当前位置：文档之家 › 第15章虚位移原理例题

第15章虚位移原理例题

  • 格式：ppt
  • 大小：1.86 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

材料力学课件-虚位移习题解

材料力学课件-虚位移习题解


Fp
2m
2m 1m
3m
δrD D
δrB δrE δθ B E 45o
FEF
M C
图1
Fp
2m
2m 1m
3m
D δrD
δθ M
B E 45o
C
δrB
F
FCG
图2
FEF = −0.943kN (值为负，表明真
正指向与假定的相反)。
(2)由虚位移原理，有：
A
FPδrD + FCGδrE − Mδθ = 0 (2)
由图 2 所示几何关系：
δrC = 3δθ , δrB = δθ , δrD = δθ / 2
将上述关系式代入(2)中得：
FCG = 1.167kN
解毕。
虚位移原理
1 附图中,连接Ｄ，Ｅ两点的弹簧的弹簧常数为ｋ，ＡＢ
＝ＢＣ＝ l ，ＢＤ＝ＢＥ＝ｂ。当ＡＣ＝ａ时，弹簧拉 力为零。设在Ｃ处作用一水平力 F ，使系统处于平衡，
求Ａ，Ｃ间的距离ｘ（杆ＡＢ，ＢＣ的质量不计，摩擦 不计）。
解：作用于机构上的力除主动力F外，还有弹性力FD,FE, 它们的元功之和不为 0。以ϕ为广义坐标，建立图示坐
B
b l
y
FD
D
ϕ Ax
FE E
x
图1
xC = 2l cos ϕ
δxC = −2l sinϕδϕ .
代入(1)式，并约去δϕ得：
x = a + F ⎜⎛ l ⎟⎞2 k ⎝b⎠
解毕。
C F
2 由ＡＢ和ＢＣ在Ｂ点铰连而成的梁，用铰
支座Ａ及杆ＥＦ和ＣＧ支承，受力 F 及力偶
Ｍ作用。已知Ｆ＝１ｋＮ，Ｍ＝４ｋＮ·ｍ， 梁的重量不计，求杆ＥＦ和ＣＧ的内力。
理论力学课件 虚位移原理

理论力学课件 虚位移原理

f k ( x i ) 0, i 1 ,2 , ,3 n ； k 1,2, , r (约束数 )
x
A
f k ( xi，t ) 0,
i 1,2 , ,3n；k 1,2, , r (约束数)
y B 0 (单侧约束)
y O
B
x
y
只能限制质点或质点系单一方向运动的约束称为单侧约束。
δW Fi δri 0
r A
δW Fi δri 0
M δ F δrB 0
M δ F rδ 0
M F r
例题：例15-3
图示椭圆规机构，连杆AB长l，杆重和滑道摩擦不计，在主动力 F1 和 F2 作用下于图示位置平衡，求主动力之间的关系。 解：研究整个机构。系统的所有约束都是 完整、定常、理想的。 1） 采用分析法。选取角度为广义坐标，有
虚位移可以是线位移，也可以是角位移。通常用变分符号 表示 虚位移。同样也可以定义虚速度。 虚位移视约束情况，可以有多个，甚至无穷多个。
与实位移不同，虚位移是约束允许的，与主动力和运动初始条件 无关的，不需经历时间的假想的微小位移。定常约束下，实位移一定 是虚位移中的一个。 F (多种形式)
δ2
k =3n-m-l k =6n-s, k =3n-s s =m+l
n——刚体数 s——约束数
空间刚体系 平面机构
自由度数为1
*自由度计算
k=?
A
解：
k=2n-s=2×3-5=1
B
k=3n-s=3×4-(2×5+1)=1
O1
O2
C
k=3×5-(2×6+2)=1
三种算法，结果相同。
15.虚位移原理

15.虚位移原理


( 3) 双面约束 – 约束条件用方程给出 约束条件用方程给出. 条件用不等式给出. 单面约束 – 约束 条件用不等式给出 x L A
mg
0
A点的约束方程 点的约束方程: 点的约束方程
x +y ≤L
2 A 2 A
y
可积分的运 动约束 圆轮的直线纯滚动. 圆轮的直线纯滚动
(4) 完整约束 – 几何约束和可积分的运动约束 几何约束和可积分的运动约束. 不可积分的运动约束. 非完整约束 – 不可积分的运动约束
E
A
B
l Q = q ⋅ = 800 N 4
l 8
l 8
l 8
l 8
l 8
l 8
l 4
P
Q
Q M
A
B
C
D
q=400N/m , P = 200N . M = 200 m.N . l = 8m l Q = q ⋅ = 800 N 4 E 去掉B 支座代之以F 去掉 支座代之以 B , 原结构变成一个自由 度的系统. 杆绕E 度的系统 设CE杆绕 杆绕 点有一个虚角位移δϕ δϕ, 点有一个虚角位移δϕ 则各处有关的虚位移 如图. 如图
实位移
m
dr
v
t
δr
m t+dt
虚位移
3. 虚功 虚功.
δw = F ⋅ δ r
实功. 实功
δw = F ⋅ d r
△: 理想约束 : 若其约束反力的功或约束反力的功之和为零, 定义 : 若其约束反力的功或约束反力的功之和为零 这种约束称 为理想约束. 为理想约束 △△: 虚位移的求法: △△ 虚位移的求法 1. 几何法 - 用几何学或运动学的条件直接求得 用几何学或运动学的条件直接求得. 例一. 试用 杆的转角的变分δφ 各点的虚位移, 例一 试用OA杆的转角的变分 表示 、B、C、D各点的虚位移 杆的转角的变分 表示A、 、 、 各点的虚位移 已知OA = r. 已知 解: δr = r ⋅ δϕ
15 理论力学--虚位移原理及其应用

15 理论力学--虚位移原理及其应用


(i = 1, 2,⋯, n )
O θ1 l1 M1(x1，2) y θ2 y l2 M2(x2，y2) x
如图15-5所示双摆。质点系由两个 质点组成，受到两个几何约束，广义坐 标数（或自由度数）为 2 ，可以选取角
ϕ 1和 ϕ 2作为广义坐标， ϕ 1和 ϕ 2相互
独立。
图 15-5
15.2.4 虚位移分析 15.2.4.1 几何法 应用几何学或运动学的方法求各点虚位移间的关 系。首先根据系统的约束条件，确定自由度，给定虚 位移，画出虚位移图，然后应用运动学的方法求有关 点虚位移间的关系。 质点的无限小位移与该点的速度成正比，即dr = v dt。 两质点无限小位移大小之比等于两点速度大小之比。 两质点虚位移大小之比等于对应点虚速度大小之比。 可以应用运动学中的速度分析方法（如瞬心法、速度 投影法、速度合成定理等）去建立虚位移间的关系。
本章重点 虚位移、理想约束的概念，应用虚位移原理 求解物体系的平衡问题。 本章难点 广义坐标、广义力的概念，广义坐标形式的 虚位移原理。
15.1 约束及其分类 . 15.1.1 约束与约束方程 位形（Configuration）： 位形 质点系内各质点在空间的位置的集合。 约束（Constraints）： 约束 在非自由质点系中，那些预先给定的限制质点系 位形或速度的运动学条件。 例如，限制刚体内任意两点间的距离不变的条件 ，限制车轮在直线轨道上滚动而不滑动的条件 约束方程（Contraint equations）： 约束方程 限制条件的数学方程式。
f j ( x1 , y1 , z1 ; ⋯; xn , yn , zn ) = 0
( j = 1, 2,⋯, s )
（15-3）
15.2 虚位移与自由度 . 15.2.1 虚位移 质点或质点系在给定位置（或瞬时），为约束所 容许的任何无限小位移，称为质点或质点系在该位置 的虚位移 虚位移（Virtual displacement）。 虚位移 虚线位移：δ r ， δ r = δ x i + δ y j + δ z k 。 虚角位移：δϕ ， δθ 。
第十五章虚位移原理

第十五章虚位移原理

F 2l δφ
F'
B
A
W
FN s 2Fl 0


2π
s
h
h s 2π
δs FN
FN h W (2Fl 2π ) 0
FN h 2 Fl 0 2π
1 FN 4π Fl h
例题
第15章 虚位移原理
例 题 1
例题
第15章 虚位移原理
2 1 2 1
2
2 1
y
x22 y22 l32 ( x1 x2 ) ( y1 y2 ) l
2 2 2
l2 m1
m2 （x ，y ） 2 2
l3 x
l1
（x1，y1）
例3：曲柄连杆机构 约束方程为：
2 2 xA yA r2
y

r φ
A （xA，yA） l
B x （xB，yB）
xC
xC
例题
第15章 虚位移原理
例 题 7
已知图所示结构，各杆都以光滑铰链连接，且有 AC=CE=BC=CD=DG=GE=l。在点G作用一铅直方向的力F，求 支座B的水平约束反力FBx。
sin ( ) M FAr cos FB r 0 cos
例：图示平面等腰三角形机构，在C点作用主动力P,系统 处于平衡，求A、B两处的约束反力。
A、B两处共有4个反力，应逐个求之。 先求哪个反力，则解除该方向的约束，代 之以对应的反力。暂时不求的则不要解除， 仍保持原约束的性质。
力学小魔术
一根重为F的均质杆简支于A,B支座上，支座的反力 分别为F/2。如果突然将支座B撤去，显然在重力矩 作用下AB杆将绕A点顺时针转动而掉下。现在，允 许在AB杆上采取一些措施，但不能对系统施加绕A 点的外力矩，使得在支座B撤去后，AB杆仍能维持 水平而不掉下。你能做到吗？
虚位移原理例题

虚位移原理例题

虚位移原理例题虚位移原理是力学中的一个重要概念，它是描述物体在受力作用下发生位移的原理。

虚位移原理在力学、静力学、动力学等领域都有着广泛的应用。

下面我们通过一些例题来深入理解虚位移原理的应用。

例题一，弹簧振子。

一根质量为m的弹簧上挂着一个质量为M的物体，当物体受到外力F时，弹簧发生形变。

求弹簧的位移x。

解析，根据虚位移原理，我们可以假设弹簧的位移为x，那么弹簧所受的弹力为-kx，其中k为弹簧的弹簧系数。

根据牛顿第二定律，物体所受的合外力为F-kx，根据虚位移原理，这个合外力所做的虚功等于零。

因此，我们可以得到F-kx=0，解得x=F/k。

例题二，斜面上的物体。

一个质量为m的物体沿着无摩擦的斜面向下滑动，斜面的倾角为θ，斜面的高度为h。

求物体滑动的位移s。

解析，根据虚位移原理，我们可以假设物体沿着斜面滑动的位移为s，那么物体所受的重力分解成沿斜面方向的分力为mgsinθ，垂直斜面方向的分力为mgcos θ。

根据虚位移原理，物体所受的合外力为mgsinθ，这个合外力所做的虚功等于零。

因此，我们可以得到mgsinθs=0，解得s=0。

例题三，简谐振动。

一个质量为m的物体挂在一个弹簧上，弹簧的劲度系数为k。

求物体振动的最大位移A。

解析，根据虚位移原理，我们可以假设物体振动的位移为x，那么物体所受的弹力为-kx。

根据牛顿第二定律，物体所受的合外力为-mg-kx，根据虚位移原理，这个合外力所做的虚功等于零。

因此，我们可以得到-mg-kA=0，解得A=mg/k。

通过以上例题的分析，我们可以看到虚位移原理在力学问题中的重要作用。

它通过假设物体的虚位移，使得问题的分析变得简单而直观。

虚位移原理的应用不仅仅局限于上面的例题，它在静力学、动力学、弹性力学等领域都有着广泛的应用。

因此，掌握虚位移原理对于理解力学问题、解决实际问题具有重要意义。

总结：虚位移原理是力学中的一个重要概念，它描述了物体在受力作用下发生位移的原理。

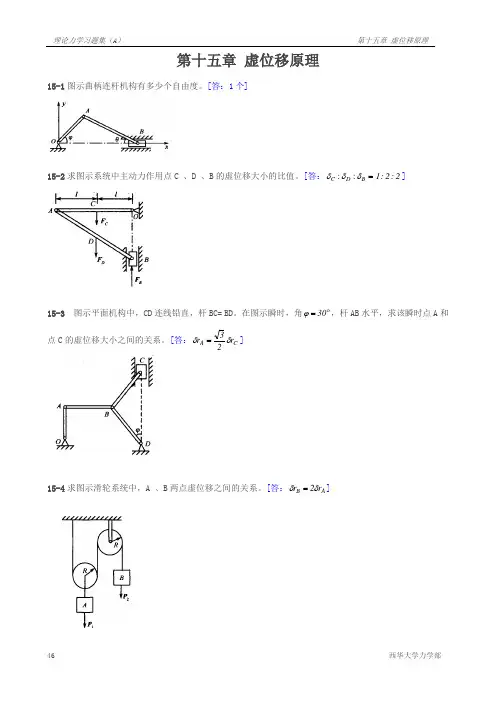
第15章 虚位移原理(古)

第15章 虚位移原理(古)

第十五章 虚位移原理15-1图示曲柄连杆机构有多少个自由度。

[答：1个]15-2求图示系统中主动力作用点C 、D 、B 的虚位移大小的比值。

[答：=B D C δδδ::2:2:1]15-3 图示平面机构中，CD 连线铅直，杆BC= BD 。

在图示瞬时，角 30=ϕ，杆AB 水平，求该瞬时点A 和点C 的虚位移大小之间的关系。

[答：C A r 23r δδ=]15-4求图示滑轮系统中，A 、B 两点虚位移之间的关系。

[答：A B r 2r δδ=]15-5重为P 、长为l 的均质杆AB 放置如图。

设各处光滑，在A 点处的水平力F 作用下保持平衡， 60=ϕ，今给A 点一向右的虚位移x δ，试由虚位移原理建立的虚功方程。

[答：0x F -63P=δδ]15-6 杆OA 和AB 各长l ，在A 点用铰链连接，在点O 和B 间连接一根刚度系数为 k 的铅直弹簧，弹簧的原长为0l 。

当在A 点作用铅垂力A F 时，机构处于图所示的平衡位置，且弹簧被拉伸。

如果不计各构件的重量和摩擦，用虚位移原理求机构处于平衡位置时的角度ϕ。

[答：4kl2kl F arcsinA +=ϕ]15-7 如图所示，两等长杆AB 和BC 在点B 用铰链连接。

在杆的点D 和点E 连接水平弹簧，弹簧的刚度系数为k ；从当距离AC a =时，弹簧的拉力等于零。

已知 AB=l , BD=b ，今在点C 作用水平力F 1使系统处于平衡。

若不计构件重量和摩擦，试用虚位移原理求距离AC 的值x 。

[答：21b l kFa x ⎪⎭⎫ ⎝⎛+=]15-8 在图示机构中，已知：力F ，l GC EG DE DC BC AC ======，弹簧的原长为l ，刚度系数为k 。

试用虚位移原理求机构平衡时，力F 与角θ的关系。

[答：()12sin kl 32F -=θ]15-9 平面机构在力F 1和F 2的作用下，在图所示的角度θ位置平衡。

已知1l BD OD ==，2l AD =，如果不计各构件重量和摩擦，试用虚位移原理求F 1 / F 2的比值。

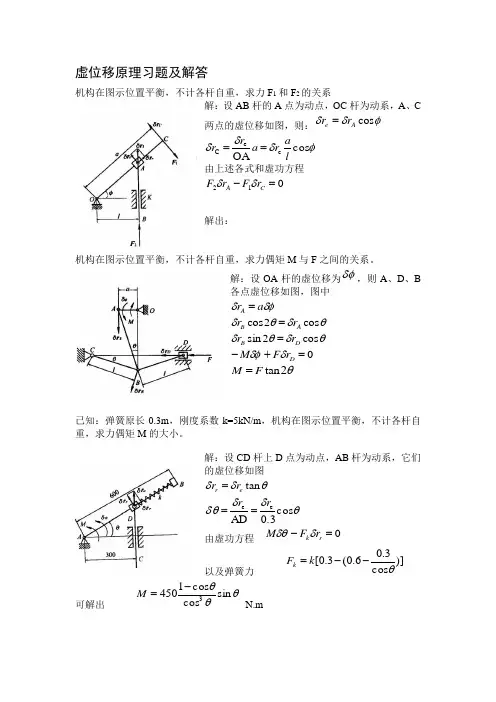
工程力学A 参考习题之虚位移原理习题及解答

工程力学A 参考习题之虚位移原理习题及解答

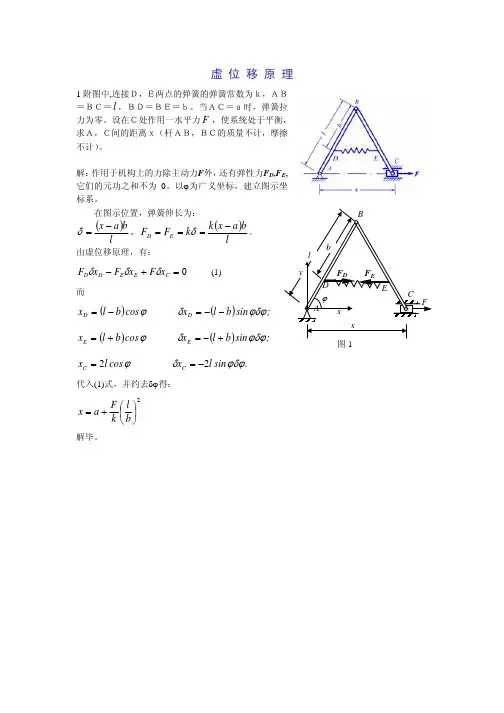
虚位移原理习题及解答机构在图示位置平衡，不计各杆自重，求力F 1和F 2的关系解：设AB 杆的A 点为动点，OC 杆为动系，A 、C两点的虚位移如图，则：φδδcos A e r r =φδδδcos OAeeC l ar a r r ==由上述各式和虚功方程012=-C A r F r F δδ解出：机构在图示位置平衡，不计各杆自重，求力偶矩M 与F 之间的关系。

解：设OA 杆的虚位移为δφ，则A 、D 、B各点虚位移如图，图中δφδa r A =θδθδcos 2cos A B r r = θδθδcos 2sin D B r r = 0=+-D r F M δδφ θ2tan F M =已知：弹簧原长0.3m ，刚度系数k=5kN/m ，机构在图示位置平衡，不计各杆自重，求力偶矩M 的大小。

解：设CD 杆上D 点为动点，AB 杆为动系，它们的虚位移如图θδδtan e r r r =θδδδθcos 0.3AD e e rr ==由虚功方程 0=-r k r F M δδθ以及弹簧力)]cos 3.06.0(3.0[θ--=k F k可解出 θθθs i n c o s c o s14503-=M N.m已知：BC=AB=L ，BE=BD=b ，弹簧刚度为k ，当x=a 时，弹簧拉力为零，该系统在力F 作用下平衡，杆重不计，求平衡时x=?解：弹簧力如图，其中)(a x l bk F F k k -='=各力作用点横向坐标及其变分为θcos )(b l x D -= θδθδs i n )(b l x D --= θcos )(b l x E +=θδθδs i n )(b l x E +-=θcos 2l x C = θδθδs i n2l x C -= 代入虚功方程0=∑x F xδ0=+'-C E KD K x F x F x F δδδ 解得：22kb Fl a x += 已知：已知均质杆长，杆重皆为P ，滑块C 重P2，滑轨倾角为θ，求平衡时角φ为多大？φsin 2l x D = δφφδ.cos 2l x D = φcos 2l y D = δφφδ.sin 2l y D -=φsin 2lx E = δφφδ.cos 2l x E =φcos 23l y E = δφφδ.sin 23l y E -= 0=C x 0=C x δφcos 2l y C = δφφδ.sin 2l y C -=把它们代入虚功方程 0)(=+∑y F x F y xδδ得：0sin sin cos sin cos 21111=++++C E E D D y P y P x P y P x P θδθδθδθδθδ解得： θφc o t)(2t a n 211P P P +=15-15 用虚位移原理求图示桁架中杆3的内力。

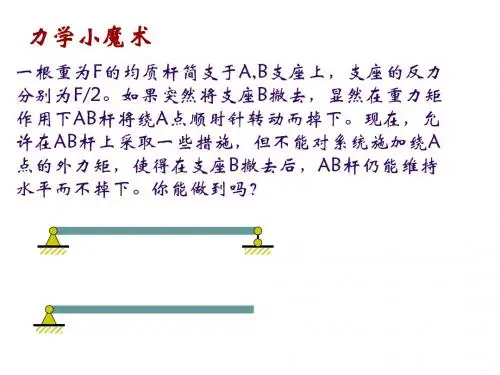
第十五章 虚位移原理(2)

第十五章 虚位移原理(2)

第十五（1）章 虚位移原理虚位移原理应用功的概念分析系统的平衡问题，是研究静力学平衡问题的另一途径。

虚位移原理与达朗贝尔原理结合起来组成动力学普遍方程，为求解复杂系统的动力学问题提供了另一种普遍的方法，构成了分析力学的基础。

本书只介绍虚位移原理的工程应用，而不按分析力学的体系追求其完整性和严密性。

§15-1 约束·虚位移·虚功1．约束及其分类在第一章，我们将限制物体位移的周围物体称为该物体的约束。

为研究上的方便，现将约束定义为：限制质点或质点系运动的条件称为约束，表示这些限制条件的数学方程称为约束方程。

我们从不同的角度对约束分类如下。

（1）几何约束和运动约束 限制质点或质点系在空间的几何位置的条件称为几何约束。

例如图15-1所示单摆，其中质点M 可绕固定点O 在平面Oxy 内摆动，摆长为l 。

这时摆杆对质点的限制条件是：质点M 必须在以点O 为圆心、以l 为半径的圆周上运动。

若以x ，y 表示质点的坐标，则其约束方程为222l y x =+。

又如，质点M 在图15-2所示固定曲面上运动，那么曲面方程就是质点M 的约束方程，即()0,,=z y x f又例如，在图15-3所示曲柄连杆机构中，连杆AB 所受约束有：点A 只能作以点O 为圆心，以r 为半径的圆周运动；点B 与点A 间的距离始终保持为杆长l ；点B 始终沿滑道作直线运动。

这三个条件以约束方程表示为()()0222222==-+-=+B A B A B A A y l y y x x r y x上述例子中各约束都是限制物体的几何位置，因此都是几何约束。

在力学中，除了几何约束外，还有限制质点系运动情况的运动学条件，称为运动约束。

例如，图5-4所示车轮沿直线轨道作纯滚动时，车轮除了受到限制其轮心A 始终与地面保持距离为r 的几何约束r y A =外，还受到只滚不滑的运动学的限制，即每一瞬时有0=-ϖr v A上述约束就是运动约束，该方程即为约束方程。

虚位移原理例题

虚位移原理例题

虚位移原理例题虚位移原理是物理学中一个非常重要的概念，它描述了光学中光线的传播规律，也是解决光学问题的基本工具之一。

下面我们通过一些例题来深入理解虚位移原理。

例题一：一根直立的圆柱形玻璃杯里装满了水，现在在玻璃杯旁边放置一个小的物体。

当我们从玻璃杯的一侧观察时，看到的物体会出现在玻璃杯的哪个位置？解析：根据虚位移原理，我们知道光线在从一种介质射向另一种介质时会发生折射。

在这个例子中，当我们从玻璃杯的一侧观察时，光线会从空气中射入水中，然后再从水中射出。

根据虚位移原理，我们可以得出结论，在观察时，物体会出现在实际物体所在位置的上方，这就是虚位移的原理。

例题二：一束光线从空气中射入玻璃中，入射角为30°，折射角为20°。

求玻璃的折射率是多少？解析：根据折射定律，我们知道入射角和折射角之间有一个固定的关系，即折射率n等于正弦入射角与正弦折射角的比值。

根据虚位移原理，我们可以通过求解这个例题来验证虚位移原理的正确性。

根据已知条件，我们可以得出：n = sin(30°) / sin(20°) ≈ 1.5。

因此，玻璃的折射率约为1.5。

例题三：一束光线从空气中射入水中，入射角为45°，求折射角和折射率是多少？解析：根据折射定律和虚位移原理，我们可以通过这个例题来进一步验证虚位移原理的正确性。

根据折射定律，我们可以得出：sin(折射角) = sin(入射角) / n。

代入已知条件，我们可以得出：sin(折射角) = sin(45°) / 1.33 ≈ 0.707 / 1.33 ≈ 0.531。

折射角约为 arcsin(0.531) ≈ 32°。

因此，光线在从空气射入水中时，折射角约为32°，折射率约为1.33。

通过以上例题的分析，我们可以更加深入地理解虚位移原理在光学中的应用。

虚位移原理是解决光学问题的重要工具，它帮助我们理解光线在不同介质中传播的规律，也为光学领域的研究提供了重要的理论基础。

工程力学：虚位移原理2015

工程力学：虚位移原理2015

给出所有广义坐标方向上的虚位移计算虚功前面的系数就是sincossincosmglmglmglmglsincosmglmglsincosmglmgl给出所有广义坐标方向上的虚位移计算虚功前面的系数就是取一组特定虚位移除不为零其余广义坐标虚位移均为零计算虚功则
研究 该平衡问题
图示杠杆平衡，求F1与F2关系
r r
W
F
•dr
k(r
lO )
r r
•dr
代入得到 W k(r lO )d r
因为 r • d r d( r • r )
2
d r2 rdr
2
积分
W
l0 2 l0 1
k(r
lO
)dr
1 2
k[12
22]
结论：弹性力的功只与弹簧的起始和终了变形有关，与质
点运动路径无关.
5
例：固定圆环半经为R，小球套在圆环上，被长度为l 2R 的弹簧约束在O点。试求：小球从A到B的功，又从B到C的功。
问题：内力做功一定是零吗？
B d rB
什么条件下内力做功是零呢？
只要AB之间距离保持不变，内力功为零
例如：刚体、不可伸长的柔索、二力杆
W内 0
10
问题：若做功的力为有势力，则有势力的功与势能有什么关系？
有势力的功
势能
势力场与势能
势力场(potential force field)：场力所做的功与质点经过的
（b）
条件（a）和条件（b）是等价的
猜想： 平衡条件
虚位移
虚功
力在微小位移中所作的功的关系来建立
虚位移原理
2
准备知识（动能定理部分内容）
力的功与元功
功是度量力在一段路程上对物体作用的累积效应，是标量。

文库最新发布：虚位移原理

8xQ = -xP
计算虚功得: W(P) = P xP
O
y
A
B
P
C
W(Q) = Q xQ
Q
由虚位移原理得: P xP + Q xQ = 0
x
代入上述变分结果得: - 8 P xQ + Q xQ = 0
Q/P = 8 21
例题7.在图示结构中,曲柄OA上作用一力偶, 其力偶矩为m,另在滑块D上作用一水平力P. 结构尺寸如图所示.求当平衡时,力P与力偶矩 m的关系.
4
(2) 解析法
先把各质点的坐标表示成广义坐标的函数,再将各式 对广义坐标求变分(与求微分相似)，得到各虚位移在相 应坐标轴上的投影。
例题.求图示机构A点和B点的虚位移.OA=AB=l ;
y
解: xA=l cos yA=l sin
xB=2l cos
yB=0 xA = -lsin
O
yA = lcos
I
解: 应用几何学和运动学来求A点
和B点的虚位移rA和 rB
2
OA杆作定轴转动
rA
2
rA = OA 1
(1)
AB杆作平面运动 , I为瞬心
A 1
rA = IA 2
(2)
O
rB
B
3
由(1)(2)式得:
I
2
=
OA IA
1
rB = IB 2
=
OA IA
IB
1
2
rA
2
A
1
O
rB
B
当然也可以取1 的转向为顺时针转向,画 出虚位移图得出的 rA和 rB的表达式与转向 为逆时针是一致的.
B是AC杆的瞬心. E是CE杆的瞬心.

高中物理竞赛经典讲义 虚位移原理

第15章 虚位移原理15-1 图示曲柄式压缩机的销钉B 上作用有水平力F ，此力位于平面ABC 内。

作用线平分ABC ∠。

设AB = BC ，θ2=∠ABC ，各处摩擦及杆重不计，求对物体的压缩力。

解：令B 有虚位移AB B ⊥r δ，而C 有铅直向上的虚位移C r δ，如图（a ）。

将B r δ及C r δ向BC 方向投影，为简单起见，以B r δ表示B r δ的绝对值B r δ，以C r δ表示C r δ，则有)902cos(δ)90cos(δ︒-=-︒θθB C r r即 θcos 21δδ=C B r r （1） 由虚位移原理得 0δsin δN =-C B r F r F θ θsin δδN F F r r C B = （2） 将式（1）代入（2）得 θtan 2N F F =15-3 挖土机挖掘部分示意如图。

支臂DEF 不动，A 、B 、D 、E 、F 为铰链，液压油缸AD 伸缩时可通过连杆AB 使挖斗BFC 绕F 转动，EA = FB = a 。

当︒==3021θθ时杆DF AE ⊥，此时油缸推力为F 。

不计构件重量，求此时挖斗可克服的最大阻力矩M 。

解：由虚功原理： 0δδcos 1=-⋅ϕθM r F A （1）式中 a r B δδ=ϕ （2）A 、B 的虚位移向AB 投影 22sin δcos δθθB A r r =2tan δδθB A r r = （3）式（2），（3）代入（1）得 0δδtan cos 21=⋅-⋅⋅a r M r F B B θθ Fa M Fa M 21,sin ,30221==︒==θθθ15-5 在图示机构中，当曲柄OC 绕O 轴摆动时，滑块A 沿曲柄滑动，从而带动杆AB 在铅直导槽K 内移动。

已知：OC = a ，OK = l ，在点C 处垂直于曲柄作用一力F 1；而在点B 沿BA 作用一力F 2。

求机构平衡时F 2与F 1的关系。

解：用解析法解，选取ϕ为广义坐标，则滑块A 的约束方程ϕtan l y A =ϕϕδsecδ2l y A = （1） 由虚位称原理 0δδ)(21=+-A y F a F ϕ （2）把式（1）代入（2）得 0δsec δ221=+-ϕϕϕl F a F因 0δ≠ϕ，于是有 0sec 221=+-ϕl F a F故 ϕ221cos a l F F =15-7 图示滑套D 套在光滑直杆AB 上，并带动杆CD 在铅直滑道上滑动，已知︒=0θ时弹簧为原长，弹簧刚性系数为5 kN/m 。

第15章 虚位移原理_例题


δ y D = − 2 a sin ϕδϕ − b sinψδψ x B = 2 a sin ϕ + 2 b sinψ , δ x B = 2 a cos ϕδϕ + 2 b cosψδψ
代入(a)式，得：
( − P a sin ϕ − P2 2a sin ϕ + F 2a cos ϕ )δϕ + ( − P2b sin ψ + F 2b cosψ )δψ = 0 1
h 4、列虚功方程： δW = 2 Flδϕ − FN δs = (2 Fl − FN ) ⋅ δϕ = 0 2π
δϕ 是任意的，有： 2 Fl − h F = 0 由于 N 2π 也即：
l ∴ FN = 4π F h
讨论： 1）利用约束力不做功避免了所有约束力的出现， 这是虚位移原理解题与矢量静力学解题相比的巨大优点。 2）本题求虚位移间关系的方法为：由物理关系直接给 出法。
− M δθ − F δx B = 0
注意：几何法时，主动力与虚位移方向一致为正；
力偶、角度逆时针为正 解析法时主动力、坐标变分各自沿坐标轴方向为正，力偶、角度逆时针为正。 力偶
例4 均质杆OA及AB在A点用铰连接，并在O点用固定铰 支座，如图所示。两杆各长2a和2b，各重P1及P2，设在B点 加水平力 F 以维持平衡，求两杆与铅直线所成的角ϕ及ψ 。
而
δ rC = a δϕ , δ rB = δ rD = δ rA = 2 a δϕ
代入上式后，得：
( F cosϕ ⋅2a − P1 ⋅asinϕ − P2 ⋅2asinϕ )δϕ = 0
tgϕ =
2F P1 + 2 P2
讨论：其它可能虚位移与真实位移
例5 ：升降机构，

虚功(虚位移)原理复习与例题

由虚功方程，得
FAsA 2qlsE
M
sE
l
A
0
P
q
M
B
D
C
sC sE
其中
FA
sA sC 2sE
代入虚功方程，得
(FA
ql
M 2l
)sA
0
解得
FA
M 2l
ql
§5.2.3 用广义坐标表示的质点系平衡条件
xi xi (q1, q2 ,qs , t) yi yi (q1, q2,qs ,t)(i 1,2,, n)
虚位移与实位移的区别和联系
实位移——质点或质点系在其真实运动中，在一定的时间间 隔内发生的位移。
（1）在完整定常约束下，实位移是诸多虚位移中的一个； （2）在完整定常约束下，虚位移方向沿其速度方向。
dr ——实位移 r ——虚位移
M dre
dr
r
M1
2. 虚 功
质点或质点系所受的力在虚位移上所作的功——虚功。
自 由 度 —— 在完整约束条件下，确定质点系位置的独立参变 量的数目等于系统的自由度数。
N=3n—s
对于稳定的完整约束，各质点的坐标可以写成广义坐标的 函数形式
xi xi (q1, q2 ,qk , t) yi yi (q1, q2,qk ,t)(i 1,2,, n) zi zi (q1, q2 ,qk , t)
2l
P
q
M
BC
sE
D
sD
FD
(2) 解除B处约束，代之以反力
P
q
M
FB ，并将其视为主动力。
A
D
BC
由虚功方程，得
sB sC sE
PsB FBsB

工程力学-材料力学-第15章 虚位移原理(邱清水)

一旦确定了质点系的广义坐标，则也隐含地描述了质点系的 几何约束方程 。
15.2 虚位移与虚功
1．虚位移
虚位移：是指在某瞬时，质点系在约束所容许的条件下， 可能实现的任意无限小的位移。
虚位移可以是线位移，也可以是角位移。通常用变分符号
表示虚位移。
如下图所示的杠杆AB，如令杆绕Ｏ轴转动微小角度δ，
y x
O
B
15.1质点系的自由度· 约束及约束的分类
4) 完整约束与非完整约束
几何约束和可积分的运动约束称为完整约束。 若运动约束不可积分为有限形式，则称为非完整约束。 y vC C*
xC R 0
C
O
R
可以积分为 xC R 0
x
x
圆轮所受约束为完整 约束。
15.1质点系的自由度· 约束及约束的分类
xA 0, y A l sin xB l cos , yB 0
进行变分运算，可得
x A 0 y A l cos xB l sin
将数据代入虚功方程，可得
y B 0
FA cos FB sin l 0
由于 的任意性，故可解得
rA v A AC l rB v B BC 2l sin
由虚位移原理，可得
P1 rA P2 rB 0
即得
P1 cos 2P2 sin rA 0
P 2P2 tan 1
由于rA的任意性，故可解得 本题也可通过解析法求解
15.3 虚位移原理—例题分析
1.求结构平衡时的主动力和平衡位置
例15-2 如图所示椭圆规机构中，刚性连杆AB长l。
杆AB、滑块A、B的重量均不计，所有接触光滑，机

虚位移原理


M F xC 0
xC h cot BC
xC
h sin 2
解得
M
Fh
sin 2
例15-5 求图所示无重组合梁支座Ａ的约束力。 求： FA
解：解除A处约束，代之 FA ，给虚位移，如图
WF FA sA F1 s1M F2 s2 0
sA ,
8
s1
3
3
8
sA,
sM
11
11 8
wF FBxxB FyG 0
F
xB 2l cos , yG 3l sin xB 2l sin, yG 3l cos
带入虚功方程
FBx 2lsin F 3lcos 0
FBx
3 2
F cot
如图在CG间加一弹簧，刚度K，且已有伸长量 0 ， 仍求FBX 。
在弹簧处也代之 以力，acoΒιβλιοθήκη bcos 2（）a
I1
O
2
A m1
利用虚位移图 计算虚功.
2
rA
C
rD
D
P
W(m) = -m1
3
b
B
b
W(P) = 2bPsin4
4
rB
4
I2
由虚位移原理得:
-m1+ 2bPsin4 = 0
把式代入式得: m = aPtg2
另解：设A点虚位移为δyA，B点虚位移为δrB，D点 虚位移为δxD。根据虚位移原理知：
a
I1
O
2
A m1
2
rA
C
rD
D
P
b
B
b
4
rB
4
I2
a
I1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例2 图示椭圆规机构，连杆AB长l，杆重和滑道摩擦不计， 铰链为光滑的，求在图示位置平衡时，主动力大小P和Q之间 的关系。
解：研究整个机构。 系统的所有约束都是 完整、定常、理想的。
1、几何法：使A发生虚位移 rA ，
B的虚位移 rB ，则由虚位移原理，
得虚功方程：
rA
PrA QrB 0
虚功方程 M FrB 0
arcsin M
2Fl
xB 2l cos xB 2l sin
( x轴向右为正，xB向右，
rB xB 2l sin)
当然，几何法
也可以假设 顺时针，
求解结果相同。
虚功方程 M FxB 0
内移动，不计各构 件自 衡时力F1与F2的关系。
解：给出力
F1
、F2
处的虚位移 rC、rA
几何法：ra rA re rr rA cos re
rC
re
a l / cos
y

rArC C
M 0.45 cos3
(kN m)
例8：书15-8 图示之机构中，弹簧
的刚度系数为k ，当AC 距离等于 d 时，
弹簧拉力为零。如在C点作用一水平力F，
杆系处于平衡，求距离x之值。设
，
，
杆重不AB计。BC a BD b
解：1 、以整个系统为研究对象 2、分析受力，去掉弹簧，暴露出弹簧 作用在AB与BC上的两力。
θ
θCrC D F
Fθ

rB
B
P
rD
F P ctg P
2
选择AB杆、CD杆和滑套D的系统为研究对象。

re

300
cos

rr
re
tan

300sin cos2

去掉弹簧，暴露出弹簧力 F和
F
ra re
rB F rr
F

弹簧原长 (600 300 )mm
弹簧后来长
(600

300 cos
)mm
k a
讨论： 有弹簧存在时，必须计入弹性力虚功， 此时，将弹性力视为常力。
例9：三铰拱上有载荷作用力P及力偶M， 各尺寸如图，求B铰的约束力。 解：（1）求B 铰水平约束力：
解除B 铰的水平约束，代之以水平力FBx 分析主动力：M，P，FBx ，
给虚位移，求虚位移关系：
C*为刚体CDB的瞬心，
弹簧缩短
(
300 cos
300 )mm
弹簧力 F

k
(
300
cos
300 )
由虚 位移原理：
M F
ra

F


rB

0
M Frr 0 0
[M
1.5(
1 cos
1)

0.3
sin cos2
0]

0
sin (1 cos )
re

A rr
F1
由虚功原理 F1rC F2rA 0

F1

a
F2l cos2

φD x
O
解析法：建立如图直角坐标系 yA l tan
求变分 y A

l
cos2

又rC
由虚功原理 F1rC F2yA 0
a
F1
F2l
a cos2
Py A QxB 0 ,
(Pcos Qsin )l 0
由于 任意，故 PQ tg
注意：几何法时，主动力与虚位移方向一致为正； 解析法时主动力、坐标变分各自沿坐标轴方向为正

OA
vA
vB
例3：两均质杆 OA AB l ，均不计重，构成曲柄滑块
机构。今在OA杆上作用力偶 M ，在滑块B上作用力 F ，使 机构处于平衡状态，如例图所示。试求平衡位置角 。
解：将杆BD截断，暴露出内力
F
、F
给出力
P
、
F
处的虚位移 rD、rB
几何法： rC cos rD
rC cos(90 2 ) rB cos A
由虚功原理 PrD FrB 0 0 PrC cos F 2sinrC 0 (P cos 2F sin )rC 0

2Fl

FNs

(2Fl
h
2
FN )

0
由于 是任意的，有： 2Fl
也即：
h
2
FN

0
FN
4
l h
F
讨论： 1）利用约束力不做功避免了所有约束力的出现， 这是虚位移原理解题与矢量静力学解题相比的巨大优点。
2）本题求虚位移间关系的方法为：由物理关系直接给 出法。
xD a bcos , xE a bcos
xD (a b)sin (2) xE (a b)sin (3)
4、列虚功方程： FxC T xD TxE 0 (4)
联立（1）~（4），得：
x

AC

d

F

b
2

M
FNB
而
r1 rB

1 2
,
rC rB
181
,
rB
rG
4
1rB
rE
6
1rB
rC
12
1rB

1 12
181

11 96
1 11 11

FNB

2
P1

8
P2

M 96
例11： 书15-15
用虚位移原理求图示桁架中杆BD的内力，
已知ctgθ =2。
M F 2l sin 0
注意：几何法时，主动力与虚位移方向一致为正；
解析法时主动力、坐标变分各自沿坐标轴方向为正，力偶、角度逆时针为正。
例4 均质杆OA及AB在A点用铰连接，并在O点用固定铰 支座，如图所示。两杆各长2a和2b，各重P1及P2，设在B点
加水平力 F 以维持平衡，求两杆与铅直线所成的角及 。
设弹簧为原长l0 ，则：
当
d l0
时ba，,弹簧l0长度ba为dl ：
有：AC x
x a, lb
l b x a
故弹簧力 T k b x b d kb x d (1)
a a a
3、给虚位移 xC 、 求各虚位移间的关系(解析法简单)
xC 2a cos xC 2a sin
P1asin P2 2asin F2acos 0 P2 bsin F2bcos 0
由此解得：
tg

P1
2F 2P2
,
tg 2F
P2
解法二： 应用虚位移原理，几何法
先使 保持不变，而使 获得变分 ，得到系统的一
组虚位移，如图所示。
FrB cos P2rD sin 0
代入(a)式，得：
(P1a sin P2 2a sin F 2a cos) (P2bsin F 2b cos ) 0
(P1asin P2 2asin F2a cos) (P2bsin F2bcos ) 0 由于 , 是彼此独立的，所以：
B
F2
例7： 书15-7
滑套D套在光滑直杆AB上，并带动杆
CD在铅直滑道上滑动。已知=0o时，
弹簧等于原长，弹簧刚度系数为
5(kN/m)，求在任意位置（ 角）平衡
时，加在AB杆上的力偶矩M ？
解：这是一个已知系统平衡，求作用于系统上主动力之间关系 的问题。将弹簧力计入主动力，系统简化为理想约束系统，故 可以用虚位移原理求解。
解：1、对象：系统 2、分析受力：M，F
3、给虚位移： ， rB ，求虚位移关系：

几何法(虚位移投影法或者瞬心法)：
rA l
OA
vA
rA cos(90 ) rA sin 2 rB cos
vB
2rA sin rB
解析法：
rB 2l sin
例1：螺旋压榨机中螺杆的螺距为 h 。如果
在手柄上作用一在水平面内的力偶，其
力偶矩为 2Fl ，求平衡时作用于被压榨
物体上的压力。（忽略摩擦）
解：
1、对象：由手柄、螺杆及压板组成的系统
23、、分给析系受统力以：虚主位动移力：（F和, F’s有 )及，：压s板阻h力FN
2
4、列虚功方程： W
rD 5a
rB 2a
M PrD
a 5a

FByrB

0
M Pa FBy 2a 0
FBy

1 2
P

M a

讨论：虚位移原理可用于求解约束反力，只需将约束解除，代 之以约束反力，并将其视为主动力即可。（注：每次只可解 除一个约束）
而 rB 2b , rD b
代入上式，得
tg

F 2b P2 b

2F P2
再使 保持不变，而使 获得变分 ，得到系统的另
一组虚位移，如图所示。 图示中：
rA rD rB
FrB cos P1rC sin P2rD sin 0
例10 多跨静定梁，
M
求支座B处反力。
解：将支座B 除
去，代入相应的
约束反力
FNB
。

M