下载文档原格式
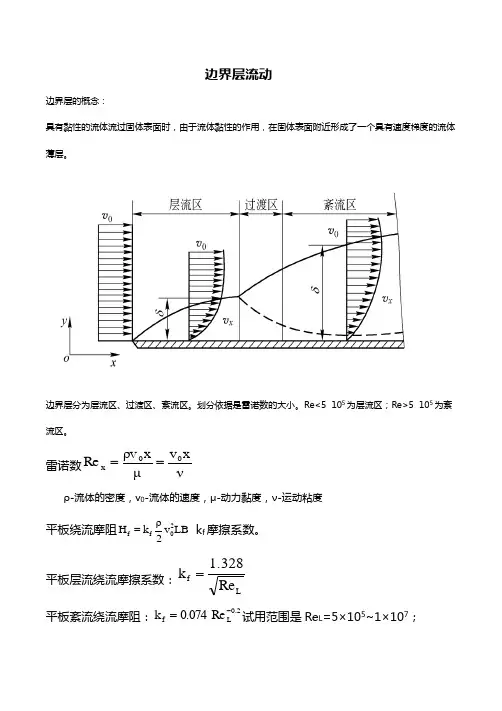
边界层流动边界层的概念：具有黏性的流体流过固体表面时，由于流体黏性的作用，在固体表面附近形成了一个具有速度梯度的流体薄层。
边界层分为层流区、过渡区、紊流区。
划分依据是雷诺数的大小。
Re<5×105为层流区；Re>5×105为紊流区。
雷诺数νx v μx ρv Re 00x ==ρ-流体的密度，v 0-流体的速度，μ-动力黏度，ν-运动粘度 平板绕流摩阻LB v 2ρk H 20f f = k f 摩擦系数。
平板层流绕流摩擦系数：L f Re 1.328k =平板紊流绕流摩阻：0.2L f Re 0.074k -=试用范围是Re L =5×105~1×107；58.2)Re (lg 455.0k -=L f 适用范围Re L =1×105~1×109；平板混合边界层摩擦阻力系数：L 0.2L f Re 1700Re 0.074k -=Re L =5×105~1×107； L2.58L f Re 1700)(lgRe 0.455k -= Re L =1×105~1×109； 球体绕流摩阻H f20f 2f f πR 2ρk πR h H v =⋅=-----------------我是分割线-------------------香蕉球是怎么回事？香蕉球是在踢球时给球施加一个旋转的力。
上旋球的落点会比不旋转的球落点要近些。
下旋球的落点会比不旋转的球落点要远些。
上旋为逆时针旋转,如图力F1作用在1点时产生上旋球。
在飞行过程中球表面会形成一层很薄速度边界层。
上旋球的上表面V 空方向与ω球方向相反，所以空气被减速，下表面V 空方向与ω球方向相同，所以空气被加速。
根据伯努利方程可知，速度大的地方压强小，速度小的地方压强大。
即P 上大于P 下，球被迫向压强小的一侧转弯了。
----------------我是分割线----------------------由管流连续性方程可知流量q v 和流速v 与截面A 都是正相关 ⎭⎬⎫⎩⎨⎧∝∝A q v q v vV 2211q A v A v ==上课期间，打开的水龙头很少，流量q v 总很小，总管道的流速v 很小； 下课期间，用水高峰期时，打开的水龙头增多，流量q v 总增大，总管道内水的流速v 很大。
For personal use only in study and research; not for commercial use第四章1. 常压下温度为20℃的水以5m/s 的流速流过一光滑平面表面，试求由层流边界层转变为湍流边界层的临界距离c x 值的范围。
解： 0/()c c x x Re u μρ=c x Re 的范围：56210~310⨯⨯由物性数据表查得，常压下20℃水的物性 3998.2kg/m ρ=，3100.510Pa s μ-=⨯⋅∴ c x 的范围为：0.04～0.60m 。
2. 流体在圆管中流动时，“流动已经充分发展”的含义是什么？在什么条件下会发生充分发展的层流，又在什么条件下会发生充分发展了的湍流？答：当流体以均匀一致的流速在圆管中流动时，在管内壁周围形成边界层，且逐渐加厚，在离进口某一距离（L e ）处，四周的边界层在管中心汇合，此后便占有管的全部截面，而边界层的厚度也维持不变，这时的流动称为充分发展了的流动。
若边界层汇合时，流体的流动为层流，则管内的流动为充分发展了的层流；若边界层汇合时的流体已是湍流，则管内流动为充分发展了的湍流。
在2000d Re <，L ＞L e 的光滑管条件下，会发生充分发展了的层流；当10000d Re >，L > L e 光滑管条件下会发生充分发展了的湍流。
3. 已知二维平面层流流动的速度分布为0(1)cy x u u e =-，00(0)y y y u u u =<，式中c 为常数。
试证明该速度分布普兰德边界层方程（4-13）的正确解，并以流动参数表示c 。
解：由 0(1)cy x u u e =-，00(0)y y y u u u =<可知0x u x∂=∂，0y u y∂=∂∴0y x u u xy∂∂+=∂∂满足连续性方程。
依题意，普兰德边界层方程左端为右端为若两端相等，则常数c 为4. 常压下温度为30℃的空气以10m/s 的流速流过一光滑平板表面，设临界雷诺数53.210cx Re =⨯，试判断距离平板前缘0.4m 及0.8m 两处的边界层是层流边界层还是湍流边界层? 求出层流边界层相应点处的边界层厚度。
流体流动的边界层理论与应用引言流体流动是自然界中普遍存在的现象，广泛应用于各个领域，如航空航天、机械工程、气象学等。
边界层是流体流动中十分重要的概念，它描述了流动的边缘区域，包括流动的速度梯度和压力变化。
边界层理论和应用研究的目的是为了更好地理解流体流动的本质和优化相关应用。
边界层理论的基本原理边界层理论是描述流体流动的边缘区域的理论框架。
它的基本原理包括以下几个方面：粘性边界层理论中的基本假设之一是流体具有一定的粘性。
粘性导致了流体的内摩擦力和黏滞性。
在流体流动中，粘性扮演着重要的角色，影响了流动的速度分布和边界层的厚度。
动量守恒边界层的形成是由于流体在固体表面附近的动量交换。
边界层理论基于动量守恒原理，描述了流体速度的变化情况。
边界层内的速度梯度决定了局部的动量传输。
能量守恒边界层理论还基于能量守恒原理，描述了流体流动中的热传输现象。
热量可以通过边界层传递，影响流体的温度分布。
边界层理论的应用边界层理论在各个领域都有广泛的应用，以下列举了其中几个典型的应用：空气动力学在航空航天工程中，边界层理论被广泛用于研究飞行器的气动性能。
通过分析边界层的厚度和速度分布，可以评估飞行器的阻力和升力特性，并进行优化设计。
涡街流量计涡街流量计是一种常用的流量测量仪器，利用边界层理论原理实现流量的测量。
通过将流体引导到一个弯曲的管道内，使流体形成旋涡，并通过测量旋涡的频率来计算流体的流量。
边界层控制边界层控制是一种改变流动边界层结构的技术，通过控制或改变边界层内的速度分布和压力变化，可以实现对流体流动的操控。
边界层控制在飞行器设计和汽车空气动力学中有着重要的应用，可以减少阻力、增加升力以及改善气动性能。
污染扩散在大气科学中，边界层理论被用于研究大气中污染物的扩散和传输现象。
通过分析边界层内的流动特性，可以预测污染物的传播范围和浓度分布，为环境管理和污染控制提供科学依据。
结论流体流动的边界层理论是研究流体流动基本原理和应用的重要工具。
第6章 层流的解析解与近似解粘性流动基本方程组的解析解有着它固有的数学困难，真正能做解析解的流动为数不多，而且都是比较简单的流动。
本章将介绍几种粘性流动的解析解，有助于我们开阔思路，认识多种实际流动的性质。
首先先介绍一下粘性流研究的意义和研究的特点以及粘性流动的基本方程组，接着介绍一些解析解。
在介绍解析解时先考虑常特性不可压缩流体，通过基本方程，解得流场的速度和温度分布，最后求出摩擦阻力系数和热交换系数。
为了认识可压缩流动的特性，介绍两种简单的可压缩流动的解析解。
另外本章只限于雷诺数不大的流动。
6.1 粘性流研究的意义一切流体都具有粘性，但是人类最经常接触的流体，如水和空气其粘性都很小，要考虑粘性的影响就会使数学问题变得非常复杂；另外，对于这些粘性小的流体，忽略其粘性所得到的结果又能在一定程度上符合实际情况，因此，理想无粘性流体理论最先得到了发展，它比粘性流体理论要成熟得多。
应当指出，虽然理想流体理论取得了重大的成就，但在某些方面却有不可逾越的先天性缺陷。
例如，它不能预估管道流动的压力损失，也不能计算在流体中运动的物体所受到的阻力。
后一问题与著名的达朗伯疑题有关。
达朗伯对理想流体进行了严谨的研究后得出了如下结论：当任意形状的固体在静止的充满无限空间的无粘性流体中作匀速直线运动，它不承受沿运动方向的作用力，即物体所受阻力为零。
在他所做假设的前提下，这一结论的逻辑推理是完全正确的，但它却与实际完全不符，因为所有的物体在流动中运动时都受到阻力作用。
这从反面说明了考虑粘性的必要性。
例1 圆柱绕流对于理想不可压缩流体，()22214sin s p p p C U θρ∞∞-==- 其中 p ∞——远前方静压，ρ——流体密度。
流动边界层的定义流动边界层的定义流动边界层是指在固体表面附近，由于粘性效应而形成的一种特殊的流场。
它通常出现在高速气体或液体与固体表面接触的情况下。
流动边界层对于工程领域中诸如空气动力学、水力学、热力学等方面的问题都具有重要意义。
1. 流动边界层的基本概念1.1 流动边界层的形成原因当高速气体或液体与固体表面接触时，由于粘性效应，会在固体表面附近产生一层非常薄的流场，这就是流动边界层。
1.2 流动边界层的特征流动边界层通常具有以下几个特征：（1）速度梯度大；（2）温度梯度小；（3）压力梯度小；（4）密度梯度小。
1.3 流动边界层的分类根据不同情况下流场中粘性效应所占比例不同，可以将流动边界层分为以下两类：（1）无粘流动边界层：当粘性效应可以忽略时，流动边界层可以看作是无粘的。
（2）粘性流动边界层：当粘性效应不能忽略时，流动边界层就是粘性的。
2. 流动边界层的结构2.1 流动边界层的结构特征流动边界层通常具有以下几个结构特征：（1）速度剖面：在流场中，速度从固体表面到自由流场逐渐增加，形成了一个速度剖面。
（2）压力分布：由于黏性效应，在流场中存在一个压力梯度，这导致了压力沿着法向方向发生变化。
（3）温度分布：在高速气体或液体与固体表面接触时，会产生一定的热量，并导致温度沿着法向方向发生变化。
2.2 流动边界层的三个区域根据速度剖面和压力分布的不同情况，可以将流动边界层分为以下三个区域：（1）黏性亚层：在靠近固体表面处，由于黏性效应非常显著，形成了一个非常薄的黏性亚层。
在这个区域内，速度剖面呈现线性分布。
（2）平衡层：在黏性亚层之上，由于惯性效应和黏性效应的平衡作用，形成了一个平衡层。
在这个区域内，速度剖面呈现对数分布。
（3）外层：在平衡层之上，流场的特征逐渐趋向于自由流场，在这个区域内，速度剖面呈现指数分布。
3. 流动边界层的控制方程3.1 流动边界层的基本方程流动边界层的基本方程包括质量守恒方程、动量守恒方程和能量守恒方程。
