当前位置：文档之家 › 第6章 边界层流动.

第6章 边界层流动.

  • 格式：ppt
  • 大小：1.27 MB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

流体力学第6章讲解

流体力学第6章讲解

2、射孔的形状，圆孔口和方孔显然其扩张的情况不会相同。不同的射口形状有 不
同的实验值。用φ表示这个影响因素， 对圆断面射流 φ＝3.4，长条缝射孔 φ＝2.44。
圆孔综口合射这流两：个t影g响因素K：x k＝Kφα 3.4a
x
R 1 3.4 as 3.4( as 0.294)
r0
vm
vm r0 1
1
v0 R
2
1
[(11.5 )2 ]2d
0
9
第二节圆断面射流的运动分析
1
n
1
n
[(1 1.5 )2 ] d Bn; [(1 1.5 )2 ] d Cn
0
0
n
1
1.5
2
2.5
3
Bn
0.0985
0.064
0.0464
0.0359
0.0286
第一节无限空间淹没紊流射流特性
二、紊流系数a及几何特征
其斜率即：tga＝常数＝k。 对于不同的条件，k值是不同的常数，也叫实验常数。 通过实验发现，k值的影响因素有两个主要的因素：
1、射孔出口截面上气流的紊流强度。 紊流强度的大小用紊流系数a（A）来表示：a大紊流的强度就大，因此，紊
流 系数的大小可以反映出射流的扩张能力，所以，a也叫表征射流流动结构的 特征系数。另一方面，由于a反映的是射流混合能力的大小，因此，a还可以反 映孔口出口截面上的速度均匀程度。a越小，则混合能力越差，说明流速越均匀 。
二、断面流量Q
R
微环面的流量表达式 Q 2vydy Q0 r02v0
0
主体段：
R
Q
v r 0
y
y
2 ( )( )d( )

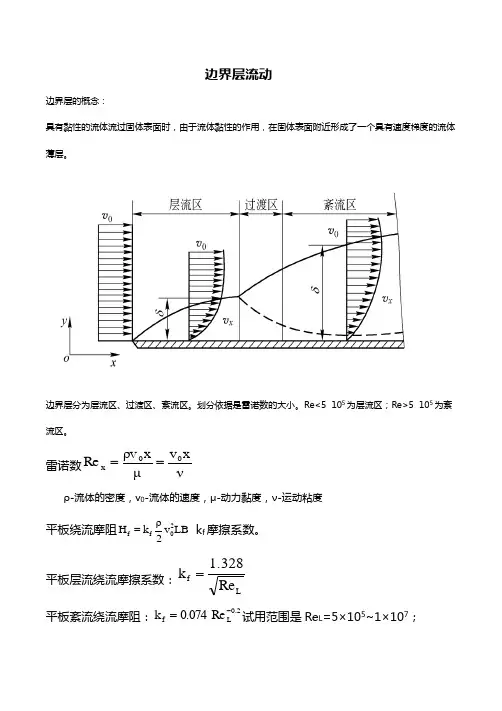
边界层流动

边界层流动

边界层流动边界层的概念：具有黏性的流体流过固体表面时，由于流体黏性的作用，在固体表面附近形成了一个具有速度梯度的流体薄层。

边界层分为层流区、过渡区、紊流区。

划分依据是雷诺数的大小。

Re<5×105为层流区；Re>5×105为紊流区。

雷诺数νx v μx ρv Re 00x ==ρ-流体的密度，v 0-流体的速度，μ-动力黏度，ν-运动粘度 平板绕流摩阻LB v 2ρk H 20f f = k f 摩擦系数。

平板层流绕流摩擦系数：L f Re 1.328k =平板紊流绕流摩阻：0.2L f Re 0.074k -=试用范围是Re L =5×105~1×107；58.2)Re (lg 455.0k -=L f 适用范围Re L =1×105~1×109；平板混合边界层摩擦阻力系数：L 0.2L f Re 1700Re 0.074k -=Re L =5×105~1×107； L2.58L f Re 1700)(lgRe 0.455k -= Re L =1×105~1×109； 球体绕流摩阻H f20f 2f f πR 2ρk πR h H v =⋅=-----------------我是分割线-------------------香蕉球是怎么回事？香蕉球是在踢球时给球施加一个旋转的力。

上旋球的落点会比不旋转的球落点要近些。

下旋球的落点会比不旋转的球落点要远些。

上旋为逆时针旋转,如图力F1作用在1点时产生上旋球。

在飞行过程中球表面会形成一层很薄速度边界层。

上旋球的上表面V 空方向与ω球方向相反，所以空气被减速，下表面V 空方向与ω球方向相同，所以空气被加速。

根据伯努利方程可知，速度大的地方压强小，速度小的地方压强大。

即P 上大于P 下，球被迫向压强小的一侧转弯了。

----------------我是分割线----------------------由管流连续性方程可知流量q v 和流速v 与截面A 都是正相关 ⎭⎬⎫⎩⎨⎧∝∝A q v q v vV 2211q A v A v ==上课期间，打开的水龙头很少，流量q v 总很小，总管道的流速v 很小； 下课期间，用水高峰期时，打开的水龙头增多，流量q v 总增大，总管道内水的流速v 很大。

边界层内外流动的特点

边界层内外流动的特点

边界层内外流动的特点
）。

边界层是大气层的一种说法，它指的是介于大气层和海洋之间的一层
非常有规律的温度、海盐、水分组成的那一层。

边界层内外流动特点如下：1）边界层内水温、盐度等特征流动比较稳定，边界层内的交换流量
要比邻近的大气层或海洋流量小得多，但依然会受到潮汐流的影响；
2）边界层外的水温、盐度有很大的变化，但与边界层内的流动保持
平衡；
3）边界层的流速因层的厚度而异，厚的层的流速要比薄的层的流速
要快得多；
4）受风流和日照的影响，边界层的流动经常会上升或下降；
5）夏季海温较高、陆地表面特别热，海水受热容易持续升温，边界
层流动弱，边界层会上升；
6）冬季海温较低，陆地表面特别冷，海水比较耗热，边界层流动强，边界层会下降。

流体力学张兆顺课后答案

流体力学张兆顺课后答案

流体力学张兆顺课后答案【篇一：流体力学知识点大全】书籍：《全美经典-流体动力学》《流体力学》张兆顺、崔桂香《流体力学》吴望一《一维不定常流》《流体力学》课件清华大学王亮主讲目录：第一章绪论第二章流体静力学第三章流体运动的数学模型第四章量纲分析和相似性第五章粘性流体和边界层流动第六章不可压缩势流第七章一维可压缩流动第八章二维可压缩流动气体动力学第九章不可压缩湍流流动第十章高超声速边界层流动第十一章磁流体动力学第十二章非牛顿流体第十三章波动和稳定性第一章绪论1、牛顿流体：剪应力和速度梯度之间的关系式称为牛顿关系式，遵守牛顿关系式的流体是牛顿流体。

2没有内摩擦，也就没有内耗散和损失。

层流：纯粘性流体，流体分层，流速比较小；湍流：随着流速增加，流线摆动，称过渡流，流速再增加，出现漩涡，混合。

因为流速增加导致层流出现不稳定性。

定常流：在空间的任何点，流动中的速度分量和热力学参量都不随时间改变，3、欧拉描述：空间点的坐标；拉格朗日：质点的坐标；4、流体的粘性引起剪切力，进而导致耗散。

5、无黏流体—无摩擦—流动不分离—无尾迹。

6、流体的特性：连续性、易流动性、压缩性不可压缩流体：d??0dtconst是针对流体中的同一质点在不同时刻保持不变，即不可压缩流体的密度在任何时刻都保持不变。

是一个过程方程。

7、流体的几种线流线：是速度场的向量线，是指在欧拉速度场的描述；同一时刻、不同质点连接起来的速度场向量线；dr?u?x,tdr?u?0迹线：流体质点的运动轨迹，是流体质点运动的几何描述；同一质点在不同时刻的位移曲线；涡线：涡量场的向量线，u,dr???x,t??dr???0涡线的切线和当地的涡量或准刚体角速度重合，所以，涡线是流体微团准刚体转动方向的连线，形象的说：涡线像一根柔性轴把微团穿在一起。

第二章流体静力学1、压强：p?lim?fdf??a?0?ada静止流场中一点的应力状态只有压力。

2、流体的平衡状态：1）、流体的每个质点都处于静止状态，==整个系统无加速度；2）、质点相互之间都没有相对运动，==整个系统都可以有加速度；由于流体质点之间都没有相对运动，导致剪应力处处为零，故只有：体积力(重力、磁场力)和表面力(压强和剪切力)存在。

边界层流动特性分析

边界层流动特性分析
▪ 边界层方程
1.边界层方程是描述边界层内流体运动规律的基本方程，主要包括Navier-Stokes 方程和连续方程。 2.边界层方程的求解通常需要采用数值模拟或者近似解析方法，如普适函数法和相 似理论法。 3.边界层方程的研究对于揭示边界层流动的内在机制和预测流动行为具有关键作用 。
边界层概念与定义
▪ 边界层厚度测量方法
1.热膜风速计法：通过测量热膜上的热量传递来推算流体的速 度分布，从而得到边界层的厚度。 2.皮托管法：利用皮托管测量总压和静压差，计算出平均速度 ，再根据速度分布推导出边界层厚度。 3.激光多普勒测速技术（LDV）：通过发射激光束并接收反射 光的多普勒频移信号，精确测量流场速度，进而确定边界层厚 度。
边界层分离
1.边界层分离是指当流体流过曲率半径较小的固体表面时，边 界层内的流体由于离心力的作用而从固体表面分离的现象。 2.边界层分离会导致流体在分离点后方形成涡旋，从而增加流 体与固体表面的摩擦阻力并影响流体的整体流动性能。 3.边界层分离的研究对于理解和控制流体流动中的能量损失、 噪声辐射以及流体机械的性能具有重要的实际意义。
边界层的分类
1.根据流体运动的特征，边界层可以分为层流边界层和湍流边 界层。层流边界层是指流体流动呈现有序、稳定的流动状态， 而湍流边界层则表现为无序、随机的流动状态。 2.根据流体与固体表面的相对运动关系，边界层还可以分为静 止边界层和动边界层。静止边界层是指固体表面静止不动时形 成的边界层，而动边界层则是指固体表面运动时形成的边界层 。 3.根据流体与固体表面的接触方式，边界层可以进一步细分为 光滑表面边界层和粗糙表面边界层。
边界层控制技术
1.边界层控制技术是通过改变边界层的流动特性来提高流体机 械效率、降低能耗和减少环境污染的一类技术。 2.常见的边界层控制技术包括流动诱导分离控制、湍流减阻技 术和热边界层控制等。 3.边界层控制技术在航空航天、能源、交通等领域具有广泛的 应用前景，对于推动相关行业的技术进步和可持续发展具有重 要作用。

船舶流体力学第六章 势流理论

船舶流体力学第六章 势流理论

= Vx
- iVy
= V
\W
(z)=

dW dz
dz
=
V dz
=
V
z
6.5.2 点源
Q向四周流出 +
Q从四周流入 -
Vq =0
Q
Vr = 2pr
pqp qp 公式6.4.6
dw dz
=（Vr
－
iV q
） e-iq
d w = ( Q - i 0 ) · e - i = Q = Q d z 2 r 2 r e i 2 z
=0
\ V 2 +-U = C 2
（关于流线的常数）
条件 3）无旋 柯西 —— 拉格朗日积分
V=(f)=f
t t
t
V t +V22
+ -U+VV=0
\ft +V22+ -U=0
f \
ft +V22
+ -U
6.2 不可压势流的基本方程和边界条件
6.2.1 ．不可压势流的质量守恒方程
V x
+ Vy
+ Vz
=0
x y z
f
Vx = x \
2f 2f 2f
x2 + y 2 + z 2 = 0
2f = 0 （拉普拉斯算子 2 ） 调和函数叠加性
6.2.2 ．拉普拉斯 边界条件 速度场 压力分布 流体对固体的力
在空间中不变，只是时间的函数
V 2 + - U + = C ( t )
2 t
4）定常 则 V 2 +- U = C 在全部空间适用
2
6.2.3 边界条件和解法概述

第6章层流的解析解与近似解

第6章层流的解析解与近似解

第6章 层流的解析‎解与近似解‎粘性流动基‎本方程组的‎解析解有着‎它固有的数‎学困难，真正能做解‎析解的流动‎为数不多，而且都是比‎较简单的流‎动。

本章将介绍‎几种粘性流‎动的解析解‎，有助于我们‎开阔思路，认识多种实‎际流动的性‎质。

首先先介绍‎一下粘性流‎研究的意义‎和研究的特‎点以及粘性‎流动的基本‎方程组，接着介绍一‎些解析解。

在介绍解析‎解时先考虑‎常特性不可‎压缩流体，通过基本方‎程，解得流场的‎速度和温度‎分布，最后求出摩‎擦阻力系数‎和热交换系‎数。

为了认识可‎压缩流动的‎特性，介绍两种简‎单的可压缩‎流动的解析‎解。

另外本章只‎限于雷诺数‎不大的流动‎。

6.1 粘性流研究‎的意义一切流体都‎具有粘性，但是人类最‎经常接触的‎流体，如水和空气‎其粘性都很‎小，要考虑粘性‎的影响就会‎使数学问题‎变得非常复‎杂；另外，对于这些粘‎性小的流体‎，忽略其粘性‎所得到的结‎果又能在一‎定程度上符‎合实际情况‎，因此，理想无粘性‎流体理论最‎先得到了发‎展，它比粘性流‎体理论要成‎熟得多。

应当指出，虽然理想流‎体理论取得‎了重大的成‎就，但在某些方‎面却有不可‎逾越的先天‎性缺陷。

例如，它不能预估‎管道流动的‎压力损失，也不能计算‎在流体中运‎动的物体所‎受到的阻力‎。

后一问题与‎著名的达朗‎伯疑题有关‎。

达朗伯对理‎想流体进行‎了严谨的研‎究后得出了‎如下结论：当任意形状‎的固体在静‎止的充满无‎限空间的无‎粘性流体中‎作匀速直线‎运动，它不承受沿‎运动方向的‎作用力，即物体所受‎阻力为零。

在他所做假‎设的前提下‎，这一结论的‎逻辑推理是‎完全正确的‎，但它却与实‎际完全不符‎，因为所有的‎物体在流动‎中运动时都‎受到阻力作‎用。

这从反面说‎明了考虑粘‎性的必要性‎。

例1 圆柱绕流对于理想不‎可压缩流体‎，()22214sin s p p p C U θρ∞∞-==- 其中 p ∞——远前方静压‎，ρ——流体密度。

流体力学第六章 流动阻力及能量损失

流体力学第六章 流动阻力及能量损失

第六章流动阻力及能量损失本章主要研究恒定流动时，流动阻力和水头损失的规律。

对于粘性流体的两种流态——层流与紊流，通常可用下临界雷诺数来判别，它在管道与渠道内流动的阻力规律和水头损失的计算方法是不同的。

对于流速，圆管层流为旋转抛物面分布，而圆管紊流的粘性底层为线性分布，紊流核心区为对数规律分布或指数规律分布。

对于水头损失的计算，层流不用分区，而紊流通常需分为水力光滑管区、水力粗糙管区及过渡区来考虑。

本章最后还阐述了有关的边界层、绕流阻力及紊流扩散等概念。

第一节流态判别一、两种流态的运动特征1883年英国物理学家雷诺（Reynolds O.）通过试验观察到液体中存在层流和紊流两种流态。

1.层流观看录像1-层流层流（laminar flow），亦称片流：是指流体质点不相互混杂，流体作有序的成层流动。

特点：（1）有序性。

水流呈层状流动，各层的质点互不混掺，质点作有序的直线运动。

（2）粘性占主要作用，遵循牛顿内摩擦定律。

（3）能量损失与流速的一次方成正比。

（4）在流速较小且雷诺数Re较小时发生。

2.紊流观看录像2－紊流紊流（turbulent flow），亦称湍流：是指局部速度、压力等力学量在时间和空间中发生不规则脉动的流体运动。

特点：（1）无序性、随机性、有旋性、混掺性。

流体质点不再成层流动，而是呈现不规则紊动，流层间质点相互混掺，为无序的随机运动。

（2）紊流受粘性和紊动的共同作用。

（3）水头损失与流速的1.75~2次方成正比。

（4）在流速较大且雷诺数较大时发生。

二、雷诺实验如图6-1所示，实验曲线分为三部分：（1）ab段：当υ<υc时，流动为稳定的层流。

（2）ef段：当υ>υ''时，流动只能是紊流。

（3）be段：当υc<υ<υ''时，流动可能是层流（bc段），也可能是紊流（bde段），取决于水流的原来状态。

图6-1图6-2观看录像3观看录像4观看录像5实验结果（图6-2）的数学表达式层流：m1=1.0, h f=k1v , 即沿程水头损失与流线的一次方成正比。

第6章 边界层流动

第6章 边界层流动

6.2 二维平面边界层流动
因为d << L，相对于边界层厚度而言，平板就是无 限长的这样而在边界层流动问题中就找不到一个x方向的 特征长度；因此可以设想在任一x断面流速分布都是相似 的并可作以下变换
微 分 方 程 及 其 精 确 解
将边界层微分方程简化为 边界条件h = 0: f (h) = f '(h) = 0; h = ∞: f '(∞) = 1。 上式是一个非线性三阶常微分方程，有对应于 边界条件的确定解；它由布拉休斯在1908年首次得 出并采用幂级数和渐近方法获得精确解。
微 分 方 程 及 其 精 确 解
6.2 二维平面边界层流动
边界层厚度：
边界层位移厚度：
边界层动量厚度： 壁面切应力系数：
微 分 方 程 及 其 精 确 解
摩擦阻力系数：
t0为壁面切应力、FDf为整个平板受到的力，即
6.2 二维平面边界层流动
以上结果得到试验的证实。图6-5表示顺流放置平 板层流边界层的布拉休斯精确解，以及据此绘制的边 界层厚度的沿程变化和流速分布。
图6-4 平板层流边界层
6.2 二维平面边界层流动
微分方程的精确解 如图6-4所示，取平板前缘为直角坐标系的原点，则 平板前方未受扰动的均匀来流速度U∞与平板平行。由伯努 利方程知，在绕平板流动的势流部分，U = U∞、dp/dx = 0； 而由边界层微分方程知，在边界层中压强沿y方向是均匀 分布的，即边界层内任一点处的压强都与同x坐标处边界 层外势流的压强相等。
微 分 方 程 及 其 精 确 解
g 为另一积分常数。
类似还可得三阶渐近解f = f1 + f2 + f3甚至更高 阶渐近解，本问题中仅考虑到二阶。

传热学第六章

传热学第六章

流动全部为紊流
局部传热系数关联式 Nuxm 0.0296Rex4m/5Prm1/3
平均传热系数关联式 Num 0.037Rem4/5Prm1/3
Rex=0≥108 0.6 Prm 60
混合边界层
h

1 l

xc
0
hcx
dx
1
l
xc
hcx
2 dx
Rem

u d o
层流 Rem 1.4 105
层流、紊流的转变
特征速度 来流速度 u∞ 特征尺寸 管外径 d0
Rem＞1.4 105
定性温度 热边界层的平均温度 tm=1/2(t∞+tw)
1.流动的特征
圆柱前半部，沿流动方向流体处于加速减压状态，沿流向压 力逐渐减小。圆柱后半部，沿流向压力逐渐增加。最大粘滞 摩擦力处于圆柱表面处，因而圆柱表面附近的流体受到的阻 力最大。
小结：利用关联式获取表面换热系数的关键步骤
1，熟悉对象：如流过平板、圆柱、球或管束； 2，确定特征温度，查表获取特征温度下流体的热物理参数； 3，确定特征长度，计算Re数； 4，确定要获取局部、还是平均表面换热系数； 5，选择合适的关联式计算无量纲表面换热系数，即Nu数； 6，计算换热系数。
2017/10/23
第六章 单相对流换热的实验关联式
Convection Heat Transfer
§6-1 管内强制对流传热
6.1.1管内强制对流流动和换热的特征
入口段 充分发展段
1. 层流和湍流判别
层流： Re 2300 过渡区： 2300 Re 10000 旺盛湍流： Re 10000
Nu f

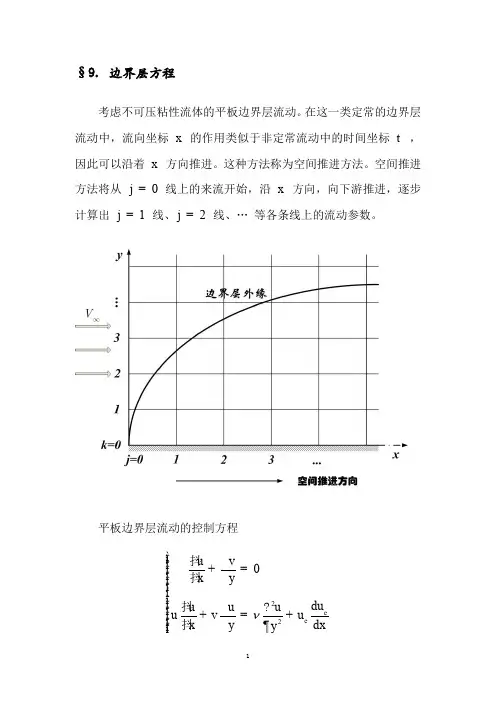
6-边界层方程

6-边界层方程

§9. 边界层方程考虑不可压粘性流体的平板边界层流动。

在这一类定常的边界层流动中，流向坐标 x 的作用类似于非定常流动中的时间坐标 t ，因此可以沿着 x 方向推进。

这种方法称为空间推进方法。

空间推进方法将从 0j = 线上的来流开始，沿 x 方向，向下游推进，逐步计算出 1j = 线、2j = 线、… 等各条线上的流动参数。

平板边界层流动的控制方程220e euvx ydu u u uu v u x y dx yìï抖ï+=ïï抖ïïíïï抖 ï+=+ïï抖¶ïî这里 ()e e u u x = 是边界层外缘处的速度分布。

通过求解边界层外的无粘流动，可事先求得 e u 。

因此在边界层流动的求解中，ee du u dx这一项是已知的。

边界层流动控制方程的初始条件是在平板前缘（0j = 线），给定来流速度 u V ¥= ，0v = 而边界条件是沿壁面（0k = 线），速度 0u = ，0v =取特征速度 V ¥ 和特征长度 1L = ，将方程无量纲化，平板边界层流动的控制方程成为2201Re e e u v x y du u u u u v u x y dx y ìï抖ï+=ïï抖ïïíïï抖 ï+=+ïï抖¶ïî方程中u u V ¥=、 v v V ¥= 、 e e u u V ¥= ， x x L = 、 y y L =而Re V L¥=是（来流）雷诺数。

下面为了简洁起见，省略所有无量纲量上方的横杠。

按照空间推进的观点，流向坐标 x 是类时间坐标。

流动边界层的定义

流动边界层的定义

流动边界层的定义流动边界层的定义流动边界层是指在固体表面附近，由于粘性效应而形成的一种特殊的流场。

它通常出现在高速气体或液体与固体表面接触的情况下。

流动边界层对于工程领域中诸如空气动力学、水力学、热力学等方面的问题都具有重要意义。

1. 流动边界层的基本概念1.1 流动边界层的形成原因当高速气体或液体与固体表面接触时，由于粘性效应，会在固体表面附近产生一层非常薄的流场，这就是流动边界层。

1.2 流动边界层的特征流动边界层通常具有以下几个特征：（1）速度梯度大；（2）温度梯度小；（3）压力梯度小；（4）密度梯度小。

1.3 流动边界层的分类根据不同情况下流场中粘性效应所占比例不同，可以将流动边界层分为以下两类：（1）无粘流动边界层：当粘性效应可以忽略时，流动边界层可以看作是无粘的。

（2）粘性流动边界层：当粘性效应不能忽略时，流动边界层就是粘性的。

2. 流动边界层的结构2.1 流动边界层的结构特征流动边界层通常具有以下几个结构特征：（1）速度剖面：在流场中，速度从固体表面到自由流场逐渐增加，形成了一个速度剖面。

（2）压力分布：由于黏性效应，在流场中存在一个压力梯度，这导致了压力沿着法向方向发生变化。

（3）温度分布：在高速气体或液体与固体表面接触时，会产生一定的热量，并导致温度沿着法向方向发生变化。

2.2 流动边界层的三个区域根据速度剖面和压力分布的不同情况，可以将流动边界层分为以下三个区域：（1）黏性亚层：在靠近固体表面处，由于黏性效应非常显著，形成了一个非常薄的黏性亚层。

在这个区域内，速度剖面呈现线性分布。

（2）平衡层：在黏性亚层之上，由于惯性效应和黏性效应的平衡作用，形成了一个平衡层。

在这个区域内，速度剖面呈现对数分布。

（3）外层：在平衡层之上，流场的特征逐渐趋向于自由流场，在这个区域内，速度剖面呈现指数分布。

3. 流动边界层的控制方程3.1 流动边界层的基本方程流动边界层的基本方程包括质量守恒方程、动量守恒方程和能量守恒方程。

流体力学第六章边界层流动5

流体力学第六章边界层流动5
2018/10/31 10
层流与紊流、雷诺数
在不同的初始和边界条件下，粘性流体质点的运动会出现两种不同
的运动状态，一种是所有流体质点作定向有规则的运动，另一种是
作无规则不定向的混杂运动。前者称为层流状态，后者称为湍流状 态（别称紊流状态）。首先是英国物理学家雷诺在1883年用实验证
明了两种流态的存在，确定了流态的判别方法。
u???????????????????????用量纲分析的方程分析法可得一般二维流动无量纲方程组用量纲分析的方程分析法可得一般二维流动无量纲方程组621平板层流边界层微分方程精确解0??????yuxuyxre12222yuxuxpeuyuuxuuxxxyxx???????????????1121?11?11?11???2?2015112924忽略第二方程最后一项第三方程除压强项的其他项
vc d Re c
Re c
vc d

Re 2320时，管中是层 流； Re 2320时，管中是紊 流。
2018/10/31 13
根据实验结果可知，同管流一样，边界层内也存在着层流和紊流两种 流动状态，若全部边界层内部都是层流，称为层流边界层;若全部边界层 内部都是湍流，称为湍流边界层；若在边界层起始部分内是层流，而在 其余部分内是紊流，称为混合边界层。如图所示，在层流变为紊流之间 有一过渡区。在紊流边界层内紧靠壁面处也有一层极薄的层流底层。
dp dU U dx dx
②第二式右边得到简化（x方向二阶偏导数消失），有利于数值计算。 利用该方程就可计算壁切应力和流动阻力，具有里程碑式意义。
2018/10/31 25
布拉修斯利用相似性解法，引入无量纲坐标：
Rex
*
*

传热学-第六章3-4

传热学-第六章3-4
Re f = 2300 − 106 Pr f = 0.6 − 105
非圆形截面槽道 用当量直径作为特征尺度应用到上述准 则方程中去。 则方程中去。 4
de = A c P
式中： 式中：
为槽道的流动截面积； 为湿周长。 A 为槽道的流动截面积；P 为湿周长。 c
对截面上出现尖角的流动区域， 注 ： 对截面上出现尖角的流动区域 ， 采用当 量直径的方法会导致较大的误差。 量直径的方法会导致较大的误差。
3、影响管内强制对流换热的几个主要因素 1）入口段的影响：对紊流，当L/d <60，h受入口段影 ）入口段的影响：对紊流， ， 响较大； 不再随管长变化。 响较大；当L/d>60，平均h不再随管长变化。由实验 得出h的经验公式 的经验公式， 的长管， 得出 的经验公式，一般是对L/d>60的长管，若对短 管，需乘上修正系数CL。进口的断面形状对换热系数
4）管壁粗糙度的影响：粗糙度越大，换热越强。工程 ）管壁粗糙度的影响：粗糙度越大，换热越强。
上常采用内壁做成沙砾状的螺旋管加强换热。 上常采用内壁做成沙砾状的螺旋管加强换热。
4、强化换热措施
由
N uf =
h=
0 . 0 2 3 R e0.8 P r
f
0 . 4 0 . 6
n f
0 . 0 2 3
Cp 0 . λ 0 . 2 ρ u 4 µ d
2、紊流换热关联式的修正
（1）短管修正
入口段的传热系数较高。 入口段的传热系数较高。对于通常的工业设备 中的尖角入口，有以下入口效应修正系数： 中的尖角入口，有以下入口效应修正系数：
cL =
1
0 . 7
+
d L
（2）弯管修正

传热学讲义对流换热——第六章

传热学讲义对流换热——第六章

第六章 单相流体对流换热及准则关联式第一节 管内受迫对流换热本章重点：准确掌握准则方程式的适用条件和定性温度、定型尺寸的确定。

1-1 一般分析),,,,,,,,(l c t t u f h p f w μαρλ=流体受迫在管内对流换热时，还应考虑以下因素的影响：① 进口段与充分发展段，② 平均流速与平均温度，③ 物性场的不均匀性，④ 管子的几何特征。

一、进口段与充分发展段1．流体在管内流动的主要特征是，流动存在着两个明显的流动区段，即流动进口（或发展）段和流动充分发展段，如图所示。

（1）从管子进口到边界层汇合处的这段管长内的流动称为管内流动进口段。

（2）进入定型流动的区域称为流动充分发展段。

在流动充分发展段，流体的径向速度分量v 为零，且轴向速度u 不再沿轴向变化，即：0=∂∂xu， 0=v 2．管内的流态（1）如果边界层在管中心处汇合时流体流动仍然保持层流，那么进入充分发展区后也就继续保持层流流动状态，从而构成流体管内层流流动过程。

2300Re <用νdu m =Re 判断流态, 式中 m u 为管内流体的截面平均流速， d 为管子的内直径，ν为流体的运动黏度。

（2）如果边界层在管中心处汇合时流体已经从层流流动完全转变为紊流流动，那么进入充分发展区后就会维持紊流流动状态，从而构成流体管内紊流流动过程。

410Re >（3）如果边界层汇合时正处于流动从层流向紊流过渡的区域，那么其后的流动就会是过渡性的不稳定的流动，称为流体管内过渡流动过程。

410Re 2300<<3．热进口段和热充分发展段当流体温度和管壁温度不同时，在管子的进口区域同时也有热边界层在发展，随着流体向管内深入，热边界层最后也会在管中心汇合，从而进入热充分发展的流动换热区域，在热边界层汇合之前也就必然存在热进口区段。

随着流动从层流变为紊流， 热边界层亦有层流和紊流热边界层之分。

热充分发展段的特征对常物性流体，在常热流和常壁温边界条件下，热充分发展段的特征是：)(1x f t f =及)(2x f t w =与管内任意点的温度),(r x f t =组成的无量纲温度⎪⎪⎭⎫⎝⎛--x f x w w t t t t ,,x ,随管长保持不变，即： 0,,x ,=⎪⎪⎭⎫ ⎝⎛--∂∂x f x w w t t t t x 式中，t —管内任意点的温度，),(r x f t = ⇒xf x w w t t tt ,,x ,--仅是r 的函数。

层流边界层流动与换热的相似解

层流边界层流动与换热的相似解

当Pr→ 0时，上式的解为：
则：
整个平板长度L的平均对流表面传热系数可以由下式计 算获得：
得到：
即：
在整个Pr数范围内，可以整理出：
需要注意的是，在边界层前缘(x→0)，边界层的基本 假设不再成立，因此边界层微分方程不适用。否则， 此处的局部对流表面传热系数将无限大，与实际不符。 因此，边界层分析主要用于高Re数范围。
从哈里斯用数值方法得到的结果分析可知： ( l ) β =0，即m =0，对应的是U∞=常数，即前面讨论的外掠平 壁的层流边界层流动。 (2 ) β＞0，即m＞0,是外掠楔形物的边界层层流流动，在x=0处 主流速度为零，沿流动方向速度加速，在壁面上边界层内速度 分布的斜率较外掠平壁时大。随β的增大，速度分布的斜率更大， 边界层愈薄。 (3 ) β＝π描述的是面对平壁的流动，称为滞止流动。 ( 4 ) β＜0 表明，边界层主流速度在x=0处为无穷大，沿流动方 向减少，夹角是负值。 通过在平壁吸气使边界层消失，保证主流速度恒定，进入扩充 段，主流速度将沿流动方向减少。在β＝－0.1988 时，速度分 布呈S形，在壁面处(y=0)速度梯度为零。当β ＜－0.1988时， 流动边界层从壁面脱离并在贴壁处产生回流，因而β＝－0.1988 称为脱体的临界角。
。
式(8-3-36)表明 是Pr数的函数，波尔豪森给出 了一系列 的数值。表7-2 给出了不同Pr数时外 掠平壁的 的数值。可以发现，在Pr = 0.6 ～15 的范围内， 可以十分精确地用 表 示。
即：
对于Pr < 0.6的低普朗数流体，其导热性能很好，前 面边界层分析已说明，当 Pr << 1时速度边界层厚度 远小于温度边界层厚度，可以近似认为温度边界层内 速度为主流速度U∞，即 。代入方程(8-3-32)得：

第六章 层流对流换热

第六章 层流对流换热

u max
= − r02 4μ
d ( p + ρ gh ) dL
（6－8）
由于旋转抛物体的体积恰好等于它的外切圆柱体体积的一半，因此，平均流速等于最大流速 的一半，即
U
=
1 2
u max
= − r02 8μ
d ( p + ρ gh ) dL
（6－9）
同时，无量纲速度的分布为
φ= u U
=
⎡ 2 ⎢1
ρc
p
(
w
∂T ∂r
+u
∂T ) ∂x
=
λ
(
∂ 2T ∂r 2
+
1 r
∂T ∂r
+
∂ 2T ∂x 2
)
（6－15）
因为是充分发展的层流流动，故 w = 0 ， ∂ T ∂x
沿x
不再变化，
∂2T ∂x2
=0
，上述能量方
程即成为
ρc
pu
∂T ∂x
=λ r
∂ (r ∂T ) ，根据 ∂T
∂r ∂r
∂x
=
d T~ dx
3
流动，由于流体的物性不随温度变化，即动量方程与能量方程之间没有藕合作用，因而可以
先求速度场，后求温度场，而速度场已由上述方法求得，
再利用能量方程就可求出温度分布。
三、 恒热流密度时对流换热系数的确定
t
tw
tm
恒热流密度下的换热，如电加热、辐射加热、以及换
tc
热器中单位面积换热量为常量的情况，其温度（壁温、容
和u
=
2U
⎡ ⎢1 ⎣
−
(
r r0
)2
⎤ ⎥ ⎦

知识点：流动边界层PPT

知识点：流动边界层PPT

w xc Re c v
知识点：流动边界层
的开始处距离平壁前端的距离x0称为临界距离。它由临界雷 诺数确定
对于外掠平板的流动，一般情况下可取Rec=5×105。 3.流动边界层的特征 （1）边界层厚度δ 沿流体流动方向逐渐增厚且与壁面特 性尺寸l相比是极小值； （2）边界层内存在较大的速度梯度； （3）边界层内的流态分层流和紊流，紊流边界层紧靠壁 面处仍有薄层流体保持层流，称为层流底层； （4）只有在边界层内才显示流体粘性的影响。
知识点：流动边界层
y
w∞ w
y w∞ w∞ x(w) x0
层流边界层 过渡段 紊流边界层
w∞层流底层Βιβλιοθήκη δ0x(w)
图1 流动边界层示意图
图2 流体外掠平板时流动 边界层的形成和发展
知识点：流动边界层
2.流动边界层的形成和发展 流动边界层的形成和发展过程可以用速度均匀的流体外 掠平板时反映出来。如图2，当流体与平壁前端x=0处接触时 流动边界层厚度δ =0。随随着流体进入平壁后，由于粘性的 切应力的作用，在壁面上形成层流边界层，其厚度δ 随着距 平壁前端距离x的增加而增加，在距前端x0之前始终保持层流 状态。随着边界层厚度的增加，粘滞阻力对边界层外边缘处 流体的影响开始减弱，相反惯性力的影响相对加强。这使得 层流边界层从其边缘开始，逐渐变得不稳定起来，即层流边 界层开始向紊流边界层过渡。开始形成紊流区，除靠近壁面 处有一薄层层流底层外，主要是紊流核心，紊流区成为边界 层的主体，这种边界层称为紊流边界层。由层流向紊流过渡
流动边界层的概念当粘性流体流过固体壁面时固体壁面附近的流体流动速度变化较大由于壁面摩擦阻力的阻滞作用靠近固体壁面的流体速度下降形成一个速度有明显变化的流体薄层称为流动边界层或称速度边界层
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6.2.1 微分方程及其精确解 微分方程 在直角坐标系，定常、不可压、不计重 力的二维流动N-S方程为
边 界 层 流 动
6.2 二维平面边界层流动
根据小粘度二维平面边界层流动的特点——d << L 以及uy<< ux——对 N-S方程中各变量和参数作数量级估 计，有 量级1的量： 量级e 2的量：
边 界 层 流 动
图6-1 翼型绕流
6.1 边界层基本概念
6.1.1 边界层流态 边界层流动可以是层流或湍流。实际中更一般地是 混合边界层，即边界层前缘为层流，经过一过渡区(称为 转捩区)后转变为湍流；在湍流区，紧挨物面附近还有一 层流底层。图6-2所示为一均匀来流绕过平板一侧所形成 的边界层流动。
微 分 方 程 及 其 精 确 解
边 界 层 流 动
图6-2 平板边界层流动
6.1 边界层基本概念
在湍流区，若平板表面粗糙度D大于层流底层的厚 度dl，则称之为粗糙(表面)平板；否则称为光滑(表面)平 板。当层流区的范围很小时，可近似地把整个边界层看 成为湍流边界层。 为了便于判断边界层的流态，通常假定由层流到湍 流的转捩是在某一截面突变完成的，并称此截面为临界 截面，它离边界层前缘的距离称为临界长度x*，临界截 面边界层的厚度称为临界厚度d*。（图6-2） 边界层流态用临界雷诺数Re*来判断， Re*有两种形 式：Rex* = U∞x*/u和 Red* = U∞d*/u，对于平板绕流，Rex* = 5105 ~ 3106，Red* 2800。
微 分 方 程 及 其 精 确 解
dx, dx2; ux, dux, d2ux; p, dp; r dy2; u
量级e << 1的量：dy; uy, duy, d2uy
依照以上量级对N-S方程进行简化分析，可得
6.2 二维平面边界层流动
以上就是二维平面边界层流动的微分方程，由普 朗特在1904年首次提出。虽然普朗特边界层微分方程 相对N-S方程大为简化，但仍然是非线性的，只能对 特殊情况下的某些层流边界层求得精确解。 求解边界层微分方程时，首先要得到边界层外部 势流的速度，使压强p成为已知量，这样未知量只有 ux和uy，由边界层微分方程x分式和连续方程一起构成 封闭的求解系。 注意：普朗特边界层微分方程不适用于d /x << 1条件 得不到满足的边界层前缘部分，该部分对应的雷诺数 范围一般为Rex ≤ 25。
边 界 层 流 动
6.1 边界层基本概念
边界层位移厚度也称边界层排挤厚度。在边界层 内，流速受到壁面的阻滞作用而减小，使通过边界层 内的流量比理想流动时减少，这相当于固体壁面沿其 法线方向朝流场内移动了一个距离d1后理想流动所通 过的流量，这个d1就是边界层位移厚度，如图6-3所 示。根据位移厚度d1的定义，对不可压流动有
第 6 章 边界层流动
6.1 边界层基本概念 6.1.1 边界层流态 6.1.2 边界层各特征厚度 6.2 二维平面边界层流动 6.3 二维曲面边界层流动 6.4 二维圆柱滑动轴承润滑 6.5 圆柱和圆球绕流阻力
6.1 边界层基本概念
实际流体绕任何形状物体的大雷诺数流动都会在 物面附近形成边界层。图6-1所示为空气绕某一翼型的 流动，整个流场可分为边界层、边界层脱离翼型物面 以后形成的尾流、以及边界层和尾流以外的势流。
边 界 层 各 特 征 厚 度
即
图6-3 边界层位移厚度
6.1 边界层基本概念
边界层动量厚度 与理想流动相比，边界层内流 速降低一方面使通过的流体质量减少，另一方面也使 通过的流体动量减少。这种动量减小也可以看成是相 当于将固体壁面向流场内移动了一个距离d2：
边 界 层 各 特 征 厚 度
即 称d2为动量损失厚度，简称动量厚度。边界层的 位移厚度与动量厚度之比称为边界层形状因子： H = d1/d2。
微 分 方 程 及 其 精 确 解
6.2 二维平面边界层流动
微分方程的精确解 应用边界层微分方程解决粘性流动问题的一个最 简单的例子，是流体绕顺流放置平板的层流边界层流 动，即均匀来流绕过沿平行于流动方向放置的一块薄 平板(其厚度假设为零)并在平板一侧附近所产生的流 动。
微 分 方 程 及 其 精 确 解
边 界 层 流 态
6.1 边界层基本概念
6.1.2 边界层各特征厚度 边界层厚度 边界层理论将大雷诺数流动的流 场分为粘性区和无粘区两部分，分别称为边界层和 主流区，它们的交界面称为边界层(外)边界，并人 为地规定边界层边界上流速为主流区的99％(或 99.5%), 边界层边界到物面的距离称为边界层厚度d， 用数学式表示即有 边界层未脱离物面的情况下，边界层厚度沿流 程是增加的，即在迎流的前缘点为零，然后沿流动 方向逐渐增加，到送流的后缘点达到最大。
第 6 章 边界层流动
6.1 边界层基本概念 6.2 二维平面边界层流动 6.2.1 微分方程及其精确解 6.2.2 积分方程及其近似解 6.3 二维曲面边界层流动 6.4 二维圆柱滑动轴承润滑 6.5 圆柱和圆球绕流阻力
6.2 二维平面边界层流动
二维平面不可压边界层流动是最简单的一类粘性流 动，即便如此也只有极少数情况能通过边界层微分方程 求得精确解，大多数情况只能通过边界层积分方程求近 似解。
ቤተ መጻሕፍቲ ባይዱ
图6-4 平板层流边界层
6.2 二维平面边界层流动
微分方程的精确解 如图6-4所示，取平板前缘为直角坐标系的原点，则 平板前方未受扰动的均匀来流速度U∞与平板平行。由伯努 利方程知，在绕平板流动的势流部分，U = U∞、dp/dx = 0； 而由边界层微分方程知，在边界层中压强沿y方向是均匀 分布的，即边界层内任一点处的压强都与同x坐标处边界 层外势流的压强相等。
6.1 边界层基本概念
边界层能量厚度即边界层能量损失厚度。与理想流体 的流动相比，边界层内流速的降低还使流体的动能通量减 少。类似于动量厚度，可以定义不可压流动的边界层能量 厚度d3：
边 界 层 各 特 征 厚 度
即
以上定义式表示边界层实际的流量具有的理想流 动动能与实际流动动能之差。容易证明，在边界 层任一截面，恒有：d > d1> d3 > d2。