第5章 边界层流动

流体力学张兆顺课后答案【篇一：流体力学知识点大全】书籍：《全美经典-流体动力学》《流体力学》张兆顺、崔桂香《流体力学》吴望一《一维不定常流》《流体力学》课件清华大学王亮主讲目录：第一章绪论第二章流体静力学第三章流体运动的数学模型第四章量纲分析和相似性第五章粘性流体和边界层流动第六章不可压缩势流第七章一维可压缩流动第八章二维可压缩流动气体动力学第九章不可压缩湍流流动第十章高超声速边界层流动第十一章磁流体动力学第十二章非牛顿流体第十三章波动和稳定性第一章绪论1、牛顿流体：剪应力和速度梯度之间的关系式称为牛顿关系式，遵守牛顿关系式的流体是牛顿流体。

2没有内摩擦，也就没有内耗散和损失。

层流：纯粘性流体，流体分层，流速比较小；湍流：随着流速增加，流线摆动，称过渡流，流速再增加，出现漩涡，混合。

因为流速增加导致层流出现不稳定性。

定常流：在空间的任何点，流动中的速度分量和热力学参量都不随时间改变，3、欧拉描述：空间点的坐标；拉格朗日：质点的坐标；4、流体的粘性引起剪切力，进而导致耗散。

5、无黏流体—无摩擦—流动不分离—无尾迹。

6、流体的特性：连续性、易流动性、压缩性不可压缩流体：d??0dtconst是针对流体中的同一质点在不同时刻保持不变，即不可压缩流体的密度在任何时刻都保持不变。

是一个过程方程。

7、流体的几种线流线：是速度场的向量线，是指在欧拉速度场的描述；同一时刻、不同质点连接起来的速度场向量线；dr?u?x,tdr?u?0迹线：流体质点的运动轨迹，是流体质点运动的几何描述；同一质点在不同时刻的位移曲线；涡线：涡量场的向量线，u,dr???x,t??dr???0涡线的切线和当地的涡量或准刚体角速度重合，所以，涡线是流体微团准刚体转动方向的连线，形象的说：涡线像一根柔性轴把微团穿在一起。

第二章流体静力学1、压强：p?lim?fdf??a?0?ada静止流场中一点的应力状态只有压力。

2、流体的平衡状态：1）、流体的每个质点都处于静止状态，==整个系统无加速度；2）、质点相互之间都没有相对运动，==整个系统都可以有加速度；由于流体质点之间都没有相对运动，导致剪应力处处为零，故只有：体积力(重力、磁场力)和表面力(压强和剪切力)存在。

对于实际流体的流动，无论流动形态是层流还是紊流，真正能求解的问题很少。

这主要是由于流体流动的控制方程本身是非线性的偏微分方程，处理非线性偏微分方程的问题是当今科学界的一大难题，至今还没有找到一套完整的求解方案。

但在实际工程中的大多数问题，是流体在固体容器或管道限定的区域内的流动，这种流动除靠近固体表面的一薄层流体速度变化较大之外，其余的大部分区域内速度的梯度很小。

对于具有这样特点的流动，控制方程可以简化。

首先，由于远离固体壁面的大部分流动区域流体的速度梯度很小，可略去速度的变化，这部分流体之间将不考虑粘性力的存在，视为理想流体，用欧拉方程或伯努利方程就可求解。

而靠近固体壁面的一个薄层——称为流动边界层，在它内部由于速度梯度较大，不能略去粘性力的作用，但可以利用边界层很薄的特点，在边界层内把控制方程简化后再去求解。

这样对整个区域求解的问题就转化为求解主流区内理想流体的流动问题和靠近壁面的边界层内的流动问题。

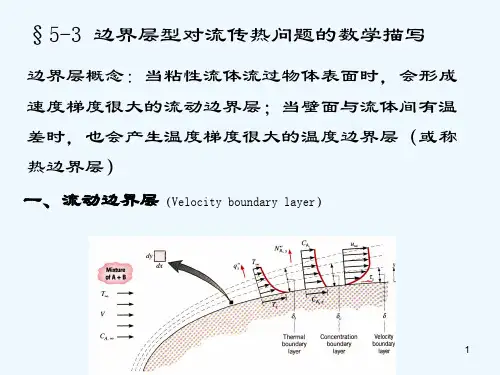
第一节边界层理论的基本概念一、边界层的定义流体流经固体表面时，靠近表面总会形成一个薄层，在此薄层中紧贴表面的流体流速为零，但在垂直固体表面的方程（法向）上速度增加得很快，即具有很大的速度梯度，甚至对粘度很小的流体，也不能忽略它表现出来的粘性力。

（因此，流体在绕流过固体壁面流动时，紧靠固体壁面形成速度梯度较大的流体薄层称为边界层。

）而在此边界层外，流体的速度梯度很小，甚至对粘度很大的流体，其粘性力的影响也可忽略，流体的流速与绕流固体表面前的流速v0一样。

可以把这部分在边界层外流动的流体运动视为理想流体运动，不考虑粘性力的影响。

边界层内、外区域间没有明显的分界面，而把边界层边缘上的流体流速v x视为v x=0.99v0，因此从固体表面至v x=0.99v0处的垂直距离视为边界层的厚度δ。

二、边界层的形成与特点边界层内的流动可以是层流，也可以是带有层流底层的紊流，还可以是层流、紊流混合的过渡流。

评判边界层层流或紊流的参数为雷诺数Re=vxρ/η，式中v为边界层外边界上流体流速，x为距边界层起点的距离（即流体进入平板的长度）。

1、什么是内部流动？什么是外部流动？答：所谓内部流动，是指流体流过与之换热的管壁内部，其流动边界层与热边界层不能自由发展，最后汇合于管道中心。

而外部流指的是换热壁面上的流动边界层和热边界层可以自由发展，存在一个边界层外的区域。

2、试说明管槽内对流换热的入口效应并解释其原因。

答：管槽内强制对流换热的入口效应：入口段由于热边界层较薄而具有比较充分的发展段高的表面传热系数。

入口段的热边界层较薄，局部表面传热系数较高，且沿着主流方向逐渐降低。

充分发展段的局部表面传热系数较低。

3、对流动现象而言，外略单管的流动与管道内的流动有什么不同？答：外掠单管流动的特点：边界层分离、发生绕流脱体而产生回流、漩涡和涡束。

4、对于外接管束的换热，整个管束的平均表面传热系数只有在流动方向管排数大于一定值后才与排数无关，试分析原因。

答：因后排管受到前排管尾流的影响（扰动）作用对平均表面传热系数的影响直到10排管子以上的管子才能消失。

5、什么叫大空间自然对流换热？什么叫有限自然对流换热？这与强制对流中的外部流动和内部流动有什么异同？答：大空间作自然对流时，流体的冷却过程与加热过程互不影响，当其流动时形成的边界层相互干扰时，称为有限空间自然对流。

这与外部流动和内部流动的划分有类似的地方，但流动的动因不同，一个由外在因素引起的流动，一个是由流体的温度不同而引起的流动。

6、如果把一块温度低于环境温度的大平板竖直地置于空气中，试画出平板上流体流动及局部表面传热系数分布的图像。

7.什么叫膜状凝结，什么叫珠状凝结?膜状凝结时热量传递过程的主要阻力在什么地方？答：凝结液体在壁面上铺展成膜的凝结叫膜状凝结，膜状凝结的主要热阻在液膜层，凝结液体在壁面上形成液珠的凝结叫珠状凝结。

8．在努塞尔关于膜状凝结理论分析的8条假定中，最主要的简化假定是哪两条?答：第3条，忽略液膜惯性力，使动量方程得以简化；第5条，膜内温度是线性的，即膜内只有导热而无对流，简化了能量方程。

2 转捩的试验现象圆管的转捩1883年，雷诺公布了著名圆管转捩实验。

发现，圆管流动的下临界雷诺数接近于2000～2300。

上临界雷诺数与来流条件、试验装置Re增加间歇因子在临界雷诺数附近的一个范围内时，流动具有间歇性(intermittence)1956年，罗塔(J Rotta)的试验结果全部时间作湍流运动的时间=γ1956年，罗塔(J Rotta)的试验结果边界层的转捩3 层流稳定性理论从数学上看，可以得到层流解物理上不存在或很难存在，因此物理上存在的层流解加的流动稳定性条件。

讨论：NS方程的解势流解满足N-S方程本身，但不满足边界条件流动稳定性条件层流稳定性理论认为：扰动便会迅速发展，并逐渐过渡到湍流。

系统激励(外界扰动)(体现为流态变化)系统的响应特性由Re决定：两种稳定性分析方法小扰动法（获得广泛应用）考虑二维不可压恒定平行流动的扰动问(),0,()(,,),(,,),(,,)U U y V P P x u u x y t v v x y t p p x y t =≡=′′′′′′===p P p w W w v V v u U u ′+=′+=′+=′+= 小扰动的基本方程222222221()1()0u u u p u u u v t x y x x y v v v p v v u v t x y y x y u v x yνρνρ∂∂∂∂∂∂++=−++∂∂∂∂∂∂∂∂∂∂∂∂++=−++∂∂∂∂∂∂∂∂+=∂∂③式u U u v V v v p P p ′=+′′=+=′=+①式代入忽略二阶项小量222211()110u u dU P p d U U v u t x dy x x dy v v P p U v t x y y u v x yνρρνρρ′′′∂∂∂∂′′++++=+∇∂∂∂∂′′′∂∂∂∂′+++=∇∂∂∂∂′′∂∂+=∂∂22110P d Ux dy Pyνρρ∂=∂∂=∂⑤式22110u u dU p U v u t xdy x v v p U v t x y u v x yνρνρ′′′∂∂∂′′+++=∇∂∂∂′′′∂∂∂′++=∇∂∂∂′′∂∂+=∂∂222()()()0u v u v d U u v U v t y x x y x dy y xu v x yν′′′′′′∂∂∂∂∂∂∂∂′−+−+=∇−∂∂∂∂∂∂∂∂′′∂∂+=∂∂0u v ′′==此即小扰动应该遵守的方程⑦式边界条件(固壁、无穷远处均成立)奥尔－佐默费尔德方程(Orr －Sommerfeld equation)（实际上三维扰动所得到的临界雷诺数更高）()()(,,)()()i r r i x t t i x t x y t y e y e e αββαβψ−−=Φ=Φu v y x ψψ∂∂′′==−∂∂，其中，为实数代表扰动波数,为扰动的圆频率，则为放大系数，<0，扰动被衰减，层流稳定>0，扰动被放大，层流不稳定α2/απλ=2/r T βπ=i βi βi β方程推导据此可以推导出关于扰动幅度四阶常微分方程：此即研究层流不稳定理论的出发点，通常称为Orr-Sommerfeld 方程。