空间力系。重心
- 格式:ppt
- 大小:2.05 MB
- 文档页数:41



三者定义1、重心:物体的重力的合力作用点称为物体的重心。
(与组成该物体的物质有关)重心只在重力场中才有意义,一旦物体离开重力场,重心就没有任何意义;而质心是反映质点系质量分布情况的一个几何点,它与作用力无关,无论质点系是否在重力场中,质心总是存在的。
在重力场中,物体的重心和质心的位置是重合的。
2、质心:指物质系统上被认为质量集中于此的一个假想点。
与重心不同的是,质心不一定要在有重力场的系统中。
值得注意的是,除非重力场是均匀的,否则同一物质系统的质心与重心不通常在同一假想点上。
说明白一点,质心就是物体质量集中的假想点(对于规则形状物体就是它的几何中心),重心就是重力的作用点,通常情况下,由于普通物体的体积比之于地球十分微小,所以物体所处的重力场可看作是均匀的,此时质心与重心重合;如果该物体的体积比之于地球不可忽略(例如一个放在地面上半径为3000km的球体),则该球体所处的重力场就不均匀了,具体说是由下自上重力场逐渐减小,此时重力的作用点靠下,也就是重心低于质心. 如果物体所处的位置不存在重力场(如外太空),则物体就无所谓重心了,但由于质量仍然存在,所以质心仍然存在。
质心和重心的关系就好象质量与重量的关系3、形心:物体的几何中心。
(只与物体的几何形状和尺寸有关,与组成该物体的物质无关)。
一般情况下重心和形心是不重合的,只有物体是由同一种均质材料构成时,重心和形心才重合。
当截面具有两个对称轴时,二者的交点就是该截面的形心。
据此,可以很方便的确定圆形、圆环形、正方形的形心;只有一个对称轴的截面,其形心一定在其对称轴上,具体在对称轴上的哪一点,则需计算才能确定。
对于一些常见的简单图形,如圆形、矩形、三角形、正方形等,其形心都是熟知的,利用这些简单图形的形心,由叠加法即可确定由这些简单图形组成的组合图形的形心。
重心重心在工程中具有重要的意义。
例如,水坝的重心位置关系到坝体在水压力作用下能否维持平衡;飞机的重心位置设计不当就不能安全稳定地飞行;构件截面的重心(形心)位置将影响构件在载荷作用下的内力分布规律,与构件受力后能否安全工作有着紧密的联系。




2、空间任意力系的平衡方程及常见的空间约束空间任意力系平衡的充要条件:空间任意力系的平衡方程:00xy z F FF ===ååå00xyzMMM===ååå空间任意力系平衡的充要条件:力系中各力在任一坐标轴上的投影的代数和等于零,以及各力对每一个坐标轴的力矩的代数和也等于零.该力系的主矢、主矩分别为零.(1) 空间任意力系的平衡方程(基本式)常见的空间约束00xy z F FF===ååå00xyzM M M ===ååå空间任意力系的平衡方程(基本式)平衡方程除了基本式之外,还有四矩式、五矩式、六矩式。
有几个力矩平衡方程,称之为几矩式。
各种形式应该根据实际情况灵活运用。
基本式以外的方程形式,通常不再给限定条件,一般的情况下只要列出的方程能求解出未知量即是未违反限制条件。
常见的空间约束00zxyF MM===ååå空间平行力系的平衡方程各种力系的独立平衡方程个数空间任意力系6个空间汇交力系3个空间平行力系3个空间力偶系3个平面任意力系3个平面汇交力系2个平面平行力系2个平面力偶系2(1)个最一般情形:空间、任意一级特殊情形(包含一种特殊情况):空间问题+特殊力系,或者任意力系+平面情形二级特殊情形(包含两种特殊情况):平面问题+特殊力系。
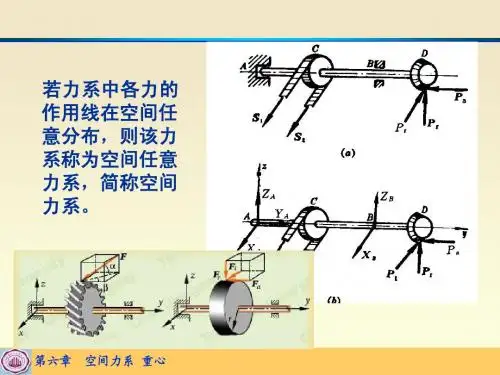
2、空间任意力系的平衡方程及常见的空间约束(2) 空间常见约束类型柔索二力杆2、空间任意力系的平衡方程及常见的空间约束2、空间任意力系的平衡方程及常见的空间约束径向轴承圆柱铰链铁轨蝶铰链球铰链导向轴承带有销子的夹板导轨空间任意力系及重心的计算f. 6个未知约束量空间固定端约束分析实际的约束时,需要忽略一些次要因素,抓住主要因素,做一些合理的简化。
比如导向轴承和径向轴承之间的区别;蝶铰链和止推轴承之间的区别。
如果刚体只受平面力系的作用,则垂直于该平面的约束力和绕平面内两轴转动的约束力偶都应该为零,相应减少了约束量的数目。


机械基础强度名词解释《机械设计基础》名词解释1.机械:机器、机械设备和机械工具的统称。
2.机器:是执行机械运动,变换机械运动方式或传递能量的装置。
3.机构:由若干零件组成,可在机械中转变并传递特定的机械运动。
4.构件:由若干零件组成,能独立完成某种运动的单元5.零件:构成机械的最小单元,也是制造的最小单元。
6.标准件:是按(或部标准等) 大批量制造的常用零件。
7.自由构件的自由度数:自由构件在平面内运动,具有三个自由度。
.约束:起限制作用的物体,称为约束物体,简称约束。
9.运动副:构件之间的接触和约束,称为运动副。
10.低副:两个构件之间为面接触形成的运动副。
11.高副:两个构件之间以点或线接触形成的运动副。
12.平衡:是指物体处于静止或作匀速直线运动的状态。
13.屈服极限:材料在屈服阶段,应力波动最低点对应的应力值,以σs表示。
14.强度极限:材料σ-ε曲线最高点对应的应力,也是试件断裂前的最大应力。
15.弹性变形:随着外力被撤消后而完全消失的变形。
16.塑性变形:外力被撤消后不能消失而残留下来的变形。
17.延伸率:δ=(l1-l)/l×100%,l为原标距长度,l1为断裂后标距长度。
1.断面收缩率:Ψ=(A-A1)/ A×100%,A为试件原面积,A1为试件断口处面积。
19.工作应力:杆件在载荷作用下的实际应力。
20.许用应力:各种材料本身所能安全承受的最大应力。
21.安全系数:材料的机限应力与许用应力之比。
22.正应力:沿杆的轴线方向,即轴向应力。
23.剪应力:剪切面上单位面积的内力,方向沿着剪切面。
24.挤压应力:挤压力在局部接触面上引起的压应力。
25.力矩:力与力臂的乘积称为力对点之矩,简称力矩。
26.力偶:大小相等,方向相反,作用线互相平行的一对力,称为力偶27.内力:杆件受外力后,构件内部所引起的此部分与彼部分之间的相互作用力。
2.轴力:横截面上的内力,其作用线沿杆件轴线。
空间力系和重心空间力系和重心各力的作用线不在同一平面内的力系,称为空间力系。
与平面力系类似,空间力系可分为空间汇交力系、空间力偶系和空间任意力系来研究。
空间力系和重心6.1空间力沿坐标轴的分解与投影直接投影法zF= Fx+ Fy+ Fz= Xi+ Yj+ Zk其中,FzαγZkFxFβ Y FyX= F cosα Y= F cosβ Z= F cosγXjixy空间力系和重心二次投影法zX= Fxy cos = F sinγ cos Y= Fxy sin = F sinγ sin Z= F cosγZγkFYj i X Fxyy注意,力在轴上的投影是代数量,而力在平面上的投影是矢量。
x空间力系和重心力的大小和方向余弦:zF= X 2+Y 2+ Z2X cos( F, i )= F Y cos( F, j )= F Z cos( F, k )= FZγkFYj i X Fxyyx空间力系和重心6.2力对点之矩和力对轴的矩6.2.1力对点之矩力对点的力矩矢等于矩心到该力作用点的矢径与该力的矢量积,表示为,M O (F )FOrMO ( F )= r× F空间力系和重心若矢径rz和力F分别为M O (F )B Fr= xi+ yj+ zk F= Xi+ Yj+ Zki则,M O ( F )= r× F= x X j y Y k z Z kOrA( x, y, z )ijyx= ( yZ zY )i+ ( zX xZ ) j+ ( xY yX )k空间力系和重心由此可知力矩矢M O (F )在三个坐标轴上的投影分别为:M Ox ( F )= yZ zY M Oy ( F )= zX xZ M Oz ( F )= xY yX(6 1)力矩矢的始端必须在矩心,不可任意移动,为一定位矢量。
空间力系和重心6.2.2力对轴之矩为度量力对绕定轴转动刚体的作用效应,引入力对轴的矩的概念。
空间力系和重心力对轴的矩的概念作用于刚体的力F对z轴的定义为:M Z ( F )= M O ( Fxy )=± Fxy hM z (F )F这样,空间力对轴之矩归结为平面上的力对点之矩,即力F对任一轴z之矩,等于这力在垂直于z轴的平面内的分量Fxy对该平面和z轴交点O之矩。
第六章空间力系和重心教学目标1 能熟练地计算力在空间直角坐标轴上的投影和力对轴之矩。
2 了解空间力系向一点简化的方法和结果。
3 能应用平衡条件求解空间汇交力系、空间任意力系、空间平行力系的平衡问题。
4 能正确地画出各种常见空间约束的约束力。
5 对重心应有清晰的概念,能熟练地应用组合法求物体的重心。
本章重点1 力在空间直角坐标轴上的投影和力对轴之矩。
2 空间汇交力系、空间任意力系、空间平行力系平衡方程的应用。
3 各种常见空间约束的约束力。
4 重心的坐标公式。
本章难点空间矢量的运算,空间结构的几何关系和立体图。
教学过程(下页)一、空间力系的简化 1.空间力系向一点简化刚体上作用空间力系),,(21n F F F,将力系中各力向任选的简化中心O 简化。
主矢:∑∑='=C i F F F,与O 点选择无关。
(6-1)主矩:∑∑∑⨯===)()(00i i i i F r F M M M,与O 点的选择有关。
(6-2) 主矢F和主矩0M 的解析表达式222)()()(∑∑∑++=iz iy ix F F F F (6-3) FFx F ix∑=),cos(,FFy F iy∑=),cos(,FFz F iz∑=),cos(2220))(())(())((i z i y i x F M F M F M M ∑∑∑++= (6-4)0)(),cos(M F Mx M i x∑=,00)(),cos(M F My M i y∑=,00)(),cos(M F Mz M i z∑=结论:空间力系向任一点简化,一般可得到一力和一力偶,该力通过简化中心,其大小和方向等于力系的主矢,该力偶的力偶矩矢等于力系对简化中心的主矩。
2.空间力系简化的最后结果 (1)空间力系平衡0=F ,00=M,此空间力系为平衡力系。
(2)空间力系简化为一合力偶0=F ,00≠M ,此空间力系简化为一合力偶,合力偶矩矢等于力系主矩0M与简化中心的位置无关。