工程力学之空间力系和重心
- 格式:pdf
- 大小:1.25 MB
- 文档页数:28

工程力学重点总结—期末考试、考研必备!!第一章静力学的基本概念和公理受力图一、刚体P2刚体:在力的作用下不会发生形变的物体。
力的三要素:大小、方向、作用点。
平衡:物体相对于惯性参考系处于静止或作匀速直线运动。
二、静力学公理1、力的平行四边形法则:作用在物体上同一点的两个力,可以合成为仍作用于改点的一个合力,合力的大小和方向由这两个力为边构成的平行四边形的对角线矢量确定。
2、二力平衡条件:作用在同一刚体上的两个力使刚体保持平衡的必要和充分条件是:这两个力的大小相等、方向相反,并且作用在同一直线上。
3、加减平衡力系原理:作用于刚体的任何一个力系中,加上或减去任意一个平衡力系,并不改变原来力系对刚体的作用。
(1)力的可传性原理:作用在刚体上某点的力可沿其作用线移动到该刚体内的任意一点,而不改变该力对刚体的作用。
(2)三力平衡汇交定理:作用于刚体上三个相互平衡的力,若其中两个力的作用线汇于一点,则此三个力必在同一平面内,且第三个力的作用线通过汇交点。
4、作用与反作用定律:两个物体间相互作用的力,即作用力和反作用力,总是大小相等,方向相反,作用线重合,并分别作用在两个物体上。
5、刚化原理:变形体在某一力系作用下处于平衡状态时,如假想将其刚化为刚体,则其平衡状态保持不变。
三、约束和约束反力1、柔索约束:柔索只能承受拉力,只能阻碍物体沿着柔索伸长的方向运动,故约束反力通过柔索与物体的连接点,方位沿柔索本身,指向背离物体。
2、光滑面约束:约束反力通过接触点,沿接触面在接触点的公法线,并指向物体,即约束反力为压力。
3、光滑圆柱铰链约束:①圆柱、②固定铰链、③向心轴承:通过圆孔中心或轴心,方向不定的力,可正交分解为两个方向、大小不定的力;④辊轴支座:垂直于支撑面,通过圆孔中心,方向不定。
4、链杆约束(二力杆):工程中将仅在两端通过光滑铰链与其他物体连接,中间又不受力作用的直杆或曲杆称为连杆或二力杆,当连杆仅受两铰链的约束力作用而处于平衡时,这两个约束反力必定大小相等、方向相反、沿着两端铰链中心的连线作用,具体指向待定。



《工程力学(一)》串讲讲义】课程介绍一、课程的设置、性质及特点《工程力学(一)》课程,是全国高等教育自学考试机械等专业必考的一门专业课,要求掌握各种基本概念、基本理论、基本方法,包括主要的各种公式。
在考试中出现的考题不难,但基本概念涉及比较广泛,学员在学习的过程中要熟练掌握各章的基本概念、公式、例题。
本课程的性质及特点:1.一门专业基础课,且部分专科、本科专业都共同学习本课程;2.工程力学(一)课程依据《理论力学》、《材料力学》基本内容而编写,全面介绍静力学、运动学、动力学以及材料力学。
按重要性以及出题分值分布,这几部分的重要性排序依次是:材料力学、静力学、运动学、动力学。
二、教材的选用工程力学(一)课程所选用教材是全国高等教育自学考试指定教材(机械类专业),该书由蔡怀崇、张克猛主编,机械工业出版社出版(2008年版)。
三、章节体系依据《理论力学》、《材料力学》基本体系进行,依次是第1篇理论力学第1章静力学的基本概念和公理受力图第2章平面汇交力系第3章力矩平面力偶系第4章平面任意力系第5章空间力系重心第6章点的运动第7章刚体基本运动第8章质点动力学基础第9章刚体动力学基础第10章动能定理第2篇材料力学第11章材料力学的基本概念第12章轴向拉伸与压缩第13章剪切第14章扭转第15章弯曲内力第16章弯曲应力第17章弯曲变形第18章组合变形第19章压杆的稳定性第20章动载荷第21章交变应力●静力学公理和物体受力分析静力学公理:二力平衡公理:作用在刚体上的二力使刚体平衡的充要条件是:大小相等、方向相反、作用在一条直线上。
应用此公理,可进行简单的受力分析。
加减平衡力系公理:在作用于刚体的已知力系中加上或减去任何平衡力系,并不改变原力系对刚体的效应。
力的平行四边形法则:作用于物体上某一点的两力,可以合成为一个合力,合力亦作用于该点上,合力的大小和方向可由这两个力为邻边所构成的平行四边形的对角线确定。
力的可传性原理:作用于刚体上的力可沿其作用线移至同一刚体内任意一点,并不改变其对于刚体的效应。





第四章 空间力系作用在物体上各力的作用线不在同一平面内,称该力系为空间力系。
按各力的作用在空间的位置关系,空间力系可分为空间汇交力系、空间平行力系和空间任意力系。
前几章介绍的各种力系都是空间力系的特例。
第一节 力的投影与分解一、力在空间直角坐标轴上的投影已知力F 与x 轴如图4-1(a)所示,过力F 的两端点A 、B 分别作垂直于x 轴的平面M 及N ,与x 轴交于a 、b ,则线段ab 冠以正号或负号称为力F 在x 轴上的投影,即F x =±ab符号规定:若从a 到b 的方向与x 轴的正向一致取正号,反之取负号。
已知力F 与平面Q ,如图4-1(b)所示。
过力的两端点A 、B 分别作平面Q 的垂直线AA ′、BB ′,则矢量B A ''称为力F 在平面Q 上的投影。
应注意的是力在平面上的投影是矢量,而力在轴上的投影是代数量。
(a) (b)图4- 1图4-2现在讨论力F 在空间直角坐标系Oxy 中的情况。
如图4-2(a)所示,过力F 的端点A 、B 分别作x 、y 、z 三轴的垂直平面,则由力在轴上的投影的定义知,OA 、OB 、O C 就是力F 在x 、y 、z 轴上的投影。
设力F 与x 、y 、z 所夹的角分别是α、β、γ,则力F 在空间直角坐标轴上的投影为:⎪⎭⎪⎬⎫±=±=±=γβαcos cos cos F F F F F F z y x (4-1) 用这种方法计算力在轴上的投影的方法称为直接投影法。
一般情况下,不易全部找到力与三个轴的夹角,设已知力F 与z 轴夹角为γ ,可先将力投影到坐标平面Oxy 上,然后再投影到坐标轴x 、y 上,如图4-2(b )所示。
设力F 在Oxy 平面上的投影为F xy 与x 轴间的夹角为θ,则⎪⎭⎪⎬⎫±=±=±=γθγθγcos sin sin cos sin F F F F F F z y x (4-2) 用这种方法计算力在轴上的投影称为二次投影法。

第一章静力学基础第一节静力学的基本概念1、静力学是研究物体在力系作用下平衡规律的科学。
2、力是物体之间的相互机械作用,这种作用使物体的机械运动状态发生变化,同时使物体的形状或尺寸发生改变。
前者称为力的运动效应或外效应,后者称为力的变形效应或内效应。
3、力对物体作用的效应,取决于力的大小、方向(包括方位和指向)和作用点,这三个因素称为力的三要素。
4、力是矢量。
5、力系:作用在物体上的若干个力总称为力系。
6、等效力系:如果作用于物体上的一个力系可用另一个力系来代替,而不改变原力系对物体作用的外效应,则这两个力系称为等效力系或互等力系。
7、刚体就是指在受力情况下保持其几何形状和尺寸不变的物体,亦即受力后任意两点之间的距离保持不变的物体。
8、平衡:工程上一般是指物体相对与地面保持静止或做匀速直线运动的状态。
9、要使物体处于平衡状态,作用于物体上的力系必须满足一定的条件,这些条件称为力系的平衡条件;作用于物体上正好使之平衡的力系则称为平衡力系。
第二节静力学公理1、二力平衡公理:作用于同一刚体上的两个力,使刚体处于平衡状态的必要与充分条件是:这两个力大小相等,方向相反,且作用于同一条直线上(简称等值、反向、共线)。
2、对于刚体来说,这个条件既是必要的又是充分的,但对于变形体,这个条件是不充分的。
3、加减平衡力系公理:在作用于刚体的力系中,加上或减去任意平衡力系,并不改变原力系对刚体的效应。
4、力的可传性原理:作用于刚体上的力,可沿其作用线移动至该刚体上的任意点而不改变它对刚体的作用效应。
5、力的平行四边形法则:作用于物体上同一点的两个力,可以合成为一个合力,合理也作用在该点上,合力的大小和方向则由以这两个分力为邻边所构成的平行四边形的对角线来表示。
6、这种合成力的方法叫矢量加法。
7、作用与反作用定律:两物体间相互作用的力,总是大小相等,方向相反,且沿同一直线。
8、刚化原理:变形体在已知力系作用下处于平衡,如设想将此变形体刚化为刚体,则其平衡状态不会改变。
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P N θ==+=∑故:161.2R F N==1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故:3R F KN== 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑ sin 300ACAB FF -=0Y =∑ cos300ACFW -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700ACAB FF -=0Y =∑ sin 700ABFW -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑ cos 60cos300ACAB FF -=0Y =∑ sin 30sin 600ABAC FF W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑ sin 30sin 300ABAC FF -=0Y =∑ cos30cos300ABAC FF W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑cos 450RA F P -=15.8RA F KN∴=由Y =∑sin 450RA RB F F P +-=7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑cos 45cos 450RA RB F F P --= 0Y =∑sin 45sin 450RA RB F F P -=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN= (压力) 5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑ sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x=∑cos60cos300AC ABF F W⋅--= 0Y=∑sin30sin600AB ACF F W+-=联立上二式,解得:7.32ABF KN=-(受压)27.3ACF KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D,B点分别列平衡方程(1)取D点,列平衡方程由x=∑sin cos0DBT Wαα-=DBT Wctgα∴==(2)取B点列平衡方程:由Y=∑sin cos0BDT Tαα'-=230BDT T ctg Wctg KNαα'∴===2-10解:取B为研究对象:由0Y =∑ sin 0BC F P α-= sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CE F F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑ cos 75cos 750ABAD FF P +-=联立后可得:2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑ sin sin 300RAFP α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q =联立方程后解得:RD F =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑ sin 450RBRA FF P --=且RE REF F '=联立上面各式得:RA F =2RB F Q P=+(3)取BCE 部分。
!"#!$%&$'(')*+&,-./&$01$21(3$&)%)$%3%31基于智慧职教云平台线上教学课程建设与实践探索(((以+工程力学,课程为例马辉4王媛4杨晶六安职业技术学院汽车与机电工程学院!安徽六安!"@D#C E摘4要!+工程力学,是机械类等相关专业重要的职业技术基础课程!它与工程技术联系极为紧密!重点在于解决工程实际问题!具有理论性*基础性和应用性等特点"面对+互联网X教育,快速发展的新时代!传统的教学模式现已不能完全满足教师教学和学生学习的现实需求"本课程线上教学充分合理利用信息化技术!重点从课程建设目标任务*线上教学资源建设*教学过程实施及考核评价等三个方面介绍了基于智慧职教平台的线上教学的课程建设"通过教学实践探索开启了+云平台X 直播,的线上教学新模式!实现了课程建设的目标任务!取得了很好的教学效果!能为其他课程线上教学的开展*建设和实践提供有益的参考和借鉴作用"关键词!智慧职教平台#线上教学#工程力学#课程建设44随着计算机技术"通信技术和各种移动终端的飞速发展升级及普及#物联网的时代正向我们走来#,互联网X-被广泛关注&国家出台一系列相关政策以促进,互联网X教育-的快速发展#使其更好地服务社会&互联网和各类网络教学平台也为教学改革提供了全新的载体#教师的教和学生的学都围绕其开展&$$%传统的教学模式已不能完全满足教师教学和学生学习的现实需求#如何能够更好地促进基于互联网的,平台X课程-改革建设#开展实施线上教学指引学生进行有效的学习成为一种全新的课题&,工程力学-在我校机械类和建筑类专业群中开设#是必修的职业技术基础课程之一#主要研究分析物体的受力情况"机械运动的一般规律及工程构件的承载能力'具有足够的"强度和满足一定稳定性要求(&$)%本课程与工程技术联系极为紧密#重点在于解决工程实际问题#具有理论性"逻辑性"系统性和应用性较强的特点#为进一步学习其他专业课程提供必须的力学知识和工程分析与计算能力#在专业学习中起到桥梁和纽带的作用$(%& #课程建设目标任务面对,师生时空隔离和课时相对不足的现状#高职学生基础差异大"学习主动性不足"积极性不高的学情#加之工程力学课程公式相对较多"理论性又较强-等情况#教学团队提出了,基于智慧职教平台4工程力学2课程建设与直播相结合-的线上教学改革思路&在,互联网X-的时代背景下#充分合理利用信息化技术手段#如智慧职教平台"l l"钉钉"微信"仿真软件等平台#积极探索与实践,云平台X直播-方式线上教学改革&使得线上教学既具有传统课堂教学师生间情感沟通的温度#又能够解决传统教学模式对教学时间"空间的限制#满足学生个性化学习需求&最终达成,以学生主动参与#老师积极讲解引导的平台自主学习与在线课堂直播授课相结合的互动式信息化教学新模式及校内"外优质特色教学资源共建共享共用-的课程建设目标&从而推动,工程力学-教学方法改革#不断创新优化教学模式#进一步提升课程教学质量&"线上教学资源建设,智慧职教-是一个整合国家,职业教育专业教学资源库-项目建设成果#面向全社会的职业教育数字教学资源共享平台和在线教学服务平台#由高等教育出版社负责建设和运营#具有网页版和手机端两种方式#方便师生登录使用&$3%建设课程教学资源是能否顺利进行线上教学的先决条件#,工程力学-线上教学资源建设主要依托我校的智慧职教平台进行&首先基于智慧职教平台功能设立专属课程#主要进行课程名称"课程简介"教学团队"创建班级"导入学生"教材信息"课程设计"题库作业等栏目建设&其次#在之前,工程力学-学习领域课程教学改革验收合格的基础上#再次修订了课程标准#优化学习情境#分解设计学习任务#拆解知识'技能(重难点#建设线上教学资源&,工程力学-课程设计如表$所示&根据课程改革及建设计划#课题组又重新优化修改课件"丰富题库资源"编写学习任务书和制作创新型微课#其中创新型微课涉及每个学习情境#学生可反复观看#帮助对重要知识'技能(点的理解掌握&,工程力学-课程各类资源建设数量如表)所示&最后#智慧职教平台本身自带资源库包含有大量优质的教学资源及服务线上教学功能#也便于教师整合平台资源库资源和自建资源#快速高效组建自己的专属课程#顺利实施线上教学&除此之外#教师还可以分享更多的学习资料"电子书等资源给学生#满足学生在无任何教学参考资料情况下的学习需求#进一步丰富学生学习内容&表$+工程力学,课程设计一览情境名称学习任务工程力学导学工程力学导论学习情境一!刚体静力分析任务一!静力学基本概念认知任务二!静力学基本公理认知与实践任务三!刚体静力学分析与受力图绘制CF:科技风;<;=年;月电子信息44续表情境名称学习任务学习情境二!平面力系任务一!应用平面汇交力系的平衡方程解决工程实际问题任务二!应用平任意力系的平衡方程解决工程实际问题任务三!应用平面力偶系的平衡条件解决工程实际问题学习情境三!空间力系及重心任务一!空间力系任务二!力对轴之矩学习情境四!工程构件的基本变形与强度计算任务一!应用轴向拉压强度条件解决工程中拉压杆的设计问题任务二!应用剪切"挤压强度条件解决工程连接件的设计问题任务三!圆轴扭转的设计计算任务四!直梁弯曲的设计计算表)+工程力学,课程资源建设情况一览资源名称单位数量课件个$R学习任务书个$(课程微课个R题库资源道1$0d<B A8及视频个$5@教学过程实施及考核评价,工程力学-教学过程的实施#技术层面主要依托学校智慧职教平台"技能微课云平台和钉钉直播平台等信息技术相融合来实施开展的#打造一个,多平台融合的空中课堂-线上教学学习环境*教学设计方面主要设置课前'任务驱动#线上自学("课中'直播互动#答疑解惑(和课后'巩固提升#拓展评价(三个闭环学习环节&课前#教师认真备课#精心设计教学过程#借助平台发布学习任务"课件"参考资料等教学文件#根据学习任务需要设置相关教学活动和学习思考#引导学生进行线上自学#完成相关课前任务要求#学生遇到疑难点时应及时反馈#便于老师调整设置直播教学内容#重点讲解*课中#教师利用云课堂和钉钉直播等开展直播教学"答疑解惑#教学过程中要注意避免教师一言堂#尽量把知识体系进行分解"碎片化#加强和学生线上沟通交流#并与签到"预习讨论"讲授"随机提问"头脑风暴"抢答"小组S a"投票"测验等教学活动有机结合起来#增加师生之间的线上互动#激发学生的学习自觉性和学习兴趣#主动参与到线上教学中从而提高直播课堂教学的温度和活力*课后#巩固提高与拓展评价#鼓励学生#完成课后作业习题#总结上传学习成果#对学生进行客观科学的评价及反馈#也可设置拓展提升模块#拓展学生学习广度和深度#进一步提高学习效果&最后#利用平台的自动统计功能#导出平台记录的学生学习和教师教学全过程数据$R%#分析学生学习情况#进行课后小结"诊改#以便于优化组织下一次教学#构建高效互动优质的空中课堂&,考核评价-是高职院校课程教学改革不可或缺的组成部分"重要的环节之一#构建科学合理的课程考核评价体系具有重要的意义&我校,工程力学-课程实行过程性"开放性"多元化的考核评价模式#可以对学生进行全面"客观"量化的全过程性考核&在教学实施过程中#学生浏览课件"观看视频"互动答题"题库作业完成情况"学习任务书填写情况和期末考试等教学环节均设置对应的权重和分值&利用智慧职教云"钉钉等平台的数据记录统计功能#老师能够随时了解学生的线上学习情况#学生也可以实时掌握自己的学习进度&最后学生课程学习总体评价通过智慧职教平台设置考核权重后生成统计分和最终分&合理可视动态的课程考核评价#能够激发学习者学习的潜能和自觉性#也有助于老师改进教学#提升教学质量&A结语依托互联网通过基于智慧职教云平台对,工程力学-进行线上课程建设与教学实践探索#经过第一轮教学改革的实施开启了,云平台X直播-的线上教学新模式&最终实现了课程的建设目标任务#形成了课前'线上学习("课中'直播讲解(和课后'线上学习(三个闭环的教学学习环节#促进老师和学生能够进行真诚沟通"良好交流和有效互动*提高了学生学习兴趣"学习自觉性和教学活动参与度#养成了自主自立好的学习习惯#也有利于学生自学能力的培养和提升&同时#教师综合素养显著增强#教育教学和信息化教学能力水平也得到了很大提高#进一步提升课程教学质量&面对互联网教育快速发展的新时代#如何更好地依托互联网开展,工程力学-的,教-与,学-#促进信息技术与教育教学的应用与深度融合#仍有许多工作需要做#也将在今后的混合式教学改革中进行不断探索和实践&参考文献%$&刘炜!张林&大学英语线上教学的学情分析与学习评价%[&&湖北开放职业学院学报!)%)%'0($$R32$RR!$R5& %)&张定华&工程力学%\&&北京$高等教育出版社!)%$3& %(&郭空明!章云!徐亚兰&对高校工程力学课程的多方位思考%[&&教育教学论坛!)%$0'(1($$'R2$'0&%3&陈梅!刘江越!李自臣&基于+智慧职教云,的混合式教学探索%[&&黑龙江科学!)%$''$($)R2)1&%R&刘超&基于云课堂e S S的高职课程的教学过程探索)))以-飞机构造基础.课程为例%[&&科技创新导报!)%$5'3($30235&基金项目 安徽省高等学校省级质量工程重大线上教学改革研究项目)))+2云课堂X直播0线上教学改革创新与实践)))以-工程力学.课程为例,')%)%o:P A+C((1(作者简介 马辉'$'5))4(!男!安徽泗县人!硕士!讲师!研究方向$机械加工与制造#王媛'$'51)4(!女!安徽六安人!硕士!讲师!研究方向$机械加工与制造#杨晶'$'50)4(!男!安徽合肥人!硕士!讲师!研究方向$机械加工与制造"$F电子信息科技风;<;=年;月。
工程力学4.1力在空间坐标轴上的投影4.2力对轴的矩·合力矩定理4.3 空间任意力系的平衡方程4.4 平行力系的中心物体的重心工程中常常存在着很多各力的作用线不在同一平面内的力系,即空间力系,空间力系是最一般的力系。
(a)图为空间汇交力系;(b)图为空间任意力系;在(b)图中去了风力即为空间平行力系。
迎面风力侧面风力b4.1 力在空间坐标轴上的投影4.1.1力在空间的表示:力的三要素:大小、方向、作用点(线)大小:作用点:在物体的哪点就是哪点方向:①由α、β、g 三个方向角确定②由仰角θ与俯角ϕ来确定。
F F=4.1 力在空间坐标轴上的投影4.1.1力在空间的表示:1、一次投影法(直接投影法)由图可知:cos ,cos ,cos x y z F X F F Y F F Z F αβg==⋅==⋅==⋅4.1.2力在空间坐标轴上的投影2、二次投影法(间接投影法)当力与各轴正向夹角不易确定时,可先将投影到xy 面上,然后再投影到x 、y 轴上,即Fsin cos cos cos cos x xy F X F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅sin sin sin cos sin y xy F Y F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅cos sin z F Z F F g θ==⋅=⋅ 4.2 力对轴的矩⋅合力矩定理一、力对轴的矩的概念与计算定义:()()2''z O xy xy m F m F F d OA B ==±⋅=∆的面积由于力和都不能使门转动,所以得出力与轴平行或相交时,力对轴之矩为零。
亦即力与轴共面时,力对轴之矩为零。
y F z F 力对轴的矩是力使刚体绕该轴转动效应的度量,是代数量,其大小等于在垂直于转轴的平面内的分量的大小和它与转轴间垂直距离的乘积,其正负号按右手规则确定,即大拇指方向与轴的正向一致的为正,反之为负。
4.2.2合力矩定理与平面力系情况类同,空间力系的合力矩定理为:12()()()()()z z z z n z i m R m F m F m F m F =+++=∑即:空间力系的合力对某一轴的矩,等于力系中所有各分力对同一轴的矩的代数和。
sin 45cos 45cos 45sin 60cos 45cos 60z xy x y P P P P P P P P =⋅︒=⋅︒=-︒⋅︒=⋅︒⋅︒解:例4-1 已知:P =2000N,C 点在Oxy 平面内。
求:力对三个坐标轴的矩。
P()()()()6(5)06cos 45sin 605cos 45cos 6038.2(N m)x y z z z z z x y m P m P m P m P P P P P =++=⨯+-⨯+=︒︒-︒︒=⋅()()()()0066sin 4584.8(N m)x y z x x x x zm P m P m P m P P P =++=++=︒=⋅()()()()0055sin 4570.7(N m)x y z y y y y zm P m P m P m P P P =++=++=︒=⋅4.2.3力对轴之矩的解析表达式在最一般的情况下,位于空间的力对于三个坐标轴都可以产生力矩。
由合力矩定理可以推导出力对轴之矩的解析表达式:()()()x z y y x z z y x M F F y F z M F F z F xM F F x F y⎧=-⎪⎪=-⎨⎪=-⎪⎩式中F x 、F y 、F z 是力在坐标轴上的投影,x 、y 、z 是力作用点的坐标。
建立空间任意力系平衡方程的方法与平面力系的方法相同,都是采取力系向一点简化的方法。
只是对于空间力系推导平衡条件的过程比较复杂。
这里只用比较直观的方法得出空间任意力系平衡方程。
4.3空间任意力系的平衡方程123,,nF F F F 设作用在刚体上有空间任意力系4.3.1空间任意力系平衡方程的建立如果该物体平衡,则必须要使该物体不能沿x 、y 、z 三轴移动,也不能绕x 、y 、z 三轴转动。
即满足:0, ()00, ()00, ()0x x y y z z F m F F m F F m F ======∑∑∑∑∑∑空间任意力系的平衡方程空间任意力系平衡的充要条件是:各力在三个坐标轴上的投影的代数和及各力对此三个轴力矩的代数和都必须分别等于零。
共六个独立方程,只能求解独立的六个未知数。
对于空间汇交力系:(设各力汇交于原点)则()0()0()0x i y i z i m F m F m F ≡≡≡∑∑∑成为恒等式故空间汇交力系的平衡方程为:x y z F F F ===∑∑∑4.3.2空间汇交力系的平衡方程对于空间平行于z 轴的平行力系:则()000zi x ym F F F≡≡≡∑∑∑成为恒等式Oxyz故空间平行于z 轴的平行力系的平衡方程为:0()0()0z x i yFm F mF ===∑∑∑3F 2F 1F nF 4.3.3空间平行力系的平衡方程4.3.4空间任意力系的平衡方程平面解法及应用当空间任意力系平衡时,它在任意平面上的投影所组成的平面任意力系也是平衡的。
因而在工程中,常将空间力系投影到三个坐标平面上,画出构件受力图的主视、俯视和侧视等三视图,分别列出它们的平衡方程,同样可解出所求的未知量。
这种将空间问题转化为平面问题的研究方法,称为空间问题的平面解法。
这种方法特别适用于受力较多的轴类构件。
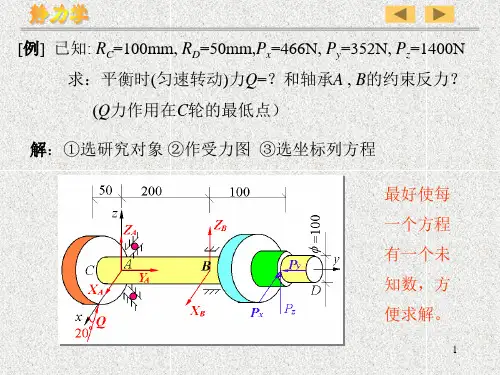
例4-2 已知:R C =100mm, R D =50mm,P x =466N, P y =352N, P z =1400N求:平衡时(匀速转动)力Q =?和轴承A , B 的约束反力?最好使每一个方程有一个未知数,方便求解。
(Q 力作用在C 轮的最低点)解:①选研究对象②作受力图③选坐标列方程0;0,352(N)0;501000,746(N)y A y A y yz x F Y P Y P mP Q Q =-====-⨯+⨯=∴=∑∑由00; 3005020050 cos 200, 437(N)0; cos 200, 729(N)0; 20030050 sin 200, 2040(N)0; sin 200, 385(N)AAz x y B B yA B x A x B z B zA B z A m P P X Q X F X X P Q X m Z P Q Z FZ Z P Q Z =---=∴==+--=∴==+-=∴=-=+++=∴=∑∑∑∑方法(二) :将空间力系投影到三个坐标平面内,转化为平面力系平衡问题来求解,请自己试着求解。
本节小结:1.力在空间直角坐标轴上投影的计算方法:直接投影法、间接投影法。
2.力对轴之矩是力使物体绕某轴转动效果的度量,其计算方法有:根据定义计算、应用合力矩定理计算。
3.空间力系平衡问题的解法:直接利用空间力系平衡方程求解、把空间力系的平衡问题转化为平面力系的平衡问题求解。
4.4平行力系的中心物体的重心4.4.1空间平行力系的中心、物体的重心空间平行力系,当它有合力时,合力的作用点C就是此空间平行力系的中心。
而物体重心问题可以看成是空间平行力系中心的一个特例。
1、平行力系的中心由合力矩定理可得:iiC i i C i iC F xx R F y y R F z z R===∑∑∑如果把物体的重力都看成为平行力系,则求重心问题就是求平行力系的中心问题。
由合力矩定理:C i i C ii P x P x P y P y ⋅=∆⋅=∆∑∑2、重心坐标公式根据平行力系中心位置与各平行力系的方向无关的性质,将力线转成与y 轴平行,再应用合力矩定理对x 轴取矩得:, i iC i i C PzPz Pz z P∆=∆∴=∑∑综合上述得重心坐标公式为:,,i iiii iC C C PxP yPzx y z PPP∆∆∆===∑∑∑若以△P i = △m i g , P =Mg 代入上式可得质心公式:,,iiiiiiCCCm x m y m z x y z MMM∆∆∆===∑∑∑4.4.2物体的质心公式和形心公式设ρi 表示第i 个小部分每单位体积的质量,⊿V i 第i 个小体积,则i i im V ρ∆=∆代入上式则可得:又若该物体还是均质体,则其形心(几何中心)坐标为:,,iiiiiiCCCV x V y V z x y z VVV∆∆∆===∑∑∑ii iC iiii iC iiiiiCiiV x x V V y y V V z z Vρρρρρρ∆=∆∆=∆∆=∆∑∑∑∑∑∑同理,可写出均质板,均质杆的形心(几何中心)坐标分别为::,,iiiiiiC C C A xA yA zx y z AAA∆∆∆===∑∑∑平板:,,iiiiiiCCCl x l y l z x y z lll∆∆∆===∑∑∑细杆iCiC iC Px x P Py y P Pz z P∆=∆=∆=∑∑∑物体分割的越多,每一小部分体积越小,求得的重心位置就越准确。
在极限情况下,(n-),常用积分法求物体的重心位置。
∞4.4.3物体的重心的精确公式设g i 表示第i 个小部分每单位体积的重量,⊿V i 第i 个小体积,则,,VVVCCCx dV y dV z dV x y z PPPg g g ===⎰⎰⎰i i i P V g ∆=∆代入重心坐标公式并取极限,可得:上式为重心C 坐标的精确公式。
VP dVg =⎰式中,对于均质物体,g =恒量,上式成为:,,VVVC C C x dV y dV z dV x y z VVV⋅⋅⋅===⎰⎰⎰同理对于薄平面和细长杆均可写出相应的公式:,,AAAC C C x dA y dA z dA x y z AAA⋅⋅⋅===⎰⎰⎰,,LLLC C C x dL y dL z dL x y z LLL⋅⋅⋅===⎰⎰⎰解:由于对称关系,该圆弧重心必在Ox 轴,即y C =0。
取微段dL R d θ=⋅2cos 2LC x dL x LRd Rααθθα-⋅∴=⋅⋅⋅=⎰⎰sin C R x αα=下面用积分法求物体的重心实例:例4-3 求半径为R ,顶角为2α的均质圆弧的重心。
Ocos x R θ=⋅解:取坐标系O xy 如图所示,将L 形界面分割成I 、II 两部分。
【例4-4】求如图所示L 形界面的形心位置,图中单位尺寸为cm 。
2211122222103cm 30cm 1.5cm 5cm 53cm 15cm 5.5cm 1.5cmA x y A x y ∆=⨯===∆=⨯===,,,,1122C 121122C 1230 1.515 5.52.83cm301530515 1.53.83cm3015iiiix AA x A x x AA A y AA y A y y AA A ∆∆+∆⨯+⨯====∆+∆+∆∆+∆⨯+⨯====∆+∆+∑∑如果物体被切去一部分,则其重心和形心仍可用组合法的公式去求,只是切去部分的形体要代负值。