当前位置：文档之家 › 郝桐生--第6章空间力系和重心(执行)

郝桐生--第6章空间力系和重心(执行)

  • 格式：pdf
  • 大小：1.03 MB
  • 文档页数：45

下载文档原格式

  / 45

合集下载

空间力系和重心.ppt

空间力系和重心.ppt


有各力在任意相互垂直的三个坐标轴的每一个轴上的
投影的代数和等于零，以及力系对于这三个坐标轴的
矩的代数和分别等于零。
Fx 0 Fy 0
Fz 0
Mx F 0 My F 0 Mz F 0
§5.4 空间平行力系的中心和物体的重心
一、空间平行力系的中心
若空间力系各合力的作用线相互平行称为空间平行 力系。若力系为一合力，合力的作用点，即是平行力系 的中心。
式中，Rx、Ry、Rz表示合力在各轴上的投影。
已知各力在坐标轴上的投影，则合力的大小和方 向可按下式求得
R Rx2 Ry2 Rz2
2
2
2
Fx Fy Fz
cos Fx / R cos Fy / R
cos Fz / R
式中，α、β、γ分别表示合力与x、y、z轴正向 的夹角。
二、重心的概念
重力的作用点即是空间平行力系的中心，称为物体 的重心。
三、重心和形心的坐标公式
物体重心C的坐标公式为
xC
x i .Wi W
yC
y i .Wi W
zC
z i.Wi W
四、求重心的方法
几种常用的方法：
1.对称法 2.积分法 3.组合法
（按照右手螺旋法则决定之）
空间力对轴的矩等于零的条件
1、力通过轴线
FLeabharlann Fz2、力与轴线平行
Fy Fx
二、合力矩定理
力对轴的矩的解析表示式为
Mx F Fz.yA Fy.zA My F Fx.zA Fz.xA
Mz F Fy.xA Fx.yA
§ 5.3 空间力系的平衡方程及应用
空间任意力系平衡的必要和充分条件是:力系中所
可求出力F 的大小和方
力偶矩的大小

力偶矩的大小

第6章 空间力系和重心
※ 空间任意力系的平衡方程 ※ 空间约束和约束反力 ※ 空间力系平衡问题举例 ※ 重心 ※ 结论与讨论
§6-1 空间汇交力系
1. 空间力的投影和分解
z
直接投影法
X F cos
Y

F
cos


Z F cos
F

O
y
x
F=Fx+Fy+Fz=Xi+Yj+Zk
M z (F ) Fxb Fy a
Fb cos sin Fa cos cos
MO(F) Mx(F) i M y(F) j Mz(F)k
Fbsin i Fa sin j (Fb cos sin Fa cos cos ) k
§6-3 空间力偶

2. 空间汇交力系的合成与平衡条件(解析法)
空间汇交力系的合力等于各分力的矢量和，合力的作用线
通过汇交点。
n
FR F1 F2 Fn Fi i 1 X ii Yi j Zik
FR
( X )2 (Y )2 ( Z)2
MO (F )
MO(F) =Fh=2△OAB
r xi yj zk
z
F Xi Yj Zk
i jk
MO(F)
MO(F) r F x y z
XYZ
( yZ zY )i (zX xZ) j (xY yX )k O
r
h
BF
A(x,y,z) y
x
MO (F )
二次投影法
z
F

O
y
Fxy
建筑力学课件 第六章 空间力系的平衡

建筑力学课件 第六章 空间力系的平衡

Fz= Fz×sin30° =200×sin30°=100N
6.2 空间一般力系
因分力Fxy与x、y轴都相 交，它对x、y轴之矩都
为零，因此
Mx（F） =Mx（Fxy）+Mx（Fz）
= Mx（Fz） =100×2=200N·m
6.2 空间一般力系
My（F） =My（Fxy）+My（Fz） = My（Fz） =－100×2 =－200N·m
6.1 空间汇交力系
根据平衡条件，建 立平衡方程并求解
6.1 空间汇交力系
F2
1 2
F3
1 2
0力对轴之矩 在生活和生产实际中，经常会遇到物体绕定轴转 动的问题。门的开启和关闭即是最常见的例子。 如图所示的门，设力F作用于门上的A点，为了 研究力F使门绕z轴转动的 效应，可将它分解为一个 与转轴z平行的分力Fz和 一个通过A点且垂直于z 轴的平面上的分力Fxy。
6.1 空间汇交力系
如果力F与三条坐标轴的夹角分别为α、β、γ，根 据力在坐标轴上投影的定义,显然力在x、y、z坐 标轴上的投影Fx、Fy、Fz 的大小分别为
6.1 空间汇交力系
上面式中cosα、cosβ、cosγ称为力 矢量F的方向余弦。所以力在某 轴上的投影等于力矢量与该轴 正方向之间的夹角的余弦与力 的大小的乘积。
6.1 空间汇交力系
二、空间汇交力系平衡
根据平面汇交力系平衡的解析条件，同理 可得，空间汇交力系平衡的充分与必要条 件是合力等于零，或者空间汇交力系的各 分力在空间直角坐标系三个坐标轴上的投 影的代数和都等于零。其表达式为
6.1 空间汇交力系
例6-1 如图所示， 重为W的物体用 三根连杆支承， 求每根连杆所受 的力。
即平 F矢投有面量影xFo到xyy，上z轴的和投xy影坐F标xy与平x面轴上得，夹分角别得，到则投可影先F将z 力和 FFzxy＝＝FFcsoins
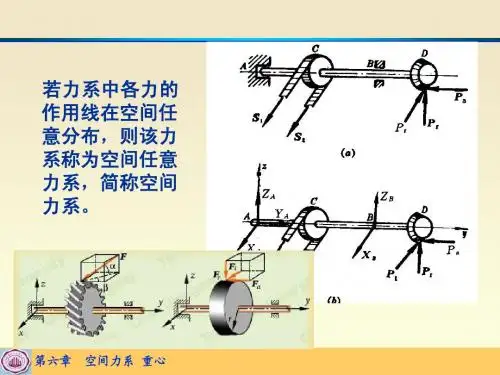
lllx第六章静力学空间力系重心-精选文档

lllx第六章静力学空间力系重心-精选文档

z
F

B
b C c y
D
力对轴之矩 a A M ( F ) yF zF x z y x b F sin a 0 F sin b M ( F ) zF xF y x z


a ( F cos ) ( c ) F sin Fc sin Fa cos
Northeastern University
第六章 空间力系
重心
1
工程中的空间力系问题
2
力在空间坐标轴上的投影 力对轴之矩
3
4 5
空间力系的平衡方程
重心
PAG 1
Northeastern University
§6-1
工程中的空间力系问题
空间力系:力系各分力的作用线分布在空间,而且不能 简化到某一平面的力系。
y
F3
' ' F , i ) F F 方向 cos( R ix R
PAG 9
Northeastern University
§6-4
空间力系的平衡方程
MO
一、空间一般力系向一点的简化
空间力偶系的合力偶之矩 — 主矩
z M1
B
M M o O i C M i M j M k Ox Oy Oz x M3 [ M ( F )] i [ M ( F )] j [ M ( F )] k x i y i z i ( y F z F ) i ( z F x F ) j ( x F y F ) k i iz i iy i ix i iz i iy i ix
一、空间的力对轴之矩 — 代数量
静力学 第6章空间力系及重心

静力学 第6章空间力系及重心

3
,
y2
4r
3
b
,
y3
0
yC
Ai yi A
yC
A1 y1 A2 y2 A3 y3 A1 A2 A3
40.01mm
3)． 实验法 （1） 悬挂法
（2） 称重法
P xC F1 l
xC
F1 P
l
xC
F1 P
l
整理后，得
zC
r
F2 F1 P
1 H
l2 H2
作业
•6-2,6-3,6-5
MO 0
FR MO 成 角
FR 0 MO 0
ห้องสมุดไป่ตู้
力螺旋 平衡
力螺旋中心线通过简化中心
简化中心到力螺旋中心轴距离
d MO sin / FR
与简化中心的位置无关
2. 空间一般力系的平衡条件
空间任意力系平衡的充分必要条件：
空间任意力系的平衡方程
3. 特殊力系的平衡条件
⑴.空间汇交力系的平衡方程 力多变形法则对空间汇交力系仍然适用
力螺旋力螺旋中心线通过简化中心主矩最后结果说明合力合力作用线过简化中心合力偶平衡与简化中心的位置无关与简化中心的位置无关空间任意力系的简化结果简化中心到力螺旋中心轴距离sin空间一般力系的平衡条件空间任意力系的平衡方程
第六章 空间力系与重心
§6.1 工程中的空间力系问题 §6.2 力在空间坐标轴上的投影 §6.3 力对轴之矩 §6.4 空间力系的平衡方程 §6.5—物体的重心坐标公式与求法
§6.3 力对轴之矩 ( moment of a force about an axis )
M z F MO Fxy Fxy h
F
力与轴相交或与轴平行（力
空间力系 重心

空间力系 重心


（2）方向:转动方向
（3）作用面：力矩作用面.
MO ( F ) r F
第六章 空间力系 重心
§6–3 力对点的矩和力对轴的矩
力对轴的矩
M z ( F ) M O ( Fxy ) Fxy h
力与轴相交或与轴平行（力与轴在同一平面内），力 对该轴的矩为零。
重心C的矢径
Pi ri rC Pi
式中的ΔPi可以是物体中任一部分的重量，而不仅限于微元体。 对由简单形体组成的物体，可用这种方法求重心，称为分割法。
第六章 空间力系 重心
1．计算重心坐标的公式 对y轴用合力矩定理
P xC P x1 P x2 .... P xn P xi 1 2 n i
（1)实际重心偏后，飞机拉起时尾部摩擦跑道导致起火； （2)实际重心偏前，飞机冲到跑道尽头仍然拉起困难；
（3)直升机重心偏离旋翼轴心，使飞行员难以操纵飞机。
第六章 空间力系 重心
•重心：物体所受的重力是一种体积 分布力。不论物体如何放置，其重力 的合力作用线相对于物体总是通过一 个确定的点，这个点称为物体的重 心 。
如一空间力系由F1、F2、…、Fn组成，其合
力为FR，则合力FR对某轴之矩等于各分力对同
一轴之矩的代数和。
M z ( FR ) M z ( Fi )
i
第六章 空间力系 重心
§6–4 空间任意力系向一点的简化· 主矢和主矩
•简化过程：
将力系向已知点 O 简化 —— O 点称为简化中心。
R
z
Rx
第六章 空间力系 重心
活页铰
第六章
空间力系 重心
滑动轴承
第六章
第六章空间力系

第六章空间力系

Fx Fy Fz
kr Oj
ih x
A(x,y,z) y
( yFz zFy )i (zFx xFz ) j (xFy yFx )k
4.2.1 力对点的矩以矢量表示－力矩矢
力矩矢MO(F)在三个坐标轴上的投
z
影为
[M O (F )]x yFz zFy
MO(F)
[M O (F )]y zFx xFz [M O (F )]z xFy yFx
求力F在三轴上的投影和对三轴的矩。
z
解：
Fx F cos cosj
Fa a2 b2 c2
c
Fy F cos sinj
Fb a2 b2 c2
x
Fz F sin
Fc a2 b2 c2
M x (F ) M x (Fx ) M x (Fy ) M x (Fz ) Fyc
MO F'R
＝ F'R
O
O
4.4.2 空间任意力系的简化结果分析
F'R ≠ 0，MO≠0 ，同时两者既不平行，又不垂直，此时 可将MO分解为两个分力偶M"O和M'O，它们分别垂直 于F'R和平行于F'R，则M"O和F'R可用作用于点O'的力 FR来代替，最终得一通过点O '的力螺旋。
MO
F'R

O
a
FB
y b Fxy
符号规定：从z轴正向看，若力使刚体逆时针转则取正号，反之 取负。也可按右手螺旋法则确定其正负号。
由定义可知：(1)当力的作用线与轴平行或相交(共面)时，力 对轴的矩等于零。(2)当力沿作用线移动时，它对于轴的矩不变。
理论力学 第六章 空间力系.ppt

理论力学 第六章 空间力系.ppt


r = x i + y j + z k 则：
z
i x MO(F) = r F =
jk yz
B
MO(F）
F
Od y
Fx Fy Fz
rA
x
=( y·Fz - z ·Fy ) i + (z·Fx - x ·Fz ) j + (x·Fy - y ·Fx ) k
其中 [MO (F)] x = y·Fz - z ·Fy [MO (F)] z = x·Fy - y ·Fx
使-R=R')
③由反向平行力合成得：
F1与R合成得F2，作用在d点 F1'与R'合成得F2'，作用在c点
且R-F1=F2 ，R'- F1'= F2'
④在I内的力偶（F1，F1'）等效变成II内的（ F2， F2' ）
14
由此可得出，空间力偶矩是自由矢量，它有三个要素：
①力偶矩的大小= m
②力偶矩的方向——与力偶作用面法线方向相同 ③转向——遵循右手螺旋规则。 三、空间力偶系的合成与平衡 由于空间力偶系是自由矢量，只要方向不变，可移至任意 一点，故可使其滑至汇交于某点，由于是矢量，它的合成符合 矢量运算法则。
[MO (F)] y = z·Fx - x ·Fz 为力矩式在坐标轴上的投影。
19
二 力对轴的矩
z
力对物体绕轴转动效果的度量
1)定义:力对轴的矩等于此力在垂直
于矩轴的平面上的投影矢量对
于矩轴与这平面的交点的距 。
o
用FXY表示F在XY平面上的投影，
则力F对Z轴的矩为
x
mZ (F) Fxyd
各力偶矩矢在三个坐标轴的每一坐标轴上投影的代数和等于零.
工程力学第6章 空间力系重心

工程力学第6章 空间力系重心


载荷F。钢丝OA和OB所构成的
平面垂直于铅直平面Oyz，并与
该 平 面 相 交 于 OD ， 而 钢 丝 OC
则沿水平轴y。已知OD与轴z间
的 夹 角 为 β ， 又 ∠ AOD =
∠BOD = α，试求各钢丝中的
拉力。
空间汇交力系
例题4
A
D
Bz F3
F2 αα β
x
O
yC F1
解： 取O点为研究对象，受
力分析如图所示，这些力构 成了空间共点力系。
F
空间汇交力系
例题4
力F2与x轴之间 的 夹 角 为 90o － α ， 故它在该轴上的投 影为：
F2x F2 cos (90o ) F2 sin
空间汇交力系
例题4
DB z
A
F' F3
F2 αα β
x
O
yC F1
列平衡方程
Fx 0， F2 sin F3 sin 0 Fy 0,
例题3
Fx
Fz
6-4 空间力系的平衡方程
空间力系的平衡方程为：
Fx 0, mx (F ) 0 Fy 0, my (F ) 0 Fz 0, mz (F ) 0
空间汇交力系
例题4
如图所示为空气动力天平
上测定模型所受阻力用的一个
悬挂节点O，其上作用有铅直
Fz 0,
FAz FBz (F3 F4 ) cos 30 (F1 F2 ) 0
Mx 0, FAZ 0.25 m FBZ 1.25 m (F3 F4) cos 30 0.75 m 0
M y 0, (F1 F2 ) 0.4 m (F3 F4 ) 0.2 m 0 Mz 0, FAx 0.25 m FBx 1.25 m (F3 F4 )sin 30 0.75 m 0
工程力学之空间力系和重心

工程力学之空间力系和重心

工程力学4.1力在空间坐标轴上的投影4.2力对轴的矩·合力矩定理4.3 空间任意力系的平衡方程4.4 平行力系的中心物体的重心工程中常常存在着很多各力的作用线不在同一平面内的力系，即空间力系，空间力系是最一般的力系。

(a)图为空间汇交力系；(b)图为空间任意力系；在(b)图中去了风力即为空间平行力系。

迎面风力侧面风力b4.1 力在空间坐标轴上的投影4.1.1力在空间的表示：力的三要素：大小、方向、作用点(线)大小：作用点：在物体的哪点就是哪点方向：①由α、β、g 三个方向角确定②由仰角θ与俯角ϕ来确定。

F F=4.1 力在空间坐标轴上的投影4.1.1力在空间的表示：1、一次投影法（直接投影法）由图可知：cos ,cos ,cos x y z F X F F Y F F Z F αβg==⋅==⋅==⋅4.1.2力在空间坐标轴上的投影2、二次投影法（间接投影法）当力与各轴正向夹角不易确定时，可先将投影到xy 面上，然后再投影到x 、y 轴上，即Fsin cos cos cos cos x xy F X F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅sin sin sin cos sin y xy F Y F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅cos sin z F Z F F g θ==⋅=⋅ 4.2 力对轴的矩⋅合力矩定理一、力对轴的矩的概念与计算定义：()()2''z O xy xy m F m F F d OA B ==±⋅=∆的面积由于力和都不能使门转动，所以得出力与轴平行或相交时，力对轴之矩为零。

亦即力与轴共面时，力对轴之矩为零。

y F z F 力对轴的矩是力使刚体绕该轴转动效应的度量，是代数量，其大小等于在垂直于转轴的平面内的分量的大小和它与转轴间垂直距离的乘积，其正负号按右手规则确定，即大拇指方向与轴的正向一致的为正，反之为负。

4.2.2合力矩定理与平面力系情况类同，空间力系的合力矩定理为：12()()()()()z z z z n z i m R m F m F m F m F =+++=∑即：空间力系的合力对某一轴的矩，等于力系中所有各分力对同一轴的矩的代数和。

06空间力系 重心(new)

06空间力系 重心(new)


合力偶Ｍo称为力系的主矩
M ox M x F M oy M oz
空间力系的平衡方程：
y
M F M F
z
Fx 0, Fy 0, Fz 0
M x F 0, M y F 0, M z F 0



空间汇交力系的平衡方程：
Fx 0 Fy 0 Fz 0
§6-3 力对轴之矩
1、力对轴之矩概念
定义:力使物体绕某一轴转动效应的量度,称为力对该轴 之矩，是用来量度力使物体绕轴转动效应的物理量。
F对转轴z的矩：
mz F mo F2 F2 d

Fz
Fy
Fx
通常规定：从z轴 的正向看去，逆 时针方向转动的 力矩为正，顺时 针方向转动的力 矩为负。
y
xC
重心坐标式
xi Ai A y A yC i i A
o
xc
C yc
x
§6-7 物体重心的求法
1、对称性法—当研究的物体具有对称轴、对称面或对称中心的均抽物体，其
重心一定在对称轴、对称面或对称中心上。
2、分割法—将形状较复杂的物体分成具有简单几何形状的几个部分，每一部 分容易确定，然后，再根据重心坐标求出组合形体的重心（简单几何图形的重 心坐标公式可以查表）。
mx W
W1
Wn W2 z 2 zn x1 W xc x2
c
m W ,
n x i i 1
z1 z
y1 y2 X
Y xn
y
c
W . yC W1 y1 W2 y 2 Wn y n my W
m W ,
n y i i 1 n z i i 1

第六章 空间力系 重心


z
F5 O x F4 m2 y F2 F1 m1
F6 F3
M z ( R) m z ( F i ) ( a F a 2a F a ) ( a F a a F a ) 2a F a a F a a F a (0 m3) a F a m3
三、空间力系平衡的充要条件 力系中诸力在坐标轴上的投影的代数和为零，对各轴 之矩代数和为零。 四、空间一般力系的平衡方程
§ 6-3
一、力对点之矩
力对点之矩和力对轴之矩
z F
mO(F) = r×F
力矩是(定位于矩心的) 定位矢量，其方向由右 手螺旋定则确定。 设r=xi+yj+zk， F=Fxi+Fyj+Fzk，
i j y Fy k z Fz
x
O
y
mO(F) 在坐标轴上 的投影为：
[mO ( F )]x yFz zFy [mO ( F )]y zFx xFz [mO ( F )]z xFy yFx
【例6-4】不计杆件和圆盘自重，求图示结构中夹紧端 A处的约束反力。
【解】1)对结构作受力分析。
2)列平衡方程：
F iz P F A 0 m x ( F i ) Pl m Ax 0 m y ( F i ) m Ay P (l D 2) 0
m (F ) 0 m (F ) 0
x i
y i
z
O未知数 其平衡方程为： F iy 0 m z ( F i ) 0
空间平行力系是空间一般力系的特例。 即： F ix 0
y
F
iz
0
m (F ) 0
mz (F xy) mz (F x) mz (F y)

第六章 空间力系和重心


F
x
0, Fy 0, Fz 0,
例6-2
已知：物重P=10kN，CE=EB=DE；
30
0
求：杆受力及绳拉力 解：画受力图，列平衡方程
F
x
0
F1 sin 45 F2 sin 45 0
FFy0源自FA sin 30 F1 cos 45 cos 30 F2 cos 45 cos 30 0
z
0

F1 cos 45 sin 30 F2 cos 45 sin 30 FA cos 30 P 0
F1 F2 3.54kN
FA 8.66kN
例6-3 已知：P=1000N ,各杆重不计. 求：三根杆所受力. 解：各杆均为二力杆，取球铰O，画受 力图。
F F
M O ( F , F ) (rA rB ) F M
（3）只要保持力偶矩不变，力偶可在其作用面内任意移转 ，且可以同时改变力偶中力的大小与力偶臂的长短，对刚体 的作用效果不变.
=
=
=
) rBA FR rBA ( F1 F2 ) M ( FR , FR rBA F1 rBA F2 rBA F1 M ( F1 , F1)
(4)只要保持力偶矩不变，力偶可从其所在平面移至另 一与此平面平行的任一平面，对刚体的作用效果不变.
=
=
F1 F1 F2
F2 F3 F3
=
=
定位矢量 滑移矢量 自由矢量 力偶矩矢是自由矢量 力偶矩矢相等的力偶等效——空间力 偶等效定理 (5)力偶没有合力，力偶只能由力偶来平衡.
例6-4 已知：在工件四个面上同时钻5个孔，每个孔所受切削力 偶矩均为80N·m. 求：工件所受合力偶矩在 x, y, z 轴上的投影 解：把力偶用力偶 矩矢表示，平行移 到点A .

大学本科理论力学课程第6章 空间力系和重心(执行)


Fx
Fxy
Fxy cos
F
sin
F sin
cos
Fy Fxy sin F sin sin
Fz F cos
反之 F Fx2 Fy2 Fz2
cos Fx / F, cos Fy / F, cos Fz / F
这里注意力向坐标轴投影是代数量 而力向某平面投影是矢量。P103
空间力偶的等效定理：凡矩 矢相等的力偶均为等效力偶。
P108
理论力学电子教程
第六章 空间力系和重心
例 6-3 图示的三角柱刚体是正方体的一半。在其中三个侧面各自
作用着一个力偶。已知力偶（F1 ，F 1）的矩M1=20 N·m；力偶 （F2， F 2 ）的矩M2=10 N·m；力偶（F3 ，F 3）的矩M3=30 N·m 。试求合力偶矩矢M。又问使这个刚体平衡，还需要施加怎样一
若引入单位矢量，则力F沿直角 坐标轴分解的表达式为
z Fz
F
Fx
Fy
Fxy y
x
F Fx Fy Fz Fxi Fy j Fzk
理论力学电子教程
测验
(1) 判断下列桁架中的零杆; （2） 计算图示桁架中5杆的内力。
第六章 空间力系和重心
A 4 PB
a
7
53
1
E6 a
D2 C a
理论力学电子教程
理论力学电子教程
第六章 空间力系和重心
第六章 空间力系和重心
§6－1 空间力沿坐标轴的分解与投影 §6－2 空间汇交力系的合成与平衡 §6－3 空间力偶理论 §6－4 力对于点之矩与力对于轴之矩
§6－5 空间任意力系向已知点的简化·主 矢 与主矩·空间力系的合力矩定理 §6－6 空间任意力系的平衡条件与平衡方程 §6－7 平行力系的中心与重心

08_空间力系和重心II

第6章空间力系和重心(II)•空间力的分解与投影•空间汇交力系•空间力偶理论•力对点之矩与力对轴之矩•空间任意力系的简化与平衡空间平行力系，，重心•空间平行力系1、空间任意力系向已知点的简化其中其中：：i i i i F F ′=r r i o i()i o i M M F =r r r 一空间汇交力系与一空间力偶系等效代替一空间任意力系一空间汇交力系与一空间力偶系等效代替一空间任意力系。

§6-5 空间任意力系向已知点的简化·主矢与主矩·空间力系的合力矩定理1F 2F 3F 力线平移定理力线平移定理（（力矩矢量力矩矢量））R i ix iy izR i ix iy iz F F F i F j F k ′==++∑∑∑∑r r r r r r r r 称为力系称为力系（（对O 点）的主矩o i o i ()o i o i M M M F ==∑∑r r r r 称为力系的主矢空间空间（（附加附加））力偶系的合力偶矩力偶系的合力偶矩（（矢）由力对点的矩与力对轴的矩的关系由力对点的矩与力对轴的矩的关系，，有:空间汇交力系的合力空间汇交力系的合力（（作用于作用于O O 点）矢量()()()k F M j F M i F M M i z i y i x O r r r r r r r ∑∑∑++=对x x ，，y y ，，z 轴的矩轴的矩。

式中式中::，，分别表示分别表示力力()i x F M r ()i y F M r ()i z F M r i F r—有效推进力RxRx F ′r 飞机向前飞行RyRy F ′r —有效升力飞机上升Rz Rz F ′r —侧向力飞机侧移Ox OxM r —滚转力矩飞机绕飞机绕x x 轴滚转Oy Oy M r —偏航力矩飞机转弯Oz Oz M r —俯仰力矩飞机俯仰2．空间任意力系的简化结果分析（1）当时R O 0,0R O F M ′==r r 则为平衡力系则为平衡力系（（与简化中心无关与简化中心无关）。

空间力系与重心


轴上的力和力矩平衡条件。只有当这六个方程同时满足时，空间一般力
系才处于平衡状态。
04
重心位置确定方法
几何法确定重心位置
01
02
03
悬挂法
将物体悬挂于一点，通过 测量悬线的长度和方向， 利用几何关系确定重心位 置。
支撑法
将物体支撑于两点，测量 支撑点的位置和支撑力的 大小，通过几何关系求解 重心位置。
度的基础。
06
重心在工程中应用举例
建筑结构稳定性分析
重心位置与结构稳定性
案例分析
在建筑设计中，通过调整结构布局和 构件尺寸，可以改变结构的重心位置， 从而提高结构的稳定性。
以高层建筑为例，通过优化结构布局 和构件设计，降低重心高度，提高结 构的整体稳定性。
地震作用下的重心影响
地震时，建筑物受到水平地震力的作 用，重心位置的高低直接影响结构的 抗震性能。
THANKS
感谢观看
航空航天领域应用
重心与飞行器稳定性
在航空航天领域，飞行器的重心位置对其稳定性和操控性 具有重要影响。合理设计重心位置可以提高飞行器的稳定 性和操控性。
重心与燃料消耗
飞行器的重心位置不仅影响稳定性和操控性，还影响燃料 消耗。通过优化重心位置可以降低飞行器的燃料消耗。
案例分析
以飞机设计为例，通过精确计算和调整机身、机翼等部件 的质量和布局，实现重心的合理分布，提高飞机的稳定性 和经济性。
力多边形封闭
如果将各力矢量按照一定顺序首 尾相接，可以形成一个封闭的力 多边形，这也是空间汇交力系平 衡的一个必要条件。
空间平行力系平衡条件
各力在任意轴上的投影之和为零
对于空间平行力系，所有力在任意选定的轴上的投影之和必须为零，这是平衡 的一个必要条件。

《工程力学》空间力系与重心


Fz F cos
F
Fxy
F sin
Fx Fy
Fxy cos F sin cos Fxy sin F sin sin
（3-2）
反之，如果已知力F在x、y、z三个坐标轴上的投影 Fx 、Fy 、Fz
F Fx2y Fz2 Fx2 Fy2 Fz2
，也可以求出F的大小和方向。其形式为 （3-3）
FX 0, F1 sin 45 F2 sin 45 0 FY 0, FA sin 30 F1 cos45 cos30 F2 cos45 cos30 0 FZ 0, F1 cos45 sin 30 F2 cos45 sin 30 FA cos30 P 0
求解上面的三个平衡方程，得
所以
zc
Gi zi G
由以上得到重心坐标的一般公式为：
xc
Gi xi G
yc
Gi yi G
zc
Gi zi G
（3-12）
xc
mi xi M
在式（3-12）中，如以
Gi
mi g、G Mg
代入，在分子和分母中消去g，即得到公式：
yc
mi
M
yi
zc
mi zi M
设有一个空间力F，作用点A的坐标为（x，y，z）,该力在三个坐标轴上的分力大小（即该力在x，y，z轴
上的投影）分别为Fx , Fy , Fz ，则该力对三个坐标轴的矩为（证明从略）
M M
x y
(F (F
) )
yFz zFx
zFy xFz
M
z
(F
)
xFy
yFx
（3-8）
例3-3 如图3-5所示，手柄ABCD在平面内，在D点作用一个力F，该力平行于xz平面，已知F=200N， 30，AB＝ 20cm，BC＝30cm，CD＝15cm，试求F对x，y，z轴之矩。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

理论力学电子教程
第六章 空间力系和重心
§6－3 空间力偶理论
1、空间力偶的等效定理，力偶矩矢的概念
同平面内力偶等效条件：力偶矩大小相等，转向相同。
平行平面间的力偶的等效条件：作用面平行的两个力偶，若其力 偶矩大小相等，转向相同，则两力偶等效。P107
注意：分别作用在不平行平 面内的两个力偶对于刚体的 效应是不同的 空间力偶的三要素：P107 大小、力偶在作用面内的转向 和力偶作用面在空间的方位。
Fx FR
cos
FRy FR
Fy FR
y
cos
FRz FR
Fz FR
x
Fn
理论力学电子教程
第六章 空间力系和重心
平衡的必要与充分条件：该力系的合力为零。 空间汇交力系的平衡方程
FR ( Fx )2 ( Fy )2 ( Fz )2 0
Fx 0, Fy 0, Fz 0,
各力首尾连接形成封闭空间力多边形。P105
理论力学电子教程
第六章 空间力系和重心
§6－2 空间汇交力系的合成与平衡
空间汇交力系的几何法与平面汇交力系类似。
FR F1 F2 F3 Fi
各力首尾连接形成 空间力多边形，封闭边 代表合力；P104
注意合力作用线通 过汇交点。
理论力学电子教程
第六章 空间力系和重心
空间汇交力系的解析法 各分力 Fi Fixi Fiy j Fizk
力偶矩矢是一矢量。
理论力学电子教程
第六章 空间力系和重心
力偶矩矢是一矢量。 力偶的矢量方向用右手螺旋法则确定。从力偶矢末端看去，
逆时针转动为正。 空间力偶是一个自由矢量（在作用面内或平行平面可自由移转）。 P107
力对刚体来讲是滑动矢量，可沿作用线移动。
力对变形体来讲是定位矢量
空间力对点之矩是定位矢量 空间力偶的等效定理：凡矩
rOA(x,y,z) OA AB FAB(Fx,Fy ,Fz )
x
y Fy
z Fz
理论力学电子教程
第六章 空间力系和重心
２.力对轴之矩P109
理论力学电子教程
第六章 空间力系和重心
§6－1 空间力沿坐标轴的分解与投影
空间力系：各力的作用线不在同一平面内的力系。可 分为空间汇交力系，空间平行力系，空间力偶系，空间任 意力系。
其研究方法：与平面力系研究的方法相同，但由于各 力的作用线分布在空间，因此平面问题中的一些概念、理 论和方法要作推广和延伸。
3.合力偶矩矢M 的大小和方向。
M
M
2 x
M
2 y
z
M
2 z
42.7N m
M1 M3
M2
45° 45°
y
O
x
理论力学电子教程
第六章 空间力系和重心
§6－4 力对于点之矩与力对于轴之矩
1. 空间力对于点之矩矢量：P108
M
O
( FAB
)
FAB
AB
rOA
FAB
矩心、力矩作用面、力矩矢量三要素(力矩大小、力矩作用面在空间方位、力使
理论力学电子教程
第六章 空间力系和重心
第六章 空间力系和重心
§6－1 空间力沿坐标轴的分解与投影 §6－2 空间汇交力系的合成与平衡 §6－3 空间力偶理论 §6－4 力对于点之矩与力对于轴之矩
§6－5 空间任意力系向已知点的简化·主矢 与主矩·空间力系的合力矩定理
§6－6 空间任意力系的平衡条件与平衡方程 §6－7 平行力系的中心与重心
空间合力投影定理 合力在某一轴上的投影，等于力系中所有各
力在同一轴上的投影的代数和
FRx Fx FRy Fy
FRz Fz
则合力
FR FRxi FRy j FRzk
z
F1
FR
F2
FRx2 FRy 2 FRZ 2 ( Fx )2 ( Fy )2 ( Fz )2
F
cos
FRx FR
矢相等的力偶均为等效力偶。 P108
理论力学电子教程
第六章 空间力系和重心
例 6-3 图示的三角柱刚体是正方体的一半。在其中三个侧面各自
作用着一个力偶。已知力偶（F1 ，F 1）的矩M1=20 N·m；力偶 （F2， F 2 ）的矩M2=10 N·m；力偶（F3 ，F 3）的矩M3=30 N·m 。试求合力偶矩矢M。又问使这个刚体平衡，还需要施加怎样一 个力偶。
若引入单位矢量，则力F沿直角 坐标轴分解的表达式为
F Fx Fy Fz Fxi Fy j Fzk
z Fz
F
Fx
Fy
Fxy y
x
理论力学电子教程
第六章 空间力系和重心
图示斜五面体OABCDE沿坐标轴正向三个棱边的长度OA＝4，OC ＝3，OE＝3（单位m），斜平面ABDE沿对角线EB间作用一力P ＝10kN，则该力在x轴上的投影Px=_______kN。在y轴上的投影 Py=_______kN。在z轴上的投影Pz=_______kN。
z
F2
F2
F3
O
y
F3
F1
x
F1
理论力学电子教程
第六章 空间力系和重心
解： 1.画出各力偶矩矢。 2.合力偶矩矢M 的投影。
M x M1x M 2x M3x 0
M y M1y M 2 y M 3y 0 10 30 cos 450 11.2N m
M z M1z M 2z M 3z 20 0 30 sin 450 41.2N m
物体在力矩作用面内绕过矩心且垂直于力矩作用面的轴转动的转向)
空间力对点之矩由右手法则确定矢量方向，以矩心为力矩矢
量起点。由于力对点之矩大小和方向均与矩心有关因此是一个 定位矢量；而力偶矩是自由矢量。P109
空间力对点之矩矢量与矩心位置有关；
而空间力偶矩矢量与矩心位置无关。
i jk
M (F ) r ຫໍສະໝຸດ Fx O AB理论力学电子教程
第六章 空间力系和重心
1、研究空间力的合成。
FR F1 F2 F3
2、研究空间力沿坐标轴的投影。
（1）直接投影法P102
Fx F cos , Fy F cos , Fz F cos x
z
Fz
F
Fx Fy
y
理论力学电子教程
第六章 空间力系和重心
（2）二次投影法(先向包括投影轴在内的平面投影)P103
Fx
FFxy xcy os
F
sin
F sin
cos
Fy Fxy sin F sin sin
Fz F cos
反之 F Fx2 Fy2 Fz2
cos Fx / F, cos Fy / F, cos Fz / F
这里注意力向坐标轴投影是代数量 而力向某平面投影是矢量。P103