第四章 空间力系和重心
- 格式:ppt
- 大小:1.10 MB
- 文档页数:20



第四章空间力系一、要求1、能熟练地计算力在空间直角坐标轴上的投影和力对轴之矩。
2、对空间力偶的性质及其作用效应要有清晰的理解。
3、了解空间力系向一点简化的方法和结果。
4、能应用平衡条件求解空间汇交力系、空间任意力系、空间平行力系的平衡问题。
5、能正确地画出各种常见空间约束的约束反力。
二、重点、难点1、本章重点:力在空间直角坐标轴上的投影和力对轴之矩。
空间汇交力系、空间任意力系、空间平行力系的平衡方程的应用。
各种常见的空间约束及约束反力。
2、本章难点:空间矢量的运算,空间结构的几何关系与立体图。
三、学习指导1、空间力系的基本问题及其研究方法空间力系研究的基本问题仍然是静力学的三个基本问题,即:物体的受力分析、力系的等效替换和力系的平衡条件。
空间力系是力系中最普遍的情形,其它各种力系都是它的特殊情形。
按由浅入深、由特殊到一般的认识规律研究空间力系,是从理论上对静力学作一个系统而完整的总结。
与平面力系的研究方法相似,这里也采用力向一点平移的方法将空间任意力系分解为空间汇交力系和空间力偶系,再应用这两个力系的合成方法来简化原力系,然后根据简化结果推导出平衡条件。
由于空间力系各力作用线分布在空间,因而使问题复杂化。
出现了力在坐标轴上的二次投影法、力对轴的矩以及用向量表示力对点的矩和力偶矩等新问题,简化的结果和平衡方程也复杂了。
2、各类力系的平衡方程各类力系的独立的平衡方程的数目不变。
但是平衡方程的形式可以改变。
上表列出的是一般用形式。
解题指导1、对于解力在直角坐标轴上投影或力沿直角坐标轴分解这类问题,重要的是确定力在空间的位置。
一般解题的思路如下:(1)认清题意,仔细查看结构(或机构)的立体图,它由哪些部件组成,各部件在空间的位置,以及它们和坐标轴的关系。
(2)认清力的作用线在结构(或机构)的哪个平面内,寻找它与坐标面的交角,然后找力与坐标平面的夹角及力与坐标轴的夹角。
(3)考虑用一次投影或二次投影的方法求解。
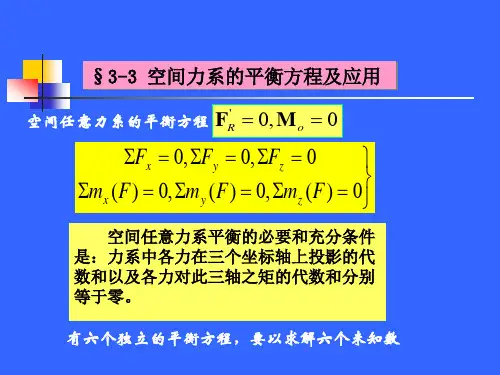


工程力学4.1力在空间坐标轴上的投影4.2力对轴的矩·合力矩定理4.3 空间任意力系的平衡方程4.4 平行力系的中心物体的重心工程中常常存在着很多各力的作用线不在同一平面内的力系,即空间力系,空间力系是最一般的力系。
(a)图为空间汇交力系;(b)图为空间任意力系;在(b)图中去了风力即为空间平行力系。
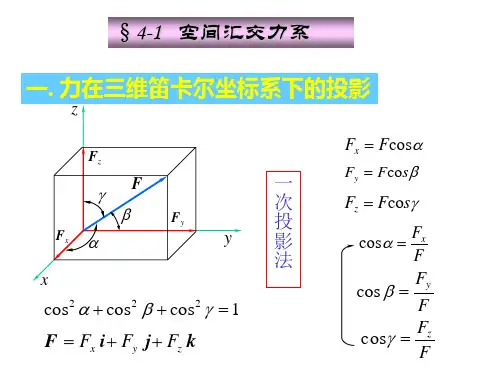
迎面风力侧面风力b4.1 力在空间坐标轴上的投影4.1.1力在空间的表示:力的三要素:大小、方向、作用点(线)大小:作用点:在物体的哪点就是哪点方向:①由α、β、g 三个方向角确定②由仰角θ与俯角ϕ来确定。
F F=4.1 力在空间坐标轴上的投影4.1.1力在空间的表示:1、一次投影法(直接投影法)由图可知:cos ,cos ,cos x y z F X F F Y F F Z F αβg==⋅==⋅==⋅4.1.2力在空间坐标轴上的投影2、二次投影法(间接投影法)当力与各轴正向夹角不易确定时,可先将投影到xy 面上,然后再投影到x 、y 轴上,即Fsin cos cos cos cos x xy F X F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅sin sin sin cos sin y xy F Y F F F g ϕϕθϕ==⋅⋅=⋅=⋅⋅cos sin z F Z F F g θ==⋅=⋅ 4.2 力对轴的矩⋅合力矩定理一、力对轴的矩的概念与计算定义:()()2''z O xy xy m F m F F d OA B ==±⋅=∆的面积由于力和都不能使门转动,所以得出力与轴平行或相交时,力对轴之矩为零。
亦即力与轴共面时,力对轴之矩为零。
y F z F 力对轴的矩是力使刚体绕该轴转动效应的度量,是代数量,其大小等于在垂直于转轴的平面内的分量的大小和它与转轴间垂直距离的乘积,其正负号按右手规则确定,即大拇指方向与轴的正向一致的为正,反之为负。
4.2.2合力矩定理与平面力系情况类同,空间力系的合力矩定理为:12()()()()()z z z z n z i m R m F m F m F m F =+++=∑即:空间力系的合力对某一轴的矩,等于力系中所有各分力对同一轴的矩的代数和。




第四章空间力系的平衡及重心第五节物体的重心及其求法一、物体重心的概念地球上的物体都受到地球的吸引力,这个吸引力就是重力。
严格地讲,物体的重力是一个分布力,分布在物体的各个部分,我们通常所说的重力是指这个分布力的合力。
可以证明,无论物体如何放置,其重力(合力)均通过一个确定的点,这个点就是物体的重心。
重心是力学中的一个十分重要的概念,在工程实际中有着很重要的意义。
物体的平衡和稳定,物体旋转时振动的大小等均涉及到重心的位置。
二、物体重心坐标公式1、物体重心坐标的一般公式假象地将物体分割成若干个微小部分,每部分的重力分别为DG1、D G2……D G n,各力的作用点的坐标分别为(x1,y1,z1)、(x2,y2,z2)……(x n,y n,z n),该物体的重力G=D G1+D G2+……+D G n。
由合力矩定理可得其重心坐标公式为:2、均质物体重心坐标公式设均质物体的密度为r,体积为V,则其重力G=rVg,每一微小部分的重力Gi=rV i g,将此关系代入式(4-8),可得均质物体的重心坐标公式:3、均质薄板的重心坐标公式设均质薄板的厚度为d,面积为A,则其体积V=dA,V i=dA i,将此关系代入式(4-9),可得均质薄板的重心坐标公式:可见,对均质物体而言,其重心位置完全取决于其几何形状,而与其重量无关,物体的重心就是其形心。
三、物体重心(形心)的求法1、查表法对于简单几何形状的均质物体,其重心可从有关手册中查到,可直接查表。
见表4-2。
2、对称法对于具有对称面、对称轴或对称中心的均质物体,其重心就在对称面、对称轴或对称中心上。
若物体有两个对称面,则其重心就在这两个对称面的交线上;若物体有两个对称轴,则其重心就在这两个对称轴的交点上。
空间力系和重心空间力系和重心各力的作用线不在同一平面内的力系,称为空间力系。
与平面力系类似,空间力系可分为空间汇交力系、空间力偶系和空间任意力系来研究。
空间力系和重心6.1空间力沿坐标轴的分解与投影直接投影法zF= Fx+ Fy+ Fz= Xi+ Yj+ Zk其中,FzαγZkFxFβ Y FyX= F cosα Y= F cosβ Z= F cosγXjixy空间力系和重心二次投影法zX= Fxy cos = F sinγ cos Y= Fxy sin = F sinγ sin Z= F cosγZγkFYj i X Fxyy注意,力在轴上的投影是代数量,而力在平面上的投影是矢量。
x空间力系和重心力的大小和方向余弦:zF= X 2+Y 2+ Z2X cos( F, i )= F Y cos( F, j )= F Z cos( F, k )= FZγkFYj i X Fxyyx空间力系和重心6.2力对点之矩和力对轴的矩6.2.1力对点之矩力对点的力矩矢等于矩心到该力作用点的矢径与该力的矢量积,表示为,M O (F )FOrMO ( F )= r× F空间力系和重心若矢径rz和力F分别为M O (F )B Fr= xi+ yj+ zk F= Xi+ Yj+ Zki则,M O ( F )= r× F= x X j y Y k z Z kOrA( x, y, z )ijyx= ( yZ zY )i+ ( zX xZ ) j+ ( xY yX )k空间力系和重心由此可知力矩矢M O (F )在三个坐标轴上的投影分别为:M Ox ( F )= yZ zY M Oy ( F )= zX xZ M Oz ( F )= xY yX(6 1)力矩矢的始端必须在矩心,不可任意移动,为一定位矢量。
空间力系和重心6.2.2力对轴之矩为度量力对绕定轴转动刚体的作用效应,引入力对轴的矩的概念。
空间力系和重心力对轴的矩的概念作用于刚体的力F对z轴的定义为:M Z ( F )= M O ( Fxy )=± Fxy hM z (F )F这样,空间力对轴之矩归结为平面上的力对点之矩,即力F对任一轴z之矩,等于这力在垂直于z轴的平面内的分量Fxy对该平面和z轴交点O之矩。