X-s控制图_实例
- 格式:xls
- 大小:68.50 KB
- 文档页数:15

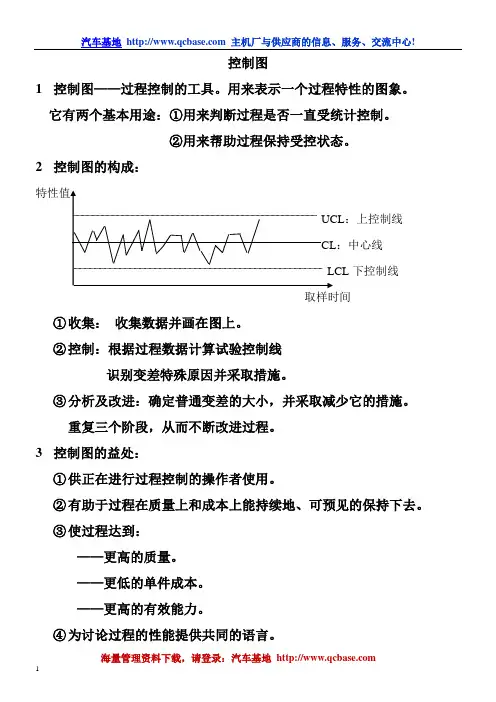
控制图1控制图——过程控制的工具。
用来表示一个过程特性的图象。
它有两个基本用途:①用来判断过程是否一直受统计控制。
②用来帮助过程保持受控状态。
2控制图的构成::上控制线:中心线下控制线取样时间①收集:收集数据并画在图上。
②控制:根据过程数据计算试验控制线识别变差特殊原因并采取措施。
③分析及改进:确定普通变差的大小,并采取减少它的措施。
重复三个阶段,从而不断改进过程。
3控制图的益处:①供正在进行过程控制的操作者使用。
②有助于过程在质量上和成本上能持续地、可预见的保持下去。
③使过程达到:——更高的质量。
——更低的单件成本。
——更高的有效能力。
④为讨论过程的性能提供共同的语言。
⑤区分变差的特殊原因和普通原因,作为采取局部措施或对系统采取措施的指南。
第二章计量型数据控制图第一节均值和极差图参见“均值和极差控制图”1.收集数据1.1子组大小:一般为4-5件(连续生产的产品的组合)。
各子组样本应一样。
选择原则:一子组各样本间出现的变差的机会小。
子组内变差主要由普通原因造成。
1.2子组频率:应在适当时间收集足够的子组,能反映潜在的变化。
过程处于稳定,频率可减少。
(每班两次、每小时一次或其他频率)。
1.3子组组数:≧25个。
总单值≧100个。
2.控制图及记录原始数据:①X图绘在R图的上方。
下面再接一个数据栏。
②X和R值为纵坐标,时间为横坐标。
③数据栏应包括:每个读数空间、读数、和、均值、极差以及日期/时间或其他识别子组的代码的空间等。
3.计算均值(X)和极差(R):X=( X1+X2+…+X n)/n R=X MAX﹣X MINX1,X2,…X n——测量值。
n——子组容量。
4.控制图刻度;①对X图:坐标刻度最大值-最小值≧2(X max–X min)②对R图:坐标刻度最大值≧2R max5.计算控制限:①平均极差(R)及过程平均值(X)R=(R1+R+2…+R K)/K(1X2+…+X K)/KK——子组的数量。

《质量统计技术》习题第一章概论1-1 质量的含义是什么?1-2 不合格和缺陷的关系是什么? 1-3 检验、试验和验证概念上有什么区别?1-4 质量管理、质量控制和质量检验的关系是什么?1-5 什么是统计技术?可以分为几类?1-6 组织应用统计技术应该具备哪些基本条件? 1-7 质量管理和质量管理体系的关系是什么?1-8 质量管理经历了哪几个阶段?各个阶段的特点是什么? 1-9 统计技术在质量管理中有哪些重要作用?第二章统计技术基础知识一、思考与练习2-1 质量特性数据有哪些特点?2-2 分层随机抽样主要解决什么问题,如何应用? 2-3 什么是必然事件、不可能事件、随机事件? 2-4 什么是小概率事件实际不可能性原理?2-5 设有10件产品,其中有3件不合格品,现从中任取4件。
求恰好抽到2件不合格品的概率;求至少抽到1件不合格品的概率。
2-6 离散型随机变量概率分布与连续型随机变量概率分布有何区别?2-7 什么是正态分布?标准正态分布?正态分布的密度曲线有何特点? 2-8 已知随机变量u服从N(0,1),求P(u<-=, P(u≥),u|≥), P(-≤u<),并作图示意。
P P(u<-u?=+P(u≥u?)=; P(-u?≤u<u?)=;2-10 设X变量服从正态分布,总体平均数μ=10,P(x ≥12)=,试求X在区间内取值的概率。
2-11 什么是二项分布?如何计算二项分布的平均数、方差和标准差? 2-12 已知随机变量X服从二项分布B,求μ及σ。
(10,3) 2-13 已知随机变量X服从二项分布B(10,),求P(2≤X≤6),P(X≥7),P(X 2-14 什么是泊松分布?其平均数、方差有何特征?2-15 已知随机变量X服从泊松分布P(4),求P(X=1),P(X=2),P(X≥4)。
2-16 某种产品的不合格品率为。
试问在360件此产品中,(a)有3件或3件的不合格品的概率;(b)恰有3件不合格品的概率。
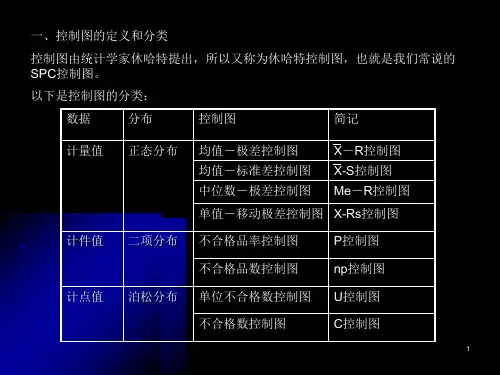
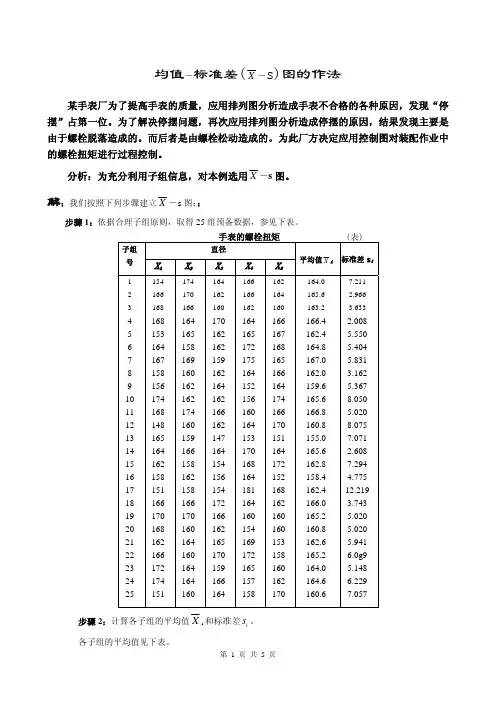



控制图(control charts)又名:统计过程控制( statistical process control)方法演变:EQ \o(\s\up5(-),\s\do2(x))计量值控制图:⎺X-R控制图(又名均值极差控制图),⎺X-s控制图,单值控制图(又名X 控制图,X-R控制图,IX-MR控制图,XmR控制图,移动极差控制图),移动均值-移动极差控制图(又名MA-MR控制图),目标偏差控制图(又名差异控制图、偏差控制图、名义值偏差控制图),CUSUM(又名累计和控制图),EWMA(又名指数加权移动平均控制图),多元控制图(又名Hotelling T2控制图)。
计数值控制图:p控制图(又名不良品率控制图),np控制图,c控制图(又名缺陷数控制图),u控制图。
两种数据都适用的控制图:短期过程控制图(又名稳定控制图或者Z控制图),组控制图(又名多属性值控制图)。
概述控制图是一种对过程变异进行分析和控制的图形工具。
数据按时间顺序绘制在图上,控制图一般有一条代表均值的中心线,一条上控制限位于中心线上方,一条下控制限位于中心线下方,这些线是根据过程数据确定的。
通过当前数据和由历史数据计算所得的控制限的比较,我们可以判定当前过程变异是稳定的(受控制)还是不稳定的(不受控制,受到某个特定因素的干扰)。
控制图分为很多种,不同的过程、不同的数据,我们采用不同的控制图。
计量值数据的控制图经常是成对应用,其中常绘制在上方的一张控制图监测均值,或者说过程数据的分布中心,而绘制在下方的一张控制图监测极差,或者说分布的波动程度。
如果借助于练习打靶的例子来说明,那么均值就是靶子上射击集中的地方,极差是射击点的离散程度。
计量值数据要成对使用控制图,计数值数据则通常只使用一张控制图就足够了。
适用场合·当你希望控制当前过程,问题出现时能察觉并能对其采取补救措施时;·当你希望对过程输出的变化范围进行预测时:·当你判断一个过程是否稳定(处于统计受控状态)时;·当你分析过程变异来源是随机性(偶然事件)还是非随机性(过程本身固有)时;·当你决定怎样完成一个质量改进项目时——防止特殊问题的出现,或对过程进行基础性的改变。

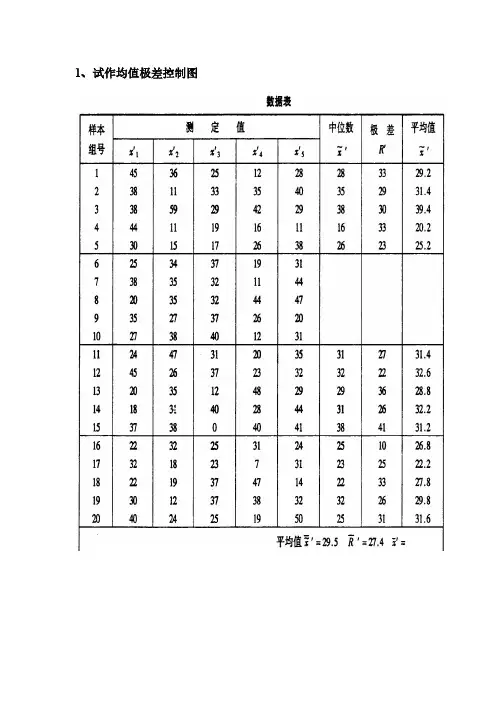
1、试作均值极差控制图
2、试作均值极差控制图、中位数极差控制图和均值标准差控制图
3、试作移动极差控制图
4、试作样本大小n 相等时的p
控制图
5、试作样本大小n 相等时的pn
控制图
6. 试作样本大小n不相等时的p控制图
〔案例〕
某电机厂生产洗衣机用小型电机,构成交验批的批量各不相等,现每隔1
小时抽取一个样本,共25批,经检验将不合格品数及不合格品率记入数据
表,试作分析用控制图。
7. 试作C控制图
某电线生产过程中,每隔一定时间对100m导线进行检查,检查的结果如表所示,试作C控制图。
8. 试作U控制图
某电子产品检查的结果如表所示,试作U控制图。
