下载文档原格式
实验室质量控制方法—-质控图的应用摘要通过使用质量控制图来对实验室的监测工作实施质量控制，保证日常质量监测工作的成果正确可靠性，同时为实验室的工作人员的比对检测、期间核查等分析工作的质量管理活动提供了成果评价的重要依据，是在实验室中日正常检测中有效的质控方式。
关键字质量控制图；绘制；应用分析质量控制图，最早于20世纪40年代初就用于实验室的质量控制工作中，它的研究理论基础为数理统计学中的统计学与质量检验理论知识。
该图主要作用是对各类实验中所得到的数据和成果进行监测，并对实验的有效质量展开针对性监控。
从实际的使用效果而言，质量控制图具有简洁、简单、简明的特点，能够快速及时准确反应实验中分析误差的各类变化及变化趋势，从而“提醒”实验人员采取正确措施进行处理。
正因质控图既能够有效保障日常实验过程的质量监测工作的成果正确和可靠性，又能为科研人员提供实验结果比对检测、过程核查等科研活动提供成果评价的重要依据，目前已经是我国实验室中的主流质控措施方法之一。
此外，在中国合格评定国家认可委员会中发布的《CNAS-CL01:2018检测和校准实验室能力认可准则》和《CNAS-CL01-A002:2018检测和校准实验室能力认可准则在化学检测领域的应用说明》里明确规定了试验室应该监控结果有效性的程序以及实验室人员对于测试结果有效性进行监控，可以通过制作质量控制图进行核查和监控，来对实验室的检测有效准确进行保证。
1质量控制图的绘制和判断1.1质量控制图的类型实验室中最常使用的控制图表大致有两类，即是X-图(单值图或均值图)和R-图(极差图)。
当是利用标准物质、样品的空白值、回收率和某一固定浓度标准物质的数值进行监控时，可以采用制作X-图。
X-图是用来监控控制值的系统效果和随机效应。
但X-图的不足之处是难以区分批间与批间的精密度。
当是利用双样或多个样重复分析数值时，则采用制作R-图（极差(R)）。
R-图是用来监控重复性问题。
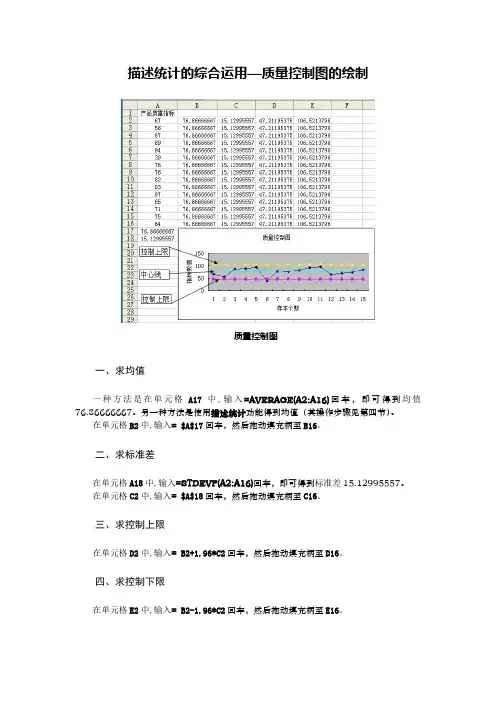
描述统计的综合运用—质量控制图的绘制质量控制图一、求均值一种方法是在单元格A17中,输入=AVERAGE(A2:A16)回车，即可得到均值76.86666667。
另一种方法是使用描述统计功能得到均值（其操作步骤见第四节）。
在单元格B2中,输入= $A$17回车，然后拖动填充柄至B16。
二、求标准差在单元格A18中,输入=STDEVP(A2:A16)回车，即可得到标准差15.12995557。
在单元格C2中,输入= $A$18回车，然后拖动填充柄至C16。
三、求控制上限在单元格D2中,输入= B2+1.96*C2回车，然后拖动填充柄至D16。
四、求控制下限在单元格E2中,输入= B2-1.96*C2回车，然后拖动填充柄至E16。
五、做质量控制图1、绘制折线图（1）点击图表向导，进入图表向导步骤1对话框；（2）选择折线图→数据点折线图，点击下一步，进入图表向导步骤2对话框；（3）在数据区域输入A2:A16，点击下一步，进入图表向导步骤3对话框；（4）点击标题，在图表标题项中输入质量控制图，在分类（X）轴项中输入样本个数，在分类（Y）轴项中输入指标数值；（5）点击网格线，去掉网格线；（6）点击图例，去掉图例，点击完成，得到折线图。
2、绘制质量控制图的中心线选中单元格B2:B16，将鼠标移至所选单元格的边缘，直到变成一个四向箭头，按住鼠标左键，将其拖放到折线图中，即可得到质量控制图的中心线。
3、绘制质量控制图的上控制线选中单元格E2:E16，将鼠标移至所选单元格的边缘，直到变成一个四向箭头，按住鼠标左键，将其拖放到折线图中，即可得到质量控制图的上控制线。
4、绘制质量控制图的下控制线选中单元格D2:D16，将鼠标移至所选单元格的边缘，直到变成一个四向箭头，按住鼠标左键，将其拖放到折线图中，即可得到质量控制图的下控制线。
5、利用绘图功能，标出控制上限、中心线、控制下限及其指向箭头（绘制方法见第三章第四节K线图部分），完成最终的质量控制图。
质量控制(QC)流程图引言概述：质量控制（QC）流程图是一个重要的工具，用于确保产品或者服务的质量符合预期标准。
它提供了一个清晰的视觉表示，展示了质量控制过程中的各个环节和步骤。
本文将详细阐述质量控制流程图的五个大点，包括质量目标设定、质量计划制定、质量控制执行、质量数据分析和质量改进措施。
正文内容：1. 质量目标设定1.1 确定质量目标：首先，制定一个明确的质量目标，以确保产品或者服务能够满足客户的需求和期望。
这个目标应该是具体、可衡量和可达到的。
1.2 确定质量指标：在设定质量目标的基础上，确定一些关键的质量指标，用于衡量产品或者服务的质量水平。
这些指标可以包括缺陷率、客户满意度、产品可靠性等。
2. 质量计划制定2.1 制定质量计划：根据质量目标和指标，制定一个详细的质量计划，包括质量控制的具体步骤、所需资源和时间安排等。
这个计划应该是可操作的，并且能够满足质量目标。
2.2 制定质量检查标准：在制定质量计划的过程中，制定一套质量检查标准，用于判断产品或者服务是否符合要求。
这些标准应该是明确的，并且能够被操作人员理解和执行。
3. 质量控制执行3.1 进行质量检查：按照质量计划和质量检查标准，对产品或者服务进行检查。
这包括对关键环节、关键参数进行监控和测量，以确保产品或者服务的质量符合要求。
3.2 记录质量数据：在质量控制执行过程中，及时记录质量数据，包括缺陷数量、不合格品数量等。
这些数据是后续质量分析和改进的重要依据。
4. 质量数据分析4.1 分析质量数据：对记录的质量数据进行分析，找出其中的规律和趋势。
通过统计分析和数据挖掘等方法，发现潜在的质量问题和改进机会。
4.2 制定改进措施：根据质量数据分析的结果，制定相应的改进措施。
这些措施可以包括优化生产工艺、改进设备性能、加强员工培训等。
5. 质量改进措施5.1 实施改进措施：根据制定的改进措施，进行相应的实施。
这包括对生产工艺、设备和人员进行相应的调整和改进，以提高产品或者服务的质量水平。
工程质量控制网络图工程质量控制网络图是一种用于监控和管理工程质量的工具，它通过图形化的形式展示了工程质量控制的各个环节和流程。
本文将详细介绍工程质量控制网络图的标准格式，包括图形元素的定义和使用，以及网络图的绘制步骤和注意事项。
一、工程质量控制网络图的标准格式1. 图形元素定义：(1) 活动（Activity）：表示工程质量控制的具体任务或活动，通常用矩形框表示，框内标注活动名称。
(2) 事件（Event）：表示工程质量控制的里程碑或重要节点，通常用圆形表示，圆内标注事件名称。
(3) 箭头（Arrow）：表示活动之间的逻辑关系或依赖关系，箭头从前置活动指向后置活动，箭头上可以标注活动之间的时间或顺序关系。
(4) 里程碑（Milestone）：表示工程质量控制的重要阶段或目标，通常用菱形表示，菱形内标注里程碑名称。
2. 标准格式示例：```活动1 --箭头--> 活动2活动2 --箭头--> 活动3活动3 --箭头--> 事件1事件1 --箭头--> 活动4活动4 --箭头--> 里程碑1```二、工程质量控制网络图的绘制步骤1. 确定活动和事件：根据工程质量控制的具体需求，确定需要进行控制和监管的活动和事件。
2. 确定活动之间的逻辑关系：根据活动之间的依赖关系，确定箭头的方向和顺序。
3. 绘制网络图：按照标准格式，使用适当的图形元素绘制网络图。
4. 标注活动和事件名称：在各个图形元素内部标注相应的活动和事件名称。
5. 标注箭头上的关系：在箭头上标注活动之间的时间或顺序关系。
6. 标注里程碑：在里程碑所在的菱形内标注里程碑名称。
7. 优化网络图：根据实际情况，对网络图进行优化和调整，使其更加清晰和易读。
三、工程质量控制网络图的注意事项1. 确保逻辑关系的准确性：在确定活动之间的逻辑关系时，要充分考虑各个活动之间的依赖关系，确保网络图的准确性。
2. 清晰明了的标注：在绘制网络图时，要使用清晰明了的字体和标注方式，确保活动和事件的名称能够清晰可读。
控制图的原理及应用教案一、控制图的概述•控制图是用来监测和分析过程稳定性的工具。
它能够帮助我们判断过程是否受到了特殊因素的影响，从而帮助我们定位问题和改进过程。
•控制图包括过程监控图、变动图、普通图等，每种图形都有其特定的使用场景和目的。
二、控制图的基本原理•均值控制图的原理：通过收集和分析过程数据，确定过程的中心线和控制上下限，根据数据的离散程度来判断过程的稳定性。
•范围控制图的原理：通过跟踪样本范围的变化，来评估过程的稳定性和一致性。
•动态测量控制图的原理：通过在过程控制中，采样循环中检测结果的变化，来判断过程的稳定性。
•经济控制图的原理：通过分析与经济因素相关的数据，来优化过程并减少资源的浪费。
三、控制图的应用场景1.生产过程监控：通过定期采样和测量关键参数，将数据绘制在控制图上，及时发现过程异常和问题并采取相应的纠正措施。
2.产品质量控制：通过控制图来监测产品参数的变化和偏离，确保产品质量在可接受范围内，并及时发现潜在问题。
3.供应链管理：通过掌握供应链中各个环节的数据，绘制控制图来分析供应链的稳定性和可靠性，及时处理延迟和异常情况。
4.服务质量监控：对于服务行业，可以使用控制图来衡量并监控关键指标，及时发现异常情况并采取相应的改进措施。
5.实验过程控制：在实验过程中，采用控制图能够帮助我们评估实验结果的稳定性和一致性，从而提高实验的可靠性。
四、控制图的应用步骤1.收集数据：需要收集与需要监控的过程相关的数据。
2.绘制控制图：选择适当的控制图类型并将数据绘制在控制图上。
3.判断过程稳定性：通过分析控制图数据的模式和规律，判断过程的稳定性。
4.分析过程问题：如果控制图中存在异常点或趋势，说明过程可能存在问题，需要进一步分析和排查。
5.纠正和改进：根据分析结果采取纠正措施，并对过程进行改进以提高稳定性和一致性。
6.持续监控：持续收集数据并绘制控制图，监控过程的稳定性和持续改进。
五、控制图的优势和局限性优势•提供直观的数据展示和分析方式，便于快速理解和判断过程稳定性。
质量控制图的绘制及使用[2,5,7]根据误差为正态分布的原理，在统计学上X±1S占正态曲线下面积的68.26%，以此作为上辅助限和下辅助限；X±2S占总面积的95.45%，以此作为上警戒限和下警戒限；X±3S占总面积的99.73%，以此作为控制图的上控制限和下控制限（图21.2）；超过3倍S的概率总共只占0.27%，以乃属于小概率事件，亦即同一总体中出现如此大偏差的概率极小，可以认为它不是这个总体中的一个随机样品，这个结论具有99.73%的把握是正确的。
既然不能作为同一总体中的一个随机组成者，而在分析测试中是用同一分析方法，在相同条件下所测得的同一个样品（例如空白试验）的检测值，则必然发生了某种影响较大因素的作用，从而有根据否定这一测定值。
图21.2 质量控制图图21.2中质量控制图的形式与正态曲线形式完全相同，即将正态曲线向逆时针方向旋转了90度，以正态曲线的中心m被X所代替，作为理想的预期测定值；将68.26%概率保证的置信区间作为目标值（即上、下辅助限之间的区域）；以95.45%概率保证的置信区间作为可接受范围（即上、下警戒限之间的区域）；将上、下警戒限至上、下控制限的区间作为可能存在“失控”倾向，应进行检查并采取相应的校正措施；在上、下控制限以外，则表示测定过程已失去控制，应立即停止检测，待查明原因加以纠正后对该批样品全部重新测定。
对于质量控制检查样品和实验室控制样品的控制图，是把算术平均值作为中心值统计。
最初控制限制是用平均值的百分数表示，通常系列测定算术平均值±10%。
然而，最少进行7个测定值后才能建立统计控制限度。
警戒限度设在来自平均数(X)±2Sx (标准误，来自质量控制样品的95%）；控制限度设在离平均数(X)±3 Sx应包含质量控制样品的99.7%）。
质量控制样品数据的5%将落在警戒限外面，如果两个连续测定值落在警戒限外面被认为是“失控”状态(Taylor, 1987)。
由于99.7%的数据应该落在X±3Sx以内，控制限外面的点是最可能失控的，矫正活动是有根据的。
例如，如果失控值是标准参考物质或其它质量控制样品，即这一批完整的分析样应重新测定。
这可能需要对新的校正标准再分析、或要求通过完整的制备方法采取新的测定部分。
然而，如果失控结果是对连续标定检验（CCV），那么前面在控的实验室控制样品需要重测。
通常这种状态是由于仪器漂移或其它决定时间特征的因素引起的。
在质量控制中一个系统的趋势也代表一个失控状态。
这种趋势可以通过发生在平均值上下7个系列值或出现在数据的方式表现出来。
这可能与变量有关，例如室温、一天内时间的变化或分析者等。
警戒和控制限度需要根据周期进行重新修改。
根据产生数字的量，这个修订日期可以是每周，每月，每年一次，或者在获得一定数目的数据之后，以检查控制限是否适当。
如果数值连续地落在X±1Sx以内，控制限太宽了，以致于在控制的分析系统没有用处了。
同样地，如果大于5%的数值落在X±2Sx外面，那么控制限没有充分落在分析系统变化范围内，需要修改或者该系统严重失控。
当控制限被重新修正以后，已经累积的所有资料（数据）应该用于平均数和标准差的测定。
这最好是通过集中测定来完成。
当控制图在分析时间上被保持和评估时，应采取立即校正，以节省时间。
因为当测定系统失控时，不能测定常规样品。
某些样品在测定某些参数时可能容易拖延时间，不能在有效分析时间内绘制控制图，影响对分析过程的控制。
因为拖延时间是在样品失效前，因此必须在真正分析时间内测定质量控制检查样品并绘制控制图。
由于控制图的制作是以正态分布假设为基础的，所以制作一个控制图应对一份控制样品至少作15～20组的重复测定，低于15组的控制图是不可靠的。
这20组数据应由20天的分析测出，或20批分析测出，不能一天进行数组或一批样进行数组测定。
控制样品的测定条件应与样品的测定条件完全一致。
在精密度控制图中常用的有均值控制图（即X质控图），均值极差质控图(即X－R值控图)和临界限Rc值控制精密度。
1. 均值质控图[2,3]对控制样品进行多次重复测定（一般重复测定20次），由所得结果计算出控制样的X及S，就可以绘制精密度控制图（图21.3）。
纵坐标为测定值，横坐标为获得数据的顺序。
将均值X作成与横坐标平行的中心线CL，X±3S x为上、下控制限UCL及LC L，X±2S x为上、下警戒限UWL及LWL。
在进行试样例行分析时，每批带入控制样，其测定数据在控制图上打点，如果打在上、下警戒限范围内，则测定结果合格；如果点落在控制限之外（如第5批），叫“超控”，该批结果全部为错误结果，必须立即找出原因，采取适当措施，等“回控”后再重新测定。
如果控制样品的结果落在控制限和警戒限之间（如第10批），说明精密度已不理想，应引起注意。
均值质控图制作比较简单，是化学分析中常用的一种质控图。
这种图是以一种浓度的控制样绘制的，并以控制样与样品处在相同条件下分析为依据，从而根据控制样品的受控与否来肯定或否定这批分析样品的，只能看出批间的变异，故所得信息较少。
在例行分析中经常用实验室控制样品做空白试验的均值质控图，每次作两份空白样品，以首次合格值考查其稳定性，如符合要求者，取其平均值，并积累20次以上的数值，计算出平均空白值X b和空白值标准差S b。
X b+3S b上控制限；X b+2S b上警戒限；X b+S b上辅助限；X b控制基线。
图21.3 均值质控图图中没有控制下限，因空白值愈小愈好，但绘图时应保留< X b的部分，当实测空白值低于控制基线且逐渐稳步下降时，说明实验水平有所提高，可酌情用较小空白值取代较大空白值，重新计算绘制。
2. 均值一极差质控图[2]是最常用、最重要的控制图。
在这种控制图中，即可通过均值(X)表示测定结果的集中趋势，又可通过极差(R)表示离散程度，因而所得信息更多，能及早发现异常。
制作X——R质控图至少应对一种控制样品作20组重复分析，每组平行2～5份，而且每天只能测一组，20天后将资料整理、计算(表21.5)和绘制X——R质控图(如图21.4)。
图21.4 X——R质控图计算X——R质控图的中心线：X=∑X/n=52.939/20=2.647R=∑R/n=2.21/20=0.110计算X——R质控图的上、下控制限和上、下警戒限，计算式中所用的计算因子A2、D3、D4列于表21-6。
对X图：上控制限= X + A2R =2.647+1.023×0.110=2.760下控制限= X- A2R =2.647-1.023×0.110=2.534计算式中：A2─利用R求X分布的警戒限、控制限的系数，其数值取决于每组平行测定的份数n；D3、D4─利用R求R分布的系数，也取决于n。
对于R图来说，重要的是分析结果是否超过上警戒限，所以下警戒限不必计算。
对于R图来说，重要的是分析结果是否超过上警戒限，所以下警戒限不必计算。
(1)X——R质控图的绘制：将上述计算值用方格计算纸作图，两图之间应有30mm左右的间距。
(2)X——R质控图的应用：在进行样品分析时，将控制样（质量控制检查样）插入样品组内，在相同条件下共同分析，并将控制样的X及R点于图中，极差愈小愈好，故极差控制图部分（R图）没有下警戒限，但仍有下控制限。
在使用R控制图的过程中，如R值稳步下降逐次变小，以至于R≈D3 R，即接近于下控制限，则表明测定的精密度已有所提高，原质量控制图已失去作用。
此时应使用新的测定值重新计算X、R和各相应的统计量，重新绘制X ——R质控图。
如果均值和极差中有任意点超出控制限，即为失控，应停止分析，待查明原因恢复控制后再继续测定。
在有些情况下，虽然所有的点都在控制范围之内，但有7点连续在中心线相应的一侧，亦为异常情况。
异常判断的依据是调查测定结果是否接近控制限。
一般测定结果超出警戒限的概率为5%，所以判断异常的基准是：A. 连续3点中有2点超出警戒限；B. 连续7点中有3点超出警戒限；C. 连续10点中有4点超出警戒限。
如果出现上述异常现象，亦应立即停止分析，查明原因，使测定过程回到控制之中。
在均值─极差质控图中的极差部分，由于实际监测样品的浓度不是固定不变的，而统计量R 值类似均值控制图中的X值，会随样品浓度的变动而改变，在重复测定单一浓度的质量控制检查样品所得R值的代表意义有一定局限性，而绘制一系列不同浓度水平的R图又太繁锁。
因为在使用R图中主要是观察R值是否超出上控制限，故可对每个监测项目绘制一系列各种浓度范围的上控制限表格，并把高浓度范围内的上控制限按照“数字修约规则”修约到最接近的整数单位；把低浓度范围的上控制限也同样处理到最近的整数单位。
这一系列的R 值称为“临界限”（R c），用它来作为不同浓度水平的极差控制是很方便实用的。
(3)用临界限Rc值来控制精密度[2]R值的控制是检查重复分析的减差值（R）是否超出上控制限(D4R)。
更实际的方法是在日常工作中积累各种浓度范围的R值，在达到一定数量时计算出各种浓度范围的R值的均值，把相似R值的浓度范围分组并求出加数均值，按公式UCL（上控制限）=D4 R计算出临界Rc值。
表21.8为三种测定指标的上控制限计算实例，其中R=|X1 -X2|／(X1 +X2)/2，即重复样的差(绝对值)除以重复样结果的均值。
在计算出UC L值后，应检查所有数据，弃去其中超出UCL的值，并将弃去极端值后的数据重新计算，UCL值作为临界控制限。
准确度控制图确度用加标回收率表示，控制图以加标回收率均值绘制，在控制样品中（常规样品）加入一定已知含量的标准溶液或标准物质，标准参考物质进行分析（一般最大加入量约为试样含该物质浓度的2倍），进行15～20次回收率试验，每次双样平行，求出各次回收率P，再计算出平均回收率P和回收率的标准差S p 。
以P为中心线；P±3S p为上、下控制限；P±2S p 为上、下警戒限；P±S p为上、下辅助限绘制成图（从略）。
如果回收率落在设定的控制限以内，测定过程在统计控制以内。
当回收率变化或没有落在设立的控制限以内，必须进行校正。
如果有任一点回收率超出控制限，或连续7点在中心线相同的一侧，表示测定过程失控，应停止分析，查找失控原因，采取必要措施，使测定回到控制之中。
单一加标回收率控制图的适用性常因样品浓度悬殊而受到限制。
在中、高浓度时，加标回收率受样品浓度波动的影响非常小；但低浓度样品的浓度波动对加标回收率的影响较大。
因此对低浓度样品通常分别绘制不同浓度范围的加标回收率控制图。
如果不考虑监测样品中的基体、干扰等因素对准确度的影响，可先对质量控制样品中某种组分进行20次以上的测定，取所测浓度的均值作为中心线，再于距离中心线上、下各一个标准差绘出上、下辅助限，并以此限控制单纯分析过程的准确度。
