北师大版初中数学七年级上册《第四章 基本平面图形 3 角》 赛课教案_0

数学北师大版七年级上册4.3角教学设计第一篇：数学北师大版七年级上册4.3角教学设计七年级上册第四章基本平面图形4.3角教学设计灵璧县大路中学李磊 2016-11-2《4.3 角》教学设计教学目标: 知识与技能目标：1.理解角的有关概念，熟悉角的四种表示方法；认识度、分、秒并能进行简单的换算。

2.创设角及度、分、秒的思维情境，利用小组活动培养学生的探究能力和运算能力。

过程与方法目标：经历从现实生活中认识角的过程，培养学生的观察能力和动手操作能力。

情感态度与价值观目标：在合作交流的学习过程中，进一步培养学生的观察、想象、探究的能力，激发学生对数学的好奇心及求知欲。

教学重点：理解角的概念，掌握角的表示方法.教学难点：进行简单的度、分、秒的换算.教学方法：观察法、情境教学法.教学手段：多媒体课件教学过程：一、巧妙设疑，复习引入问题1.在小学我们已经认识了“角”，你能在图中找到角吗？幻灯片2显示图片问题2.生活中存在着许许多多的角，我们一起看一看，谁能从这些图中找出角？幻灯片3显示图片二、讲授新课 1.问题引入问题1：上节课我们认识了射线，从一点可以引出多少条射线？问题2：如果从一点出发任意取两条射线，那出现的是什么图形？2.角的定义学生在练习本上画出一个角，并思考自己是怎样画成一个角的？教师在黑板上同步演示角的画法，学生归纳，观察后给出角的定义.教师板书角的定义：角是由两条具有公共端点的射线所组成的图形.3.角的表示问题1：所有的角都一样吗？为什么？问题2：既然角有异同，能不能想办法把它们分别表示出来，加以区别？（1）角的符号：“∠”表示，读作“角”；（2）角的表示方法通常有以下几种：CCBBOαβB21O图1AO图2A图3Aa.用三个大写英文字母表示：如图1，可记作∠AOB或∠BOA，其中O是角的顶点，必须写中间，A、B分别是角的两边上的一点，写在两边，可以交换位置.b.用一个大写英文字母表示：如图1，可记作∠O.用这种方法表示的前提是同一个点作顶点的角只有一个时，否则不能用这种表示方法.如图2，∠AOC就不能记作∠O，因为此时以O为顶点的角不止一个，容易引起混淆。

3 角1．理解角的相关概念，会根据具体情境恰当地表示一个角；能进行简单的度、分、秒的互化．2．会在实例中找角，体会角在实际生活中的应用．重点掌握角的相关概念及表示方法．难点理解角的换算关系．一、复习导入教师：在小学时，我们已经认识了角，你能说一说你理解的角的概念，并举一些角的例子吗？学生思考后举手回答，教师点评．二、探究新知1．角的相关概念教师：在小学，我们说从一个顶点起画的两条射线，可以组成角．换句话说，角由两条具有公共端点的射线组成，两条射线不能乱摆，一定要有公共端点．那么，构成角的两个要素是什么呢？学生思考后举手回答，教师点评，并进一步讲解：构成角的两个要素为角的顶点和边，公共的端点就是角的顶点；两条射线叫做角的两边．说明：初中阶段，没有特别说明，我们只研究小于或等于180°的角.教师：前面在静止的情况下，通过观察角，我们给角下定义，下面我们在运动的情况下观察角的形成(课件演示)．教师：一条射线绕着其端点旋转，我们可以发现初始位置和最终位置作为始边和终边，也会形成不同的角．因此角又可以看成是一射线绕其端点旋转所形成的图形，那么，旋转时有无特殊情况呢？教师课件演示并讲解：当终边和始边成一条直线时，所成的角叫做平角．终边继续旋转，当它又和始边重合时，所成的角叫做周角．说明：(1)平角与直线、周角与射线是两个不同的概念，它们的图形表面上看起来一样，但本质上不同，角含有两条射线．(2)本书中所说的角，除非特殊注明，都是指没有旋转到成为平角的角．2．角的表示方法课件出示：教师：我们在前面知道，用一个大写字母表示点，而由于两点确定一条直线，因此我们用两个大写字母表示线(包括射线)，角应该怎样表示呢？学生：角内一弧线，标1，表示∠1.教师：有没有别的方法表示角呢？学生思考后回答，教师进一步讲解：角是由两条具有公共端点的射线组成，仿照射线的表示方法，我们也可以用大写字母表示端点和射线上的点，用三个大写字母表示角，记为∠BAC，注意三个字母的顺序有规定，顶点的字母必须写在中间，当然还可以只用顶点一个字母表示角，记为∠A.课件出示练习：指出图中(包含平角在内)有几个角，并用适当的方法表示这些角．学生回答后，教师点评：用顶点的一个字母表示角虽然很方便，但在顶点处有多个角时就不适用，否则会造成歧义．用三个字母表示角时顶点字母要放中间．找角的时候可以按一定顺序来，这样不容易遗漏，可以先找单个角，再找两个、三个角拼成的大角．教师引导学生总结角的表示方法：(1)在角的内部靠近角的顶点处画一弧线，用一个数字或小写的希腊字母(如α，β，γ)表示角；(2)用三个大写字母表示角，中间的字母表示顶点，其他两个字母表示角的两边上的点；(3)如果一个顶点只对应一个角时(即不歧义时)可只用顶点的大写字母表示角．3．度、分、秒的换算课件出示教材第116页图4－16，提出问题：(1)请用字母表示图中的每个城市．(2)请用字母分别表示以北京为中心的每两个城市之间的夹角．(3)请用量角器测量出西安和福州、哈尔滨和上海两城市之间的夹角，与同伴交流自己的量法和读法．学生独立完成，教师点评．强调：用三个大写字母表示角；量角时需注意：一对，角的顶点对准量角器的中心，二重，角的一边与量角器的零刻度线重合，三读数，读出角的另一边所指的度数．终边所指度数读始边指着0°的那一圈的刻度．教师：想一想，如何测量哈尔滨在北京的北偏东多少度？学生：先以北京为中心画个十字架，上北下南、左西右东，量正北方向所在射线与北京和哈尔滨所连射线的夹角．教师：在测量角的度数时我们发现，有时候量角器量出来的度数不是整数，还有没有比“度”更小的单位，让测量得更精确些？教师：在实际生活中，有时我们要求角的测量结果更精确，这时就要用比度数更小的单位表示结果．比度还小的角的单位是分、秒，它们之间的换算关系是1°＝60′，1′＝60″，右上角的小圆圈表示度，一撇表示分，两撇表示秒．三、举例分析例(课件出示教材第115页例题)学生完成后教师点评．四、练习巩固教材第116页“随堂练习”第1，2题．五、小结1．什么是角？2．如何表示角？3．度、分、秒之间怎样换算？六、课后作业教材第117页习题4.3第1～3题．本节课的内容是角，是在学生已经初步认识长方形、正方形、三角形的基础上进行教学的．在教学过程中，使用课件及实物图进行演示，并联系实际让学生理解角的概念，切实感受到数学来源于生活，生活中处处有数学．课堂上，以学生为主，教师引导学生探索角的初步知识，为学生提供足够的时间和空间，使学生在轻松愉快的环境下学习．。

第四章基本平面图形3．角一、学生起点分析本节课是教材第四章《平面图形及其位置关系》的第三节，学生在学习了直线、射线和线段性质的基础上，学习由它们组成新的几何图形——角，同时使学生认识：几何图形是由简单到复杂的组合过程。

本课主要通过丰富的实例理解角的概念（包括角的静态描述和动态描述），知道角的多种表示方法和角的度量单位及其简单换算。

二、教学目标和重难点教学目标：1.通过丰富的实例，理解角的静态定义，能在具体情境中表示角。

2.通过实物演示，理解角的动态定义，进一步认识锐角、钝角、直角、平角、周角及其大小关系。

3.认识角的常用度量单位：度、分、秒，并会进行简单的换算。

教学重点：角的概念及表示方法，角的度量单位换算。

教学难点：在不同环境中恰当地表示角。

三、教学过程设计本节课由五个教学环节组成，它们是①直观感知“角”，描述角的静态定义；②归纳角的四种表示方法；③演示动态，引出角的动态定义；④角的度量单位及换算；⑤达标反思，归纳交流。

其具体内容与分析如下：（一）直观感知“角”，描述角的静态定义内容：1、“角”在我们生活中随处可见，你能在图中找到角吗？2.活动：画一个角。

问题：大家都是画了两条什么线？（射线）这两条射线有什么关系？（有公共端点）3.角的定义：角是由两条具有公共端点的射线所组成的图形，两条射线的公共端点叫这个角的顶点，两条射线是这个角的两边。

目的：用丰富的实例，让学生对角有直观认识，激发学生进一步探索的兴趣。

通过画角引出角的静态定义。

效果：角的概念的表述是一个难点。

让学生先画角，回顾画角的过程启发学生描述角的定义，显得自然，水到渠成。

（二）归纳角的四种表示方法BAC ∠ , A ∠ α∠ 1∠1.归纳角的四种表示方法：（1）用三个大写字母；如∠BAC ；（2）用一个大写字母，如∠A ；（3）用一个希腊字母，如∠α；（4）用一个数字，如∠1。

2.下面每幅图中各有几个角？用适当方法分别表示下图中的每个角。

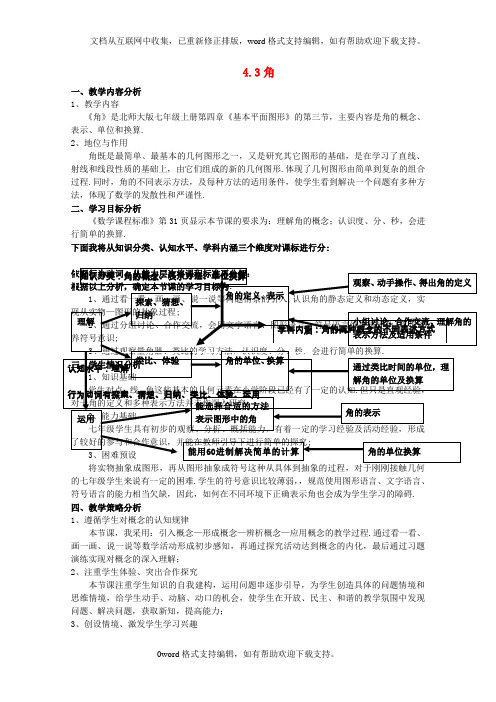
4.3角一、教学内容分析1、教学内容《角》是北师大版七年级上册第四章《基本平面图形》的第三节，主要内容是角的概念、表示、单位和换算.2、地位与作用角既是最简单、最基本的几何图形之一，又是研究其它图形的基础，是在学习了直线、射线和线段性质的基础上，由它们组成的新的几何图形.体现了几何图形由简单到复杂的组合过程.同时，角的不同表示方法，及每种方法的适用条件，使学生看到解决一个问题有多种方法，体现了数学的发散性和严谨性.二、学习目标分析《数学课程标准》第31页显示本节课的要求为：理解角的概念；认识度、分、秒，会进行简单的换算.下面我将从知识分类、认知水平、学科内涵三个维度对课标进行分:将实物抽象成图形，再从图形抽象成符号这种从具体到抽象的过程，对于刚刚接触几何的七年级学生来说有一定的困难.学生的符号意识比较薄弱，，规范使用图形语言、文字语言、符号语言的能力相当欠缺，因此，如何在不同环境下正确表示角也会成为学生学习的障碍.四、教学策略分析1、遵循学生对概念的认知规律本节课，我采用：引入概念—形成概念—辨析概念—应用概念的教学过程.通过看一看、画一画、说一说等数学活动形成初步感知，再通过探究活动达到概念的内化，最后通过习题演练实现对概念的深入理解；2、注重学生体验、突出合作探究本节课注重学生知识的自我建构，运用问题串逐步引导，为学生创造具体的问题情境和思维情境，给学生动手、动脑、动口的机会，使学生在开放、民主、和谐的教学氛围中发现问题、解决问题，获取新知，提高能力；3、创设情境、激发学生学习兴趣本课我从和学生谈到“换个角度看人生”的话题开始，以告诉学生在生活中要学会“换位思考”结尾，即首尾呼应，又进行了情感教育，使学生意识到数学能启迪智慧，点亮人生，激发学生学习数学、应用数学的热情.五、教学过程依据“目标导引教学”这一理念，本节课采取“目标、教学、评价一致性”的教学设计,同时采用“点拨式自主学习”的教学方法：布置作业:必做： 习题4.3 一、知识技能1、2 二、问题解决3四、随堂练习，巩固提高 检测目标1、2、3的达成通过让学生板画：将每个景点抽象成点，画出几何示意图，从而正确的表示出角1、这是一个公园的示意图（1）海洋世界在大门的正东方向，你能说出它在大门的北偏东多少度吗？（2）虎豹园、猴山、大象馆分别在大门的北偏东（或南偏东）多少度？（3）在图中连接各个景点与大门，并用适当方式表示各角2、（1）0.25°等于多少分? 等于多少秒?（2）2700″等于多少分? 等于多少度?设计意图通过练习帮助学生加快熟练角的各种表示方法，单位换算，逐步渗透具体到抽象的数学思想方法.五、师生交流，归纳小结 培养归纳能力、激发学习热情通过提问，让学生总结、归纳本节课学习的主要内容一、请学生总结这节课的收获二、老师送给学生的一段话：当你因为老师的严厉批评而心生不满时，换个角度想一想，成长的路上，怎能缺少老师的辛勤培育！当你因为父母的严格要求而满腹牢骚时，换个角度想一想，父母是这个世上最爱你的人！当你在学习上遭遇挫折而沮丧气馁时，换个角度想一想，不经历风雨，怎能见彩虹？当你因为一道数学题百思不得其解时，换个角度想一想，也许柳暗花明又一村！设计意图培养学生及时复习、梳理知识点的习惯.小结的形式符合学生的思维发展规律，能优化认知结构，提高学生的思维水平. 同时，进行情感教育，用数学联系生活，使学生意识到数学能够启迪智慧，点亮人生，激发学生学习数学的热情.选作：一、如图1，数一数图中有多少个角，你是怎样数的？二、如图2，怎样表示图中的角？。

第四章基本平面图形3．角一、学生起点分析本节课是教材第四章《平面图形及其位置关系》的第三节，学生对点、线、角这些基本的几何元素在小学阶段已经有了一定的认知水平，在此基础上进一步对这些几何元素进行再认知、再探索，通过螺旋上升的方式加深拓展。

本课主要通过丰富的实例回顾和理解角的概念（包括角的静态描述和动态描述），知道角的多种表示方法。

具体讲，角就是在学习了直线、射线和线段性质的基础上，由它们组成新的几何图形，从而使学生认识：几何图形是由简单到复杂的组合过程。

通过角的不同表示法，使学生看到解决一个问题有多种方法以及每一种方法的适用条件，培养学生思维的发散性和严谨性。

二、教学任务分析本课时的教学内容安排，首先引导学生回顾小学阶段对于角的概念的认知，通过生活中角的实例的例举和展示，让学生比较、讨论角的特征，认识到角就是在学习了直线、射线和线段的基础上，由它们组成新的几何图形。

再帮助学生归纳出角的定义，通过角的不同表示方法的比较，在学生充分对比、讨论、交流的基础上，归纳出角的不同表示方法的特点和适用条件，最后在巩固练习和评价小结的基础上结束。

教学中要通过创设适当的情境激发学生的求知欲，引导学生在充分比较讨论的基础上解决问题并归纳结论。

根据以上分析,确定本节课的教学目标如下：1.通过丰富的实例，进一步理解角的有关概念；会根据具体环境恰当的表示一个角。

认识角的常用度量单位：度、分、秒，并会进行简单的换算。

（知识与技能）2.通过实际操作，体会角在实际生活中的应用，培养学生的抽象思维。

（过程与方法）3.通过在图片、实例中找角，培养学生的观察力，能把实际问题转化为数学问题，培养学生对数学的好奇心与求知欲。

（情感与态度）教学重点：角的概念及表示方法；教学难点：在不同环境中恰当地表示角。

三、教学过程设计本节课由五个教学环节组成，它们是①情景引入；②感知定义；③自学归纳，思辨求真；④动手操作、解决问题；⑤师生交流，归纳小结。

第四章基本平面图形3角教学目标1.让学生理解角的定义及有关概念.2.让学生用运动的观点理解角、直角、平角、周角等概念.3.使学生掌握角的表示方法.4.让学生学会度、分、秒的转化和运算.教学重难点重点：角的定义及有关概念，角度的测量，以及度、分、秒的互化.难点：度、分、秒的互化.教学过程导入新课问题1：以前我们曾经认识过角，你们能从这些图形中指出角吗？问题2：我们已经认识了射线，从一点可以引出多少条射线？问题3：如果从一点出发任意取两条射线，那出现的是什么图形？（通过后面两个问题，使学生认识到几何图形都是由基本元素构成的，这是建模思想的初步渗透）探究新知(一)角的定义探究1：学生在练习本上画出一个角，并思考自己是怎样画成一个角的？（教师在黑板上同步演示角的画法，学生归纳、观察后给出角的定义1）角的定义1：角由两条具有公共端点的射线组成.探究2：教师拿出教学用的圆规演示角的动态形成过程，从而生成一个角.学生观察、归纳并总结出角的定义2.角的定义2：角也可以看成是一条射线绕着它的端点旋转而成的.起始位置的射线叫做这个角的始边；终止位置的射线叫做这个角的终边.(二)角的表示探究：如图，（1）用适当的方式分别表示图中的每个角.（2）∠BAC，∠CAD和∠BAD能用∠A来表示吗？（学生通过观察、分析，进一步掌握角的表示方法）结论：一个角可以有以下表示方法：图1（1）如图1，用三个大写字母表示：∠AOB或∠BOA .注意:顶点的字母必须写在中间.（2）如图1，用一个大写字母表示：∠O .注意:当两个或两个以上的角有同一个顶点时，不能用一个大写字母表示. （3）如图1，用一个数字表示：∠1.注意：在角的内部靠近角的顶点处画一弧线，写上数字.（4）如图2，用一个希腊字母表示：∠α.图2注意：在角的内部靠近角的顶点处画一弧线，写上希腊字母.(三)直角、平角、周角探究：裁纸刀在开合过程中形成了大小不同的角.你还能举出其他类似的例子吗？结论：角也可以看成是由一条射线绕着它的端点旋转而成的，如图.当终边旋转到与始边垂直时，所成的角叫做直角.当终边和始边成一条直线时，所成的角叫做平角.终边继续旋转，当它又和始边重合时，所成的角叫做周角.一个直角=90°，一个平角=180°， 一个周角=360°. 例1 下列说法正确的是 ( ) A.平角就是一条直线 B.周角就是一条射线 C.小于平角的角是钝角D.一个周角的度数等于四个直角的度数和解析：平角不是一条直线，故A 错；角和射线不是一个概念，故B 错；小于平角的角不一定是钝角，还可能是直角和锐角，故C 错；一个周角=360°，一个直角=90°，故D 正确. 答案：D (四) 角度的换算把一个周角分成360等份，每一份就是1度的角，记作1°. 把1°的角分成60等份，每一份叫做1分的角，记作1′. 把1′ 的角分成60等份，每一份叫做1秒的角，记作1″. 所以，角的度、分、秒是60进制的，这和时间的时、分、秒是一样的.1°的160 为1分，记作1′，1°＝60′. 1′的160为1秒，记作1″，即1′＝60″.例2 (1)把25.72°用度、分、秒表示; (2)把45°12′30″化成度.解： (1)0.72°=0.72×60′=43.2′，0.2′=0.2×60″=12″， ∴ 25.72°=25°43′12″.(2)30″=30×(160)′=0.5′，12.5′=12.5×(160)°≈0.21°，∴ 45°12′30″=45.21°.总结：（1）是由高级单位向低级单位化；（2）是由低级单位向高级单位化.它们都必须是逐级进行的，“越级”化单位容易出错，转化时，要熟记它们之间的换算关系，将度、分、秒化为度的一般公式为a°b′c″=[a+b+c6060]°.(五)角的度量阅读并完成课本第116页做一做.(学生自主完成，教师指导总结)角的度量步骤：（1）对中：顶点对中心.（2）对线：一边与刻度尺的零度线重合.（3）读数.课堂练习1.下列语句正确的是（）A.两条直线相交，组成的图形叫做角B.两条有公共端点的线段组成的图形叫角C.两条有公共点的射线组成的图形叫角D.从同一点引出的两条射线组成的图形叫角2.下列说法正确的是（）A.平角是一条直线B.一条射线是一个周角C.两条射线组成的图形叫做角D.两边成一直线的角是平角3. 下列四个图中，能用∠1、∠AOB、∠O三种方法表示同一个角的是（）A BC D4.（1）131°28′﹣51°32′15″=.（2）58°38′27″+47°42′40″=.5.（1）用度、分、秒表示48.26°；（2）用度表示37°24′36″；（3）42°16′+18°23′×2；（4）90°−19°12′÷6.6. 某火车站的钟楼上装有一个电子报时钟，在钟面的边界上，每一分钟的刻度处都装有一只小彩灯.(1)晚上9时30分时，时针与分针所夹的角内有多少只小彩灯(包括分针处的彩灯)?(2)晚上9时35分20秒，时针与分针所夹的角内有多少只小彩灯?参考答案1.D2.D3.D4.（1）79°55′45″（2）106°21′7″5. 解：（1）48.26°=48°+0.26×60′=48°15′+0.6×60″=48°15′36″；（2）根据1°=60′，1′=60″得，36″÷60=0.6′，24.6′÷60=0.41°，所以37°24′36″用度来表示为37.41°；（3）42°16′+18°23′×2=42°16′+36°46′=78°62′=79°2′；（4）90°−19°12′÷6=90°−18°72′÷6=90°−3°12′=86°48′.6. 解：(1)晚上9时30分时，时针与分针之间有(45+3060×5)−30=17.5（个）小格，中间有17个分钟刻度，而每一个分钟刻度处装有一只小彩灯，连同分针处的彩灯，时针与分针所夹的角内共有18只小彩灯.(2)晚上9时35分20秒，时针与分针之间有202035 45366056060⎛⎫-+⎪⎝⎭÷×111218＝（个）小格，中间有12个分钟刻度，而每一个分钟刻度处装有一只小彩灯，所以晚上9时35分20秒时，时针与分针所夹的角内有12只小彩灯.课堂小结布置作业完成教材习题4.3.板书设计第四章基本平面图形3 角(一) 角的定义角的定义1：角是两条具有公共端点的射线所组成的图形角的定义2：角也可以看成是由一条射线绕着它的端点旋转而成的图形(二)角的表示（1）用三个大写字母表示；（2）用一个大写字母表示；（3）用一个数字表示；（4）用一个希腊字母表示.(三) 直角、平角、周角(四) 角度的换算1°的160为1分，记作1′，即1°＝60′.1′的160为1秒，记作1″，即1′＝60″.(五) 角的度量。

7年级数学上册北师版第4章基本平面图形教案、学案、说课稿、教学设计目录4.1 线段、射线和直线【教案】4.1 线段、射线和直线【学案】4.2 比较线段的长短【教案】4.2 比较线段的长短【说课稿】4．3 角【教案】4．3 角【说课稿】4．3 角【学案】4.4 角的比较【教案】4.4 角的比较【学案】4.4 角的比较【说课稿】4.5.1多边形【教案】4.5.1多边形【教学设计】4.5.1多边形【说课稿】4.5.1多边形【学案】4.5.2 圆的初步认识【教案】4.5.2圆的初步认识【说课稿】第四章达标测试卷4.1 线段、射线和直线【教案】【教学目标】知识与技能1．理解线段、射线和直线的概念,并能理解它们的区别与联系。

2．能用几何语言描述直线的性质.3．会用字母表示线段、射线、直线,会根据语言描述画出图形.过程与方法1．通过对直线、射线、线段概念的教学培养学生的几何想象能力和观察能力,用运动的观点看待几何图形.2．通过操作活动获得两点确定一条直线等实践操作活动的实验.情感、态度与价值观初步体验图形是有效描述现实世界的重要手段,并能应用空间与图形知识解决生活中的现象并解决简单的实际问题,体会研究几何图形的意义.【教学重难点】重点:理解并掌握直线的两条性质,会用字母表示图形,并根据语言描述画出图形.难点:直线的两条性质的理解与应用.【教学过程】一、创设情境,引入新课“神舟十号”载人飞船发射成功,人们为之欢欣鼓舞,为了保障它的安全运行,科研人员时刻都在监视着它的一举一动.可是在飞船上天后,肉眼、望远镜无法看清它时怎么办呢?即使在先进的科研装备中,飞船也只是显示为一个点,科研人员正是利用这个点运动成的线路来研究飞船的运行状况的,利用点动成线来研究问题,竟是这般神奇!这节课我们就来学习线的相关知识.知识回顾,问题展示:师:1.六棱柱由什么围成?面与面相交成什么?线与线相交成什么?2.点动成什么?线动成什么?面动成什么?学生回答.生活情景展示(图片):师:竖琴中绷紧的琴弦,马路上的人行横道线,还有六棱柱的棱,都可以近似地看作线段.线段有两个端点.将线段向一个方向无限延伸,就形成了射线.如:手电筒打开后,有一束光线,它可以射向很远的地方,这束光线可近似地看作射线,探照灯也是一样.射线有一个端点.将线段向两个方向无限延伸,就形成直线.如笔直的铁轨向两方无限延长,它可以近似地看作直线,直线没有端点.师:生活中哪些物体可以近似地看作线段、射线、直线?学生回答.二、讲授新课看一看下面分别是什么图形,有什么特征.1.线段:有两个端点,能度量大小.2.射线:有一个端点,并向一方无限延伸,不能度量大小.3.直线:没有端点,并向两个方向无限延伸,不能度量大小.师:在几何中,我们怎样表示线段、射线和直线呢?学生阅读课本,举手回答.师:在几何中,我们常用字母表示图形,一个点可以用一个大写字母表示,如图(1)中的两点分别用字母A和B表示,这两点分别记作点A和点B.如图(1)中,以A、B为端点的线段,记作线段AB或线段BA.有时一条线段也可以用一个小写字母表示,如图(2),记作线段a.由此可知,线段有两种表示方法:一条线段可以用它的两个端点的大写字母表示,也可用一个小写字母表示.师:表示线段的两个字母没有顺序性,如线段BA与线段AB表示的是同一条线段;表示线段时,在字母的前面一定要写上“线段”两字.一条射线可以用它的端点和射线上的另一点表示,如图(3)中的射线,记作射线OM,其中表示端点的字母必须写在另一个字母的前面,而且在两个字母的前面要写上“射线”两字.师:1.表示射线的两个大写字母中第一个一定是端点.2.同一条射线有不同的表示方法,如下图中的射线,可以表示为射线AB,也可表示为射线AC.3.端点相同的射线不一定是同一条射线,端点不同的射线一定不是同一条射线.4.两条射线为同一条射线必须具备的条件:(1)端点相同;(2)延伸的方向相同.一条直线可以用在这条直线上的两个点来表示,如图(4)中的直线记作直线AB或直线BA,一条直线也可以用一个小写字母表示,如图(5),可以记作直线l.所以直线也有两种表示方法.师:1.字母前要注明直线两字.2.表示直线的两个字母也可交换位置,但射线不行,它具有方向性,端点在前,射线上任意一点在后.三、变式训练1.如图所示:射线AB、射线AC、射线BC是不是同一条射线?2.如图所示:(1)图中有几条直线?有几条线段?如何表示它们?(2)图中有几条射线?能表示的射线有几条?如何表示?问题展示:已知点A,B,C,D,按要求画图.画直线BC.连接AB,AC.画射线AD.延长线段AB,反向延长射线AD.如图所示:图中有条线段, 条射线, 条直线.学生回答,教师点评.四、再引入新课出示墨盒:请一个同学演示使用墨盒弹出一条直线的过程.提出问题:为什么这样拉出的线是直的,其关键是什么?这节课我们就来解决这个问题.师:请同学们总结一下,直线、射线、线段之间的区别与联系?学生回答,教师点评.活动(一) 两点确定一条直线师:请同学们按要求画出直线,你们从中发现了什么吗?1.过一点A画直线.2.过两点A、B画直线.学生画图探究,得出结论.教师找两位同学上黑板画图.师:利用动画展示过一点可以画出无数条直线.过两点可以画一条直线,即两点确定一条直线.如果将一根木条固定在墙上,至少需几个钉子?学生回答.师:你还能举出一些生活中的例子吗?学生举例回答.师:建筑工人砌墙,如何拉参照线?木工师傅锯板时,怎样弹线?教师总结:经过两点有且只有一条直线,即两点确定一条直线.学生回答:活动(二) 两直线相交,只有一个交点师:两条直线相交,有几个交点?学生回答.师:两条直线相交,会有两个交点吗?学生交流探讨,举手回答.师:(反证法)若两直线相交,有两个交点,由直线的性质“两点确定一条直线”知,过这两个交点的直线为同一条直线,这与假设相矛盾.所以两直线相交,只有一个交点.五、变式训练1.平面内三点可确定多少条直线?2.请你探究:(1)平面上有两条直线,最多有多少个交点?(2)平面上有三条直线,最多有多少个交点?(3)平面上有n条直线,最多有多少个交点?学生画图回答.师:问题1中的三个点要分类讨论:看是否在同一直线上;问题2中要看增加一条直线,与其他直线最多有几个交点.问题展示:1.已知线段AB,按下列要求画出图形.(1)延长线段AB到C;(2)在直线AB外取一点D;(3)连接BD;(4)作射线DA.2.已知平面内的三个点A,B,C,过其中每两个点画直线,可以画出几条直线?六、课堂小结1.这节课主要学习了哪些内容?2.通过本节课的学习,你有什么体会?能否与同学们交流一下?学生回答.教师总结:(1)线段、射线、直线的概念;(2)它们的两种表示方法:两个大写字母,一个小写字母.（3）直线的两条性质.（4）直线性质的应用.（5）描述图形及其表示.4.1 线段、射线和直线【学案】【学习目标】1．使学生在了解直线概念的基础上，理解射线和线段的概念，并能理解它们的区别与联系．2．通过直线、射线、线段概念的教学，培养几何想象能力和观察能力，用运动的观点看待几何图形．3．培养对几何图形的兴趣，提高学习几何的积极性．【学习重难点】重点：直线、射线、线段的概念．难点：对直线的“无限延伸”性的理解．【学习方法】小组合作学习【学习过程】模块一预习反馈一、学习准备1.请同学们阅读教材，并完成随堂练习和习题2．（1）绷紧的琴弦、人行横道线都可以近似地看做。

3 角【知识与技能】1.通过实际情境，理解角的有关概念，掌握角的表示方法.2.会进行角的度量，以及度、分、秒的互化.3.进一步认识锐角、钝角、直角、平角、周角及其大小关系.【过程与方法】通过问题情境，认识角、表示角、度量角、进行角的互化，经历角的静态定义到动态定义的形成过程，体会运动变化的思想方法.发展学生的符号感和数感.【情感态度】结合本课教学特点，教育学生热爱生活，热爱学习，激发学生学习兴趣.【教学重点】理解角的概念与表示方法，学会角度的测量，以及度、分、秒的互化.【教学难点】度、分、秒的互化.一、情境导入，初步认识教材第114页最上方的彩图及相关问题.【教学说明】学生很容易从生活中的图形中找到角.初步感受角的形象，体会角与生活的紧密联系.二、思考探究，获取新知1.角的概念与表示方法问题1 角是由什么图形组成的？角有哪些表示方法？【教学说明】学生在小学对角的概念与表示方法有一定的了解，此时教师加以规范，有助于学生进一步掌握角的概念及表示方法.【归纳结论】角由两条具有公共端点的射线组成，两条射线的公共端点是这个角的顶点，这两条射线是角的两边.角的表示方法常见的有三种：（1）用三个或一个大写的英文字母表示；（2）用一个小写的希腊字母表示；（3）用数学标注.注意：顶点处只有一个角时才能用一个大写的英文字母表示.问题2 教材第114页下方“做一做”.【教学说明】学生通过观察，分析，进一步掌握角的表示方法.2.用旋转的观点描述角及认识平角，周角问题3 教材第115页“议一议”.【教学说明】学生通过观察，从旋转的角度体会角的形成.【归纳结论】角可以看成是由一条射线绕着它的端点旋转而成的.3.角的度量及度、分、秒的换算问题4 在小学数学中，我们已知道：1平角=180°，1周角=360°.度量角的单位除了度，还有哪些？相邻单位间的进率又是多少呢？【教学说明】教师引导学生了解角的度量单位，掌握相邻单位间的进率.【归纳结论】为了更精密地度量角，我们规定：问题5 计算：（1）1.45°等于多少分？等于多少秒？（2）1800″等于多少分？等于多少度？【教学说明】学生通过计算，与同伴进行交流，熟练掌握度、分、秒的计算.问题6 教材第116页“做一做”.【教学说明】学生通过观察，动手操作，进一步掌握角的表示方法和角的度量，会用角度来表示方位.三、运用新知，深化理解1.下列说法正确的是（）A.平角是一条直线B.一条射线是一个周角C.两边成一条直线时组成的角是平角D.一个角不是锐角就是钝角2.教材第116页下方的“随堂练习”第1题.3.教材第116页下方的“随堂练习”第2题.【教学说明】学生自主完成，检测对角的有关知识的掌握情况，加深对新学知识的理解，对学生的疑惑、教师应及时指导.完成上述题目后，教师引导学生完成练习册中本课时练习的课堂作业部分.【答案】1.C2.(1)北偏东90°(2)虎豹园在南偏东0°（正南方），猴山在北偏东0°（正北方），大象馆在北偏东45°；（3）图略.∠AOC=∠AOB=90°，∠AOD=∠BOD=45°，∠COD=135°,∠BOC=180°；（4）锐角有∠BOD、∠AOD、∠AOC,钝角为∠COD、∠BOC,直角为∠AOB、∠AOC,平角为∠BOC.3.(1)15 ′，900″；（2）45′，0.75°.四、师生互动，课堂小结通过这节课的学习，你掌握了哪些新知识？还有哪些疑问？【教学说明】教师引导学生回顾知识点，让学生大胆发言，积极与同伴交流，加深对知识的理解.【板书设计】1.布置作业：从教材“习题4.3”中选取.2.完成练习册中本课时的相应作业.本节课从学生了解角的概念及表示方法，到角的度量及度、分、秒的换算，培养学生动手动脑习惯，激发学生学习兴趣.第一章测评(时间:45分钟,满分:100分)一、选择题(本大题共8小题,每小题4分,共32分.下列各题给出的四个选项中,只有一项符合题意)1.(2018·湖北咸宁中考)咸宁冬季里某一天的气温为-3 ℃~2 ℃,则这一天的温差是()A.1 ℃B.-1 ℃C.5 ℃D.-5 ℃2.杨梅开始采摘啦!每筐杨梅以5千克为基准,超过的千克数记为正数,不足的千克数记为负数,记录如图,则这4筐杨梅的总质量是()A.19.7千克B.19.9千克C.20.1千克D.20.3千克3.下列说法正确的有()①一个数不是正数就是负数;②海拔-155 m表示比海平面低155 m;③负分数不是有理数;④零是最小的数;⑤零是整数,也是正数.A.1个B.2个C.3个D.4个4.小灵做了以下4道计算题:①-6-6=0;②-3-|-3|=-6;③3÷×2=12;④0-(-1)2 020=-1.则她做对的道数是()A.1B.2C.3D.45.(2018·黑龙江齐齐哈尔中考)“厉害了,我的国!”2018年1月18日,国家统计局对外公布,全年国内生产总值(GDP)首次站上82万亿元的历史新台阶.把82万亿用科学记数法表示为()A.8.2×1013B.8.2×1012C.8.2×1011D.8.2×1096.有理数a,b,c在数轴上对应的点如图所示,则下列式子正确的是()A.ac>bcB.|a-b|=a-bC.-a<-b<cD.-a-c>-b-c7.已知①1-22;②|1-2|;③(1-2)2;④1-(-2),其中相等的是()A.②和③B.③和④C.②和④D.①和②8.若(-ab)2 019>0,则下列各式正确的是()A.<0B.>0C.a>0,b<0D.a<0,b>0二、填空题(本大题共4小题,每小题4分,共16分)9.-2的相反数是,倒数是,绝对值是.10.在数轴上,与-3对应的点距离4个单位长度的点有个,它们表示的数是.11.近似数20.995精确到百分位是.12.某品种兔子,一对兔子每个月能繁殖3对小兔子,而每对小兔子一个月后也能繁殖3对新小兔子,总之,所有的每对兔子都是每月繁殖3对小兔子.如果开始只有一对兔子,那么半年后有对兔子(不考虑意外死亡).三、解答题(本大题共5小题,共52分)13.(12分)计算:(1)(-49)-(+91)-(-5)+(-9);(2)-17+17÷(-1)11-52×(-0.2)3;(3)-5-.14.(10分)某人用400元购买了8套儿童服装,准备以一定价格出售.如果每套儿童服装以55元的价格为标准,实际出售时超出的记作正数,不足的记作负数,记录如下:+2,-4,+2,+1,-2,-1,0,-2.(单位:元)(1)通过计算说明当他卖完这8套儿童服装后是盈利还是亏损.(2)每套儿童服装的平均售价是多少元?15.(10分)观察下列各式:13=12,13+23=32,13+23+33=62,13+23+33+43=102,……(1)说出等式左边各个幂的底数与右边幂的底数之间有什么关系;(2)利用上述规律,计算13+23+33+43+…+1003的值.16.(10分)利用运算律有时能进行简便计算.例198×12=(100-2)×12=1 200-24=1 176;例2-16×233+17×233=(-16+17)×233=233.请你参考黑板中老师的讲解,用运算律简便计算:(1)999×(-15);(2)999×118+999×-999×18.17.(10分)如图,小玉有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:-3 -5 0 +3 +4(1)从中抽出2张卡片,使这2张卡片上的数字的乘积最大,则应如何抽取?最大的乘积是多少?(2)从中抽出2张卡片,使这2张卡片上的数字相除的商最小,则应如何抽取?最小的商是多少?(3)从中抽出2张卡片,使这2张卡片上的数字经过加、减、乘、除、乘方中的一种运算后,得到一个最大的数,则应如何抽取?最大的数是多少?(4)从中抽出4张卡片,用学过的运算方法,要使结果为24,则应如何抽取?写出运算式子(一种即可).参考答案第一章测评一、选择题1.C2-(-3)=5 ℃.2.C3.A4.C5.A6.D7.A因为①1-22=1-4=-3;②|1-2|=|-1|=1;③(1-2)2=(-1)2=1;④1-(-2)=1+2=3,所以相等的是②和③.8.A因为(-ab)的奇次幂大于0,所以-ab>0,则ab<0,即a,b异号,商为负数,但不能确定a,b谁正谁负.二、填空题9.2-210.2-7和1满足要求的点有2个,分别位于-3的两侧且到-3对应的点的距离都是4,右边的数为-3+4=1,左边的数为-3-4=-7.11.21.00精确到百分位即保留两位小数,根据四舍五入法可得20.995≈21.00.12.4 096结合乘方的定义可知:开始有兔子的对数是1,1个月后有4对兔子,以后每一个月后每一对兔子都变成4对兔子,依次类推,可得6个月后有46对小兔子.三、解答题13.解(1)原式=-49-91+5-9=-49-91-9+5=-149+5=-144.(2)原式=-17+17÷(-1)-25×=-17+(-17)-=-34+=-33.(3)原式=-5-=-5-=-5-=-5+=-4.14.解(1)售价总额为55×8+2-4+2+1-2-1+0-2=440-4=436(元).436-400=36(元),即当他卖完这8套儿童服装后盈利了36元.答:他卖完这8套儿童服装后是盈利.(2)436÷8=54.5(元).答:每套儿童服装的平均售价是54.5元.15.解(1)左边各个幂的底数之和等于右边幂的底数.(2)原式=(1+2+3+4+…+100)2=5 0502=25 502 500.16.解(1)原式=(1 000-1)×(-15)=-15 000+15=-14 985.(2)原式=999×=999×100=99 900.17.解(1)抽取-3,-5,最大的乘积是15.(2)抽取-5,+3,最小的商是-.(3)抽取-5,+4,最大的数为(-5)4=625.(4)答案不唯一,如抽取-3,-5,0,+3,运算式子为{0-[(-3)+(-5)]}×(+3)=24.有理数的乘法（完成时间：45分钟，满分：100分）一、选择题（每题5分，共25分）1．（-2）×（-5）的运算结果是 （ ）A.2B.5C.10D.-102．（2010·福建福州）2的倒数是( )A ．12B ．－12C ．2D ．－23．下列运算错误的是 （ ） A.31×(－3)=-1 B.－5×(－21)=－25C.8×(－2)=-10D.0×(－3)=04．若干个不等于0的有理数相乘，积的符号 ( )A.由因数的个数决定B.由正因数的个数决定C.由负因数的个数决定D.由负因数和正因数个数的差为决定5．（2010·广东广州）下列命题中，正确的是 （ ）A ．若a·b＞0，则a ＞0，b ＞0B ．若a·b＜0，则a ＜0，b ＜0C ．若a·b＝0，则a ＝0，且b ＝0D ．若a·b＝0，则a ＝0，或b ＝0二、填空题（每题5分，共25分）6．如果0a b >>，则ab ______0；如果0b a <<，则ab ______ 0．7．_______的倒数是2，31-的倒数是________.8．在-2，3，4，-5这四个数中，任取两个数相乘，所得的积最大的是 ________．9．（10-11）（11-12）（12-13）·…·（99-100）=_______．10．若0a b +<，且0ab >，则a ______ 0，b ______ 0三、解答题（每题10分，共50分）11．计算：（1）（-15）×（+13）（2）（+334）×（-1625）（3）（-2.5）×213（4）-9×[-（-13）]12．计算：（1）123×（-49）×（-2.5）×（-325）; （2）（-0.8）×（-7.82）×12.513．计算：11111 (1)(1)(1)(1)(1) 20082007200632 -----14．计算：（1）()()80181125.073-⨯⨯-⨯⎪⎭⎫⎝⎛-；（2）()()()()()84255.2125-⨯-⨯⨯-⨯-⨯-．15．2009年1月，我国北方发生了严重的干旱，若某水库的水位每天下降0.1米，经过7天后水库的水位共下降多少米？参考答案1．C；2．A；3．B；4．C；5．D；6．＞；7．-3；8．12；9．1；10．＜，＜；11．（1）原式=-5；（2）原式=125-；（3）原式=356-；（4）原式=-3；12．（1）原式=29-；（2）原式=78.2；13．原式=（20072008-）×（20062007-）×……×（23-）×（12-）=12008-；14．（1）原式=-142；（2）原式=-100000；15．7×（-0.1）=-0.7（米）答：7天后水库的水位共下降0.7米.．11。

北师大版七年级上册第四章基本平面图形课程设计一、教学目标•了解基本平面图形（三角形、四边形、五边形、六边形、圆）•能够正确使用基本平面图形的名称•能够正确区分基本平面图形的特性•能够绘制基本平面图形并计算其面积和周长二、教学重难点•教学重点：熟悉基本平面图形的名称、特性、绘制方法、计算公式等。

•教学难点：正确使用基本平面图形的名称、正确区分基本平面图形的特性。

三、教学内容和方法1. 教学内容课程内容对应课程章节三角形的认识第1节四边形的认识第2节五边形和六边形第3节圆的认识和绘制第4节2. 教学方法•授课法：通过课堂讲解和举例，认识基本平面图形的名称和特性。

•实验法：借助实验，提高学生对基本平面图形的认知，了解基本平面图形的绘制方法和计算公式。

•活动法：通过小组讨论、合作，进行互相检验、共同提升。

四、教学过程安排教学环节具体内容时间（分钟）导入激发学生学习兴趣，回顾上节课知识，介绍本节课学习5目标课堂讲解讲解基本平面图形的名称和特性30图形绘制展示基本平面图形的绘制方法和计算公式，学生跟着老20师一起练习学生自主进行不同基本平面图形的实验，巩固知识点20知识点实验活动环节学生分组合作讨论生活中的应用场景，学生互相展示25总结总结本节课学习内容，查漏补缺，明确下节课内容预习10要求五、板书设计•三角形：定义、分类、性质、图形•四边形：定义、分类、性质、图形•五边形和六边形：定义、性质、图形•圆：定义、性质、图形、圆周率六、作业布置•完成作业集锦练习册中的习题•通过自己的生活实例找到一些基本平面图形•预习下节课内容，准备好相关学习材料七、教学评估•通过课堂综合评价和作业评价，了解学生对基本平面图形的掌握情况•通过讲解、实验和活动等教学方法，开展小组互相检验的活动，提高学生学习兴趣和能力水平。