含有圆的组合图形

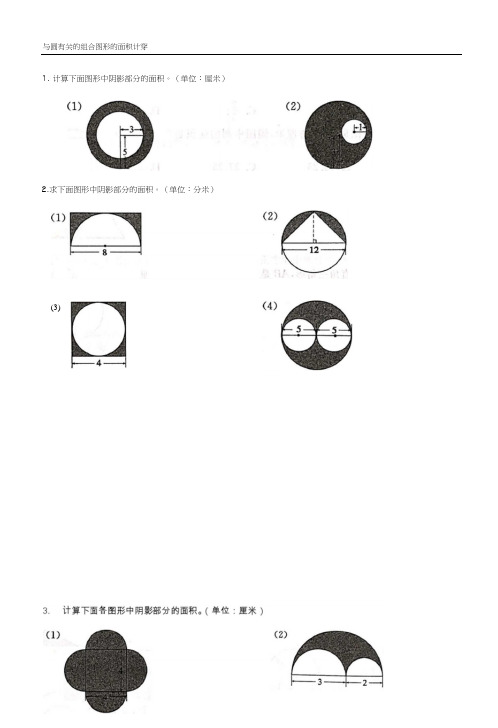
1.计算下面图形中阴影部分的面积。

（单位：厘米）2.求下面图形中阴影部分的面积。

（单位：分米）(3)位：米)(4)1.计算下面图中阴影部分的面积。

(单2.下面两个圆中直角等腰三角形的面积都是5平方厘米,求圆的面积。

3.已知扇形的面积是3.14平方厘米，求图中阴影部分的面枳。

4.如囹,己知廈角等腰三角形ABC的底边AC K 20厘爪，求阴影部分的面积。

与圈有关的组合图形的面积计算5.如图,已知扇形DEC的半径为18厘米,扇形BCF的半径为6厘米，四边形ABCD为长方形。

求阴影部分的面积。

与圈有关的组合图形的面积计算6.如图，三个圆的半径分别为1厘米、2厘米、3厘米,AB与CD垂直且过这三个圆的共有圆形0,图中阴影部分的面积是多少？7.如图，0为圆心，CO垂直于AB ,C为另一个圆的圆心f AC =BC ,三角形ABC 的面积为45平方厘爪，求阴影部分的面积。

C1.图中五个相同的圆的圆心连线构成一个边长为10厘米的正五边形,求五边形的内阴影部分-6-与圈有关的组合图形的面积计算的面积。

2.如图，两个扌圆形AOB与A'0'B'^放一起，POQO'是面积为5平方厘米的正方形，那么畫合后的图中阴影部分的面积为多少平方厘米？3.计算图中阴影部分的面积。

（单位：厘米）4.如图,已知六个圆的面积相等,而阴影部分的面积为60平方厘米。

六个圆的面积为多少平方厘米？20A fB-8-5.如图,已知大正方形的面积为100平方厘米，小正方形的面积为50平方厘米，求阴影部分的面积。

6.如图，圆0的半径是15厘米,zAOB =90° , zCOD =120° , CD =26厘米，求阴影部分的面积。

7.如图,zAOB =90° , C为AB弧的中点,已知阴影甲的面积为16平方厘米,阴影乙的面积是多少？AB与圈有关的组合图形的面积计穿8.如图,在长方形ABCD中,AD=DE=3厘米,AE=AB ,求阴影部分的面积。

圆与组合图形的面积杭州市胜利小学徐丹芳教学目标：1、在设计面积相等的图案活动中，建立基本图形组合的数学思想，并能用于解题。

2、在解题过程中归纳出求和、去空、求差、转化（对称）的算法，并能初步综合运用解题。

3、进一步培养学生空间观念，初步建立解题模型。

4、小组合作中，体验合作的力量、提升与组员沟通的能力。

教学重难点：解题方法的归纳和综合应用。

教学准备：1、课前学生完成《圆与组合图形的面积》练习整理，收集学生作业，用于上课导入。

2、准备课件。

3、学生准备学具（尺、圆规等）教学过程：一、课前练习整理导入。

出示：板书：S圆：S正=π：4T：课前，请你在这个正方形中，设计出与阴影部分面积相等的图案吗？收集整理后，发现同学们很有数学思考，我们一起来看看。

展示学生作品：……提问：1、这里有哪些基本图形？（圆、正方形、长方形、半圆、四分之一圆）2、S圆：S长是多少？（π：4）S圆：S长是多少？（π：4）师小结：这些基本的内切图形间的关系都是π：4，由基本图形直接拼成的图形关系也是π：4。

2个基本图形可以组合成多种组合图形，请看，算一算。

二、归纳基本算法。

1、★例题正方形边长是20厘米，求阴影部分面积。

去空求差求和重叠（去空求差）等2、★★例题2题，（1）翻转对称出现第一题，整体出现第二题。

学生独立解答。

同桌交流（2）上台操作讲解。

★★★（1）展示各种方法（2）总结（回顾整理）★★★★1、独立思考。

2、学生讲解。

三、拓展1、1题【例 2】草场上有一个长20米、宽10米的关闭着的羊圈，在羊圈的一角用长30米的绳子拴着一只羊(见如图)．问：这只羊能够活动的范围有多大？(圆周率取3.14)【解析】此题是小升初的一道原题，也是近些年比较新颖的一种梯形，经常会在此基础上做一些改变。

在做题之前，我们首先将羊活动的范围画出来，如图所示，接下来，根据扇形的大小，将羊活动的范围可以分成A 、B 、C、三部分，其中A是半径30米的个园，B、C分别是半径为20米和10米的个圆。

与圆有关的组合图形的面积计算--------------------------------------------------------------------------作者: _____________1.计算下面图形中阴影部分的面积。

（单位：厘米）2.求下面图形中阴影部分的面积。

（单位：分米）3.计算下面各图形中阴影部分的面积。

（单位：厘米）1.计算下面图中阴影部分的面积。

（单位：米）2.下面两个圆中直角等腰三角形的面积都是5平方厘米，求圆的面积。

3.已知扇形的面积是3.14平方厘米，求图中阴影部分的面积。

4.如图，已知直角等腰三角形ABC的底边AC长20厘米，求阴影部分的面积。

5.如图，已知扇形DEC的半径为18厘米，扇形BCF的半径为6厘米，四边形ABCD为长方形。

求阴影部分的面积。

6.如图，三个圆的半径分别为1厘米、2厘米、3厘米，AB与CD垂直且过这三个圆的共有圆形O，图中阴影部分的面积是多少？7.如图，O为圆心，CO垂直于AB，C为另一个圆的圆心，AC＝BC，三角形ABC的面积为45平方厘米，求阴影部分的面积。

1.图中五个相同的圆的圆心连线构成一个边长为10厘米的正五边形，求五边形的内阴影部分的面积。

2.如图，两个圆形AOB与叠放一起，POQ是面积为5平方厘米的正方形，那么叠合后的图中阴影部分的面积为多少平方厘米？3.计算图中阴影部分的面积。

（单位：厘米）4.如图，已知六个圆的面积相等，而阴影部分的面积为60平方厘米。

六个圆的面积为多少平方厘米？5.如图，已知大正方形的面积为100平方厘米，小正方形的面积为50平方厘米，求阴影部分的面积。

6.如图，圆O的半径是15厘米，∠AOB＝90°，∠COD＝120°，CD＝26厘米，求阴影部分的面积。

7.如图，∠AOB＝90°，C为AB弧的中点，已知阴影甲的面积为16平方厘米，阴影乙的面积是多少？8.如图，在长方形ABCD中，AD＝DE＝3厘米，AE＝AB，求阴影部分的面积。

圆的组合图形面积姓名：【知识与方法】要解决与圆有关的题目，需要注意以下几点:1、熟练掌握有关圆的概念和面试公式：圆的面积＝圆的周长=扇形的面积= 扇形的弧长=（ｎ是圆心角的度数）2、掌握解题技巧和解题方法：加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。

例1.求阴影部分的面积。

（单位:厘米)ﻫ解:这是最基本的方法:圆面积减去等腰直角三角形的面积，×-2×１＝1.14(平方厘米）ﻫﻫﻫ例２．正方形面积是7平方厘米,求阴影部分的面积。

(单位：厘米)ﻫ解:这也是一种最基本的方法用正方形的面积减去圆的面积。

ﻫ设圆的半径为r，因为正方形的面积为7平方厘米,所以=７,所以阴影部分的面积为:7-＝7－×7＝1.50５平方厘米ﻫﻫ例3．求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆,用正方形的面积减去圆的面积，所以阴影部分的面积：2×2－π＝0.8６平方厘米。

ﻫ例4.求阴影部分的面积。

(单位：厘米)ﻫ解：同上，正方形面积减去圆面积,16-π()＝16-4π=３.44平方厘米ﻫﻫ例5.求阴影部分的面积。

（单位:厘米）ﻫ解：这是一个用最常用的方法解最常见的题，为方便起见,ﻫ我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形, π()×2－16=8π-１6=９.1２平方厘米另外：此题还可以看成是１题中阴影部分的8倍。

ﻫ例6.如图:已知小圆半径为2厘米，大圆半径是小圆的3倍，问:空白部分甲比乙的面积多多少厘米?ﻫ解：两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π(）=1０0.4８平方厘米ﻫ（注：这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。

(单位:厘米）ﻫ解:正方形面积可用(对角线长×对角线长÷2，求）ﻫ正方形面积为:5×５÷2=12.5所以阴影面积为:π÷4-12.５=７.1２5平方厘米ﻫ(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形）ﻫ例8．求阴影部分的面积。

圆的组合图形面积姓名：知识与方法要解决与圆有关的题目,需要注意以下几点：1、熟练掌握有关圆的概念和面试公式：圆的面积= 圆的周长=扇形的面积= 扇形的弧长=n是圆心角的度数2、掌握解题技巧和解题方法：加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法;例1.求阴影部分的面积;单位:厘米解：这是最基本的方法：圆面积减去等腰直角三角形的面积,×-2×1=1.14平方厘米例2.正方形面积是7平方厘米,求阴影部分的面积;单位:厘米解：这也是一种最基本的方法用正方形的面积减去圆的面积;设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积;单位:厘米解：最基本的方法之一;用四个圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部分的面积：2×2-π＝0.86平方厘米;例4.求阴影部分的面积;单位:厘米解：同上,正方形面积减去圆面积,16-π=16-4π=3.44平方厘米例5.求阴影部分的面积;单位:厘米解：这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍;例6.如图：已知小圆半径为2厘米,大圆半径是小圆的3倍,问：空白部分甲比乙的面积多多少厘米解：两个空白部分面积之差就是两圆面积之差全加上阴影部分π-π=100.48平方厘米注：这和两个圆是否相交、交的情况如何无关例7.求阴影部分的面积;单位:厘米解：正方形面积可用对角线长×对角线长÷2,求正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形例8.求阴影部分的面积;单位:厘米解：右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆, 所以阴影部分面积为：π=3.14平方厘米例9.求阴影部分的面积;单位:厘米解：把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形, 所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积;单位:厘米解：同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米注: 8、9、10三题是简单割、补或平移11、例13.求阴影部分的面积;单位:厘米解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为：8×8÷2=32平方厘米12、例14.求阴影部分的面积;单位:厘米解：梯形面积减去圆面积,4+10×4-π=28-4π=15.44平方厘米 .13、例16.求阴影部分的面积;单位:厘米解：π＋π－π=π116-36=40π=125.6平方厘米14、例17.图中圆的半径为5厘米,求阴影部分的面积;单位:厘米解：上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和;所以阴影部分面积为：5×5÷2+5×10÷2=37.5平方厘米15、例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长;解：阴影部分的周长为三个扇形弧,拼在一起为一个半圆弧,所以圆弧周长为：2×3.14×3÷2=9.42厘米16、例19.正方形边长为2厘米,求阴影部分的面积;解：右半部分上面部分逆时针,下面部分顺时针旋转到左半部分,组成一个矩形;所以面积为：1×2=2平方厘米17、例25.如图,四个扇形的半径相等,求阴影部分的面积;单位:厘米分析：四个空白部分可以拼成一个以２为半径的圆．所以阴影部分的面积为梯形面积减去圆的面积,4×4+7÷2-π=22-4π=9.44平方厘米18、例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积;解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+π÷4-2=π-1+π-1=π-2=1.14平方厘米19、例28.求阴影部分的面积;单位:厘米解法一：设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=12.5弓形面积为:π÷2-5×5÷2=7.125所以阴影面积为:12.5+7.125=19.625平方厘米20、例30.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米;求BC的长度;解：两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米21、例33.求阴影部分的面积;单位:厘米解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE面积,为π+π-6=×13π-6=4.205平方厘米22、例34.求阴影部分的面积;单位:厘米解：两个弓形面积为：π-3×4÷2=π-6 阴影部分为两个半圆面积减去两个弓形面积,结果为π+π-π-6=π4+-+6=6平方厘米。

3. 计算下面各图形中阴影部分的面积。

（单位：厘米）1. 计算下面图形中阴影部分的面积。

（单位：厘米）2. 求下面图形中阴影部分的面积。

（单位：分米）1. 计算下面图中阴影部分的面积。

（单位：米）2. 下面两个圆中直角等腰三角形的面积都是5 平方厘米，求圆的面积。

3. 已知扇形的面积是3.14 平方厘米，求图中阴影部分的面积。

4. 如图，已知直角等腰三角形ABC 的底边AC长20厘米，求阴影部分的面积。

5. 如图，已知扇形DEC的半径为18厘米，扇形BCF的半径为6厘米，四边形ABCD 为长方形。

求阴影部分的面积。

6. 如图，三个圆的半径分别为1 厘米、2 厘米、3厘米，AB与CD垂直且过这三个圆的共有圆形O，图中阴影部分的面积是多少？7. 如图，O 为圆心，CO 垂直于AB，C 为另一个圆的圆心，AC＝BC，三角形ABC 的面积为45平方厘米，求阴影部分的面积。

1. 图中五个相同的圆的圆心连线构成一个边长为10 厘米的正五边形，求五边形的内阴影部分的面积。

2. 如图，两个1圆形AOB 与′′′叠放一起，POQ′是面积为 5 平方厘米的正方形，那么叠合后的图中阴影部分的面积为多少平方厘米？3. 计算图中阴影部分的面积。

（单位：厘米）如图，已知六个圆的面积相等，而阴影部分的面积为60平方厘米。

六个圆的面积为多少平方厘米？5. 如图，已知大正方形的面积为100 平方厘米，小正方形的面积为50 平方厘米，求阴影部分的面积。

6. 如图，圆O 的半径是15 厘米，∠AOB＝90°，∠COD＝120°，CD＝26 厘米，求阴影部分的面积。

7. 如图，∠AOB＝90°，C 为AB弧的中点，已知阴影甲的面积为16平方厘米，阴影乙的面积是多少？8. 如图，在长方形ABCD 中，AD＝DE＝3厘米，AE＝AB，求阴影部分的面积。

9. 如图是一个古座钟的图画，如果内圆的半径为12厘米，阴影部分的面积是多少？4.。

含有圆的组合图形的面积凌津滩中学：张帆教学目标：1、让学生结合具体情境认识组合图形的特征，掌握计算组合图形的面积的方法，并能准确掌握和计算简单组合图形的面积。

2、通过自主合作，培养学生独立思考、合作探究的意识。

3、让学生在解决实际问题的过程中，进一步体验图形和生活的联系，感受平面图形的学习价值，提高数学学习的举和学习好数学的自信心。

教学重难点：组合图形的认识及面积计算、图形分析。

教具学具准备：多媒体课件、各种基本图形纸片。

教学设计：⊙创设情境，认识圆环1．师：我们来欣赏一组美丽的图片。

课件出示圆形花坛、圆形水池外的圆形甬路、奥运五环标志、光盘……2．同学们，你们从图中发现了什么？(它们都是环形的)3．教师拿出环形光盘说明：像这样的图形，我们称它为圆环或环形。

你还知道生活中有哪些环形的物体？它们给我们的生活带来了怎样的变化？(学生结合生活实际谈谈已经知道的环形物体以及它给我们的生活带来的乐趣)4．导入新课：这节课我们一起来探讨环形的知识。

(板书课题：圆环的面积)设计意图：从学生掌握的常识和熟悉的事物入手，使其感受到数学就在我们身边，学生从直观上也感受到了环形的特点，为后面学习环形的面积奠定基础。

⊙探索交流，解决问题1．画一画，剪一剪，发现环形特点。

(1)画一画。

让学生在硬纸板上用同一个圆心分别画一个半径为10厘米和5厘米的圆。

(学生按照要求画圆)(2)剪一剪。

指导学生先剪下所画的大圆，再剪下所画的小圆。

问：剩下的部分是什么图形？(环形)师：我们也称它为圆环。

(3)教师手拿学生剪的圆环提问：这个圆环是怎样得到的？生明确：圆环是从外圆中去掉一个内圆得到的。

(4)借助图示认识圆环的各部分名称。

你知道圆环各部分的名称吗？(出示图示引导学生明确相关内容并板书)①外圆：又名大圆，它的半径用R表示。

②内圆：又名小圆，它的半径用r表示。

③环宽：指外圆半径和内圆半径相差的宽度。

2．探究圆环面积的计算方法。

(1)小组讨论，怎样求圆环的面积？(2)汇报讨论结果。