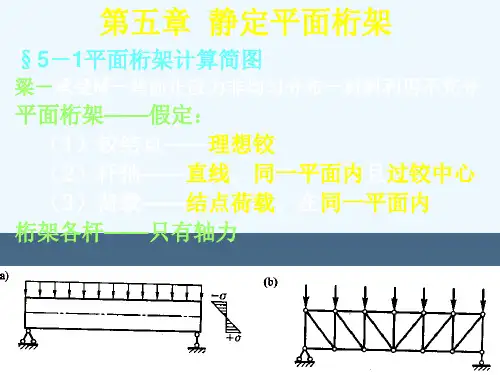
一、工程背景混凝土屋架长沙市体育馆的屋盖承重结构南京长江大桥主体结构图5-1第一节概述二、静定平面桁架结构的主要受力特征图5-2直杆铰接体系且只受结点荷载作用，其受力特性是结构内力只有轴力，而没有弯矩和剪力。
三、静定平面桁架结构的计算简图取桁架计算简图时采用的假定：（1）各杆两端用理想铰联结；（2）各杆轴线绝对平直，在同一平面内且通过铰的中心。
（3）荷载和支座反力都作用在结点上并位于桁架平面内。
通常把理想情况下计算出的应力称为“初应力”或“基本应力”；因理想情况不能完全实现的而出现的应力称为“次应力”。
四、桁架各部分的名称及分类1、名称：上弦杆下弦杆竖杆斜杆桁高（h)节间长度(d)跨度（l）2、分类：（1）按外形分：平行弦、折弦、三角形等。
图5-4（2）按竖向荷载作用下支座是否产生水平推力分：（a）无推力桁架（梁式桁架）；（b ）有推力桁架（拱式桁架）。
图5-6图5-7（3）按几何组成分：a)简单桁架：由基础或基本铰结三角形开始，依次增加二元体而形成的桁架。
b)联合桁架：若干个简单桁架按几何不变体系组成规则铰结而成的桁架。
图5-8c)复杂桁架：不属于以上两类的静定桁架（可采用“零载法”分析）。
图5-91、定义：利用各结点的平衡条件求解桁架内力的方法。
2、实质：作用在结点上的各力组成一平面汇交力系。
3、注意点：（1）轴力以拉力为正，即离开隔离体方向为正。
（2）一般结点上的未知力不能多余两个。
（3）可利用比例关系求解各轴力的铅直、水平分量。
Ny N Nx x y F F F l l l ==F N αl xl y l F NF NxF N F Ny α第二节静定平面桁架计算的结点法4、结点法举例：例1 计算图示各杆的轴力。
解：求支座反力∑∑∑===0018M M F x )(100)(800811↑=↑==KN F KN F F y y x 校核：080100806040=--++=∑yF F 1x =0F 1y =80kN F 8y =100kN 40kN 60kN 80kN 4m 4×3m=12m 图5-11分别以各结点为研究对象，求各杆之轴力：3F34y100kN80kN60kN40kNF N34F34xF N35180kNF N12F13yF13xF N13F N23F N24260kN40kN(b)3(c)(a)图5-12将计算结果标在桁架计算简图上：轴力（kN）图5-13例2 计算图示各杆的轴力。
