浙江工业大学_离散数学测_验(含答案)

《离散数学》试题及答案一、选择题（每题5分，共25分）1. 下列关系中，哪个是等价关系？（）A. 小于等于（≤）B. 大于等于（≥）C. 整除（|）D. 模2同余（≡）答案：D2. 下列哪个图是完全图？（）A. 无向图B. 有向图C. 简单图D. n阶完全图答案：D3. 设A和B为集合，若A∪B=A，则下列哪个结论成立？（）A. A⊆BB. B⊆AC. A=BD. A∩B=∅答案：B4. 下列哪个命题是永真命题？（）A. (p→q)∧(q→p)B. (p∧q)→(p∨q)C. (p→q)∧(p→¬q)D. (p∧¬q)→(p→q)答案：B5. 设G=(V,E)是一个连通图，其中V={v1,v2,v3,v4,v5}，E={e1,e2,e3,e4,e5,e6}，若G的最小生成树的边数是（）。

A. 4B. 5C. 6D. 7答案：B二、填空题（每题5分，共25分）6. 设A={1,2,3,4,5}，B={3,4,5,6,7}，则A∩B=_________。

答案：{3,4,5}7. 设图G的顶点集V={a,b,c,d}，边集E={e1,e2,e3,e4,e5}，其中e1=(a,b)，e2=(a,c)，e3=(b,d)，e4=(c,d)，e5=(d,a)，则G的邻接矩阵为_________。

答案：[0 1 1 0 0; 1 0 0 1 0; 1 0 0 1 0; 0 1 1 0 1;0 0 0 1 0]8. 设p为真命题，q为假命题，则(p∧q)∨(¬p∧¬q)的值为_________。

答案：真9. 设G=(V,E)是一个连通图，其中V={v1,v2,v3,v4,v5}，E={e1,e2,e3,e4,e5,e6}，若G的度数序列为（3,3,3,3,3,3），则G的边数是_________。

答案：1510. 下列命题中，与“若p，则q”互为逆否命题的是_________。

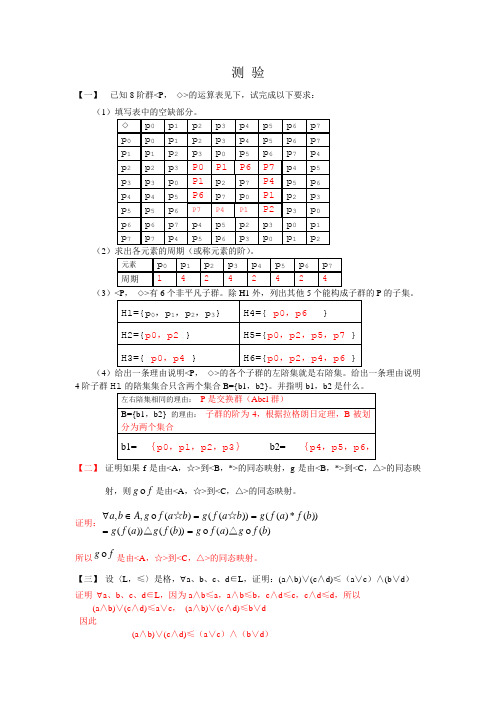
测 验【一】 已知8阶群<P ， ◇>的运算表见下，试完成以下要求：（1）填写表中的空缺部分。

（2（3 ◇P 的子集。

（4）给出一条理由说明<P ， ◇>的各个子群的左陪集就是右陪集。

给出一条理由说明4阶子群【二】 证明如果f 是由<A ，☆>到<B ，*>的同态映射，g 是由<B ，*>到<C ，△>的同态映射，则f g 是由<A ，☆>到<C ，△>的同态映射。

证明：)(△)())((△))(())(*)(())☆(()☆(,,b f g a f g b f g a f g b f a f g b a f g b a f g A b a ====∈∀所以f g 是由<A ，☆>到<C ，△>的同态映射。

【三】 设〈L ，≤〉是格，∀a 、b 、c 、d ∈L ，证明：(a ∧b)∨(c ∧d)≤（a ∨c ）∧(b ∨d ） 证明 ∀a 、b 、c 、d ∈L ，因为a ∧b ≤a ，a ∧b ≤b ，c ∧d ≤c ，c ∧d ≤d ，所以 (a ∧b)∨(c ∧d)≤a ∨c ， (a ∧b)∨(c ∧d)≤b ∨d 因此(a ∧b)∨(c ∧d)≤（a ∨c ）∧（b ∨d ）【四】 设S 是30的因子集合，S 上关系“|”是整除关系。

a)请画出该关系所对应的格的Hasse 图; b)判断是否存在子格为布尔格;c)如果存在子格为布尔格，请给出这些子格并写出布尔格的原子。

解（1）G={1，2，3，5，6，10，15，30}，其哈斯图见图 7.4.1。

(2)〈G ，|〉的所有元素个数大于等于4的不同构的子格的Hasse 图见图7.4.2。

（3）所有的子格均是分配格、模格。

图7.4.2（b ）、（f ）所示的格还是有补格。

（4）图（b ）、（f ）所示的格是布尔代数。

其中，图（b ）的原子集合为{15，6}，图（f ）的原子集合为{2，3，5}。

离散数学考试试题（A、B卷及答案）离散数学考试试题(A卷及答案)一、证明题(10分)1) (P∧Q∧A→C)∧(A→P∨Q∨C)? (A∧(P?Q))→C。

P<->Q=(p->Q)合取(Q->p)证明: (P∧Q∧A→C)∧(A→P∨Q∨C)(?P∨?Q∨?A∨C)∧(?A∨P∨Q∨C)((?P∨?Q∨?A)∧(?A∨P∨Q))∨C反用分配律((P∧Q∧A)∨(A∧?P∧?Q))∨C( A∧((P∧Q)∨(?P∧?Q)))∨C再反用分配律( A∧(P?Q))∨C(A∧(P?Q))→C2) ?(P↑Q)??P↓?Q。

证明:?(P↑Q)??(?(P∧Q))??(?P∨?Q))??P↓?Q。

二、分别用真值表法与公式法求(P→(Q∨R))∧(?P∨(Q?R))的主析取范式与主合取范式,并写出其相应的成真赋值与成假赋值(15分)。

主析取范式与析取范式的区别:主析取范式里每个括号里都必须有全部的变元。

主析取范式可由析取范式经等值演算法算得。

证明:公式法:因为(P→(Q∨R))∧(?P∨(Q?R))(?P∨Q∨R)∧(?P∨(Q∧R)∨(?Q∧?R))(?P∨Q∨R)∧(((?P∨Q)∧(?P∨R))∨(?Q∧?R))分配律(?P∨Q∨R)∧(?P∨Q∨?Q)∧(?P∨Q∨?R)∧(?P∨R∨?Q)∧(?P ∨R∨?R) (?P∨Q∨R)∧(?P∨Q∨?R)∧(?P∨?Q∨R)4M使(非P析取Q析取R)为0所赋真值,即100,二进制为4M∧6M∧50m∨1m∨2m∨3m∨7m所以,公式(P→(Q∨R))∧(?P∨(Q?R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。

真值表法:0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1 0111111111111111111为000、001、010、011、111:成假赋值为:100、101、110。

《离散数学》考试题库及答案一、填空 20% （每小题2分）1．设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且（N ：自然数集，E + 正偶数） 则 =⋃B A 。

2．A ，B ，C 表示三个集合，文图中阴影部分的集合表达式为 。

3．设P ，Q 的真值为0，R ，S 的真值为1，则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。

4．公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。

5．若解释I 的论域D 仅包含一个元素，则 )()(x xP x xP ∀→∃ 在I 下真值为 。

6．设A={1，2，3，4}，A 上关系图为则 R 2 = 。

7．设A={a ，b ，c ，d}，其上偏序关系R 的哈斯图为则 R= 。

8．图的补图为 。

9．设A={a ，b ，c ，d} ，A 上二元运算如下：A BC* a b c d a b c da b c d b c d a c d a b d a b c那么代数系统<A ，*>的幺元是 ，有逆元的元素为 ，它们的逆元分别为 。

10．下图所示的偏序集中，是格的为 。

二、选择 20% （每小题 2分）1、下列是真命题的有（ ） A ． }}{{}{a a ⊆；B ．}}{,{}}{{ΦΦ∈Φ；C ． }},{{ΦΦ∈Φ；D ． }}{{}{Φ∈Φ。

2、下列集合中相等的有（ ）A ．{4，3}Φ⋃；B ．{Φ，3，4}；C ．{4，Φ，3，3}；D ． {3，4}。

3、设A={1，2，3}，则A 上的二元关系有（ ）个。

A ． 23 ； B ． 32 ； C ． 332⨯； D ． 223⨯。

4、设R ，S 是集合A 上的关系，则下列说法正确的是（ ） A ．若R ，S 是自反的， 则S R 是自反的； B ．若R ，S 是反自反的， 则S R 是反自反的； C ．若R ，S 是对称的， 则S R 是对称的； D ．若R ，S 是传递的， 则S R 是传递的。

离散数学一、填空题(本大题共48分，共16小题，每小题3分)1.--公式为之充分必要条件是其合取范式之每一合取项中均必同时包含一命题变元及其否定2.无向图G具有是生成树，当且仅当的，若G为(n,m)连通图，要确定G的一棵生成树必删掉G的条边。

3.一个无向图的欧拉回路要求经过图中一次且仅一次，汉密顿图要求经过图中一次且仅一次。

4.设P：我生病，Q：我去学校(1)命题“我虽然生病但我仍去学校”符号化为o (2)命题“只有生病的时候，我才不去学校”符号化为o (3)命题"如果我生病，那么我不去学校”符号化为o5.设有33盏灯，拟公用一个电源，则至少需要5个插头的接线板数6.若HlAH2A-AHn是 ,则称Hl, H2, -Hn是相容的，若HlAH2A-AHn是 ,则称H1.H2, -Hn是不相容的7.设f,g,h 是N 到N上的函数(N 为自然数集合),f(n)=n+l;g(n)=2n;h(n)=0；贝lj(fdg)oh=8.K5的点连通度为 ,边连通度为o9.A={1, 2, 3, 4, 5, 6, 8, 10, 24, 36}, R 是A 上的整除关系。

子B={1, 2, 3, 4},那么B的上界是； B的下界是；：6的上确界是; B的下确界为10.命题公式P-*QAR的对偶式为11.设入={1, {2}, <t>},则A的幕集有元素个。

12.设A={0, 1,2, 3}, B={4,6, 7}, C={8, 9, 12, 14}, R1 是由A 到B 的关系,R2 是由B到C原关系，分别定义为Rl={<2, 6>, <3, 4>, <0, 7>} ;R2={<4, 8>, <4, 12>, <6, 12>,〈7, 14〉},则复合关系RloR2 为：13.设A= {<i)}, B={<t>, (<!>}},贝i]P(A) nP(B)= 。

离散数学考试题及答案一、单项选择题（每题2分，共10分）1. 在集合{1,2,3}和{3,4,5}的笛卡尔积中，元素(3,4)属于（）。

A. {1,2,3}B. {3,4,5}C. {1,2,3,4,5}D. {1,2,3}×{3,4,5}答案：D2. 命题“若x>2，则x>1”的逆否命题是（）。

A. 若x≤2，则x≤1B. 若x≤1，则x≤2C. 若x≤1，则x≤2D. 若x≤2，则x≤1答案：C3. 函数f: A→B的定义域是集合A，值域是集合B的（）。

A. 子集B. 真子集C. 任意子集D. 非空子集答案：D4. 以下哪个图是无向图（）。

A. 有向图B. 无向图C. 完全图D. 树答案：B5. 以下哪个命题是真命题（）。

A. 所有的马都是白色的B. 有些马是白色的C. 没有马是白色的D. 以上都不是答案：B二、填空题（每题2分，共10分）6. 集合{1,2,3}的子集个数为______。

答案：87. 命题“若x>0，则x>1”的逆命题是：若x>1，则______。

答案：x>08. 函数f: A→B中，若A={1,2}，B={3,4}，则f的值域可以是{3}或{4}或{3,4}，但不能是______。

答案：{1,2}9. 在有向图中，若存在从顶点A到顶点B的有向路径，则称A到B是______的。

答案：可达10. 命题逻辑中，合取（AND）的符号是______。

答案：∧三、解答题（每题15分，共30分）11. 证明：若p∧q为真，则p和q都为真。

证明：根据合取（AND）的定义，p∧q为真当且仅当p和q都为真。

因此，若p∧q为真，则p和q都为真。

12. 给定函数f: A→B，其中A={1,2,3}，B={4,5,6}，且f(1)=4，f(2)=5，f(3)=6。

请找出f的值域。

答案：根据函数的定义，f的值域是其所有输出值的集合。

因此，f的值域为{4,5,6}。

《离散数学》考试试卷（试卷库20卷）及答案第 1 页/共 4 页《离散数学》考试试卷（试卷库20卷）试题总分： 100 分考试时限：120 分钟、选择题（每题2分，共20分）1. 设论域为全总个体域，M(x)：x 是人，Mortal(x)：x 是要死的，则“人总是要死的”谓词公式表示为( )（A ）)()(x Mortal x M → （B ）)()(x Mortal x M ∧（C ）))()((x Mortal x M x →?（D ）))()((x Mortal x M x ∧?2. 判断下列命题哪个正确？( )（A ）若A∪B＝A∪C，则B ＝C （B ）{a,b}={b,a}（C ）P(A∩B)≠P(A)∩P (B)（P(S)表示S 的幂集）（D ）若A 为非空集，则A ≠A∪A 成立3. 集合},2{N n x x A n∈==对( )运算封闭（A ）乘法（B ）减法（C ）加法（D ）y x -4. 设≤><,N 是偏序格，其中N 是自然数集合，“≤”是普通的数间“小于等于”关系，则N b a ∈?,有=∨b a ( )（A ）a（B ）b（C ）min(a ，b)（D ） max(a ，b)5. 有向图D=，则41v v 到长度为2的通路有( )条（A ）0 （B ）1 （C ）2 （D ）36. 设无向图G 有18条边且每个顶点的度数都是3，则图G 有( )个顶点（A ）10 （B ）4 （C ）8 （D ）127. 下面哪一种图不一定是树？（）（A ）无回路的连通图（B ）有n 个结点n-1条边的连通图（C ）每对结点间都有通路的图（D ）连通但删去一条边则不连通的图 8. 设P ：我将去镇上,Q ：我有时间。

命题“我将去镇上,仅当我有时间”符号化为（）（A ）P →Q （B ）Q →P （C ）P Q （D ）Q P ?∨? 9. 下列代数系统中,其中*是加法运算,（）不是群。

离散数学试题及答案一、单项选择题（每题2分，共20分）1. 在集合论中，空集的表示符号是（）。

A. {0}B. ∅C. {}D. Ø答案：B2. 如果A和B是两个集合，那么A∩B表示（）。

A. A和B的并集B. A和B的交集C. A和B的差集D. A和B的补集答案：B3. 命题逻辑中，p ∧ q的真值表中，当p和q都为假时，p ∧ q的值为（）。

A. 真B. 假C. 不确定D. 无定义答案：B4. 在图论中，如果一个图中的任意两个顶点都由一条边相连，则称这个图为（）。

A. 连通图B. 无向图C. 完全图D. 有向图答案：C5. 布尔代数中，逻辑或运算符表示为（）。

A. ∧B. ∨C. ¬D. →答案：B6. 一个关系R是从集合A到集合B的二元关系，如果对于A中的每个元素x，B中都存在唯一的元素y与之对应，则称R为（）。

A. 单射B. 满射C. 双射D. 单满射答案：C7. 在命题逻辑中，如果p是假命题，那么¬p的值为（）。

A. 真B. 假C. 不确定D. 无定义答案：A8. 一个有向图是无环的，那么它一定是（）。

A. 有向无环图B. 无向无环图C. 有向有环图D. 无向有环图答案：A9. 在集合论中，如果集合A是集合B的子集，那么A⊆B表示（）。

A. A包含于BB. A是B的真子集C. A是B的超集D. A与B相等答案：A10. 命题逻辑中，p → q的真值表中，当p为真，q为假时，p → q 的值为（）。

A. 真B. 假C. 不确定D. 无定义答案：B二、多项选择题（每题3分，共15分）1. 在集合论中，以下哪些符号表示的是集合的并集（）。

A. ∪B. ∩C. ⊆D. ⊂答案：A2. 在图论中，以下哪些说法是正确的（）。

A. 有向图可以是无环的B. 无向图可以是无环的C. 有向图一定是连通的D. 无向图一定是连通的答案：A B3. 在命题逻辑中，以下哪些符号表示的是逻辑与（）。

离散考试试题及答案一、选择题（每题5分，共20分）1. 在离散数学中，下列哪个概念不是布尔代数的基本运算？A. 与B. 或C. 非D. 模答案：D2. 集合论中，下列哪个符号表示“属于”关系？A. ∈B. ∉C. ⊆D. ⊂答案：A3. 命题逻辑中，下列哪个符号表示“蕴含”关系？A. ∧B. ∨C. →D. ↔答案：C4. 关系R在集合A上是自反的，意味着什么？A. 对于所有a∈A，(a, a)∈RB. 对于所有a∈A，(a, a)∉RC. 对于所有a∈A，(a, b)∈RD. 对于所有a∈A，(a, b)∉R答案：A二、填空题（每题5分，共20分）1. 一个集合的基数是集合中元素的________。

答案：数量2. 在有向图中，如果存在一条从顶点u到顶点v的路径，则称顶点v 是顶点u的________。

答案：可达的3. 一个图是连通的，当且仅当图中任意两个顶点都是________。

答案：连通的4. 在命题逻辑中，一个命题的否定是________。

答案：它的对立命题三、简答题（每题10分，共30分）1. 请解释什么是图的哈密顿回路。

答案：哈密顿回路是一个图中的闭合回路，它恰好访问图中的每个顶点一次。

2. 描述一下什么是二元关系，并给出一个例子。

答案：二元关系是定义在两个集合上的一个关系，它关联了第一个集合中的元素和第二个集合中的元素。

例如，小于关系是数字集合上的一个二元关系。

3. 什么是图的生成树？答案：图的生成树是图的一个子图，它包含图中的所有顶点，并且是一棵树，即它是连通的且没有环。

四、计算题（每题15分，共30分）1. 给定一个集合A={1,2,3,4,5}，计算它的幂集。

答案：幂集P(A)={∅, {1}, {2}, {3}, {4}, {5}, {1,2}, {1,3}, {1,4}, {1,5}, {2,3}, {2,4}, {2,5}, {3,4}, {3,5}, {4,5},{1,2,3}, {1,2,4}, {1,2,5}, {1,3,4}, {1,3,5}, {1,4,5}, {2,3,4}, {2,3,5}, {2,4,5}, {3,4,5}, {1,2,3,4}, {1,2,3,5}, {1,2,4,5}, {1,3,4,5}, {2,3,4,5}, {1,2,3,4,5}, A}。

浙江工业大学期终考试命题稿2010 /2011 学年第 1 学期命题注意事项：一、命题稿请用A4纸电脑打印，或用教务处印刷的命题纸，并用黑墨水书写，保持字迹清晰，页码完整。

二、两份试题必须同等要求，卷面上不要注明A、B字样，由教务处抽定A、B卷。

三、命题稿必须经学院审核，并在考试前两周交教务处。

浙江工业大学2012/2013 学年第1学期试卷课程＿＿＿＿＿＿＿＿姓名＿＿＿＿＿＿＿＿班级＿＿＿＿＿＿＿＿学号＿＿＿＿＿＿＿＿一、选择 15分（每小题 3分）1．下列语句是命题的是（ A ）。

A、离散数学是重要的一门必修课。

B、1+101=110？C、我正在说谎。

D、全体起立！2．图的邻接矩阵为( C )。

A、 B、 C、 D、3．下列排列能构成图的顶点度序列的是（ A ）。

A、1,2,2,3,4B、2,3,4,5,6,7C、2,1,1,1,2D、3,3,5,6,04．设，则IA =（ D ）。

A、 A ；B、A×IA；C、IA×A；D、。

5．下述命题公式中，是重言式的为（ C ）。

A、；B、；C、；D、。

二、填空题15分（每小题 3分）1已知一棵无向树T有三个3度顶点,一个2度顶点,其余的都是1度顶点, 则T中有 5 个1度顶点。

2．设A={1，2，3，4}，A上二元关系R={<2,2>,< 2,3>, < 3,2>, <3,1>}，则S(R)={<2,2>,<2,3>,<3,2>,<3,1>,<1,3>}。

3．A={1，2，3，4，5，6}，A上二元关系，则用列举法给出T={<2,1>,<3,1>,<1,1>,<2,2>,<3,3>,<4,4>,<5,5>,<6,6>,<4,2>,<6,3>,<5,1>, <6,2>}。