一阶电路和二阶电路的时域分析

一阶电路和二阶电路的时域分析一、一阶电路的时域分析：一阶电路指的是由一个电感或电容与线性电阻串联或并联而成的电路。

对于串联的一阶电路，其特征方程为：L di(t)/dt + Ri(t) = V(t) ---------- (1)其中，L是电感的感值，R是电阻的电阻值，i(t)是电路中的电流，V(t)是电路中的输入电压。

通过对上述方程进行求解可以得到电路中电流与时间的关系。

对于并联的一阶电路，其特征方程为：1/R C dq(t)/dt + q(t) = V(t) ---------- (2)其中，C是电容的电容值，q(t)是电路中电荷的变化，V(t)是电路中的输入电压。

同样，通过对上述方程进行求解可以得到电路中电荷与时间的关系。

一阶电路的响应可以分为自由响应和强迫响应两部分。

自由响应指的是由于电路中初始条件的存在，电流或电荷在没有外部输入电压的情况下的变化。

强迫响应指的是由于外部输入电压作用而产生的电流或电荷的变化。

对于一个初始处于稳定状态的电路，在有外部输入电压作用时，电路中电流或电荷会从初始值开始发生变化，最终趋于一个新的稳定状态。

这一过程可以由电流或电荷的指数递减或递增的形式表示。

在分析一阶电路的时域特性时，可以利用巴塞尔函数法或拉普拉斯变换法。

巴塞尔函数法主要是通过巴塞尔函数的表达式计算电压或电流的变化情况；拉普拉斯变换法则通过将时域的微分方程转化为复频域的代数方程，然后求解代数方程，最后再对求得的结果进行逆变换获得电流或电压的表达式。

二、二阶电路的时域分析：二阶电路是指由两个电感或电容与线性电阻串联或并联而成的电路。

对于串联的二阶电路，其特征方程为：L₁L₂ d²i(t)/dt² + (L₁R₁+L₂R₂+L₁R₂+L₂R₁) di(t)/dt + R₁R₂i(t) = V(t) ---------- (3)其中，L₁和L₂分别是两个电感的感值，R₁和R₂分别是两个电阻的电阻值，i(t)是电路中的电流，V(t)是电路中的输入电压。

0=t ：换路时刻，换路经历的时间为0_到+0；-=0t ：换路前的最终时刻；+=0t ：换路后的最初时刻；5.1.2动态电路的初始条件设0=t 时电路换路，若换路前后电容电流和电感电压为有限值的条件下，则在换路瞬间电容元件的电压和电感元件的电流不能跃变，这就是换路定律。

其数学表达式为)0()0()0()0(-+-+==u u q q c 电容上电荷和电压不发生跃变！ ①若-=0t 时，0)0(q q C =-,0)0(U u C =-,则有0)0(q q C =+,0)0(U u C =+,故换路瞬间，电容相当于电压值为0U 的电压源；②若-=0t 时，0)0( ,0)0(==--C C u q ,则应有0)0( ,0)0(==++C C u q ,则换路瞬间，电容相当于短路。

⎩⎨⎧==-+-+)0( )0( )0()0(L L L L i i ψψ电感的磁链和电流不发生跃变！ ①若-=0t 时，00)0( ,)0(I i L L ==--ψψ，则有00)0( ,)0(I i L L ==++ψψ,故换路瞬间，电感相当于电流值为0I 的电流源；②若-=0t 时，0)0( ,0)0(==--L L i ψ，则应有0)0( ,0)0(==++L L i ψ,则换路瞬间，电感相当于开路。

换路后初始瞬间+=0t 时刻，电路中电压和电流值称为初始值。

换路定律仅适用于电容电压和电感电流初始值的确定。

独立初始条件)0(+C u 和)0(+L i ：由-=0t 时的)0(-C u 和)0(-L i 确定。

非独立初始条件（电阻电压或电流、电容电流、电感电压）需要通过已知的初始条件求得。

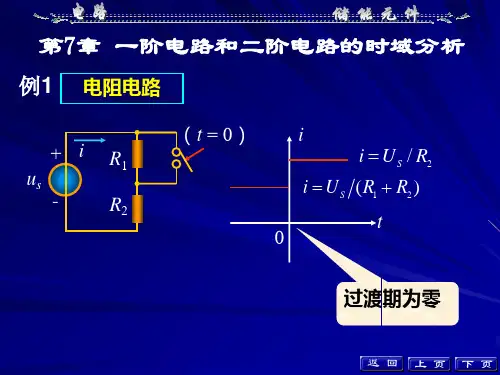
本节重点：动态电路初始值的确定，电路和换路情况复杂时，容易出错5.2一阶电路的时域分析5.2.1一阶电路的零输入响应零输入响应：无外施激励，由动态元件的初始值引起的响应。

电路的微分方程为⎪⎩⎪⎨⎧=≥=+0)0(0 0U u t u dt du RC C C C 0 )( 0≥=∴-t e U t u RC tC0 )(0≥=-=-t e RU dt du C t i RC t C 这里，特征方程RCs +1=0，特征根 1 RCs -=，时间常数RC =τ 。

第七章 一阶电路和二阶电路的时域分析一、是非题1.若电容电压(0)0c u -=,则接通时电容相当于短路。

在t=∞时,若电路中电容电流0c i =,则电容相当于开路。

2. 换路定则仅用来确定电容的起始电压(0)c u +及电感的起始电流(0)L i +,其他电量的起始值应根据(0)c u +或(0)L i +按欧姆定律及基尔霍夫定律确定。

3. 在一阶电路中，时间常数越大，则过渡过程越长。

4.一阶电路的时间常数只有一个，即一阶电路中的各电压、电流的时间常数是相同的。

5. 零输入的ＲＣ电路中,只要时间常数不变,电容电压从100V 放电到50V 所需时间与从150V 放电到100V 所需时间相等。

6.在Ｒ、Ｃ串联电路中，由于时间常数与电阻成正比，所以在电源电压及电容量固定时，电阻越大则充电时间越长，因而在充电过程中电阻上消耗的电能也越多。

7.单位冲激函数是单位阶跃函数的一阶导数，因此线性电路的单位冲激响应是单位阶跃响应的一阶导数。

（ ） 8.一阶RL 电路在冲激函数()t δ作用下，换路定律()()00L L i i +-=不再适用。

（ ）二、选择题1.RC 电路在零输入条件下，时间常数的意义是A 、响应的初始值衰减到0.632倍时所需时间B 、响应的初始值衰减到0.368倍时所需时间C 、过渡过程所需的时间D 、过渡过程结束所需的时间c2.一阶电路的零状态响应，是指： (A) 电容电压()00VC u +=或电感电压()00VL u += (B) 电容电压()00VC u +=或电感电流()00VL i +=(C) 电容电流()00VC i +=或电感电压()00V L u += (D) 电容电流()00V C i +=或电感电流()00VL i +=3.R 、C 放电电路经过1.2秒后，电容器电压降为原来的36.8%，则其时间常数τ为 (A) 0.4s (B) 1.2s (C) 0.8s (D) 0.6s4. R 、C 串联电路，已知全响应()()1083V 0tC u t et -=-≥，其零状态响应为：( )(A) 1088V te-- (B) 1083V te-- (C) 103V te-- (D) 105V te-5.电压波形的数值表达式为_____. (Ａ) -2ε(t)+ε(t-1) (Ｂ) -2ε(t)+3ε(t+1)-ε(t+3)(Ｃ) -2ε(t)+3ε(t-1)-ε(t-3) (Ｄ) -2ε(t)+3ε(t-1)6.一阶电路的全响应u C (t)＝[10-6 e-10t]Ｖ,初始状态不变而若输入增加一倍，则全响应u C (t)为______。