一阶电路的时域分析
- 格式:ppt
- 大小:710.50 KB
- 文档页数:36



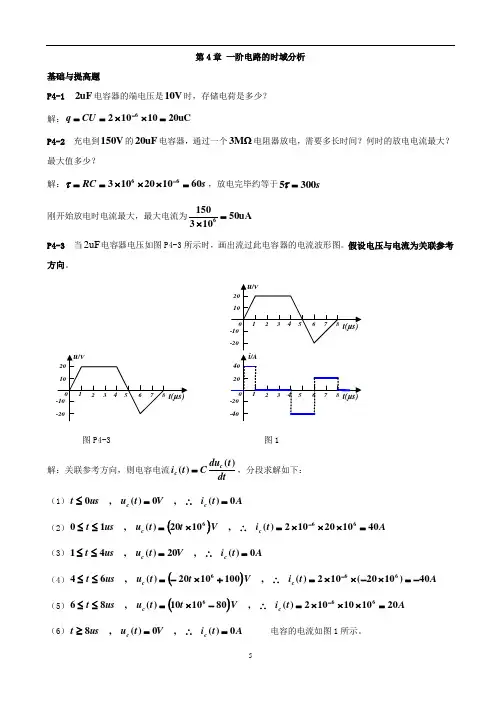
第4章 一阶电路的时域分析基础与提高题P4-1 uF 2电容器的端电压是V 10时,存储电荷是多少? 解:uC 20101026=⨯⨯==-CU qP4-2 充电到V 150的uF 20电容器,通过一个M Ω3电阻器放电,需要多长时间?何时的放电电流最大?最大值多少?解:s RC 60102010366=⨯⨯⨯==-τ,放电完毕约等于s 3005=τ 刚开始放电时电流最大,最大电流为uA 501031506=⨯ P4-3 当uF 2电容器电压如图P4-3所示时,画出流过此电容器的电流波形图。
假设电压与电流为关联参考方向。
图P4-3 图1解:关联参考方向,则电容电流dtt du C t i c c )()(=,分段求解如下: (1)A t i V t u ust c c 0)(,0)(,0=∴=≤(2)()A t i Vt t u us t c c 401020102)(,1020)(,10666=⨯⨯⨯=∴⨯=≤≤-(3)A t i V t u us t c c 0)(,20)(,41=∴=≤≤(4)()A t i V t t u us t c c 40)1020(102)(,1001020)(,64666-=⨯-⨯⨯=∴+⨯-=≤≤-(5)()A t i Vt t u us t c c 201010102)(,801010)(,86666=⨯⨯⨯=∴-⨯=≤≤-(6)A t i V t u ust c c 0)(,0)(,8=∴=≥ 电容的电流如图1所示。
P4-4 0.32tA 电流流过150mH 电感器,求s t 4=时,电感器存储的能量。
解:电感器存储的能量()23232.0101502121t Li W ⨯⨯⨯==- 当s t 4=时,电感器存储的能量为0.123WP4-5 由20V 电源与Ω2电阻、H 6.3电感组成的串联电路,合上开关后经过多长时间电流达到其最大值,最大值多少?设合上开关前电感无初始储能。

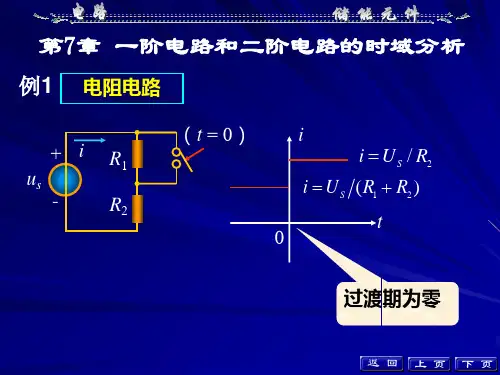


一阶电路和二阶电路的时域分析一、一阶电路的时域分析:一阶电路指的是由一个电感或电容与线性电阻串联或并联而成的电路。
对于串联的一阶电路,其特征方程为:L di(t)/dt + Ri(t) = V(t) ---------- (1)其中,L是电感的感值,R是电阻的电阻值,i(t)是电路中的电流,V(t)是电路中的输入电压。
通过对上述方程进行求解可以得到电路中电流与时间的关系。
对于并联的一阶电路,其特征方程为:1/R C dq(t)/dt + q(t) = V(t) ---------- (2)其中,C是电容的电容值,q(t)是电路中电荷的变化,V(t)是电路中的输入电压。
同样,通过对上述方程进行求解可以得到电路中电荷与时间的关系。
一阶电路的响应可以分为自由响应和强迫响应两部分。
自由响应指的是由于电路中初始条件的存在,电流或电荷在没有外部输入电压的情况下的变化。
强迫响应指的是由于外部输入电压作用而产生的电流或电荷的变化。
对于一个初始处于稳定状态的电路,在有外部输入电压作用时,电路中电流或电荷会从初始值开始发生变化,最终趋于一个新的稳定状态。
这一过程可以由电流或电荷的指数递减或递增的形式表示。
在分析一阶电路的时域特性时,可以利用巴塞尔函数法或拉普拉斯变换法。
巴塞尔函数法主要是通过巴塞尔函数的表达式计算电压或电流的变化情况;拉普拉斯变换法则通过将时域的微分方程转化为复频域的代数方程,然后求解代数方程,最后再对求得的结果进行逆变换获得电流或电压的表达式。
二、二阶电路的时域分析:二阶电路是指由两个电感或电容与线性电阻串联或并联而成的电路。
对于串联的二阶电路,其特征方程为:L₁L₂ d²i(t)/dt² + (L₁R₁+L₂R₂+L₁R₂+L₂R₁) di(t)/dt + R₁R₂i(t) = V(t) ---------- (3)其中,L₁和L₂分别是两个电感的感值,R₁和R₂分别是两个电阻的电阻值,i(t)是电路中的电流,V(t)是电路中的输入电压。


Chapter 7 一阶电路主要内容1.动态电路的方程及其初始条件;2.一阶电路(RC 电路、RL 电路)的时间常数;3.零输入响应、零状态响应、全响应、瞬态分量、稳态分量;4.三要素法;5.阶跃响应、冲激响应。
§7-1 动态电路的方程及其初始条件一、动态电路的方程1.动态电路:含有动态元件(电容或电感)的电路。
2.动态电路的方程: 电路中有储能元件(电容或电感)时,因这些元件的电压和电流的约束关系是通过导数(或积分)表达的。
根据KCL 、KVL 和支路方程式(VAR )所建立的电路方程是以电流、电压为变量的微分方程或微分-积分方程。
一阶动态电路:仅含一个动态元件的电路(RC 电路、RL 电路)。
3.动态电路的特征:当电路的结构或元件的参数发生改变时(如电源或无源元件的断开或接入,信号的突然注入等),可能使电路改变原来的工作状态,而转变到另一个工作状态。
换路:电路或参数的改变引起的电路变化。
0=t :换路时刻,换路经历的时间为 0_ 到 +0;-=0t :换路前的最终时刻; +=0t :换路后的最初时刻;4.经典法(时域分析法):根据KCL ,KVL 和VAR 建立描述电路的以时间为自变量的线性常微分方程,然后求解常微分方程,从而得到所求变量(电流或电压)的方法。
用经典法求解常微分方程时,必须根据电路的初始条件确定解答中的积分常数。
电路独立初始条件:)0(+C u 和 L i )0(+。
二、电路的初始条件1.电容的电荷和电压⎪⎪⎩⎪⎪⎨⎧+=+=⎰⎰ξξξξd tt i C t u t u d tti t q t q C C C C C C 0000)(1)()()()()(取 +-==0 ,00t t , 则⎪⎩⎪⎨⎧+=+=⎰⎰+-+--+-+ξξξξd i c u u d i q q C C C C C C 0000)(1)0()0()()0()0(若有限)( M i C ≤, 则 0)(00=⎰+-ξξd i C ,且⎩⎨⎧==-+-+)0()0()0()0(C C C C u u q q 电容上电荷和电压不发生跃变!① 若 -=0t 时,0)0(q q C =-, 0)0(U u C =-, 则有 0)0(q q C =+,)0(U u C =+, 故换路瞬间,电容相当于电压值为 0U 的电压源;② 若 -=0t 时,0)0( ,0)0(==--C C u q , 则应有)0( ,0)0(==++C C u q , 则换路瞬间,电容相当于短路。

一阶电路动态过程的时域分析1、典型一阶电路一阶电路仅包含一个动态元件,假设将动态元件别离出来,那么由戴维南或诺顿定理 可得到如下两种典型一阶电路:注意:图中N 是线性含源单口网络.2、一阶电路的电路方程及其一般形式一阶RC 电路:一阶RL 电路一阶电路方程的一般形式从上可知,一阶电路的电路方程都是一阶常系数微分方程. 励为x(t),响应为y ⑴,那么一阶电路方程一般形如:誓 y(t) = x(t)式中,七因具有时间的单位而称为一阶电路的时间常数 (time constant).并且,对 于一阶RC 电路,①关于u c 的电路方程: RC臂…US②关于i c 的电路方程: RCd Ci c "皿dt ③关于U R 的电路方程:RC ®R dtdtU R = RC 眄 dt①关于i L 的电路方程: 丹 iL 4US②关于U L 的电路方程: L dU L __ L dU s U L — R dt R dt5+L 5 tt L③关于U R 的电路方程:L d^R U R = U SR dt并且,假设记电路的激典型一阶RL 电路+ 1 +h]=[RCi欧雌…欧情卜欧]芳卜秒]对于一阶RL电路,=[秒]3、常系数一阶微分方程的经典时域解法对于常系数一阶微分方程七婴+ y(t) = x(t),其解(即电路的响应)由通解和特解dt 两局部构成通解:是对应齐次方程的解,与鼓励无关,称为电路的自由响应.管+ ;y(t)=0=通解y h(t) = Ae pt = Ae 之式中,A为待定积分系数,可根据初始条件来确定.特解:与电路鼓励x(t)有关,Mt)不同,特解形式就不同.因此特解也称为强制响应.在高等数学中,特解一般可以采用常数变异法求得,即:令非齐次微分方程的解为y(t) = m(t)eT ,求出誓后代入原微分方程,得到m⑴:m(t) =1 x(t)e dtX所以,常系数一阶微分方程7黎十y(t) = x(t)的解为t 上Ae -;1e x(t)e dty(t)=通解自由响应)解(强制响应)4、直流鼓励下的一阶电路时域分析同时考虑电路的外部鼓励和动态元件的初始储能, 直流一阶电路的响应存在以下3种情况:①零输入响应(Zero-input response)无外部鼓励(x(t)=0)但动态元件有初始储能时,仅由初始储能引起的电路响应^dy(y + y(t)= 0 [ + -t Tdty(t) = y(0 )e+y(0 ) ;0RC 里u c = 0』 」dtu c (t) = u c (0 )e^C =Uo e+u c (0 )= U 0 =0i c (t)=cdu^=UCpe -工 = dt * U R (t) = -u c (t) = -U °e一阶RL 电路零输入响应波形分析及结论: 无论一阶RC 还是一阶RL,也无论电路的响应是何变量,一阶电路的零输入响 应都具有如下特点:所有变量的零输入响应与其初始值成正比.例如,一阶RC 电路的零输入响应 一阶RC 电路零输入响应波形又如,一阶RL 电路的零输入响应—dL i L= 0 + -占 --R dt i 0= i L (t) = i L (0+)eE =1论 i L (0+) = l 0 =0di L (t) 」U L (t) = L = - RI 0e 二 dt上U L (t)= —RI»cK ⑴=火色〞F同一电路,所有变量的零输入响应按同一指数规律衰减,并最终必衰减至00所有变量零输入响应的衰减快慢取决于电路的时间常数T,或者说,一阶电路过渡过程时间的长短取决于电路的时间常数To并且,E大一过渡过程时间长;T小一过渡过程时间短.由于所以,E是响应衰减到原来电压36.8%所需的时间.并且工程上可以认为,经过3 T- 57,过渡过程即可结束.另外,可以证实,T等于响应衰减指数曲线的次切距长.②零状态响应(Zero-state response)有外部鼓励(x(t)用)但动态元件无初始储能时,仅由外部鼓励引起的电路响应.-皿(t) _____________M __________ _ ________ Me_t ° _________忑出+y⑴=M>= y(t)特解,强制(稳态)分量通解自由(暂态)分量y(0+)=0 J =y(8)(1 -e-t)例如,一阶RC电路直流鼓励下的零状态响应iRCdUC(t ) + U C (t ) = U S J dtlu c (0+) = 0分析及结论:一阶动态电路的零状态响应由稳态〔强制〕和暂态〔自由〕两局部构成. 同一电路,不同变量的零状态响应中的暂态分量按同一指数规律衰减,并 且衰减快慢取决于电路的时间常数丁.E 越大,响应变化越慢,否那么响应变化越快.③全响应〔complete response 〕既有外部鼓励〔x 〔t 〕力〕,也有动态元件初始储能时,由两者共同作用引起的电路响应ottu c (t) = U s —U s e飞.,i c (t) = U S e-c又如,一阶RL 电路直流鼓励下的零状态响应I L diL(t) + i L (t )= u S* ** *R R dt - R = i L (t)=谭--j^e II i L (0+) = 0R R_ t,U L (t) = U s e L R一阶RC 电路零状态响应波形一阶RL 电路零状态响应波形y(t) = M I y(s)(=M) [y(0 +)_y(g)]门 『y(t)-特解,强制(稳态)分量+通解,自由(暂态)分量注1:上述一阶电路的全响应是从微分方程解结构角度进行分解的.除此以外, 一阶电路的全响应还可以按鼓励与响应间的因果关系进行如下分解:v(t)= y(0+)…+ y9)(i-e -『八 零输入响应零状态响应因此,零输入响应和零状态响应都是全响应的特例.注2:假设定义时间常数T 、响应初值y(0+)和响应稳态值y(8为一阶电路的三要素, 那么一阶电路的全响应可直接根据以上公式得到. 这种求解全响应的方法称为三要 素解法.并且,三要素法的一般步骤为:除去动态元件,求取所得网络的等效电阻R,并计算动态电路的时间常数T :R 是除掉动态元件后所得网络的等效电阻.利用换路定那么及0+等效电路,求取响应初值 y(0+); 根据换路并稳定后的电路,求取响应的稳态值 y(3 ;按三要素法公式,写出全响应的表达式.例1:(零输入响应问题):1) t=0时,翻开开关S,求u v .2)假设电压表量程为50V,试判断其是否会被损坏 3)讨论电路的改良举措dy(t) + + ----- + dt y(0)= 0时间常数广RC 电路:r^RC. RL 电路:HRq H & "H .*)H 0]:产0, 〞40+) H 0u s w 0,尸 05、正弦鼓励下一阶电路的时域分析电路方程仍为常系数一阶微分方程:F 彗詈+ y(t) = x(t),故x(t)= Msin (乳+,dt时,_t t工_t.y(t) = Ae .+1e 〞Msin(8t + *)e z dt = Ae .十——Mr^[sin(^t + ^) -COT cos ®t+*)] 122根据初始条件可求得A = y(0+)-M 2 2bin 中一⑴lUcoS 】1+⑴7于是,正弦鼓励下一阶动态电路的响应为:例2 (零状态响应问题):t=0开关K 翻开,求t >0后i L 、UL 及电流源的电压.例3(全响应问题):t=0时开关由1-2,求换路后的u c (t)Mc(O + ) = Ug 或MO* ) = Io换路时,电路如何响应? 以.).。
自动控制实验一一阶系统的时域分析二阶系统的瞬态响应实验目的:1.了解一阶系统的时域分析方法。
2.掌握二阶系统的瞬态响应特性。
3.学习使用实验仪器进行实验操作。
实验仪器和材料:1.一台一阶系统实验装置。
2.一台二阶系统实验装置。
3.示波器、函数发生器等实验仪器。
实验原理:一阶系统的时域分析:一阶系统的传递函数形式为:G(s)=K/(Ts+1),其中K为增益,T为系统的时间常数。
一阶系统的单位阶跃响应可以用下式表示:y(t)=K(1-e^(-t/T)),其中t为时间。
通过绘制单位阶跃响应曲线的方法可以得到一阶系统的时域参数。
二阶系统的瞬态响应:二阶系统的传递函数形式一般为:G(s) = K/(s^2 + 2ξωns +ωn^2),其中K为增益,ξ为阻尼系数,ωn为自然频率。
二阶系统的单位阶跃响应可以用下式表示:y(t) = (1 - D)e^(-ξωnt)cos(ωnd(t - φ)),其中D为过渡过程的衰减因子,φ为过渡过程的相角。
实验步骤:一阶系统的时域分析:1.将一阶系统实验装置连接好,并接通电源。
2.设置函数发生器的输出信号为单位阶跃信号,并将函数发生器连接到一阶系统实验装置的输入端。
3.调节函数发生器的幅值和时间参数,使得单位阶跃信号满足实验要求。
4.将示波器的探头连接到一阶系统实验装置的输出端。
5.调节示波器的时间和幅值参数,观察并记录单位阶跃响应信号。
6.根据记录的单位阶跃响应信号,计算得到一阶系统的时域参数。
二阶系统的瞬态响应:1.将二阶系统实验装置连接好,并接通电源。
2.设置函数发生器的输出信号为单位阶跃信号,并将函数发生器连接到二阶系统实验装置的输入端。
3.调节函数发生器的幅值和时间参数,使得单位阶跃信号满足实验要求。
4.将示波器的探头连接到二阶系统实验装置的输出端。
5.调节示波器的时间和幅值参数,观察并记录单位阶跃响应信号。
6.根据记录的单位阶跃响应信号,计算得到二阶系统的瞬态响应特性,包括过渡过程的衰减因子和相角。