高二数学(理)40分钟限时训练一

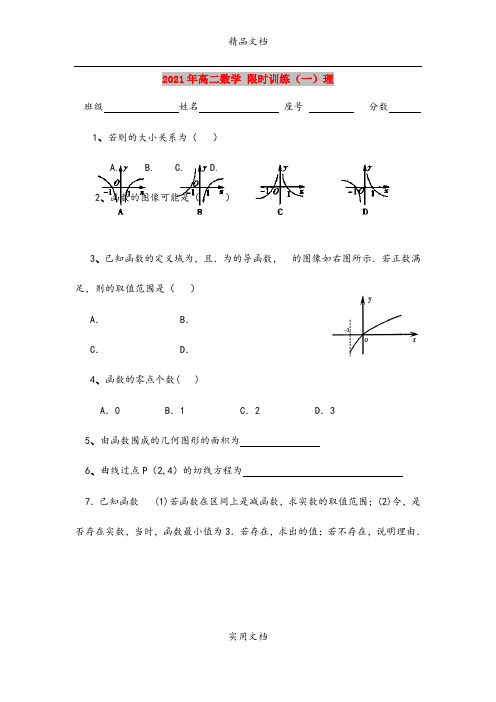
2021年高二数学限时训练（一）理班级姓名座号分数1、若则的大小关系为（）A. B. C. D.2、函数的图像可能是（）3、已知函数的定义域为，且．为的导函数，的图像如右图所示．若正数满足，则的取值范围是（）A． B．C． D．4、函数的零点个数( )A．0 B．1 C．2 D．35、由函数围成的几何图形的面积为6、曲线过点P（2,4）的切线方程为7．已知函数 (1)若函数在区间上是减函数，求实数的取值范围；(2)令，是否存在实数，当时，函数最小值为3．若存在，求出的值；若不存在，说明理由．信丰中学xx--xx年高二下学期数学理科限时训练（一）xx.3.10 BBAD 4x-y-4=0或x-y+2=07、解：（1）由条件可得在上恒成立，即在上恒成立，而在上为减函数，所以故的取值范围为………………5分（２）设满足条件的实数存在，，当时，，在上递减，，即有（舍去）………………………７分当，即时，，在上递减，，即有（舍去）…………………９分当即时，令，解得，则有在上递减，在上递增，即有………………………１１分[综上，满足条件的实数存在且为………………………１２分信丰中学xx--xx年高二下学期数学理科限时训练（二）2015.3.12班级姓名座号分数1．函数f(x)＝2x＋101－x＋lg(3x＋1)的定义域是( )A. B. C.(-1,1) D .2．已知函数的图像与轴恰有两个公共点,则( )A．或2 B．或3 C．或1 D．或1 3 ．已知二次函数的图象如图所示,则它与轴所围图形的面积为( )A．B．C．D．4．函数y＝11－x的图象与函数y＝2sin πx(－2≤x≤4)的图象所有交点的横坐标之和等于( )．A．2 B．4 C．6 D．8yx O第3题5.已知函数是定义在实数集R上的奇函数，且当时成立（其中的导函数），若，，则的大小关系是( )A．B．C．D．6．已知函数（a)（1）当时，求的单调区间；（2）对任意的恒成立，求的最小值；信丰中学xx--xx年高二下学期数学理科限时训练（二）xx.3.12BA B D A6解：（1）当时，由，由故的单调减区间为单调增区间为（2）即对恒成立。

信丰中学2021--2021年高二下学期(xu éq ī)数学理科限时训练〔一〕班级 姓名 座号 分数 1、假设那么的大小关系为〔 〕A.B.C.D.2、函数的图像可能是〔 〕3、函数的定义域为，且．为()f x 的导函数，()f x 的图像如右图所示．假设正数满足，那么的取值范围是〔 〕A ．B ．C ．D ．4、函数的零点个数( )A ．0B ．1C ．2D ．3 5、由函数围成的几何图形的面积为6、曲线过点P 〔2,4〕的切线方程为7．函数(1)假设函数)(x f 在区间上是减函数，务实数的取值范围；(2)令，是否存在实数a ，当时，函数最小值为3．假设存在，求出a 的值；假设不存在，说明理由．BBAD4x-y-4=0或者(hu òzh ě)x-y+2=07、解：〔1〕由条件可得在[]2,1上恒成立，即在[]2,1上恒成立，而在[]2,1上为减函数，所以故a 的取值范围为………………5分（２） 设满足条件的实数a 存在，(]e x ,0∈，当时，，)(x g 在(]e x ,0∈上递减，， 即有 〔舍去〕………………………７分 当，即时，0)(/<x g ，)(x g 在(]e x ,0∈上递减，3)()(min ==∴e g x g ， 即有ea 4=〔舍去〕…………………９分 当即时，令0)(/<x g ，解得，那么有)(x g 在上递减，在上递增，即有………………………１１分[综上，满足条件的实数(sh ìsh ù)a 存在且为2e a =………………………１２分信丰中学2021--2021年高二下学期数学理科限时训练〔二〕201班级 姓名 座号 分数1．函数f (x )＝2x ＋101－x＋lg(3x ＋1)的定义域是( ) A. B.C.(-1,1) D .2．函数的图像与轴恰有两个公一共点,那么( ) A ．或者2B ．或者3C ．或者1D ．或者13 ．二次函数的图象如下图,那么它与轴所围图形的面积为( )A ．B ．C ．D ．4．函数y ＝11－x的图象与函数y ＝2sin πx (－2≤x ≤4)的图象所有交点的yxO第3题1横坐标之和等于( )．A．2 B．4 C．6 D．8是定义(dìngyì)在实数集R上的奇函数，且当时成立〔其中的导函数〕，假设，，那么的大小关系是() A．B．C．D．6．函数〔a)〔1〕当时，求()f x的单调区间；〔2〕对任意的恒成立，求a的最小值；BA B D Aa 时，6解：〔1〕当1由，由故()f x的单调减区间为单调增区间为〔2〕即对恒成立。

40-分钟限时训练1.已知21,F F 为平面内两定点,|21F F |=6,动点M 满足12||||||6MF MF -=,则M 的轨迹是( ) A ．两条射线 B ．椭圆 C ．双曲线 D ．抛物线2.有关命题的说法错误．．的是 ( ) A.命题“若, 则”的逆否命题为：“若，则 B.“”是“”的充分不必要条件. C.若为假命题，则、均为假命题.D.对于命题：使得. 则：均有.3.设椭圆22221(0)x y a b a b +=>>的离心率为12e =，右焦点为F （c, 0），方程20ax bx c +-=的两个实根分别为x 1和x 2，则点P （x 1, x 2）（）A ．必在圆222x y +=内B ．必在圆222x y +=上C ．必在圆222x y +=外D ．以上三种情形都有可能4．,k R ∈曲线11622=--ky k x 表示双曲线，则k 的取值范围为. 5.是椭圆2212516x y +=的上一点，点分别是圆()2231x y -+=和()2234x y ++=上的动点，则PM PN +的最大值为.6.如图，SD ⊥正方形ABCD 所在平面，AB = 1，SB ．(1) 求证：BC ⊥SC ；(2) 设棱SA 的中点为M ，求异面直线DM 与SB 所成角的大小．0232=+-x x 1=x 1≠x 0232≠+-x x 1=x 0232=+-x x q p ∧p q p x R ∃∈，210x x ++<⌝p x R ∀∈，210x x ++≥P N M , ABCSMD7.如图，已知椭圆的中心在坐标原点，焦点F 1、F 2在x 轴上，长轴A 1A 2的长为4，左准线l 与x 轴的交点为M ，1||MA ∶11||A F =2∶1． (3) 求椭圆的方程；若点P 在直线l 上运动，求12tan F PF 的最大值．B 1A 1 CB AC 1D F40-分钟限时训练1．在三棱柱ABC －A 1B 1C 1中，D 是CC 1的中点，F 是A 1B 的中点，且βα+=，则( )A ．1,21-==βα B ．1,21=-=βαC ．21,1-==βαD ．21,1=-=βα 2.若l 、m 、n 是互不相同的空间直线，α、β是不重合的平面，则下列命题中为真命题的是（ ）A.若//,,l n αβαβ⊂⊂，则//l nB.若,//l l αβ⊥，则αβ⊥C.若,l αβα⊥⊂，则l β⊥D.若,l n m n ⊥⊥，则//l m3.已知双曲线的准线过椭圆的焦点，则直线与椭圆至多有一个交点的充要条件是( )A. B.C. D. 4l 过抛物线24y x =的焦点且与该抛物线交于A ，B 两点，则|AB|=.5．已知非零实数a 、b 、c 成等差数列，直线0ax by c ++=与曲线2221(0)9x y m m +=>恒有公共点，则实数m 的取值范围为___________________．22122x y -=22214x y b +=2y kx =+11,22K ⎡⎤∈-⎢⎥⎣⎦11,,22K ⎛⎤⎡⎫∈-∞-+∞⎪⎥⎢⎝⎦⎣⎭K ⎡∈⎢⎣⎦,K ⎛⎫∈-∞+∞ ⎪ ⎪⎝⎦⎣⎭6.已知命题2p :"x [1,2],x a 0",∀∈-≥命题2000q :"x R,x 2ax 2a 0"∃∈++-=若命题“p 且q ”为假命题，“p 或q ”是真命题，求实数a 的取值范围.7.如图，在长方体1111ABCD A B C D -中，11,2AD AA AB ===，点E 在棱AB 上移动.（1）证明：11D E A D ⊥；（2）若=2AE 1D EC D --的大小。

浙江省杭州第十四中学2024-2025学年高二上学期限时训练（一）数学试卷一、单选题1．已知复数z 满足z i=3+2i ， 则复数z (1－i)的虚部为（ ）A ．－5B ．－5iC ．－3D ．－3i2．已知{},,a b c r r r 为空间的一组基底，则下列向量也能作为空间的一组基底的是（ ） A ．,,a b b c a c ++-r r r r r rB ．2,,a b b a c +-r r r r rC ．2,2,a b b c a b c ++++r r r r r r rD ．,2,2a c b a b c ++-r r r r r r3．某产品售后服务中心选取了10个工作日，分别记录了每个工作日接到的客户服务电话的数量（单位：次）：67573740466281473130则这组数据的（ ） A ．众数是30B ．10%分位数是30.5C ．极差是37D ．中位数是434．已知直线1l ：310ax y ++=，2l ：()20x a y a +-+=，则“3a =”是“12l l ∥”的（ ） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．已知()()()()1,0,0,0,1,0,0,0,1,1,1,2A B C D ，则点D 到平面ABC 的距离为（ ）AB C D 6．著名数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休．”事实上，有很多代数问题可以转化为几何问题加以解决，(),M x y 与点(),N a b 的距离．结合上述观点，可得y ）A ．B ．CD ．37．某校课外活动期间开展跳绳、踢键子、韵律操三项活动，甲、乙两位同学各自任选其中一项参加，则他们选择同一项活动的概率是（ ）A ．19B ．29C ．13D ．238．过定点M 的直线10ax y +-=与过定点N 的直线210x ay a -+-=交于点P ，则PM P N ⋅的最大值为( )A ．4B ．3C ．2D ．1二、多选题9．下列说法正确的是（ ）A ．直线sin 20x y α++=的倾斜角θ的取值范围是π3π0,,π44⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭B ．“1a =-”是“直线210a x y -+=与直线20x ay --=互相垂直”的充要条件C ．两个非零向量与任何一个向量都不能构成空间的一个基底，则这两个向量共线D ．已知向量()9,4,4a =-r ，()1,2,2b =r ，则a r 在b r 上的投影向量为()1,2,210．某社团开展“建党100周年主题活动——学党史知识竞赛”，甲、乙两人能得满分的概率分别为34，23，两人能否获得满分相互独立，则（ ） A ．两人均获得满分的概率12B ．两人至少一人获得满分的概率712C ．两人恰好只有甲获得满分的概率14D ．两人至多一人获得满分的概率1211．扎马钉（图1），是古代军事战争中的一种暗器.如图2所示，四个钉尖分别记作A B C D ､､､，连接这四个顶点构成的几何体为正四面体，组成该“钉”的四条等长的线段公共点为O ，设1OA =，则下列结论正确的是（ ）A ．AB CD ⊥B ．O 为正四面体ABCD 的中心C ．1BC =D ．四面体ABCD 的外接球表面积为π三、填空题12．如图，在平行六面体1111ABCD A B C D -中，底面是边长为1的正方形，若1160A AB A AD ∠=∠=o ，且13AA =，则1AC 的长为.13．将一张坐标纸对折，如果点()0,m 与点()()2,22m m -≠重合，则点()4,1-与点重合. 14．学校为了解学生身高(单位：cm)情况，采用分层随机抽样的方法从4000名学生（男女生人数之比为3:2）中抽取了一个容量为100的样本.其中，男生平均身高为175，方差为184，女生平均身高为160，方差为179，用样本估计总体，则该学校学生身高的方差为．四、解答题15．如图，在四棱锥P ABCD -中，AD BC ∥，224PA BC AD AB ====，AD ⊥平面PAB ，PA AB ⊥，E 、F 分别是棱PB 、PC 的中点．(1)证明：//DF 平面ACE ；(2)求平面ACE 与平面PAD 的夹角的正弦值．16．为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者.从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄的分组区间是：第1组[)20,25、第2组[)25,30、第3组[)30,35、第4组[)35,40、第5组[]40,45.(1)求图中x 的值并根据频率分布直方图估计这500名志愿者中年龄在[)35,40的人数；(2)估计抽出的100名志愿者年龄的第75百分位数；(3)若在抽出的第2组、第4组和第5组志愿者中，采用按比例分配分层抽样的方法抽取6名志愿者参加中心广场的宣传活动，再从这6名中采用简单随机抽样方法选取2名志愿者担任主要负责人.求抽取的2名志愿者中恰好来自同一组的概率.17．已知点()1,2P -，直线1:430l x y ++=和2:3550l x y --=(1)过点P 作1l 的垂线PH ，求垂足H 的坐标；(2)过点P 作l 分别于12,l l 交于点A B 、，若P 恰为线段AB 的中点，求直线l 的方程．18．已知函数()2(0,1)ax f x a b x b =>>+满足()11f =，且()f x 在R (1)求a ，b 的值；(2)当[]1,2x ∈时，不等式()()232m f x x x m ≤+-恒成立，求实数m 的取值范围. 19．已知ABC V 中，角A ，B ，C 的对边分别是a ，b ，c ，120C =︒. （1）若2a b =，求tan A 的值； （2）若ACB ∠的平分线交AB 于点D ，且1CD =，求ABC V 周长的最小值.。

1.已知,a b 是实数，则“0a >且0b >”是“0a b +>且0ab >”的 ( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 答案：C解析 对于“0a >且0b >”可以推出“0a b +>且0ab >”，反之也是成立的2.“0x >”是“0x ≠”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 答案 A【命题意图】本小题主要考查了命题的基本关系，题中的设问通过对不等关系的分析，考查了命题的概念和对于命题概念的理解程度． 解析 对于“0x >”⇒“0x ≠”；反之不一定成立，因此“0x >”是“0x ≠”的3.下列命题是真命题的为A ．若11x y=,则x y = B ．若21x =,则1x = C ．若x y =,则x y = D ．若x y <,则 22x y < 答案：A4.（2009天津卷理）命题“存在0x ∈R ，02x ≤0”的否定是A. 不存在0x ∈R, 02x >0 B. 存在0x ∈R, 02x ≥0C. 对任意的x ∈R, 2x ≤0D. 对任意的x ∈R, 2x >0【考点定位】本小考查四种命题的改写，基础题。

解析：由题否定即“不存在R x ∈0，使020≤x ”，故选择D 。

5.若非空集合,,A B C 满足A B C = ，且B 不是A 的子集， 则( )A.“x C ∈”是“x A ∈”的充分条件但不是必要条件B.“x C ∈”是“x A ∈”的必要条件但不是充分条件C.“x C ∈”是“x A ∈”的充要条件D.“x C ∈”既不是“x A ∈”的充分条件也不是“x A ∈”必要条件 答案 B6.已知椭圆C:2244x y +=,过点()2,0P -与椭圆C 只有一个交点的直线方程是 （ ）（A ）x+2=0 （B ）x-2=0 （C ）y+2=0 （D ） y-2=07．直线1y kx k =-+与椭圆22194x y +=的位置关系为（A ）相切 （B ）相交 （C ）相离 （D ）不确定8.直线1y kx =+与焦点在x 轴上的椭圆2219x y m+=总有公共点，则实数m的取值范围是 （ ）（A ）21≤m<9 （B ）9<m<10 （C ）1≤m<9（D ）1<m<99．椭圆221164x y +=上的点到直线220x y +-=的最大距离是（ ）（A ）3 （B ）11 （C ）22 （D ）1010.直线1y x =+被椭圆2224x y +=所截的弦的中点坐标是（ ）（A ）(31, －32) （B ）(－32, 31) （C ）(21, －31)（D ）(－31, 21)11.已知椭圆221369x y +=，椭圆内一点(4,2)P ,则以P 为中点的弦所在的直线的斜率是 （ ）（A ）21 （B ）－21 （C ）2（D ）－212．若P 在椭圆1222=+y x 上，1F 、2F 是椭圆的两焦点，且 9021=∠PF F ，则21PF F ∆的面积是。

40分钟限时练习（1）一．选择题（共8小题，满分24分，每小题3分）1．（3分）﹣8的倒数是（ ）A ．8B ．18C ．−18D ．﹣8 2．（3分）若√x+2x有意义，则实数x 的取值范围为（ ） A ．x ＞﹣2 B ．x ≥﹣2 C ．x ＞﹣2且x ≠0 D ．x ≥﹣2且x ≠03．（3分）2022年11月5日，“长征三号”运载火箭在西昌卫星发射中心点火起飞，随后将“中星19号”卫星准确送入高度为35800千米的预定轨道，发射任务取得圆满成功．该卫星主要为跨太平洋重要航线、东太平洋海域及北美西海岸等覆盖区域提供通信服务．数据35800用科学记数法表示为（ ）A ．0.358×105B ．358×102C ．3.58×104D ．3.58×105 4．（3分）分式方程1x−2=3x 的解为（ ） A ．x ＝3 B ．x ＝2C ．x ＝1D ．无解 5．（3分）已知点（﹣2，3）在反比例函数y =k x 的图象，则下列各点也在该图象上的是（ ）A ．（2，3）B ．（1，﹣6）C ．(6，−12)D ．（0，0）6．（3分）计算2sin 30°的值为（ ）A ．1B ．√3C ．2D ．2√37．（3分）一个多边形的内角和的度数可能是（ ）A ．1700°B ．1800°C ．1900°8．（3分）下列图形中，既是轴对称图形也是中心对称图形的有（ ）A ．4个B ．3个C ．2个D ．1个二．填空题（共8小题，满分32分，每小题4分）9．（4分）因式分解：ma 2﹣2am +m ＝ ．10．（4分）化简：3m 2n9m = ．11．（4分）如图，四边形OABC 是矩形，OC 在x 轴上，OA 在y 轴上，函数y ＝x 的图象与AB 交于点D （3，3），点E 是射线BC 上一点，沿DE 折叠点B 恰好落在函数y ＝x 的图象上，且BE ＝2CE ，则点B 的坐标为 ．12．（4分）已知下列命题：①若a2＝b2，则a＝b；②2022年全年鄂尔多斯市一般公共预算累计完成842.8亿元，用科学记数法表示为8.428×1010元；③二元一次方程2x+y＝6的正整数解有3对；④连接两点之间的线段叫做两点之间的距离．是真命题的是.（只填序号）13．（4分）为了落实“双减”政策，减轻学生作业负担，某学校领导随机调查了九（1）班学生每天在作业上共花费的时间，随机调查了该班10名学生，其统计数据如下表：则这10名学生每天在作业上花费的平均时间是小时．时间（小时）43210人数2421114．（4分）如图，四边形ABCD中，E、F、G、H依次是各边中点，O是四边形内一点，若S四边形AEOH＝3，S四边形BFOE＝4，S四边形CGOF＝5，则S四边形DHOG＝．15．（4分）如图，在▱ABCD中，∠ABC＜90°，⊙O与它的边BA，BC相切，射线BO交边AD于点E．当AB＝6，AD＝8时，DE的长等于．16．（4分）如图，点A是反比例函数y=kx（k≠0，x＜0）图象上一点，过点A作AB⊥y轴于点D，AD＝DB．若点C为x轴上任意一点，且S△ABC＝9，则k的值为．三．解答题（共4小题，满分44分）17．（10分）计算：（1）（√12−√13）×√3+(12)0；（2）（m ﹣1）2﹣m （m ﹣3）．18．（10分）计算．（1）{x −y =12x +5y =9；（2）3x +2≤﹣2（x ﹣2）．19．（12分）为了解市民对全市创卫工作的满意程度，某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计，将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，得到下列不完整的统计图．请结合图中信息，解决下列问题：（1）求此次调查中接受调查的人数，并补全条形统计图．（2）若本市人口300万人，估算该市对市创卫工作表示满意和非常满意的人数．（3）兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访，已知4位市民中有2位来自甲区，另2位来自乙区，请用列表或用画树状图的方法求出选择的市民均来自同区的概率．20．（12分）如图，在△ABC中，AB＝AC，D是边BC延长线上一点，连接AD．AE∥BD，∠BAC＝∠DAE，连接CE交AD于点F．（1）若∠D＝36°，求∠B的度数；（2）若CA平分∠BCE，求证：△ABD≌△ACE．。

分钟课时作业一、选择题：每小题5分，共30分・1.如果等差数列｛如｝中，。

3 +他+。

5=12,那么等于（）A. 2B. 3C. 4 D・ 5解析：^3+04+05 = 3%= 12，血=4・答案：C2.等差数列｛©｝中，若Q] 两根，则血+⑷006+ °2 010 = (A. 10B. 15C. 20D. 40,«2 oil 为方程x2— 10x+16 = 0 的)解析：由等差数列的性质，得。

1 +。

2011=。

2 +。

2010 = 2如006・因为尙，"2011是方程F_10x+16二0的两根，所以。

1+。

2011 = 1°・3 _所以a2+^ioo6+«2oio=2X 10=15*答案：B3.等差数列｛如｝中，«1+«2-----------------4101=°'则有（）A・ di+dioi>O B・ di+dioiVOC・ °1+如0]=0 D・ «5i —51解析：Va1+«ioi = 2a5p ^.ai+a2 ------------- aioi = lOla5i=O, •••尙+。

101=°・答案：C4.已知等差数列｛给｝中，01+如+。

13=4兀，则tan（6z2+«i2）的值为（）答案：D5・在。

和b之间插入〃个数构成一个等差数列，则其公差为)b—a A.——nb — a C ------n+1a —b B・^TTD.解析：•=给+2 = 4 •・Z? = a + (zi+ l)d,.” b一a•••〃=吊・答案：C6.设数列他小｛仇｝都是等差数列,且如=25,饷=75, a2 + />2=100,则037 + ^37 等于（）A. 0 B・ 37C・ 100D・—37解析：V ｛a n｝, ｛b“｝都是等差数列,・°・｛。

a =2b =3c =4 a =b b =c +2 c =b +3()/3d a b c =++PRINT “d =”；d河南宏力学校高二数学限时训练(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分150分 考试时间120分钟 2012—9—6第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符号题目要求的)1、直线cos 1()y x R αα=⋅+∈的倾斜角的取值范围是（ ）A ．[0，2π] B ．[0，π) C ．[-4π，6π] D ．[0，4π]∪[43π，π)2、将十进制下的数72转化为八进制下的数 ( )A 、011B 、101C 、110D 、1113、图（1）程序运行的结果是（ ）图（1）A. 5B. 6C.7D. 8 4、用秦九韶算法计算多项式1876543)(23456++++++=x x x x x x x f当4.0=x 时的值时，需要做乘法和加法的次数 分别是（ ）A ．6，6 B. 5, 6 C. 5, 5 D. 6, 5 5、如图（2），该程序运行后输出的结果为（ ） A.1 B.10 C.19 D.28 6、直线()110a x y +++=与圆2220x y x +-=相切，则a 的值为（ ）A . 1，1-B . 2-C . 1D . 1- 图（2） 7、将两个数17,8==b a 交换,使8,17==b a ,下面语句中正确的一组是 （ ） A. B. C. D.8、数4557，1953，5115的最大公约数为（ ）．A ．93B ．31C ．651D ．2179、若圆222)5()3(r y x =++-上有且只有两个点到直线234=-y x 的距离为1，则 半径r 的取值范围是 ( ))6,4.(A )6,4.[B ]6,4.(C ]6,4.[D10、圆心为1,32C ⎛⎫-⎪⎝⎭的圆与直线:230l x y +-=交于P 、Q 两点，O 为坐标原点，且满足0OP OQ ⋅=u u u v u u u v，则圆C 的方程为（ ）A ．2215()(3)22x y -+-= B ．()2532122=-+⎪⎭⎫ ⎝⎛+y xC ．22125()(3)24x y ++-=D ．22125()(3)24x y +++=11、设入射光线沿直线 y=2x+1 射向直线 y=x, 则被y=x 反射后,反射光线所在的直线方程是( ) A ．x-2y-1=0 B ．x-2y+1=0 C ．3x-2y+1=0 D ．x+2y+3=0 12、若A )12,5,(--x x x ，B )2,2,1(x x -+，当AB 取最小值时，x 的值等于（ ）A 19B 78-C 78D 1419第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13、下面语句编写的是求函数f(x)的函数值的算法，这个函数f(x)=________________。

数学基础小题限时40分钟训练(一)班级： 姓名： 得分：一、选择题(本大题共12小题，每小题5分，共60分)1．已知集合A ＝{x |1<x <3}，B ＝{x |1<log 2x <2}，则A ∩B 等于( )．A ．{x |0<x <3}B ．{x |2<x <3}C ．{x |1<x <3}D ．{x |1<x <4}2．复数z ＝x ＋3i 1－i(x ∈R ，i 是虚数单位)是实数，则x 的值为( )． A ．3 B ．－3 C ．0 D. 33．“k ＝1”是“直线x －y ＋k ＝0与圆x 2＋y 2＝1相交”的( )．A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件4．已知函数f (x )＝⎩⎪⎨⎪⎧e x ，x <0，ln x ，x >0，则f ⎣⎡⎦⎤f ⎝⎛⎭⎫1e ＝( )． A.1e B ．e C ．－1eD ．－e 5．若圆C 的半径为1，圆心在第一象限，且与直线4x －3y ＝0和x 轴相切，则该圆的标准方程是( )．A ．(x －3)2＋⎝⎛⎭⎫y －732＝1 B ．(x －2)2＋(y －1)2＝1 C ．(x －1)2＋(y －3)2＝1 D.⎝⎛⎭⎫x －322＋(y －1)2＝1 6．已知某几何体的三视图如下图，其中正(主)视图为半径为1，则该几何体体积为( )．A ．24－32πB ．24－π3C ．24－πD ．24－π27．已知函数f (x )＝2cos ⎝⎛⎭⎫2x ＋π6，下面四个结论中正确的是( )． A ．函数f (x )的最小正周期为2πB ．函数f (x )的图象关于直线x ＝π6对称 C ．函数f (x )的图象是由y ＝2cos 2x 的图象向左平移π6个单位得到 D ．函数f ⎝⎛⎭⎫x ＋π6是奇函数 8．执行如图所示的程序框图，则输出的n 为( )．A ．3B ．4C ．5D ．69．实数x ，y 满足⎩⎪⎨⎪⎧ x ≥1，y ≤a ，a >1，x －y ≤0，若目标函数z ＝x ＋y 取得最大值4，则实数a 的值为( )．A ．4B ．3C ．2 D.3210．已知数列{a n }，{b n }满足a 1＝1，且a n ，a n ＋1是函数f (x )＝x 2－b n x ＋2n 的两个零点，则b 10等于( )．A ．24B ．32C ．48D ．6411．已知函数f (x )＝a x －1＋3(a >0且a ≠1)的图象过一个定点P ，且点P 在直线mx ＋ny －1＝0(m >0，且n >0)上，则1m ＋4n的最小值是( )． A ．12 B ．16 C ．25 D ．2412．已知点F 1，F 2分别是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左、右焦点，过F 1且垂直于x 轴的直线与双曲线交于A ，B 两点，若△ABF 2是锐角三角形，则该双曲线离心率的取值范围是( )．A ．(1，3)B ．(3，22)C ．(1＋2，＋∞)D ．(1,1＋2)13．抛物线y ＝2x 2的准线方程是_______________________________________．14．（文）如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人比赛得分的中位数之和是________．（理）某中学从6名品学兼优的同学中选出4名去进行为期三天的环保知识宣传活动，每人一天，要求星期天有2人参加，星期五、星期六各有1人参加，则不同的选派方案的种数为________．15．（文）某商场举行抽奖活动，从装有编号0,1,2,3四个小球的抽奖箱中，每次取出一个小球后放回，连续取两次，取出的两个小球号码相加之和等于5中一等奖，等于4中二等奖，等于3中三等奖，则中奖的概率为________．（理）袋中有3个黑球，1个红球．从中任取2个，取到一个黑球得0分，取到一个红球得2分，则所得分数ξ的数学期望E (ξ)＝________.16．已知 2＋23＝223， 3＋38＝338， 4＋415＝4415，…，若 6＋a t ＝6a t (a ，t 均为正实数)，类比以上等式可推测a ，t 的值，则a ＋t ＝________.数学基础小题限时40分钟训练(一)参考答案1．B [B ＝{x |1<log 2x <2}＝{x |2<x <4}，A ∩B ＝{x |2<x <3}．]2．B [因为z ＝x ＋3i 1－i＝(x ＋3i )(1＋i )2＝(x －3)＋(x ＋3)i 2，且是实数，所以x ＝－3，选B.] 3．A [若直线x －y ＋k ＝0与圆x 2＋y 2＝1相交，则有圆心(0,0)到直线x －y ＋k ＝0的距离为|k |2<1，解得－2<k <2，故选A.]4．A [因为f ⎝⎛⎭⎫1e ＝ln 1e ＝－1，所以f ⎣⎡⎦⎤f ⎝⎛⎭⎫1e ＝f (－1)＝1e.] 5．B [设圆心坐标为(a ，b )，则|b |＝1且|4a －3b |5＝1.又b >0，故b ＝1，由|4a －3|＝5得a ＝－12(圆心在第一象限、舍去)或a ＝2，故所求圆的标准方程是(x －2)2＋(y －1)2＝1.]6．A [由三视图可知，几何体是一个长、宽、高分别为4、3、2的长方体挖去了一个半径为1的半圆柱，故V ＝4×2×3－12×3×π×12＝24－32π.] 7．D [令g (x )＝f ⎝⎛⎭⎫x ＋π6＝2cos ⎣⎡⎦⎤2⎝⎛⎭⎫x ＋π6＋π6＝2cos ⎝⎛⎭⎫2x ＋π2＝－2sin x ．] 8．B [执行程序框图可知：n ＝1，s ＝0，p ＝30，s <p 成立；s ＝3，n ＝2，s <p 成立；s ＝3＋9，n ＝3，s <p 成立；s ＝3＋9＋27，n ＝4，s <p 不成立，因此输出的n 的值为4.]9．C [画出可行域得直线y ＝－x ＋z 过(a ，a )点时取得最大值，即2a ＝4，a ＝2.]10．D [由题意知：a n ·a n ＋1＝2n ，所以a n ＋1·a n ＋2＝2n ＋1，故a n ＋2a n＝2，所以a 1，a 3，a 5，…成等比数列，a 2，a 4，a 6，…也成等比数列，所以a 10＝2·24＝32，a 11＝32，故b 10＝64，选D.]11．C [由题意知，点P (1,4)，所以m ＋4n －1＝0，故1m ＋4n ＝m ＋4n m ＋4(m ＋4n )n ＝17＋4n m ＋4m n≥25，所以所求最小值为25.]12．D [A ⎝⎛⎭⎫－c ，b 2a ，B ⎝⎛⎭⎫－c ，－b 2a ，F 2A →＝⎝⎛⎭⎫－2c ，b 2a ，F 2B →＝⎝⎛⎭⎫－2c ，－b 2a .F 2A →·F 2B →＝4c 2－⎝⎛⎭⎫b 2a 2>0，e 2－2e －1<0,1<e<1＋ 2.] 13． y ＝－18 解析 由题意知：抛物线的开口方向向上，且2p ＝12，所以准线方程为y ＝－18. 14．（文）64解析 由图可知甲与乙两人比赛得分的中位数分别为28,36，其和为28＋36＝64. （理）180解析 第一步，从6人中选出4人有C 46种不同的方法，第二步，从选出的4人中选2人安排在星期天有C 24种不同的方法，第三步，安排剩余的两人有A 22种不同的方法，所以共有C 46C 24A 22＝15×6×2＝180种不同的选派方案．15．（文）916解析 从四个小球中连续抽取两次小球，取后放回，共有16种抽法，其中中一等奖的为23,32两种抽取方法；中二等奖的为13,31,22三种抽取方法；中三等奖的为12,21,30,03四种抽取方法，则中奖的概率为P ＝2＋3＋416＝916. （理）1解析 由题得ξ所取得的值为0或2，其中ξ＝0表示取得的球为两个黑球，ξ＝2表示取得的球为一黑一红，所以P (ξ＝0)＝C 23C 24＝12，P (ξ＝2)＝C 13C 24＝12，故E (ξ)＝0×12＋2×12＝1. 16．41解析 由推理可得a ＝6，t ＝62－1，故a ＋t ＝41.。

40分钟测试（3）一、选择题（每空5 分，共40 分）1、已知是等差数列的前项和，则2，则（）A. 66B. 55C. 44D. 332、已知等比数列的前项和为，且满足，则的值为（）A．4 B．2 C ． D．3、已知命题p：x∈R，x＋6＞0，则p是( )A ．x∈R，x＋6≥0B ．x∈R，x＋6≤0C ．x∈R，x＋6≥0D ．x∈R，x＋6≤04、．已知p：{1}{0,1}，q：{1}∈{1,2,3}，由它们构成的新命题“p∧q”“p∨q”“p”中，真命题的个数为( )A．0 B．1 C．2 D．35、在数列中，满足，，则( )A． 9 B． 11 C． 25 D．366、已知等差数列的前项和为，则使数列前项和最大的等于（）A．7 B．8 C.9 D．107、若{a n}为等比数列，，则( )A.B. C.24 D.488、已知α，β是不同的两个平面，直线a⊂α，直线b⊂β.p：a与b无公共点；q：α∥β，则p是q的( )A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件二、填空题（每空5 分，共20 分）9、若为等比数列的前项的和，，则= ．10、若等差数列的前5项和，且，则 _.11、已知命题p、q，则“命题p∨q为真”是“命题”p∧q为真的_________条件.12、命题“若．”的逆否命题是参考答案一、选择题1、 D2、C【解析】根据题意，当时，，故当时，，数列是等比数列，则，故，解得，故选C．3、D4、B5、C6、C7、C8、B二、填空题9、-710、1311、必要不充分12、若。