3-4割集分析法

§3-6 割 集 分 析 法一、割集与基本割集1）、割集 割集是支路的集合，它必须满足以下两个条件： （1） 移去该集合中的所有支路，则图被分为两部分。

（2） 当少移去该集合中的任何一条支路，则图仍是连通的。

需要说明的是，在移去支路时，与其相连的结点并不移去。

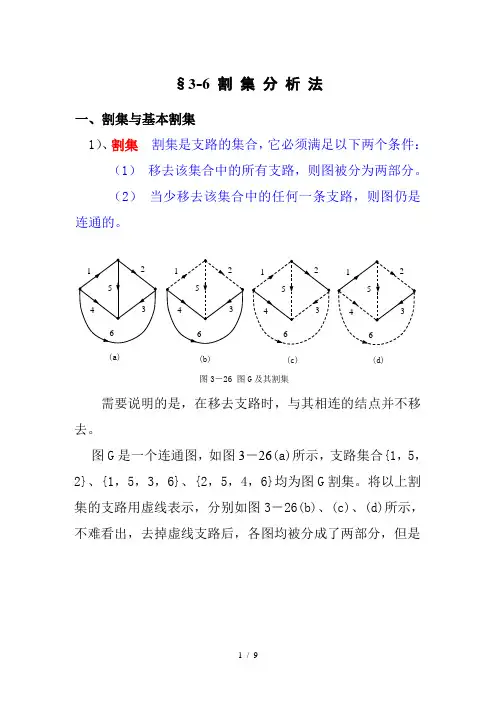
图G 是一个连通图，如图3－26(a)所示，支路集合{1，5，2}、{1，5，3，6}、{2，5，4，6}均为图G 割集。

将以上割集的支路用虚线表示，分别如图3－26(b)、(c)、(d)所示，不难看出，去掉虚线支路后，各图均被分成了两部分，但是图3－26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路，图仍然是连通的，故满足割集所要求的条件。

而支路集合{1，5，4，6}、{1，2，3，4，5}不是图G 的割集。

将集合中的支路用虚线表示后如图3－27(a)和(b)所示。

对于图3－27(a)来说，移去支路1、5、4、6后，图虽说被分为两部分（结点①为其中的一部分），但如不移去支路5，图仍被分为两部分；而对于图3－27(b)来说，将支路1、2、3、4、5移去后，图则被分成了三部分，故以上两种支路集合不是割集。

2）、作高斯面确定割集在图G 上作一个高斯面（闭合面），使其包围G 的某些节点，而每条支路只能被闭合面切割一次，去掉与闭合面相切割的支路，图G 将被分为两部分，那么这组支路集合即为图G 的一个割集。

在图G 上画高斯面（闭合面）C 1、C 2、(a)(b)图3－27 非割集说明①②①②C 3如图3－28所示，对应割集C 1、C 2、C 3的支路集合为{1，5，2}、{1，5，3，6}、{2，5，4，6}。

3）、基本割集基本割集又称单树支割集，即割集中只含一条树支，其余均为连支。

如选支路1、5、3为树支，如图3－29所示，则割集C 1，C 2，C 3为基本割集，基本割集的方向与树支的参考方向一致。

当树选定后，对应的基本割集是唯一确定的。

安全系统工程（第三版）模拟试题二一、选择题（每小题1分，共10分）1.系统的特征不包括（）A.整体性B.相关性C.目的性D.复杂性2.预先危险性分析法（PHA）可以用于工程活动的（）A.日常运行阶段B.建造投产阶段C.事故调查期间D.方案设计阶段3.下列不是引导词的是（）A. 否B. 多C. 少D. 并且4.在故障树分析中，某些基本事件都不发生，则导致顶事件不发生，这些基本事件的集合称为（）A. 径集B. 割集C. 最小径集D. 最小割集5. 预先危险性分析是在一个工程项目的设计、施工和投产之前，对系统存在的危险性类别、出现条件、导致事故的后果等做出概略的分析。

通常情况下这种分析方法将系统的危险和危害划分为（）个等级。

A．4 B. 5 C．6 D．76. 以下各种评价方法中不属于定量评价方法的有（）A. 故障类型及影响分析B. 事故树分析C. 作业条件危险性评价法D. 危险指数评价法7. 在事故树分析中，反映基本事件发生概率的增减对顶事件发生概率影响的敏感程度的是（）A．结构重要度B．临界重要度C．概率重要度D．最小径集8. 在火灾爆炸指数法中，物质在由燃烧或其他化学反应引起的火灾和爆炸中其潜在能量释放速率的度量，被称为（）A. 物质系数B. 爆炸系数C. 工艺系数D. 物质危险9. 对现有的设备设施进行安全评价，可以采取的评价方法是（）A. 安全验收评价B. 安全现状评价C.安全预评价D.专项安全评价10.下列评价方法中不能提供评价后果的是（）A.预先危险性分析B.ETAC.FTAD.安全检查表法二、名词解释（每小题4分，共20分）1、系统工程2、预先危险性分析3、最小割集4、故障5、安全决策三、简答题（每小题6分，共30分）1、在作故障类型及影响分析时，划分故障类型和评定故障危险度等级应分别从哪些方面进行考虑？2、安全系统工程的优点有哪些？3、最小割集和最小径集的主要作用有哪些？4、简述事故树分析的步骤5、什么是风险型决策？风险型决策问题一般应具备哪5个条件？四、计算题（20分）已知事故树如图1所示，其中q1=0.01，q2=0.02,q3=0.03,q4=0.04,q5=0.05,试求该事故树的最小割集，最小径集，顶事件发生的概率，结构重要度，概率重要度和关键重要度，并对结果进行分析。

第三章电阻电路的一般分析◆重点：1、支路法2、节点法3、网孔法和回路法◆难点：1、熟练掌握支路法、网孔法和割集分析法的计算思路，会用这几种方法列写电路方程。

2、熟练地运用节点法和回路法分析计算电路。

3-1 电网络中的基本概念网络图论与矩阵论、计算方法等构成电路的计算机辅助分析的基础。

其中网络图论主要讨论电路分析中的拓扑规律性，从而便于电路方程的列写。

1．支路——Branch流过同一个电流的电路部分为一条支路。

2．节点——node三条或者三条以上支路的汇集称为节点。

4．网络的图——graph节点和支路的集合，称为图，每一条支路的两端都连接到相应的节点上。

6．回路——loop电路中的任意闭合路径，称为回路。

8．网孔——mesh一般是指内网孔。

平面图中自然的“孔”，它所限定的区域不再有支路。

例如：在下图中，支路数6，节点数4，网孔数3，回路数79．树一个连通图G的树T是指G的一个连通子图，它包含G的全部节点，但不含任何回路。

树中的支路称为“树支”——tree branch，图G中不属于T 的其他支路称为“连支”——link，其集合称为“树余”。

一个连通图的树可能存在多种选择方法。

10．基本回路只含一条连支的回路称为单连支回路，它们的总和为一组独立回路，称为“基本回路”。

树一经选定，基本回路唯一地确定下来。

对于平面电路而言，其全部网孔是一组独立回路。

3-2 2B 法与1B 法3.2.1 支路法（2B 法）介绍1．方法概述以支路电压和支路电流作为变量，对节点列写电流（KCL ）方程，对回路列写电压（KVL ）方程，再对各个支路写出其电压电流关系方程，简称支路方程。

从而得到含2b 个变量的2b 个独立方程。

又称为“2b 法”。

2．思路由上述方法可见，“2b 法”实际上清晰地体现了求解电路的两个不可或缺的方面，即电路的解一是要满足网络的拓扑约束，二是要满足电路中各个元件的伏安关系约束。

3．方程结构b 个支路方程，)1(-n 个电流（KCL ）方程，))1((--n b 个电压（KVL ）方程。

危害、危险辨识与评价之————危险性分析评价法之——事故树分析一、事故树分析（FTA）－定性分析事故树定性分析就是对事故树中各事件不考虑发生概率多少，只考虑发生和不发生两种情况。

通过定性分析可以知道哪一个或哪几个基本事件发生，顶上事件就一定发生，哪一个事件发生对顶上事件影响大，哪一个影响少，从而可以采取经济有效的措施，防止事故发生。

事故树定性一分析包括求最小割集和最小径集，计算各基本事件的结构重要度，在此基础上确定安全防灾对策。

（1）最小割集和最小径集在事故树中，如果所有的基本事件都发生则顶上事件必然发生。

但是在很多情况下并非如此，往往是只要某个或几个事件发生顶上事件就能发生。

凡是能导致顶上事件发生的基本事件的集合就叫割集。

割集也就是系统发生故障的模式。

在一棵事故树中，割集数目可能有很多，而在内容上可能有相互包含和重复的情况，甚至有多余的事件出现，必须把它们除去，除去这些事件的割集叫最小割集。

也就是说凡能导致顶上事件发生的最低限度的基本事件的集合称为最小割集。

在最小割集里，任意去掉一个基本事件就不成其为割集。

在事故树中，有一个最小割集，顶上事件发生的可能性就有一种。

事故树中最小割集越多，顶上事件发生的可能性就越多，系统就越危险。

相反地，在事故树中，有一组基本事件不发生，顶上事件就不发生，这一组基本事件的集合叫径集。

径集是表示系统不发生故障而正常运行的模式。

同样在径集中也存在相互包含和重复事件的情况，去掉这些事件的径集叫最小径集。

也就是说，凡是不能导致顶上事件发生的最低限度的基本事件的集合叫最小径集。

在最小径集中，任意去掉一个事件也不成其径集。

事故树有一个最小径集，顶上事件不发生的可能性就有一种。

最小径集越多，顶上事件不发生的途径就越多，系统也就越安全。

上述所谓的集合，就是满足某种条件或具有某种属性的事物的全体。

集合的每一个成员称为这个集合的元素。

例如一个班级全体学生构成了一个集合，一个车队的全部汽车也构成一个集合。

§3-6 割 集 分 析 法一、割集与基本割集1）、割集 割集是支路的集合，它必须满足以下两个条件： （1） 移去该集合中的所有支路，则图被分为两部分。

（2） 当少移去该集合中的任何一条支路，则图仍是连通的。

需要说明的是，在移去支路时，与其相连的结点并不移去。

图G 是一个连通图，如图3－26(a)所示，支路集合{1，5，2}、{1，5，3，6}、{2，5，4，6}均为图G 割集。

将以上割集的支路用虚线表示，分别如图3－26(b)、(c)、(d)所示，不难看出，去掉虚线支路后，各图均被分成了两部分，但是图3－26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路，图仍然是连通的，故满足割集所要求的条件。

而支路集合{1，5，4，6}、{1，2，3，4，5}不是图G 的割集。

将集合中的支路用虚线表示后如图3－27(a)和(b)所示。

对于图3－27(a)来说，移去支路1、5、4、6后，图虽说被分为两部分（结点①为其中的一部分），但如不移去支路5，图仍被分为两部分；而对于图3－27(b)来说，将支路1、2、3、4、5移去后，图则被分成了三部分，故以上两种支路集合不是割集。

2）、作高斯面确定割集在图G 上作一个高斯面（闭合面），使其包围G 的某些节点，而每条支路只能被闭合面切割一次，去掉与闭合面相切割的支路，图G 将被分为两部分，那么这组支路集合即为图G 的一个割集。

在图G 上画高斯面（闭合面）C 1、C 2、(a)(b)图3－27 非割集说明①②③①②C 3如图3－28所示，对应割集C 1、C 2、C 3的支路集合为{1，5，2}、{1，5，3，6}、{2，5，4，6}。

3）、基本割集基本割集又称单树支割集，即割集中只含一条树支，其余均为连支。

如选支路1、5、3为树支，如图3－29所示，则割集C 1，C 2，C 3为基本割集，基本割集的方向与树支的参考方向一致。

当树选定后，对应的基本割集是唯一确定的。

1.系统工程定义：系统工程是以系统为研究对象，以达到总体最佳效果为目标，为达到这一目标而采取组织、管理、技术等多方面的最新科学成就和知识的一门综合性的科学技术。

2.安全系统工程：是指采用系统工程方法，识别、分析、评价系统中的危险性，根据其结果调整工艺、设备、操作、管理、生产周期和投资等因素，使系统可能发生的事故得到控制，并使系统安全性达到最好的状态。

3.系统安全分析是安全系统工程的核心内容。

4.安全检查表：根据有关安全规范、标准、制度及其他系统分析方法分析的结果，系统地对一个生产系统或设备进行科学的分析，找出各种不安全因素，依据检查项目把找出的不安全因素以问题清单的形式制成表，以便于实施检查和安全管理，称为安全检查表。

5.预先危险分析pha：一般是指在一个系统或子系统运转活动之前，对系统存在的危险源、出现条件及可能造成的结果，进行宏观概略分析的方法。

6.危险源是指导致事故的根源，包括三个要素：潜在危险性、存在状态和触发因素。

7.故障：元件、子系统或系统在规定期限内和运行条件下未按设计要求完成规定的功能或功能下降，称为故障。

8.危险和可操作性研究：(HAZOP)是一种基于引导词的、由多专业人员组成的研究组通过一系列的会议来实施的、对系统工艺或操作过程中存在的可能导致有害后果的各种偏差加以系统识别的定性分析方法。

9.引导词：系统偏差产生联想的简短词汇。

10.割集：事故树中某些事件构成的集合，且当集合中的事件都发生时，顶事件必然发生。

11.最小割集：如果某个割集中任意除去一个基本事件就不在是割集，则称该割集为最小割集。

12.径集：事故树中某些基本事件的集合，当这些基本事件都不发生时，顶事件必不发生。

13.最小径集：又称最小通集，在最小径集中，去掉任何一个基本事件它就不在是径集。

则称这个径集为最小径集。

因此最小径集表达了系统的安全性。

14.可靠性：指系统、设备或元件等在规定的时间内、规定的条件下，完成其规定功能的能力。

第三章网孔分析法和节点分析科学家研究世界工程师创造崭新世界西奥多•冯•卡曼(Theodore von Karman)美籍匈牙利力学家,近代力学奠基人之一。

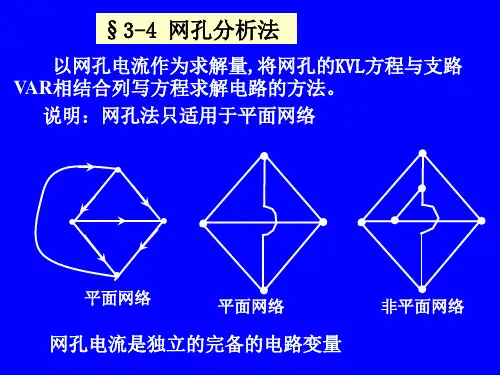
第三章网孔分析法和结点分析法3－1 网孔分析法(重点）3－2 结点分析法（重点）3－3 含受控源的电路分析（重点）3－4 回路分析法和割集分析法3－5 计算机分析电路实例3－6 树支电压与连支电流法§3－1 网孔分析法(重点)本章介绍利用独立电流或独立电压作变量来建立电路方程的分析方法，可以减少联立求解方程的数目，适合于求解稍微复杂一点的线性电阻电路，是求解线性电阻电路最常用的分析方法。

网孔方程：用网孔电流作变量建立的电路方程。

求解网孔方程得到网孔电流后，用KCL 方程可求出全部支路电流，再用VCR 方程可求出全部支路电压。

一、网孔电流设想电流i 1、i 2和i 3沿每个网孔边界闭合流动而形成，如图中箭头所示。

这种在网孔内闭合流动的电流，称为网孔电流。

为何提出网孔电流作为求解变量？是因为网孔电流具有如下令人感兴趣的特点：（1）完备性——网孔电流一旦求出，各支路电流就被唯一确定。

（2）独立性——网孔电流自动满足KCL 。

这一特点的意义在于：求解i 1、i 2、i 3时，不必再列写KCL 方程，只需列出三个网孔的KVL 方程。

因而可用较少的方程求出网孔电流。

二﹑网孔方程⎪⎭⎪⎬⎫=++−=−++=−++0003S 4466332S 6655221S 445511u i R i R i R u i R i R i R u i R i R i R 将以下各式代入上式，消去i 4、i 5和i 6后可以得到：326215314 i i i i i i i i i −=+=+=网孔方程⎪⎭⎪⎬⎫++−−+++=+++3S 314326332S 326215221S 31421511)()()()()()(i i R i i i i R i i R u i i i i R i R 1S 34251541)(u i R i R i R R R =++++S236265215)(u i R i R R R i R =−+++3S 36432614)(u i R R R i R i R −=+++−以图示网孔电流方向为绕行方向，写出三个网孔的KVL 方程分别为：﹑将网孔方程写成一般形式：⎪⎭⎪⎬⎫=++=++=++S3333323213122S 32322212111S 313212111u i R i R i R u i R i R i R u i R i R i R 其中R 11,R 22和R 33称为网孔自电阻，它们分别是各网孔内全部电阻的总和。