割集分析法

最小割集计算：T=A1+A2+A3=B1B2+X6X7+X8X9=（X1+X2+X3）（X4+X5）+X6X7+X8X9= X1X4+X1X5+X2X4+X2X5+X3X4+X3X5+X6X7+X8X9则最小割集有8个，即K1=｛X1，X4｝；K2=｛X1，X5｝；K3=｛X2，X4｝；K4=｛X2，X5｝；K5=｛X3，X4｝；K6=｛X3，X5｝；K7=｛X6，X7｝；K8=｛X8，X9｝。

最小径集计算：T′=A1′·A2′·A3′=（B1′+B2′）（X6′+X7′）（X8′+X9′）=（X1′X2′X3′+X4′X5′）（X6′+X7′）（X8′+X9′）=（X1′X2′X3′X6′+X1′X2′X3′X7′+X4′X5′X6′+X4′X5′X7′）（X8′+X9′）= X1′X2′X3′X6′X8′+ X1′X2′X3′X6′X9′+ X1′X2′X3′X7′X8′+ X1′X2′X3′X7′X9′+ X4′X5′X6′X8′+ X4′X5′X6′X9′+ X4′X5′X7′X8′+ X4′X5′X7′X9′则故障树的最小径集为8个，即P1=｛X1，X2，X3，X6，X8｝；P2=｛X1，X2，X3，X6，X9｝；P3=｛X1，X2，X3，X7，X8｝；P4=｛X1，X2，X3，X7，X9｝；P5=｛X4，X5，X6，X8｝；P6=｛X4，X5，X6，X9｝；P7=｛X4，X5，X7，X8｝；P8=｛X4，X5，X7，X9｝；起重钢丝绳断裂事故发生概率计算：根据最小割集计算顶上事件的概率即g=1－（1－qk1）（1－qk2）（1－qk3）（1－qk4）（1－qk5）（1－qk6）（1－qk7）（1－qk8）=1－（1－q1q4）（1－q1q5）（1－q2q4）（1－q2q5）（1－q3q4）（1－q3q5）（1－q6q7）（1－q8q9）由于q1=q2=q3=q4=q5=q6=q7=q8=q9=0.1则g=1－（1－0.1×0.1）（1－0.1×0.1）（1－0.1×0.1）（1－0.1×0.1）（1－0.1×0.1）（1－0.1×0.1）（1－0.1×0.1）（1－0.1×0.1）=1－（1－0.1×0.1）8=1－0.998=0.07726山东科技大学2005年招收硕士学位研究生入学考试安全系统工程试卷（共2页）一、问答题（共25分）1、说明事故法则的概念，它对安全工作的启示是什么？分析其在安全工作中的应用。

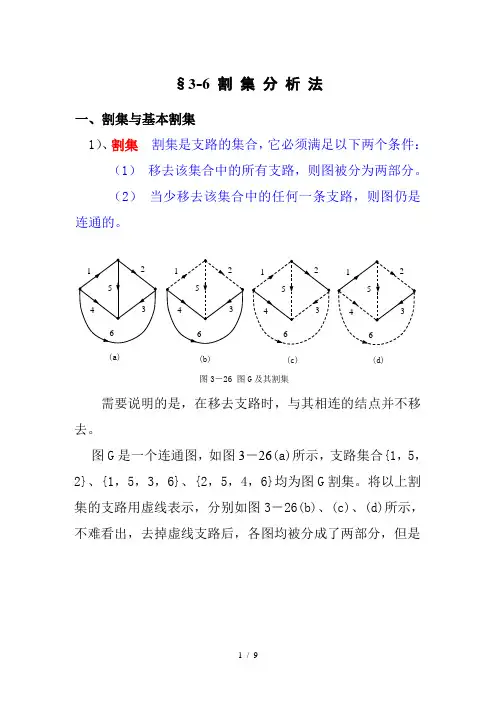
§3-6 割 集 分 析 法一、割集与基本割集1）、割集 割集是支路的集合，它必须满足以下两个条件： （1） 移去该集合中的所有支路，则图被分为两部分。

（2） 当少移去该集合中的任何一条支路，则图仍是连通的。

需要说明的是，在移去支路时，与其相连的结点并不移去。

图G 是一个连通图，如图3－26(a)所示，支路集合{1，5，2}、{1，5，3，6}、{2，5，4，6}均为图G 割集。

将以上割集的支路用虚线表示，分别如图3－26(b)、(c)、(d)所示，不难看出，去掉虚线支路后，各图均被分成了两部分，但是图3－26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路，图仍然是连通的，故满足割集所要求的条件。

而支路集合{1，5，4，6}、{1，2，3，4，5}不是图G 的割集。

将集合中的支路用虚线表示后如图3－27(a)和(b)所示。

对于图3－27(a)来说，移去支路1、5、4、6后，图虽说被分为两部分（结点①为其中的一部分），但如不移去支路5，图仍被分为两部分；而对于图3－27(b)来说，将支路1、2、3、4、5移去后，图则被分成了三部分，故以上两种支路集合不是割集。

2）、作高斯面确定割集在图G 上作一个高斯面（闭合面），使其包围G 的某些节点，而每条支路只能被闭合面切割一次，去掉与闭合面相切割的支路，图G 将被分为两部分，那么这组支路集合即为图G 的一个割集。

在图G 上画高斯面（闭合面）C 1、C 2、(a)(b)图3－27 非割集说明①②①②C 3如图3－28所示，对应割集C 1、C 2、C 3的支路集合为{1，5，2}、{1，5，3，6}、{2，5，4，6}。

3）、基本割集基本割集又称单树支割集，即割集中只含一条树支，其余均为连支。

如选支路1、5、3为树支，如图3－29所示，则割集C 1，C 2，C 3为基本割集，基本割集的方向与树支的参考方向一致。

当树选定后，对应的基本割集是唯一确定的。

故障树割集下行法摘要：1.故障树割集下行法的定义与概述2.故障树割集下行法的基本原理3.故障树割集下行法的应用实例4.故障树割集下行法的优缺点分析5.故障树割集下行法在我国的发展现状与前景正文：故障树割集下行法是一种基于故障树理论的安全评估方法，主要用于分析和计算系统故障概率，以及确定系统的安全关键部件。

该方法通过构建故障树，分析树中各节点的割集，从而找出可能导致系统故障的最小割集，进而为系统安全管理提供依据。

下面将从五个方面对故障树割集下行法进行详细介绍。

首先，故障树割集下行法的定义与概述。

故障树是一种特殊的决策树，用以表示系统中各部件的故障模式及其对系统整体功能的影响。

故障树割集下行法通过分析故障树中各节点的割集，找出导致系统故障的最小割集，从而计算出系统的故障概率。

其次，故障树割集下行法的基本原理。

该方法的基本原理是利用故障树的结构特征，分析树中各节点的割集，从而找出可能导致系统故障的最小割集。

在此基础上，可以计算出系统的故障概率，并据此评估系统的安全性能。

再次，故障树割集下行法的应用实例。

故障树割集下行法广泛应用于航空航天、核能、化工、电力等高安全风险领域。

例如，在航空航天领域，可以通过该方法分析飞机各部件的故障概率，从而确定哪些部件是安全关键部件，为飞机的设计和维修提供依据。

接着，故障树割集下行法的优缺点分析。

该方法的优点在于可以直观地表示系统的故障模式，便于分析和理解；计算简便，速度快；能够准确找出安全关键部件，为系统安全管理提供依据。

缺点在于，对于复杂的系统，构建故障树需要花费较多时间和精力；此外，该方法对于不确定性因素的处理能力较弱。

最后，故障树割集下行法在我国的发展现状与前景。

故障树割集下行法在我国已经得到广泛应用，并在相关领域的研究中取得了显著成果。

§3-6 割 集 分 析 法一、割集与基本割集1）、割集 割集是支路的集合，它必须满足以下两个条件： （1） 移去该集合中的所有支路，则图被分为两部分。

（2） 当少移去该集合中的任何一条支路，则图仍是连通的。

需要说明的是，在移去支路时，与其相连的结点并不移去。

图G 是一个连通图，如图3－26(a)所示，支路集合{1，5，2}、{1，5，3，6}、{2，5，4，6}均为图G 割集。

将以上割集的支路用虚线表示，分别如图3－26(b)、(c)、(d)所示，不难看出，去掉虚线支路后，各图均被分成了两部分，但是图3－26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路，图仍然是连通的，故满足割集所要求的条件。

而支路集合{1，5，4，6}、{1，2，3，4，5}不是图G 的割集。

将集合中的支路用虚线表示后如图3－27(a)和(b)所示。

对于图3－27(a)来说，移去支路1、5、4、6后，图虽说被分为两部分（结点①为其中的一部分），但如不移去支路5，图仍被分为两部分；而对于图3－27(b)来说，将支路1、2、3、4、5移去后，图则被分成了三部分，故以上两种支路集合不是割集。

2）、作高斯面确定割集在图G 上作一个高斯面（闭合面），使其包围G 的某些节点，而每条支路只能被闭合面切割一次，去掉与闭合面相切割的支路，图G 将被分为两部分，那么这组支路集合即为图G 的一个割集。

在图G 上画高斯面（闭合面）C 1、C 2、(a)(b)图3－27 非割集说明①②③①②C 3如图3－28所示，对应割集C 1、C 2、C 3的支路集合为{1，5，2}、{1，5，3，6}、{2，5，4，6}。

3）、基本割集基本割集又称单树支割集，即割集中只含一条树支，其余均为连支。

如选支路1、5、3为树支，如图3－29所示，则割集C 1，C 2，C 3为基本割集，基本割集的方向与树支的参考方向一致。

当树选定后，对应的基本割集是唯一确定的。

3.6 矿井通风网络解算的计算方法3.6.1算法概述3.6.1.1通风网络解算的内容通风网络解算就是在已知通风网络中的几何结构（网络图）、各分支风阻、各风机特性曲线、矿井的自然风压等基础数据的情况下，要求：（1） 计算网络中各分支的风量和阻力；（2） 计算各扇风机在该网络上工作时的工况参数。

除了计算矿井在设计和正常生产情况下的通风状况外，还可计算出矿井在冒顶、火灾、风机故障等非正常情况下和各种可预见的情况（如工作面贯通、采完封闭等）下网络的通风状况。

但不论在什么情况下，所计算的都是空气在网络中自然流动状况，所以矿井通风网络解算又称为自然分风计算。

3.6.1.2网络自然分风计算的数学模型在3.5节中已经给出了用不同形式描述的风压、风量平衡定律，它们是任何矿井通风网络分析问题的基本数学模型。

风量平衡定律：01=∙∑=nj j ijq b（i=1,2,3,…,m-1），BQ=0 （3-10）风压平衡定律：01=∑=nj ij i h c（i=1,2,3,…,b ） ，CH=0 （3-15）通风网络解算的目的就是要计算出同时满足以上两式的一组风量和一组风压：T Q =（q 1，q 2，q 3，…，q n ，） T H =（h 1，h 2，h 3，…，h n ，） 式（3-10）有m-1个独立风量方程，式（3-15）有n-m+1个独立风压方程式，两式联立有：独立方程数：（m-1）+(n-m+1)=n 个；又知在n 个未知风量中，只有n-m+1个是独立的。

在n 个未知风压中，只有m-1个是独立的。

因此：独立变量数：(n-m+1)+（m-1）=n 个所以两式联立后，独立方程数正好等于独立变量数，故方程组是有解的。

因在式（3-15）中j N j f j j j j h h h q r h --∆+=2，所以，所得方程组是非线性的。

对这样一个非线性方程组，一般均无法直接用解析法求解（除简单并联外）。

因而只能用数值解法求其数值解。

割集法计算题一、割集法的基本概念割集法是一种在图论或者网络分析中超级有用的方法呢。

简单来说呀，割集就是能把一个连通图分成两个不连通部分的边的集合。

这就像是在一个大的交通网络里，你把某些关键的道路给堵住了，整个交通就被分成了两块不能互相到达的区域啦。

二、割集法计算题的类型1. 简单连通图的割集计算比如说给你一个简单的三角形的连通图，让你找出所有的割集。

这种情况下呢，这个三角形的三条边就分别是三个割集啦，因为你去掉任何一条边，这个三角形就不再是一个连通的图形啦。

这就好比在一个三角形的小岛，有三条桥连接着，你拆掉任何一座桥，这个岛就被分成了两块啦。

2. 复杂连通图的割集计算当图变得复杂起来，比如有好多节点和边的那种图。

这时候找割集就没那么容易啦。

你得一个一个地去分析哪些边组合起来可以把图断开。

就像是在一个超级大的迷宫里，你要找到哪些墙推倒了就能把迷宫分成两块一样难呢。

三、割集法计算题的解题步骤1. 观察图形先仔细看看这个图长啥样，有多少个节点和边。

这就像是你要去探索一个新地方，得先看看这个地方的大概布局一样。

2. 从简单边入手先看看那些单独去掉就可能把图断开的边。

这就像是在一个连锁结构里，先找找那些最脆弱的一环。

3. 组合边的分析然后再分析一些边的组合，看看它们能不能把图断开。

这就像是在玩拼图，你要试试不同的碎片组合起来能不能达到你想要的效果。

四、割集法的实际应用1. 电路分析中的应用在电路里呀，割集法可以用来分析电流的流向呢。

比如说一个复杂的电路网络，你可以把某些线路看成是割集，这样就能更好地理解电流是怎么在这个网络里流动的啦。

2. 交通网络规划中的应用在交通规划的时候呢，割集法可以帮助规划者找到那些关键的道路。

如果这些道路出现问题，整个交通就会瘫痪，所以要重点保护或者规划好这些道路的备份呢。

五、割集法计算题的易错点1. 遗漏割集有时候在复杂的图里，很容易就漏掉一些边的组合可以成为割集。

这就像是在找宝藏的时候，可能忽略了一些小角落一样。

故障树最小割集Company number：【0089WT-8898YT-W8CCB-BUUT-202108】故障树定性分析—最小割集及其求法故障树分析，包括定性分析和定量分析两种方法。

在定性分析中，主要包括最小割集、最小径集和重要度分析。

限于篇幅，以下仅介绍定性分析中的最小割集和最小径集。

最小割集及其求法割集：它是导致顶上事件发生的基本事件的集合。

最小割集就是引起顶上事件发生必须的最低限度的割集。

最小割集的求取方法有行列式法、布尔代数法等。

现在，已有计算机软件求取最小割集和最小径集。

以下简要介绍布尔代数化简法。

图8－9为一故障树图，以下是用布尔代数化简的过程。

图8－9 故障树T=A1＋A2=X1 X2 A3＋X4 A4=X1 X2 (X1＋X3)＋ X4 (X5＋X6)=X1 X2 A1＋X1 X2 A3＋ X4 X5＋X4 X6=X1 X2＋ X4 X5＋X4 X6所以最小割集为{X1，X2}，{X4，X5}，{X4，X6}。

结果得到三个交集的并集，这三个交集就是三个最小割集E1={X1，X2}，E2={X4，X5}，E3={X4，X6}。

用最小割集表示故障树的等效图如图8－10。

故障树定性分析—最小割集和最小径集在故障树分析中的应用（1）最小割集表示系统的危险性求出最小割集可以掌握事故发生的各种可能，了解系统的危险性。

每个最小割集都是顶上事件发生的一种可能，有几个最小割集，顶上事件的发生就有几种可能，最小割集越多，系统越危险。

从最小割集能直观地、概略地看出，哪些事件发生最危险，哪些稍次，哪些可以忽略，以及如何采取措施，使事故发生概率下降。

例：共有三个最小割集{X1} 、{X2，X3} 、{X4，X5，X6，X7 ，X8}，如果各基本事件的发生概率都近似相等的话，一般地说，一个事件的割集比两个事件的割集容易发生，五事件割集发生的概率更小，完全可以忽略。

因此，为了提高系统的安全性，可采取技术、管理措施以便使少事件割集增加基本事件。

西南交通大学考研电路分析大纲本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March电路分析大纲一、绪论，电路的基本概念及基本定律1、电路模型。

2、基本变量及参考方向。

3、电路元件，独立电源，受控源，基尔霍夫定律。

二、电阻电路的等效变换1、电路元件的联接，Y- 接互换。

2、电路的简化。

3、实际电压源、电流源的等效互换。

三、常用网络分析法1、支路电流法，结点电压法。

2、网孔电流法，网络图论知识，回路分析法。

3、割集分析法。

四、线性网络的几个定理1、叠加定理，叠代定理。

2、戴维南-诺顿定理，特勒根定理。

3、互易定理，对偶原理。

五、含运算放大器的电路分析1、运算放大器，理想运算放大器。

2、含理想运算放大器的电路分析与计算。

六、正弦稳态电路1、正弦量的振幅、频率与相位及有效值。

2、相量分析法，正弦量的相量表示，向量图。

3、R、L、C元件的相量电路、相量表达式、向量图。

4、感抗、容抗、感纳，容纳的概念及与频率的关系。

5、复阻抗、复导纳的概念及其欧姆定律。

6、以阻抗或导纳判断电路的性质。

7、简单及复杂电路的分析计算。

8、正弦稳态电路的功率和能量。

9、有功功率，无功功率，视在功率，复功率和功率因数。

10、最大功率传输。

11、串联、并联谐振，串，并联谐振频率特性。

12、谐振电路的品质因数。

七、具有耦合电感的电路1、互感及互感电压，互感电压的参考方向。

2、电路的伏安关系式。

3、同名端，耦合电感的串、并联、去耦。

4、空心变压器电路的分析。

5、理想变压器与全耦合变压器。

八、三相交流电路1、三相电源，相序，星形、三角形联接。

2、对称三相电路中相电压与线电压，相电流与线电流的关系。

3、对称三相电路的计算，有功功率。

4、无功功率。

瞬时功率，视在功率。

5、不对称三相电路的分析计算。

九、周期性非正弦电流电路1、周期性非正弦函数的傅里叶级数。

2、波形的对称性与傅里叶级数的关系。

“电路分析基础”教材各章小结第一章小结：1.电路理论的研究对象是实际电路的理想化模型，它是由理想电路元件组成。

理想电路元件是从实际电路器件中抽象出来的，可以用数学公式精确定义。

2.电流和电压是电路中最基本的物理量，分别定义为电流tqidd=，方向为正电荷运动的方向。

电压qwudd=，方向为电位降低的方向。

3.参考方向是人为假设的电流或电压数值为正的方向，电路理论中涉及的电流或电压都是对应于假设的参考方向的代数量。

当一个元件或一段电路上电流和电压参考方向一致时，称为关联参考方向。

4.功率是电路分析中常用的物理量。

当支路电流和电压为关联参考方向时，ui p=；当电流和电压为非关联参考方向时，uip-=。

计算结果0>p表示支路吸收（消耗）功率；计算结果<p表示支路提供（产生）功率。

5.电路元件可分为有源和无源元件；线性和非线性元件；时变和非时变元件。

电路元件的电压-电流关系表明该元件电压和电流必须遵守的规律，又称为元件的约束关系。

（1）线性非时变电阻元件的电压-电流关系满足欧姆定律。

当电压和电流为关联参考方向时，表示为u=Ri；当电压和电流为非关联参考方向时，表示为u=－Ri。

电阻元件的伏安特性曲线是u-i平面上通过原点的一条直线。

特别地，R→∞称为开路；R＝0称为短路。

（2）独立电源有两种电压源的电压按给定的时间函数u S(t)变化，电流由其外电路确定。

特别地，直流电压源的伏安特性曲线是u-i平面上平行于i轴且u轴坐标为U S的直线。

电流源的电流按给定的时间函数i S(t)变化，电压由其外电路确决定。

特别地，直流电流源的伏安特性曲线是u-i平面上平行于u轴且i轴坐标为I S的直线。

（3）受控电源受控电源不能单独作为电路的激励，又称为非独立电源，受控电源的输出电压或电流受到电路中某部分的电压或电流的控制。

有四种类型：VCVS、VCCS、CCVS和CCCS。

6.基尔霍夫定律表明电路中支路电流、支路电压的拓扑约束关系，它与组成支路的元件性质无关。

isograph计算二级割集摘要：1.ISOGRAPH简介2.二级割集概念阐述3.ISOGRAPH计算二级割集方法4.实例分析5.总结与展望正文：【1】ISOGRAPH简介ISOGRAPH（等高线图）是一种用于表示图形中某一方面属性的图形，通过等高线可以直观地反映出数据的变化规律和分布情况。

在地理信息系统（GIS）、遥感、地图制图等领域具有广泛的应用。

【2】二级割集概念阐述二级割集是指在原始数据集中，通过一定的规则将数据划分为两个子集，其中一个子集包含一类目标，另一个子集包含另一类目标。

在ISOGRAPH 中，二级割集常用于区分不同地物类型、地貌特征等。

【3】ISOGRAPH计算二级割集方法计算二级割集的主要方法有以下几种：1.基于地形指数的方法：通过计算地形指数（如高程、坡度等）将数据划分为不同区域。

2.基于水系分析的方法：利用水系网络将数据划分为山地区域和平原区域。

3.基于地貌单元的方法：根据地貌单元（如山地、丘陵、平原等）进行划分。

4.基于土地利用类型的方法：根据土地利用类型（如耕地、林地、草地等）进行划分。

【4】实例分析以土地利用类型为例，假设我们有一幅包含多种土地利用类型的遥感图像，我们可以通过以下步骤计算二级割集：1.预处理：对原始图像进行辐射校正、大气校正等预处理，提高图像质量。

2.特征提取：从图像中提取感兴趣区域（如建筑用地、水体等），作为划分依据。

3.分类：利用分类算法（如最小距离分类、支持向量机等）对图像进行分类，得到初步的二级割集。

4.优化：根据实际情况对分类结果进行调整，使划分更加合理。

5.绘制等高线图：根据分类结果，绘制等高线图，直观地展示土地利用类型的分布情况。

【5】总结与展望ISOGRAPH在计算二级割集方面具有显著优势，能够直观地反映数据分布规律和地物类型差异。

随着遥感技术、GIS和计算机视觉等领域的不断发展，ISOGRAPH在二级割集计算方面的应用将更加广泛。