我所认识的应力应变关系

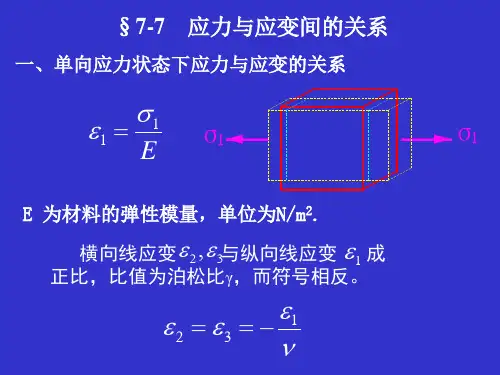
应力应变的关系
应力和应变是力学中的两个重要概念，它们之间存在着一定的关系。

应力是指物体在受到外部力的作用下产生的内部阻力，即单位面积上的力的大小。

应力可以分为三种：拉应力、压应力和剪应力。

拉应力是指在物体受到拉伸力的作用下产生的内部阻力；压应力是指物体在受到压缩力的作用下产生的内部阻力；剪应力是指在物体受到剪切力的作用下产生的内部阻力。

应变是指物体在受到外力作用下，因其分子重新排列或形变而产生的变形量，即单位长度的形变。

应变可以分为线性应变和剪切应变。

线性应变是指物体在受到拉伸或压缩力的作用下产生的长度变化；剪切应变是指物体在受到剪切力的作用下产生的形变。

应力和应变之间的关系可以通过物体的材料性质来描述。

弹性材料的应力和应变之间存在线性关系，即受到的应力与应变成正比。

这个比例常数称为弹性模量，用来描述物体的弹性性质。

对于非弹性材料，应力和应变之间的关系则更加复杂，通常需要使用材料的本构方程进行描述。

总之，应力和应变之间的关系取决于物体的材料性质，并可以通过弹性模量或材料的本构方程来描述。

立，即可求出与给定主应力 i 对应的主方向。
1、 2、 3是方程（5-7）的三个根，所
以，也可以将特征方程写成
( 1 )( 2 )( 3 ) 0
展开后有 3 ( 1 2 3 ) 2 ( 1 2 2 3 3 1 ) 1 2 3 0
与式（5-7）比较，得
I1 I2
方程（7）有三组解：
第一组是 m0, n0
第二组是 m0, n1/ 2
第三组是 m1/ 2, n0
有了m、n就可以从（4）中求得相应的l，并运用
（5）式得到相应的极值剪应力 ，由（2）式
得到极值剪应力面上的正应力 。 同理可从（3）和（4）中分别消去m和n，按上述 方法又可以得到六组解，但其中三组是重复的， 独立的解答一共六组，如表5-1所示。 表中前三组解答对应于主平面，其上剪应力为零； 而后三组解答对应于经过主轴之一而平分其他两 主轴夹角的平面，如图5-5示，其上剪应力为
1 和 2 的方向可取与 ν (3) 垂直平面上的任
意方向。即与ν (3) 垂直的方向都是主方向。
如果 123，则 ν (1)ν (2)、ν (2)ν (3)、
ν (3)ν (1)三者可以是零，也可以不是零，这
说明三个主方向可以相互垂直，也可以不垂 直，也就是说，任何方向都是主方向。
（3）主应力的极值性 命题1：最大（或最小）主应力是相应点处任 意截面上正应力的最大（或最小）值。
r r
这就是极坐标下的应力分量与直角坐标下应力 分量的转换公式。
反过来，取直角坐标系为新坐标系，极坐标系 旧坐标系，根据（5-2）式，用极坐标应力分量 表示直角坐标应力分量的关系为：
x xrxrr xx 2xrxr
cos2 r sin2 2sin cosr

生物医学工程：利用应变和应力原理，开发出更符合人体生理需求的医疗 器械和生物材料，提高医疗效果和人体健康水平。
新能源技术：利用应变和应力原理，优化风力发电机叶片设计，提高风能 利用率和发电效率。
机器人技术：通过研究应变和应力与机器人关节运动的关系，提高机器人 的灵活性和稳定性，拓展机器人的应用领域。
应变和应力对未来科技发展的影响
增强材料性能：通过深入研究应变和应力，可以开发出性能更强的新型材 料，为未来的科技发展提供物质基础。
智能制造：利用应变和应力的知识，可以优化制造过程中的材料性能，提 高生产效率和产品质量，推动智能制造的发展。
生物医学应用：在生物医学领域，应变和应力的研究有助于更好地理解和 控制人体生理机制，为未来的生物医学应用提供支持。
压痕法：利用压痕仪在物体表面压出一定形状的压痕，通过测量压痕的尺寸来计算应力
应变和应力的相互影响
应变和应力之间的关系：应变是应力作用下的物体形状变化，应力是抵抗变形的力。
应变和应力的测量方法：通过应变计和应力计进行测量，应变计测量物体变形，应力计测量物 体受到的力。
应变和应力的相互影响：应变和应力之间存在相互影响，例如在材料屈服点附近，应变和应力 之间会发生突变。
应力的概念
分类：正应力、剪应力、弯 曲应力等
定义：物体受到外力作用时， 内部产生的反作用力
单位：帕斯卡（Pa） 作用效果：使物体产生形变
应变和应力的关系
应变是物体形状 的改变，应力是 物体内部抵抗变
形的力
应变和应力之间 存在线性关系， 即应变正比于应
力
应变和应力之间 的关系可以用胡 克定律表示，即 应力=弹性模量
应变和应力关系
汇报人：XX
应变和应力的定义 应变和应力的测量方法 应变和应力的应用领域 应变和应力的研究进展 应变和应力的未来展望

我所认识的应力与应变机械与动力工程学院动力工程专业学号602430107013 杨栋君一点的应力与应变是材料力学与弹塑性力学两门课程中两个非常重要的基本概念，材料力学主要讨论平面应力状态以及平面应力状态下的应变分析，而弹塑性力学则研究空间应力状态与应变状态。

我最先接触应力与应变是在材料力学的绪论中，材料力学中的应力首先是由研究构件（组成机械的零件或结构物的构件统称为构件，如建筑物的梁和柱，机床的轴等）截面处某一点的强弱程度而逐渐引入的。

应力定义为“单位面积上所承受的附加内力”。

材料力学中物体因受外力作用而变形，其内部各部分之间因相对位置改变而引起的相互作用称为内力，在m 上，围绕点取微小面积，上分布截面{ EMBED Equation.KSEE3 \* MERGEFORMAT |m内力的合力为（的方向和大小与点的位置和的大小有关），平均应力，代表在范围内，单位面积上内力的平均集度。

通过引入数学的极限法，随着的逐渐缩小，当趋于零时，平均应力的大小和方向都趋向于一定极限，即，称为点的应力。

应力是一个矢量，一般既不与截面垂直，也不与截面相切。

在弹塑性力学中，针对应力首先引入了体力（作用在物体微粒体积上的力）和面力（沿着物体表面的分布力）的概念。

可变形固体在外力等因素的作用下，其内部各部分之间就要产生相互的作用，内力指物体内的一部分与其相邻的另一部分之间相互作用的力。

应力就是载荷引起的物体内单位面积上的内力，表示内力在截面上某一点的分布集度。

这点与材料力学中的应力的定义基本一致。

但弹塑性力学中更细化的从空间（取平行于坐标面的3个两两垂直的微元平面）研究一点处的应力状态，当微元面趋于零时，上面作用的应力就代表过点任何截面上的应力，由爱因斯坦的求和约定引入了应力张量。

每一行为过点的一个面上的3个应力分量，便构成应力张量。

或者（应力张量的9个分量必须满足正交坐标系中二阶张量的变换公式）。

由此可以看出应力不是一个简单的矢量，它是对某点内力的精确描述。

应力应变关系我所认识的应力应变关系一在前面两章的分别学习了关于应力与应变的学习，第三章的本构关系讲述了应力与应变的关系从而构成了弹塑性力学的本构关系。

在单向应力状态下，理想的弹塑性材料的应力应变关系及其简单满足胡克定律即,E ,,XX在三维应力状态下需要9个分量，即应力应变需要9个分量，于是可以把单向应力应变关系推广到三维应力状态，及推广到广义的胡克定律本式应该是91个应变分量单由于切应力互等定理，此时后面的三个应力与式中的切应力想等即现在剩余36个应变分量。

(1)具有一个弹性对称面的线弹性体的应力应变公式如下(2)正交各向异性弹性体的弹塑性体公式如下(3)各向同性弹性体的本构方程各向同性弹性体在弹性状态下，主应力方向与主应变方向重合容易证明。

在主应变空间里，由于应变主轴与应力主轴重合，各向同性弹性体体内任意一点的应力和应变之间满足:,,,,,，，CCCxxyz111213,,,,,，，CCCyxyz212223,,,,,，，CCCzxyz313233 (2-3),,,,,,yyxzxz对的影响与对以及对的影响是相同的，即有,CCC==,CC=CC=,y112233x12132123z;和对的影响相同，即，同理有和CC=3132等，则可统一写为:CCCa==,112233CCCCCCb=====,122113312332 (2-4)所以在主应变空间里，各向同性弹性体独立的弹性常数只有2个。

在任意的坐标系中，同样可以证明弹性体独立的弹性参数只有2个。

广义胡可定律如下式,,xy1,,,,,,,,,,，[()]xy,xxyz,2GE,,,,1,yz, ,,，[()],,,,,,,,yzyyxz2GE,,,1,zx,,,,，[()]zx,,,,,,,zzxy,2GE,,EGv泊松比剪切模量 E:弹性模量/杨氏模量 ,2(1),，,,,E虎克定律 ,G,,对于应变能函数理解有点浅在此就不多做介绍了。

2 屈服条件拉伸与压缩时的应力——应变关系曲线P,,A0,ll0,,lBC:屈服阶段,,CD:强化阶段塑性阶段,,DE:局部变形阶段,弹性变形时应力应变关系的特点1.应力与应变完全成线性关系;即应力主轴与全量应变主轴重合2.弹性变形是可逆的，与应变历史(加载过程)无关，即某瞬时的物体形状、尺寸只与该瞬时的外载有关，而与该瞬时之前各瞬间的载荷情况无关。

τ xy
右侧面
σx τ xz
x
γ xy
γ yz
γ zx
O
∠ xOy ∠ yOz
∠zox 。
z
σz
前面
2、各向同性材料的广义胡克定 、 律
(1)线应变的推导 线应变的推导 分别单独存在时, 在σx σy σz 分别单独存在时 x 方 依次为: 向的线应变 εx 依次为
x σ
z
x
x σ
εx ' =
σx
τ = Gγ
或
γ=
τ
G
τ γ γ τ
为剪切弹性模量，单位为N/m G 为剪切弹性模量，单位为N/m2.
三、复杂应力状态下应力与应变的关系 σx σy σz τ x y τ y z τ z x εx ε y ε z γ x y γ y z γ z x
1、各向同性材料的广义胡克定律 （1）符号规定 ） (a)三个正应力分量 拉应力为正 (a)三个正应力分量 三个正应力分量：拉应力为正
因此, 该圆筒变形后的厚度并无变化, 因此 该圆筒变形后的厚度并无变化 仍然为 t =10mm .
G G G
在线弹性范围内, 小变形条件下, 在线弹性范围内 小变形条件下 各向同性材料。 各向同性材料。
1 εx = σx ν (σ y +σz ) E 1 E
[
]
公式的适用范围 : 在线弹性范围内,小 在线弹性范围内 小 变形条件下, 变形条件下 各向同性材 料。
ε y = [σ y ν (σz +σx )]
ν ν ε z = (σ x + σ y ) = (τmax + τmax ) = 0 E E
同理可得,圆筒中任一点 该点到圆筒横截面中心的距离为 该点到圆筒横截面中心的距离为ρ 同理可得 圆筒中任一点 (该点到圆筒横截面中心的距离为ρ) 处 的径向应变为

我所认识的应力与应变的关系机械与动力工程学院我所认识的本构关系可以从三个不同的受力条件下进行分析，第一是在弹性变形下的应力与应变的关系，第二是在屈服条件下的应力与应变的关系，第三是在塑性条件下的应力与应变的关系，而对应力与应变的关系的研究也可以归结为对本构关系的研究。

首先，弹塑性力学分别从静力学和几何学的角度出发，导出了平衡方程的和几何方程，这些方程均与物体的材料性质（物理性质）无关，因而适用于任何连续介质。

但仅仅依靠平衡方程和几何方程来解决实际中的工程问题是不够的。

由于平衡方程仅建立了力学参数（应力分量与外力分量）之间的联系，而几何方程也仅建立了运动学参数（位移分量与应变分量）之间的关系，所以平衡方程与几何方程式两类完全相互独立的方程，他们之间还缺乏必要的联系。

对于所求解的问题来讲，因为您未知量的数目多于任何一类方程的个数，所以无法利用这两类方程求的全部未知量。

平衡方程：⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎭⎫ ⎝⎛∂∂=+∂∂+∂∂+∂∂⎪⎪⎭⎫ ⎝⎛∂∂=+∂∂+∂∂+∂∂⎪⎪⎭⎫ ⎝⎛∂∂=+∂∂+∂∂+∂∂222222000t w Z z y x t v Y z y x t u X z y x z zy zx yz y yx xz xy x ρσττρτστρττσ （1） 几何方程：⎪⎪⎪⎭⎪⎪⎪⎬⎫∂∂+∂∂=∂∂=∂∂+∂∂=∂∂=∂∂+∂∂=∂∂=x w z u z w z v y w y v y u x v x u zx z yz y xy x γεγεγε （2） 为了求解具体的力学问题，还必须引进一些关系式，这些关系式即所谓的本构关系。

本构关系反映可变形体材料的固有特此那个，故也称为物理关系，它实际上是一组联系力学参数和运动学参数的方程式，即所谓的本构方程。

本构方程实际上就是一组反映可变形体材料应力和应变之间关系的方程。

在单向应力状态下，理想弹性材料的应力和应变之间的关系极其简单。

我所认识的应力应变关系应力应变都是物体受到外界载荷产生的响应。

物体由于受到外界载荷后，在物体内部各部分之间要产生互相之间的力的作用，由于受到力的作用就会产生相应的变形；或者由于变形引起相应的力的作用。

则一定材料的物体其产生的应力和应变也必然存在一定的关系。

一 应力-应变关系影响本构关系的因素有很多，例如材料、环境、加载类型（载荷、温度）、加载速度（动载荷、静载荷）等，当然，本构关系有很多类型，包括弹性、塑性、粘弹性、粘塑性、各向同性、各向异性本构关系，那么首先来叙述一下简单情况本构关系，所谓简单情况就是六个应力分量x y xy yz zx σσστττ、、z 、、、只有一个不为零，六个应变分量x y xy yz zx εεεγγγ、、z 、、、只有一个自由变化，应力应变关系图1-1。

图1-1 应力应变关系图图中OA 为线弹性阶段，AB 为非线弹性阶段，故OB 为初始弹性阶段，C 点位初始屈服点，()s σ+为初始屈服应力，CBA 为弹性阶段卸载，这一阶段中E σε=，初始弹性阶段结束之后，应力继续增大，进入塑性阶段，CDE 为强化阶段，应变强化硬化，EF 为颈缩阶段，应变弱化软化。

如果在进入塑性阶段卸载后再加载，例如在D 点卸载至零，应力应变关系自D 点沿'DO 到达'O 点，且'DO ∥OA ，其中'O O 为塑性应变p ε，DG 为弹性应变e ε，总应变为它们之和。

此后再继续加载，应力应变关系沿ODEF 变化，D 点为后继屈服点，OD 为后继弹性阶段，()'s σ+为后继屈服应力，值得一提的是初始屈服点只有一个，而后继屈服点有无数个（由加载历史决定）。

若在卸除全部载荷后反向加载，弹性阶段'COC ，()()s s σσ+-=，而在强化阶段'DOD ，()()s s σσ+->，称为Bauschinger 效应。

从上述分析得出材料弹塑性行为有一定的特殊性，主要表现在：弹性应力应变关系是线性，且是单值对应关系，而塑性应力应变关系是非线性的非单值对应。

理论上参数1强度来源强度来源应力应力应变关系应变关系变形特性变形特性泊松比泊松比强度特征强度特征疲劳特征疲劳特征常用的沥青混合料类型沥青混凝土ac抗滑磨耗层aksmaogfc抗滑磨耗层多孔沥青路面pac?沥青混合料是一种粘弹塑性材料其应力应变关系受温度时间等外界因素和沥青含量沥青性质集料级配和集料性质等自身因素的影响所以与一般材料不同对沥青混合料的应力应变关系讨论其蠕变特性?典型蠕变关系曲线见图
动态模量 动态模量的试验过程与上图中的（b）类似。
t 0 sint t 0 sint
动态模量： E * 0 0
注意：1、试验时间不可太长，否则不是常数， 而是时间的函数。 2、 (t)反映了材料的流变特性，对弹 性体，相位差为“0”
级配要求
应满足一定的级配要求，可参见有关手册或规范
测试与计算 测试采用三轴试验
计算： tg
2、应力-应变关系
测定方法
三轴试验
应力-应变关系

ε
注意：该曲线与土的应力-应变曲线的区别
粒料的模量与 受力状态有关
Er k1 k2
θ为主应力之和
1 2 3 1 2 2 3 3
低应力为零：常用方式，沥青路面方式 低应力>零：水泥路面方式 低应力<零：双向加载方式，不常用
• 随着荷载作用次数的增加，材料的抗力（强度、 模量）在不断降低。
• 疲劳寿命与加荷方式、波形、频率等因素有关。 荷载级位越大，疲劳寿命越短；荷载级位越小， 疲劳寿命越长。当然还与材料自身的特性有关， 与黏结料的性质有关，与集料的性质也有关。 一般而言，影响弯拉强度的因素都将影响疲劳 特性。
• 疲劳特性一般用应力或应变与疲劳寿命之间的 关系来表示，两者之间在半对数或双对数坐标 上一般呈线性关系。见图。

应力应变关系矩阵现代工程学中，应力应变关系矩阵是一个非常重要的概念。

它是描述材料在受力情况下的应变与应力之间的关系的工具。

通过对应力应变关系矩阵的研究，我们可以更好地理解材料的力学性能，为工程设计提供科学依据。

应力应变关系矩阵是指材料在受力作用下所表现出的应变与应力之间的关系。

在材料受力的过程中，会产生内部的应力场，导致材料发生相应的变形，这种变形就是应变。

而应力则是描述单位面积上的力的大小，是导致材料发生变形的根本原因。

应力应变关系矩阵可以用数学形式表示，通过矩阵的运算可以推导出材料的应变与应力之间的关系。

在工程实践中，应力应变关系矩阵起着至关重要的作用。

通过对材料的应力应变关系进行研究，我们可以预测材料在受力情况下的力学性能，比如弹性模量、屈服强度、断裂强度等。

这些参数对工程设计和材料选择都具有重要意义。

只有深入了解材料的力学性能，才能确保工程设计的可靠性和安全性。

除了在工程设计中的应用，应力应变关系矩阵也被广泛应用于材料科学和力学研究领域。

通过对不同材料的应力应变关系进行研究，科学家们可以揭示材料的力学性质和变形规律，为新材料的设计和合成提供理论依据。

同时，应力应变关系矩阵还可以帮助我们理解材料在不同载荷下的变形行为，为材料力学的研究提供新思路和方法。

在实际工程中，对应力应变关系矩阵的认识也是至关重要的。

工程师们需要根据材料的应力应变特性来选择合适的材料和设计结构，以确保工程项目的安全性和可靠性。

只有深入了解材料的应力应变关系，才能准确预测材料在受力情况下的行为，为工程设计提供科学依据。

让我们总结一下本文的重点，我们可以发现，应力应变关系矩阵在材料科学和工程领域具有重要意义。

通过对这一概念的研究，我们可以更好地理解材料的力学性能，为工程设计和材料选择提供科学依据。

希望未来能够有更多的科研人员投入到这一领域的研究中，为材料科学和工程技术的发展做出贡献。

广义虎克定律--应力应变曲线 其中E是与材料有关的弹性常数，通常称为弹性 模量，E的量纲与 相同，一般用GN/m2。 A 则称为 比例极限，上式即为虎克定律的数学表达式。 A点与B点非常接近，工程上弹性极限 B 和比例极限 A并不严格区分。这种情况下，横向应变 ' 与轴向 应变 绝对值之比一般是常数，即
过了屈服阶段以后，材料又恢复了抵抗变形的能力 ，要使它增加变形必须增加拉力，这种现象称为材料的 强化，强化阶段中的最高点D所对应的 D 称为强度极 限。
广义虎克定律--应力应变曲线 (四)局部变形阶段——DG段
过了D点以后，在局部范围内，横截面急剧缩小，
继续伸长需要拉力相应减小，到G点处，试件被拉断。
地球物理场论 I
海洋地球科学学院 地球探测信息与技术系
宋 鹏
第四章 应力与应变关系
4.1 广义虎克定律 4.2 工程弹性常数及相互间关系式 4.3 简单和复杂应力状态下弹性应变能和应变能密度 4.4 能量密度与能通量密度
应力与应变关系
在前几章中，从静力学、动力学和几何学的观点 分别研究了应力和应变。前面知道联结应力分量(6个)
l1 n3 cos180 1 m2 cos 0 1 l2 l3 m1 m3 n1 n2 cos 90 0
各向同性体的广义虎克定律 因此新坐标轴也指向应变主轴方向，剪应变也应该 等于零，且因各向同性时，弹性系数C41，C42和C43应 该不随方向面改变，故取 x, y, z 分别为1′，2′和3′ 轴，同样由式（4-3）第4式得：
2 t 2 2 3 t 2 3
(j)
常数 和 称为拉梅(Lame)弹性常数，简称拉梅 常数。

应力和应变的关系曲线
描述
应力和应变的关系曲线是描述应力与应变之间关系的图形表示。
形状
在弹性范围内，曲线呈直线上升；超过弹性极限后，曲线出现弯曲。
应用
通过应力和应变的关系曲线，可以确定材料的弹性模量、屈服点和 极限强度等机械性能参数。
04
应力和应变的应用
弹性力学
弹性力学是研究弹性物体在外力作用下 变形和内力的规律的科学。在弹性力学 中，应力和应变是描述物体变形和受力 状态的基本物理量。
公式
σ=Eεsigma = E varepsilonσ=Eε
解释
σ为应力，E为弹性模量，ε为应变。 当应力增加时，应变也相应增加， 且两者成正比关系。
非线性关系
描述
当材料受到超过其弹性极限的应力时 ，应力与应变之间的关系不再是线性 的，而是呈现非线性关系。
特征
在非线性阶段，应变随应力的增加而 急剧增加，可能导致材料发生屈服或 断裂。
设计优化
优化结构设计
通过对应力和应变的分析，优化结构设计，提高结构的承载能力 和稳定性。
考虑材料特性
在设计过程中，充分考虑材料的力学特性和性能，合理选择和使 用材料，以降低应力和应变对结构的影响。
引入减震和隔震措施
通过引入减震和隔震措施，降低地震等外部载荷对结构产生的应 力和应变，提高结构的抗震性能。
时间
蠕变
在长期恒定应力作用下，材料会发生 缓慢的塑性变形，即蠕变。蠕变会影 响材料的应力和应变关系，特别是在 高温和长期载荷作用下。
时间依赖性
某些材料的力学性能会随时间发生变 化，对应力和应变的关系产生影响。 例如，疲劳和时效等现象会导致材料 性能随时间发生变化。
07
应力和应变在工程实践中的 注意事项

§7-7 应力与应变间旳关系
一、单向应力状态下应力与应变旳关系
1
1
E
σ1
σ1
E 为材料旳弹性模量，单位为N/m2.
横向线应变2,3与纵向线应变 1 成
正比，比值为泊松比γ，而符号相反。
2
3
1
二、纯剪切应力状态下应力与应变旳关系
G 或
G
τ γ γτ
G 为剪切弹性模量，单位为N/m2.
三、复杂应力状态下应力与应变旳关系
x y z x y y z z x
y
σy
上面
x y z x y y z z x
1、各向同性材料旳广义胡克定律 （1）符号要求
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量：拉应力为正
σz
x
o
压应力为负。 z
前面
(b)三个剪应力分量: 若正面(外法线与坐标轴
P a
y
z
x
y 解：铜块上截面上旳压应力为
y
P A
300 103 0.12
y x
30MPa
x
(b) Z z
1 [ ( )] 0
xE x
y
z
由
1 [ ( )] 0
zE z
x
y
解得
x
z
(1 1 2
)
y
0.34(1 0.34) 1- 0.342
(30)
-15.5MPa
特例
在平面纯剪切应力状态下：σ 1 σ 3 τ xy
代入得
1 2
E
(1
2
3)
1 2

我所认识的应力应变关系应力应变都是物体受到外界载荷产生的响应。

物体由于受到外界载荷后，在物体内部各部分之间要产生互相之间的力的作用，由于受到力的作用就会产生相应的变形；或者由于变形引起相应的力的作用。

则一定材料的物体其产生的应力和应变也必然存在一定的关系。

一 应力-应变关系影响本构关系的因素有很多，例如材料、环境、加载类型（载荷、温度）、加载速度（动载荷、静载荷）等，当然，本构关系有很多类型，包括弹性、塑性、粘弹性、粘塑性、各向同性、各向异性本构关系，那么首先来叙述一下简单情况本构关系，所谓简单情况就是六个应力分量x y xy yz zx σσστττ、、z 、、、只有一个不为零，六个应变分量x y xy yz zx εεεγγγ、、z 、、、只有一个自由变化，应力应变关系图1-1。

图1-1 应力应变关系图图中OA 为线弹性阶段，AB 为非线弹性阶段，故OB 为初始弹性阶段，C 点位初始屈服点，()s σ+为初始屈服应力，CBA 为弹性阶段卸载，这一阶段中E σε=，初始弹性阶段结束之后，应力继续增大，进入塑性阶段，CDE 为强化阶段，应变强化硬化，EF 为颈缩阶段，应变弱化软化。

如果在进入塑性阶段卸载后再加载，例如在D 点卸载至零，应力应变关系自D 点沿'DO 到达'O 点，且'DO ∥OA ，其中'O O 为塑性应变p ε，DG 为弹性应变e ε，总应变为它们之和。

此后再继续加载，应力应变关系沿ODEF 变化，D 点为后继屈服点，OD 为后继弹性阶段，()'s σ+为后继屈服应力，值得一提的是初始屈服点只有一个，而后继屈服点有无数个（由加载历史决定）。

若在卸除全部载荷后反向加载，弹性阶段'COC ，()()s s σσ+-=，而在强化阶段'DOD ，()()s s σσ+->，称为Bauschinger 效应。

从上述分析得出材料弹塑性行为有一定的特殊性，主要表现在：弹性应力应变关系是线性，且是单值对应关系，而塑性应力应变关系是非线性的非单值对应。

我所认识的应力和应变关系在这之前我认识了应力和应变的概念、性质以及从静力学和几何学的角度出发所得到的平衡方程和几何方程。

但是平衡方程仅反映了应力分量和外力分量的关系；几何方程仅建立了位移分量和应变分量的关系。

而谈到应力与应变的关系，对于可变形固体，在弹塑性力学中，在外力的作用下，其将发生变形。

变形分为两个阶段，弹性阶段和塑性阶段。

在弹性阶段，发生的弹性变形可以完全恢复，它是一个可逆过程。

此时，应力与应变的关系是一一对应的，是单值函数关系。

而在塑性阶段，所发生的塑性变形是不可以恢复的，是不可逆过程。

相对应的，塑性阶段的应力应变的关系是非线性关系，不存在一一对应的关系。

我所认识的应力和应变的关系就是本构关系。

本构关系也称为物理关系，它反应的是可变形材料的固有属性，实质上是一组联系力学参数和运动参数的方程式，也就是我们所说的本构方程。

在说应力与应变的关系之前，先说一下本构关系的相关影响因素，包括材料、环境、加载类型、以及加载速度。

即，),,(T t f εσ=。

另外，有各种各样的本构系，比如：弹性本构关系、塑性本构关系、粘弹性本构关系、粘塑性本构关系、各向同性本构关系、各向同性本构关系等等。

简单情况的本构关系：应力和应变的关系包括弹性和塑性的应力应变关系。

我们所说的是线性弹性体的应力应变关系，又分为简单应力状态和复杂应力状态。

在简单拉伸情况下，理想弹性材料的应力和应变的关系很简单，就是材料力学中的胡克定律： 。

而在塑性阶段，应力应变之间不再是简单的胡克定律，而是 。

另外，简单拉伸情况下的卸载定律是 。

在后继弹性阶段，也就是卸载后重新加载的材料会继续发生新的塑性变形，在此时的屈服称为后继屈服，相应的屈服点称为后继屈服点。

初始屈服和后继屈服的不同是：第一，应力的数值不一样，后继屈服的应力值更大；第二，屈服点的个数不一样。

初始屈服点只有一个，而后继屈服点会有好多个，则其对应的应力值也会有很多个。

最后，在卸载全部载荷后进行反向加载比如说把拉伸改成压缩，此时会产生Bauschinger 效应。

我所认识的应力和应变之间的关系在单向应力状态下，理想弹性材料的应力和应变之间的关系是满足胡克定律的一一对应的关系。

在三维应力状态下描述一点处的应力状态需要9个分量，相应的应变状态也要用9个应变分量来表示。

对于一个具体的理想弹性体来讲，如果在三维应力状态下，应力与应变之间仍然有线性一一对应关系存在，则称这类弹性体为线性弹性体。

所谓各向弹性体，从力学意义上讲，就是弹性体内的每一点沿各个方向的力学性质都完全相同的。

这类线性弹性体独立的唐兴常数只有两个。

各向同性体本构关系特点：1.主应力与主应变方向重合。

2.体积应力与体积应变成比例。

3.应力强度与应变强度成比例。

4.应力偏量与应变偏量成比例。

工程应用中，常把各向同性弹性体的本构方程写下成11()11()11()x y z xy xy y x z yz yz z y x xz xz E G E G E G εσμσσγτεσμσσγτεσμσσγτ⎧⎡⎤=-+=⎣⎦⎪⎪⎪⎡⎤=-+=⎨⎣⎦⎪⎪⎡⎤=-+=⎪⎣⎦⎩，式中分别为弹性模量、泊松比和剪切模量。

在E G μ、、这三个参数之间，实际上独立的常量只有两个，它们之间存在关系为()21E G μ=+。

屈服条件:弹性和塑性的最主要区别在于变形是可以恢复。

习惯上，根据破坏时变形的大小把工程材料分为脆性材料和塑性材料两类。

对于加载过程如图1OA: 比例阶段；线性弹性阶段AB: 非弹性变形阶段 BC ： 初始屈服阶段 s σσ≤ CDE ：强化阶段；应变强化硬化阶段EF ： 颈缩阶段；应变弱化，软化阶段s σσ≥ C 点为初始屈服点具有唯一性。

在应力超过屈服应力后，如果在曲线上任意一点D 处卸载，应力和应变之间将不再遵循原有的加载曲线规律，而是沿一条接近平行于OA 的直线DO ’变化，直到应力下降为零，这时应变并不为零，即有塑性应变产生。

如果用OD ’表示总应变ε，O ’D ’表示可以恢复的弹性应变eε，OO ’表示不能恢复的塑性应变p ε，则有e p εεε=+，即总应变等于弹性应变加上塑性应变。

1． 画出应力正方形，注出 x 和 y 面上的应力值，图 5(a)以一个假想的情况为例。下列
方向的规定仅适用于画莫尔圆时：若切应力对正方形内任意点的矩为顺时针转向，
则规定为正；而逆时针方向时规定为负。所以作用在 x 和 y 面上的切应力必定符号
相反。正应力则按常规，即拉伸时为正、压缩时为负。
图 5 当σ x = +5 ，σ y = −3 ，τ xy = +4 时画出的应力正方形
情况（平面应力状态），而且是在直角坐标系内，但式（5）对二维和三维应力状态都适用。
用数学或几何方法（见习题 3 和 4）可证明，无限小应变分量可按几乎同样的关系式进
行变换：
3
⎧ ⎪ ⎨
ε x′ ε y′
⎫ ⎪ ⎬
=
⎧ A ⎪⎨
εx εy
⎫ ⎪ ⎬
(6)
⎪ ⎩
1 2
γ
x′y′
⎪ ⎭
⎪ ⎩
1 2
γ
xy
殊性。在直径线段水平时，正应力取最大值而切应力为零。这些正应力称为主应力，记作σ p1 和σ p2 ，主应力作用的平面称为主平面。如果材料易于因拉伸断裂而失效，则当σ p1 的值超
过拉伸强度极限时,将沿主平面断裂而失效。 例 3 先用莫尔圆图解法预测粉笔在扭转时将如何断裂，再用实践来检验，这将使我们
（图（a））、莫尔圆（图（b））和斜截面上的应力状态（图（c））
2． 在以σ 为横坐标（ x 轴）、τ 为纵坐标（ y 轴）的坐标系内作图，画出与应力正方 形 x 、 y 面上的应力相对应的点作为应力圆上的两个点。由于这两个面上的切应力 的符号彼此相反，其中一个点必在σ 轴上方、而另一点在σ 轴下方。此两点到σ 轴 的距离完全相等。为便于说明，把这两点分别标为 x 和 y 。