超静定结构(精)
- 格式:doc
- 大小:886.00 KB
- 文档页数:20




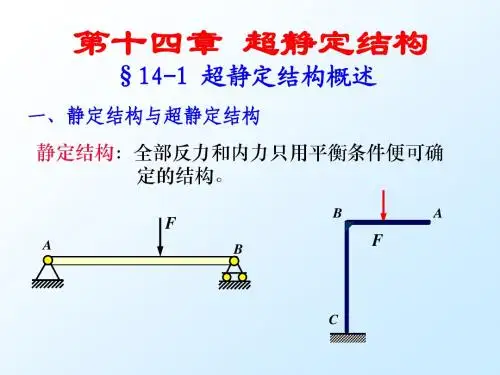
超静定结构及力学原理和方程重难点分析一、超静定结构的概念:超静定结构:从几何组成分析来说具有几何不变性而又有多余约束的结构。
超静定结构与静定结构相比较,主要有三个方面的优点:1从几何组成看,超静定结构未没有联系的几何不变体系,而超静定结构是具有多余联系的几何不变体系;2从静力特征看,静定结构仅凭静力平衡条件便可以完全确定它的反力和内力,而超静定结构仅凭静力平衡条件还不能确定全部反力和内力,必须建立附加方程式才能求解;3 当无外荷载作用时,超静定结构有产生内力的可能性超静定杆件结构的分类:超静定梁、刚架、桁架、拱以及组合结构。
二、超静定次数的确定1、超静定次数的概念超静定次数:结构中多余约束的数目2、方法去掉多余联系的常用方法如下:(1)去掉一根支杆或切断一根链杆,相当于去掉一个联系; (2)去掉一个单铰,相当于去掉二个约束;(3)切断一根弯杆或去掉一个固定支座,相当于去掉三个联系(4)将固定支座改成不动铰支座或将受弯杆切断改铰结,各相当去掉一个联系 3、举例例如图1所示的单跨静定梁,若去掉B 支座的支杆,代以多未知力B X ,则原梁变为静定的简支梁(即为基本结构),如图1(b )所示;若将固定端A 支座加一个单铰,代以多余未知力A X ,则原梁变为静定的简支梁(即为基本结构),如图1(c )所示,所有原结构一次超静定结构.同理,如图2所示的刚架,可将A 、B 两固定改成铰支座,代以多余力A X 、B X ,则得如图2(b )所示的静定三铰刚架;或者去掉铰C ,代以多余力1X 、2X ,则得如图2(c )所示的两各静定悬臂刚架;或者去掉铰C ,故原结构为二次超静定结构。
三、力法原理和力法方程1.力法的基本原理:将超静定结构转化为含多余力的静定结构 (一)一次超静定结构 (1)确定超静定次数:n=1次 (2)选基本结构⎩⎨⎧)几何不变体系(静定结构b a )((3)位移条件: 01=∆ (a) 根据叠加原理 :p1111∆+∆=∆ (b )11111x δ=∆ (c)(4)力法方程(一次):将(c )代入(b )式得:01111=∆+px δ…………(6-1)式中:--11δ系数(单位多余力1=X 作用时,B 点沿1x 方向的位移)--∆p1自由项(荷载单独作用时B 点沿1x 方向的位移)1x --基本未知量(多余未知力或多余力)系数(11δ) 和自由项(p1∆)都是基本结构(静定结构)在已知外力作用下的位移,可用上一章讲的单位荷载法或图乘法求得,代入(6-1)式后可求出多余未知力1x ,求得1x 之后其余的计算(支座反力和内力)同静定结构。



第四节超静定结构的受力分析及特性一、超静定结构的特征及超静定次数超静定结构的几何特征是除了保证结构的几何不变性所必须的约束外,还存在多余约束。
超静定结构的静力特征是仅由静力平衡条件不能唯一地确定全部未知反力和内力。
结构的多余约束数或用静力平衡条件计算全部未知反力和内力时所缺少的方程数称为结构的超静定次数。
通常采用去除多余约束的方法来确定结构的超静定次数。
即去除结构的全部多余约束,使之成为无多余约束的几何不变体系,这时所去除的约束数就是结构的超静定次数。
去除约束的方法有以下几种:(一)切断一根两端铰接的直杆(或支座链杆),相当于去除一个约束。
(二)切断一根两端刚接的杆件,相当于去除三个约束。
(三)切断——个单铰(或支座固定铰),相当于去除二个约束;切断一个复铰(连接n根杆件的铰),相当于去除2(n—1)个约束。
(四)将单刚结点改为单铰节点,相当于去除一个约束;将连接n个杆件的复刚节点改为复铰节点,相当于去除n—1个约束。
去除一个超静定结构多余约束的方法可能有几种,但不管采用哪种方法,所得超静定次数一定相同。
去除图4—1a所示超静定结构的多余约束的方法之一如图4—1b所示,去除六个多余约束后,就成为静定结构,故为超静定六次。
再用其他去除多余约束的方案确定其超静定次数,结果是相同的。
(a)(b)图4-1二、力法的基本原理(一)力法基本结构和基本体系去除超静定结构的多余约束,代以相应的未知力X i (i=1、2、…、n),X i 称为多余未知力或基本未知力,其方向可以任意假定。
去除多余约束后的结构称为力法基本结构。
力法基本结构在各多余未知力、外荷载(有时还有温度变化、支座位移等)共同作用下的体系称为力法基本体系,它是用力法计算超静定结构的基础。
选取力法基本结构应注意下面两点:1.基本结构一般为静定结构,即无多余约束的几何不变体系。
有时当简单超静定结构的解为已知时,也可以将它作为复杂超静定结构的基本结构,以简化计算。


1超静定结构的解法超静定结构是指结构的支座反力数目多于静力平衡方程的数目,即结构的自由度多余零,不能通过直接求解静力平衡方程得到结构的内力、位移等参数。
因此,需要使用超静定结构的解法来求解结构的响应。
超静定结构的解法主要有两种:力法和位移法。
在这里,我将分别介绍这两种方法的基本原理。
1.力法力法是指通过引入虚功原理,利用未知内力的线性平衡方程组与已知荷载、位移或位移力系数之间的关系,构建方程并求解未知内力的方法。
使用力法解决超静定结构的基本步骤如下:(1)确定支座反力。
根据结构的约束条件,计算支座反力数目;(2)选择剪力或弯矩作为未知内力。
在超静定结构中,选择剪力或弯矩作为未知内力比较常见;(3)建立线性平衡方程组。
将剪力或弯矩作为未知量,根据结构的几何条件和约束条件,建立线性平衡方程组;(4)引入荷载、位移或位移力系数。
根据结构的受力情况,将已知荷载、位移或位移力系数引入线性平衡方程组;(5)求解未知内力。
通过求解线性平衡方程组,得到未知内力。
2.位移法位移法是指通过引入位移的概念,利用位移与剪力/弯矩之间的关系,将超静定结构的内力求解问题转化为线性代数方程组的求解问题。
使用位移法解决超静定结构的基本步骤如下:(1)确定支座反力。
根据结构的约束条件,计算支座反力数目;(2)选择支座位移为未知量。
在超静定结构中,支座位移比较容易确定;(3)建立位移-力关系方程。
根据结构的几何条件和材料性质,建立位移-力关系方程,将剪力或弯矩表示为位移的函数;(4)引入荷载或位移。
根据结构的受力条件,将已知荷载或位移引入位移-力关系方程;(5)求解未知位移。
通过求解位移-力关系方程,得到未知位移;(6)求解未知内力。
将未知位移代入位移-力关系方程,求解出未知内力。
需要注意的是,在力法和位移法中,由于超静定结构的自由度数目大于零,未知内力或未知位移存在无穷多个解。
因此,需要加入合理的边界条件,如位移边界条件、力边界条件等,来确定唯一的解。
超静定结构的特征:
超静定结构的特征主要包括以下几点:
1.具有多余约束:超静定结构相对于静定结构,具有多余的约束,这些多余约束不是维持体系几何
不变所必需的。
2.具有几何不变性:超静定结构在去掉多余约束后,仍然是一个几何不变体系,即受到外力作用时,
其整体和局部的形状和大小都不会发生变化。
3.受力状态复杂:超静定结构的支座反力和截面内力不能完全由静力平衡条件唯一确定,因此其受
力状态相对较为复杂。
4.结构形式多样:超静定结构的样式非常多样,包括连续梁、刚架、拱、薄壳等,这些结构都可以
通过添加多余约束来转化为超静定结构。
5.稳定性好:由于超静定结构的内力分布比较均匀,因此其稳定性较好,在受到外力作用时不易发
生失稳现象。
6.调整能力强:超静定结构的内力可以通过改变多余约束的约束力进行调节,因此其调整能力较强。
常见的超静定结构形式
1. 平衡树:平衡树是一种特殊的二叉查找树,它在每个节点左右子树的高度最多相差一,也就是说每个节点的子树中叶子节点分布平衡,它可以在O(logN)时间内完成插入,删除,查找操作。
2. AVL树:AVL树也是一种特殊的二叉查找树,它具有以下特性:1)每个节点的左右子树的高度最多相差1;2)每个节点的左右子树的高度最多相差1;3)它可以在O(logN)时间内完成插入,删除,查找操作。
3. 红黑树:红黑树也是一种特殊的二叉查找树,它具有以下特性:1)每个节点的左右子树的高度相等;2)每个节点的子节点不允许相互交叉;3)它可以在
O(logN)时间内完成插入,删除,查找操作。
4. 哈夫曼树:哈夫曼树是一种最优查找树,它的每个节点的权重符合最优性原理。
哈夫曼树的最坏情况的查找时间复杂度是O(logN)。
;。
第4章超静定结构§4.1 超静定结构特性●由于多余约束的存在产生的影响1. 内力状态单由平衡条件不能惟一确定,必须同时考虑变形条件。
2. 具有较强的防护能力,抵抗突然破坏。
3. 内力分布范围广,分布较静定结构均匀,内力峰值也小。
4. 结构刚度和稳定性都有所提高。
●各杆刚度改变对内力的影响1. 荷载作用下内力分布与各杆刚度比值有关,与其绝对值无关。
2. 计算内力时,允许采用相对刚度。
3. 设计结构断面时,需要经过一个试算过程。
4. 可通过改变杆件刚度达到调整内力状态目的。
●温度和沉陷等变形因素的影响1. 在超静定结构中,支座移动、温度改变、材料收缩、制造误差等因素都可以引起内力,即在无荷载下产生自内力。
2. 由上述因素引起的自内力,一般与各杆刚度的绝对值成正比。
不应盲目增大结构截面尺寸,以期提高结构抵抗能力。
3. 预应力结构是主动利用自内力调节超静定结构内力的典型范例。
§4.2 力法原理●计算超静定结构的最基本方法超静定结构是具有多余联系(约束)的静定结构,其反力和内力(归根结底是内力)不能或不能全部根据静力平衡条件确定。
力法计算超静定结构的过程一般是在去掉多余联系的静定基本结构上进行,并选取多余力(也称赘余力)为基本未知量(其个数等于原结构的超静定次数)。
根据基本体系应与原结构变形相同的位移条件建立方程,求解多余力后,原结构就转化为在荷载和多余力共同作用下的静定基本结构的计算问题。
这里,基本体系起了从超静定到静定、从静定再到超静定的过渡作用,即把未知的超静定问题转换成已知的静定问题来解决。
●基本结构的选择(解题技巧)1. 通常选取静定结构;也可根据需要采用比原结构超静定次数低的、内力已知的超静定结构;甚至可取几何可变(但能维持平衡)的特殊基本结构。
2. 根据结构特点灵活选取,使力法方程中尽可能多的副系数δij = 0。
3. 应选易于绘制弯矩图或使弯矩图限于局部、并且便于图乘计算的基本结构。
4. 对称取基本结构;或利用对称性取半结构;或求弹性中心;以减少未知力数目,并使力法方程解耦。
●力法典型方程典型方程可写成矩阵形式:δX+ Δ = C (4.2.1) 式中,δ为柔度系数矩阵(对称方阵);X为多余未知力列阵;Δ为自由项列阵(外因作用下的广义位移列阵);C为原结构多余联系处的已知位移(不一定为零)列阵。
●力法的解题步骤1. 确定基本未知量,合理选取基本结构。
2. 根据多余联系处的位移(变形)协调条件,建立力法方程。
3. 计算力法方程中的柔度系数和自由项。
绘制基本结构的i M 图、M P 图(或写出弯矩方程),并图乘(或积分)。
其它外因下的自由项由位移公式求得。
对于桁架结构,只考虑相应的轴力图。
对于超静定拱,求方程系数、自由项时图乘法不再适用,位移系数计算时往往要考虑轴力或曲率的影响。
4. 解力法方程(线性代数方程组),求出多余未知力。
5. 绘制超静定结构的内力图。
对于受弯结构,一般先绘M 图,再按M 、Q 、N 的顺序依次作图。
可利用已有的i M 图、P M 图,根据叠加公式∑+=P i i M X M M 绘制;也可将已求的多余力和荷载加在基本结构上,按静定结构方法计算绘制最后内力图。
桁架结构按叠加公式∑+=P i iN X NN 标注轴力图。
6. 内力计算校核(包括平衡条件校核和变形条件校核)。
例1 图4.2.1a 所示连续梁为28a 号工字钢,I=7114cm 4,E=210 GPa ,l =10 m ,P=50 kN 。
若欲使梁内最大正、负弯矩的绝对值相等,问应将中间支座升高或降低多少?解:选取如图4.2.1b 所示基本体系,依题意有2/4/M Pl M -=,得6/Pl M =,作M 图(图4.2.1c )。
求中间支座B 处位移,取如图4.2.1d 所示的基本结构,作1M 图。
图乘得)(0232.0)10711410210144/(10501444421362128633↓=⨯⨯⨯⨯⨯==⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯⨯⨯-=∆-m EIPl l l Pl l Pl l EI By●形),在反对称荷载作用下只产生反对称分布的内力(变形)。
利用对称性可选取半结构计算,根据内力和变形特点,在对称轴处加上相应的支座约束,可求得原结构的解,并减少计算量。
对称结构受任意荷载作用时,也可将荷载分解成对称和反对称两组,分别利用对称性计算后,叠加所得结果即可得到原问题的解答。
例2 计算图4.2.2a 所示刚架,绘出弯矩图,并求出C 点的竖向位移。
E=常数。
解:该结构内部12次超静定(数框格),而且对称,支座本不对称,但结构外部静定,易求得支座反力H A =0。
因此,对称结构在对称力作用下(对称轴为CD 线,图4.2.2b ),取半结构计算(图4.2.2c )。
与原结构相比,A 点可以上下位移,但C 点约束,其相对位移是一致的。
若将A 处的4P 力分组为作用在A 和A ’点的对称与反对称力,对称时仅AA ’杆受轴向压力2P,反对称时再取半结构计算(图 4.2.2d )。
同样处理,还可以再取半结构(图4.2.2e )。
此时,原结构的1/8结构已降为一次超静定,选基本体系(图4.2.2f ),作1M 图和P M 图(图4.2.2g 、h ),图乘得422124722232222131311Paa a Pa EI a a a a a a a EI P -=⨯⨯⨯-=∆=⨯⨯+⨯⨯⨯⨯=δ 则 P aPa X P767244331111=⨯=∆-=δ由部分M 图按对称或反对称情况复制成原结构M 图(图4.2.2b )。
求原结构C 点竖直向下位移,就是求C 点相对于A 点的竖直向下位移,或者说是A 点相对于C 点的竖直向上位移。
因此既可以在原结构的C 点处,也可以在原结构的某一基本结构(图4.2.2f )的A 点上加单位力作M 图(图4.2.2i )与相应的部分M 图(图4.2.2j )图● 只要已知超静定结构的内力分布,即可从任一基本体系出发,按该静定结构受多种外因作用求位移的方法,求得超静定结构在某外因下的位移。
因此,基本体系的选取直接关系到求位移的计算量。
以图乘法求位移为例,选取一个便于计算的基本结构,作虚弯矩图(即M 图);将原超静定结构的最后M 图作为基本结构求位移的实际“荷载弯矩图”;M 与M 图乘得超静定结构位移,但该位移仅在原结构受荷载外因作用时才是正确的。
因为在温度变化和支座移动等外因作用时,超静定结构位移既要考虑内力(弯矩)产生的位移,也要考虑静定基本结构因温度变化和支座移动等产生的位移。
因此,超静定平面结构位移计算的一般公式为:c R ds hMt ds N t GA Qds Q k EA Nds N EI Mds M ∑∑⎰∑⎰∑⎰∑⎰∑⎰-∆++++=∆αα (4.2.2) 式中,M 、N 、Q 为超静定结构在各种外因作用下的实际内力;M 、N 、Q 为基本结构在单位力作用下的虚内力;R 为基本结构在单位力作用下的虚反力;c 为支座的实际位移。
§4.3 位移法与渐近法● 基本未知量与基本体系1. 位移法的基本未知量为结构结点处独立的角位移和线位移,与超静定次数无关,因此位移法也可解静定结构。
杆件自由端和滑动支承端的线位移及铰结端的角位移不作为基本未知量;组合结点(半铰)处的角位移应视为基本未知量;刚性梁结点处转角视为已知位移。
待求结构中若有静定部分,其内力可用平衡方程直接获得,其位移不作为基本未知量考虑;但弹性支座处位移要作为基本未知量。
为了减少基本未知量,受弯杆件一般不考虑轴向变形。
2. 在原结构刚结点上附加刚臂,在独立线位移方向上附加链杆,将结构离散成具有已知形常数和载常数的单根固端杆件处理,从而形成更高次超静定的位移法基本体系,附加约束数同基本未知量数。
要恢复原结构,附加约束上的总反力应等于零,据此建立位移法典型方程,求出结点位移(称典型方程法或基本结构法)。
● 转角位移方程用位移法计算超静定刚架时,每根杆件均可看作是单根超静定梁,因此需要计算这种梁在杆端A 、B 发生的转角φA 、φB 和侧移ΔAB (两端在垂直于杆轴方向上的相对线位移)以及在荷载等外因作用下的杆端弯矩和剪力(载常数)。
所谓转角位移方程就是求杆端弯矩的一般计算公式,由力法导出等截面杆转角位移方程中的形常数(由位移引起的杆端内力)和载常数。
结构较简单时,可逐杆写出转角位移方程,以结点或结构部分为对象,建立与各结点独立位移相应的广义力平衡条件,得到位移法方程,解决位移计算(称平衡方程法)。
● 位移法典型方程1. 一般形式:∑=+0iP jijR Zr ( i =1,2,…,n ; j =1,2,…k. ) (4.3.1)式中,n 为附加约束数,k 为基本未知量数,r ij 为反力系数(刚度系数),R iP 为自由项。
2. 矩阵形式: K Δ + R = 0 (4.3.2) 式中,K 为结构刚度矩阵(对称矩阵),Δ为未知位移列阵,R 为广义荷载反力列阵。
位移法方程实际上是每个刚结点处与转角相应的力矩平衡方程和与独立结点线位移相应的截面平衡方程(力的投影方程),平衡方程的个数与基本未知量的个数彼此相等,可解出全部基本未知量。
● 位移法的解题步骤1. 确定基本未知量,附加约束形成基本结构。
2. 利用基本体系建立位移法典型方程。
3. 由基本结构的i M 图、M P 图求系数和自由项。
4. 解位移法方程,求结点位移 Z i .5. 按 ∑+=P iiM ZM M 叠加得最后弯矩图。
6. 用平衡条件校核内力图。
例3 用位移法计算如图4.3.1a 所示刚架,绘制弯矩图。
E=常数。
解:取基本体系如图4.3.1b 。
设E 结点转角为Z 1,DF 杆水平位移为Z 2,作1M 图、2M 图、M P 图(图4.3.1c 、d 、e )。
计算系数和自由项: l i r r i i i i r /6,16466211211-===++=ql R R lil i l i l i r P P 83,0,18123321222222-===++=代入位移法方程,得⎪⎪⎭⎪⎪⎬⎫=-+-=-083186********ql li Z l i Z l iiZ 解得 iql Z iql Z 42,1122221==由 P M Z M Z M M ++=2211 ,作M 图(图4.3.1f)。
● 位移法的解题技巧1. 利用结构对称性,取半结构计算。
2. 与力法结合,简化计算(联合法与混合法)。
例4 试举例说明联合法与混合法的应用。
解:⑴联合法应用 分析如图4.3.2a 所示一般荷载作用下的对称刚架。
不论用力法或位移法都有六个基本未知量。
若将荷载按对称和反对称分组,在正对称情况下取半结构(图4.3.2b ),无侧移刚架宜用位移法计算,只有两个基本未知量(用力法则有四个多余力)。