静定结构与超静定结构

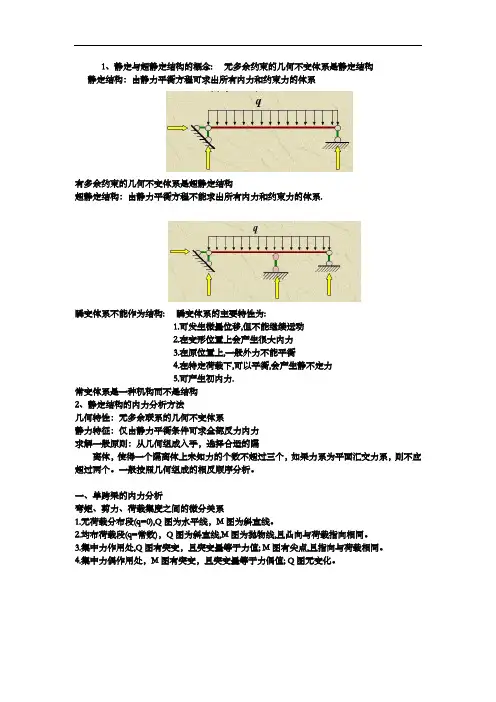
1、静定与超静定结构的概念:无多余约束的几何不变体系是静定结构静定结构：由静力平衡方程可求出所有内力和约束力的体系有多余约束的几何不变体系是超静定结构超静定结构：由静力平衡方程不能求出所有内力和约束力的体系.瞬变体系不能作为结构:瞬变体系的主要特性为:1.可发生微量位移,但不能继续运动2.在变形位置上会产生很大内力3.在原位置上,一般外力不能平衡4.在特定荷载下,可以平衡,会产生静不定力5.可产生初内力.常变体系是一种机构而不是结构2、静定结构的内力分析方法几何特性：无多余联系的几何不变体系静力特征：仅由静力平衡条件可求全部反力内力求解一般原则：从几何组成入手，选择合适的隔离体，使得一个隔离体上未知力的个数不超过三个，如果力系为平面汇交力系，则不应超过两个。

一般按照几何组成的相反顺序分析。

一、单跨梁的内力分析弯矩、剪力、荷载集度之间的微分关系1.无荷载分布段(q=0),Q图为水平线，M图为斜直线。

2.均布荷载段(q=常数)，Q图为斜直线,M图为抛物线,且凸向与荷载指向相同。

3.集中力作用处,Q图有突变，且突变量等于力值; M图有尖点,且指向与荷载相同。

4.集中力偶作用处，M图有突变，且突变量等于力偶值; Q图无变化。

内力计算的关键在于:正确区分基本部分和附属部分. 熟练掌握单跨梁的计算.单体刚架(联合结构)的支座反力(约束力)计算方法:切断约束，取一个刚片为隔离体，假定约束力的方向，由隔离体的平衡建立三个平衡方程。

四.刚架弯矩图的绘制做法:拆成单个杆,求出杆两端的弯矩,按与单跨梁相同的方法画弯矩图. 分段定点连线六.由做出的剪力图作轴力图做法: 逐个杆作轴力图,利用结点的平衡条件,由已知的杆端剪力和求杆端轴力,再由杆端轴力画轴力图.注意:轴力图画在杆件那一侧均可,必须注明符号和控制点竖标.。

结构力学静定结构与超静定结构结构力学是研究结构承受外力后的力学性能的学科，它在建筑、机械、航空航天等领域都扮演着重要的角色。

在结构力学中，我们可以将结构分为两类：静定结构和超静定结构。

静定结构是指在确定边界条件下，结构的所有支反力以及结构内部的应力分布等参数都可以通过静力平衡方程唯一求解出来的结构。

在静定结构中，支反力的计算可以通过平衡方程解决，而应力的计算可以通过弹性力学理论求解。

以简支梁为例，简支梁的两端固定支承，中间用力作用时，通过平衡方程可以求解出支反力。

而根据梁的几何形状和荷载的大小，可以计算出梁内部的应力分布。

在静定结构中，支反力和应力可以通过简单的数学计算求解，因此设计和分析起来相对简单。

而超静定结构则相对复杂一些。

超静定结构是指在确定边界条件下，结构的参数无法通过静力平衡方程唯一求解出来的结构。

这意味着在求解超静定结构时，不仅需要静力平衡方程，还需要考虑结构的变形和材料的本构关系等。

以悬臂梁为例，悬臂梁的一端固定支承，另一端悬空。

在悬臂梁上增加一个附加支承，形成一个超静定结构。

在这种情况下，由于支承力未知，无法通过静力平衡方程唯一求解出来。

因此，我们需要考虑结构的变形情况，并将其作为一个未知数来求解。

在超静定结构中，我们通常采用的方法是引入截面变形理论和力法。

通过假设结构具有一定的变形形态，并利用力法求解出结构的变形、应力和支反力等参数。

通常情况下，超静定结构的计算需要较为复杂的数学方法和计算机仿真。

静定结构和超静定结构在工程实践中都有广泛的应用。

静定结构常常用于桥梁、楼房等普通建筑结构的设计与分析中，因其计算相对简单，容易掌握。

而超静定结构常常用于大跨度的特殊结构的设计与分析中，如悬索桥、曲线梁等。

虽然超静定结构计算较为复杂，但可以提供更多的设计自由度和结构优化的可能性。

总而言之，静定结构和超静定结构都是结构力学中的重要概念。

静定结构是可通过静力平衡方程求解出内部参数的结构，而超静定结构则需要额外的变形理论和力法求解。

第十章静定结构和超静定结构课题：第一节结构的计算简图[教学目标]一、知识目标：1、理解结构计算简图的作用和意义。

2、掌握结构计算简图基本的简化方法。

二、能力目标：通过对结构计算简图的讲解，提高学生分析问题的能力。

三、素质目标：培养学生善于区分事物的主要矛盾和次要矛盾[教学重点]1、支座的简化和节点的简化。

2、计算简图的概念和要求。

[难点分析]计算简图简化的原理。

[学生分析]学生由于缺乏实际工程知识，不太理解计算简图的作用以及这种分析方法。

[辅助教学手段]理论联系实际、分析、讨论的方法[课时安排]1课时[教学内容]一、导入新课何谓结构？结构的举例。

通过启发学生联系工程实例，理解结构的概念。

二、新课讲解1．结构的计算简图2．结构的计算简图应满足的要求（1）基本上反映结构的实际工作性能（2）计算简便3．实际结构的计算简图的简化（1）支座的简化三种形式；简支梁、阳台、柱的实例。

（2）节点的简化铰节点和刚节点的特点及其应用（3）构件的简化实际上是力学中杆件的简化（4）荷载的简化集中荷载和均布荷载三、讨论1 牛腿柱的计算简图2 雨蓬的计算简图四、小结在结构设计中，选定了结构的计算简图后，在按简图计算的同时，还必须采取相应的措施，以保证实际结构的受力和变形特点与计算简图相符。

五、作业思考题：1课题：第二节平面结构的几何组成分析[教学目标]一、知识目标：1、理解几何组成分析的作用和意义。

2、了解结构从几何组成的观点的分类。

3、了解结构几何组成分析的规则和方法。

4、了解静定结构和超静定结构的概念。

5、会对简单结构进行几何组成分析。

二、能力目标：通过对结构几何组成分析的讲解，提高学生分析问题的能力。

三、质目标：培养学生善于区分事物的主要矛盾和次要矛盾[教学重点]1、几何组成分析的意义和结果。

2、几何组成分析的方法。

[难点分析]结构几何组成分析的概念和方法都比较抽象，尤其是方法，学生学习起来比较困难。

讲解时，淡化理论，结合例题讲解。

西南交通大学应用力学与工程系材料力学教研室第八章简单的超静定问题§8-1 概述静定结构: 仅靠静力平衡方程就可以求出结构的全部未知的约束反力或内力FAB2A F1BααC平面任意力系：3个平衡方程平面共点力系：2个平衡方程独立平衡方程数：超静定结构(静不定结构): 仅凭静力学平衡方程不能求解全部未知内力或反力的结构。

超静定结构的未知力的数目多于独立的平衡方程的数目；两者的差值称为超静定的次数。

BD C A 132FααF F CF B F A BC ABCADA FααF N1y xF N3F N2BD C A 132FααF F CF B F A BC AA FααF N1y xF N3F N2•习惯上把维持物体平衡并非必需的约束称为多余约束，相应的约束反力称为多余未知力。

•超静定的次数就等于多余约束或多余未知力的数目。

•注意：从提高结构的强度和刚度的角度来说，多余约束往往是必需的，并不是多余的。

超静定的求解：根据静力学平衡条件确定结构的超静定次数，列出独立的平衡方程；然后根据几何、物理关系列出需要的补充方程；则可求解超静定问题。

F F CF B F A BC A•补充方程的数目=多余未知力的数目=多余约束数。

•根据变形几何相容条件，建立变形几何相容方程，结合物理关系（胡克定律），则可列出需要的力的补充方程。

•补充方程的获得，体现了超静定问题的求解技巧与关键。

此处我们将以轴向拉压、扭转、弯曲的超静定问题进行说明。

BD C A 132FααF F CF B F A BC AA FααF N1yxF N3F N2§8.2 拉压超静定问题1拉压超静定问题解法例两端固定的等直杆AB ，在C 处承受轴向力F 如图，杆的拉压刚度为EA ，求杆的支反力.解：一次超静定问题=−+F F F B A F BA F AB ablFC (1) 由节点A 的平衡条件列出杆轴线方向的平衡方程（2）变形：补充方程(变形协调条件)可选取固定端B 为多余约束，予以解除，在该处的施加对应的约束反力F B ，得到一个作用有原荷载和多余未知力的静定结构--称为原超静定结构的基本静定系或相当系统注意原超静定结构的 B 端约束情况，相当系统要保持和原结构相等，则相当系统在B 点的位移为零。

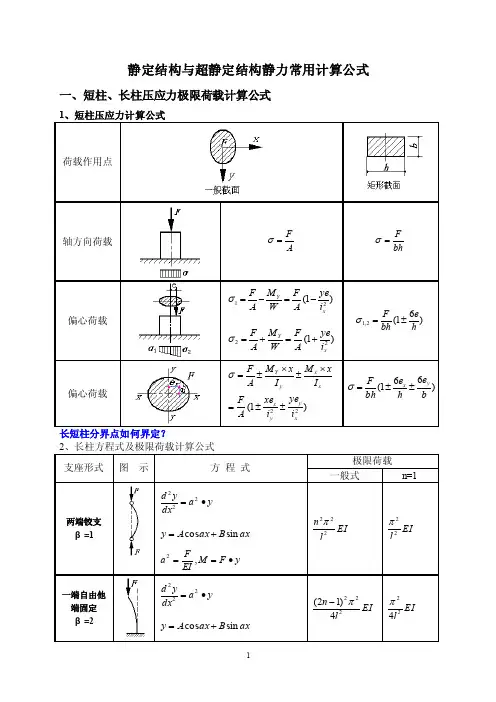
静定结构与超静定结构静力常用计算公式一、短柱、长柱压应力极限荷载计算公式1、短柱压应力计算公式荷载作用点轴方向荷载AF =σ bhF =σ 偏心荷载)1(21xY i ye A F W M A F -=-=σ )1(22xY i ye A F W M A F +=+=σ )61(2,1hebh F ±=σ 偏心荷载)1(22xy y x xx y Y i ye i xe A FI xM I x M A F ±±=⨯±⨯±=σ )661(beh ebh F yx ±±=σ长短柱分界点如何界定？2、长柱方程式及极限荷载计算公式 支座形式图 示方 程 式极限荷载 一般式 n=1两端铰支 β=1y a dxy d ∙=222 ax B ax A y sin cos +=y F M EIFa ∙==,2 EI ln 222π EI l 22π一端自由他端固定β=2y a dxyd ∙=222 ax B ax A y sin cos +=EI l n 2224)12(π-EI l 224πy F M EIFa ∙==,2 两端固定 β=0.50)(22=-+F M y a dxyd A FM ax B ax A y A++=sin cos A M y F M EIFa +∙-==,2 EI l 224π EI l 224π 一端铰支他端固定 β=0.75)(222x l EI Q y a dx y d -=∙+)(sin cos x l FQax B ax A y -++=水平荷载-=Q EIFa ,2 ——EI l227778.1π注：压杆稳定临界承载能力计算公式：EI l P cr 22)(βπ=二、单跨梁的反力、剪力、弯矩、挠度计算公式 1、简支梁的反力、剪力、弯矩、挠度计算公式荷载形式M 图V 图反力 2F R R B A == L Fb R A =L Fa R B =2qL R R B A == 4qL R R B A == 剪力V A =R A V B =-R B V A =R A V B =-R B V A =R A V B =-R BV A =R A V B =-R B弯矩4max FL M =LFabM =max 82maxqL M = 122maxqL M = 挠度EIFL 483max=ω 若a ＞b 时，3)2(932maxab a EIL Fb +=ω（在)2(3b a ax +=处） EIqL 84max=ω EIqL 1204max=ω 注：1、弯矩符号以梁截面下翼缘手拉为正（+），反之为负（—）。

静定结构与超静定结构的概念
静定结构是指由力学平衡条件完全确定的结构体系。

这种结构体系的节点数和支座数
均为定值，因此问题可以被简化为一组线性方程组，能够通过矩阵运算得到完整的结构位
移和内力。

因此，静定结构具有稳定可靠、计算简单等优点。

常见的静定结构有梁、柱、
桁架等。

超静定结构则是指节点数和支座数不足以完全确定结构体系的构件，在此基础上另外
增设一定数目的约束，即超数约束，从而使结构体系的DOF（自由度）等于零或小于零，可以通过高斯消元、截可省略算法等方法进行求解。

常见的超静定结构有悬链、钢框架、高
层建筑等。

超静定结构相对于静定结构具有以下特点：
1.灵活编排：在设计中，超静定结构通过增加适量的支承约束，可以根据实际情况安
排构件的位置，达到灵活编排的目的。

2.承载能力大：超静定结构的约束力较大，因此在承载能力方面比静定结构更有优势，能够承受更大的荷载。

3.变形小：超静定结构的约束力较大，因此在荷载下变形较小，对结构的稳定性和耐
久性都有良好的保证。

4.抗剪承载能力强：由于超静定结构的超数约束，使得其具有很好的抗剪承载能力，
因此比较适合用于高层、大跨度等大型结构的设计中。

需要注意的是，在设计超静定结构时，要考虑结构的稳定性，避免出现过度约束、约
束不当等问题，以免影响结构的受力性能和使用寿命。

同时，在考虑承重能力的同时，也
要注重结构的变形控制，以达到有效的结构控制和优化设计的目的。

静定结构超静定结构不同静定结构与超静定结构的不同1、静定结构是无多余约束的几何不变体；静定结构中，温度变化、支座移动等不会在结构中产生附加应力。

2、超静定结构是在静定结构的基础上增加了（多余）的约束；超静定结构会随温度变化及支座移动均可能在结构中产生附加应力。

附：机械设计通用的技术要求1.零件去除氧化皮。

2.零件加工表面上，不应有划痕、擦伤等损伤零件表面的缺陷。

3.去除毛刺飞边。

4.经调质处理，HRC50～55。

5.零件进行高频淬火，350～370℃回火，HRC40～45。

6.渗碳深度0.3mm。

7.进行高温时效处理。

8.未注形状公差应符合GB1184-80的要求。

9.未注长度尺寸允许偏差±0.5mm。

10.铸件公差带对称于毛坯铸件基本尺寸配置。

11.未注圆角半径R5。

12.未注倒角均为2×45°。

13.锐角倒钝。

14.各密封件装配前必须浸透油。

15.装配滚动轴承允许采用机油加热进行热装，油的温度不得超过100℃。

16.齿轮装配后，齿面的接触斑点和侧隙应符合GB10095和GB11365的规定。

17.装配液压系统时允许使用密封填料或密封胶，但应防止进入系统中。

18.进入装配的零件及部件（包括外购件、外协件），均必须具有检验部门的合格证方能进行装配。

19.零件在装配前必须清理和清洗干净，不得有毛刺、飞边、氧化皮、锈蚀、切屑、油污、着色剂和灰尘等。

20.装配前应对零、部件的主要配合尺寸，特别是过盈配合尺寸及相关精度进行复查。

21.装配过程中零件不允许磕、碰、划伤和锈蚀。

22.螺钉、螺栓和螺母紧固时，严禁打击或使用不合适的旋具和扳手。

紧固后螺钉槽、螺母和螺钉、螺栓头部不得损坏。

23.规定拧紧力矩要求的紧固件，必须采用力矩扳手，并按规定的拧紧力矩紧固。

24.同一零件用多件螺钉（螺栓）紧固时，各螺钉（螺栓）需交叉、对称、逐步、均匀拧紧。

25.圆锥销装配时应与孔应进行涂色检查，其接触率不应小于配合长度的60%，并应均匀分布。

静定结构和超静定结构优缺点及工程应用一、静定结构和超静定结构概念静定结构与超静定结构都是几何不变体系。

在几何结构方面, 二者不一样在于: 静定结构无多出联络, 而超静定结构则含有多出联络。

有多出约束( n > 0)几何不变体系——超静定结构;无多出约束( n = 0)几何不变体系——静定结构。

静定结构──几何特征为无多出约束几何不变, 是实际结构基础。

因为静定结构撤销约束或不合适更改约束配置能够使其变成可变体系, 而增加约束又能够使其成为有多出约束不变体系（即超静定结构）。

静定结构约束反力或内力均能经过静力平衡方程求解, 也就是说, 其未知约束反力或内力数目等于独立静力平衡方程数目。

静定结构在工程中被广泛应用, 同时是超静定结构分析基础。

超静定结构——几何特征为几何不变但存在多出约束结构体系, 是实际工程常常采取结构体系。

因为多出约束存在, 使得该类结构在部分约束或连接失效后仍能够负担外荷载, 但需要注意是, 此时超静定结构受力状态与以前是大不一样, 假如需要话, 要重新核实。

因为其结构中有不需要多出联络, 所以所受约束反力或内力仅凭静力平衡方程不能全部求解, 也就是未知力数目多于独立静力平衡方程个数。

二、静定结构基础特征及优缺点1、静定结构是几何不变体系, 无多出约束, 全部支座反力和内力只要用静力平衡条件就能确定, 而且解答是唯一。

2、静定结构支座反力和内力与结构所用材料性质、截面大小和形状都没相关系。

3、静定结构在温度改变、支座移动、材料伸缩和制造误差等原因影响下, 都不产温度变化（自由地产生弯曲变形，不产生内力）支座移动（刚体位移，不产生内力）制造误差生制作反力和内力。

即没有荷载作用在静定结构上时, 支座反力均为零, 所以内力也均为零。

4、静定结构局部平衡特征在一组平衡力系作用下, 假如静定结构中某一几何不变部分能够与荷载平衡, 则只会是该部分产生内力, 其它部分支座反力和内力均为零。

一次超静定结构超静定结构是指结构的自由度数量大于零但小于等于实际所需自由度数量的结构。

一次超静定结构是指结构的自由度数量为实际所需自由度数量加一的结构。

在一次超静定结构中，自由度数量比所需的自由度数量多一个，这意味着结构中存在一个多余的自由度。

在设计一次超静定结构时，需要注意将多余的自由度与结构的其他自由度相匹配，使得结构能够保持平衡和稳定。

一次超静定结构在实际工程中常见，例如在悬索桥和平衡臂桥中，由于主梁的几何形状的限制，产生了一个多余的自由度，导致结构成为一次超静定结构。

对于一次超静定结构，在结构受到外部荷载作用时，由于存在多余的自由度，结构内部会出现额外的应力和变形。

因此，在设计一次超静定结构时，需要通过合理的结构设计和计算方法，来保证结构的安全性和稳定性。

一、项目背景现代社会交通工具得到了广泛的应用，其中车辆是人们出行的主要方式之一。

由于道路状况、驾驶技术以及其他因素的限制，车辆在行驶过程中难免会遭受到撞击和冲击，这可能对车辆以及车上乘客造成伤害和损失。

因此，开发和应用车载防冲击结构成为保障车辆和乘客安全的重要举措。

二、项目目标本项目旨在设计和开发一种有效的车载防冲击结构，能够在车辆遭受撞击和冲击时减少乘客受伤和车辆损坏程度。

三、项目内容1. 研究市场上现有的车载防冲击结构，了解其设计原理和应用效果。

2. 对车辆的结构和特点进行分析，确定开发车载防冲击结构的关键要素。

3. 设计和开发车载防冲击结构的样机，包括研究材料和构造，进行模拟测试和性能评估。

4. 根据样机的测试结果进行改进和优化，确保车载防冲击结构的效果和可靠性。

5. 进行大规模生产和应用的准备工作，包括制定生产计划、建立生产线和培训工作人员等。

四、项目计划1. 第一阶段（3个月）：调研和分析阶段- 研究市场上现有的车载防冲击结构，了解其设计原理和应用效果。

- 对车辆的结构和特点进行分析，确定开发车载防冲击结构的关键要素。

2. 第二阶段（6个月）：样机设计和开发阶段- 设计和开发车载防冲击结构的样机，包括研究材料和构造，进行模拟测试和性能评估。