陕西师范大一数学分析期末考试题

大一上数学分析期末考试题及答案一、选择题（每题3分，共30分）1. 极限的定义是：如果对于任意的正数ε，都存在正整数N，使得当n>N时，都有|a_n - A| < ε，则称序列{a_n}的极限为A。

A. 正确B. 错误答案：A2. 函数f(x)=x^2在区间(-∞, +∞)上是单调递增的。

A. 正确B. 错误答案：B3. 函数f(x)=x^3在区间(-∞, +∞)上是单调递增的。

A. 正确B. 错误答案：A4. 函数f(x)=sin(x)在区间[0, π]上是单调递增的。

A. 正确B. 错误答案：B5. 函数f(x)=x^2在区间[0, +∞)上是单调递增的。

A. 正确B. 错误答案：A6. 函数f(x)=x^3在区间(-∞, +∞)上是单调递增的。

A. 正确B. 错误答案：A7. 函数f(x)=e^x在区间(-∞, +∞)上是单调递增的。

A. 正确B. 错误答案：A8. 函数f(x)=ln(x)在区间(0, +∞)上是单调递增的。

A. 正确B. 错误答案：A9. 函数f(x)=1/x在区间(0, +∞)上是单调递减的。

A. 正确B. 错误答案：B10. 函数f(x)=x^2在区间(-∞, 0)上是单调递减的。

A. 正确B. 错误答案：A二、填空题（每题4分，共20分）11. 极限lim(x→0) (sin(x)/x) = ________。

答案：112. 极限lim(x→+∞) (1/x) = ________。

答案：013. 极限lim(x→0) (1 - cos(x))/x^2 = ________。

答案：1/214. 函数f(x)=x^3在x=0处的导数为 ________。

答案：015. 函数f(x)=e^x在x=0处的导数为 ________。

答案：1三、计算题（每题10分，共40分）16. 计算极限lim(x→0) (tan(x) - sin(x))/x^3。

解：利用洛必达法则，对分子分母分别求导三次，得到极限为1/2。

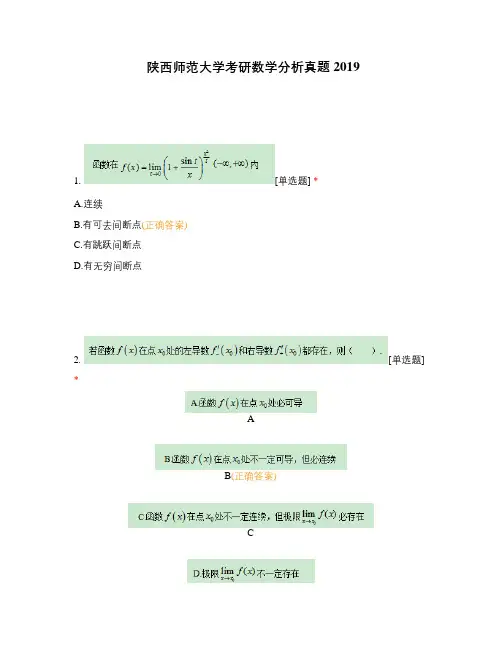
陕西师范大学考研数学分析真题20191. [单选题] *A.连续B.有可去间断点(正确答案)C.有跳跃间断点D.有无穷间断点2. [单选题] *AB(正确答案)CD3. [单选题] *AB(正确答案)CD4. [单选题] *A(正确答案)BCD5. [单选题] *AB(正确答案)CD6. [单选题] *A.①②B.③④C.②④(正确答案)D.①③7.[单选题] *AB(正确答案)CD8.[单选题] *ABCD(正确答案)9. [单选题] *ABCD(正确答案)10.[单选题] *ABCD(正确答案)11.[填空题] *答案若为分数，请用“/”作分数线，示例：三分之一写作1/3_________________________________(答案：-1)12. [填空题] *答案若为分数，请用“/”作分数线，示例：三分之一写作1/3_________________________________(答案：1/12)13.[填空题] *答案若为分数，请用“/”作分数线，示例：三分之一写作1/3；本题的两个答案之间用“，”隔开_________________________________(答案：2,0)14. [填空题] *答案若为分数，请用“/”作分数线，示例：三分之一写作1/3_________________________________(答案：2)15.[填空题] *答案若为分数，请用“/”作分数线，示例：三分之一写作1/3_________________________________(答案：10/3)。

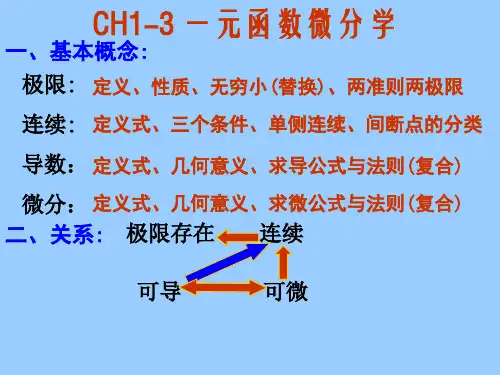
数学分析上学期期末考试试题(及答案)一、选择题（每小题2分，共20分）1. 下列哪个不是测度论中的重要定理？A. 开集的性质B. 测度的可贸易性C. 有限可加性定理D. 外测度的定义2. 设函数f(x)在[a, b]上可导，下列关于f(x)的结论中正确的是：A. f(x)在[a, b]上一定为增函数B. f(x)在[a, b]上一定为减函数C. f(x)在[a, b]上既可以是增函数也可以是减函数D. f(x)在[a, b]上一定为周期函数3. 以下哪个不是级数收敛的充要条件？A. 极限一致有界B. 积分收敛C. 极限值为零D. 部分和有界4. 若函数序列fn(x)在[a, b]上一致收敛于f(x)，则f(x)在[a, b]上一定是A. 递增的B. 递减的C. 周期函数D. 连续函数5. 下列哪个不是积分的线性性质？A. ∫[a, b](f+g)(x)dx = ∫[a, b]f(x)dx + ∫[a, b]g(x)dxB. ∫[a, b]cf(x)dx = c∫[a, b]f(x)dx (c为常数)C. ∫[a, b]f(x)g(x)dx = ∫[a, b]f(x)dx * ∫[a, b]g(x)dxD. ∫[a, b]f(x)dx = -∫[b, a]f(x)dx6. 函数f(x)=|x|/(x^2+9)的不可导点是A. x=-3B. x=3C. x=-3和x=-sqrt(3)D. x=-3和x=sqrt(3)7. 设函数u(x, y)具有二阶连续偏导数，下列哪个条件可以确保u(x, y)为调和函数？A. u_xx + u_yy = 0B. u_xx + u_yy = 1C. u_xx - u_yy = 0D. u_xx - u_yy = 18. 设实数α为2π的有理数倍数，函数f(x)的周期为2π，下列哪个函数一定是f(x)的周期函数？A. f(x + α)B. f(x - α)C. f(-x)D. f(x/2)9. 设f(x)在区间[a, b]上一阶可导，且f(a)=f(b)=0，若存在c∈(a,b)使得f(c)=0，则函数f(x)在[a, b]上的其中一个极值点为A. aB. bC. cD. 以上都可能是10. 函数f(x)对任意的x∈(-∞, +∞)满足f'(x) = f(x)，若f(x)在x=0处的值为2，则f(1)的值为A. -1B. 0C. 1D. 2二、填空题（每小题5分，共20分）1. 若函数f(x)可导，则f(x)________是可测的，且__________是可测的。

数学分析期末考试试题一、选择题（每题2分，共20分）1. 函数f(x)=x^2-3x+2在区间[1,3]上的最大值是：A. 0B. 2C. 4D. 62. 以下哪个选项不是闭区间[a, b]上连续函数的性质？A. 有界性B. 保号性C. 介值性D. 可微性3. 函数f(x)=sin(x)在x=0处的导数是：A. 0B. 1C. -1D. 24. 函数f(x)=x^3+2x^2-3x+1在x=-1处的泰勒展开式（展开到x^2项）是：A. -1+2x-x^2B. 1-2x+x^2C. -1+2x+x^2D. 1+2x-x^25. 以下哪个级数是发散的？A. 1 - 1/2 + 1/3 - 1/4 + ...B. 1^2 + 1/2^2 + 1/3^2 + ...C. 1 - 1/2 + 1/4 - 1/8 + ...D. 1 - 1/2^2 + 1/3^2 - 1/4^2 + ...6. 函数f(x)=x^2在x=1处的高阶导数f^(n)(x)（n≥2）是：A. 0B. 1C. 2D. 47. 函数f(x)=e^x的原函数是：A. e^x + CB. ln(x) + CC. sin(e^x) + CD. cos(e^x) + C8. 函数f(x)=x^2在[0,1]上的定积分是：A. 1/3B. 1/2C. 1D. 2/39. 函数f(x)=|x|在x=0处的导数是：A. 1B. -1C. 0D. 不存在10. 以下哪个函数是周期函数？A. f(x)=x^2B. f(x)=e^xC. f(x)=sin(x)D. f(x)=ln(x)二、填空题（每题2分，共10分）11. 若函数f(x)=x^3-6x^2+11x-6在x=2处取得极小值，则f'(2)=_________。

12. 若函数f(x)=x^3+bx^2+cx+d在x=-1处取得最大值，则b=_________。

13. 函数f(x)=ln(x)的原函数是_________。

数学分析试题（一）答案及评分标准一、填空（每题3分）1． ]10,0(2．2)()(x f x f −+，2)()(x f x f −− 3．52 4．，1=a 1−=b 5．0二、求极限（每题5分）1．=++++++∞→n n 313131212121222L L lim )(lim )(lim n n n n 31313121212122++++++∞→∞→L L ……………………………(1分) =3113113121121121−−−−∞→∞→))((lim ))((lim n n n n ……………………………………………………………(2分) 2=……………………………………………………………………………(2分) 2．))()((lim 22221111n n nn ++++∞→L 22221211110n n n n n +≤++++≤)()(L ……………………………………………(2分) 利用夹逼原则，…………………………………………………………………(1分) 可求得021111222=++++∞→))()((lim n n n n L ．……………………………………(2分) 3．=−−++∞→902070155863)()()(lim x x x x 9090207090155863()()(lim xx x x x x −−++∞→………………………(2分)=902070155863)()()(lim xx x x −−++∞→…………………………………………………..(1分) 902070583⋅=…………………………………………………………………..(2分) 4．x x x sin )(tan lim 0→= ………………………………………………..(1分) )ln(tan sin lim x x x e 0→x x x x e tan ln sin lim lim 00→→=x x x x e sin tan ln lim lim 100→→=………………………………………………(1分)x x x e sin sec lim 20→−=…………………………………………………………………(2分) 10==e ………………………………………………………………………(1分)5．))cos cos cos (cos lim (lim n n x x x x x 22220L ∞→→ n n n x x x x x x x x x x 22222222212sin cos cos cos sin cos cos cos sin sin L L +==== …………………………………………………………………………………..（2分）=∞→)cos cos cos (cos lim n n x x x x 2222L 12122+∞→⋅n n n x x sin sin lim …………………………….(1分) 12122+∞→⋅n n n x x sin sin lim =x x x xn n n 2222sin sin lim ⋅∞→x x 22sin =………………………………...(1分) ))cos cos cos (cos lim (lim n n x x x x x 22220L ∞→→=1220=→x x x sin lim …………………………(1分) 6．)sin (lim x x x 22011−→=)sin sin (lim xx x x x 22220−→………………………………………..(1分) =)sin sin (lim xx x x x 22220−→=x x x x x x x 2222220sin sin sin lim +−→……………………………….(1分) xx x x x x x 22222220cos sin sin cos lim++−=→……………………………………………(1分) xx x x x x x 2226232220sin cos sin sin lim −+−=→…………………………………………(1分) 31−=．…………………………………………………………………………(1分) 三、计算（每题5分）1．22xx x x x x y tan sec )tan (−=′=′ 2．)ln )11(ln()1111(ln 2′−−−=′−++−−+=′x x x x xx y ………通过分母有理化先将化简………………………………………………………………………………..(2分) y xx x x x x 1111111222−−⋅−−=′−−−)ln )(ln(………………………………(2分) 2111111x x x x xx y −=′−++−−+=′)(ln ……………………………………………(1分)3．……………………………………………………...(2分))()(ln sin sin ′=′=′x x x e x y )ln (sin )(sin ln sin ′⋅=′x x e e xinx x x …………………………………………………..(1分) )sin ln (cos )ln (sin sin sin xx x x x x x e y x xinx +=′⋅=′………………………………..(2分) 4．，则……………………………………………...(1分) 31x x f =−)(31)()(+=x x f 213()(+=′x x f )…………………………………………………………………(2分) 2)2(3)1(+=+′x x f ………………………………………………………………(1分) 231x x f =−′)(…………………………………………………………………..(1分)5．，则⎪⎩⎪⎨⎧==ta y t a x 33sin cos t t t a t t a dx dy tan sin cos cos sin −=−=2233……………………………(2分) ⎪⎩⎪⎨⎧−==x dxdy t a x tan cos 3，则t t a t t a x dx y d sin cos sin cos sec 42222313=−−=…………………...(3分) 6．设，由于x x x y −=ln x x x x y ln )ln (=′−=′………………………………(3分)xdx dy ln =……………………………………………………………………(2分)四、由于∞=−+−→13221x x x x ))((lim，1=x 是垂直渐近线……………………(1分) 21322=−+−∞→xx x x x )())((lim ……………………………………………………….(2分)=−−+−∞→)))(((lim x x x x x 2132241124=−−∞→x x x lim ……………………………….(2分) 因此也具有斜渐近线42+=x y ．……………………………………..(1分) 五、x x x f 2ln )(=，由0222=−=′xx x x f ln ln )(，可解出1=x ，……..(2分) 2e 当时，；当时，10<<x 0<′)(x f 21e x <<0>′)(x f ；当时， x e <20<′)(x f ……………………………………………………………………………………(2分) 所以是的极小值，1=x f 01=)(f ；是的极大值，. 2e x =f 224−=e e f )(…………………………………………………………………………………….(2分) 六、证：令⎪⎩⎪⎨⎧=∈=0120x x x x x f ,],(,sin )(π…………………………………………(1分) f 在],[20π上连续．当),(20π∈x 时，022<−=−=′xx x x x x x x x f )tan (cos sin cos )(， 所以在f ],[20π上严格递减，………………………………………………..(3分) 因此),(20π∈x 时， 1022=<<=)()()(f x f f ππ 即x x x<<sin π2．…………………………….(2分)七、不妨假设在上不恒正也不恒负，…………………………..(1分) f ],[b a 即存在，满足],[,b a x x ∈′′′0>′)(x f ，0<′′)(x f ，…………………………(2分) 由连续函数的介值定理，……………………………………………………(2分) 则存在),(x x x ′′′∈0，使得00=)(x f ………………………………………….(1分) 这与已知矛盾．……………………………………………………………….(1分)。

一、选择题（每题5分，共20分）1. 下列函数中，在区间（0，+∞）上单调递减的是：A. f(x) = x^2B. f(x) = e^xC. f(x) = ln(x)D. f(x) = 1/x2. 函数y = x^3 - 6x + 9的极值点为：A. x = -1B. x = 1C. x = -3D. x = 33. 下列积分中，结果为π的是：A. ∫(0 to π) sin(x) dxB. ∫(0 to π) cos(x) dxC. ∫(0 to π) tan(x) dxD. ∫(0 to π) cot(x) dx4. 设f(x) = x^3 - 3x，则f(x)的导数f'(x)为：A. 3x^2 - 3B. 3x^2 - 2xC. 3x^2 + 2xD. 3x^2 + 35. 下列级数中，收敛的是：A. ∑(n=1 to ∞) (1/n^2)B. ∑(n=1 to ∞) (1/n)C. ∑(n=1 to ∞) (1/n^3)D. ∑(n=1 to ∞) (n^2)二、填空题（每题5分，共20分）1. 函数f(x) = 2x^3 - 3x^2 + x在x=1处的导数值为______。

2. 极限lim(x→0) (sin(x)/x) 的值为______。

3. 若f(x) = x^2 + 1，则f'(x) = ______。

4. 函数y = e^x的导数y' = ______。

5. 级数∑(n=1 to ∞) (1/n^2) 的和为______。

三、解答题（每题10分，共40分）1. 求函数f(x) = x^3 - 3x^2 + 4x的导数。

2. 求函数y = ln(x^2 + 1)的导数。

3. 计算极限lim(x→∞) (1/x^2 + 1/x^3)。

4. 求函数y = e^(2x)的积分。

四、应用题（每题10分，共20分）1. 一辆汽车以v = 20m/s的速度匀速行驶，当刹车后，每秒减速5m/s，求汽车停止前行驶的距离。

方法一：应用数列极限的定义(证明题)用定义求数列极限有几种模式： （1），作差，解方程，解出，则取或（2）将a a n -适当放大，解出()εf n >； （3）作适当变形，找出所需N 的要求。

方法二：常用方法：约去零因子求极限，分子分母同除求极限，分子(母)有理化求极限方法三（迫敛性）设收敛数列都以为极限，数列满足：存在正整数,当时有：则数列{}c n收敛，且。

方法四：（单调有界定理）在实系数中，有界的单调数列必有极限。

方法五：两个重要极限是和方法六：（柯西收敛准则）数列收敛的充要条件是：对任给的，存在正整数N，使得当n，m时，有方法七：Stolz定理：设n>N时，且，若（为有限数或无穷大），则方法八：形如数列极限方法九：用等价无穷小量代换求极限（等价无穷小量代换,只能代换极限式中的因式．．），常见等价无穷小有：当时,,；方法十：用罗必塔法则求极限，用对数恒等式求极限，数列极限转化成函数极限求解。

算术－几何－调和平均不等式：对记(算术平均值)(几何平均值)(调和平均值)有均值不等式:等号当且仅当时成立. （3） Bernoulli 不等式: (在中学已用数学归纳法证明过)对由二项展开式（４）Cauchy－Schwarz 不等式:(),有（５），；；；导数微分及应用习题判断:1、若可微，且为上的偶函数，则必为][l l-上的偶函数；,（）2 若是上的奇函数，则)f'必为[]l l,-上的偶函数；（）(xx点的极限存在3、如果函数在点的左、右极限都存在，则函数在（）x点可导；（）4、若函数)f在(x(xf在点连续，则)5、若函数)(x f 在点0x x =连续，则)(x f 在0x 点的极限一定存在；（ ）6、若函数)(x f 在点0x x =可微，则)(x f 在0x 点可导 ； （ ）7、如果函数()x f y = 在 0x 点 的左、右 极限都存在，则)(x f 在0x 点可导 ；（ ）8、若函数)(x f 在点0x x =连续，则函数()x f y = 在 0x 点 的左、右 极限都存在且相等；（ ）9、若)(x f 在0x 点不可导，则函数)(x f 在点0x x =一定不连续；（ ） 10、若函数)(x f 在点0x x =不可微，则)(x f 在0x 点不可导 ； （ ） 11、若函数)(x f 在点0x x =不可微，则)(x f 的左、右 极限一定不存在；（ ）12、设函数)(x f 在0x 点可导，导数为，则（ ）13、设函数)(x f 在0x 点可导，导数为)(0x f '，则（ ）14、设函数)(x f 在0x 点可导，导数为)(0x f '，则（ ） 15、函数在处不可导；（ ）16、函数1-=x y 在1=x 处不连续；（ ） 17. 若)(0x f '存在，且，则（ ）18、若)(x f 在上可导，则)(x f 在],[b a 上有界； （ ）19、若)(x f 在0x 点导数不存在，则曲线在点处没有切线；（ ） 20、曲线上点处的法线的斜率为；（ ）21.设)(x f y =在0x x =可微，则当时，是关于高阶的无穷小；（ ） 22、若，则)(x f 在处不可导；（ ）23、若)0()()()(lim2+∞<<=--→l l a x a f x f ax ，则)(x f 在a x =处可导但；（ ） 24、若)0()()()(lim2+∞<<=--→l l a x a f x f ax ，则)(x f 在a x =处可导且；（ ） 25、若，则； （ ）1.设)(x f 在0x x =的某个邻域内具有二阶连续导数，则（ ）.A 、0；B 、)(0x f '；C 、；D 、；.2、设在0x 的邻域内连续，且有，则（ ）.A 、0；B 、；C 、；D 、.3.设，则（ ）. A 、； B 、； C 、； D 、.4.设)(x f 在1=x 点处可微，，则（ ）.A 、2；B 、1；C 、0；D 、.5.设，其中)(x f 为二阶可导函数，则（ ）.A 、；B 、；C 、；D 、.6.如果在区间内，，则在),(b a 内)(x f 与)(x ϕ（ ）.A 、仅相差一个常数；B 、完全相等；C 、均为常数；D 、为常数）.7.设)(x f 为可导的偶函数，则)(x f '为（ ）.A 、偶函数；B 、可能是偶函数；C 、奇函数；D 、非奇非偶函数.8、设()x f 在0x x =处可导，则（ ）. A 、0； B 、； C 、； D 、)(0x f '.9、设，则（ ）.A 、－3；B 、3；C 、0；D 、∞. 10、设()x f 在区间),(b a 内连续，，则在点0x 处()x f （ ）.A 、极限存在且可导；B 、极限不存在，但可导；C 、极限存在，但不一定可导；D 、极限不一定存在. 11.设，则在处()x f （ ）.A 、 无定义；B 、不连续；C 、连续且可导；D 、连续但不可导. 12、设，在0=x 可导，则必有（ ）.A、；B、；C、；D、.13、，则在0x处的导数（）.=A、0；B、－1；C、不存在；D、1.14、可微的周期函数其导数（）.A、一定是周期函数，且周期不变；B、一定是周期函数，但周期可能发生变化；C、不一定是周期函数； D、一定不是周期函数.15、设()xf为可微的偶函数，且对任意的，则（）.A、；B、；C、2；D、－2.16.曲线上，切线平行于直线的点的坐标为（）.A、（1，－3）；B、（3，－3）；C、（－1，5）；D、（2，0）.''y（）.17、设，其中为可微函数，则=A、；B、；C、；D、.18、设，则（）.A、；B、；C、；D、.19.设)f为可微函数，若，则（）.(uA、；B、；C、；D、.20、下列函数中导数等于的是（）.A、；B、；C、；D、.21、曲线在点处的切线与直线垂直，则此曲线在点M 处的切线方程为（ ）. A 、；B 、；C 、； D 、.22.设，则（ ）.A 、；B 、；C 、2；D 、.23、设，则=''y （ ）.A 、；B 、； C 、； D 、.24、下列函数中在点0=x 连续且可导的是（ ）.A 、；B 、；C 、；D 、.25、设方程确定是的函数，则（ ）.A 、；B 、1；C 、；D 、0.26.其中为可微函数，则=22dxyd （ ）.A 、；B 、；C 、；D 、.27.设，其中l 为有限值，则()x f 在a x =处（ ）.A 、可导且0)(='a f ；B 、可导但0)(≠'a f ；C 、不一定可导；D 、肯定不可导.28.曲线在点M 处的切线斜率为3，则M 点的坐标为（ ）.A 、（1，0）；B 、（0，1）；C 、（1，3）；D 、（1，－2）. 29、设，则=dy （ ）.A 、；B 、； C 、； D 、.30.设具有二阶导数，，则=''y （ ）. A 、； B 、； C 、； D 、.31、函数，则()x f 在0=x 处（ ）.A 、间断；B 、连续但不可导；C 、连续且导数为0；D 、连续且导数为－1. 32.设，在0=x 可导，则的值为（ ）.A 、； B 、1,2=-=b a ； C 、1,2==b a ； D 、.33、，则（ ）.A 、；B 、；C 、6；D 、－6.34.若)(x f 在0x 处不可导，则)(x f 在0x 点（ ）.A 、无意义；B 、左、右极限不相等；C 、不一定可导；D 、不可微. 35、若，则( ).A 、；B 、； C 、； D 、.36.若，且，则=)(x f （ ）.A 、； B 、； C 、； D 、．37、设函数 ，则=')0(f （ ）.A 、-1；B 、；C 、1；D 、． 38.，在0=x 处（ ）.A 、不可导；B 、连续且可导；C 、不连续但可导；D 、不连续.39、设，则)(x f 的有关论证正确的是（ ）.A 、)(x f 在点0=x 处可微；B 、，C 、，D 、)(x f 在点0=x 处可导.40.设（其中 为常数），则（ ）. A 、； B 、0； C 、1； D 、x . 41、设（其中 n a a a ,,,21 为常数），则（ ）. A 、!n ； B 、0； C 、1； D 、x .42.设，则（ ）.A 、；B 、；C 、；D 、0.43.设函数，则函数)(x f 在0=x 处（ ）.A 、不连续；B 、连续，不可导；C 、可导，但不连续；D 、可导且导数也存在.44、设，则=22dxy d （ ）. A 、；B 、；C 、；D 、.45.已知函数，则函数)(x f 在点0=x 处的导数（ ）. A 、； B 、； C 、； D 、不存在.46.设，则（ ）. A 、21； B 、； C 、1； D 、0. 47.设，则（ ）. A 、0； B 、1； C 、－1； D 、2.48、设，则=+)1(n y （ ）. A 、； B 、； C 、； D 、0. 49、设，则（ ）. A 、； B 、； C 、； D 、. 50.下列命题中正确的是（ ）.A 、若，则有；B 、若)()(x g x f =，则有)()(x g x f '='； C 、若，则； D 、若0)(0=x f ；则0)(0='x f .51.)(x f y 在点0x 处的左、右导数存在且相等是)(x f 在点0x 处可导的 （ ）.A 、必要条件；B 、充分条件；C 、充分必要条件；D 、无关条件.52.设函数，则为（ ）.A 、2；B 、3；C 、－1；D 、不存在.1. × ；2.∨；3、×；4、×；5、∨；6、∨；7、 × ；8、 ∨ ；9、 × ；10、 ∨ ；11、×；12、×；13、 ∨ ；14、×；15、∨ ；16、×；17、 ∨ ；18、∨ ；19、×；20、∨ ；21、 ∨ ；22、×；23、×；24、∨；25、× ；1、D ；2、B ；3、D ；4、A ；5、C ；6、A ；7、C ；8、B ；9、A ；10、C ；11、D ；12、D ；13、；C ；14、A ；15、B ；16、B ；17、D ；18、C ；19、D ；20、B ；21、A ；22、B ；23、D ；24、C ；25、B ；26、C ；27、A ；28、D ；29、B ；30、D ；31、D ；32、C ；33、C ；34、D ；35、A ；36、C ；37、C ；38、B ；39、C ；40、B ；41、A ；42、B ；43、B ；44、B ；45、D ；46、D ；47、D ；48、B ；49、A ；50、B ；51、C ；52、D.中值定理和罗比达法则★1.下列函数在给定区间上是否满足罗尔定理的所有条件？如满足，请求出满足定理的数值。

陕西师大附中2022—2023 学年度第二学期高一年级期终考试数学学科试题一、单项选择题：本题共8小题，每小题4分，共32分．在每小题给出的四个选项中，只有一项是符合题目要求．2．在ABC中，2BD BC=，3BE BA=，且，若CP xCA yCB=+ )R∈，则y+=（）B．35C．．已知函数()()1fA．B．C．D．++”模式，即语文、数学、外语必选，物理、历史二选7．2022年某省新高考将实行“312）图（1）π++929分．在每小题给出的选项中，有多项符合题目要求．全部选对的得4分，部分选对的得2分，有选错的得0分．9．制造业PMI指数反映制造业的整体增长或衰退，制造业PMI指数的临界点为50%．我国2021年10月至2022年10月制造业PMI指数如图所示，则（）A．2022年10月中国制造业PMI指数为49.2%，比上月下降0.9个百分点，低于临界点B．2021年10月至2022年10月中国制造业PMI指数的极差为2.9%C．2021年10月至2022年10月中国制造业PMI指数的众数为50.2%．12EF AB = ．34AF AB AD =-+．34BE AB AD =+ ．()()22916BE AF AD AB ⋅=-．在ABC 中，内角A ，C 所对的边分别为a ，b ，c ，根据下列条件判断三角形的情况，则正确的是（ 19b =，45A =︒，C ︒，有两解 B ．3a =，2b =3=，2b =，则AB AC ⋅=______ y x a =+的图象有且只有一个交点，分。

解答应写出文字说明、证明过程或演算步骤．在ABC中a的大小；（2）若，试判断ABC的形状．分）已知z是复数，均为实数，其中的共轭复数z；m对应的点在第三象限，求实数60,PA⊥2(2)求点分）已知函数(f x（2）若()12f x =，()23f x =，()128f x x =，求a 的值； （3）x ∀∈R ，()212x x f x -+≤恒成立，求a 的取值范围。