数学分析3期末测试卷

一、填空（每空2分，共20分） 1．设})1,0(|{中的无理数∈=x x E ，则 =E sup ；=E inf ；E 的聚点是 。

2．若0),(≠=∂∂a a a y f ，则=--→ax a a f a x f ax ),(),(lim3．若),(y x f 关于x 是奇函数，即),(),(y x f y x f --=，区域D 关于y 轴对称， 则=⎰⎰Ddxdy y x f ),(4．设曲面S 为)10,10(0≤≤≤≤=y x z ，下侧为正侧，),(y x f 在S 上连续， 则⎰⎰SdS y x f ),(的计算公式是 ；⎰⎰Sdxdyy x f ),(的计算公式是 ；⎰⎰Sdydz y x f ),(5．S 为球面1222=++z y x ，外侧为正侧，则=⎰⎰Sdxdy ；6．设S 为球面1222=++z y x ，则=++⎰⎰SdS z y x )(222 ；二、求偏导数或全微分（共20分） 1．（10分）证明函数⎪⎩⎪⎨⎧=+≠++=000),(2222222yx y x y x yx y x f 在原点（0, 0）连续且偏导数存在，但在此点不可微.2．（10分）设 ),,(xyz yz z f u =，求22yu ∂∂.三、（10分）求曲面 2132222=++z y x 的切平面，使其平行于平面064=++z y x . 四、（50分）求下列积分 1．（5分）交换积分次序⎰⎰⎰⎰+--122122),(),(x x dy y x f dx dy y x f dx2．（10分）求⎰Lds y 2其中L 是旋轮线的一拱]2,0[),cos 1(),sin (π∈-=-=t t a y t t a x 3．求⎰++-=Lyx x d y y d x I 22，其中L 是包含原点的任一条分段光滑封闭曲线，逆时针方向为正.4．（15分）以S 表示椭球B ：1222222=++cz by ax的上半部分（0≥z ），αc o s ，βcos ，γcos 表示S 的外法线的方向余弦，计算曲面积分⎰⎰++SdS cz by ax z )cos cos cos (222γβα.5．（10分）求⎰⎰++Szdxdy ydzdx xdydz 其中S 是球面1222=++z y x 的外侧.。

3 数学分析试卷
11sin sin 01(),
0 0x y xy y x f x xy ⎧+≠⎪=⎨⎪=⎩
当、已知当()()
000000lim (,),lim lim (,)lim lim (,),x y x x y y f x y f x y f x y →→→→→→判断及是否存在，并说明理由。

2222
2,()1z z z x y x y h z x y ∂++=∂∂、已知=()是由确定的。

试求的值。

222
22231 x y z a b c
++=、求椭球体上任一点的切平面于坐标轴所围四面体体积的最大值。

22
22223/222 0()4(,)(,) 0 0x y x y x y f x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩
当、已知，判断的连续性及可微性。

当22265,0
x y z x y z ⎧++=⎨++=⎩、已知曲线方程为求在点(1,-2,1)处的切线方程和法平面方程。

23D 36,D x dxdy y xy
+⎰⎰、求二重积分已知为如图的区域。

7I ().1x y z dxdydz x y z Ω=++Ω++=⎰⎰⎰、计算三重积分其中为平面，
与三个坐标平面围城的空间区域。

2228I cos .1
xdydz ydzdx dxdy x y z ∑++∑++=⎰⎰、求曲面积分=其中为所谓区域的外侧。

L
9I sin . L Pdx x ydy =+⎰、求曲线积分已知如图所示。

S 22I (). S 2xy yz zx dS z x y ax ++=+=⎰⎰10、求曲面积分=已知为柱面所截的曲面。

2012–2013学年第一学期期末考试题 11数学教育《数学分析》（三）一、单项选择（将正确答案地序号填在括号内，每题2分，共20分）1. 下列数项级数中收敛地是 （ ）A.211n n∞=∑； B. 21n nn ∞=+∑； C. 11n n ∞=∑； D. 0123n n n ∞=++∑. 2. 下列数项级数中绝对收敛地是 （）A. 1(1)n n n ∞=-∑B. 1n n ∞=1n n ∞=∑1sin n n n ∞=∑3.函数项级数1nn x n∞=∑地收敛域是 （）A. (1,1)-B. (1,1]-C. [1,1)-D. [1,1]-4.幂级数021nn n x n ∞=+∑地收敛半径是 （ ） . A B C D 1．2　．1 ．025.下列各区域中，是开区域地是（ ）2. {(,)|}A x y x y >. {(,)|||1}B x y xy ≤22.{(,)|14}C x y x y <+≤.{(,)|1}D x y x y +≥6.点集11{,|}E n N n n ⎛⎫=∈ ⎪⎝⎭地聚点是（ ）A.(){0,0}B.()0,0C.0,0D.{}{}0,07.点函数()f P 在0P 连续，是()f P 在0P 存在偏导数 （ ）A.必要条件B.充分条件C.充要条件D.既不充分也不必要条件 8.函数(,)f x y 在()00,x y 可微，则(,)f x y 在()00,x y 不一定 ( ) A.偏导数连续 B.连续C. 偏导数存在 D.存在方向导数 9.设函数)()(y v x u z =，则zx∂∂等于（ ） A.()()u x v y x y ∂∂∂∂ B. ()()du x v y dx y ∂∂ C.()()du x v y dxD.()()u x v y x y ∂∂+∂∂10. 函数(,)f x y 在()00,x y 可微地充分必要条件是( )A.偏导数连续;B.偏导数存在;C.存在切平面;D.存在方向导数.二、填空题（将正确答案填在横线上，每题2分，共20分）11.若数项级数11np n n ∞=-∑（）绝对收敛，则p 地取值范围是；12. 幂级数0(1)n n n x ∞=+∑地和函数是；13．幂级数201(1)n n x n∞=-∑地收敛域是 .； 14．平面点集22{(,)|14}E x y x y =<+≤地内点是_________ ___ __ _______； 15．函数33(,)3f x y x y xy =+-地极值点是______________________. 16．曲面221z x y =+-在点（2,1,4）地切平面是 ______________________17．函数y z x =，则zy∂=∂ ______________________； 18．函数u xyz =在（1,1,1）沿方向(cos ,cos ,cos )l αβγ=地方向导数是 ___________；19．设cos sin x r y r ϕϕ=⎧⎨=⎩，则x x r y y r ϕϕ∂∂∂∂=∂∂∂∂； 20．若arctany x =，则dydx=______________________.三、判断题（请在你认为正确地题后地括号内打“√”，错误地打“×”，每题1分，共10分）21.绝对收敛地级数一定一致收敛； ( ) 22.条件收敛地级数实质上就是发散地级数； （ ） 23.变号级数一定条件收敛； （ ） 24.收敛地数值级数一定是有界地； （ ）25.若P 是点集E 地界点，则一定有P E ∈； （ ） 26.点集E 地内点一定是E 地聚点；（ ） 27.若函数(,)f x y 在()00,x y 存在偏导数，且0000(,)(,)0f x y f x y x y∂∂==∂∂，则()00,x y 是函数(,)f x y 极值点； ( )28.若()'',xy f x y 和()'',yx f x y 都存在，则()()'','',xy yx f x y f x y =； （ ） 29.任何一个幂级数地收敛域都不是空集； （ ）30.2R 中地有界无限点集E 至少有一个聚点（ ） 四、计算题（请写出必要地步骤或过程，每题8分，共32分） 31.判断数项级数1821nn n n ∞=+⎛⎫ ⎪+⎝⎭∑地敛散性；32.求函数22sin()u x y xy =+地偏导数；33.设函数2ln(),,23u x y x ts y t s =+==+，求,u us t∂∂∂∂；34.求曲面222x z y =-在点（2，-1,1）地切平面和法线；五、证明题（请写出必要地步骤或过程，每题9分，共18分）35.证明函数项级数20sin 1n nxn∞=+∑在R 一致收敛；36.证明方程(,)0x y F x y xy e e =+-=在点x=0地某邻域内确定一个隐函数()y x ϕ=，并求'()x ϕ版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.b5E2R。

数学分析第三学期期末复习卷两套卷五卷六卷五一、选择题（每小题3分，共15分）1．设函数⎪⎩⎪⎨⎧=≠+=)0,0(),(0)0,0(),(),(263y x y x y x y x y x f ，则它在点 (0, 0) 处是（ ）(A) 连续的； (B) )0,0(),(lim )0,0(),(f y x f y x ≠→(C) 二重极限不存在； (D)),(lim)0,0(),(y x f y x →存在，但)0,0(f 不存在2．),(y x f z =在点),(00y x 处的偏导数x z ∂∂及yz∂∂存在且连续是),(y x f 在该点可微的（ ）(A) 充分条件； (B) 必要条件； (C) 充要条件； (D) 以上都不是 3．设22z xy u -=，则u 在点 ( 2, -1, 1 ) 处的方向导数的最大值为（ ） (A) 62 (B) 4 (C) (-2, -4, -2) (D) 6 4．设233y x x z +-=，则它在点 (1, 0) （ ） (A) 取得极大值； (B) 不取得极值；(C) 取得极小值； (D) 不能确定是否取得极值 5．设有空间区域}0,|),,({22221≥≤++=z R z y x z y x V ，}0,0,0,|),,({22222≥≥≥≤++=z y x R z y x z y x V ，则有 (A) ⎰⎰⎰⎰⎰⎰=214V V dv x dv x (B) ⎰⎰⎰⎰⎰⎰=214V V dv y dv y(C)⎰⎰⎰⎰⎰⎰=214V V dv z dv z (D) ⎰⎰⎰⎰⎰⎰=214V V dv xyz dv xyz二、填空（每空2分，共20分） 1．设}2|{2<=x x E ，则 =E sup ；=E inf ；E 的聚点是 。

2．若0),(≠=∂∂a a a y f ，则=--→ax a a f a x f a x ),(),(lim3．设V 是锥面22y x z +=与平面1=z 围成的区域，在直角坐标系下将 下列积分化为三次积分=⎰⎰⎰Vdxdydzz y x f ),,(4．设V 是锥面22y x z +=与平面1=z 围成的区域，将下列积分化为柱面 坐标变换的三次积分=⎰⎰⎰Vdxdydzz y x f ),,(5．设V 是锥面22y x z +=与平面1=z 围成的区域，将下列积分化为球坐标变换的三次积分=⎰⎰⎰Vdxdydzz y x f ),,(6．S 为球面1222=++z y x ，外侧为正侧，则=⎰⎰Sdxdy ；7．设S 为球面1222=++z y x ，则=++⎰⎰SdS z y x )(222 ；8．第二类曲面积分⎰⎰++Sdxdy R dzdx Q dydz P 化成第一类曲面积分是其中γβα,,为有向曲面S 在点 (x , y , z ) 处的 方向角.三、求偏导数或全微分（共15分） 1．（5分）求函数 0)()()(>=x f x f z y g 的全微分。

运城学院应用数学系2008—2009学年第一学期期末考试《数学分析Ⅲ》试题（B ）适用范围：数学与应用数学专业 0701、0702班 命题人：王文娟，王莲花信息与计算科学专业 0703班 审核人：一、单选题（每题2分，共10分）1、设(,)ln(f x y x =-，(0,0)x y >>其中则(,)f x y x y +-=（ ）A 、ln()x y -B 、C 、1(ln ln )2x y - D 、2ln()x y - 2、(,)z f x y =在00(,)x y 处不连续，则(,)f x y 在该点处 （ ）A 、必无定义B 、极限必不存在C 、偏导数不存在D 、必不可微3、若(,)f x y 与(,)g x y 在曲线L 上满足(,)(,)f x y g x y ≤，则下列说法中成立的是（ ）A 、(,)(,)LL f x y dx g x y dx ≤⎰⎰B 、|(,)(,)||(,)||(,)|L L L L f x y dx g x y dy f x y dx g x y dy +≤+⎰⎰⎰⎰C 、(,)(,)L L f x y ds g x y ds ≤⎰⎰D 、A 、B 、C 都不对4、设域22:1,D x y +≤f 是D上的连续函数，则Df dxdy =⎰⎰（ ）A 、102()r f r dr π⎰B 、104()r f r dr π⎰ C 、1202()f r dr π⎰ D 、04()r r f r dr π⎰ 5、设2()f x x =在[1,1]-的傅立叶级数是22114(1)cos 3nn n x n ππ∞=-+∑，该级数的和函数是()s x ，则（ ）A 、(1)1,(2)4s s ==B 、 1(1),(2)42s s == C 、1(1),(2)02s s == D 、(1)1,(2)0s s == 二、判断题（每题2分，共10分）1、若(,)f x y 在00(,)x y 的两个累次极限00lim lim (,)x x y y f x y →→与00lim lim (,)y y x x f x y →→都存在且相等,则二重极限也必存在. （ ）2、有界的无限点列{}2n P R ⊂必存在收敛子列{}nk P . （ ）3、如果曲面:(,)S z f x y =在000(,,)Q x y z 存在切平面，则(,)z f x y =在000(,)P x y 处可微. （ ）4、若(,)f x y 在点(,)x y 处二阶偏导(,)xy f x y 及(,)yx f x y 都存在, 则(,)xy f x y 与(,)yx f x y 在点(,)x y 处连续的充要条件是(,)(,)xy yx f x y f x y =. （ ）5、若(,)f x y 在有界闭区域D 上连续,且(,)0f x y >,则(,)0Df x y dxdy >⎰⎰.（ ）三、填空题（每空2分，共10分）1、4422(,)4f x y x y x y =+-, 则(1,1)|df =____________2、22(,)(0,0)1lim ()sin x y x y x y→+=+ ____________ 3、L 是按逆时针方向绕行圆域:221(1)(1)4x y -+-=,则22L xdy ydx x y -=+⎰ _________4、改变累次积分的顺序220(,)y dy f x y dx =⎰⎰ 5、1210lim (1)x dx ααα→+=⎰________________ 四、解下列各题（每题6分，共36分）1、 xyzu e =, 求3u x y z ∂∂∂∂ 2、22260()0x y z y z x y z ⎧++-=⎪≠⎨⎪++=⎩, 求dz dx ,dy dx3、设2222(2)(2)du x xy y dx x xy y dy =+-+--，求函数(,)u x y4、计算VI zdxdydz =⎰⎰⎰,其中V 由上半球面2224x y z ++=与0z =所围成.5、计算dxdy xz y dzdx x dydz z x y S)()(22+++-⎰⎰,其中S 是边长为a 的正立方体表面并取外侧.6、计算2()LI xydx x y dy x dz =+-+⎰.其中L 是螺旋线cos ,x t =sin ,y t z t ==从0t =到t π=上的一段.五、应用题（每题7分，共21分）1、用钢板制造容积为V 的无盖长方形水箱,问怎样选择水箱的长、宽、高才最省钢板.2、求arctany z x =在(1,1,)4π处的切平面与法线方程.3、求密度函数为(,)1x y x y μ=--的平面薄板D 的质量，其中D 是xy 平面上0,0,1x y x y ==+=所围.六、证明题（共13分）1、(6分) 证明:230cos (110)t tx dx t x t+∞≤≤+⎰是一致收敛的. 2、(7分) 证明:222222(0(,)00x y x y f x y x y ⎧++≠⎪=⎨⎪+=⎩在点(0,0)处连续、偏导数存在且可微.。

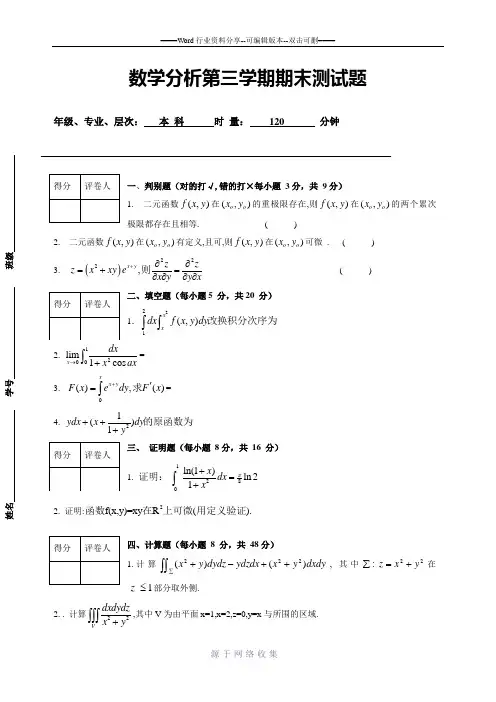
数学分析第三学期期末测试题年级、专业、层次： 本 科 时 量： 120 分钟一、判别题（对的打√,错的打×每小题 3分，共 9分） 1. 二元函数(,)f x y 在(,)o o x y 的重极限存在,则(,)f x y 在(,)o o x y 的两个累次极限都存在且相等. ( ) 2. 二元函数(,)f x y 在(,)o o x y 有定义,且可,则(,)f x y 在(,)o o x y 可微 . ( ) 3. ()222,x y z z z x xy e x y y x +∂∂=+=∂∂∂∂则 ( ) 二、填空题（每小题5 分，共20 分） 1．221(,)______________x x dx f x y dy ⎰⎰改换积分次序为 2. 1200lim 1cos x dx x ax →+⎰=_____________ 3. 0 (),()x x y F x e dy F x +'=⎰求=_____________ 4. 21()__________1ydx x dy y +++的原函数为 三、 证明题（每小题 8分，共 16 分） 1. 证明：1820ln(1)ln 21x dx x π+=+⎰ 2. 证明:2f(x,y)=xy R ().函数在上可微用定义验证四、计算题（每小题 8 分，共 48分） 1.计算⎰⎰∑++-+dxdy y x ydzdx dydz y x )()(222, 其中22:y x z +=∑在1≤z 部分取外侧.2. . 计算22Vdxdydz x y +⎰⎰⎰,其中V 为由平面x=1,x=2,z=0,y=x 与所围的区域.3. 改变下列积分的积分次序⎰⎰--22933),(x x dy y x f dx 4.求(L ln ,y xy x dy ⎡⎤+++⎢⎥⎣⎦其中L 为曲线sin ,0y x x π=≤≤与直线段0,0y x π=≤≤围区域D 的正向边界,. 5. (,)y w g x x =，求：)1,1(22x w ∂∂ 6. 2211441x y z z x y -+=+==-求在某点与垂直的切平面方程.五、讨论题（每小题 7 分，共 7分） (,,),1.f x y z xy x y =+=讨论在条件的极值。

一、填空题(每空3分，共24分)1、 设z x u ytan =，则全微分=u d __________________________。

2、 设32z xy u =，其中),(y x f z =是由xyz z y x 3333=++所确定的隐函数，则=x u _________________________。

3、 椭球面14222=-+z y x 在点)1,1,2(M 处的法线方程是__________________。

4、 设,d ),()(sin 2y y x f x F xx⎰=),(y x f 有连续偏导数，则=')(x F __________________。

5、 设L 是从点(0,0)到点(1,1)的直线段，则第一型曲线积分⎰=Ls x yd _____________。

6、 在xy 面上，若圆{}122≤+=y x y x D |),(的密度函数为1),(=y x ρ，则该圆关于原点的转动惯量的二重积分表达式为_______________，其值为_____________。

7、 设S 是球面1222=++z y x 的外侧，则第二型曲面积分=⎰⎰dxdy z S2_______。

二、计算题(每题8分，共56分) 1、 讨论yx y x y x f 1sin 1sin )(),(-=在原点的累次极限、重极限及在R 2上的连续性。

2、 设),(2xy y x f u =具有连续的二阶偏导数，求二阶偏导数xx u 和xy u 。

3、 求22333),(y x x y x f --=在}16|),{(22≤+=y x y x D 上的最大值和最小值。

4、 求x x x e x xd sin e2⎰∞+---。

提示：C bx b bx a ba e x bx e ax ax+-+=⎰)cos sin (d sin 22。

5、 利用坐标变换求⎰⎰+-Dy x yx yx d d sec2，其中D 由1=+y x ，0=x 及0=y 围成。

2021-2022年度大学期末考试试卷 《数学分析三》大学考试试题B 卷及参考答案一、单项选择题（从给出的四个答案中，选出一个最恰当的答案填入括号内，每小题2分，共20分）1、 函数)(x f 在[a,b ]上可积的必要条件是（ ） A 连续 B 有界 C 无间断点 D 有原函数2、函数)(x f 是奇函数，且在[-a,a ]上可积，则（ ） A ⎰⎰=-a aa dx x f dx x f 0)(2)( B 0)(=⎰-aa dx x fC⎰⎰-=-aaadx x f dx x f 0)(2)( D )(2)(a f dx x f aa=⎰-3、 下列广义积分中，收敛的积分是（ ） A⎰11dx xB⎰∞+11dx xC⎰+∞sin xdx D⎰-1131dx x4、级数∑∞=1n na收敛是∑∞=1n na部分和有界且0lim =∞→n n a 的（ ）A 充分条件B 必要条件C 充分必要条件D 无关条件 5、下列说法正确的是（ ） A∑∞=1n na和∑∞=1n nb收敛，∑∞=1n nn ba 也收敛 B∑∞=1n na和∑∞=1n nb发散，∑∞=+1)(n n nb a发散C∑∞=1n na收敛和∑∞=1n nb发散，∑∞=+1)(n n nb a发散 D ∑∞=1n n a 收敛和∑∞=1n n b 发散，∑∞=1n nn ba 发散6、)(1x an n∑∞=在[a ，b ]收敛于a （x ），且a n （x ）可导，则（ ）A)()('1'x a x an n=∑∞= B a （x ）可导C⎰∑⎰=∞=ban ban dx x a dx x a )()(1D∑∞=1)(n nx a一致收敛，则a （x ）必连续7、下列命题正确的是（ ） A)(1x an n∑∞=在[a ，b ]绝对收敛必一致收敛B)(1x an n∑∞=在[a ，b ] 一致收敛必绝对收敛C 若0|)(|lim =∞→x a n n ，则)(1x an n∑∞=在[a ，b ]必绝对收敛D)(1x an n∑∞=在[a ，b ] 条件收敛必收敛8、∑∞=++-012121)1(n n nx n 的和函数为 A xe B x sin C )1ln(x + D x cos9、函数)ln(y x z +=的定义域是（ ） A {}0,0|),(>>y x y x B {}x y y x ->|),( C {}0|),(>+y x y x D {}0|),(≠+y x y x 10、函数f (x,y )在（x 0,,y 0）偏可导与可微的关系（ ） A 可导必可微 B 可导必不可微 C 可微必可导 D 可微不一定可导二、计算题：（每小题6分，共30分） 1、⎰=914)(dx x f ，求⎰+22)12(dx x xf2、计算⎰∞++02221dx xx 3、计算∑∞=11n nx n 的和函数并求∑∞=-1)1(n n n4、设023=+-y xz z ，求)1,1,1(xz ∂∂5、求2220lim yx yx y x +→→ 三、讨论与验证题：（每小题10分，共20分）1、 讨论⎪⎩⎪⎨⎧=≠+-=)0,0(),(0)0,0(),(),(2222y x y x y x y x xyy x f 在（0，0）点的二阶混合偏导数2、 讨论∑∞=+-221sin 2)1(n n n n nx的敛散性 四、证明题：（每小题10分，共30分）1、设)(1x f 在[a ，b ]上Riemann 可积，),2,1()()(1 ==⎰+n dx x f x f ban n ，证明函数列)}({x f n 在[a ，b ]上一致收敛于02、设yx e z =，证明它满足方程0=∂∂+∂∂yz y x z x 3、 设)(x f 在[a ，b ]连续，证明⎰⎰=πππ)(sin 2)(sin dx x f dx x xf ，并求⎰+π2cos 1sin dx xxx参考答案一、1、B 2、B3、A4、C5、C6、D7、D8、C9、C10、C 二、1、⎰⎰++=+202222)12()12(21)12(x d x f dx x xf （3分）令122+=x u ，⎰⎰==+91222)(21)12(du u f dx x xf （3分）2、⎰∞++02221dxx x =4)1arctan(lim )1()1(11lim 002π=+=+++∞→∞→⎰A A A A x x d x （6分） 3、解：令)(x f =∑∞=11n n x n ，由于级数的收敛域)1,1[-（2分），)('x f =x x n n -=∑∞=-1111，)(x f =)1ln(110x dt t x-=-⎰（2分），令1-=x ，得2ln )1(1=-∑∞=n n n 4、解：两边对x 求导02232=--x x xz z z z （3分）x z z z x 2322-=（2分）2)1,1,1(=∂∂x z（1分）5、解：x yx yx ≤+≤||0222（5分）0lim 22200=+→→y x y x y x （1分）由于x =-2，x =2时，级数均不收敛，所以收敛域为（-2，2）（3分）三、1、解、⎪⎩⎪⎨⎧=+≠++-+=000)(4),(22222222224y x y x y x y y x x yy x f x （2分）⎪⎩⎪⎨⎧=+≠++--=000)(4),(22222222224y x y x y x y y x x xy x f y (4分）1)0,0(),0(lim )0,0(02-=∆-∆=∂∂∂→∆y f y f x y zx x y1)0,0()0,(lim )0,0(02=∆-∆=∂∂∂→∆xf x f y x zy y x （6分）2、解：由于x nx n n n n n 221sin 2|sin 2)1(|lim =-+∞→（3分），即1sin 22<x 级数绝对收敛1sin 22=x 条件收敛，1sin 22>x 级数发散（7分）所以原级数发散（2分）四、证明题（每小题10分，共20分）1、证明：因为)(1x f 在[a ，b ]上可积，故在[a ，b ]上有界，即0>∃M ，使得]),[()(1b a x M x f ∈∀≤，（3分）从而)(|)(|)(12a x M dt t f x f xa-≤≤⎰一般来说，若对n 有)!1()()(1--≤-n a x M x f n n （5分）则)()!1()()(1∞→--≤-n n a b M x f n n ，所以)}({x f n 在[a ，b ]上一致收敛于0（2分）⎰⎰⎰=+++=+aa Ta Tdt t f T t d T t f t T x dx x f 0)()()()(（2）（4分）将式（2）代入（1）得证（2分）2、 y e x z y x 1=∂∂，2y x e y zy x -=∂∂，（7分）则012=-=∂∂+∂∂yx ye y xe y z y x z x y xy x （3分） 3、 证明：令t x -=π⎰⎰⎰⎰-=---=πππππππ0)(sin )(sin ))(sin()()(sin dt t tf dt t f dt t f t dx x xf 得证（7分）8cos 1sin 2cos 1sin 20202ππππ=+=+⎰⎰dx xx dx x x x （3分）。