当前位置：文档之家 › 作业2拉压

作业2拉压

  • 格式：ppt
  • 大小：240.50 KB
  • 文档页数：12

下载文档原格式

  / 12

合集下载

【材力】2拉压变形(1)

【材力】2拉压变形(1)
例题 作图示杆件的轴力图，并求1-1、2-2、3-3截面的应力。
1 f 30
60kN 2 f 20 40kN 3 f 35 30kN 50kN
FN1 0 FN 2 60 kN FN 3 50 kN
FN1 0 A1
1
2
60
3 50 20
kN
FN图
1
+
FN 2 60 10 3 4 2 191MPa A2 (20 10 3 ) 2 FN 3 50 10 3 4 3 52 MPa 3 2 A3 (35 10 )
x+dx A B' x
d x d d x x lim x 0 x dx
材料力学
河南城建学院土木工程系力学教研室 §2-4 轴向拉伸或压缩时的变形
d1
F
2、横向变形 l l1
d
F
横向绝对变形 横向线应变
d d1 - d
d d
材料力学
河南城建学院土木工程系力学教研室 §2-4 轴向拉伸或压缩时的变形
F FN A A
FN：横截面上的轴力 A：横截面面积
拉应力为正，压 应力为负。
对于等直杆：
当有多段轴力时，最大轴力所对应的 截面-----危险截面。
危险截面上的正应力----最大工作应力
材料力学 max
A
FN,max
河南城建学Leabharlann 土木工程系力学教研室3、拉压杆斜截面上的应力
河南城建学院土木工程系力学教研室 §2-4 轴向拉伸或压缩时的变形
1、纵向变形 当杆件因荷载或截面尺寸变化的原 因而发生不均匀变形时，不能用总长度内的平均线 应变代替各点处的纵向线应变。 y x截面处沿x方向的纵向平 d x 均线应变为 C x O x截面处沿x方向的纵向线应 x z A x B 变为

材料力学习题册答案-第2章-拉压

材料力学习题册答案-第2章-拉压
第二章 轴向拉压
一、 选择题
1．图 1 所示拉杆的外表面上有一斜线，当拉杆变形时，斜线将（
A.平动
B.转动
C.不动
D.平动加转动
D）
2．轴向拉伸细长杆件如图 2 所示,则正确的说法是 （ C ）
A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C. 1-1 面上应力非均匀分布，2-2 面上应力均匀分布 D.1-1 面上应力均匀分布，2-2 面上应力非均匀分布
30KN 1
300mm
l1 解：(1) 轴力图如下
2
400mm
l2
10KN
-
40KN
50KN 3
400mm
l3
10KN
+
10KN
（2）
(3)右端面的位移
=
= 即右端面向左移动 0.204mm。
8.一杆系结构如图所示，试作图表示节点 C 的垂直位移，设 EA 为常数。
A
30
C
30 ΔL2 60 ΔL1
CD 段：σ3＝ ＝
Pa＝25MPa
2.图为变截面圆钢杆 ABCD，已知 =20KN， = =35KN， = =300mm， =400mm,
D
3
C
P3
2
，绘出轴力图并求杆的最大最小应力。
B
1 P2
A
P1
l3 解：
-
50KN
l2 15KN
l1
20KN
+
AB 段：σ1＝
＝
＝176.9MPa
BC 段：σ2＝
反力均匀分布，圆柱承受轴向压力 P，则基座剪切面的剪力
。ห้องสมุดไป่ตู้

第2章拉压作业参考解答

第2章拉压作业参考解答

aEADj + 4.5aEADj = 2aF ， Dj = 2F 5.5EA
4. 再由 Hooke 定律：
FN1
=
EADj
=
2F 5.5
=
0.3636F
FN 2
= 1.5EADj
=
1.5´ 2F 5.5
2
（1）图（a）为开槽拉杆，两端受力 F=14kN，b=20mm，b0＝10mm，δ=4mm。 （2）图（b）为阶梯形杆，AB 段杆横截面面积为 80mm2，BC 段杆横截面面积为 20mm2， CD 段杆横截面面积为 120mm2。 （3）图（c）为变截面拉杆，上段 AB 的横截面面积为 40mm2，下段 BC 的横截面面积为
DG
=
Dl2
-
2 3
Dl1
-
1 3
Dl3＝6.89 ´10-4
m
5
2-15 求附图示圆锥形杆在轴向力 F 作用下的伸长量。弹性模量为 E。
解答 对于截面缓变的圆锥形杆可假设横截面上正应力均匀分布。横截面面积为
A(x)
=
1 4
p [d1l
-
(d1
-
d2 )x]2
/l2
ò ò ò Dl =
l
edx =
FN1
FN3
FN2
D
(2)
（b） 整体分析，示力图见附图（3）。
å M Ai = 0 : FN1 ´1 + 3´ 3´1.5 = 0
FN1 = -13.5kN
FAx A
FAy FN1
B
s1
=
FN 1 A1
=
-13.5 ´103 850 ´10-6
=
-15.88MPa

第二章拉压(1)

第二章拉压(1)
7来自AC1kN
B
x
李禄昌 例2-2 求图示杆各截面上的轴力
解：
N 1 = 10 kN
A
B
C
D
N 2 = 10 − 15 = −5kN
N 3 = −20 kN
N 注意确定控制面。 注意确定控制面。
10KN ㈩
x
5KN ㈠ 20KN
8
李禄昌
5、绘制轴力图的方法与步骤如下： 、绘制轴力图的方法与步骤如下： ⑴、确定作用在杆件上的外载荷与约束力； 确定作用在杆件上的外载荷与约束力； ⑵、根据杆件上作用的载荷以及约束力，确定控制 根据杆件上作用的载荷以及约束力，确定控制 确定轴力图的分段点： 轴力图的分段点 面，确定轴力图的分段点：在有集中力作用处即为 轴力图的分段点； 轴力图的分段点； 应用截面法， 用假想截面从控制面之间 从控制面之间将杆 ⑶ 、 应用截面法 ， 用假想截面 从控制面之间 将杆 件截开， 在截开的截面上， 画出未知轴力， 并假设 件截开 ， 在截开的截面上 ， 画出未知轴力， 为正方向； 对截开的部分杆件建立平衡方程， 为正方向 ； 对截开的部分杆件建立平衡方程 ， 确定 轴力的大小与正负 ； 坐标系， ⑷、建立FN－x坐标系，将所求得的轴力值标在坐 标系中，画出轴力图。 标系中，画出轴力图。
问题：直杆上作用有 个载荷 而且AB段与 个载荷， 段与BC段杆横截面面积 问题：直杆上作用有4个载荷，而且 段与 段杆横截面面积 不相等，材料不同。各段杆的横截面上的轴力如何分布？哪个横 不相等，材料不同。各段杆的横截面上的轴力如何分布？ 截面上的正应力最大？哪个横截面上承载能力最差、最危险？ 截面上的正应力最大？哪个横截面上承载能力最差、最危险？
6
李禄昌 设一杆轴线同时受力P 的作用， 例2-1 设一杆轴线同时受力 1 , P2 , P3 的作用，其作用点分别为 A、C、B , 求杆的轴力画轴力图。 求杆的轴力画轴力图。 P2=3kN 只计算内力时， 只计算内力时，不 P1=2kN P3=1kN 设正法与绘内力图 考虑面积影响， 实际集中力并非 考虑面积影响，故 A B 有机结合起来。 有机结合起来。 C 集中在一点处。 用等直杆件。 集中在一点处 用等直杆件。 。

建筑力学-作业2

建筑力学-作业2

一、单项选择题（每小题2分，共20分）题目11．两根材料不同、截面面积不同的杆件，在相同轴向外力作用下，轴力是（）。

选择一项：A. 不相等B. 可能相等C. 可能不相等D. 相等题目22．胡克定律应用的条件是（）。

选择一项：A. 只适用于塑性材料B. 只适用于轴向拉伸C. 应力不超过屈服极限D. 应力不超过比例极限题目33．工程上习惯将EA称为杆件截面的（）。

选择一项：A. 抗拉刚度B. 抗弯刚度C. 抗剪刚度D. 抗扭刚度题目44．低碳钢的拉伸过程中，（）阶段的特点是应力几乎不变。

选择一项：A. 颈缩B. 弹性C. 强化D. 屈服题目55．低碳钢的拉伸过程中，（）阶段的特点是应力与应变成正比。

选择一项：A. 屈服B. 颈缩C. 弹性D. 强化题目66．低碳钢的拉伸过程中，胡克定律在（）范围内成立。

选择一项：A. 弹性阶段B. 强化阶段C. 屈服阶段D. 颈缩阶段题目77．低碳钢材料在拉伸试验过程中，所能承受的最大应力是（）。

选择一项：A. 强度极限σbB. 屈服极限σsC. 比例极限σpD. 许用应力[σ]题目88．直径为D的圆形截面，则其对形心轴的惯性矩为（）。

选择一项：C题目99．构件抵抗变形的能力称为（）。

选择一项：A. 极限强度B. 强度C. 刚度D. 稳定性题目1010．构件抵抗破坏的能力称为（）。

选择一项：A. 稳定性B. 强度C. 刚度D. 极限强度二、判断题（每小题2分，共20分）题目111．杆件变形的基本形式有轴向拉伸与压缩、剪切、扭转和弯曲四种。

选择一项：对错题目122．轴向拉伸（压缩）时与轴线相重合的内力称为剪力。

选择一项：对错题目133．梁的正应力是由剪力引起的。

选择一项：对错题目144．轴向拉伸（压缩）的正应力大小和轴力的大小成正比。

选择一项：对错题目155．任意平面图形对某轴的惯性矩一定大于零。

选择一项：对错题目166．平面图形对所有平行轴的惯性矩中，其对其形心轴的惯性矩为最大。

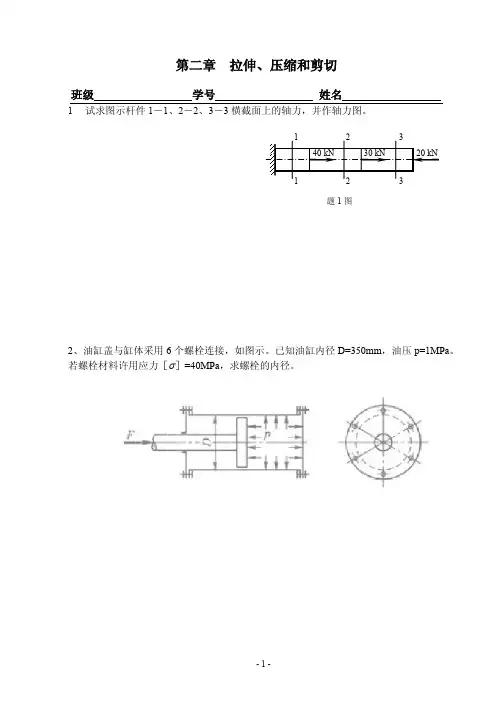
材料力学-第二章 拉压与剪切

材料力学-第二章 拉压与剪切

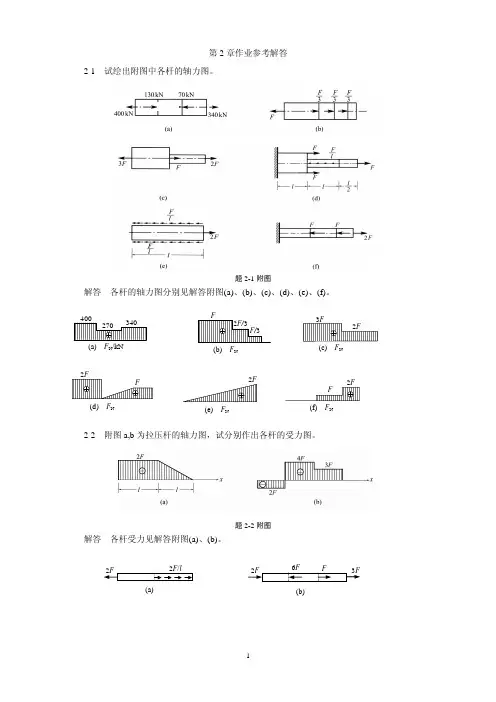
班级 学号 姓名1 试求图示杆件1－1、2－2、3－3横截面上的轴力，并作轴力图。

2、油缸盖与缸体采用6个螺栓连接，如图示。

已知油缸内径D=350mm ，油压p=1MPa 。

若螺栓材料许用应力［ ］=40MPa ，求螺栓的内径。

题1图140 kN 30 kN20 kN122 33班级 学号 姓名3 图示木制桁架受水平力P 作用。

已知P=80kN[][]MPa MPa 10,8==压拉σσ，试设计AB 、AD 两杆的横截面积。

4 图示结构，杆1、2的横截面均为圆形，直径分别为d 1=30mm , d 2=20mm 。

两杆材料相同，许用应力[σ]=160MPa ，在节点A 处受铅直力P=80kN 。

试校核结构的强度。

A B C D P60° 60° 30° 30°BC A P 12 30° 45°班级学号 姓名5、某铣床工作台进给油缸如图示，缸内油压p=2MPa ，油缸内径D=75mm ，活塞杆直径 d=18mm 。

已知活塞材料的许用应力［σ］=50MPa ，试校核活塞杆的强度。

6、简易吊车如图所示。

AB 为木杆，横截面积 21cm 100=A ，许用压应力[]MPa 71=σ。

BC 为钢杆，横截面积22cm 6=A ，许用拉应力[]MPa 1602=σ。

试求许可吊重F 。

F30°AB C木杆 钢杆第二章 拉伸、压缩和剪切班级 学号 姓名7、 图示拉杆沿斜截面m －m 由两部分胶合而成。

设在胶合面上许用拉应力[]MPa 100=σ，许用切应力[]MPa 50=τ，并设胶合面的强度控制杆件的拉力。

试问：为使杆件承受最大拉力F ，α角的值应为多少？若杆件横截面面积为4cm 2，并规定α≤60°，试确定许可载荷F 。

8、变截面杆如图所示。

已知：21cm 8=A ，22cm 4=A ， GPa 200=E 。

试求杆的总伸长l ∆。

材料力学2-2拉压静不定

材料力学2-2拉压静不定
1
ቤተ መጻሕፍቲ ባይዱ
7）组合体伸长： 6）应力： （压） （拉）
作业： P73
P81
2.43
2.47
P81
2.48
九、应力集中的概念
P
P 0 A
P
max
P
P
P
P
理论应力集中系数：k
max 0
习 题 课
例题1：图示构架，两杆的材料相同，其横截面面积之 比为A1：A2=2：3，承受载荷为P，试求： 1)为使两杆内的应力相等,夹角应为多大? 2)若P=10kN，A1=100mm2，则杆内的应力为多大?
0.06 10 3 L1 0 .1 L2 0 .3
作业：
P82 2.51
P84 2.53
soc
1
L

1L 3L soc , 3L
)2 ( 0 soc 1 N 2 3 N，0 Y )1(
2
已知三杆的EA相同，3杆制造短了长度， 若将三杆用铰A装配，试求装配后各杆的受力。
解： 1）平衡方程
2）装配后的变形几何关系(变形图)
3
L N L 1N soc 3 A 3E soc 1A 1E
3
L N 3L 3 N , 1 1 1L 3L A A 3E 1 1E
3
soc 3L 2L 1L
2)变形几何关系、变形图：
3)物理关系：
5)联立求解：
4)补充方程：
3. 静不定问题特征： 1）各杆的受力与刚度有关； 2）静不定问题可能产生初应力或温度应力。
tAE R tE B t A A
例1： D1=45mm，t = 3mm，d2=30mm，E1=210GPa， 1=1210 -61/oC， E2=110GPa， 2=16 10 - 61/oC， t从30o升高至180o（30o为装配时温度），求钢管和铜 杆内的应力以及组合体的伸长。 解：1）

建筑力学形成性考核作业2

建筑力学形成性考核作业2

一、选择题1．D 2．C 3．B 4．D 5．A 6．C 7．B 8．B 9．D 10．C二、填空题1．轴向拉压、剪切、扭转和弯曲。

2．扭矩 M n 扭矩矢量指向与截面外法线一致 3．杆件轴线方向4．剪力 弯矩 5．零杆6．水平直 斜直 7．斜直 抛物 8．剪力 集中力 9．弯矩 集中力偶 10．弯矩三、计算题1．解：（1）用1-1截面将杆截开，保留左段，受力如图：由xF=0∑ N1F 2F =0- N1F 2F()=拉再用2-2截面将杆截开，保留左段，受力如图： 由xF=0∑ N2F 2F+2F =0-N2F =0最后用3-3截面将杆截开，保留左段，受力如图： 由xF=0∑ N3F 2F+2F F =0-- N3F =F （拉） 作轴力图：2FABD∙∙C2FF1 122332F A1 1F N12FAB∙2F22F N22FAB∙∙C2F F33F N32F F N 图⊕⊕F（2）用1-1截面将杆截开，保留左段，受力如图： 由xF=0∑ N1F 10=0-N1F 10kN()=拉再用2-2截面将杆截开，保留左段，受力如图：由xF=0∑ N2F 10+30=0- N2F 20kN()=-压最后用3-3截面将杆截开，保留右段，受力如图： 由xF=0∑ N3F 40=0-- N3F =40kN()-压 作轴力图：10kNABD∙∙C1 1 22 3320kN30kN40kN10kN A1 1F N110kNAB∙22F N230kND 3340kNF N310F N 图（kN ）⊕Ө2040（3）用1-1截面将杆截开，保留右段，受力如图： 由x F =0∑ N1F 604010=0-++- N1F =90kN()拉再用2-2截面将杆截开，保留右段，受力如图：由xF=0∑ N2F 4010=0-+- N2F =30kN()拉最后用3-3截面将杆截开，保留右段，受力如图： 由xF=0∑ N3F 10=0-- N3F =10kN()-压作轴力图：2．解：（1）求支座反力， 由AM=0∑ B F 440220420-⨯-⨯⨯= B F 60k N ()=↑ 由xF=0∑ Ax F 400+= Ax F 40kN()=-←ABD∙∙C60kN1 1 223310kN 40kNBD∙∙C60kN1 110kN 40kNF N1 D∙C2210kN 40kN F N2D33 10kN F N390 F N 图（kN ） ⊕Ө3010由yF=0∑ Ay F 602040+-⨯= Ay F 20kN()=↑分别作出AC 、CD 、DB 各段受力平衡图如下：作F Q 图、M 图、F N 图如下：40kN C 20kN/m2m 2m4mA DB 40kN AC40kN20kN20kN 80kN/m C20kN/mD20kN 80kN/m60kN B D60kN60kNC A DB ⊕Ө⊕ 20 40 60F Q 图（kN ） C ADB8040M 图（kN ∙m ）8080（2）求支座反力，由力偶的平衡，得：B M F =()l ↑ A M F =()l↓ 作分段平衡受力图：作F Q 图、M 图、F N 图如下：C A DBӨ 20 60 F N 图（kN ） ӨC AB l l M CAM MM l MlM l MlC BMC A B F Q 图 ӨM l C A BM 图 M3．解：（1）求支座反力， 由AM=0∑ B F 485420--⨯⨯= B F 12k N ()=↑ 由yF=0∑ A F 12540+-⨯= A F 8k N ()=↑ 作F Q 图，计算弯矩极值M D ： 由yF=0∑ 85x =0- x =1.6mD M =8 1.65 1.60.8 6.4k N m ⨯-⨯⨯= 作M 图，C A BF N 图M l ⊕ 5kN/mD C8kN ∙mA B4m2m⊕ Ө1.6m8F Q 图（kN ）125kN/m DAM Dx 8kN6.4M 图（kN ∙m ）8（2） B M =4010130k N m -⨯= A M =40104103 1.545kN m -⨯-⨯⨯=-作F Q 图、M 图如下：（3）求支座反力， 由BM=0∑ A F 42020210630--⨯+⨯⨯= -A F 30kN()=↑由yF=0∑ B 30F 106200+-⨯-= B F 50k N ()=↑ 作F Q 图计算弯矩极值M E ： 由y F =0∑ 502010(x 2)0--⨯-=x =5mE M =503205103 1.55kN m ⨯-⨯-⨯⨯= A M =2010210-⨯⨯= B M =20240kN m -⨯=- 作M 图10kNDC 40kN ∙mAB 1m 3m1m10kN/mӨF Q 图（kN ）1040 204045M 图（kN ∙m ）10kN/mDC 20kN ∙mA B4m2m 2m20kN10kN/mECM EB x20kN 50kNӨF Q 图（kN ）1020 Ө2030⊕⊕ 40205M 图（kN ∙m ）4．解：求支座反力，由整体平衡条件，得：yF=0∑ C F F F F 0---= C F 3F ()=↑用Ⅰ-Ⅰ截面将桁架截开，保留右边部分，受力如图：由yF=0∑ N2F sin 45F F+3F 0︒--= N2F 2F()=-压 由DM=0∑ N1F a F a +3F a 0-= N1F 2F()=-压 由xF=0∑ N 1N 2N 3F F c o s 45F 0--︒-= N3F 3F()=拉 由零杆判别法，可知：N4F 0=1 2 3a ABCFDaaa4F FⅠ Ⅰ C DFFF N1 F N2 F N33F。

材力讲稿第2章拉压2.2

材力讲稿第2章拉压2.2

小结与讨论
失效原因的初步分析
第二章 轴向拉伸和压缩
小结与讨论
低碳钢试样拉伸至屈服时，如果试样表面具有足够的 光洁度，将会在试样表面出现与轴线夹角为45º 的花纹，称 为滑移线。通过拉、压杆件斜截面上的应力分析，在与轴 线夹角为45º 的斜截面上切应力取最大值。 因此，可以认为，这种材料的屈服是由于切应力最大 的斜截面相互错动产生滑移，导致应力虽然不增加、但应 变继续增加。 灰铸铁拉伸时，最后将沿横截面断开，显然由于拉应 力拉断的。但是，灰铸铁压缩至破坏时，却是沿着约55º 的 斜截面错动破坏的，而且断口处有明显的由于相互错动引 起的痕迹。这显然不是由于正应力所致，而是与切应力有 关。
第二章 轴向拉伸和压缩
极限应力值－强度指标
条件屈服应力
对于没有明显屈服阶段的塑 性材料，工程上则规定产生0.2 ％塑性应变时的应力值为其屈服 应力，称为材料的条件屈服应力 (offset yield stress)，用σ 0.2表示。
0.2
第二章 轴向拉伸和压缩
极限应力值－强度指标
第二章 轴向拉伸和压缩
弹性力学性能
比例极限与弹性极限
线弹性阶段之后，应力－应变 曲线上有一小段微弯的曲线，这表 示应力超过比例极限以后，应力与 应变不再成正比关系，但是，如果 在这一阶段，卸去试样上的载荷， 试样的变形将随之消失。 这表明这一阶段内的变形都是 弹性变形，因而包括线弹性阶段在 内，统称为弹性阶段。弹性阶段的 应 力 最 高 限 称 为 弹 性 极 限 (elastic limit)，用σ e表示。
压缩时材料的力学行为
第二章 轴向拉伸和压缩
压缩时材料的力学行为
铸铁压缩时的应力一应变曲线，与拉伸时的应 力一应变曲线不同的是，压缩时的强度极限氏却 远远大于拉伸时的数值，通常是拉伸强度极限的4 －5倍。对于拉伸和压缩强度极限不等的材料，拉 伸强度极限和压缩强度极限分别用 bt和 bc 表示。 这种压缩强度极限明显高于拉伸强度极限的脆性 材料，通常用于制作受压构件。

北京交通大学材料力学2拉压剪-课2

北京交通大学材料力学2拉压剪-课2

Fl Δl1 Δ A A A 2 cos 2 EA cos 1.293mm ( )
柯燎亮
北京交通大学工程力学研究所
§2-5 杆件在轴向载荷作用下的强度 设计
北京交通大学工程力学研究所
柯燎亮
一、强度概述
例：三角架结构，已计算出拉杆BD和压杆 CD横截面上的正应力，可能关心的问题：
FP x A
（物理方程、本构方程）
FP---作用在杆件两端的载荷； E----杆材料的弹性模量(与正应力具有相同的单位)； EA--为杆件的抗拉/压刚度;
“＋”---伸长变形；“－”---缩短变形。
北京交通大学工程力学研究所 柯燎亮
FP l Δl EA
l x l
（物理方程）
b1 b
？
max
F N max A
？
柯燎亮
北京交通大学工程力学研究所
三、拉压杆件的强度计算 2、强度设计
当作用在构件或结构上的载荷以及材料的许用应力均为已 知时，计算构件所必需的横截面面积，进而设计出构件横截面 各部分的尺寸。这一类强度问题又称为截面设计或尺寸设计。
F N x1 400 10 3 6 ＝ 160 10 Pa 160 MPa 6 A1 2500 10
FNx 2 －100 10 3 6 ＝ － 40 10 Pa －40 MPa 6 A2 2500 10 FN x 3 200 10 3 6 ＝ 200 10 Pa 200 MPa 6 A3 1000 10
FN3l 200103 300103 -3 Δl3 m 0.12 10 m＝0.12mm 9 6 EA3 20010 250010
Δl Δl i 0.24－0.06 0.12 mm＝0.3mm

《建筑力学》第二次作业及答案

《建筑力学》第二次作业及答案

(60分及格就行)一、单项选择题。

本大题共20个小题，每小题2.0 分，共40.0分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.杆拉压变形中横截面上应力均布的结论是从（）假设得到的：A.各向同性B.小变形C.平面D.单向受力2.弹性极限，比例极限，屈服极限和强度极限中最小的是（）：A.弹性极限B.比例极限C.屈服极限D.强度极限3.弹性极限，比例极限，屈服极限和强度极限中最小的是（）：A.弹性极限B.比例极限C.屈服极限D.强度极限4.如果一个材料的拉伸强度和压缩强度相差较大,说明这个材料可能是（）：A.弹性材料B.塑性材料C.脆性材料D.不能确定5.拉压杆的强度公式不能用于解决哪个问题（）：A.强度校核B.截面尺寸设计C.受力分析D.确定许用载荷6.在杆件的拉压实验中，如果断口呈45度左右倾斜，则材料应该是（）：A.弹性材料B.塑性材料C.脆性材料D.不能确定7.名义剪应力和名义挤压应力中“名义”二字的含义指（）：A.最大B.最小C.精确D.近似8.在连接件的近似计算中，通常考虑剪切强度，挤压强度和（）：A.弯曲强度B.板的拉伸强度C.屈服强度D.极限强度9.圆轴逆时针方向旋转时，横截面45度角分线上某点的剪应力与x轴正向（假设水平向右）之间的夹角为（）：A.45度B.90度C.135度D.0度10.电动机功率为200KW，转速为100转/分，则其输出扭矩为（）：A.19.1NmB.19.1kNmC.4.774NmD.4.774kNm11.在外载荷及梁横截面面积不变的前提下，若将截面从圆形改成矩形，则梁的最大剪应力从8MPa变为（）：A.7MPaB.8MPaC.9MPaD.10MPa12.在梁的弯曲应力分析中，通常以（）作为设计截面尺寸的依据：A.剪应力B.正应力C.最大弯矩D.最小弯矩13.欧拉公式中的惯性矩是指横截面的（）惯性矩：A.最小B.最大C.平均D.任意14.在载荷不变的前提下，将悬臂梁的直径由d改为2d，则自由端处的位移是原位移的（）：A.1/4B.1/8C.1/16D.1/3215.悬臂梁在自由端处作用集中力，假设将此力由端部移至悬臂梁的中部，此时自由端的转角是原先的（）：A.1/2B.1/4C.1/8D.1/1616.如果用单位载荷法求结构中某点的水平位移，应在该点施加（）：A.单位力偶矩B.垂直方向的单位载荷C.水平方向的单位载荷D.任意方向的单位载荷17.刚架和梁使用单位载荷法时通常只考虑（）引起的位移：A.轴力B.扭矩C.弯矩D.剪力18.力法方程的基本意义是基本结构在多余未知力和荷载的共同作用下，与原结构多余未知力作用处的（）相同：A.力B.力矩C.支反力D.位移19.在使用图乘法计算力法方程中的系数时，如果一个弯矩图为对称图形,另一个为反对称图形,则系数应该（）：A.为正B.为负C.为零无法计算20.直杆转角位移方程的研究对象都是（）：A.简支梁B.悬臂梁C.静定梁D.超静定梁二、多项选择题。

材料力学第二章+拉压

材料力学第二章+拉压

FN4
20kN
第二章 轴向拉伸和压缩
§2.2 内力计算
40kN A B 300 50
55kN 25kN C 500 D 400
20kN E
FN
(kN) 10
FN1=10kN （拉力） FN2=50kN （拉力） FN3= - 5kN （压力） FN4=20kN （拉力）
+
20
+
5
FNmax 50( kN ) 发生在BC段内任一横截面上
寸。）
第二章 轴向拉伸和压缩 圣维南原理：
§2.3 拉压杆的应力
在静力等效条件下，不同的加载方式只对加载处附近区 域的应力分布有影响，离开加载处较远的部分，其应力分布 并没有显著的差别。
第二章 轴向拉伸和压缩
§2.3 拉压杆的应力
例题2-3 试求此正方 形砖柱由于荷载引起的横 截面上的最大工作应力。 已知F = 50 kN。
FN
O
x
第二章 轴向拉伸和压缩
§2.2 内力计算
例题1
一等直杆其受力情况如图所示， 作杆的轴力图.
40kN A 600 B 300
55kN 25kN C 500 D 400
20kN E
第二章 轴向拉伸和压缩
40kN
§2.2 内力计算
55kN 25kN
300
20kN D 400
E
A
600
B
C
500
§2.2 内力计算
1、截面法
截开 在求内力的截面m-m 处， 假想地将杆截为两部分. 代替 取左部分为研究对象。弃去 右部分。弃去部分对研究对 象的作用，以截开面上的内 m F m FN m
F
m

工程力学作业2

工程力学作业2

A
3 2F
2 2F
1 F
3 l/3
B2
l/3
C l/3 1 D
解：
20kN
20kN
-20kN
D

FN 1l1 EA

FN 2l2 EA

FN 3l3 EA

20103 0.3
2.11011 0.032
0.04m m
BC

FN 2l2 EA

20103 0.3
2.11011 0.032
F
F
解：

F
bl
50103 0.25l
1MPa
a

l

50 103 0.25 1 106

0.2m

200m m
ll
PF b
FP
bs

F ab

50 103 a 0.25

bs
10MPa
50 103 a 0.2510106 0.02m 20mm
Me
T
A
A τA
100
Me
B
CB
O τC τB
解:(1)
max
T
Wp

14 103
0.13
71.3MPa
16


Tl GI p

14103 1
8 1010 0.14

0.0178rad
1.020
32
25
(2)
A B max 71.3MPa
C
A z
B

材料力学(长学时)_2-拉压、剪切

材料力学(长学时)_2-拉压、剪切

第二章 拉伸、压缩与剪切2-1 求图示各杆指定截面的轴力，并作轴力图。

2-2图示杆的横截面面积为A ，弹性模量为E 。

作轴力图，并求杆的最大正应力及伸长。

N(x)=x lP21l l l ∆+∆=∆ =⎰+l 0lEA PxdxEA 2Pl =EAPl.2-3 图示一正方形截面的阶梯形混凝土柱。

设重力加速度g=9.8m/s 2, 混凝土的密度为33m /kg 1004.2⨯=ρ，P=100kN ，许用应力[]MPa 2=σ。

试根据强度条件选择截面宽度a 和b 。

选a ：62233102a4a 8.91004.210100⨯=⨯⨯⨯+⨯ a=0.2283m. 选b:6223233102bb8.91004.242283.08.91004.24101003⨯=⨯⨯⨯+⨯⨯⨯⨯+⨯⨯ b=0.3980m.2-4 图示一面积为100mm ⨯200mm 的矩形截面杆，受拉力P=20kN 的作用，试求：（1）6π=θ的斜截面m-m 上的应力；（2）最大正应力max σ和最大剪应力max τ的大小及其作用面的方位角。

max 3MPa 12.01.01020σ==⨯⨯=σMPa 75.030cos 1o 6=⨯=σπMPa 433.060sin 21o 6==τπ MPa 5.0121045max =⋅=τ=τ.2-5 在图示杆系中，AC 和BC 两杆的材料相同，且抗拉和抗压许用应力相等，同为[]σ。

BC 杆保持水平，长度为l ，AC 杆的长度可随θ角的大小而变。

为使杆系使用的材料最省，试求夹角θ的值。

;sin PN 1θ-= θ=cot P N 2 材料最省时，两杆可同时达到许用应力 [];cot P A 1σθ=[]σθ=sin PA 2 结构的总体积为[]⎪⎪⎭⎫⎝⎛θθθ+⋅σ=+=cos sin cos 1Pl l A l A V 22211 0d dV=θ0cos 2sin 22=θ-θ ∴ o 73.54=θ.2-6 图示一三角架，在结点A 受P 力作用。

材料力学作业及答案

材料力学作业及答案
二、 杆件受力如图所示，计算 BC 段的轴力时分离体的最佳取法是（ ）
【A】
【B】
【C】
【D】 解：正确答案为【D】； 【A】 分离体上不能带有支座，因为支座处的支反力要影响分离体的平衡（如下图所示），
因此必须将支座去除，用相应的支反力取而代之； 【B】 用截面法计算轴力时，不要在集中力作用点上取截面，因为此处的受力比较复杂，
为了保险起见，建议大家用 的公式来计算线应变。从这个公式可以看出，当材料相同的时， E
线应变的变化规律与正应力的变化规律相同，正应力发生变化的截面上，线应变也将发生变化。
三、图示立柱由横截面面积分别为 A 和 2A 的 AB 和 BC 段组成，已知材料的容重为 ，弹性模量为 E，则
解：正确答案为【A】。 [B]问题出在分子上的 3，在用胡克定律计算变形时分子上要用轴力，而不能用杆件上作用的外力。 [C]这是一个常见的错误，很多同学会仿照对变形进行分段累加的算法来计算线应变，要注意变形有累 加意义，即一段杆件的总的变形量等于每个分段变形量的代数和；但是线应变指的是在一个很小的范围 内杆件的变形程度，可以简单地将线应变理解成是属于某个截面的。当一段杆件受力均匀时，这段杆件 各个横截面上的线应变都是相等的，你可以笼统地说这段杆件的线应变是多少，但是当两段杆件的轴力 不同时，只能说两段杆件的线应变个各是多少，而不能把两段杆件的线应变加起来。不要说是两段杆件 的线应变，即便是把两个截面不同的线应变加起来都没有任何力学意义。就像汽车在公路上行驶，在第 一段上是一个速度，在第二段上是另一个速度，显然把这两个速度加起来是没有什么意义的。 [D]当两段杆件的变形程度不同时，不能像本选项那样将两段杆件连在一起，一次性计算线应变，必须 是各算各的。
在材料力学中采用“突变”的形式来处理。在这种处理方式下，这个截面上的轴力 是不确定的，在材料力学中绘制出来的集中力作用截面附近的轴力图，如下图所示， 此时只需要求出集中力作用截面左右两条线代表的轴力值即可，因此，应该在集中 力作用截面的左右两侧取计算截面。，而不要把计算截面取在集中力的作用截面上。

材料力学 第2章_拉压

材料力学 第2章_拉压
解：1． 确定螺栓所受轴力 FN＝FP＝20 kN 2． 计算螺栓横截面上的正应力 FN FP 4 FP 4 20 103 N ＝ ＝ 2 ＝ 2 ＝ ＝113.2MPa 2 2 A πd πd π 15 mm 4 3．许用应力 ＝ S 240 160MPa n 1.5 4．强度校核
FN1 F1 10kN
F
x
0
FN2 F1 F2 10kN
CD段
FN kN
FN3 F4 25kN
x
F
x
0
2.绘制轴力图
返回
例题 2-1 1 B 1 F2 FN1 FN2 F2 FN3
25 10 10
已知 F1=10kN；F2=20kN；
F3=35kN；F4=25kN； 2 C 2 3 D F4 3.用截面一侧外力计算轴力
A A1 l1 l 100% 100% 断面收缩率 A l
式中，l1为断裂后标距长度；A1为断口处最小面积。
≥5%为塑性材料
＜5%为脆性材料
返回
3. 低碳钢拉伸时的主要性能指标

e
b
P
a
c
s
b
f
弹性常数 弹性模量：

o

E tan
泊松比：
返回
4. 卸载定律

d
e
b
f
卸载定律——在卸载过程中， 应力和应变按直线规律变化。 d点卸载后，弹性应变消 失，留下塑性应变。d点的 应变包括两部分：
P
a
o

d g
f h
弹性应变： d ’g

塑性应变： od ’ f点的应变与断后伸长率有何不同？

工程力学作业2拉压

工程力学作业2拉压

FN2 FN3
30°
FN1
60°
A F
两个方程，三个未知数，所以是一次超静定问题。
工程力学电子教案
第七章 拉伸和压缩
12
(2) 画变形关系图，列出变形协调方程；
1
1 2
∆l1 +
3 2
∆l3 = ∆l2
2 3
A
(3) 根据胡克定律，由变形协调方程得补充方程；
FN 1l1 FN 2l2 FN 3l3 ∆l1 = , ∆l2 = , ∆l3 = EA1 EA2 EA3
∆l2 = −0.04 mm
工程力学电子教案
9
7-13 试求图示杆系节点B的位移，已知两杆的横截面面积均为 A=100mm2，且均为钢杆（σp=200MPa，σs=240MPa， C D E=2.0×105MPa）。 解：BD杆的轴力为F，被拉伸，BC 杆的轴力为零。
30°
∆lBD = 0.75mm
A’
代入变形协调条件，得补充方程
1 4 3 FN 1 + 8 FN 3 = 2 FN 2 3
工程力学电子教案
第七章 拉伸和压缩
13
(4) 联立平衡方程和补充方程，解出全部未知力。
− FN 2 cos 30o − FN 3 = 0 FN 1 + FN 2 sin 30o − F = 0
1 4 3 FN 1 + 8 FN 3 = 2 FN 2 3
F
B
3m
A
4m
C
2m
D
工程力学电子教案
4
7-6 结构如图所示，杆件AB，AD均由两根等边角钢组成。已 知材料的许用应力[σ]=170MPa，试为AB，AD杆选择等边角钢 的型号。 B 解：对DE杆作平衡分析知：

2.拉压

2.拉压
以塑性应变02所对应的应力作为名义屈服极限记作0236金属材料压缩时的力学性能比例极限mpa2004000102应变曲线低碳钢拉伸应力应变曲线37bl灰铸铁的拉伸曲线灰铸铁的压缩曲线铸铁抗压性能远远大于抗拉性能断裂面为与轴向大致成45铸铁压缩实验
1
工程实例
2
工程实例
3
大仓货架
4
5
6
埃菲尔铁塔
7
斜 拉 桥
8
9
本章要点
（1）横截面上正应力计算公式 （2）拉压虎克定律 （3）拉压静不定问题求解
重要概念
平面假设、轴力、拉压虎克定律、拉压静不定问题、 应力集中、拉压变形能
10
目录
§2-1. 轴向拉伸和压缩的概念 §2-2. 轴向拉压时横截面上的内力和应力 §2-3. 直杆轴向拉伸或压缩时斜截面上的应力 §2-4. 材料在拉伸和压缩时的力学性能 §2-5. 许用应力, 安全系数, 拉压强度 §2-6. 轴向拉伸或压缩时的变形 §2-7. 直杆轴向拉伸或压缩时的变形能 §2-8. 应力集中的概念
A1——试件拉断后断口处的 最小横截面面积 δ ＜5%—脆性材料
32
δ ≥5%—塑性材料
冷作硬化现象
构件处于强化阶段实施卸载。如卸载后重新加载， 曲线将沿卸载曲线上升。 如对试件预先加载, 使其达到强化阶段, 然后卸载, 当再加载时, 试件的线弹性阶段将增加, 同时其塑性降低。 ——称为冷作硬化现象
29
二. 材料拉伸实验 标准试件（低碳钢、铸铁）
工作段长度 l
do
lo=10do 或 5do
标距 lo
1. 低碳钢 (C≤0.3%) 拉伸实验及力学性能 σ 屈服阶段 σb 颈缩阶段 — 典型的塑性材料 拉 伸 σe σp—比例极限 σs 曲 σp 强化阶段 线 σe—弹性极限
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

12 cm 1cm 11 cm 0 . 5 cm

2

120×10
4
I z I z , 22 a I z ,120 10 ,120 10 I z , 22 a 120 12
7
240
3
220
7
3

3 . 4 10 3 . 176 10 6 . 576 10
F
x F
从轴力图中可以看出，AB段被拉伸，BC段被压缩，CD段被拉伸。 杆端D的水平位移DD为： D D l1 D l 2 D l 3 0 . 04 mm D BC段被压缩，于是B，C两横截面的相对纵向位移DBC即为Dl2。
D l 2 0 . 04 mm
工程力学电子教案
6
7-13：试求图示杆系节点B的位移，已知两杆的横截面面积均为 A=100mm2，且均为钢杆(p=200MPa，s=240MPa， E=2.0×105MPa)。 C D 解：对B点受力分析知BD杆被拉伸，力的 大小等于F。BC杆受力为零。 进而BD杆的轴力为F，BC杆的轴力为零。
2 3
FN 2
D
3
4m
A F
F N 1 35 . 5 kN F N 2 8 . 96 kN F N 3 7 . 76 kN
1 2 3
A
1 177 . 6 MPa 2 29 . 9 MPa 3 19 . 4 MPa
A'
工程力学电子教案
5
7-10：一根等截面直杆如图所示，其直径为d=30mm。已知F=20kN， l=0.9m，E=2.1×105MPa。作轴力图，并求杆端D的水平位移DD以 及B，C两横截面的相对纵向位移DBC。
A 2F B l/3 l/3 2F C l/3 D F
解：首先作出杆件的轴力图。 F
N
F

75 kN 3000 mm 125 kN 3000 mm 100 kN 3000 mm 75 kN 3000 mm
2 2 2 2
25 MPa 41 . 7 MPa 33 . 3 MPa 25 MPa
FAC
BC
AC
可得：F
N , AC
100 kN ,
F N , CD 75 kN
1 4
FN 1
3 8
FN 3
2 3
FN 2
工程力学电子教案
第七章
拉伸和压缩
9
(4) 联立平衡方程和补充方程，解出全部未知力。
F N 2 cos 30 F N 3 0 F N 1 F N 2 sin 30 F 0
1 4
C
B 2
60°
1
30°
FN 1
3 8
FN 3
F B FBC FAB
3m
解得： F
AB
75 kN ,
F BC 125 kN
A
4m
C
2m
进而得杆的内力，F
N , AB
75 kN ,
F N , BC 125 kN
D
于是各杆横截面上的正应力为： 对C点作受力分析：
F'BC C FCD

AB

F N , AB A F N , BC A F N , AC A F N , CD A
C B 2
60°
1
30°
解：(1) 画受力图，列出独立的平衡 方程，并确定超静定次数；
D
3
4m
A F
F N 2 cos 30 F N 3 0 F N 1 F N 2 sin 30 F 0


FN2 FN3
30°
FN1
60°
A F
两个方程，三个未知数，所以是一次超静定问题。
工程力学电子教图示组合截面对于水平形心轴z的惯性矩Iz。
I z I z , 22 a 2 I z ,120 10 I z , 22 a 2 I zC Aa 3400 cm 6576 cm
4

2

3
22a
12 cm 1cm 2 12
CD
注意判断内力和应力的正负。
工程力学电子教案
4
7-6：结构如图所示，杆件AB，AD均由两根等边角钢组成。已知材 料的许用应力[]=170MPa，试为AB，AD杆选择等边角钢的型号。 解：对DE杆作平衡分析知， F 300 kN 进而， 假设AB，AC杆均被拉伸， 对A点作受力分析：
7
mm
4
工程力学电子教案
2
7-1：试作图示各杆的轴力图，并分别指出最大拉力和最大压力的 值及其所在的横截面（或这类横截面所在的区段）。
10kN 5kN
(c)
A
0.5m
B
0.5m
C
1m 15kN 10kN
D
FN +
x
最大拉力值为15kN，位于CD段。
工程力学电子教案
3
7-4：在图示结构中，各杆的横截面面积均为3000mm2。力F为 F B 100kN。试求各杆横截面上的正应力。 解：假设各杆均被拉伸，对B点作受力分析：
第七章
拉伸和压缩
8
(2) 画变形关系图，列出变形协调方程；
1
1 2
D l1
3 2
D l3 D l 2
2 3
A
(3) 根据胡克定律，由变形协调方程得补充方程；
D l1 F N 1 l1 EA 1 , D l2 FN 2l2 EA 2 , D l3 F N 3l3 EA 3
A’
代入变形协调条件，得补充方程
N , AD
F AD 300 kN
B
FAB C FAC A FAD 30° 300kN/m
2m
A
E FEy
D FAD
由分析可知， F 600 kN , F 300 进而， F 600 kN , F 300 3 kN
AB AC
N , AB N , AC
3 kN
300kN/m FEx
D l BD 0 . 75 mm D l BC 0
B' F=15kN
30°
B
按小位移近似，变形后B点的位置为B'点，于是
D By 0 . 75 mm D Bx 0 . 75 3 mm 1 . 3 mm
B'
1m
B
工程力学电子教案
7
7-17：图示杆系中各杆材料相同。已知：三根杆的横截面面积分别 为A1=200mm2，A2=300mm2，A3=400mm2，荷载F=40kN。试求各杆 横截面上的应力。
2m
2 A AB
F N , AB

F N , AD

600 kN 170 MPa
35 . 3 cm
2
E
D
AAB≥17.6cm2，AB杆应该选择100×100×10的等边角钢。
2 A AD


300 kN 170 MPa
17 . 6 cm
2
AAD≥8.8cm2，AD杆应该选择80×80×6的等边角钢。