F
各点线应变相同 F
F
根据静力平衡条件: F NdF A dAA
即
FN
A
FN
A
正负号规定:拉应力为正,压应力为负.
FN 的适用条件:
A
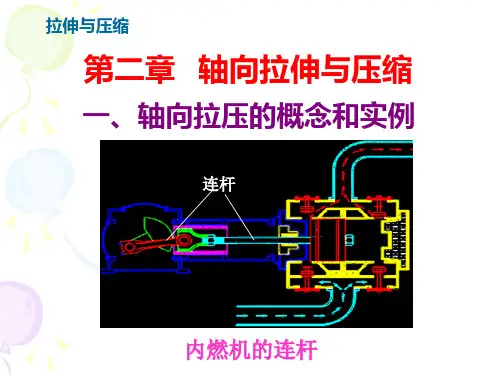
1、只适用于轴向拉伸与压缩杆件,即杆端处力的合 力作用线与杆件的轴线重合.
2、只适用于离杆件受力区域稍远处的横截面.
4、 实验验证
拉伸与压缩/横截面上的内力和应力
卸载
卸载定律:在卸载
过程中,应力与应
变满足线性关系.
p e
应变关系
e p
拉伸与压缩/材料的力学性能
低碳钢Q235拉伸时的力学行为
断裂 冷作<应变>硬化现象:
应力超过屈服极限后
卸 载 与
卸载,再次加载,材 料的比例极限提高,
再
再加载
而塑性降低的现象.
加
载
拉伸与压缩/材料的力学性能
名义屈服应力
p0.
n
(n>1) 引入安全系数的原因:
1、作用在构件上的外力常常估计不准确;构件的外形及所受 外力较复杂,计算时需进行简化,因此工作应力均有一定 程度的近似性;
2、材料均匀连续、各向同性假设与实际构件的出入,且小试样 还不能真实地反映所用材料的性质等.
构件拉压时的强度条件
maxFNAmax[]
拉伸与压缩/拉〔压〕时的强度计算
1.5m B
A 1
FN1
B
FN 2
F
2m
F
2
C
FFN2 cos 0 FN1 FN2 sin 0
解得
FN1
3 4
F(拉) ,
FN2
5 4
F(压)