3-2 拉压应力变形习题课(14年用)

第一章绪论（1）1-2 现代机械系统由哪些子系统组成, 各子系统具有什么功能？（2）答: 组成子系统及其功能如下:（3）驱动系统其功能是向机械提供运动和动力。

（4）传动系统其功能是将驱动系统的动力变换并传递给执行机构系统。

第二章执行系统其功能是利用机械能来改变左右对象的性质、状态、形状或位置, 或对作业对象进行检测、度量等, 按预定规律运动, 进行生产或达到其他预定要求。

第三章控制和信息处理系统其功能是控制驱动系统、传动系统、执行系统各部分协调有序地工作, 并准确可靠地完成整个机械系统功能。

第四章机械设计基础知识2-2 什么是机械零件的失效？它主要表现在哪些方面？答：（1）断裂失效主要表现在零件在受拉、压、弯、剪、扭等外载荷作用时, 由于某一危险截面的应力超过零件的强度极限发生的断裂, 如螺栓的断裂、齿轮轮齿根部的折断等。

（2）变形失效主要表现在作用在零件上的应力超过了材料的屈服极限, 零件产生塑性变形。

（3）表面损伤失效主要表现在零件表面的腐蚀、磨损和接触疲劳。

2-4 解释名词: 静载荷、变载荷、名义载荷、计算载荷、静应力、变应力、接触应力。

答: 静载荷大小、位置、方向都不变或变化缓慢的载荷。

变载荷大小、位置、方向随时间变化的载荷。

名义载荷在理想的平稳工作条件下作用在零件上的载荷。

计算载荷计算载荷就是载荷系数K和名义载荷的乘积。

静应力不随时间变化或随时间变化很小的应力。

变应力随时间变化的应力, 可以由变载荷产生, 也可由静载荷产生。

（1）2-6 机械设计中常用材料选择的基本原则是什么？（2）答：机械中材料的选择是一个比较复杂的决策问题, 其基本原则如下：①材料的使用性能应满足工作要求。

使用性能包含以下几个方面:②力学性能③物理性能④化学性能①材料的工艺性能应满足加工要求。

具体考虑以下几点:②铸造性③可锻性④焊接性⑤热处理性⑥切削加工性①力求零件生产的总成本最低。

主要考虑以下因素:②材料的相对价格③国家的资源状况④零件的总成本2-8 润滑油和润滑脂的主要质量指标有哪几项？答: 衡量润滑油的主要指标有: 粘度（动力粘度和运动粘度）、粘度指数、闪点和倾点等。

《工程力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】：本课程《工程力学》（编号为09004）共有单选题,填空题1,计算题,简答题,填空题2,填空题3等多种试题类型，其中，本习题集中有[填空题2,填空题3]等试题类型未进入。

一、单选题1.工程力学材料力学部分的基本研究对象是（）A.刚体B.质点C.弹性变形体D.变形杆件2.工程力学静力学部分的基本研究对象是（）A.刚体B.质点C.弹性变形体D.变形杆件3.两个力大小相等、方向相反、作用在两个相互作用物体的一条直线上，这是（）。

A.二力平衡公理B.力偶的定义C.作用力和反作用力公理D.二力杆约束反力的特性4.两个力大小相等、方向相反、作用在同一物体的一条直线上，这是（）。

A.二力平衡公理B.力偶的定义C.作用力和反作用力公理D.二力杆约束反力的特性5.两个力大小相等、方向相反、作用在同一物体的两条直线上称为（）。

A.二力平衡公理B.力偶的定义C.作用力和反作用力公理D.二力杆约束反力的特性6.刚体上作用着三个力并且保持平衡，则这三个力的作用线一定满足（）。

A.共线B.共面C.共面且不平行D.共面且相交于同一点7.下列四图中矢量关系符合F4=F1+F2+F3的是图（）。

F1F2F4F3F1F2F4F3F1F2F4F3F1F2F4F3A B C D8.下列四图中矢量关系符合F2+F1=F4+F3的是图（）。

F1F2F4F3F1F2F4F3F1F2F4F3F1F2F4F3A B C D9.下列四图中矢量关系符合F3+F1=F4+F2的是图（）。

F1F2F4F3F1F2F4F3F1F2F4F3F1F2F4F3A B C D10.柔所约束的约束反力大小未知、作用点是柔索的联接点、方向在柔索的（）方向。

A.垂直B.平行C.牵拉D.倾斜11.柔所约束的约束反力大小未知、作用点是柔索的联接点、方向在柔索的（）方向。

A.垂直B.平行C.牵拉D.倾斜12.光滑铰链约束的约束反力大小和方向的特征是（）A.一个大小方向均未知B.两个大小未知C.两个大小未知方向已知D.一个未知13.光滑铰链约束的约束反力大小和方向均未知，受力分析中常将其表达为（）的力。

材料力学第五版课后答案[习题2-2]一打入基地内的木桩如图所示，杆轴单位长度的摩擦力f=kx**2，试做木桩的后力图。

解：由题意可得：33233110,,3/()3/(/)ll N fdx F kl F k F l F x Fx l dx F x l =====⎰⎰1有3[习题2-3] 石砌桥墩的墩身高m l10=，其横截面面尺寸如图所示。

荷载kN F 1000=，材料的密度3/35.2m kg =ρ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：g Al F G F N ρ--=+-=)( 2-3图 )(942.31048.935.210)114.323(10002kN -=⨯⨯⨯⨯+⨯--=墩身底面积：)(14.9)114.323(22m A =⨯+⨯=因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

MPa kPa m kNA N 34.071.33914.9942.31042-≈-=-==σ[习题2-7] 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：)()(x EA Fdx l d =∆ ，⎰⎰==∆l l x A dxE F dx x EA F l 00)()(l xr r r r =--121，22112112d x l d d r x l r r r +-=+⋅-=，2211222)(u d x l d d x A ⋅=⎪⎭⎫ ⎝⎛+-=ππ，dx l d d du d x l d d d 2)22(12112-==+-du d d ldx 122-=，)()(22)(221212udu d d l du u d d l x A dx -⋅-=⋅-=ππ 因此，)()(2)()(202100udu d d E Fl x A dx E F dx x EA F l l l l⎰⎰⎰--===∆π lld x l d d d d E Fl u d d E Fl 011221021221)(21)(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+--=⎥⎦⎤⎢⎣⎡-=ππ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+--=21221)(2111221d d l l d d d d E Fl π⎥⎦⎤⎢⎣⎡--=122122)(2d d d d E Fl π214dEd Fl π=[习题2-10] 受轴向拉力F 作用的箱形薄壁杆如图所示。

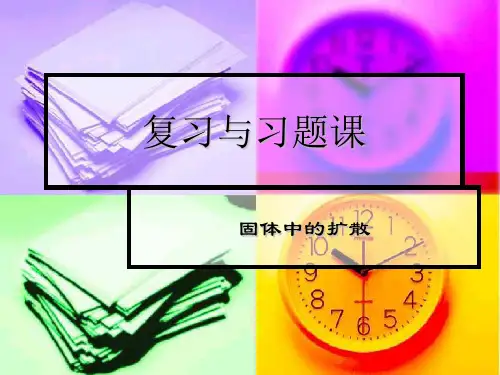
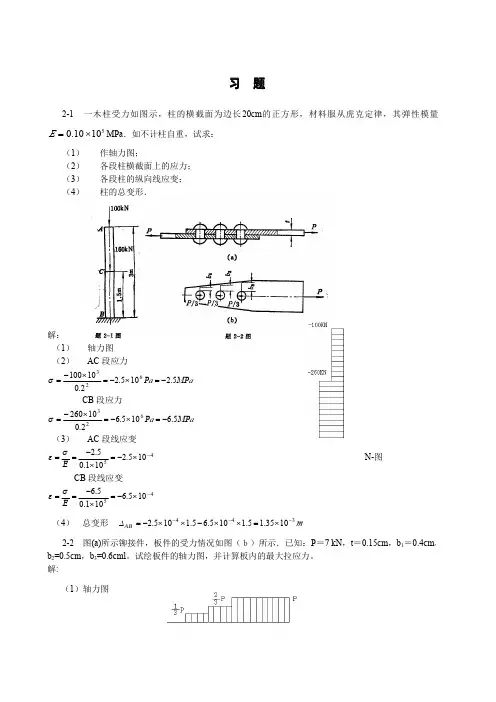
习题2-1一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量MPa ．如不计柱自重，试求：51010.0×=E （1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形．解：（1）轴力图（2）AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=（3）AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε（4）总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。

试绘板件的轴力图，并计算板内的最大拉应力。

解:（2）aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为１cm 的圆杆，在拉力P ＝10kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为＝30o 的斜截面上的正应力与剪应力。

α解:（1）最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−（2）界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。

《材料力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】：本课程《材料力学》（编号为06001）共有单选题,计算题,判断题,作图题等多种试题类型，其中，本习题集中有[判断题]等试题类型未进入。

一、单选题1.构件的强度、刚度和稳定性________。

(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关(C)与二者都有关(D)与二者都无关2.一直拉杆如图所示，在P力作用下。

(A) 横截面a上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上，各点的剪应力。

(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中，图所示杆是轴向拉伸杆。

(A) (B)(C) (D)P5.图示拉杆承受轴向拉力P的作用，斜截面m-m的面积为A，则σ=P/A为。

(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力6.解除外力后，消失的变形和遗留的变形。

(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍，则抗拉。

(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。

P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示，已知上下两面的剪应力为τ则左右侧面上的剪应力为。

(A)τ/2(B)τ(C)2τ(D)010.下图是矩形截面，则m—m线以上部分和以下部分对形心轴的两个静矩的。

(A)绝对值相等，正负号相同(B)绝对值相等，正负号不同(C)绝对值不等，正负号相同(D)绝对值不等，正负号不同11.平面弯曲变形的特征是。

(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内；(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上，各个截面上的。

第6章弯曲应力6-1 选择题答案：Aa σb σ材料和横截面均相同的两根梁，变形后其轴线为两同心圆弧，如图所示。

梁a 、b 内的最大弯曲正应力分别为和 ，则比较二者可知_____。

R aabR ba bσσ<a b σσ=a bσσ>A. B. C. D. 其大小关系不定 1=,,a a b b a b a b a bM EIR R M M M EI ρρρρσσρρ==>=<<，，显然，由知，所以6-2 选择题答案：C图示截面的抗弯截面模量 A.B.C. z W =_____。

32π1326d bh -43π16412d bh -431π1326d bh d ⎛⎫-⎪⎝⎭431π1326d bh h ⎛⎫-⎪⎝⎭D. 43max max π1,,64122z z z I d dW I bh y y ==-=其中bhzd6-3 选择题答案：B三根正方形截面梁如图所示，其长度、横截面面积和受力状态相同，其中(b)、(c)梁的截面为两个形状相同 的矩形拼合而成，拼合后无胶接。

在三根梁中，____梁内的最大正应力相等。

FAB(a)Fz(b)Fz 1 z 1b /2 (c)Fzb /2b /2 b /2A ．(a)和(b) B. (a)和(c) C. (b)和(c) D. (a)、 (b)和(c)max,(a)(c)z M Fl W =与相同。

3max 336=,6/6z b Fl FlW b bσ==max σ(b)12331max 3112,,/6224224z b b Fl b Flz W b bσ⎛⎫⎛⎫=⋅=== ⎪ ⎪⎝⎭⎝⎭所以 相等。

而 的两层截面各自的中性轴为(a)a Aa aBM 06-4 选择题答案：CA. B. C. D. 200GPa E =0M 43.010ε-=⨯max σ=图(a)所示工字钢简支梁，弹性模量 。

若在力偶矩 作用下测得横截面A 处梁顶面的纵向应变，则梁内最大弯曲正应力 _____。

第二章 习题与思考题17、在邓肯-张的非线性双曲线模型中，参数a 、b 、i E 、t E 、13-ult σσ（）以及f R 各代表什么意思？答：参数i E 代表三轴试验中的起始变形模量，a 代表i E 的倒数；ult )(31σσ-代表双曲线的渐近线对应的极限偏差应力，b 代表ult )(31σσ-的倒数；t E 为切线变形模量；f R 为破坏比。

18、饱和粘土的常规三轴固结不排水实验的应力应变关系可以用双曲线模拟，是否可以用这种实验确定邓肯-张模型的参数？这时泊松比ν为多少？这种模型用于什么情况的土工数值分析？答：可以，这时ν=0.49，,用以确定总应力分析时候的邓肯-张模型的参数。

19、是否可以用饱和粘土的常规三轴固结不排水试验来直接确定用有效应力表示的邓肯-张模型的参数？对于有效应力，上述的131()/d d σσε-是否就是土的切线模量t E ？用有效应力的广义胡克定律来推导131()/d d σσε-的表达式。

答：不能用饱和粘土的常规三轴固结不排水试验来直接确定用有效应力表示的邓肯-张模型的参数；在有效应力分析时，邓肯-张模型中的131()/d d σσε-不再是土的切线模量，而需做以下修正：131()/=1-(1-2)t t E d d A σσευ- 具体推导如下：'''11231231231231=[-(d +d )]1=[(-du)-(d +d -2du)]1=[(-du)-(d +d )-2du)]1=[-(d +d )-(1-2)du)]d d Ed E d Ed Eεσυσσσυσσσυσσυσυσσυ 又由于23=d =0d σσ；且B=1.0时，13=(-)u A σσ∆，则：13=(-)du Ad σσ，代入上式，可得：1313131=[d(-)-(1-2)Ad(-)]1=[1-(1-2)A]d(-)d E Eεσσυσσυσσ 可知131(-)=1-(1-2)t t d E d A σσευ 20、土的3σ为常数的平面应变试验及平均主应力为常数的三轴压缩试验〔1σ增加的同时，3σ相应的减少，保持平均主应力p 不变〕、减压的三轴伸长试验〔围压1σ保持不变，轴向应力3σ不断减少〕的应力应变关系曲线都接近双曲线，是否可以用这些曲线的切线斜率131(-)/d d σσε直接确定切线模量t E ？用广义胡克定律推导这些试验的131(-)/d d σσε表达式。

3到13章答案 免费下载 0财富值西北工业大学机械原理及机械零件教研室 编著第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-ζ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。

[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N ζζNM P a 3.324105.2105180946920112=⨯⨯⨯==--N N ζζNM P a 0.227102.6105180956930113=⨯⨯⨯==--N N ζζN3-2已知材料的力学性能为MPa 260=s ζ，MPa 1701=-ζ，2.0=ζΦ，试绘制此材料的简化的等寿命寿命曲线。

[解] )170,0('A )0,260(C 0012ζζζΦζ-=-ζΦζζ+=∴-1210M P a 33.2832.0117021210=+⨯=+=∴-ζΦζζ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。

如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。

[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=αζ，查附图3-1得78.0≈ζq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=ζζζq查附图3-2，得75.0=ζε；按精车加工工艺，查附图3-4，得91.0=ζβ，已知1=q β，则 35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q ζζζζββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =ζ，应力幅MPa 20a =ζ，试分别按①C r =②C ζ=m ，求出该截面的计算安全系数ca S 。

弹塑性⼒学习题集（有图）·弹塑性⼒学习题集$殷绥域李同林编!…中国地质⼤学·⼒学教研室⼆○○三年九⽉⽬录—弹塑性⼒学习题 (1)第⼆章应⼒理论.应变理论 (1)第三章弹性变形.塑性变形.本构⽅程 (6)第四章弹塑性⼒学基础理论的建⽴及基本解法 (8)第五章平⾯问题的直⾓坐标解答 (9)第六章平⾯问题的极坐标解答 (11)第七章柱体的扭转 (13)(第⼋章弹性⼒学问题⼀般解.空间轴对称问题 (14)第九章* 加载曲⾯.材料稳定性假设.塑性势能理论 (15)第⼗章弹性⼒学变分法及近似解法 (16)第⼗⼀章* 塑性⼒学极限分析定理与塑性分析 (18)第⼗⼆章* 平⾯应变问题的滑移线场理论解 (19)附录⼀张量概念及其基本运算.下标记号法.求和约定 (21)习题参考答案及解题提⽰ (22){前⾔弹塑性⼒学是⼀门理论性较强的技术基础课程，它与许多⼯程技术问题都有着⼗分密切地联系。

应⽤这门课程的知识，能较真实地反映出物体受载时其内部的应⼒和应变的分布规律，能为⼯程结构和构件的设计提供可靠的理论依据，因⽽受到⼯程类各专业的重视。

《弹塑性⼒学习题集》是专为《弹塑性⼒学》（中国地质⼤学李同林、殷绥域编，研究⽣教学⽤书。

）教材的教学使⽤⽽编写的配套教材。

本习题集紧扣教材内容，选编了170余道习题。

作者期望通过不同类型习题的训练能有助于读者理解和掌握弹塑性⼒学的基本概念、基础理论和基本技能，并培养和提⾼其分析问题和解决问题的能⼒。

鉴于弹塑性⼒学课程理论性强、内容抽象、解题困难等特点，本书对所编习题均给出了参考答案，并对难度较⼤的习题给出了解题提⽰或解答。

…编者2003年9⽉%弹塑性⼒学习题第⼆章应⼒理论·应变理论~2—1 试⽤材料⼒学公式计算：直径为1cm 的圆杆，在轴向拉⼒P = 10KN 的作⽤下杆横截⾯上的正应⼒σ及与横截⾯夹⾓?=30α的斜截⾯上的总应⼒αP 、正应⼒ασ和剪应⼒ατ，并按弹塑性⼒学应⼒符号规则说明其不同点。

8-1 试求图示各杆的轴力，并指出轴力的最大值。

解：(a)(1) 用截面法求内力，取1-1、2-2截面；(2) 取1-1截面的左段；110 0 xN N FF F F F =-==∑(3) 取2-2截面的右段；220 0 0xN N FF F =-==∑(4) 轴力最大值：max N F F =(b)(1) 求固定端的约束反力；0 20 xR R FF F F F F =-+-==∑(2) 取1-1截面的左段；(a)(c)(d)N 1F RF N 1110 0 xN N FF F F F =-==∑(3) 取2-2截面的右段；220 0 xN R N R FF F F F F =--==-=-∑(4) 轴力最大值：max N F F =(c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1截面的左段；110 20 2 xN N FF F kN =+==-∑(3) 取2-2截面的左段；220 230 1 xN N FF F kN =-+==∑(4) 取3-3截面的右段；330 30 3 xN N FF F kN =-==∑(5) 轴力最大值：max 3 N F kN =(d)(1) 用截面法求内力，取1-1、2-2截面；F RF N 211F N 1N 2F N 3(2) 取1-1截面的右段；110 210 1 xN N FF F kN =--==∑(2) 取2-2截面的右段；220 10 1 xN N FF F kN =--==-∑(5) 轴力最大值：max 1 N F kN =8-2 试画出8-1所示各杆的轴力图。

解：(a)(b) (c) (d)FN 1F N 2F FFFF 1kN8-5 图示阶梯形圆截面杆，承受轴向载荷F 1=50 kN 与F 2作用，AB 与BC 段的直径分别为d 1=20mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。