江苏省海安高级中学2018-2019学年高一3月月考数学试卷(附答案)

江苏省海安高级中学2018-2019学年高一数学上学期第一次月考试题一、填空题：本大题共14小题，每小题5分，共70分.请把答案填写在答题卡相应位置上. 1. 已知集合，，则= ▲ ． {}13A x x =≤≤{}24B x x =≤≤A B I 2. 函数的定义域是 ▲ ． ()f x =3. 若函数是奇函数，则实数的值为 ▲ ． ()2220x x x f x x ax x ìï-ï=íï-+<ïî，≥0，a 4. 下列对应为函数的是 ▲ ．（填相应序号）①R ；②其中R ,R ；213x x x ®-Î，x y ®，y x =Îy Î③R ；④其中N ,R .x x ®Îx y ®，y x x =Î，y Î5. 已知 若，则实数的取值范围是 ▲ ．()110210x x f x x xìï-ïïï=íïï<ïïî，≥，，，()2f a ≤a 6. 设集合，则满足条件的集合的个数是{}M a b =，{}M N a b c d e f =U ，，，，，N ▲ ．7. 已知函数为一次函数，且，若，则函数的解析式为()f x ()21f =-()43f f x x éù=-ëû()f x ▲ ．8. 已知函数在是单调增函数，则实数的取值集合是 ()()2123f x a x x =--+()4-¥，a ▲ ．9. 已知函数满足，则 ▲ ．()f x ()()112223f f x x x -++=()2f -=10.规定记号“”表示一种运算，即，R ，若V a b a b =+V a b Î，，则函数的值域是 ▲ ．13k =V ()()32x f x k x =-V 11. 设函数，R ，且在区间上单调递增，则满足()()()F x f x f x =+-x Î()F x [)0+¥，的取值范围是 ▲ ． ()()211F x F -<x 12. 下列说法中不正确的序号为 ▲ ．①若函数在上单调递减，则实数的取值范围是； ()33ax f x x +=+()3+-¥，a ()1-¥，②函数是偶函数，但不是奇函数；()f x =③已知函数的定义域为，则函数的定义域是； ()21y f x =-[]33-，()y f x =[]12-，④若函数在上有最小值－4，（， 为非零常数），则函数()31f x ax bx =++()0-¥，a b b 在上有最大值6． ()y f x =()0+¥，13.如果对于函数f (x )的定义域内任意两个自变量的值，，当时，都有≤ 且存在两个不相等的自变量，，使1x 2x 12x x <()1f x ()2f x 1m 2m 得，则称为定义域上的不严格的增函数．已知函数的定义域、值域分()()12f m f m =()g x 别为，，，且为定义域上的不严格的增函数，那么这样的A B {}123A =，，B A Í()g x A 函数共有 ▲ 个． ()g x14．函数的最小值为 ▲ ．()f x =二、解答题：本大题共6小题，共计90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤. 15. （本小题满分14分）已知全集U =R ，集合 ，． {}12A x x x =<->，或{}213U B x x p x p =<->+，或ð （1）若，求；12p =A B I （2）若，求实数的取值范围． A B B =I p16. （本小题满分14分） 已知函数．()()2321x f x x A x -=Î- （1）若，请根据其图象，直接写出该函数的值域； (()101+2A =¥U ，，（2）若，求证：对任意实数，为定值；()()1122A =-¥+¥U ，，x A Î()()1f x f x +-（3）若，求值：()()1122A =-¥+¥U ，，． (()(()()(()()1234201420152016201720182018201820182018201820182018f f f f f f f f +++++++17. （本小题满分15分）海安市江淮文化园是以江淮历史文化为底蕴的人文景观，整个园区由白龙故里、先贤景区、凤山书院、中国名人艺术馆群四大景区组成．据估计，其中凤山书院景区每天的水电、人工等固定成本为1000元，另每增加一名游客需另外增加成本10元，凤山书院景区门票单价x （元）（x ∈N *）与日门票销售量（张）的关系如下表，并保证凤山书院景区每天盈利．()y g x =x 20 35 40 50 y400250200100（1）在所给的坐标图纸中，根据表中提供的数据，描出实数对的对应点，并确定y 与x 的函数关系式； ()x y ， （2）求出的值，并解释其实际意义；()()1g x g x -+ （3）请写出凤山书院景区的日利润的表达式，并回答该景区怎样定价才能获最大日利()f x 润？18.（本小题满分15分）设函数满足2()3()()b c f x ax g x a b x x =-=+∈R ，，()1(0)(1)0.2f g g +--=（1）求的值；(1)g - （2）判断函数的奇偶性，并说明理由；()f x （3）若b =1，且函数在上是单调增函数，求a 的取值范围.()()()F x f x g x =+)12⎡+∞⎢⎣，19．（本小题满分16分）定义在R 上的函数满足，且当时，，对任意R ，均有()f x ()00f ¹0x >()1f x >a b Î，． ()()()f a b f a f b +=×（1）求证：；()01f =（2）求证：对任意R ，恒有； x Î()0f x >（3）求证：是R 上的增函数；()f x （4）若，求的取值范围． ()()221f x f x x ×->x20．（本小题满分16分）已知函数（，R ，），且对任意实数，恒成2()f x x bx c =++b c ∈0b >x ()2f x x b ≥+立.（1）求证：； 244b c b ≥≥+（2）若当时，不等式对满足条件的，恒成立，求的c b ≠22()()()M c b f c f b ≥--b c M 最小值.高一年级阶段检测一 数学试卷答案一、填空题：本大题共14小题，每小题5分，共70分.请把答案填写在答题卡相应位置上.答案：1、 2、 3、-2 4、①②③ 5、 6、4个 []23，(]11-，6a ≤7、 8、 9、 10、 11、 ()23f x x =-+Æ34-(32ù-¥û，01x <<12、②③ 13、9 14二、解答题：本大题共6小题，共计90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤. 15.解：因为，{}213U B x x p x p =<->+，或ð所以.-----------------------------------------------2(){}213U U B B x p x p ==-+≤≤ðð分 （1）当时，，所以12p =702B éù=êúëû，(7=22A B ùûI ，-------------------------------------------4分 （2）当时，可得.A B B =I B A Í当时，2p -1＞p +3，解得p ＞4，满足题意；B =Æ---------------------------------7分当时，应满足或 B ≠∅21331p p p ì-+ïïíï+<-ïî≤213212p p p ì-+ïïíï->ïî≤ 解得或； 即或44p p ìïïíï<-ïî≤432p p ìïïïíï>ïïî≤4p <-.--------------------------------------12分342p <≤综上，实数p 的取值范围．-----------------------------------------------14分342p p <->或16.解：(()(()()(()()1234201420152016201720182018201820182018201820182018ff f f f f f f +++++++. ()23112112x f x x x -==---（1） 由图象可知，函数的值域为；()()111+-¥U ，，--------------------------------------5分（2） ------------9()()()11111=112211111f x f x x x x x +--+-=-+=-----分（3） 由（2）得：()()12f x f x +-=则：()()()()(()()()((1234201420152016201720182018201820182018201820182018120174201820188f f f f f f f f f f +++++++æö÷ç=+÷çèø=----------------------------------------------------------------------------------------------------------------14分 17. 解:（1） 由题表作出四点的对应点，-------------------------------------------2分它们分布在一条直线上，如图所示．设它们共线于，则取两点的坐标代入得： ()0y kx b k =+¹()()2040040200，，，.204001040200600k b k y k b b ìì+==-ïïïï=Þííïï+==ïïîî所以（N*）10600y x =-+160x x <Î≤，且--------------------------------------------------6分经检验，也在此直线上． ()()3525050100，，，故所求函数解析式为（N*）． --------------------7分 ()10600g x x =-+160x x <Î≤，且（2）由（1）可得，实际意义表示：销售单价每上涨元，日销售量减少10()()110g x g x -+=张． -------------------------------------------------------------------------9分 （3）依题意:()()()210600101000107007000f x x x x x =-+×--=-+- （N*）160x x <Î≤，且-----------------------------------------------------11分 图象开口向下，对称轴为.35x =当时，函数单调递增；当时，函数单调递减. 故当时，有最()135x Î，()3560x Î，35x =()f x 大值，---------------13分5250答：当时，有最大值，故单价定为元时，才能获得日最大利润． 35x =()f x 525035------------------------------------------------------------------------14分 18.解：（1）因为，所以，即.()1(0)(1)02f g g +--=3()(24)0b c b c -++--+=10b c --=所以(1) 1.g b c -=-+=-------------------------------------------------------------------------------3分（2）当时，，即，为偶函数；------------6分0a =()3f x =-()()3f x f x =-=-()f x 当时，0a ¹()()1313f a f a =--=--，， ，即函数不是偶函数； ()()()()113360f f a a +-=-+--=-¹ ，即函数不是奇函数；--10分 ()()()()113320f f a a a --=----=¹综上所述：当时，为偶函数；当时，为非奇非偶函数----11分 0a =()f x 0a ¹()f x （3）若b =1，则c =0，于是.1()g x x=所以.1()()()3F x f x g x ax x =+=+-在上是单调减函数，1()3F x ax x =+-)12⎡+∞⎢⎣，任取，且， [)122+x x Î¥，，12x x <.121212121212()(1)11()()330x x ax x F x F x ax ax x x x x --⎛⎫⎛⎫-=+--+-=< ⎪ ⎪⎝⎭⎝⎭因为，有，所以.1212x x <≤120x x -<，120x x ×>1210ax x ->即，解得.121a x x >4a ≥故a 的取值范围是. -------------------------------------- 15分 [)4+∞，19．（1）求证：；()01f =（2）求证：对任意R ，恒有； x Î()0f x >（3）求证：是R 上的增函数；()f x （4）若，求的取值范围． ()()221f x f x x ×->x 解：（1）证明：令a ＝b ＝0，得f (0)＝f 2 (0)，又因为f (0) ≠ 0，所以 f (0)＝1.----------------------------------------------------------------3分 （2）当x < 0时，－x >0，所以f (0) ＝f (x ) f (－x ) ＝1，即， ()()10f x f x =>-又因为时，， 0x ≥()10f x >≥所以对任意x ∈R ，恒有 f (x )>0.--------------------------------------------------------------9分（3）证明：设，则，所以f (x 2)＝f [(x 2－x 1)＋x 1]＝f (x 2－x 1) f (x 1)． 12x x <210x x ->因为x 2－x 1>0，所以f (x 2－x 1)>1，又f (x 1) > 0，则f (x 2－x 1) f (x 1) > f (x 1)，即f (x 2) > f (x 1)． 所以f (x )是R 上的增函数．---------------------------------------------------------------------13分（4）由f (x )·f (2x －x 2) >1， f (0)＝1得f (3x －x 2) > f (0)，又由f (x ) 为增函数，所以3x －x 2 > 0 ⇒ 0 < x < 3.故x 的取值范围是(0，3)．-------16分 20．解：（1）因为对任意实数x ，恒成立，()2f x x b ≥+所以对任意实数x ，，即恒成立. 22x bx c x b ≥+++2(2)0x b x c b ≥+-+-即，即. --------------------- 4分 2(2)4()0b c b △＝≤---2440b c ≤-+所以，244c b ≥+又因为，即，故--------8分()22+4420b b b ≥-=-24440c b b ≥≥+>c b ≥（2）由c b ≠以及（1）知，0c b >>.所以恒成立，等价于恒成立.--- 12分 22()()()M c b f c f b ≥--22()()f c f b M c b≥--设c t b =，则2222()()()(2)221111f c f b c b c b c b t c b c b c b t t --+++====+--+++.由1c t b =>，知22()()111f c f b c b t -=+-+的取值范围为3(12，. 即32M ≥，M 的最小值为32. ---------------------------------------16分。

阶段测试（二）数 学一、选择题：(本大题共13小题，每小题4分，其中1-10题为单选题，11-13为多选题.） 1．已知集合A ={x |-1≤x ≤3}，B ={x ∈Z |x 2<5}，则A ∩B=( )A ．{0，1}B ．{-1，0，1，2}C ．{0，1，2}D ．{-2，-1，0，1，2} 2．函数f (x 24x-x +1)的定义域为 ( )A ．[12-，2]B ．[12-，2)C ．(12-，2]D ．(12-，2)3.2πsin()=3-（ ） A. 3B. 12-C.32 D.124．向量a =(1，x +1)，b =(1- x ，2)，a ⊥b ，则(a +b )∙(a -b )=( )A ．-15B ．15C ．-20D ．20 5. 已知a =log 52，b =log 73，c =125，则a ，b ，c 的大小关系是( )A ．a < b < cB ．a < c < bC ．b < a < cD ．c < b < a6．已知将函数f (x )=sin(2ωx +π6)(ω>0)的图象向左平移π3个单位长度得到函数g (x )的图象，若函数g (x )图象的两条相邻的对称轴间的距离为π2，则函数g (x )的—个对称中心为( ) A ．(-π6，0) B ．(π6，0) C ．(-π12，0) D ．(π12，0)7．如图，已知△ABC 与△AMN 有一个公共顶点A ，且MN 与BC 的 交点O 平分 BC,若AB mAM =uu u ruuu r，AC nAN =uuu ruuu r，则m n +的值为( ) A ．4 B ．3 C ．2 D ．6 8．已知函数f (x )=log a x (a >0，a ≠1)的图象经过点(22，12).若函数g (x )的定义域为R ，当x ∈[-2，2]时，有g (x )=f (x )，且函数g (x +2)为偶函数，则下列结论正确的是：( ) A ．g (π)<g (3)<g 2 B ．g (π)<g 2g (3) C ．g 2)<g (3)<g (π) D ．g 2g (π)<g (3)9．已知函数()f x 是定义域为R 的奇函数且(1)()f x f x +=-，则(1)(2)(3)(4)(5)(6)f f f f f f +++++=（ ）A ．4B ．0C ．3D ．210．对于实数a ，b 定义运算“⊗”:22,b a a ba b b a a b-<⎧⊗=⎨-⎩≥，设f (x )=(2x -3)⊗(x -3)，若关于x的方程f (x )=k (k ∈R)恰有三个互不相同的实根x 1，x 2，x 3则x 1x 2x 3取值范围为( )A ．(0，3)B ．(-1，0)C ．(-∞，0)D ．(-3，0)11．下列四个说法中，错误的选项有（ ）.A ．若函数()f x 在(,0]-∞,(0,)+∞上都是单调增函数，则函数()f x 在R 上是单调增函数B ．已知函数的解析式为2y x =，它的值域为[1,4]，这样的函数有无数个C ．把函数22x y =的图像向右平移2个单位长度，就得到了函数222x y -=的图像D ．若函数()f x 为奇函数，则一定有(0)0f = 12．下列命题中，正确的是（ ）.A.已知非零向量,a b rr 满足4a b =r r ，且()2b a b ⊥+r r r ，则a r 与b r 的夹角为56π.B.若,,a b c v v v是平面内三个非零向量，则()()a b c a b c ⋅=⋅v v v v v v ；C.若(sin a θ=v，(b =v ，其中3,2πθπ⎛⎫∈ ⎪⎝⎭，则a b ⊥v v ；D.若O 是ABC ∆所在平面上一定点，动点P 满足AB AC OP OA AB AC λ⎛⎫⎪=++ ⎪⎝⎭u u u v u u u v u u u v u u u vu u u v u u u v ，()0,λ∈+∞，则直线AP 一定经过ABC ∆的内心. 13．函数()()()2a xb f x x b c-=-+()0,,0a b R c ≠∈>，()()2g x m f x n =-⎡⎤⎣⎦()0mn >，下列结论：A.函数()f x 的图像关于x 轴上某点成中心对称；B.函数()f x 在R 上单调递增；C.存在实数q p ,，使得()p f x q ≤≤对于任意的实数x 恒成立；D.关于x 的方程()0g x =的解集可能为{}4,2,0,3--．正确结论为( )二、填空题：本大题共4个小题，每小题4分，共20分． 14. 函数()f x =的单调递减区间为 ▲ ．15.已知角θ的终边过点(3,4)-，则cos θ=_____▲______.16.已知函数(21),(1)()1log ,(01)3a a x x f x x x ->⎧⎪=⎨-<≤⎪⎩，当120,0x x >>且12x x ≠时，()()12120f x f x x x -<-，则实数a 的取值范围是 ▲ ．17.已知函数()()sin f x x ωϕ=+(016ω<<，02πϕ-<<),()04f π-=,对任意x R ∈恒有()()4f x f π≤且()f x 在区间(,)3216ππ上单调，则ϕ=____,ω的可能值有__________．三、解答题（本大题共6小题，共82分．解答应写出文字说明、证明过程或演算步骤．） 18．已知实数a 为常数，U =R ，设集合A ={x |31x x -+＞0}，B ={x |y=}，C ={x |x 2﹣(4+a )x +4a ≤0}．（1）求A ∩B ；（2）若∁U A ⊆C ，求a 的取值范围．19．设a =(x ，1)，b =(2，-1)，c =(x -m ，m -1)(x ∈R ，m ∈R).（1）若a 与b 的夹角为钝角，求x 的取值范围； （2）解关于x 的不等式|a +c |<|a -c |.20．我国西部某省4A 级风景区内住着一个少数民族村，该村投资了800万元修复和加强民俗文化基础设施，据调查，修复好村民俗文化基础设施后，任何一个月内（每月按30天计算）每天的旅游人数()f x 与第x 天近似地满足()88f x x=+（千人），且参观民俗文化村的游客人均消费()g x 近似地满足()g 14322x x =--（元）．(1)求该村的第x 天的旅游收入()p x ,并求最低日收入为多少？（单位：千元，130x ≤≤，*N x ∈）； (2)若以最低日收入的20%作为每一天的纯收入计量依据，并以纯收入的5%税率收回投资成本，试问该村在两年内能否收回全部投资成本？21．已知函数())f x x ϕ=+02πϕ⎛⎫-<< ⎪⎝⎭的图象过点(0,1).（1）求724f π⎛⎫⎪⎝⎭的值；（2）利用五点作图作出函数在一个周期内的图像； （3）当5,248x ππ⎡⎤∈-⎢⎥⎣⎦时，方程()f x k =恰有两个不同的实数解，求实数k 的取值范围.22．对于函数f 1(x )，f 2(x )，h (x )，如果存在实数a ，b 使得h (x )=af 1(x )+bf 2(x )，，那么称h (x )为f 1(x )，f 2(x )，的生成函数. （1）给出函数f 1(x )=lg 10x，f 2(x )=lg(10x )，h (x )=lg x ，h (x )是否为f 1(x )，f 2(x )的生成函数？并说明理由.（2）设f 1(x )=log 2x ，f 2(x )=log 12x ，a =2，b =1，生成函数.若不等式3h 2(x )+2h (x )+t >0在x ∈[2，4]上恒成立，求实数t 的取值范围.23．已知函数()2327mx n h x x +=+为奇函数，()13x mk x -⎛⎫ ⎪⎝⎭=，其中m n R ∈、.(1)若函数()h x 的图像过点()1,1A ，求实数m 和n 的值； (2)若3m =，试判断函数()()()11f x h x k x =+在[3,)x ∈+∞上的单调性并证明； (3)设函数()()(),39,3h x x g x k x x ⎧≥⎪=⎨<⎪⎩若对每一个不小于3的实数1x ，都恰有一个小于3的实数2x ，使得()()12g x g x =成立，求实数m 的取值范围.阶段测试（二）一、选择题：(本大题共13小题，每小题4分，其中1-10题为单选题，11-13为多选题.） 1． B 2． D 3. A 4． A 5. A 6．D 7． C 8. C 9． B 10． D 11． ACD 12． CD 13． AC三、填空题：本大题共4个小题，每小题5分，共20分． 14. (],3-∞- ． 15. ________35___. 16. 10,3⎛⎤ ⎥⎝⎦．17ϕ=__4π-__, ____3,7,11______．三、解答题（本大题共6小题，共82分．解答应写出文字说明、证明过程或演算步骤．） 18．解：(1)()()[)3,,1,2,A B =+∞⋃-∞-=+∞则[)2,A B ⋂=+∞. (2) []1,3U C A =-，当[]{}[]4,4,;4,4;4,,4a C a a C a C a >===<=因为∁U A ⊆C ,则4,1a a <⎧⎨≤-⎩解得1a ≤-.19．解：（1）依题意得0a b •<r r 且,a b r r 不反向共线，即210,2x x -<⎧⎨≠-⎩解得12x <且 2.x ≠- （2）依题意得0a c •<r r ，即210x mx m -+-=当2,m =不等式的解集为空集； 当2m >，不等式的解集为()1,1m -；当2m <不等式的解集为()1,1m -.20．解：(1)依据题意，有()()()()8g 814322x f x x x p x ⎛⎫=⋅=+⋅-- ⎪⎝⎭(130x ≤≤,*N x ∈) 即()**9688976,122,N 132081312,2230,N x x x xp x x x x x ⎧++≤≤∈⎪⎪=⎨⎪-++<≤∈⎪⎩， 01当*122,N x x ≤≤∈时，()96889769761152x p x x =++≥= (当且仅当11x =时，等号成立) ． 因此，()()p 111152min p x == (千元) ．2当*2230,N x x <≤∈时，()132081312p x xx =-++． 易知函数132081312xy x =-++ 在(]22,30上单调递减，于是，()()301116min p x p == (千元) ． 又11521116>，所以，日最低收入为1116千元．(2)该村两年可收回的投资资金为111620%5%301228035.2⨯⨯⨯⨯⨯=(千元)= 803.52 (万元)．因为803.52万元> 800万元，所以，该村两年内能收回全部投资资金． 21．【详解】（1）由题知()01fϕ==，∴cosϕ=，又02πϕ-<<，∴4πϕ=-，∴772242442fπππ⎛⎫⎛⎫=⨯-=⎪ ⎪⎝⎭⎝⎭.(2)作图略（3）∵5,2,24843x xπππππ⎡⎤⎡⎤∈-∴-∈-⎢⎥⎢⎥⎣⎦⎣⎦当2,043xππ⎡⎤-∈-⎢⎥⎣⎦即在区间,248ππ⎡⎤-⎢⎥⎣⎦上f(x)为增函数;[]20,,4xππ-∈即在区间5,88ππ⎡⎤⎢⎥⎣⎦上f(x)为减函数，又242fπ⎛⎫-=⎪⎝⎭，8fπ⎛⎫=⎪⎝⎭58fπ⎛⎫=⎪⎝⎭∴当方程()f x k=恰有两个不同实根时，2k∈⎣.22．解:(1)由题意得lg lg lg(10)()lg10xx a b x a b x b a=+=++-由1a bb a+=⎧⎨-=⎩解得1212ab⎧=⎪⎪⎨⎪=⎪⎩所以h(x)是f1(x)，f2(x)的生成函数.（2）由题意得,2()log xh x=,令[]2log,1,2xm m=∈即232t m m>--在[]1,2m∈上恒成立解得5t>-.23．解;()1()2327mx nh xx+=+Q为奇函数()()h x h x ∴-=-，即22()327327mx n mx nx R x x -++=+∈-+恒成立，0n ∴=()h x Q 的图像过点()1,1A()11,h ∴=130m n += 30,0m n ∴==()2有题意知()393x f x x x-=++，()f x 在[)3,+∞上单调递增证明：任取123x x ≤≤，则()()12331212129933x x f x f x x x x x --⎛⎫⎛⎫-=+-++- ⎪ ⎪⎝⎭⎝⎭ ()()1221123312933x x x x x x x x ----=+-123x x ≤≤Q210x x ∴->，129x x >，1233x x -<-()()21121290x x x x x x -∴-<123333x x --<()()12f x f x ∴<，函数()f x 在区间[3,)+∞上单调递增；()3当3x ≥时，()()2273273mx mg x h x x x x===++当3x <时，()()1993x mg x k x -⎛⎫==⋅ ⎪⎝⎭① 当0m ≤时， 3x ∀≥，()211111027327(3)mx mg x x h x x x ===≤++不满足条件()()2213,9903x mx g x k x -⎛⎫∀<==⋅> ⎪⎝⎭，舍；②当0 3m <<时，3x ∀≥，()211111()0,27327183mx m m g h x x x x x ⎛⎤===∈ ⎥+⎝⎦+ 23,0,x x m ∀<-≥()()(]221990,93x mg x k x -⎛⎫==⋅∈ ⎪⎝⎭由题可知(]0,0,918m ⎛⎤∈ ⎥⎝⎦，即918m ≤，162m ≤ 03m ∴<<③当3m ≥时，3x ∀≥，()211111()0,27327183mx m m g h x x x x x ⎛⎤===∈ ⎥+⎝⎦+23,30,x x m m ∀<->-≥()()32211990,933x mm g x k x --⎛⎤⎛⎫⎛⎫==⋅∈⋅ ⎥ ⎪⎪ ⎝⎭⎝⎭⎥⎝⎦ 由题可知310,0,9183m m -⎛⎤⎛⎤⎛⎫∈⋅ ⎥ ⎪⎥ ⎝⎦⎝⎭⎥⎝⎦，即5318mm -<令()5318xxH x -=-单调递减，()60H = 5318x x-<，可得6m < 36m ∴≤< 综上:()0,6m ∈。

海安县高中2018-2019学年高三下学期第三次月考试卷数学一、选择题1． 已知f （x ）=4+a x ﹣1的图象恒过定点P ，则点P 的坐标是（ ） A ．（1，5） B ．（1，4） C ．（0，4） D ．（4，0） 2． “x ＞0”是“＞0”成立的（ ）A ．充分非必要条件B ．必要非充分条件C ．非充分非必要条件D ．充要条件3． 设n S 是等差数列{}n a 的前项和，若5359a a =，则95SS =（ ） A ．1 B ．2 C ．3 D ．44． 设βα,是两个不同的平面，是一条直线，以下命题正确的是（ ） A ．若α⊥l ，βα⊥，则β⊂l B ．若α//l ， βα//，则β⊂l C ．若α⊥l ，βα//，则β⊥l D ．若α//l ，βα⊥，则β⊥l5． 如图，在正六边形ABCDEF 中，点O 为其中心，则下列判断错误的是（ ）A．= B．∥ C． D．6． 若函数f （x ）=2sin （ωx+φ）对任意x 都有f（+x ）=f （﹣x ），则f（）=（ ）A ．2或0B ．0C ．﹣2或0D ．﹣2或27． 将函数f （x ）=3sin （2x+θ）（﹣＜θ＜）的图象向右平移φ（φ＞0）个单位长度后得到函数g （x ）的图象，若f （x ），g （x ）的图象都经过点P （0，），则φ的值不可能是（ ）A．B ．πC．D．8． 将函数)63sin(2)(π+=x x f 的图象向左平移4π个单位，再向上平移3个单位，得到函数)(x g 的图象， 则)(x g 的解析式为（ ）A ．3)43sin(2)(--=πx x g B ．3)43sin(2)(++=πx x g C ．3)123sin(2)(+-=πx x g D ．3)123sin(2)(--=πx x g【命题意图】本题考查三角函数的图象及其平移变换理论，突出了对函数图象变换思想的理解，属于中等难度. 9． 在复平面内，复数1zi+所对应的点为(2,1)-，i 是虚数单位，则z =（ ） A ．3i --B ．3i -+C ．3i -D ．3i +10．设x ∈R ，则“|x ﹣2|＜1”是“x 2+x ﹣2＞0”的（ ）班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件11．某种细菌在培养过程中，每20分钟分裂一次（一个分裂为两个）．经过2个小时，这种细菌由1个可繁殖成（ ）A ．512个B ．256个C ．128个D ．64个12．已知椭圆，长轴在y 轴上，若焦距为4，则m 等于（ ） A ．4 B ．5C ．7D ．8二、填空题13．【2017-2018第一学期东台安丰中学高三第一次月考】在平面直角坐标系xOy 中，直线l 与函数()()2220f x x a x =+>和()()3220g x x a x =+>均相切（其中a 为常数），切点分别为()11,A x y 和()22,B x y ，则12x x +的值为__________．14．设某双曲线与椭圆1362722=+y x 有共同的焦点，且与椭圆相交，其中一个交点的坐标为 )4,15(，则此双曲线的标准方程是 .15．过抛物线y 2=4x 的焦点作一条直线交抛物线于A ，B 两点，若线段AB 的中点M 的横坐标为2，则|AB|等于 ．16．在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，若6a=4b=3c ，则cosB= ．17．对于函数(),,y f x x R =∈,“|()|y f x =的图象关于y 轴对称”是“()y f x =是奇函数”的 ▲ 条件． （填“充分不必要”， “必要不充分”，“充要”，“既不充分也不必要”） 18．如图，在矩形ABCD中，AB =，点Q 为线段CD （含端点）上一个动点，且DQ QC λ=,BQ 交AC 于P ，且AP PC μ=，若AC BP ⊥，则λμ-= ． 三、解答题19．已知点（1，）是函数f （x ）=a x（a ＞0且a ≠1）的图象上一点，等比数列{a n }的前n 项和为f （n ）﹣c ，数列{b n }（b n ＞0）的首项为c ，且前n 项和S n 满足S n ﹣S n ﹣1=+（n ≥2）．记数列{}前n项和为T n ，（1）求数列{a n }和{b n }的通项公式；（2）若对任意正整数n ，当m ∈[﹣1，1]时，不等式t 2﹣2mt+＞T n 恒成立，求实数t 的取值范围（3）是否存在正整数m ，n ，且1＜m ＜n ，使得T 1，T m ，T n 成等比数列？若存在，求出m ，n 的值，若不存在，说明理由．ABC D PQ20．（本题满分15分）如图，已知长方形ABCD 中，2AB =，1AD =，M 为DC 的中点，将ADM ∆沿AM 折起，使得平面⊥ADM 平面ABCM ．（1）求证：BM AD ⊥；（2）若)10(<<=λλDB DE ，当二面角D AM E --大小为3π时，求λ的值．【命题意图】本题考查空间点、线、面位置关系，二面角等基础知识，意在考查空间想象能力和运算求解能力．21．（本题满分15分）如图AB 是圆O 的直径，C 是弧AB 上一点，VC 垂直圆O 所在平面，D ，E 分别为VA ，VC 的中点. （1）求证：DE ⊥平面VBC ；（2）若6VC CA ==，圆O 的半径为5，求BE 与平面BCD 所成角的正弦值.【命题意图】本题考查空间点、线、面位置关系，线面等基础知识，意在考查空间想象能力和运算求解能力．22．已知函数．（1）求f（x）的周期和及其图象的对称中心；（2）在△ABC中，角A、B、C的对边分别是a、b、c，满足（2a﹣c）cosB=bcosC，求函数f（A）的取值范围．23．设不等式的解集为.（1）求集合；（2）若，∈，试比较与的大小。

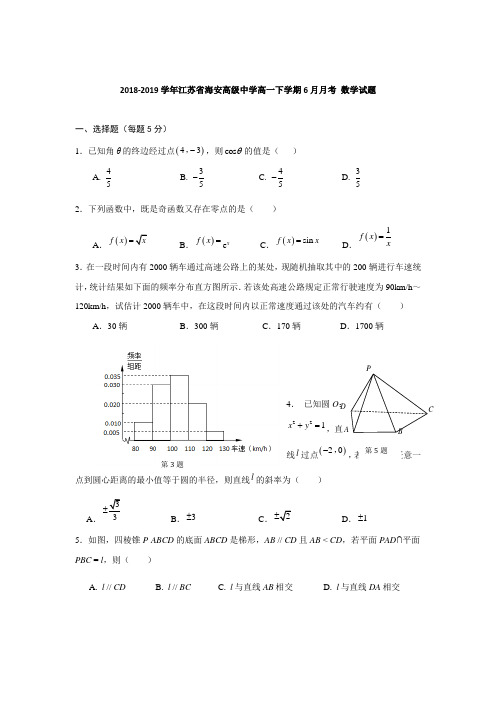
PABDC2018-2019学年江苏省海安高级中学高一下学期6月月考 数学试题一、选择题（每题5分）1．已知角θ的终边经过点()43，-，则cos θ的值是（ ） A.45 B. 35-C. 45-D.352．下列函数中，既是奇函数又存在零点的是（ ）A ．()f x x= B ．()f x =e x C ．()sin f x x= D ．()1f x x =3．在一段时间内有2000辆车通过高速公路上的某处，现随机抽取其中的200辆进行车速统计，统计结果如下面的频率分布直方图所示．若该处高速公路规定正常行驶速度为90km/h ～120km/h ，试估计2000辆车中，在这段时间内以正常速度通过该处的汽车约有（ ）A ．30辆B ．300辆C ．170辆D ．1700辆4． 已知圆O ：221x y +=，直线l 过点()20，-，若直线l 上任意一点到圆心距离的最小值等于圆的半径，则直线l 的斜率为（ ）A ．3±B ．3±C ．2±D ．1±5．如图，四棱锥P -ABCD 的底面ABCD 是梯形，AB // CD 且AB < CD ，若平面PAD ∩平面PBC = l ，则（ ）A . l // CDB . l // BC C . l 与直线AB 相交D . l 与直线DA 相交第5题 第3题6．设全集(){}I x y x y R ，，，=∈集合()312y A x y x ，，⎧-⎫==⎨⎬-⎩⎭ (){}1B x y y x ，，=≠+则C I()A B =（ ）A . ∅B .(){}23， C . ()23，D .(){}1x y y x ，=+ 7．已知()0x ，∈π，()cos 6x π-=，则()cos 3x π-=（ ）A． B．C．D．8．函数2ln 12y x x x=-+-的所有零点之和是（ ）A ．4-B ．2-C ．2D ．49．已知函数()()212f x a x x =-≤≤与()1g x x =+的图象上存在关于x 轴对称的点，则实数a 的取值范围是（ ）A ．)54，⎡-+∞⎢⎣ B ．[]13， C ．514，⎡⎤-⎢⎥⎣⎦D ．[]11，- 10．已知A B ，是圆O ：224x y +=上两点，点(12)P ，且0PA PB ⋅=,则AB 最小值是（ ）A1 BC- D二、填空题（每题5分） 11．()121lg 25lg 4=9-++▲ ．12．在△ABC 中，角A ，B ，C 所对的边为a ，b ，c ，若1=b，=c ，23π=C ，则=a ▲ ．13．已知平面向量(10)，=a，(12=-b ，则a 与+a b 的夹角 为 ▲ ．14．已知函数()f x 的部分图象如图所示，若不等式2()4f x t -<+<第14题C的解集为(12)，-，则实数t 的值为 ▲ ． 15．它的侧棱与底面所成的角为3π，则它的体积为 ▲ ． 16．已知111C B A ∆的三个内角的余弦值与222C B A ∆的三个内角的正弦值分别对应相等，其中2A 为222C B A ∆中的最大角，若1||22=C B ，则22223+B A C 的最大值为 ▲ ． 三、解答题（共70分） 17．（本题满分10分）已知向量a ＝()sin cos 2sin θθθ-，，b ＝(2，1)，其中0＜θ＜π．（1）若a ∥b ，求sin cos θθ的值；（2）若∣a ∣=∣b ∣，求θ的值．18．（本题满分11分）如图所示，在五面体ABCDEF 中，四边形ABCD （1）求证：EF //平面ABCD ；（2） 若CF ⊥AE ，AB ⊥AE ，求证：平面ABFE ⊥平面CDEF ．19．（本题满分12分）已知集合A ＝{x |(x －2)(x －3a －1)＜0}，函数)1(2lg2+--=a x xa y 的定义域为集合B .（1） 若a ＝2，求集合B ； （2） 若A ＝B ，求实数a 的值．20．（本题满分12分）已知函数()221x f xm=-+是定义在R 上的奇函数，（1）求实数m 的值；（2）如果对任意x ∈R ，不等式2(2cos )(4sin 217)0f a x f x a ++---<恒成立，求实数a 的取值范围．21．（本题满分12分）某沿海地区的海岸线为一段圆弧AB ，对应的圆心角3π∠=AOB ，该地区为打击走私，在海岸线外侧2海里内的海域ABCD 对不明船只进行识别查证(如图：其中海域与陆地近似看作在同一平面内),在圆弧的两端点A ，B 分别建有监测站，A 与B 之间的直线距离为10海里．（1）求海域ABCD 的面积；（2）现海上P 点处有一艘不明船只，在A 点测得其距A 点4海里，在B 点测得其距B 点219海里.判断这艘不明船只是否进入了海域ABCD ？ 请说明理由．22．（本题满分13分）已知函数1y x x=+在()01，上是减函数，在()1+∞，上是增函数．若函数()1()f x x a a x=--∈R ，利用上述性质， （1）当1a =时，求()f x 的单调递增区间（只需判定单调区间，不需要证明）；（2）设()f x 在区间(]02，上最大值为()g a ，求()y g a =的解析式； （3）若方程()=2f x a -恰有四解，求实数a 的取值范围．第21题171819.2021.22。

2018-2019学年江苏省南通市海安高级中学高一3月月考数学试题一、单选题1．设集合U=R，A={x|0<x<2}，B={x|x<1}，则图中阴影部分表示的集合为（）．A．B．{x|x C．{x|0<x≤1}D．【答案】D【解析】根据图可知求解的集合为，根据定义可求得结果.【详解】由图可知所求阴影部分集合为：又本题正确选项：【点睛】本题考查集合的运算中的交集和补集，属于基础题.2．已知函数，则函数的值域为（）．A．(0，+∞)B．[0，+∞)C．(2，+∞)D．[2，+∞)【答案】B【解析】根据，可知，由此可得值域.【详解】设，则值域为本题正确选项：【点睛】本题考查值域的求解问题，属于基础题.3．函数的定义域为（）．A．(2，3)∪(3，+∞)B．[2，3)∪(3，+∞)C．[2，+∞)D．(3，+∞)【答案】B【解析】解不等式组可求得函数定义域.【详解】由题意可得：本题正确选项：【点睛】本题考查函数定义域的基本要求，关键在于能够明确偶次根式被开方数大于等于零，分式分母不等于零，属于基础题.4．函数则f(f(-2018))= （）．A．1 B．-1 C．2018 D．-2018【答案】B【解析】由题意可得：，代入即可求解【详解】由题意可得：故选【点睛】本题主要考查了分段函数的函数值的求解，属于基础题。

5．若关于x的一元二次方程x2 - 4x + m =0没有实数根，则m的取值范围为（）．A．m <2 B．m >4 C．m >16 D．m <8【答案】B【解析】根据一元二次方程的根与判别式的关系可判断．【详解】∵一元二次方程x2﹣4x+m=0没有实数根，∴△=16﹣4m＜0，即m＞4，故选：B．【点睛】本题考查了一元二次方程根的分布情况，属于基础题.6．函数y =|x2-1|与y =a的图象有4个交点，则实数a的取值范围是（）．A．(0，) B．(-1，1) C．(0，1) D．(1，)【答案】C【解析】作函数图象，根据函数图像确定实数a的取值范围.【详解】作函数图象，根据函数图像得实数a的取值范围为（0，1），选C.【点睛】利用函数图象可以解决很多与函数有关的问题，如利用函数的图象解决函数性质问题，函数的零点、方程根的问题，有关不等式的问题等.解决上述问题的关键是根据题意画出相应函数的图象，利用数形结合的思想求解.7．已知函数，若关于的不等式的解集为空集，则实数的取值范围是（）．A．(-3，-2) B．(-∞，-1) C．(-∞，-2) D．(-∞，-2]【答案】D【解析】求得的解集，以及二次函数的值域，结合题意可得解集与的值域的交集为空集，可得关于的不等式，解不等式即可得结果.【详解】函数由，即，解得，那么不等式，①又，当时，取得最小值-1 ,即函数的值域为，若不等式的解集为空集，则①的解集为空集，那么与值域的交集为空集，，，即实数的取值范围是，故选D.【点睛】本题主要考查一元二次不等式的解法、二次函数的值域以及转化与划归思想的应用，意在考查综合应用所学知识，解答问题的能力，属于难题.8．函数f(x)定义域为R，且对任意x，y∈R，恒成立.则下列选项中不恒成立的是（）．A．B．C．D．【答案】D【解析】由于函数满足，故可以特殊选择函数为f(x)=x,故用排除法，可得为D9．已知函数，若关于的方程[f(x)]2+af(x)=0(a∈R)有n个不同实数根，则n的值不可能为（）．A．3 B．4 C．5 D．6【答案】A【解析】先将函数写成分段函数的形式，并做出其图像，再由得：或，所以方程的解的个数，即转化为函数与轴以及直线交点个数的问题，由图像讨论的范围，即可求出结果.【详解】因为函数，作出的图像如下：由得：或，所以方程的解的个数，即为函数与轴以及直线交点个数，由图像可得：与轴有2个交点，①当,即时，函数与直线无交点，故原方程共2个解；②当，即时，原方程可化为，故原方程共2个解；③当，即时，函数与直线有4个交点，故原方程共6个解；④当，即时，函数与直线有3个交点，故原方程共5个解；⑤当，即时，函数与直线有2个交点，故原方程共4个解；综上，原方程解的个数可能为2,4,5,6.故选A【点睛】本题主要考查函数与方程的综合，解决此类问题的关键在于将方程有实根转化为两个函数有交点的问题，由数形结合即可求解，属于常考题型.10．设f(x)与g(x)是定义在同一区间[a，b]上的两个函数，若函数y=f(x)- g(x)在x∈[a，b]上有两个不同的解，则称f(x)和g(x)在[a，b]上是“关联函数”，区间[a，b]称为“关联区间”．若f(x)=x2-3x+4与g(x)=2x+m在[0，3]上是“关联函数”，则m的取值范围为（）．A．B．C．D．【答案】A【解析】本题的意思是y=f(x)与y=g(x)的图像在[0,3]上有两个不同的交点，求m的取值范围。

江苏省南通市海安高级中学高一下学期3月线上考试数学试题一、单选题1．某地区对当地3000户家庭的2018年所的年收入情况调查统计，年收入的频率分布直方图如图所示，数据（单位：千元）的分组依次为[20，40），[40，60），[60，80），[80，100]，则年收入不超过6万的家庭大约为（）A．900户B．600户C．300户D．150户【答案】A【解析】先计算年收入不超过6万的家庭的频率,再根据样本估计总体的方法求解即可. 【详解】由频率分布直方图可得,年收入不超过6万的家庭的频率为（0.005+0.010）×20＝0.3.可得年收入不超过6万的家庭大约为3000×0.3＝900户.故选：A.【点睛】本题主要考查了频率分布直方图的应用,属于基础题.2．计算sin133cos197cos47cos73︒︒+︒︒的结果为（）A．12B．12-C．32D．3【答案】B【解析】先用诱导公式将sin133cos197cos47cos73︒︒+︒︒化为cos47cos73+sin43sin17-︒︒︒︒，然后用余弦的差角公式逆用即可. 【详解】sin133cos197cos47cos73︒︒+︒︒cos43cos17+sin43sin17=-︒︒︒︒1cos 43cos17sin 43sin17)co (s 602=︒︒-︒︒=-︒--=故选：B 【点睛】本题考查诱导公式和和角的三角函数公式的应用，属于基础题.3．已知向量a ，b 满足a =（x ，1），b =（1，﹣2），若a ∥b ，则a 2b +（ ） A ．（4，﹣3） B ．（0，﹣3） C ．（32，﹣3） D ．（4，3）【答案】C【解析】根据a =（x ，1），b =（1，﹣2），且a ∥b ，求得向量a 的坐标，再求a 2b +的坐标. 【详解】因为a =（x ，1），b =（1，﹣2），且a ∥b ， 所以21x -= ， 所以12x =- ，所以a =（12-，1）， 所以a 32,32⎛⎫+=- ⎪⎝⎭b . 故选：C 【点睛】本题主要考查向量的坐标运算，还考查了运算求解的能力，属于基础题.4．已知某种商品的广告费支出x （单位：万元）与销售额y （单位：万元）之间有如下对应数据：根据上表可得回归方程y bx a =+，计算得7b =，则当投入10万元广告费时，销售额的预报值为 A ．75万元 B ．85万元 C ．99万元D ．105万元【答案】B【解析】分析：根据表中数据求得样本中心(,)x y ，代入回归方程ˆ7ˆyx a =+后求得ˆa ，然后再求当10x =的函数值即可． 详解：由题意得11(24568)5,(3040506070)5055x y =++++==++++=， ∴样本中心为(5,50)．∵回归直线ˆ7ˆyx a =+过样本中心(5,50)， ∴ˆ5075a=⨯+，解得ˆ15a =， ∴回归直线方程为ˆ715yx =+． 当10x =时，710158ˆ5y=⨯+=， 故当投入10万元广告费时，销售额的预报值为85万元． 故选B ．点睛：本题考查回归直线过样本中心这一结论和平均数的计算，考查学生的运算能力，属容易题．5．已知函数f （x ）＝3x +x ，g （x ）＝log 3x +x ，h （x ）＝x 3+x 的零点分别为a ，b ，c ，则a ，b ，c 的大小顺序为（ ） A ．a ＞b ＞c B ．b ＞c ＞aC ．c ＞a ＞bD ．b ＞a ＞c【答案】B【解析】分别求解三个函数的零点满足的关系式,再数形结合利用函数图像的交点比较大小即可. 【详解】f （x ）＝3x +x ＝0,则x ＝﹣3x ,g （x ）＝log 3x +x ,则x ＝﹣log 3x ,h （x ）＝x 3+x ,则x ＝﹣x 3,∵函数f （x ）,g （x ）,h （x ）的零点分别为a ,b ,c , 作出函数y ＝﹣3x ,y ＝﹣log 3x ,y ＝﹣x 3,y ＝x 的图象如图, 由图可知：b ＞c ＞a ,故选：B. 【点睛】本题主要考查了函数零点的运用以及数形结合求解函数值大小的问题,属于中档题. 6．酒驾是严重危害交通安全的违法行为．为了保障交通安全，根据国家有关规定：100mL 血液中酒精含量低于20mg 的驾驶员可以驾驶汽车，酒精含量达到20～79mg 的驾驶员即为酒后驾车，80mg 及以上认定为醉酒驾车．假设某驾驶员喝了一定量的酒后，其血液中的酒精含量上升到了1mg /mL ．如果在停止喝酒以后，他血液中酒精含量会以每小时30%的速度减少，那么他至少经过几个小时才能驾驶汽车？（ ）（参考数据：lg 0.2≈﹣0.7，1g 0.3≈﹣0.5，1g 0.7≈﹣0.15，1g 0.8≈﹣0.1） A ．1 B ．3C ．5D ．7【答案】C【解析】根据题意先探究出酒精含量的递减规律，再根据能驾车的要求，列出模型0.70.2x ≤ 求解.【详解】因为1小时后血液中酒精含量为（1-30%）mg /mL , x 小时后血液中酒精含量为（1-30%）x mg /mL 的，由题意知100mL 血液中酒精含量低于20mg 的驾驶员可以驾驶汽车， 所以()3002%1.x-<，0.70.2x <，两边取对数得，lg 0.7lg 0.2x < ，lg 0.214lg 0.73x >= ，所以至少经过5个小时才能驾驶汽车.【点睛】本题主要考查了指数不等式与对数不等式的解法，还考查了转化化归的思想及运算求解的能力，属于基础题.7．已知ω＞0，0＜φ＜π，直线4x π=和54x π=是函数f （x ）＝sin （ωx +φ）图象的两条相邻的对称轴，若将函数f （x ）图象上每一点的横坐标变为原来的12倍，纵坐标变为原来的2倍，则得到的图象的函数解析式是（ ） A ．224y sin x π⎛⎫=+⎪⎝⎭B ．1224y sin x π⎛⎫=+⎪⎝⎭C ．y ＝2cos2xD ．1228y sin x π⎛⎫=+⎪⎝⎭【答案】A【解析】根据题意先求得()()sin f x x ωϕ=+的周期,再根据三角函数图像变换的方法求解析式即可. 【详解】 ∵直线4x π=和54=x π是函数f （x ）＝sin （ωx +φ）图象的两条相邻的对称轴, ∴周期T ＝2×（544ππ-）＝2π,即22ππω=,得ω＝1, 则f （x ）＝sin （x +φ）,由五点对应法得4π+φ2π=,得φ4π=,即f （x ）＝sin （x 4π+）,若将函数f （x ）图象上每一点的横坐标变为原来的12倍,得到y ＝sin （2x 4π+）, 然后纵坐标变为原来的2倍,得到y ＝2sin （2x 4π+）,故选：A. 【点睛】本题主要考查了根据函数性质求解参数以及三角函数变换的方法等.属于中档题.8．已知ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，若222c a b -=，且c =a -的取值范围是（ ）A ．(1,0)-B ．(1-C ．(D ．【解析】分析：利用222c a b -=求得,4C π=由正弦定理a 转化为A 、B 的表达式，利用三角形内角和定理华为同一个角的三角函数，即可得到2a -的取值范围.详解：由题，222c a b -=，可得222cos ,0,22a b c C C ab π+-==<<,4C π∴=由正弦定理可得2,2sin ,2sin sin sin sin c b ab B a A C B A===∴==， 且3,44A B B πππ=--=-则32sin 2sin 4a A B B B π⎛⎫==- ⎪⎝⎭B B B B =30,4B π<<2cos 1,12B B ∴-<<-<< 故选B.点睛：本题主要考查了正弦定理，余弦定理，三角函数恒等变形的应用，属于基础题． 9．已知函数f （x ）＝x 2+bx ，若f （f （x ））的最小值与f （x ）的最小值相等，则实数b 的取值范围是（ ） A ．[0，2]B ．[﹣2，0]C ．（﹣∞，﹣2]∪[0，+∞）D ．（﹣∞，0]∪[2，+∞）【答案】D【解析】先求得()f x 的最小值,再根据二次函数对称轴与值域的关系列出不等式求解即可. 【详解】由于f （x ）＝x 2+bx ,x ∈R.则当x 2b =-时,f （x ）min 24b =-, 又函数y ＝f （f （x ））的最小值与函数y ＝f （x ）的最小值相等,则函数y 必须要能够取到最小值,即242b b-≤-,得到b ≤0或b ≥2,所以b的取值范围为{b|b≥2或b≤0}.故选：D.【点睛】本题主要考查了二次函数的性质运用,需要分析到对称轴满足的关系式,属于常考题. 10．给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②用一个平面去截棱锥，棱锥底面与截面之间的部分是棱台；③半圆绕着它的直径所在的直线旋转一周所形成的曲面叫做球面；④棱台的侧棱延长后交于一点，侧面是等腰梯形．其中正确命题的序号是（）A．①②④B．①②③C．②③D．③【答案】D【解析】根据常见几何体的性质逐个判定即可.【详解】对于①,棱柱的侧棱都相等,侧面都是平行四边形,但不一定是全等平行四边形,所以①错误；对于②,用一个平行于底面的平面去截棱锥,棱锥底面与截面之间的部分是棱台,所以②错误；对于③,半圆绕着它的直径所在的直线旋转一周所形成的曲面叫做球面,③正确；对于④,棱台的侧棱延长后交于一点,但侧面不一定是等腰梯形,所以④错误.综上知,正确的命题序号是③.故选：D.【点睛】本题主要考查了常见几何体的性质判定,属于基础题.二、多选题11．抛掷一枚骰子1次,记“向上的点数是4,5,6”为事件A,“向上的点数是1,2”为事件B,“向上的点数是1,2,3”为事件C,“向上的点数是1,2,3,4”为事件D,则下列关于事件A，B，C，D判断正确的有（）A．A与B是互斥事件但不是对立事件B．A与C是互斥事件也是对立事件C．A与D是互斥事件D．C与D不是对立事件也不是互斥事件【答案】AD【解析】根据互斥事件的定义以及对立事件的定义逐个判定即可. 【详解】抛掷一枚骰子1次,记“向上的点数是4,5,6”为事件A ,“向上的点数是1,2”为事件B , “向上的点数是1,2,3”为事件C ,“向上的点数是1,2,3,4”为事件D ,在A 中,A 与B 不能同时发生,但能同时不发生,是互斥事件但不是对立事件,故A 正确； 在B 中,A 与C 是对立事件,故B 错误；在C 中,A 与D 能同时发生,不是互斥事件,故C 错误；在D 中,C 与D 能同时发生,不是对立事件也不是互斥事件,故D 正确. 故选：AD. 【点睛】本题主要考查了互斥与对立事件的判定,属于基础题. 12．下列说法中正确的有（ ）A ．设正六棱锥的底面边长为1，侧棱长为B ．用斜二测法作△ABC 的水平放置直观图得到边长为a 的正三角形，则△ABC 面积2 C ．三个平面可以将空间分成4，6，7或者8个部分 D ．已知四点不共面，则其中任意三点不共线． 【答案】ACD【解析】对A,根据题意求出底面积与高再求体积判定即可. 对B,根据斜二测画法前后面积的关系求解判断即可. 对C,分析这三个平面的位置关系再逐个讨论即可. 对D,利用反证法证明即可. 【详解】对于A,正六棱锥的底面边长为1,则S 底面积＝6•12⨯1×1×sin60°=；则棱锥的高h ==2,所以该棱锥的体积为V 13=S 底面积h 13=2=正确； 对于B,水平放置直观图是边长为a 的正三角形,直观图的面积为S ′12=⨯a 2×sin60°2=,则原△ABC 的面积为S ＝′＝2a 2=a 2,所以B 错误；对于C,若三个平面互相平行,则可将空间分为4部分；若三个平面有两个平行,第三个平面与其它两个平面相交,则可将空间分为6部分； 若三个平面交于一线,则可将空间分为6部分；若三个平面两两相交且三条交线平行（联想三棱柱三个侧面的关系）,则可将空间分为7部分；若三个平面两两相交且三条交线交于一点（联想墙角三个墙面的关系）,则可将空间分为8部分；所以三个平面可以将空间分成4,6,7或8部分,C 正确；对于D,四点不共面,则其中任意三点不共线,否则是四点共面,所以D 正确； 综上知,正确的命题序号是ACD. 故选：ACD. 【点睛】本题主要考查了立体几何中的基本性质与空间中线面的关系问题,属于基础题. 13．下列函数()f x 对任意的正数1x ，2x ，3x 满足123123()()()()f x x x f x f x f x ++≤++的有（ ）A ．()42sin f x x =+B ．()f x =C ．()xf x e =D ．()ln(1)f x x =+【答案】ABD【解析】根据四个选项中的函数证明不等式123123()()()()f x x x f x f x f x ++≤++成立或举反例说明不成立(举反例时中让123x x x ==)． 【详解】A ．123123()42sin()6f x x x x x x ++=+++≤，123123()()()42sin 42sin 42sin 6f x f x f x x x x ++=+++++≥，A 正确；B ．2123123x x x x x x =+++>++，B 正确；C ．1231x x x ===时，1233x x x e e e e e ++=>++，C 错；D ．123123122313123123(1)(1)(1)11x x x x x x x x x x x x x x x x x x +++=+++++++>+++，∴123123123ln[(1)(1)(1)]ln(1)ln(1)ln(1)ln(1)x x x x x x x x x +++=+++++>+++，D 正确． 故选：ABD ． 【点睛】本题考查正弦函数、幂函数、指数函数、对数函数的性质，对于函数的性质123123()()()()f x x x f x f x f x ++≤++，正确的需进行证明，错误的可举一反例说明．三、填空题14．连掷两次骰子得到的点数分别为m 和n ，记向量(),a m n =与向量()1,1b =-的夹角为θ，则θ为锐角的概率是__________． 【答案】512【解析】连掷两次骰子分别得到点数m ,n ,所组成的向量(m ,n )的个数共有36种由于向量(m ,n )与向量(1,−1)的夹角θ为锐角,∴(m ,n )⋅(1,−1)>0， 即m >n ，满足题意的情况如下： 当m =2时，n =1； 当m =3时，n =1，2； 当m =4时，n =1，2，3； 当m =5时，n =1，2，3，4；当m =6时，n =1，2，3，4，5；共有15种， 故所求事件的概率为：1553612= . 15．若等腰△ABC 的周长为3，则△ABC 的腰AB 上的中线CD 的长的最小值为_____【解析】画图利用三角形三边的关系以及余弦定理分析求解即可. 【详解】如图所示,设腰长AB ＝2x ,则BC ＝3﹣4x ＞0,解得0＜x34＜；由中线长定理可得：2CD2+2x2＝（2x）2+（3﹣4x）2,化为：CD2＝9（x23-）212+；∴x23=时,CD取得最小值为1222=.2.【点睛】本题主要考查了利用三角形三边之间的关系与余弦定理求解线段长度的最值问题等,需要建立关于所求线段的等式再根据函数的最值分析.属于常考题.16．用一张长为12，宽为8的铁皮围成圆柱形的侧面，则这个圆柱的体积为_____；半径为R的半圆形铁皮卷成一个圆锥筒，那么这个圆锥筒的高是_____．【答案】288π或192π3【解析】①根据底面周长等于铁皮的边长,进而求得底面半径,再计算体积即可.②根据圆锥底面周长等于扇形弧长列式求解即可.【详解】①若圆柱的底面周长为12,则底面半径为r6π=,高为h＝8,此时圆柱的体积为V＝π•r2•h288π=；若圆柱的底面周长为8cm,则底面半径为r′4π=,h′＝12,此时圆柱的体积V＝π•r′2•h′192π=；所以圆柱的体积为288π或192π；②半径为R的半圆形铁皮卷成一个圆锥筒,所以底面圆的半径r满足2πr＝πR,即2r＝R；所以该圆锥筒的轴截面是边长为R的等边三角形,则其高为h ==. 故答案为：(1)288π或192π. 【点睛】本题主要考查了圆柱与圆锥的体积与周长等的关系,属于常考题.17．对于函数y ＝f （x ），若在其定义域内存在x 0，使得x 0f （x 0）＝1成立，则称函数f （x ）具有性质M ．（1）下列函数中具有性质M 的有____ ①f （x ）＝﹣x +2②f （x ）＝sin x （x ∈[0，2π]） ③f （x ）＝x 1x+，（x ∈（0，+∞）） ④f （x）=（2）若函数f （x ）＝a （|x ﹣2|﹣1）（x ∈[﹣1，+∞））具有性质M ，则实数a 的取值范围是____．【答案】①②④ a 12≤-或a ＞0 【解析】（1）①因为f （x ）＝﹣x +2，若存在，则()0021x x -+=，解一元二次方程即可.②若存在，则00sin 1x x =，即00sin 10x x -=，再利用零点存在定理判断.③若存在，则00011x x x ⎛⎫+= ⎪⎝⎭，直接解方程.④若存在，则1x =，即10x -=，令()01f x x =-，再利用零点存在定理判断.（2）若函数f （x ）＝a （|x ﹣2|﹣1）（x ∈[﹣1，+∞））具有性质M ，则ax （|x ﹣2|﹣1）=1，x ∈[﹣1，+∞）有解，将问题转化 ：当2x ≥ 时，213a x x=- 有解，当12x -≤< 时，21a x x=-+ 有解，分别用二次函数的性质求解.【详解】（1）①因为f （x ）＝﹣x +2，若存在，则()0021x x -+=， 即200210x x -+=，所以01x = ，存在.②因为f （x ）＝sin x （x ∈[0，2π]），若存在，则00sin 1x x =， 即00sin 10x x -=， 令()00sin 1f x x x =-，因为()πππ⎛⎫=-<=->⎪⎝⎭1sin 110,sin 10222f f ， 所以存在01,2x π⎛⎫∈ ⎪⎝⎭. ③因为f （x ）＝x 1x+，（x ∈（0，+∞）），若存在，则00011x x x ⎛⎫+= ⎪⎝⎭，即()000,x =∉+∞，所以不存在. ④因为f （x）（x ∈（0，+∞）），若存在，则1x =，即10x -=， 令()1f x x =-，因为()1110,11022f f ⎛⎫=-<=-> ⎪⎝⎭，所以存在01,12x ⎛⎫∈⎪⎝⎭. （2）若函数f （x ）＝a （|x ﹣2|﹣1）（x ∈[﹣1，+∞））具有性质M ， 则ax （|x ﹣2|﹣1）=1，x ∈[﹣1，+∞）有解， 当2x ≥ 时，213a x x=- 有解， 令2239()3[2,)24g x x x x ⎛⎫=-=--∈-+∞ ⎪⎝⎭ ，所以1(,](0,)2a ∈-∞-+∞ .当12x -≤< 时，21a x x=-+ 有解， 令22111()[2,]244g x x x x ⎛⎫=-+=--+∈- ⎪⎝⎭ ，所以1(,](0,4]2a ∈-∞- .综上：实数a 的取值范围是a 12≤-或a ＞0. 故答案为：(1). ①②④ (2). a 12≤-或a ＞0【点睛】本题主要考查了函数的零点，还考查了转化化归的思想和运算求解的能力，属于中档题.四、解答题18．某校有教师400人，对他们进行年龄状况和学历的调查，其结果如下：(1)若随机抽取一人，年龄是35岁以下的概率为35，求,x y ； (2)在35-55岁年龄段的教师中，按学历状况用分层抽样的方法，抽取一个样本容量为5的样本，然后在这5名教师中任选2人，求两人中至多有1人的学历为本科的概率. 【答案】（1）20；（2）710【解析】分析：（1）(1)由由古典概型概率公式8034005x +=，解得160x =,故()4001608060404020y =-++++=；（2）由分层抽样的规律可知，需学历为研究生的2人，记为12,A A ，学历为本科的3人，记为的123,,B B B ，列举可得总的基本事件，找出符合题意得基本事件，由古典概型公式可得. 详解：(1)由已知可知8034005x +=，解得160x =, 故()4001608060404020y =-++++=.(2)由分层抽样的规则可知，样本中学历为硕士的人数为4052100⨯=人，记为12,A A , 学历为本科的人数为6053100⨯=人.记为123,,B B B , 从中任选2人所有的基本事件为121112132121222312|,|,,,,,,,,,,,,,,,,A A A B A B A B A B A B A B A B B B1323,,,?B B B B 共10个，设“至多有1人的学历为本科”为事件A ，则事件A 包含的基本事件为1211121321|,|,,,,,,,,A A A B A B A B A B 2223,,,A B A B ，共7个.所以()710P A =. 点睛：本题主要考查分层抽样的应用以及古典概型概率公式的应用，属于中档题. 总体中个体差异明显，层次分明适合分层抽样，其主要性质是，每个层次，抽取的比例相同. 19．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，且2bacosB c =-． （1）求角A ；（2）若△ABC 外接圆的面积为4π，且△ABC 的面积S =△ABC 的周长．【答案】（1）3A π=．（2）6+．【解析】(1)根据正弦定理边化角,再利用三角函数和差角公式化简求解即可.(2)利用正弦定理可得a =,再结合面积公式与余弦定理求解b c +即可. 【详解】解：（1）法一：已知2bacosB c =-,由正弦定理得2sin A cos B ＝2sin C ﹣sin B ＝2sin （A +B ）﹣sin B ,可得：2cos A sin B ﹣sin B ＝0,可得：sin B （2cos A ﹣1）＝0, ∵sin B ≠0, ∴12cosA =, ∵A ∈（0,π）, ∴3A π=. 法二：已知2b acosB c =-,由余弦定理得22222a cb ba c ac +-⋅=-,可得：a 2＝b 2+c 2﹣bc又a 2＝b 2+c 2﹣2bc cos A , ∴12cosA =, ∵A ∈（0,π）, ∴3A π=. （2）由△ABC 外接圆的面积为πR 2＝4π,得到R ＝2,由正弦定理知23243a a R sinA ===, ∴23a =. ∵△ABC 的面积1232S bcsinA ==,可得bc ＝8. 法一：由余弦定理得a 2＝b 2+c 2﹣2bc cos A ＝（b +c ）2﹣3bc ,即12＝（b +c ）2﹣24 从而b +c ＝6,故△ABC 的周长为623a b c ++=+.法二：由余弦定理得a 2＝b 2+c 2﹣2bc cos A ＝b 2+c 2﹣bc ,即b 2+c 2＝20从而42b c =⎧⎨=⎩或24b c =⎧⎨=⎩, 故△ABC 的周长为623a b c ++=+. 【点睛】本题主要考查了正余弦定理与面积公式等在解三角形中的运用,属于中档题.20．如图，在空间四边形ABCD 中，,E F 分别是,AB AD 的中点，,G H 分别在,BC CD 上，且::1:2BG GC DH HC ==.（1）求证：,,,E F G H 四点共面；（2）设EG 与FH 交于点P ，求证：,,P A C 三点共线. 【答案】（1）见解析；（2）见解析.【解析】试题分析：（1）利用三角形的中位线平行于第三边；平行线分线段成比例定理，得到EF 、GH 都平行于BD ，利用平行线的传递性得到EF ∥GH ，据两平行线确定以平面得证．（2）利用分别在两个平面内的点在两个平面的交线上，得证． 试题解析：证明：（1）因为,E F 分别为,AB AD 的中点， 所以EFBD .在BCD ∆中，BG DHGC HC=， 所以GHBD ，所以EF GH .所以,,,E F G H 四点共面.（2）因为EG FH P ⋂=，所以P EG ∈，又因为EG ⊂平面ABC ， 所以P ∈平面ABC ， 同理P ∈平面ADC ，所以P 为平面ABC 与平面ADC 的一个公共点. 又平面ABC 平面ADC AC =. 所以P AC ∈，所以,,P A C 三点共线. 21．已知奇函数f （x ）222x b x +=+，函数g （θ）＝cos 2θ+2sinθ32-，θ∈[m ，56π]．m ，b ∈R ．（1）求b 的值；（2）判断函数f （x ）在[0，1]上的单调性，并证明；（3）当x ∈[0，1]时，函数g （θ）的最小值恰为f （x ）的最大值，求m 的取值范围． 【答案】（1）b ＝0；（2）在[0，1]上的单调递增，证明见解析；（3）566ππ≤<m 【解析】（1）根据函数f （x ）222x bx +=+为奇函数，令f （0）＝0求解.（2）函数f （x ）在[0，1]上的单调递增，再利用函数的单调性定义证明.（3）根据（2）知，函数f （x ）在[0，1]上的单调递增，得到()()114max f x f ==．即g （θ）的最小值为14，再令t ＝sinθ，转化为二次函数求解. 【详解】（1）因为函数f （x ）222x bx +=+为R 上的奇函数，所以f （0）＝0，解得b ＝0．（2）函数f （x ）在[0，1]上的单调递增． 证明：设1201x x ≤≤≤则：f （x 2）﹣f （x 1）()21122122222121()1112112(1)(1)x x x x x x x x x x --⎛⎫=-=⨯⎪++++⎝⎭，因为1201x x ≤≤≤， 所以x 2﹣x 1＞0，1﹣x 1x 2＞0， 所以()21122221()1102(1)(1)x x x x x x --⨯++＞， 即f （x 2）> f （x 1），所以函数f （x ）在[0，1]上的单调递增．（3）由（2）得：函数f （x ）在[0，1]上的单调递增，所以()()114max f x f ==．所以g （θ）的最小值为14． 令t ＝sinθ，所以y 2122=-+-t t 的最小值为14，令211224=-+-=t t解得13,22==t t所以1322≤≤t ，即112sin θ≤≤， 所以5,66ππθ⎡⎤∈⎢⎥⎣⎦ 又因为θ∈[m ，56π]．m ，b ∈R ， 所以566ππ≤<m ． 【点睛】本题主要考查了函数的基本性质，还考查了转化化归的思想及运算求解的能力，属于难题.22．一走廊拐角处的横截面如图所示，已知内壁FG 和外壁BC 都是半径为1m 的四分之一圆弧，AB,DC 分别与圆弧BC 相切于B,C 两点，EF //AB,GH //CD,且两组平行墙壁间的走廊宽度都是1m.（1）若水平放置的木棒MN 的两个端点M ,N 分别在外壁CD 和AB 上，且木棒与内壁圆弧相切于点P,设CMN (rad ),θ∠=试用θ表示木棒MN 的长度f ();θ （2）若一根水平放置的木棒能通过该走廊拐角处，求木棒长度的最大值．【答案】（1）)20(cos sin 1)cos (sin 2)(πθθθθθθ<<-+=f ；（2）224-．【解析】试题分析：（1）如图，设圆弧FG 所在的圆的圆心为Q ，过Q 点作CD 垂线，垂足为点T ，且交MN 或其延长线与于S ，并连接PQ ，再过N 点作TQ 的垂线，垂足为W ．在NWS Rt ∆中用NW 和SNW ∠表示出NS ，在QPS Rt ∆中用PQ 和PQS ∠表示出QS ，然后分别看S 在线段TG 上和在线段GT 的延长线上分别表示出TS=QT-QS ，然后在STM Rt ∆中表示出MS ，利用MN=NS+MS 求得MN 的表达式和)(θf 的表达式． （2）设出)21(,cos sin ≤<=+t t θθ，则θθcos sin 可用t 表示出，然后可得)(θf 关于t 的表达式，对函数进行求导，根据t 的范围判断出导函数与0的大小，进而就可推断出函数的单调性；然后根据t 的范围求得函数的最小值． 试题解析：⑴如图，设圆弧FG 所在的圆的圆心为Q ，过Q 点作CD 的垂线，垂足为点T ，且交MN 或其延长线于S ，并连结PQ ，再过点N 作TQ 的垂线，垂足为W ，在NWS Rt ∆中，因为NW=2，θ=∠SNW ，所以θcos 2=NS ，因为MN 与圆弧FG 切于点P ，所以MN PQ ⊥，在QPS Rt ∆中，因为PQ=1，PQS ∠θ=，所以θθcos 12,cos 1-=-=QS QT QS ， ①若M 在线段TD 上，即S 在线段TG 上，则TS=QT-QS ，在STM Rt ∆中，θθsin sin QSQT TS MS -==， 因此θsin QSQT NS MS NS MN -+=+=．②若M 在线段CT 上，即若S 在线段GT 的延长线上，则TS=QS-QT ，在STM Rt ∆中，θθsin sin QTQS TS MS -==， 因此θθsin sin QSQT NS QT QS NS MS NS MN -+=--=+=．．0)(<'t g 恒成立，所以一根水平放置的木棒若能通过该走廊拐角处，则其长度的最大值为224-． 【考点】解三角形的实际应用．23．已知函数y ＝f 1（x ），y ＝f 2（x ），定义函数f （x ）()()()()()()112212f x f x f x f x f x f x ⎧≤⎪=⎨⎪⎩，，＞． （1）设函数f 1（x ）＝x +3，f 2（x ）＝x 2﹣x ，求函数y ＝f （x ）的解析式；（2）在（1）的条件下，g （x ）＝mx +2（m ∈R ），函数h （x ）＝f （x ）﹣g （x ）有三个不同的零点，求实数m 的取值范围；（3）设函数f 1（x ）＝x 2﹣2，f 2（x ）＝|x ﹣a |，函数F （x ）＝f 1（x ）+f 2（x ），求函数F （x ）的最小值． 【答案】（1）()231313x x x f x x x x +≤-≥⎧=⎨--⎩，或，＜＜；（2）()40113⎛⎫⋃ ⎪⎝⎭，，；（3）()2914211[]2229142mina a F x a a a a ⎧---⎪⎪⎪=--≤≤⎨⎪⎪-⎪⎩，＜，，＞【解析】（1）根据函数f （x ）()()()()()()112212f x f x f x f x f x f x ⎧≤⎪=⎨⎪⎩，，＞的定义，两个函数中取小的.（2）函数h （x ）＝f （x ）﹣g （x ）有三个不同的零点，即方程f （x ）＝g （x ）有三个不同的实数根，因为函数()f x 是分段函数，分类讨论，分别用一次方程和二次方程求解.（3）根据题意F （x ）2219241924x a x a x a x a ⎧⎛⎫+--≥⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪-+- ⎪⎪⎝⎭⎩，，＜．按照二次函数函数定区间动的类型，讨论对称轴与区间端点值间的关系求最值.【详解】（1）∵f 1（x ）＝x +3，()22f x x x =-， 当f 1（x ）≤f 2（x ），即x ≥3或x ≤﹣1时，f （x ）＝x +3，当f 1（x ）＞f 2（x ），即﹣1＜x ＜3时，()2f x x x =-， 综上：()231313x x x f x x x x +≤-≥⎧=⎨--⎩，或，＜＜． （2）函数h （x ）＝f （x ）﹣g （x ）有三个不同的零点，即方程f （x ）＝g （x ）有三个不同的实数根，因为函数()231313x x x f x x x x +≤-≥⎧=⎨--⎩，或，＜＜，函数g （x ）＝mx +2（m ∈R ）， 所以当x ≤﹣1或x ≥3时，mx +2＝x +3恰有一个实数解， 所以11103m x ⎛⎤-=∈ ⎥⎝⎦，或[)1110m x-=∈-，， 解得，[)40113m ⎛⎤∈⋃ ⎥⎝⎦，，． 当﹣1＜x ＜3时，mx +2＝x 2﹣x 恰有两个不同的实数解，即当﹣1＜x ＜3时x 2﹣（m +1）x ﹣2=0恰有两个不同的实数解，设函数h （x ）＝x 2﹣（m +1）x ﹣2，由题意可得()()010301132h h m ∆⎧⎪-⎪⎪⎨⎪+⎪-⎪⎩＞＞＞＜＜，所以2(1)8004335m m m m ⎧++⎪⎪⎪⎨⎪⎪-⎪⎩＞＞＜＜＜， 解得403m ⎛⎫∈ ⎪⎝⎭，， 综上，m 的取值范围为()40113⎛⎫⋃ ⎪⎝⎭，，． （3）F （x ）＝f 1（x ）+f 2（x ）＝x 2+|x ﹣a |﹣222221924221924x a x a x x a x a x x a x a x a x a ⎧⎛⎫+--≥⎪ ⎪⎧+--≥⎪⎝⎭==⎨⎨-+-⎩⎛⎫⎪-+- ⎪⎪⎝⎭⎩，，，＜，＜． ①若a 12＞，则函数F （x ）在12⎛⎫-∞ ⎪⎝⎭，上是单调减函数，在12⎛⎫+∞ ⎪⎝⎭，上是单调增函数， 此时，函数F （x ）的最小值为1924F a ⎛⎫=-⎪⎝⎭； ②若1122a -≤≤，则函数F （x ）在（﹣∞，a ）上是单调减函数，在（a ，+∞）上是单调增函数，此时，函数F （x ）的最小值为F （a ）＝a 2﹣2；③若12a -＜，则函数F （x ）在12⎛⎫-∞- ⎪⎝⎭，上是单调减函数，在12⎛⎫-+∞ ⎪⎝⎭，上是单调增函数，此时，函数F （x ）的最小值为1924F a ⎛⎫-=-- ⎪⎝⎭； 综上：()2914211[]2229142min a a F x a a a a ⎧---⎪⎪⎪=--≤≤⎨⎪⎪-⎪⎩，＜，，＞． 【点睛】本题主要考查了分段函数的应用，还考查了分类讨论，运算求解的能力，属于难题.。

高一年级阶段检测一数学（创新班）试卷一、填空题：本大题共14小题，每小题5分，共计70分．1.已知集合，则＝______．【答案】【解析】，填．2.已知数列的一个通项公式为______．【答案】【解析】【分析】将化为，然后探究分母、分子的规律，然后还有正负的交替出现【详解】由已知可以得到，则有故通项公式为【点睛】本题主要考查了通过观察分析猜想归纳求数列的通项公式的方法，属于基础题。

3.在中，，，，则此三角形的最大边长为______．【答案】【解析】试题分析：首先根据最大角分析出最大边，然后根据内角和定理求出另外一个角，最后用正弦定理求出最大边．因为B=135°为最大角，所以最大边为b，根据三角形内角和定理：A=180°-（B+C）=30°，在△ABC中有正弦定理有：考点：正弦定理4.已知角的终边经过点，则的值等于______．【答案】【解析】，所以，，故，填．5.已知向量，，，则的值为______．【答案】8【解析】，所以，所以，故，填．6.已知函数则的值为______．【答案】2【解析】【分析】先求出的值，然后代入求解【详解】由函数的表达式可知：当时，当时，故答案为2【点睛】本题主要考查了求函数的值，只需代入分段函数中即可得到结果，较为简单。

7.《九章算术》是中国古代数学名著，其对扇形田面积给出“以径乘周四而一”的算法与现代数学的算法一致，根据这一算法解决下列问题：现有一扇形田，下周长（弧长）为20米，径长（两段半径的和）为24米，则该扇形田的面积为______平方米．【答案】120【解析】扇形的半径为，故面积为（平方米），填．8.若关于的不等式的解集，则的值为______．【答案】-3【解析】试题分析：显然t<0，且是方程的两根，由韦达定理得，解得．考点：不等式的解法．9.已知函数在区间上的最大值等于8，则函数的值域为______．【答案】【解析】二次函数的对称轴为，故，所以且，对称轴为，故所求值域为，填．10.已知函数是定义在R上的偶函数，则实数的值等于____．【答案】-1【解析】因为为偶函数，故，所以，整理得到，即，又当时，有，，故，为偶函数，故填．11.如图，在梯形ABCD中，，P为线段CD上一点，且，E为BC的中点，若，则的值为______．【答案】【解析】，整理得到，又，所以，也就是，，填．12.在锐角△ABC中，若，则边长的取值范围是_________。

（第11题）D2018-2019学年江苏省海安高级中学高一上学期第一次月考数学试题（创新班）一、填空题：本大题共14小题，每小题5分，共计70分． 1．已知集合{0,1,2},{0,2,4}A B ==，则A B ＝ ▲ ．2．已知数列1157,,,221220--的一个通项公式为 ▲ ． 3．在ABC ∆中，135B =︒，15C =︒，5a =，则此三角形的最大边长为 ▲ ． 4．已知角α的终边经过点(2,4)P -，则sin cos αα-的值等于 ▲ ． 5．已知向量(,5)AB m =，(4,)AC n =，(7,6)BC =，则m n +的值为 ▲ ．6．已知函数1232e ,2,()log (1),2,x x f x x x -⎧<⎪=⎨-⎪⎩≥ 则))2((f f 的值为 ▲ ． 7．《九章算术》是中国古代数学名著，其对扇形田面积给出“以径乘周四而一”的算法与现代数学的算法一致，根据这一算法解决下列问题：现有一扇形田，下周长（弧长）为20米，径长（两段半径的和）为24米，则该扇形田的面积为 ▲ 平方米． 8．若关于x 的不等式2260tx x t -+<的解集(,)(1,)a -∞+∞，则a 的值为 ▲ ．9．已知函数2() 2 (0)f x x ax a =++>在区间[0,2]上的最大值等于8，则函数() ([2,1])y f x x =∈-的值域为 ▲ ．10．已知函数2()22x x f x x m -=+-⋅是定义在R 上的偶函数，则实数m 的值等于 ▲ ． 11．如图，在梯形ABCD 中，2DC AB =，P 为线段CD 上一点，且3DC PC =，E 为BC的中点，若1212 (,)EP AB AD λλλλ=+∈R ，则12λλ+的值为 ▲ ． 12．在锐角△ABC 中，若a =2，b =3，则边长c 的取值范围是 ▲ ． 13．将函数sin y x =的图象向左平移3π个单位长度，再将图象上每个点的横坐标变为原来的1(0)ωω>倍（纵坐标不变），得到函数()y f x =的图象，若函数()y f x =在区间π(0,)2上有且仅有一个零点，则ω的取值范围为 ▲ ． 14．已知,x y 为非零实数，()ππ,42θ∈，且同时满足：①sin cos y xθθ=，② 22103x y xy =+，则cos θ的值等于 ▲ ．（第17题）二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）已知函数1()41x f x a =++的图象过点3(1,)10-．（1）判断函数()f x 的奇偶性，并说明理由； （2）若1()6f x -≤≤0，求实数x 的取值范围．16．（本小题满分14分）如图，在四边形ABCD 中，4,2AD AB ==．（1）若△ABC 为等边三角形，且AD BC ∥，E 是CD 的中点，求AE BD ⋅； （2）若AC AB =，3cos 5CAB ∠=，45AC BD ⋅=，求||DC ．17．（本小题满分14分）如图，在海岸A处，发现南偏东45°方向距A为(23－2)海里的B处有一艘走私船，在A处正北方向，距A为22海里的C处的缉私船立即奉命以103海里/时的速度追截走私船．（1）刚发现走私船时，求两船的距离；（2）若走私船正以102海里/时的速度从B处向南偏东75°方向逃窜，问缉私船沿什么方向能最快追上走私船？并求出所需要的时间(精确到分钟，参考数据：2≈1.4，6≈2.5)．18．（本小题满分16分）已知sinα+cosβ=35，cosα+sinβ=45，求：（1）sin(α+β)的值；（2）cosα sinβ的值．19．（本小题满分16分）已知(2cos ,1),cos ,1)x x x ==+-a b ，函数()f x =⋅a b ．（1）求()f x 在区间π[0,]4上的最大值和最小值； （2）若06()5f x =，0[,]42x ππ∈，求0cos2x 的值； （3）若函数()y f x ω=在区间(,)33π2π上是单调递增函数，求正数ω的取值范围．20．（本小题满分16分）设a 为实数，设函数()5f x a =+，设t =（1）求t 的取值范围，并把()f x 表示为t 的函数()g t ； （2）若()0g t ≥恒成立，求实数a 的取值范围； （3）若存在t 使得()g t t <成立，求实数a 的取值范围．一、填空题：1.{}0,22. 121(1)(1)n n n n ---⋅+3. 524.355.86.27.1208.-39.7[,4]410.1-11.1312. 13.410(,]3310 二、解答题：15．解：（1）因为()f x 的图象过点3(1,)10-， 所以13510a +=-，解得12a =-，所以11(),412x f x =-+ ……………………2分 ()f x 的定义域为R ． ……………………4分因为114141()()4124122(41)x x xx x f x f x ---=-=-==-+++， ……………………7分 所以()f x 是奇函数． …………………………………………8分（2）因为1()06f x -≤≤， 所以11106412x--+≤≤， 所以1113412x +≤≤， …………………………………………10分 所以2413x ≤+≤，所以142x ≤≤， ……………………………………12分 解得102x ≤≤． ……………………………………14分 16．（1）法一：因为△ABC 为等边△，且,AD BC ∥所以120DAB ∠=︒．…2分又2,AD AB =所以2AD BC =，因为E 是CD 中点，所以1()2AE AD AC =+1()2AD AB BC =++11()22AD AB AD =++3142AD AB =+． ……………………………………4分 又BD AD AB =-，所以AE BD ⋅31()()42AD AB AD AB =+⋅- 22311424AD AB AD AB =--⋅ ……………………………………6分311116442()4242=⨯-⨯-⨯⨯⨯-=11. ……………………………………8分 法二：如图，以A 为原点，AB 所在直线为x 轴，建立平面直角坐标系，则(00)(2,0)A B ，，， 因为△ABC 为等边△，且,AD BC ∥所以120DAB ∠=︒． ………2分又24,AD AB ==所以2AB AC ==，所以(C D -，因为E 是CD 中点， 所以1(22E -，………………4分 所以1(22AE =-，,(4BD =- ……6 分所以1((42AE BD ⋅=-⋅-，1()(4)22=-⨯-+=11． ………………………………8分（2）因为2AB AC AB ==，，所以2AC =,因为4,5AC BD ⋅=所以4(),5AC AD AB ⋅-=所以4.5AC AD AC AB ⋅-⋅= ………………………………10分 又312cos 4.55AC AB AC AB CAB ⋅=∠=⨯=所以41655AC AD AC AB ⋅=+⋅=．……12分22222DC AC AD AC AD AC AD=-=+-⋅1641625=+-⨯685=．所以285DC =14分 17．解：（1）在△ABC 中，∵AB ＝(23－2)海里，AC ＝22海里，∠BAC ＝135°，由余弦定理，得 BC ＝(23－2)2＋(22)2－2×22×(23－2)cos 135°＝4(海里)． ……….4分 （2）根据正弦定理，可得sin ∠ABC ＝AC sin 135°BC ＝22.∴∠ABC ＝45°，易知∠ACB ＝15°，…2分设缉私船应沿CD 方向行驶t 小时，才能最快截获(在D 点)走私船，则有CD ＝103t (海里)，BD ＝10t (海里)．而∠CBD ＝120°，在△BCD 中，根据正弦定理，可得 sin ∠BCD ＝BD sin ∠CBD CD ＝102t ·sin 120°103t＝22，∴∠BCD ＝45°，∠BDC ＝15°， ………..2分 ∴根据正弦定理，得233104264t=-，解得分钟小时4778.0526≈≈+=t ．………..2分 故缉私船沿南偏东60°方向，需47分钟才能追上走私船．19．（1）()2cos cos )12cos2f x x x x x x =⋅=+-+a b π2sin(2)6x =+， …2分因为π[0,]4x ∈，所以ππ2π2663x +≤≤，所以1πsin(2)126x +≤≤， 所以max min ()2,()1f x f x ==． …………………………………………4分 （2）因为06()5f x =，所以0π62sin(2)65x +=，所以0π3sin(2)65x +=， 因为0ππ[,]42x ∈，所以02ππ7π2366x +≤≤，所以0π4cos(2)65x +==-， ………………………………6分所以0000πππ1πcos2cos[(2)])sin(2)662626x x x x =+-=+++4133()252510-=-+⨯=． ………………………………………8分 （3）()n 26πsi f x x ωω⎛⎫=+ ⎪⎝⎭令222,,26πππππ2k x k k ω-++∈Z ≤≤ 得ππ6ππ3k k x ωωωω+-≤≤， ……10分 因为函数()f x 在(π2,3π)3上是单调递增函数，所以存在0k ∈Z ，使得002(,)(ππππππ,)3336k k ωωωω⊆-+所以有00ππππ,33π2.63πk k ωωωω⎧-⎪⎪⎨⎪+⎪⎩≤≥ 即0031,614.k k ωω+⎧⎨+⎩≤≥ …………………………12分因为0,ω>所以01,6k >-又因为212332πππ2ω-⋅≤， 所以302ω<≤, 所以05.6k ≤ 14分从而有01566k -<≤，所以00k =，所以10.4ω<≤ …16分（另解：由212332πππ2ω-⋅≤，得302ω<≤. 因为2(,)33x ππ∈，所以242(,)63636x ωωωπππππ+∈++，所以4362ωπππ+≤或23362ωπππ+≥，解得104ω<≤或2ω≥.又302ω<≤，所以10.4ω<≤） 20．解：1）t =要使t 有意义，必须10x +≥且10x -≥，即11x -≤≤，∴22t =+0t ≥① ∴t的取值范围是2⎤⎦2112t =-， ∴2()3g t t at =++2t ≤≤；（2）由0g t ≥（）恒成立，即有min 0g t ≤（），注意到直线2a t =-是抛物线2()3g t t at =++的对称轴， 分以下几种情况讨论：①当2a-≤a ≥-时，()g t在2⎤⎦上为递增函数，即有t =时，取得最小值，且为5；22a<-<即4a -<<-()g t 的最小值为2()324a a g -=-；③当22a-≥即4a ≤-时，()g t在2⎤⎦上为递减函数， 即有2t =时，取得最小值，且为72a +．则50a ⎧≥-⎪⎨+≥⎪⎩或24304a a -<⎧-≥<-⎪⎨⎪⎩或4720a a ≤-⎧⎨+≥⎩，解得：a ≥-或a -≤-或a ∈∅，则有a ≥-。

2019级创新实验班阶段检测（一）数学试卷一、选择题（本大题共10小题，共50.0分）1． 设集合U =R ，A ={x |0<x <2}，B ={x |x <1}，则图中阴影部分表示的集合为（ ）．A. {x |x ≥1}B. {x |x ≤1}C. {x |0<x ≤1}D. {x |1≤x <2}2． 已知函数()f x = ）．A. (0，+∞)B. [0，+∞)C. (2，+∞)D. [2，+∞)3． 函数13y x -的定义域为（ ）． A. (2，3)∪(3，+∞) B. [2，3)∪(3，+∞) C. [2，+∞) D. (3，+∞)4． 函数⎩⎨⎧≥-<=,0,2,0,1)(2x x x x x f 则f (f (-2018))= （ ）．A. 1B. -1C. 2018D. -2018 5． 若关于x 的一元二次方程x 2 - 4x + m =0没有实数根，则m 的取值范围为（ ）．A. m <2B. m >4C. m >16D. m <8 6． 函数y =|x 2-1|与y =a 的图象有4个交点，则实数a 的取值范围是（ ）．A ．(0，+∞)B ．(-1，1)C ．(0，1)D ．(1，+∞)7． 已知函数22()21f x x ax a =-+-，若关于x 的不等式()()0f f x <的解集为空集，则实数a的取值范围是（ ）．A ．(-3，-2)B ．(-∞，-1)C ．(-∞，-2)D ．(-∞，-2] 8． 函数f (x )定义域为R ，且对任意x ，y ∈R ，()()()f x y f x f y +=+恒成立.则下列选项中不恒成立．．．．的是（ ）． A ．(0)0f = B ．(2)2(1)f f = C ．11()(1)22f f =D ．()()0f x f x -< 9． 已知函数f (x )=|1- |x -1||，若关于x 的方程 [f (x )]2+af (x )=0(a ∈R)有n 个不同实数根，则n 的值不可能为（ ）．A ．3B ．4C ．5D ．6 10．设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y =f (x )- g (x )在x ∈[a ，b ]上有两个不同的解，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )=x 2-3x +4与g (x )=2x +m 在[0，3]上是“关联函数”，则m 的取值范围为（ ）． A. 9(2]4--， B. [-1，0] C. (-∞，-2) D.9()4-+∞， 二、填空题（本大题共6小题，共30.0分）11． 函数⎪⎩⎪⎨⎧≤≤-+≤<-=,03,82,10,11)(2x x x x x x f 的值域是 ▲ ．12． 已知函数()y f x =的定义域为(22)-，，函数()(1)(32)g x f x f x =-+-．则函数()g x 的定义域 ▲ ．13． 不等式11x<的解集是 ▲ ．14． 已知函数f (x )=x 2-2x 在区间[-1，t ]上的最大值为3，则实数t 的取值范围是 ▲ ． 15． 已知关于x 的不等式20ax bx c -->的解集是(21)-，，则不等式20cx bx a -->的解集是 ▲ ．16． 定义：符合()f x x =的x 称为()f x 的一阶不动点，符合(())f f x x =的x 称为()f x 的二阶不动点．设函数()2f x x bx c =++，若函数()f x 没有一阶不动点，则函数()f x 二阶不动点的个数为 ▲ ．三、解答题：本大题共6小题，计80分．请在答题卡指定的区域内作答，解答时应写出文字说明，证明过程或演算步骤． 17．（本题满分12分）已知集合{}2+230A x x x =-≤，{}22240B x x mx m x m =-+-∈∈R R ≤，，． （1）若]1,0[=B A ，求实数m 的值； （2）若B A R C ⊆，求实数m 的取值范围．18．（本题满分12分）已知二次函数2()f x ax bx c =++最小值为1-，且(2)(2)()f x f f x -=+．（1）求()f x 的解析式；（2）若()f x 在区间[]2,1m m +上单调，求m 的取值范围．19．（本题满分12分）A 、B 、C 三位老师分别教数学、英语、体育、劳技、语文、阅读六门课，每位教两门.已知：（1）体育老师和数学老师住在一起， （2）A 老师是三位老师中最年轻的， （3）数学老师经常与C 老师下象棋，（4）英语老师比劳技老师年长，比B 老师年轻， （5）三位老师中最年长的老师其他两位老师家离学校远. 问：A 、B 、C 三位老师每人各教那几门课？20．（本题满分14分）已知Rt △ABC 中，CD 是斜边AB 上的高，BE 是角平分线并且与CD 交于F ，CH ⊥EF ，垂足为H ，延长CH 与AB 交于G .（1）求证:2BG BE BF >⋅； （2）若AC=2BC ，求证EA =5FD .21．（本题满分14分）已知关于x 的不等式组23112(27)70x x k x k ⎧<⎪+⎨⎪+++<⎩，①．②（1）求解不等式②；（2）若此不等式组的整数解集M 中有且只有两个元素，求实数k 的取值范围及相应的集合M ．22．（本小题满分16分）已知函数2()1,()|1|f x x g x a x =-=-．（1）若关于x 的方程|()|()f x g x =只有一个实数解，求实数a 的取值范围； （2）若当x ∈R 时，不等式()()f x g x ≥恒成立，求实数a 的取值范围．2019级创新实验班第一次阶段考试数学参考答案及评分建议一、选择题（本大题共10小题，共50.0分） 1． D 2．B 3． B 4． B 5． B 6． C 7． D 8． D 9． A 10.A二、填空题（本大题共6小题，共30.0分） 11． 【答案】[15)-+∞， 12． 【答案】()15,2213．【答案】(0)(1)-∞+∞，，14．（-1，3]． 15．【答案】1(1)2-，16． 【答案】0．函数()f x 没有一阶不动点，()f x x ≠，()f x 图象开口向上，则()f x x >，于是()()()f f x f x x >>．三、解答题：本大题共6小题，计80分．请在答题卡指定的区域内作答，解答时应写出文字说明，证明过程或演算步骤． 17．（本题满分12分）【解】集合{}31A x x =-≤≤，{}22B x m x m m =-+∈R ≤≤，． ………………………4分（1）因为[01]AB =，，所以20m -=，且21m +≥，于是2m =． …………………6分（2）{}22B x x m x m m =<->+∈R R ，或，ð．…………………………………………8分由于A B ⊆R ð，从而21m ->，或23m +<-，解得3m >，或5m <-． (10)分故m的取值范围(5-∞-∞，，．……………………………………………12分 18．（本题满分12分）解：(1)()222(2)(2)(4)42f x a x b x c ax a b x a b c -=-+-+=-++++因为()2(2)()f x f f x -=+所以22(4)4242ax a b x a b c a b c ax bx c -++++=+++++… ………2分(4)0a b b c -+<⎧⎨=⎩即20b ac =-⎧⎨=⎩…………………4分 所以()222(1)f x ax ax a x a=-=--…………………6分因为()2f x ax bx c =++最小值为1-，所以1a =，所以()22f x x x =-．……8分(2)若()f x 在区间[]2,1m m +上单调，所以1112m m m +⎧⎨+<⎩… 或2112m m m ⎧⎨+<⎩?………10分所以m 的取值范围是0m … 或112m <?<． …………………12分 19．（本题满分12分）A 是劳技老师，数学老师；B 老师是语文和思品；C 老师是英语老师，阅读老师。