下载文档原格式
![5[1].1频谱搬移及调幅的基本原理](https://img.taocdn.com/s1/m/173d7935eefdc8d376ee321d.png)
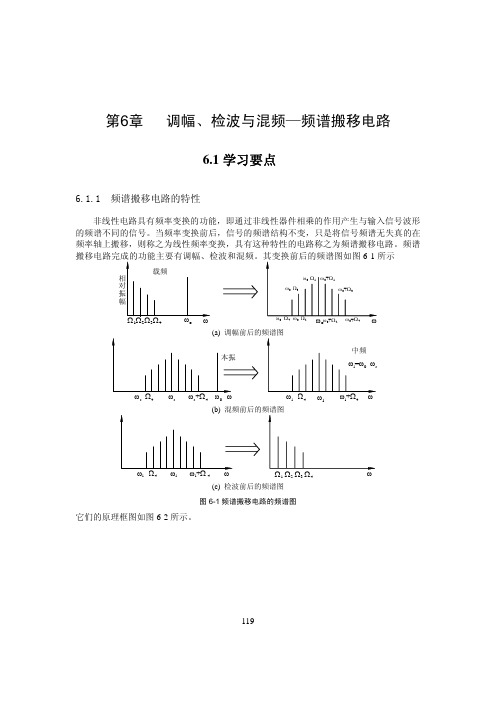
第6章 调幅、检波与混频—频谱搬移电路6.1学习要点6.1.1 频谱搬移电路的特性非线性电路具有频率变换的功能，即通过非线性器件相乘的作用产生与输入信号波形的频谱不同的信号。
当频率变换前后，信号的频谱结构不变，只是将信号频谱无失真的在频率轴上搬移，则称之为线性频率变换，具有这种特性的电路称之为频谱搬移电路。
频谱o 1 23404o 0 4 0202i 4ii 4s4s s 40i 4i i 41234(c) 检波前后的频谱图 图6-1频谱搬移电路的频谱图它们的原理框图如图6-2所示。
119max 00f1m11mfiifS(c) 混频原理图6-2 调幅、检波与混频的原理框图由以上几种频率变换电路的原理框图和频谱图可知，尽管各个电路所要完成的功能完全不同，但是这些频率变换电路之间有很多相似之处：1) 它们的实现框图几乎是相同的，都是利用非线性器件对输入信号频谱实行变换以产生新的有用频率成分后，再用适当中心频率（或截止频率）和适当带宽的滤波器获得所需频率分量并滤除无用频率分量。
2) 从频谱结构看，上述频率变换电路都只是对输入信号频谱实行横向搬移而不改变原来的谱结构，因而都属于所谓的线性频率变换。
3) 频谱的横向平移，从时域角度看相当于输入信号与一个参考正弦信号相乘，而平移的距离由此参考信号的频率决定，因此都可以用乘法电路实现。
6.1.2 振幅调制原理调制是将要传送的信息装载到某一高频振荡（载频）信号上去的过程。
按照所采用的载波波形区分，调制可分为连续波（正弦波）调制和脉冲调制。
连续波调制以单频正弦波为载波，可用数学式)t (cos A )t (ϕ+ω=a 表示，受控参数可以是载波的幅度A ，频率ω或相位ϕ。
因而有调幅（AM ）、调频（FM ）和调相（PM ）三种方式。
脉冲调制以矩形脉冲为载波，受控参数可以是脉冲高度、脉冲重复频率、脉冲宽度或脉冲位置。
相应地，就有脉冲调幅（PAM ，包括脉冲编码调制PCM ），脉冲调频（PFM ），脉冲调宽（PWM ）和脉冲调位120（PPM ）。
第5章 频谱的线性搬移电路分为频谱的线性搬移电路和非线性搬移电路。
线性搬移电路：频谱结构不发生变化，如振幅调制与解调、混频。
非线性搬移电路：频谱结构也发生了变化。
频率调制与解调、相位调制与解调等电路5.1 非线性电路的分析方法有两种分析方法：1、级数展开分析2、线性时变分析5.1.1 非线性函数的级数展开分析法//////////////////////////////////////////////////////////////////////////////////////////补充：泰勒级数1、定理 （泰勒定理） 正次幂设函数在区域D 内解析，为D 内的一点，)(z f 0z R 为到D 的边界上各点的最短距离，则当时，可展开为幂级数0z R z z <−||0)(z f n n n R z z z f n C z z C z f n n )()(00||)(!100)(−========∑∞=<−=其中 n=0，1,2,… )(z f 在处的泰勒展开式是唯一的。
0z //////////////////////////////////////////////////////////////////////////////////////////非线性器件的伏安特性，可用下面的非线性函数来表示: i =f (u ) (5-1)式中, u 为加在非线性器件上的电压。
一般情况下, u ＝E Q +u 1+u 2,其中E Q 为静态工作点，u 1和u 2为两个输入电压。
展开成E Q 处的泰勒级数，可得∑∞=+=++++++++=02212122122110)( )()()(n n n n u u a u u a u u a u u a a i LL式中，a n(n =0，1，2，…)为各次方项的系数，由下式确定: )(!1)(!1Q )(QE f n du u f d n a n E u n n n === (5-3) 由于∑=−=+nm m m n m n nu u C u u 02121)( (5-4)式中，为二项式系数，故)!(!/!m n m n C m n −=∑∑=−∞==n m m m n m n n n u u C a i 0210 (5-5)以下分析， u 2=0情况，见p144作用在非线性器件上的两个电压均为余弦信号，即u 1＝U 1cos ω1t ，u 2＝U 2cos ω2t ，利若用式(5-7)和三角函数的积化和差公式)cos(21)cos(1cos cos x y x y x ++−=2y (5-9) 由式(5-5)不难看出，i 中将包含由下列通式表示的无限多个频率组合分量5.1.2 线性时变电路分析法对式(5-1)在 E Q +u 2上对i 用泰勒级数展开，有ωp,q =|±p ω1±q ω2|++=u u E f i 1Q )(L L +++++′′++′++=n n u u E f n u u E f u u E f u E f 12Q )(212Q 12Q 2Q 2)(!1 )(!21)()( 5-11 ―――――――――――――――――――――――――――由于5-5和5-11是等价的。
