高三数学周练(贺思轩)

河南省正阳县第二高级中学2018届高三数学下学期周练（六）文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（河南省正阳县第二高级中学2018届高三数学下学期周练（六）文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为河南省正阳县第二高级中学2018届高三数学下学期周练（六）文的全部内容。

河南省正阳县第二高级中学2017—2018学年高三下期文科数学周练（六）1。

已知i 为虚数单位，则21i+=( ） A 。

—2i B 。

2i C.1—I D 。

1+i2.已知集合{|1,A x x =≤-或1}x ≥，集合{|01}B x x =<<，则()R C A B 为 A 。

(,0][1,)-∞+∞ B 。

（0,1) C. (0,1] D 。

[-1,1]3.为检测某校高一学生的身高状况，现采用先分层抽样后简单随机抽样的方法,抽取一个容量为300的样本，已知每个学生被抽取的概率为0。

25，且男女的比例为3：2，则该高校高一年级男生的人数为（ )A.600B.1200 C 。

720 D.900 4.在等比数列{}n a 中，1344a a a ==，则为6a =（ ） A 。

—6 B.8±C.-8D.85.如图所示为一个8X8的国际象棋棋盘，其中每个格子的大小都一样，向棋盘内随机抛撒100枚豆子，则落在黑方格内的豆子总数最接近（ ）A.40 B 。

50 C 。

60 D.646.空间有不重合的平面,,αβγ和直线a,b,c ，则下面四命题中正确的有1p :若αβ⊥且αγ⊥，则β∥γ;2p :若a⊥b,b⊥c,则a ∥c3p ：若,a b αα⊥⊥，则a∥b;4p ：若a⊥α，b⊥β，且αβ⊥，则a⊥bA. 1p ，2p B 。

浙江省平阳县第三中学高三数学 周练三
1、ABC ∆中，角,,A B C 对应的边分别为,,a b c ，若sin ,sin ,sin A B C 成等差数列，且22tan .C =.
(I)求
sin sin B A
的值； (II)若11c =，求ABC ∆的面积S .
2、设数列{}n a 的前n 项和为n S ，已知122n n n S a +=-(n ∈N*). （1）求证：{}2
n n a 是等差数列，并求数列{}n a 的通项公式； （2）设1log 2n n a n b +=，数列{}n b 的前n 项和为n B ，若存在整数m ，使对任意n ∈N *且n ≥2，都有320
n n m B B ->
成立，求m的最大值；
3、在某国际高端经济论坛上，前六位发言的是与会的含有甲、乙的6名中国经济学专家，他们的发言顺序通过随机抽签方式决定.
（Ⅰ）求甲、乙两位专家恰好排在前两位出场的概率；
（Ⅱ）发言中甲、乙两位专家之间的中国专家数记为ξ，求ξ的分布列和数学期望.
4、如图，三棱柱ABC－A
1B
1
C
1
的侧面A
1
ACC
1
与底面ABC垂直，AB=BC=CA=4，且AA
1
⊥A
1
C，AA
1
=A
1
C.
（Ⅰ）证明：AC⊥BA
1
；
（Ⅱ）求侧面A
1ABB
1
与底面ABC所成二面角的余弦值.。

1k （第6题图）2021年高三上学期周末练习二数学试题含答案一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答卷纸．．．相应位置．．．．上． 1．已知集合，则= ．2．已知复数z 满足：z (1－i)＝2＋4i ，其中i 为虚数单位，则复数z 的模为 ． 3．某学校高一、高二、高三年级的学生人数之比为4：3：3，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80的样本，则应从高一年级抽取 名学生．4．从2个红球，2个黄球，1个白球中随机取出两个球，则两球颜色不同的概率是 ． 5．曲线在点处的切线方程为 ．6．右图是一个算法流程图，则最后输出的k 值为 ．7．已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的渐近线方程为y ＝±3x ，则该双曲线的离心率为 ． 8．已知圆锥的侧面展开图是一个半径为2的半圆， 则这个圆锥的高是 ．9．若函数是奇函数，则使成立的的取值范围为 ．10．对于直线l ，m ，平面α，m α，则“l ⊥m ”是“l ⊥α”成立的▲________条件．（在“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”中选填一个）．11．已知函数f (x )＝13x 3＋x 2－2ax ＋1，若函数f (x )在(1，2)上有极值，则实数的取值范围为 ．12．已知等比数列{a n }的公比q ＞1，其前n 项和为S n ．若S 4＝2S 2＋1，则S 6的最小值为 ． 13．已知平行四边形ABCD 中，AD ＝2，∠BAD ＝60°．若E 为DC 中点，且AE →·BD →＝1，则BD →·BE →的值为 ．14．已知函数f (x )＝x －1－(e －1)ln x ，其中e 为自然对数的底，则满足f (e x)＜0的x 的取值范围为 ．二、解答题：本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答卷纸相应位置．．．．．．．上． 15. (本题满分14分)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且a cos B ＝b cos A ． （1）求ba的值；（2）若sin A ＝13，求sin(C －π4)的值．16. (本题满分14分)如图，在四棱锥P －ABCD 中，底面ABCD 为平行四边形，E 为侧棱PA 的中点． （1）求证：PC // 平面BDE ；（2）若PC ⊥PA ，PD ＝AD ，求证：平面BDE ⊥平面PAB ．17. (本题满分14分)已知{a n }是等差数列，其前n 项的和为S n ， {b n }是等比数列，且a 1＝b 1＝2，a 4＋b 4＝21，S 4＋b 4＝30．（1）求数列{a n }和{b n }的通项公式；（2）记c n ＝a n b n ，n ∈N*，求数列{c n }的前n 项和．PABCDE（第16题图）18. (本题满分16分)某市对城市路网进行改造，拟在原有a 个标段（注：一个标段是指一定长度的机动车道）的基础上，新建x 个标段和n 个道路交叉口，其中n 与x 满足n ＝ax ＋5．已知新建一个标段的造价为m 万元，新建一个道路交叉口的造价是新建一个标段的造价的k 倍． （1）写出新建道路交叉口的总造价y （万元）与x 的函数关系式；（2）设P 是新建标段的总造价与新建道路交叉口的总造价之比．若新建的标段数是原有标段数的20%，且k ≥3．问：P 能否大于120，说明理由．19．(本题满分16分)已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率e ＝22，一条准线方程为x = 2．过椭圆的上顶点A作一条与x 轴、y 轴都不垂直的直线交椭圆于另一点P ，P 关于x 轴的对称点为Q ． （1）求椭圆的方程；（2）若直线AP ，AQ 与x 轴交点的横坐标分别为m ，n ，求证：mn 为常数，并求出此常数．20. (本题满分16分)设函数，.（1）当时，函数与在处的切线互相垂直，求的值； （2）若函数在定义域内不单调，求的取值范围；（3）是否存在实数,使得对任意正实数恒成立？若存在，求出满足条件的实数；若不存在，请说明理由.东台市安丰中学xx 届高三数学周末练习二数学附加题（理科） （满分40分，考试时间30分钟）选题人：崔志荣 杨志青 xx.9.1821.B （本小题满分10分）已知点P (3，1)在矩阵A ＝⎣⎢⎡⎦⎥⎤a 2b －1变换下得到点P ′(5，－1)．试求矩阵A 和它的逆矩阵A －1．21.C （本小题满分10分）在平面直角坐标系xOy 中，圆C 的参数方程为⎩⎪⎨⎪⎧x=m+2cos α，y=2sin α（α为参数，m 为常数）．以原点O 为极点，以x 轴的非负半轴为极轴的极坐标系中，直线l 的极坐标方程为ρcos(θ－π4)=2．若直线l 与圆C 有两个公共点，求实数m 的取值范围．22.（本小题满分10分）如图，已知长方体ABCD －A 1B 1C 1D 1中，AB ＝3，BC ＝2，CC 1＝5，E 是棱CC 1上不同于端点的点，且＝λ．（1） 当∠BEA 1为钝角时，求实数λ的取值范围；（2） 若λ＝25，记二面角B 1－A 1B －E 的的大小为θ，求|cos θ|．23.（本小题满分10分）假定某射手射击一次命中目标的概率为23．现有4发子弹，该射手一旦射中目标，就停止射击，否则就一直独立地射击到子弹用完．设耗用子弹数为X ，求： （1）X 的概率分布； （2）数学期望E (X )．（第22题图）ABCDEA 1B 1C 1D 1东台市安丰中学xx 届高三数学周末练习二数学参考答案及评分标准 一、填空题：本大题共14小题，每小题5分，共70分．1． 2．10 3．32 4．45 5． 6．5 7．2 8． 3 9． 10．必要不充分 11．(32，4) 12．23＋3 13．3 14．(0，1)二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）解：（1）由a cos B ＝b cos A ，得sin A cos B ＝sin B cos A ， ………………………………3分 即sin(A －B )＝0．因为A ，B ∈(0，π)，所以A －B ∈(－π，π)，所以A －B ＝0，所以a ＝b ，即b a＝1． ………………………………………………………………6分 （2）因为sin A ＝13，且A 为锐角，所以cos A ＝223． ………………………………8分所以sin C ＝sin(π－2A )＝sin2A ＝2sin A cos A ＝429， ………………………………10分cos C ＝cos(π－2A )＝－cos2A ＝－1＋2sin 2A ＝－79．…………………………………12分所以sin(C －π4)＝sin C cos π4－cos C sin π4＝8＋7218． (14)分16．（本小题满分14分）证明：（1）连结AC ，交BD 于O ，连结OE ．因为ABCD 是平行四边形，所以OA ＝OC ．…………………………………………2分 因为 E 为侧棱PA 的中点，所以OE ∥PC ．…………………………………………4分 因为PC /⊂平面BDE ，OE ⊂平面BDE ，所以PC // 平面BDE ．………………………6分 （2）因为E 为PA 中点，PD ＝AD ，所以PA ⊥DE ．…………………………………8分因为PC ⊥PA ，OE ∥PC ，所以PA ⊥OE ．BC O因为OE ⊂平面BDE ，DE ⊂平面BDE ，OE ∩DE ＝E ， 所以PA ⊥平面BDE ．………………………………12分 因为PA ⊂平面PAB ，所以平面BDE ⊥平面PAB ．14分 17．（本小题满分14分）解：（1）设等差数列{a n }的公差为d ，等比数列{b n }的公比为q ．由a 1＝b 1＝2，得a 4＝2＋3d ，b 4＝2q 3，S 4＝8＋6d ．……………………………… 3分由条件a 4＋b 4＝21，S 4＋b 4＝30，得方程组⎩⎨⎧2＋3d ＋2q 3＝21，8＋6d ＋2q 3＝30，解得⎩⎨⎧d ＝1，q ＝2．所以a n ＝n ＋1，b n ＝2n，n ∈N*． ……………………………… 7分 （2）由题意知，c n ＝(n ＋1)×2n．记T n ＝c 1＋c 2＋c 3＋…＋c n ． 则T n ＝c 1＋c 2＋c 3＋…＋c n＝2×2＋3×22＋4×23＋…＋n ×2n －1＋(n ＋1)×2n， 2 T n ＝ 2×22＋3×23＋…＋(n －1)×2n －1＋n ×2n＋ (n ＋1)2n ＋1，所以－T n ＝2×2＋(22＋23＋ (2))－(n ＋1)×2n ＋1， …………………………… 11分即T n ＝n ·2n ＋1，n ∈N*． ……………………………… 14分18．（本小题满分16分）解：（1）依题意得 y ＝mkn ＝mk (ax ＋5)，x ∈N *． ………………………………………5分 （2）方法一 依题意x ＝0.2a ． …………………………………………6分所以P ＝mx y ＝x k (ax ＋5)＝0.2a k (0.2a 2＋5)＝ak (a 2＋25) (10)分≤a 3(a 2＋25)＝13(a ＋25a)≤1 3×(2a ×25a)＝130＜120． …………………………15分 答：P 不可能大于120． …………………………………………16分方法二 依题意x ＝0.2a ． …………………………………………6分 所以P ＝mx y ＝x k (ax ＋5)＝0.2a k (0.2a 2＋5)＝a k (a 2＋25)．………………………………10分假设P ＞120，得ka 2－20a ＋25k ＜0． …………………………………13分因为k ≥3，所以△＝100(4－k 2)＜0，不等式ka 2－20a ＋25k ＜0无解．……………15分 答：P 不可能大于120． …………………………………………16分19．（本小题满分16分）解： ⑴因为c a ＝22，a2c= 2，所以a ＝2，c ＝1，所以b ＝a 2－c 2＝１．故椭圆的方程为x 22＋y 2＝1． ……………………………………4分⑵解法一 设P 点坐标为(x 1，y 1)，则Q 点坐标为(x 1， – y 1)．因为k AP ＝y 1－1x 1－0＝y 1－1x 1，所以直线AP 的方程为y ＝y 1－1x 1x ＋1．令y = 0，解得m ＝－x 1y 1－1. ……………………………………8分因为k AQ ＝ －y 1－1x 1－0＝－y 1＋1x 1，所以直线AQ 的方程为y ＝－y 1＋1x 1x ＋1．令y ＝0，解得n ＝x 1y 1＋1． ……………………………………12分所以mn ＝－x 1y 1－1⨯ x 1y 1＋1＝x 211－y 21． ……………………………………14分又因为(x 1，y 1)在椭圆x 22+ y 2= 1上，所以x 212 + y 21= 1，即1－y 21= x 212，所以x 211 – y 21＝2，即mn ＝2．所以mn 为常数，且常数为2． ……………………………16分解法二 设直线AP 的斜率为k (k ≠0)，则AP 的方程为y = kx +1，令y = 0，得m ＝－1k． ………………………………6分联立方程组⎩⎪⎨⎪⎧y = kx + 1，x 22+ y 2＝1， 消去y ，得(1＋2k 2)x 2＋4kx ＝0，解得x A ＝0，x P =－4k 1 + 2k 2， …………8分所以y P ＝k ×x P ＋1＝1－2k21＋2k2，则Q 点的坐标为(－4k 1 + 2k 2，－1－2k21＋2k2)． …………………………………10分所以k AQ ＝－1－2k 21＋2k 2－1－4k 1 + 2k2＝12k ，故直线AQ 的方程为y ＝12k x ＋1．令y ＝0，得n ＝－2k ， ………………………………14分 所以mn ＝(－１k)⨯(－2k )＝2．所以mn 为常数，常数为2． ………………………………16分 20．（本小题满分16分）解：（1）当时，，在处的切线斜率，由，在处的切线斜率，， .……………4分 （2）易知函数的定义域为，又[]222212(1)2(1)11(1)()()(1)(1)(1)x m n x m n x m n x y f x g x x x x x x +--++--+-'''=-=-==+++，由题意，得的最小值为负，（注：结合函数图象同样可以得到），，，（注：结合消元利用基本不等式也可）.………………………….….…………….……………………………………………9分 （3）令2=()()()ln 2ln ln ln 22ax a xf f e f ax a ax x x a x a⋅+=⋅-⋅+-，其中 则，设在单调递减，在区间必存在实根，不妨设 即，可得（*）在区间上单调递增，在上单调递减，所以， ，代入（*）式得 根据题意恒成立.又根据基本不等式,,当且仅当时,等式成立 所以,.代入（*）式得,,即. ………………16分 (以下解法供参考，请酌情给分)解法2：ln 2ln ln ln 2(1)(ln 2ln )ax a ax x x a ax a x =⋅-⋅+-=--，其中 根据条件对任意正数恒成立 即对任意正数恒成立且，解得且，即时上述条件成立此时.解法3：ln 2ln ln ln 2(1)(ln 2ln )ax a ax x x a ax a x =⋅-⋅+-=--，其中 要使得对任意正数恒成立，等价于对任意正数恒成立，即对任意正数恒成立，设函数，则的函数图像为开口向上，与正半轴至少有一个交点的抛物线， 因此，根据题意，抛物线只能与轴有一个交点，即，所以. 数学附加题参考答案及评分标准 21解：依题意得⎣⎢⎡⎦⎥⎤a 2b －1 ⎣⎢⎡⎦⎥⎤31＝⎣⎢⎡⎦⎥⎤3a ＋23b －1＝⎣⎢⎡⎦⎥⎤5－1，……………………………………2分 所以⎩⎨⎧3a ＋2＝5，3b －1＝－1，解得 ⎩⎨⎧a ＝1，b ＝0．所以A ＝⎣⎢⎡⎦⎥⎤1 20－1． …………………………………………6分因为det(A )＝⎪⎪⎪⎪⎪⎪1 20－1＝1×(－1)－0×2＝－1，……………………………………8分所以A －1＝⎣⎢⎡⎦⎥⎤1 20－1． ………………………………………10分22. 解：圆C 的普通方程为(x －m )2＋y 2＝4． …………………………………………2分直线l 的极坐标方程化为ρ (22cos θ＋22sin θ)＝2， 即22x ＋22y ＝2，化简得x ＋y －2＝0． …………………………………………4分 因为圆C 的圆心为C (m ，0)，半径为2，圆心C 到直线l 的距离d ＝|m －2 |2，所以d ＝|m －2 |2＜2， …………………………………………8分解得2－22＜m ＜2＋22． ………………………………………10分 23．解：（1）以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立如图所示的空间直角坐标系．由题设，知B (2，3，0)，A 1(2，0，5)，C (0，3，0)，C 1(0，3因为＝λ，所以E (0，3，5λ)．从而＝(2，0，－5λ)，＝(2，－3，5－5λ)．…… 2分 当∠BEA 1为钝角时，cos ∠BEA 1＜0， 所以·＜0，即2×2－5λ(5－5λ)＜0，解得15＜λ＜45．（第22题图）即实数λ的取值范围是(15，45)． …………………………………… 5分 （2）当λ＝25时，＝(2，0，－2)，＝(2，－3，3)． 设平面BEA 1的一个法向量为n 1＝(x ，y ，z )，由 得⎩⎨⎧2x －2z ＝0，2x －3y ＋3z ＝0，取x ＝1，得y ＝53，z ＝1， 所以平面BEA 1的一个法向量为n 1＝(1，53，1)． ………………………………… 7分 易知，平面BA 1B 1的一个法向量为n 2＝(1，0，0)．因为cos< n 1，n 2>＝n 1·n 2| n 1|·| n 2|＝1 439＝34343， 从而|cos θ|＝3 4343． …………………………………… 10分 24．解：耗用子弹数X 的所有可能取值为1，2，3，4．当X ＝1时，表示射击一次，命中目标，则P (X ＝1)＝23； 当X ＝2时，表示射击两次，第一次未中，第二次射中目标，则P (X ＝2)＝(1－23)×23＝29；……2分当X ＝3时，表示射击三次，第一次、第二次均未击中，第三次击中，则P (X ＝3)＝(1－23)×(1－23)×23＝227； …………4分 当X ＝4时，表示射击四次，前三次均未击中，第四次击中或四次均未击中，则P (X ＝4)＝(1－23)×(1－23)×(1－23)×23＋(1－23)×(1－23)×(1－23)×(1－23)＝127． X 的概率分布为……………………………………………6分(2)E (X )＝1×23＋2×29＋3×227+4×127＝4027． ……………………………………10分27707 6C3B 氻ZUS26983 6967 楧34405 8665 虥 Y31810 7C42 籂 *B ~。

江苏省扬中二中2020-2021第一学期高三数学周练4姓名．．．．．．．．1． “1a <”是“210,x x a x+∀>≥”的 （ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 2．已知随机变量ξ服从正态分布2(,)XN μσ，若(2)(6)0.15P P ξξ<=>=，则(24)P ξ≤<=（ ）A ．0.3B ．0.35C ．0.5D ．0.73．已知袋中有6个除颜色外，其余均相同的小球，其中有4个红球，2个白球，从中任意取出2个小球，已知其中一个为红球，则另外一个是白球的概率为 （ ）A ．815B ．715C ．47D ．374．已知22()n x x-的二项展开式的二项式系数之和为64，则二项展开式中常数项为 （ ）A ．40B ．60C ．120D ．2405．设0,0a b >>，且21a b +=，则12aa a b++ （ ）A ．有最小值为221+B ．有最小值为21+C ．有最小值为143D ．有最小值为46．已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R ∈恒成立，且()()2f f ππ>，则()f x 的单调递减区间是 （ ）A ．[,]()63k k k Z ππππ-+∈B ．[,]()66k k k Z ππππ-+∈ C ．[,]()36k k k Z ππππ-+∈ D ．[,]()33k k k Z ππππ-+∈ 7．若函数32()231f x x ax =-+在区间(0,)+∞内有两个零点则实数a 的取值范围是 （ ） A ．1a ≤ B ．1a < C ．1a ≥ D ．1a >8．如图，已知抛物线2:y 2(0)C px p =>的焦点为F ，点00(,23)()2pP x x >是抛物线C 上一点，以P 为圆心的圆与线段PF 相交于点Q ，与过焦点F 且垂直对称轴的直线交于点,,A B AB PQ =，直线PF 与抛物线C 的另一个交点为M ，若3PF PQ =，则PQ FM= （ ）A ．1B ．3C ．2D ．5二、多选题：（每小题给出的四个选项中，不止一项是符合题目要求的，请把正确的所有选项填涂在答题卡相应的位置上）9．如图是函数()sin()f x A x ωϕ=+(A ＞0，ω＞0，ϕ＜2π)的部分图象，若()f x 在[0，2π]内有且 只有一个最小值点，ω的值可以为 （ ）A ．13B ．23C ．1D ．210．下列说法正确的是 （ ） A ．离散型随机变量ξ的方差()D ξ反映了随机变量ξ取值的波动情况； B ．随机变量2(,)XN μσ，其中σ越小，曲线越“矮胖”； C ．若A 与B 是相互独立事件，则A 与B 也是相互独立事件；D ．从10个红球和20个白球颜色外完全相同中，一次摸出5个球，则摸到红球的个数服从超几何分布； 11．如图，已知正方体ABCD-A 1B 1C 1D 1的棱长为1，动点E 在线段A 1C 1上，F 、M 分别是AD 、CD 的中点，则下列结论正确的是 （ ） . A.FM ∥A 1C 1;B.BM ⊥平面CC 1F;C.存在点E ，使得平面BEF ∥平面CC 1D 1D;D.三棱锥B-CEF 的体积为定值.12．已知函数()f x 的定义域为D ，若对于,,,(),(),()a b c D f a f b f c ∀∈分别为某三角形的三边长，则称()f x 为“三角形函数”，下列四个函数中，其中为“三角形函数”的是 （ ） A ．()(0)xf x e x => B ．2()2(01)f x x x =+≤≤C ．()(49)f x x x =≤≤D ．22()21x x f x +=+二、填空题．请把答案直接填写在答题卡相应位置上．．．．．．．．． 13．已知集合02,0,12x A x y B x x Z x x x ⎧⎫⎧+⎫⎪===≤∈⎨⎨⎬--⎩⎭⎪⎩，则A B ⋂= .14．已知等比数列{}n a 的前n 项和为n S ，前n 项积为n T ，若32154,243S a a T =+=，则1a 的值为 .15．在平面直角在平面直角坐标系xOy 中，已知圆221O x y +=：，圆22(4)4C x y -+=：，动点P 在直线320x +-=上的两点E F ，之间，过点P 分别作圆O C ，的切线，切点为A B ，，若满足2PB PA ≥，则线段EF 的长度为 ．16．已知函数4log ,04()13,42x x f x x x ⎧<≤⎪=⎨-+≥⎪⎩，若a b c <<，且()()()f a f b f c ==，则(1)cab +的取值范围是 .三、解答题．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）已知三角形ABC 的内角A ，B ，C 的对边分别为,b,c a ，且cos cos 2cos a B b A c B +=． （1）求角B ；（2）若4A π=，角B 的角平分线交AC 于点D ，BD 6，求CD 的长．18．把编号为1，2，3，4，5的五个大小、形状相同的小球，随机放入编号为1，2，3，4，5的五个盒子 里．每个盒子里放入一个小球．(1)求恰有两个球的编号与盒子的编号相同的概率；(2)设小球的编号与盒子编号相同的情况有X 种，求随机变量X 的分布列与期望．19．在①1a ，14，2a 成等差数列，②1a ，21a +，3a 成等比数列，③334S =，三个条件中任选一个，补充在下面的问题中，并作答．注：如果选择多个条件分别作答，按第一个解答计分．已知n S 为数列{}n a 的前n 项和，132n n S a a =+，(n N *∈)，10a ≠，且 ． （1）求数列{}n a 的通项公式；（2）记22log n n b a =-，求数列{}n b 的前n 项和n T ．20．已知椭圆M ：22221x y a b+=(a ＞b ＞0)的离心率为2，且过点(2)．（1）求椭圆M 的方程；（2）若A ，B 分别为椭圆M 的上，下顶点，过点B 且斜率为k (k ＞0)的直线l 交椭圆M 于另一点N （异于椭圆的右顶点），交x 轴于点P ，直线AN 与直线x ＝a 相交于点Q ．求证：直线PQ 的斜率为定值．21．如图，在长方体ABCD －A 1B 1C 1D 1中，E ，F 分别为AB ，A 1C 的中点，且AA 1＝3AD ． （1）求直线EF 与平面ABCD 所成角的大小； （2）若EF ＝23AB ，求二面角B －A 1C －D 的余弦值．22．已知21()ln 2f x x a x =+．（1）求()f x 的极值；（2）若函数()()2F x f x x =-有两个极值点1x ，2x ，且122()()2eF x F x +>--（e 为自然对数的底数）恒成立，求实数a 的取值范围．参考答案13. {}0 ； 14．1；15.3； 16．(2,64)； 三、解答题17．解：（1）因为cos cos 2cos a B b A c B +=，由正弦定理可得， sin cos sin cos 2sin cos A B B A C B +=即sin()2sin cos ,sin2sin cos A B C BC C B +=∴=，10,sin 0,cos 2B C B π<<∴>∴=，0,3B B ππ<<∴=；（2）由（1）知6ABD CBDπ∠=∠=,又755,,,4121212A ADB CDB BCD ππππ=∴∠=∠=∴∠=， BC BD ∴==在BCD ∆中，由余弦定理可得：2222cos CD BD BC BD BC CBD =+-⋅∠，即226612(3CD =+-=-=-，所以3CD =18．解：（1）记恰有2个小球与盒子编号相同为事件A ，将5个小球随机放入五个盒子中，每个盒子放一个共有55A 即120种不同的放法，事件A 共有 24220C ⨯=种放法，201()1206P A ∴== 答：恰有2个盒子与小球编号相同的概率为16，（2）随机变量X 的可能值为0,1,2,3,515(2333)4411(0)12012030C P X+++====15(333)453(1)1201208C P X++====252201(2)1201206C P X⨯====35101(3)12012012C P X====1(5)P X ==113111()012351308612120E x ∴=⨯+⨯+⨯+⨯+⨯=.19．解：（1）由已知132,2n n S a a n =+≥时，11132n n S a a --=+，两式相减得到13n n n a a a -=-，即112n n a a -=-，因为10a ≠，所以数列{}n a 是公比为12-的等比数列， 111()2n n a a -∴=-，若选①121,,4a a 成等差数列，由121,,4a a 成等差数列，可得12124a a +=⨯，即11111111,()222n n a a a a --=⇒=∴=-；若选②123,1,a a a +成等比数列，即11111,1,24a a a -+成等比数列， 221111111(1)1,()242n n a a a a -∴-+=⇒=∴=-；若选③334S =，即n 111111131()1,()2442n a a a a a -+-+=⇒=∴=-；（2）2222222211loglog ()log ()2222n n n n b a n --=-=--=-=-， 则12(022)024(22)(1).2n n n nT b b b n n n +-⋅=+++=++++-==-20．解：（1）设椭圆的焦距为2c，则2ca =①22421a b +=②又222222,8,4,4a b c a b c =+∴===，所以椭圆M 的方程为22184x y +=；（2）由（1）易知(0,2),(0,2)A B -，直线l 的方程为2y kx =-，因为直线l 不过点k ∴≠，由22222(21)8028y kx k x kx x y =-⎧⇒+-=⎨+=⎩， 所以2821N kx k =+，从而2228422(,),P(,0)2121k k N k k k -++， 直线AN 的斜率为2224221218221k k k k k --+=-+，故直线AN 的方程为122y x k =-+， 令222,222)x Q =得（，，直线AQ 的斜率为22222222222k k k k-+==-， 所以直线AQ 的斜率为定值2221．解：（1）如图，作FP ⊥平面ABCD ，所以1//FP AA ,又点F 是1A C 的中点，所以112FP AA =， FP 是1A AC 的中位线，所以点P 是AC 的中点，12EP AD =， 连接EP ，则FEP ∠即直线EF 与平面ABCD 所成的角，112tan 312AAFP FEP EP AD ∠=== 所以3FEP π∠=，即直线EF 与平面ABCD 所成的角为3π； （2）设2AD =,则123AA = 由（1）知，()2222132EF EP FP =+=+=，又23EF AB =，所以3AB =， 以点A 为原点，以AB 为x 轴、AD 为y 轴、1AA 为z 轴建立空间直角坐标系，如图，则()0,2,0D ，()3,0,0B ，(10,0,23A ，()3,2,0C ，()0,2,0BC =，(13,2,23AC =-，()3,0,0DC =， 设平面1BA C 的法向量()1111,,n x y z =，则11111112032230n BC y n A C x y z ⎧⋅==⎪⎨⋅=+-=⎪⎩， 10y =，令13z =12x =，所以(13n =，设平面1A CD 的法向量()2222,,n x y z =，则2221222303220n DC x n AC x y ⎧⋅==⎪⎨⋅=+-=⎪⎩，20x =，令21z =-，则23y =-，所以()20,1n =-， 所以向量1n 和2n 的夹角即二面角1B A C D --，121212cos ,7n n n n n n ⋅-===⋅，即二面角1B A C D --的余弦值为14-.22．解：（1）由题意知，函数()f x 的定义域为2(0,),()ax af x x x x+'+∞=+=，①当0a ≥时，()0f x '>，所以()f x 在(0,)+∞上单调递增，此时函数无极值，②当0a <时，令()0f x '=，得x =x =当0x <<时，()0f x '<， ()f x 单调递减，当x >()0f x '>， ()f x 单调递增，所以当0a <时，()f x 有极小值[ln()1]2af a =--，无极大值；（2）函数()F x 的定义域为(0,)+∞，21()ln 22F x x a x x =+-，22()2a x x aF x x x x-+'=+-=，令()0F x '=，即220(0)x x a x -+=> 当440a ∆=-≤即1a ≥时，()F x 无极值，当440a ∆=->即1a <时，设方程220x x a -+=的两根为12,x x ，则12122,x x x x a +=⋅=，①当0a ≤时，方程220xx a -+=不存在两个正根，()F x 不存在两个极值点， ②当01a <<时，解得1x =，当01x <<()0F x '>，()F x 单调递增， 当11x -<<时，()0F x '<，()F x 单调递减， 所以当01a <<时，()F x 有两个极值点12,x x ， 且12122,x x x x a +=⋅=，221211122211()F()ln 2ln 222F x x x a x x x a x x +=+-++- 2121212121()ln()2()ln 22x x x x a x x x x a a a =+-⋅+⋅--=--， 令()ln 2,()ln h a a a a h a a '=--=，当01a <<时()ln 0,()h a a h a '=<∴在(0,1)上单调递减，又12()2h e e=--，所以实数a 的取值范围为10.a e<<。

河南省正阳县第二高级中学2017-2018学年下期高三理科数学周练十四一.选择题：1.已知1z ，2z 为一对共轭复数，有以下四个命题：①21z 22z <②1212z z z z =③12()z z R +∈④12z z R ∈，其中一定正确的是（ ） A. ①② B. ②③ C. ③④ D. ①②③2.下列命题中，假命题是（ ）A.若,a b R ∈，且a+b=1,则14ab ≤B. 若,a b R ∈,则222()22a b a b ab ++≥≥恒成立2)x R ∈的最小值是若,a b R ∈,220a b ab ++<3.用S 表示图中阴影部分的面积，则S 的值为（ ）A.()ca f x dx ⎰ B.()c a f x dx ⎰ C.()()bc a b f x dx f x dx +⎰⎰ D. ()()b c a bf x dx f x dx -+⎰⎰ 4.5(1)(2)x x +-展开式中2x 的系数为（ ）A.25B.5C.-15D.-205.安排一张有5个独唱节目和3个合唱节目的节目单，要求任何2个合唱节目不相邻而且不安排在第一个节目，那么不同的节目单有（ ）个A.7200B.1440C.1200D.28806.已知x,y 为正实数，且115x y x y+++=，则x+y 的最大值为（ ） A.3 B.3.5 C.4 D.4.57.若多项式31091001910(1)...(1)(1)x x a a x a x a x +=+++++++，则9a 的值为（ ）A.9B.10C.-9D.108.随机变量(1,4)X N ，若(2)0.2P X ≥=，则(01)P X ≤≤为（ ）A.0.2B.0.6C.0.4D.0.39.若一个四位数的各位数字相加和为10，则称该数为“完美四位数”，如数字“2017”，试问数字0，1，2，3，4，5，6，7组成无重复数字且大于2017的“完美四位数”有（ ）个A.53B.59C.66D.7110.设函数f(x)=x(lnx-ax)(a 为实数)在区间（0，2）上有两个极值点，则a 的取值范围是（ ） A.1(,0)2- B.ln 21(0,)4+ C.1(,1)2 D.ln 211(,)42+11.已知点A 是抛物线24x y =的对称轴与准线的交点，点B 是抛物线的焦点，P 在抛物线上且满足PA m PB =，当m 取最大值时，点P 恰好在以A ，B 为焦点的双曲线上，则双曲线的离心率为（ ）A.121C.121 12.设函数f(x)在R 上存在导函数/()f x ，对x R ∀∈，有2()()f x f x x -+=，在(0,)+∞上 /()f x x <，若f(4-m)-f(m)≥8-4m,则实数m 的取值范围是（ ）A.[2,)+∞B.[-2,2]C. [0,)+∞D.(,2][2,)-∞-+∞二.填空题：13.已知()x x f x e=，///1211()(),()[()],...,[()]n n f x f x f x f x f f x +==，n 为正整数，照此规律()n f x =_______________14.已知F 是抛物线2:8C y x =的焦点，M 为C 上一点，FM 的延长线交y 轴于N ，若M 为FN 的中点，则FN =______________15.在区间[-1,5]上任取一个数b,则曲线32()2f x x x bx =-+在点（1，f(1)）处的切线的倾斜角为钝角的概率是（ ）16.已知在三棱锥P —ABC 中，PC ⊥平面ABC ，AB ⊥BC ，若PC=BC=8，AB=4，E ，F 分别为PA 、PB 的中点，设三棱锥P —CEF 的外接球的球心为O ，则△AOB 的面积为（ ）三.解答题：17.已知函数()2f x x a a =-+（1）若不等式()6f x ≤的解集为{|23}x x -≤≤，求实数a 的值（2）在（1）的条件下，若存在实数n,使()()f n f n m +-≤成立，求实数m 的取值范围 18.在直角坐标系xoy 中，曲线1C的参数方程是122x t y m ⎧=⎪⎪⎨⎪=+⎪⎩（t 为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程是4cos()6πρθ=-（1）写出2C 的直角坐标方程（2）设点P ，Q 分别在1C ，2C 上运动，若PQ 的最小值为1，求实数m的值19.已知矩形ABCD中，AB AD==，M为DC的中点，将△ADM折起，使得平面ADM⊥平面ABCM，求证：AD⊥BM（2）若点E为线段DB上的动点，问点E在何位置时，二面角E—AM—D从某企业生产的这种产品中抽取200件，检测后得到如下的数据：质量指标值在[165，175）中的有5件，在[175,185）中的有20件，在[185,195）中的有40件，在[195,205）中的有60件，在[205,215）中的有52件，在[215,225）中的有18件，在[225,235]中的有5件；（1）根据以上抽样调查的数据，能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92﹪的规定”（2）在样本中，按产品等级用分层抽样的方法抽取8件，再从这8件产品中随机抽取4件，求抽取的4件产品中，一，二，三等品都有的概率（3）该企业为提高产品质量，开展了“质量提升月”活动，活动后再抽样检测，产品质量指标值X近似满足X～N（218，140），则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少？21.已知椭圆C：22221(0)x ya ba b+=>>的左右焦点分别为1F，2F，过右焦点2F的直线l与C相交于P，Q两点，若△PQF的周长是短轴长的（1）求C的离心率（2）设直线l的斜率为1，在椭圆C上是否能找到一点M，使得等式2OM OP OQ=+，若存在，求出M的坐标；若不存在，说明理由。

河南省正阳县第二高级中学2018届高三数学下学期周练（十）理编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（河南省正阳县第二高级中学2018届高三数学下学期周练（十）理）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为河南省正阳县第二高级中学2018届高三数学下学期周练（十）理的全部内容。

河南正阳县第二高级中学2017-2018学年下期高三理科数学周练(十)一.选择题：1。

已知i 为虚数单位,则13ii+-=（ ） A 。

25i - B 。

25i + C 。

125i - D 。

125i +2。

曲线321y x x =-+在点（1，0)处的切线方程为（ )A 。

y=x-1B 。

y=—x+1 C.y=2x —2 D.y=—2x+23。

有下列说法：(1）a 〉b 〉0是22a b >的充分不必要条件 (2）a>b 〉0是11a b<的充要条件(3)a 〉b>0是33a b >的充要条件，则期中正确的说法有（ )个 A 。

0 B 。

1 C 。

2 D 。

34。

“直线y=x+b 与圆221x y +=相交"是“0〈b 〈1"的（ ）条件A 。

充要B 。

充分不必要 C.必要不充分 D.既不充分也不必要5。

已知抛物线22x y =的焦点与椭圆2212y x m +=的一个焦点重合，则m=（ ）A.1 B 。

2 C 。

3 D.946。

已知(12)()n x n N +-∈的展开式中第三项和第八项的二项式系数相等，则展开式所有项的系数和为（ )A.1 B 。

—1 C.0 D 。

27。

已知随机变量X 服从正态分布2(0,)N σ,若P （X>2）=0.023，则P （22X -≤≤）=( ) A 。

卜人入州八九几市潮王学校高三第二次双周练数学文科卷一、选择题：本大题一一共12个小题,每一小题5分,一共60分.在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的.1.设集合，，那么〔〕A. B. C. D.【答案】C【解析】此题选择C选项.2.假设是函数图象的一个对称中心，那么的一个取值是〔〕A.2B.4C.6D.8【答案】C【解析】，对称中心为，那么，满足要求，选C.3.函数的最小正周期为〔〕A. B. C. D.【答案】C【解析】∴最小正周期.此题选择C选项.4.定义在R上的奇函数满足：对任意的，都有，那么以下结论正确的选项是〔〕A. B.C. D.【答案】C【解析】函数满足：对任意的，都有，说明函数在上为减函数，又函数为R上奇函数，那么，且说明函数在R上为减函数，而，，，那么，又三者均为正，所以，选C.5.的内角所对的边分别是，那么“〞是“〞的〔〕A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要【答案】B【解析】，所以或者，所以“〞是“〞的必要不充分条件，应选择B.6.，使〕A. B. C. D.【答案】A7.假设函数的定义域是，那么函数的定义域是〔〕A. B. C. D.【答案】B【解析】，又，那么函数的定义域是：，选B.8.函数的单调递增区间是〔〕A. B. C. D.【答案】D【解析】由>0得(−∞,−2)∪(2,+∞)，令t=,由于函数t=的对称轴为y轴，开口向上，所以t=在(−∞,0)上递减,在(0,+∞)递增，又由函数y=是定义域内的减函数。

所以原函数在(−∞,−2)上递増。

应选：A.9.给出以下四个结论：，〞的否认是“，〞；②“假设，那么，那么〞；③一真一假；④“函数有零点〞是“函数在上为减函数〞的充要条件.其中正确结论的个数为〔〕A.1B.2C.3D.4【答案】B，那么〞，所以是错误的；③中，假设“〞或者“④中，由函数有零点，那么，而函数为减函数，那么，所以是错误的，应选A。

周周回馈练(二)对应学生用书P23一、选择题1．下列各对函数中，图象完全相同的是( )A ．y ＝x 与y ＝x 2B ．y ＝x x 与y ＝x 0C ．y ＝(x )2与y ＝|x |D ．y ＝x ＋1·x －1与y ＝x ＋x －答案 B解析 对于A ，y ＝x 2＝|x |与y ＝x 值域不同，不是同一个函数，故它们的图象不同；对于C ，函数y ＝(x )2的定义域为[0，＋∞)，函数y ＝|x |的定义域为R ，故它们的图象不同；对于D ，函数y ＝x ＋1·x －1的定义域为[1，＋∞)，而y ＝x ＋x －的定义域为(－∞，－1]∪[1，＋∞)，故它们的图象不同．故选B.2．函数f (x )＝1x ＋1＋4－2x 的定义域为( )A ．[－1,2]B ．(－1,2]C ．[2，＋∞) D．[1，＋∞)答案 B解析 要使函数有意义，则⎩⎪⎨⎪⎧ x ＋1＞0，4－2x ≥0，解得⎩⎪⎨⎪⎧ x ＞－1，x ≤2，∴－1＜x ≤2，故选B.3．若函数f (x )＝⎩⎪⎨⎪⎧ 2，x ＞0，x 2，x ≤0，则满足f (a )＝1的实数a 的值为( )A ．－1B ．1C ．－2D ．2答案 A解析 当a ＞0时，f (a )＝2不符合，当a ≤0时，a 2＝1，∴a ＝－1，故选A.4．函数f (x )＝x －1x －2的定义域为( ) A ．(1，＋∞) B．[1，＋∞)C ．[1,2)D ．[1,2)∪(2，＋∞)答案 D解析 若使函数有意义，则⎩⎪⎨⎪⎧ x －1≥0，x －2≠0，解得x ≥1且x ≠2.∴函数的定义域为[1,2)∪(2，＋∞)，选D.5．已知函数f (2x ＋1)的定义域为[1,2]，则函数f (4x ＋1)的定义域为( )A ．[3,5] B.⎣⎢⎡⎦⎥⎤12，1 C ．[5,9] D.⎣⎢⎡⎦⎥⎤0，12 答案 B解析 ∵1≤x ≤2，∴3≤2x ＋1≤5，∴3≤4x ＋1≤5.解得12≤x ≤1. ∴f (4x ＋1)的定义域为⎣⎢⎡⎦⎥⎤12，1，选B. 6．已知符号函数sgn x ＝⎩⎪⎨⎪⎧ 1，x >0，0，x ＝0，－1，x <0，则方程x ＋1＝(2x －1)sgn x 的所有解之和是( )A ．0B ．2C ．－1＋174 D.7－174答案 D解析 分情况：当x >0时，sgn x ＝1，方程为x ＋1＝2x －1，解得x ＝2；当x ＝0时，sgn x ＝0，方程为x ＋1＝1，解得x ＝0；当x <0时，sgn x ＝－1，方程为x ＋1＝12x －1，解得x ＝－1±174. 其中x ＝－1＋174舍去． 所以原方程所有解之和是2＋0＋－1－174＝7－174，选D. 二、填空题 7．已知f (x ＋1)＝x 2－3x ＋2，则f ⎝ ⎛⎭⎪⎫1x 的解析式为____________________． 答案 f ⎝ ⎛⎭⎪⎫1x ＝1x 2－5x＋6(x ≠0)解析 令x ＋1＝t ，则x ＝t －1，∴f (t )＝(t －1)2－3(t －1)＋2＝t 2－5t ＋6，∴f ⎝ ⎛⎭⎪⎫1x ＝⎝ ⎛⎭⎪⎫1x 2－5⎝ ⎛⎭⎪⎫1x ＋6＝1x 2－5x＋6(x ≠0)． 8．函数y ＝f (x )[f (x )≠0]的图象与直线x ＝1的交点个数是________．答案 0或1解析 根据函数y ＝f (x )的定义，当x 在定义域内任意取一个值，都有唯一的一个函数值f (x )与之对应，函数y ＝f (x )的图象与直线x ＝1有唯一交点，当x 不在定义域内时，函数值f (x )不存在，函数y ＝f (x )的图象与直线x ＝1无交点，所以函数y ＝f (x )的图象与直线x ＝1交点个数为0个或1个．9．若定义运算a ⊙b ＝⎩⎪⎨⎪⎧ b ，a ≥b ，a ，a <b ，则函数f (x )＝x ⊙(2－x )的值域为________． 答案 (－∞，1]解析 由题意得f (x )＝⎩⎪⎨⎪⎧ 2－x ，x ≥1，x ，x <1，画出函数f (x )的图象得值域是(－∞，1]．三、解答题10．已知f (x )＝x 2－1，g (x )＝⎩⎪⎨⎪⎧ x －1，x ＜0，2－x ，x ＞0，求f [g (x )]与g [f (x )]．解 ①当x ＞0时，g (x )＝2－x ，f [g (x )]＝(2－x )2－1＝x 2－4x ＋3.当x ＜0时，g (x )＝x －1，f [g (x )]＝(x －1)2－1＝x 2－2x ，故f [g (x )]＝⎩⎪⎨⎪⎧ x 2－2x ，x ＜0，x 2－4x ＋3，x ＞0. ②当x 2－1＜0时，即－1＜x ＜1时，f (x )＜0，所以g [f (x )]＝f (x )－1＝x 2－2.当x 2－1＞0时，即x ＞1或x ＜－1时，f (x )＞0，所以g [f (x )]＝2－f (x )＝3－x 2.故g [f (x )]＝⎩⎪⎨⎪⎧ 3－x 2，x ＞1或x ＜－1，x 2－2，－1＜x ＜1.11．(1)已知一次函数f (x )满足f [f (x )]＝4x ＋6，求f (x )的解析式；(2)已知函数f (x )满足2f (x )－f 1x＝mx ，求函数f (x )的解析式． 解 (1)设f (x )＝ax ＋b (a ≠0)，则f [f (x )]＝f (ax ＋b )＝a (ax ＋b )＋b ＝a 2x ＋ab ＋b ＝4x＋6，于是有⎩⎪⎨⎪⎧ a 2＝4，ab ＋b ＝6，解得⎩⎪⎨⎪⎧ a ＝2，b ＝2或⎩⎪⎨⎪⎧ a ＝－2，b ＝－6，所以f (x )＝2x ＋2或f (x )＝－2x－6.(2)以1x 替换等式2f (x )－f 1x ＝mx 中的x ，得2f 1x －f (x )＝m x ，与2f (x )－f 1x＝mx 联立成方程组，解得f (x )＝2mx 3＋m 3x. 故函数f (x )的解析式为f (x )＝2mx 3＋m 3x. 12．当m 为何值时，方程x 2－4|x |＋5＝m 有四个互不相等的实数根？并讨论m 为何值时，方程有三个实数根，两个实数根，没有实数根．解 直接解方程会比较麻烦，借助于图象较容易找到答案．先作出y ＝x 2－4|x |＋5的图象，如下图所示，从图中可以直接看出：当1<m <5时，方程有四个互不相等的实数根；当m ＝5时，方程有3个不相等的实数根；当m >5或m ＝1时，方程有2个不相等的实数根；当m <1时，方程没有实数根．。

河南省正阳县第二高级中学2017-2018 学年下期高三文科数学周练（十）一 . 选择题：1. 已知 i 为虚数单位，则=（）A. B. C. D.2. 已知双曲线的离心率为2，则 a=( )B. C.3.已知数列的公比 q=2, 且成等差数列，则的前 8项和为（）4.若△ ABC的三个内角满足sinA:sinB:sinC=5:11:13,则△ ABC是（）A. 锐角三角形B. 直角三角形C.钝角三角形D.锐角或钝角三角形5.4 张卡片上分别写有数字1,2,3,4，从这 4张卡片中随机抽取 2 张，则拿出的 2 张卡片上的数字之和为奇数的概率是（）A. B. C. D.6.阅读以下框图，运转相应的程序，则程序运转后输出的结果是（）7.以下命题正确的选项是（）（1 ）若命题“ p 或 q ”为真命题，则命题“p”和命题“ q ”均为真命题；（ 2）命题“”的否定是“”；（ 3）“ x=4”是“”的必需不充分条件；（ 4）命题“若，则 m=0且 n=0”的否命题是“若，则或”A.（2）（ 3）B. （ 1）（ 2）（ 3）C.（2）（ 4）D.（ 2）（ 3）（ 4）8.有一段“三段论” ，其推理是这样的。

“关于可导函数f(x), 若，则是函数 f(x)的极值点”，由于函数f(x)=满足，因此x=0是的极值点，以上推理（）A. 大前提B.小前提C.推理形式D.没有9.两千多年前，古希腊达哥拉斯学派的数学家曾在沙上研究数学。

他曾在沙上画点或用小石子表示数，依据点或小石子能摆列的形状行分。

以下中心点的个数5,9,14,20，⋯⋯梯形数。

依据形的构成，数列的第2017，=( )10.函数 f(x)的函数足关系式，的（）11.的离心率，双曲的离心率（）B. C. D.12.函数 f(x)是定在上的可函数，且函数足，不等式的解集（）A. B. C.(-2012,0) D.(-2017,-2012)二 .填空：13.在△ ABC中，∠ A=60°， BC=3， AB=，∠ C=（）14.已知 P(1,1)内必定点，P 引一条弦，使此弦以P 中点，弦所在的直方程()15.甲乙丙三人代表班参加校运会的跑步，跳，球比，每人参加一，每都有人参加，他们的身高各不同样样，现认识到以下状况：（ 1）甲不是最高的（2）最高的没报铅球（3）最矮的参加了跳远（4）乙不是最矮的，也没参加跑步，由此可以判断丙参加的竞赛项目是（）16. 已知 f(x) 是偶函数，当时，，则曲线y=f(x)在点(1,2)处的切线方程是（）三 . 解答题：17. 已知数列满足，设（ 1）证明数列是等比数列（2）求数列的前n项和18.已知 a,b,c 分别是△ ABC的内角 A、 B、C 所对的边， a=2bcosB,b c(1)求证： A=2B（ 2）若，求 A19. 近来几年来郑州空气污染教委严重，县随机抽取一年（365 天）内100 天的空气中指数的监测数据，统计结果以下表：(50,100>300空气质量优良稍微污染轻度污染重度污染中重度污染重度污染天数415183071115记某企业每日由空气污染造成的经济损失为S（单位：元），PM2.5 指数为 x, 当 x 在区间[0,100] 内时，对该企业没有造成经济损失；当x 在区间内时，对该企业造成的经济损失成直线模型（当 PM2.5 指数为150 时造成的经济损失为500 元，当 PM2.5 指数为 200 时，造成的经济损失为700 元）；当 PM2.5 指数大于300 时，造成的经济损失为 2000元（ 1）试写出S（ x）的表达式（ 2）试预计在今年内随机抽取一天，该天的经济损失大于500 元且不超出 900 元的概率（ 3）若本次抽取的样本数占有30 天是在供暖季，此中有8天为重度污染，完成下边列联表，并判断能否有95℅的掌握以为郑州市今年度空气重度污染与供暖有关附：，此中 n=a+b+c+d非重度污染重度污染合计供暖季非供暖季合计10020. 在直角坐标系XOY中，分别为椭圆的左右焦点， B（ 0，b） , 连接并延长，交椭圆于A，C与 A关于 X 轴对称（ 1）若 C（），=，求椭圆方程（2）若，求椭圆的离心率21. 已知函数（ 1）当 a=0 时，求函数在（1， f(1)））处的切线方程（ 2）令，求 g(x) 的极值22. 极坐标与直角坐标系有同样的长度单位，以原点O为极点，以x 轴正半轴为极轴已知直线l 的参数方程（t为参数），曲线C的极坐标方程为（ 1）求 C的直角坐标方程（2）设直线l 与曲线 C交于 A，B 两点，求 AB 的长23. 设函数（1）求不等式f(x)>1的解集（2）若关于x 的不等式有解，务实数m的取值范围参照答案：° 14.2x+y=315.跑步16.y=2x17.(1)略（2）18.（1）略（2）45°19. （ 1）（2）（3），有百分之九十五的掌握以为两者有关20. （1）（2）21.（1）y=2x-1（2）当时，无极值；当a>0 时，在 x=处获得极大值，无极小值22. （1）（2）23.（1）（2）[-3,4]。

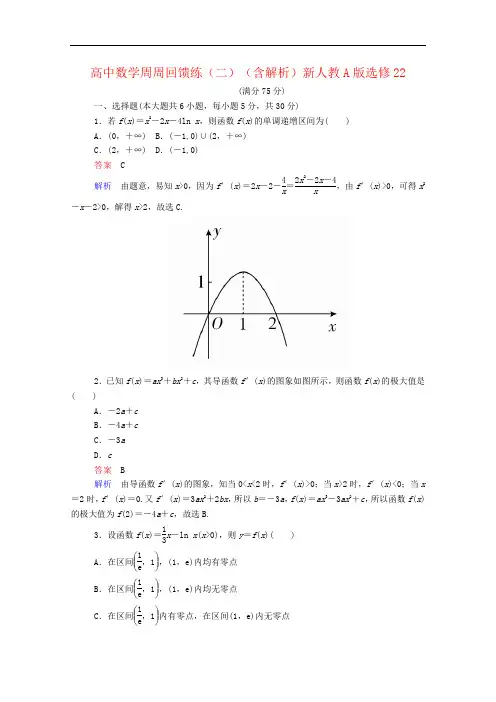
高中数学周周回馈练（二）（含解析）新人教A 版选修22(满分75分)一、选择题(本大题共6小题，每小题5分，共30分)1．若f (x )＝x 2－2x －4ln x ，则函数f (x )的单调递增区间为( ) A ．(0，＋∞) B．(－1,0)∪(2，＋∞) C ．(2，＋∞) D．(－1,0) 答案 C解析 由题意，易知x >0，因为f ′(x )＝2x －2－4x ＝2x 2－2x －4x，由f ′(x )>0，可得x2－x －2>0，解得x >2，故选C.2．已知f (x )＝ax 3＋bx 2＋c ，其导函数f ′(x )的图象如图所示，则函数f (x )的极大值是( )A ．－2a ＋cB ．－4a ＋cC ．－3aD ．c 答案 B解析 由导函数f ′(x )的图象，知当0<x <2时，f ′(x )>0；当x >2时，f ′(x )<0；当x ＝2时，f ′(x )＝0.又f ′(x )＝3ax 2＋2bx ，所以b ＝－3a ，f (x )＝ax 3－3ax 2＋c ，所以函数f (x )的极大值为f (2)＝－4a ＋c ，故选B.3．设函数f (x )＝13x －ln x (x >0)，则y ＝f (x )( )A ．在区间⎝ ⎛⎭⎪⎫1e ，1，(1，e)内均有零点B ．在区间⎝ ⎛⎭⎪⎫1e ，1，(1，e)内均无零点 C ．在区间⎝ ⎛⎭⎪⎫1e ，1内有零点，在区间(1，e)内无零点D ．在区间⎝ ⎛⎭⎪⎫1e ，1内无零点，在区间(1，e)内有零点 答案 D解析 f ′(x )＝13－1x ＝x －33x ，令f ′(x )＝0，得x ＝3，当0<x <3时，f ′(x )<0，所以函数f (x )在区间(0,3)上为减函数．又f (1)＝13>0，f (e)＝e 3－1<0，f ⎝ ⎛⎭⎪⎫1e ＝13e＋1>0，所以y ＝f (x )在区间⎝ ⎛⎭⎪⎫1e ，1内无零点，在区间(1，e)内有零点．4．函数f (x )＝x 2＋2ax ＋1在[0,1]上的最小值为f (1)，则a 的取值范围为( ) A ．(－∞，－1) B ．(－∞，－1] C ．(－1，＋∞) D．[－1，＋∞) 答案 B解析 f ′(x )＝2x ＋2a ，f (x )在[0,1]上的最小值为f (1)，说明f (x )在[0,1]上单调递减，所以x ∈[0,1]时，f ′(x )≤0恒成立，a ≤－x ， 所以a ≤－1，故选B.5．函数f (x )＝x3＋sin x 的图象大致是( )答案 C解析 显然函数f (x )为奇函数，排除B.又f ′(x )＝13＋cos x ，可知f ′(x )有无数个零点，因此函数f (x )有无数个极值点，排除A.又当x 是一个比较小的正数时，f (x )＝x3＋sin x >0，排除D.故选C.6．对于在R 上可导的函数f (x )，若满足(x －1)f ′(x )≥0，则下列说法错误的是( ) A ．f (x )在(0，＋∞)上是增函数 B ．f (x )在(－∞，0)上是减函数 C ．x ＝1时，f (x )取得极小值 D ．f (0)＋f (2)≥2f (1) 答案 A解析 当x ≥1时，f ′(x )≥0，函数f (x )在[1，＋∞)上是增函数；当x <1时，f ′(x )≤0，f (x )在(－∞，1)上是减函数，故说法A 错误，说法B 正确；当x ＝1时，f (x )取得极小值，也是最小值，说法C 正确；f (1)为函数的最小值，故有f (0)≥f (1)，f (2)≥f (1)，得f (0)＋f (2)≥2f (1)，说法D 正确．故选A.二、填空题(本大题共3小题，每小题5分，共15分)7．函数f (x )＝e x (x 2－4x ＋3)在[0,1]上的最小值是________． 答案 0解析 f ′(x )＝e x (x 2－4x ＋3)＋e x (2x －4)＝e x (x 2－2x －1)＝e x [(x －1)2－2]，当x ∈[0,1]时，f ′(x )<0，f (x )在[0,1]上是减函数，f (x )min ＝f (1)＝0.8．若函数f (x )＝mx 2＋ln x －2x 在定义域内是增函数，则实数m 的取值范围是________．答案 ⎣⎢⎡⎭⎪⎫12，＋∞解析 因为f (x )＝mx 2＋ln x －2x ， 所以f ′(x )＝2mx ＋1x－2.由题意知f ′(x )＝2mx ＋1x－2≥0在(0，＋∞)上恒成立．即2m ≥2x －1x 2在(0，＋∞)上恒成立．设t ＝－1x2＋2x＝－⎝ ⎛⎭⎪⎫1x －12＋1.故当x ＝1时，t 有最大值为1. 即2m ≥1，所以m ≥12.9．给出下列四个命题：①若f ′(x 0)＝0，则x 0是f (x )的极值点；②“可导函数f (x )在区间(a ，b )上不单调”等价于“f (x )在区间(a ，b )上有极值”； ③若f (x )＞g (x )，则f ′(x )＞g ′(x )；④如果在区间[a ，b ]上函数y ＝f (x )的图象是一条连续不断的曲线，则该函数在[a ，b ]上一定能取得最大值和最小值．其中真命题的序号是________． 答案 ④解析 ④显然是真命题；对f (x )＝x 3，有f ′(0)＝0，但x ＝0不是极值点，故①是假命题；f (x )＝|x |在(－1,1)上不单调，但x ＝0不是极小值，故②是假命题；f (x )＝x ＋1＞g (x )＝x ，但f ′(x )＝g ′(x )＝1，故③是假命题．三、解答题(本大题共3小题，每小题10分，共30分) 10．设函数f (x )＝ln (2x ＋3)＋x 2. (1)讨论f (x )的单调性；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤－34，14上的最大值和最小值． 解 易知f (x )的定义域为⎝ ⎛⎭⎪⎫－32，＋∞. (1)f ′(x )＝22x ＋3＋2x ＝4x 2＋6x ＋22x ＋3＝22x ＋1x ＋12x ＋3.当－32<x <－1时，f ′(x )>0；当－1<x <－12时，f ′(x )<0；当x >－12时，f ′(x )>0，从而f (x )在区间⎝ ⎛⎭⎪⎫－32，－1，⎝ ⎛⎭⎪⎫－12，＋∞上单调递增，在区间⎝ ⎛⎭⎪⎫－1，－12上单调递减． (2)由(1)知f (x )在区间⎣⎢⎡⎦⎥⎤－34，14上的最小值为f ⎝ ⎛⎭⎪⎫－12＝ln 2＋14.又因为f ⎝ ⎛⎭⎪⎫－34－f ⎝ ⎛⎭⎪⎫14＝ln 32＋916－ln 72－116＝ln 37＋12＝12⎝ ⎛⎭⎪⎫1－ln 499<0， 所以f (x )在区间⎣⎢⎡⎦⎥⎤－34，14上的最大值为f ⎝ ⎛⎭⎪⎫14＝116＋ln 72.11．已知f (x )＝2ln (x ＋a )－x 2－x 在x ＝0处取得极值． (1)求实数a 的值；(2)若关于x 的方程f (x )＋b ＝0的区间[－1,1]上恰有两个不同的实数根，求实数b 的取值范围．解 (1)f ′(x )＝2x ＋a－2x －1，当x ＝0时，f (x )取得极值， 所以f ′(0)＝0，解得a ＝2，检验知a ＝2符合题意． (2)令g (x )＝f (x )＋b ＝2ln (x ＋2)－x 2－x ＋b ，则g ′(x )＝2x ＋2－2x －1＝－2x ⎝ ⎛⎭⎪⎫x ＋52x ＋2(x >－2)．g (x )，g ′(x )在(－2，＋∞)上的变化状态如下表： x (－2,0) 0 (0，＋∞)g ′(x ) ＋0 － g (x )2ln 2＋b要使f (x )＋b ＝0在区间[－1,1]上恰有两个不同的实数根，只需⎩⎪⎨⎪⎧g －1≤0，g 0>0，g 1≤0，即⎩⎪⎨⎪⎧b ≤0，2ln 2＋b >0，2ln 3－2＋b ≤0，所以－2ln 2<b ≤2－2ln 3.故实数b 的取值范围是(－2ln 2,2－2ln 3]．12．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C (单位：万元)与隔热层厚度x (单位：cm)满足关系：C (x )＝k3x ＋5(0≤x ≤10)，若不建隔热层，每年能源消耗费用为8万元．设f (x )为隔热层建造费用与20年的能源消耗费用之和．(1)求k 的值及f (x )的表达式；(2)隔热层修建多厚时，总费用f (x )达到最小？并求最小值． 解 (1)由题设，每年能源消耗费用为C (x )＝k3x ＋5(0≤x ≤10)，再由C (0)＝8，得k ＝40，因此C (x )＝403x ＋5.而建造费用为C 1(x )＝6x .最后得隔热层建造费用与20年的能源消耗费用之和为f (x )＝20C (x )＋C 1(x )＝20×403x ＋5＋6x ＝8003x ＋5＋6x (0≤x ≤10)．(2)f ′(x )＝6－24003x ＋52，令f ′(x )＝0，即24003x ＋52＝6，解得x ＝5，x ＝－253(舍去)．当0<x <5时，f ′(x )<0，当5<x <10时，f ′(x )>0，故x ＝5是f (x )的最小值点，对应的最小值为f (5)＝6×5＋80015＋5＝70.当隔热层修建5 cm 厚时，总费用达到最小值70万元．。

周练卷(二)(时间:90分钟满分:120分)【选题明细表】知识点、方法题号函数的概念及映射1,2函数概念的应用3,4,7,10,12,17函数的表示方法5,9,11,13,16,20分段函数6,8,14,15,18,191.设集合A={x|0≤x≤6},B={y|0≤y≤2},则f:A→B是映射的是( B )(A)f:x→y=3x (B)f:x→y=x(C)f:x→y=x (D)f:x→y=x解析:根据映射定义A中的元素都有唯一的元素与之对应,可得B满足,故选B.2.设x取实数,则f(x)与g(x)表示同一个函数的是( B )(A)f(x)=x,g(x)=(B)f(x)=,g(x)=(C)f(x)=1,g(x)=(x-1)0(D)f(x)=,g(x)=x-3解析:A组中两函数的定义域相同,对应关系不同,g(x)=|x|≠x,故A中的两函数不为同一个函数;B 组中两函数的定义域均为所有正数构成的集合,对应关系化简为f(x)=g(x)=1,故B中的两函数是同一个函数;C组中两函数的定义域不同,f(x)的定义域为R,g(x)的定义域为{x|x≠1},故C中的两函数不为同一个函数;D组中两函数的定义域不同,g(x)的定义域为R,f(x)的定义域由不等于-3的实数构成,故D中的两函数不为同一个函数.故选B.3.函数f(x)=+的定义域为( C )(A)(-3,0] (B)(-3,1](C)[-1,3)∪(3,+∞) (D)[-1,3)解析:要使函数f(x)=+有意义,须解得x≥-1,且x≠3,所以f(x)的定义域为[-1,3)∪(3,+∞).故选C.4.设f(x)=(x≠0),则f()等于( A )(A)f(x) (B)(C)f(-x) (D)解析:f()====f(x).故选A.5.已知对于任意两个实数x,y,都有f(x+y)=f(x)+f(y)成立.若f(-3)=2,则f(2)等于( D )(A)-(B) (C) (D)-解析:令x=y=0,则f(0+0)=f(0)+f(0)⇒f(0)=0;令x=3,y=-3,则f(0)=f(3)+f(-3),且f(-3)=2⇒f(3)=-2;f(3)=f(1)+f(2),f(2)=f(1)+f(1)⇒f(2)=f(3)=-.故选D.6. 已知f(x)=则f(f(5))等于( C )(A)-3 (B)1(C)-1 (D)4解析:因为f(5)=f(5-3)=f(2)=f(2-3)=f(-1)=-2-(-1)3=-2+1=-1.所以f(f(5))=f(-1)=-1.选C.7.函数f(x)=的值域是( D )(A)(-∞,2] (B)(0,+∞)(C)[2,+∞) (D)[0,2]解析:因为函数f(x)=≥0,而且-x2-2x+3=-(x2+2x-3)=-(x+1)2+4≤4,所以≤2,所以0≤f(x)≤2.故选D.8.设集合P={x|0≤x≤2},Q={y|0≤y≤2},则图中能表示P到Q的映射的是( C )(A)(1)(2)(3)(4) (B)(1)(3)(4)(C)(1)(4) (D)(3)解析:(2)不是映射,排除选项A,(3)中当x∈(1,2]时在Q中无元素与之对应,即不表示P到Q的映射,(1)(4)表示由P到Q的映射,故选C.9.函数y=+1的图象是下列图象中的( A )解析:当x=0时,y=+1=2.故排除B,D;当x=2时,y=+1=-1+1=0.故排除C.选A.10.函数f(x)=的值域是( D )(A)R (B)[0,+∞)(C)[0,3] (D)[0,2]∪{3}解析:作出y=f(x)的图象,如图所示.由图象知,f(x)的值域是[0,2]∪{3}.故选D.11.已知f(3x+2)=9x2+3x-1,则f(x)等于( C )(A)3x2-x-1 (B)81x2+127x+53(C)x2-3x+1 (D)6x2+2x+1解析:设t=3x+2,则x=,代入解析式得,所以f(t)=9()2+3·-1=t2-3t+1,所以f(x)=x2-3x+1,故选C.12.设函数f(x)满足对任意的m,n(m,n为正整数)都有f(m+n)=f(m)·f(n)且f(1)=2,则++…+等于( C )(A)2 011 (B)2 010 (C)4 020 (D)4 022解析:因为函数f(x)满足对任意的m,n(m,n为正整数)都有f(m+n)=f(m)·f(n)且f(1)=2,所以f(m+1)=f(m)·f(1),变形可得=f(1)=2,所以++…+=2 010f(1)=4 020.故选C.二、填空题(每小题5分,共20分)13.已知f(+1)=x+2,则f(x)= .解析:因为f(+1)=x+2=x+2+1-1=(+1)2-1,则f(x)=x2-1(x≥1).答案:x2-1(x≥1)14.(2018·江苏省通东中学高三第一阶段月考)a,b为实数,集合M={,1},N={a,0},f:x→x表示把集合M中的元素x映射到集合N中仍为x,则a+b= .解析:因为f:x→x表示把集合M中的元素x映射到集合N中仍为x,所以或所以或而a=1,b=1时,M中有两个相同元素,故a=1,b=1不合题意.所以a+b=1.答案:115.某客运公司确定车票价格的方法是:如果行程不超过100千米,票价是每千米0.5元;如果超过100千米,超过部分按每千米0.4元定价,则客运票价y(元)与行程数x(千米)之间的函数关系式是 .解析:根据行程是否大于100千米来求出解析式,由题意,当0≤x≤100时,y=0.5x;当x>100时,y=100×0.5+(x-100)×0.4=10+0.4x.答案:y=16.已知函数y=f(x)是一次函数,且[f(x)]2-3f(x)=4x2-10x+4,则f(x)= .解析:因为函数y=f(x)是一次函数,所以设f(x)=ax+b(a≠0),因为[f(x)]2-3f(x)=4x2-10x+4,所以(ax+b)2-3(ax+b)=4x2-10x+4,所以a2x2+(2ab-3a)x+b2-3b=4x2-10x+4,所以所以a=-2,b=4或a=2,b=-1,所以f(x)=-2x+4或f(x)=2x-1.答案:-2x+4或2x-1三、解答题(共40分)17.(本小题满分8分)求函数的定义域:(1)f(x)=+;(2)f(x)=+x0.解:(1)要使函数有意义,只需即解得-1≤x<.所以函数的定义域为[-1,).(2)要使函数有意义,只需即所以函数的定义域为[-,0)∪(0,+∞).18.(本小题满分10分)已知f(x)=(1)作出f(x)的图象;(2)求f(x)的定义域和值域.解:(1)利用描点法,作出f(x)的图象,如图所示.(2)由条件知,函数f(x)的定义域为R.由图象知,当-1≤x≤1时,f(x)=x2的值域为[0,1];当x>1或x<-1时,f(x)=1.所以f(x)的值域为[0,1].19.(本小题满分10分)某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y 件之间有如下所表示的关系.x …30 40 45 50 …y …60 30 15 0 …个函数关系式y=f(x);(2)设经营此商品的日销售利润为P元,根据上述关系,写出P关于x的函数关系式,并指出销售单价x为多少时,才能获得最大日销售利润?解:(1)由表作出点(30,60),(40,30),(45,15),(50,0).如图,它们近似地在一条直线上,设它们共线于直线y=kx+b,所以解得所以y=-3x+150,(x∈N).经检验(30,60),(40,30)也在此直线上.所以所求函数解析式为y=-3x+150,(x∈N).(2)依题意P=y(x-30)=(-3x+150)(x-30)=-3(x-40)2+300,当x=40时,P有最大值300,故销售单价为40元/件时,才能获得日最大利润.20.(本小题满分12分)已知函数f(x)=(a,b为常数且a≠0)满足f(2)=1,方程f(x)=x有唯一解,求函数f(x)的解析式,并求f(f(-3))的值.解:根据题意f(2)=1得=1即2a+b=2. ①又=x有唯一解,即ax2+(b-1)x=0有唯一解.所以Δ=(b-1)2-4a×0=0.所以b=1,代入式①解得a=,所以f(x)=.于是f(-3)===6, 所以f(f(-3))=f(6)==.。

, , , ,河北省衡水中学201９届高三数学上学期第2周周测试题 文一、单选题第 2 周周测周测 ９、函数ﻩ的定义域为实数集 , ,关于任意的ﻩ都有 ,若在 1、已知集合 ,则A 、B 、C 、 Ｄ、２、设 为虚数单位,则复数的共轭复数是(ﻩ) A 、 B 、 C 、 D 、3。

若实数 满足ﻩ,,则ﻩ,的大小关系为(ﻩ) A 。

B 、 C 、 Ｄ、 4、函数 的图像在点处的切线斜率的最小值是( )A 、B 、C 、 1D 、 25。

已知函数是定义在区间上的可导函数, 为其导函数,当且时,,若曲线在点处的切线的斜率为,则的值为(ﻩ)A 、B 。

C 、 Ｄ。

6 、 已 知 定 义 域 为 的 奇 函 数 , 当时 , 满 足 , 则(ﻩ) A 、B 、Ｃ。

—2 D 。

０7。

函数 是幂函数,对任意的ﻩ,且,满足, 若,且,则的值( )A 、 恒大于 0ﻩB 、 恒小于 0C 。

等于 0ﻩD 。

无法判断 8、若函数 满足,且,则的解集为A 。

Ｂ。

ﻩＣ、ﻩＤ、 ﻮ区间函数恰有三个不同的零点, 则实数的取值范围是( )A 。

B 。

Ｃ、 D 、10、设 f ( x ) 为函数 f ( ｘ) 的导函数,已知 x 2 f( x ) xf ( ｘ) l ｎ x ,ｆ (e )1,则下列结论正确的ｅ是 ( )(A) f ( x )在 (0, ) 单调递增ﻩ(B) f ( ｘ) 在 (０,) 单调递减(C) f ( x ) 在 (0, ) 上有极大值 (Ｄ) f ( ｘ) 在 (０,) 上有极小值11、设函数是函数的导函数,已知,且,则使得成立的的取值范围是Ａ、B、Ｃ。

Ｄ、１2。

已知函数的导函数为,且对任意的实数都有(是自然对数的底数),且,若关于的不等式的解集中恰有两个整数,则实数的取值范围是(ﻩ)A。

B、C。

D、二、填空题13、已知命题 :ﻩ,命题:幂函数在ﻩ是减函数,若“”为真命题,“"为假命题,则实数的取值范围是ﻩ。