轴固有频率计算课件

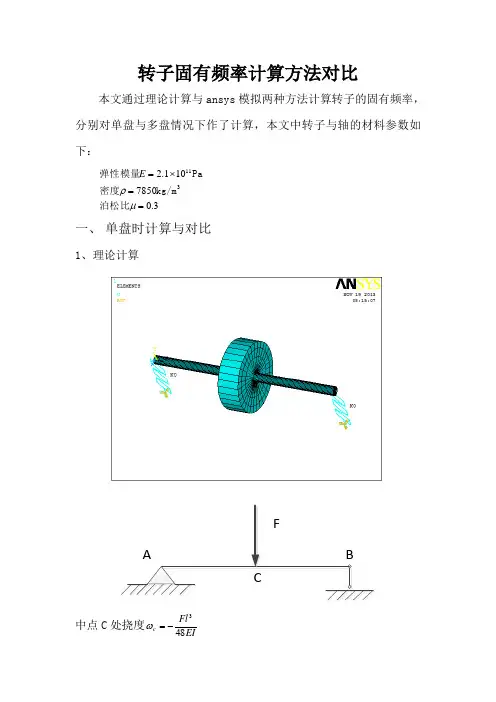
转子固有频率计算方法对比本文通过理论计算与ansys 模拟两种方法计算转子的固有频率，分别对单盘与多盘情况下作了计算，本文中转子与轴的材料参数如下：3.07850101.211==⨯=μρ泊松比kg/m 密度Pa 弹性模量3E一、 单盘时计算与对比1、理论计算中点C 处挠度EIFl c 483-=ω推出轴的刚度348l EIk =,其中l 为轴总长度，E 为弹性模量，I 为惯性矩，F 为外力644d I π=，d 为轴的轴径得：3443l d E k π=代入数据有： N/m 5341110342.4225.0401.014.3101.23⨯=⨯⨯⨯⨯⨯=k 质量kg 5.17850025.01.014.3414122=⨯⨯⨯⨯===ρπρa l D V mrad/s 5385.110342.45=⨯==m k n ωHZ 7.8528.65382===πωn f 2、ansys 模态计算固有频率约束方式：A 端铰支，即约束X 、Y 、Z 平动自由度，不约束转动自由度，B 端只约束Y 、Z 自由度用mass21单元：3、结论：1).不加集中质量结果偏差较大2).直接约束与用combin14和matrix27单元模拟与理论计算结果差不多二、多盘时计算与对比模型结构图考虑多个盘时对比较复杂，先画出本文结构如下图：理论推导示意图轴系统固有频率计算ANSYS 中模态分析直接得出固有频率通过柔度计算刚度，求固有频率根据轴挠度公式计算得柔度，得固有频率ANSYS 中静力分析求出柔度，推出固有频率1、理论推导其中：C 、D 两点为转盘所在位置，AC=CD=DB=l 31，l 为轴长，A 处铰支，B 处限制y 、z 方向自由度。

挠曲轴方程：⎪⎪⎩⎪⎪⎨⎧≤≤-+-≤≤+-=)()2(6)()0(),(622222l x a lx a x lEIx l Fa a x b l x lEIFbx ω将该系统视为两质量弹簧-阻尼系统，通过挠度公式推导柔度矩阵，继而推出刚度矩阵。

固有频率的计算方法
那什么是固有频率呢？简单说呀，就像是一个物体它自己天生就有的一种振动频率。

比如说，你拿个小弹簧，它在那晃悠的时候，就有个它自己特有的频率，这就是固有频率啦。

对于一些简单的系统，像单自由度弹簧 - 质量系统，计算固有频率就不是特别难哦。

这个系统里呀，固有频率和弹簧的劲度系数k还有质量m有关。

它的计算公式是ω = √(k / m)，这里的ω就是固有角频率啦。

你可以想象一下，弹簧硬邦邦的（k 大），质量又小，那它晃悠起来就会快快的，固有频率就高。

要是弹簧软软的，质量又很大，那晃悠起来就慢悠悠的，固有频率就低。

再说说弦振动的固有频率计算呢。

这就和弦的长度L、张力T还有线密度ρ有关啦。

它的频率公式是f = (n / 2L)×√(T / ρ)，这里的n是正整数，代表着振动的模式。

就好像弦在那弹奏的时候，不同的振动模式就有不同的固有频率，就像吉他弦，你按不同的地方，它发出的音高就不一样，这就是因为改变了弦的有效长度之类的，导致固有频率变了。

对于一些复杂的结构呢，计算就比较麻烦啦。

有时候得用到有限元分析这种高大上的方法。

不过原理也还是和那些简单系统有点联系的。

比如说一个复杂的机械结构，它可以看成是好多小的部分组成的，每个小部分都有点像咱们前面说的弹簧 - 质量系统。

然后通过一些复杂的数学计算和模拟，就能算出这个复杂结构的固有频率啦。

滚动轴承（rolling bearing）是将运转的轴与轴座之间的滑动摩擦变为滚动摩擦，从而减少摩擦损失的一种精密的机械元件。

滚动轴承一般由外圈，内圈，滚动体和保持架组成。

滚动轴承一般由内圈、外圈、滚动体和保持架四部分组成，内圈的作用是与轴相配合并与轴一起旋转；外圈作用是与轴承座相配合，起支撑作用；滚动体是借助于保持架均匀的将滚动体分布在内圈和外圈之间，其形状大小和数量直接影响着滚动轴承的使用性能和寿命；保持架能使滚动体均匀分布，防止滚动体脱落，引导滚动体旋转起润滑作用。

滚动轴承在运行过程中，由于滚动体与内圈或外圈冲击而产生振动，这时的振动频率为轴承各部分的固有频率。

固有振动中，内、外圈的振动表现最明显，如图2所示
轴承圈在自由状态下的径向弯曲振动的固有频率为：
式中n—振动阶数（变形波数），n＝2，3，…；
E—弹性模量，钢材为210GPa；
I—套圈横截面的惯性矩，mm 4；
γ—密度，钢材为7.86X10-6kg /mm³；
A—套圈横截面积，A≈bh，mm²；
D—套圈横截面中性轴直径，mm；
g—重力加速度，g＝9800mm /S2。

对钢材，将各常数代入式得
有时钢球也会产生振动，钢球振动的固有频率为：
式中R—钢球半径；
E—弹性模量，钢材为210GPa ;
γ—密度，钢材为7.86X10-6kg /mm³；
g—重力加速度，g＝9800mm /S²。

——动力学应用专题基本内容1、单自由度系统的自由振动2、固有频率的计算3、单自由度系统有阻尼的自由振动4、单自由度系统的受迫振动5、隔振与减振基本要求1、会应用动力学基本理论建立单自由度系统的振动微分方程2、掌握自由振动、受迫振动的特征3、会计算振动周期、固有频率和振幅4、掌握共振和临界转速的概念5、了解隔振的概念引言一、振动的现象与定义1、振动：物体（或系统）在其平衡位置附近周期性的往复运动。

振动是日常生活和工程实际中常见的物理现象。

例如：钟表的摆动；汽车行驶时车厢的上、下颠簸，左、右晃动；电机、机床等工作时的振动，狂风吹得旗帜哗哗作响、对瓶口吹气引起发声；以及地震时引起的建筑物的振动等。

利：振动给料机弊：磨损，减少寿命，影响强度振动筛引起噪声，影响劳动条件振动打桩机等消耗能量，降低精度等。

3. 研究振动的目的：研究并掌握振动规律，消除或减小有害的振动，充分利用振动为人类服务。

2、振动的利弊：引言一、振动的定义与现象引言二、振动的模型与分析方法xmgstlmgm k单自由度质量弹簧系统km三、振动的分类：按振动产生的原因分类：自由振动：无阻尼的自由振动，有阻尼的自由振动（衰减振动）强迫振动：无阻尼的强迫振动有阻尼的强迫振动按振动方程：可分为线性振动和非线性振动。

单自由度系统的振动多自由度系统的振动弹性体的振动按振动系统的自由度分类引言§17-1 单自由度系统的自由振动一、自由振动的概念：质量—弹簧系统一、自由振动的概念：弹簧－质量系统，物块的质量为m ,弹簧的刚度系数为k ,物块自平衡位置的初始速度为v0。

运动过程中，其方向恒指向物体平衡位置的力称为恢复力。

物体受到初干扰后，仅在恢复力作用下于其平衡位置附近的往复运动称为无阻尼自由振动。

二、自由振动微分方程及其解l0mk v0一、自由振动的概念：∑=iix F xm 0=kx xm ＋ 以弹簧未变形时的平衡位置为原点建立Ox 坐标系，将物块置于任意位置x > 0 处。

摘 要 把带有圆盘的轴分为若干段, 对圆盘厚度范围段, 可视为一特殊的段, 在这一段内, 不考虑圆盘的变形, 截面极惯性矩就等于轴的截面极惯性矩, 转动惯量为轴和盘 转动惯量之和。

每一段的扭振方程可精确求出, 然后, 根据边界条件和连续条件可将 扭振固有频率计算出来。

关键词 中图号 轴盘系统 扭转振动 固有频率 T H 133Ξ引 言在机械工程中, 轴盘系统大量存在, 其扭转振动固有频 率的计算是非常重要的, 许多学者对此进行过研究, 归纳起 来, 有这么几方面的方法: 能量法、有限元法、传递矩阵法1 和解析法2 。

在这些方法中, 有的方法较为简单, 但其结果 尤其高阶固有频率的精度较差; 而解析法精度较高, 但方法 较为复杂。

寻求一种精度高、求解原理又比较简单的方法仍 显得较为重要。

为此本文提出了一种新方法。

对于轴盘系统, 我们可把它分为若干段, 如图 1 所示。

对于每段, 可视为均质轴, 类似于式 (4) , 有( k = C k co s (Κk p Νk ) + D k si n (Κk p Νk) 1 方法 1. 1 基本假设(1) 假设在轴扭转过程中, 圆盘不产生变形。

根据这样的假设, 在圆盘厚度范围段内, 总转动惯量是轴和圆盘的转 动惯量之和, 但截面极惯性矩不变, 就是轴本身的截面极惯性矩;( 2) 假设 l 为轴的总长, G 为轴的剪切模量, J 为轴的 截面极惯性矩, I 为轴在单位长度内的转动惯量, I p i 表示第i 个圆盘厚度范围段在单位长度内的轴、盘转动惯量之和。

1. 2 求解过程 均质等截面轴扭转自振方程为(k = 式 中, Κk = ( l k ƒl ) ( I k ƒI ) 1ƒ2; 1, 2,, n )(5)p = (I ƒGJ ) 1ƒ2 l Ξ; Νk 为每段的局 部坐标, 对于每段, 总是把局部坐标建立于其左端, 这样会大大减少计算量。

在两段连接处, 连续条件为( k | Νk = 1 = ( k + 1 | Νk + 1= 0GJ (d ( k ƒd Νk ) | Νk = 1 = GJ (d ( k ƒd Νk ) | Νk + 1= 0将式 (5) 代入式 (6) , 得C k + 1 = C k co s (Κk p ) +D k sin (Κk p )(6)52 Η252 Η D k + 1 = - C k Γk sin (Κk p ) + 式中, Γk = Κk ƒΚk + 1上式可写为D k Γk co s (Κk p )5x 2 =(1)GJI5t 2令 Ν= x ƒl , 则式 (1) 变为52 Η I l 2 52 Η TT[C k + 1 D k + 1 ] =C kD k ]( ) 7F k 5Ν2 = GJ 5t 2(2)式中,再令 Η= ( e i Ξt (Ξ 为固有圆频率) , 于是, 式 (2) 变为co s (Κk p ) Γk sin (Κk p )sin (Κk p )d 2 ( I l2 Ξ [ F =(8)GJ ((3)d Ν2 = - Γk co s (Κk p )称式 (7) 为传递公式, 式 (8) 为传递矩阵。

轴承固有频率计算轴承固有频率是指轴承在运转过程中固有的振动频率。

它是轴承设计和选择的重要参数之一，对于轴承寿命的预测和故障诊断具有重要意义。

轴承固有频率的计算是基于轴承的结构特性和材料性质。

首先，我们需要了解轴承的内外径、滚子或滚珠的直径、圆周、数量以及接触角等参数。

这些参数决定了轴承的结构，并直接影响轴承的固有频率。

其次，轴承的材料性质也会对固有频率产生影响。

常见的轴承材料有钢、铜、塑料等，它们的密度、弹性模量、泊松比等特性会对轴承的固有频率产生影响。

一般来说，材料的密度越大，固有频率越高；而材料的弹性模量越小，固有频率也越高。

在计算轴承固有频率时，我们可以借助数学公式和计算工具来简化计算过程。

其中，轴承的内外径、滚子或滚珠的直径、圆周、数量等参数可以通过测量或查找轴承产品资料得到；而轴承材料的密度、弹性模量等参数可以通过材料数据库或文献查询获得。

通过计算，我们可以得到轴承的轴向固有频率、径向固有频率和倾斜固有频率。

这些固有频率对于轴承设计和选择非常重要。

它们可以帮助工程师了解轴承的振动特性，避免频率与工作环境相匹配，从而减少振动噪音和故障的发生。

值得注意的是，轴承固有频率的计算结果仅为理论值，实际工作条件下还需要结合实际振动测试数据来进行验证。

因此，在轴承设计和选择过程中，工程师们需要综合考虑轴承的固有频率、工作环境的振动要求、静载荷和工作温度等因素，以确保轴承的正常运转和寿命。

总之，轴承固有频率是轴承设计和选择的重要参考参数。

通过计算轴承的固有频率，可以了解轴承的振动特性，预测轴承的寿命，并进行故障诊断。

然而，计算结果仅为理论值，在实际工作条件下需要结合振动测试数据进行验证。

因此，在轴承设计和选择过程中，工程师们需要综合考虑多种因素，以确保轴承的正常运转和寿命。

汽车振动系统的简化，单质量系统的振动一、振动模型的建立汽车的平顺性分析，就是要研究汽车在路面不平度冲击作用下的振动情况，所有轮胎、悬架和车身各处都存在变形，这个汽车模型将非常复杂。

大部分情况下，车身左右结构和左右车轮下的道路输入都是对称的，而且路面输入的频率也较低，远低于车轮部分的固有频率。

在此条件下，可以将汽车的前轴或后轴部分的车身质量单独隔离出来，路面不平度输入直接作用在悬架上（即“轮胎贴在路面上没有动变形”），就得到最基本的单质量系统。

这个模型虽然有一定近似性，但比较简单，得到的结论也能经得起广泛的试验验证，是研究汽车平顺性的理论基础。

在这个单质量模型中：K是悬架弹簧刚度；C是减振器阻尼系数；是车身部分质量；路面不平度输入q“透过车轮”直接作用在悬架上；引起车身部分垂直位移z。

二、单质量系统的自由振动对上述单质量模型运用牛顿第二定律，可以得到微分方程，进而求得悬架系统的两个重要特性参数，固有频率和阻尼比。

固有频率，阻尼比固有频率和阻尼比是两个重要参数，由公式可知其数值仅取决于悬架系统设计参数，与路面和车速无关。

固有频率反应悬架装置做自由衰减振动时的频率，阻尼比反应振幅的衰减速度：按此图显示，可以测出车身部分自由衰减振动的周期和衰减速度，进而求得固有频率和阻尼比。

（但此图不能直接用于汽车的平顺性分析，因为汽车在路上行驶时平不是做自由振动。

）三、单质量系统频率响应特性所谓频率响应特性，系指输入频率变化时，输出与输入的关系如何变化。

具体包括：输出、输入的幅值比是频率f 的函数，称为幅频特性。

反应输出比输入放大（缩小）了多少倍。

相位差也是f 的函数，称为相频特性。

反应输出比输入导前（或滞后）了多少弧度。

平顺性分析一般不考虑相频特性两者统称为频率响应特性。

频率响应特性由微分方程求得，数学分析较复杂，不作具体介绍。

频率响应特性也无法直接指导平顺性分析，因为路面输入不是周期性的，而是随机的。

但是，我们后面会看到，频率响应特性，尤其是其中的幅频特性，对于路面随机输入下汽车的振动分析有很大帮助。

机械振动大作业（盘轴扭振系统固有频率和主振型的计算）学院：航空航天工程学部班级：04040203班姓名：李根学号：20100404020932013年5月12号盘轴扭振系统固有频率和主振型的计算一：简化简化分析分析该系统为非约束性盘轴扭振系统，并简化分析分析：：1．忽略轴的质量;2．轴的刚度对盘的影响不做考虑;3．将圆盘的质量集中于圆盘中心，不考虑圆盘厚度对系统的影响;4．系统为线弹性系统，盘为刚体。

对于非约束系统，其只存在刚度矩阵，不存在柔度矩阵，即不能对刚度矩阵求逆。

二：条件圆盘：1.几何尺寸：直径10.4d m =，厚度0.02h m =；2.材料：杨氏模量112210(/)E N m =×，剪切模量1027.6910(/)G N m =×密度37800(/)kg m ρ=轴：1.几何尺寸：直径20.04d m =，0.1a m=2.材料：杨氏模量112210(/)E N m =×，剪切模量1027.6910(/)G N m =×密度37800(/)kg m ρ=三（1）：矩阵迭代法1.1.概概述（1）：系统主振型方程为{}[]{}21A M K A ω−⎡⎤=⎣⎦，引入动力矩阵[][]1D M K −⎡⎤=⎣⎦。

任取一个经过归一化的假设阵型{}0A ,用动力矩阵[]D 前乘它，并对通过乘法运算新得到的阵型矢量进行归一化，则得：{}110[]{}D A a A =，式中1a 为新振型矢量归一化后的系数。

（2）若{}10{}A A ≠，从1{}A 开始，重复上述步骤得：{}121[]{}D A a A =，式中2a 为新振型矢量归一化后的系数。

（3）：若{}21{}A A ≠，继续重复上述步骤，进过K 次矩阵乘法运算后，得到{}1[]{}k k k D A a A −=，在规定的有效位数内，{}1{}k k A A −=时停止运算，此时的{}1k A −即为系统第一阶主振型(1){}A 的近似值，即：{}(1)1{}k A A −≈，而这时的系数k a 即是系统第一阶固有频率平方倒数的近似值，即：211/k a ω≈。