轴固有频率计算资料

固有频率影响因素相关公式固有频率是指一个物体在没有外界干扰下自然振动的频率。

它是由物体的质量、弹性系数和几何形状等因素决定的。

在工程设计和研究中，对固有频率的分析对于了解物体的振动特性以及预防共振等问题非常重要。

下面，将介绍几种常见的固有频率影响因素相关的公式。

1.杆件的固有频率：杆件的固有频率与杆件的长度和弯曲刚度相关。

杆件的固有频率可以通过以下公式计算：f=(1/2π)*(√(EI/ρA))*(m/L^2)其中，f是固有频率，E是弹性模量，I是截面惯性矩，ρ是杆件的密度，A是截面面积，m是杆件的质量，L是杆件的长度。

2.简谐振子的固有频率：简谐振子是一个理想化的振动系统，它的固有频率只与它的质量和弹性系数有关。

简谐振子的固有频率可以通过以下公式计算：f=(1/2π)*(√(k/m))其中，f是固有频率，k是系统的弹性系数，m是系统的质量。

3.平面结构的固有频率：平面结构的固有频率与结构的刚度矩阵和质量矩阵有关。

平面结构的固有频率可以通过以下公式计算：K*X=ω^2*M*X其中，K和M分别是结构的刚度矩阵和质量矩阵，X是结构的振动模态矢量，ω是固有频率。

4.悬臂梁的固有频率：悬臂梁是一种常见的结构，在分析其固有频率时，需要考虑梁的长度、质量和截面形状等因素。

悬臂梁的固有频率可以通过以下公式计算：f=1.875^2*(E*I/(ρ*A*L^4))其中，f是固有频率，E是弹性模量，I是截面惯性矩，ρ是梁的密度，A是梁的截面面积，L是梁的长度。

以上所介绍的公式是几种常见的固有频率影响因素的相关公式。

它们可以用来计算不同类型物体的固有频率，并且可以帮助工程师和研究人员了解和分析物体振动的特性。

通过对固有频率的研究和分析，可以根据具体情况来优化设计，预防共振等振动问题的发生。

——动力学应用专题基本内容1、单自由度系统的自由振动2、固有频率的计算3、单自由度系统有阻尼的自由振动4、单自由度系统的受迫振动5、隔振与减振基本要求1、会应用动力学基本理论建立单自由度系统的振动微分方程2、掌握自由振动、受迫振动的特征3、会计算振动周期、固有频率和振幅4、掌握共振和临界转速的概念5、了解隔振的概念引言一、振动的现象与定义1、振动：物体（或系统）在其平衡位置附近周期性的往复运动。

振动是日常生活和工程实际中常见的物理现象。

例如：钟表的摆动；汽车行驶时车厢的上、下颠簸，左、右晃动；电机、机床等工作时的振动，狂风吹得旗帜哗哗作响、对瓶口吹气引起发声；以及地震时引起的建筑物的振动等。

利：振动给料机弊：磨损，减少寿命，影响强度振动筛引起噪声，影响劳动条件振动打桩机等消耗能量，降低精度等。

3. 研究振动的目的：研究并掌握振动规律，消除或减小有害的振动，充分利用振动为人类服务。

2、振动的利弊：引言一、振动的定义与现象引言二、振动的模型与分析方法xmgstlmgm k单自由度质量弹簧系统km三、振动的分类：按振动产生的原因分类：自由振动：无阻尼的自由振动，有阻尼的自由振动（衰减振动）强迫振动：无阻尼的强迫振动有阻尼的强迫振动按振动方程：可分为线性振动和非线性振动。

单自由度系统的振动多自由度系统的振动弹性体的振动按振动系统的自由度分类引言§17-1 单自由度系统的自由振动一、自由振动的概念：质量—弹簧系统一、自由振动的概念：弹簧－质量系统，物块的质量为m ,弹簧的刚度系数为k ,物块自平衡位置的初始速度为v0。

运动过程中，其方向恒指向物体平衡位置的力称为恢复力。

物体受到初干扰后，仅在恢复力作用下于其平衡位置附近的往复运动称为无阻尼自由振动。

二、自由振动微分方程及其解l0mk v0一、自由振动的概念：∑=iix F xm 0=kx xm ＋ 以弹簧未变形时的平衡位置为原点建立Ox 坐标系，将物块置于任意位置x > 0 处。

固有频率公式
固有频率，又称自振频率，是指一个特定系统（如振子装置）存在的共振振动频率，这种共振振动是由该系统存在的惯性外力和弹性外力所致。

固有频率一般可以用一个公式来表达：
固有频率公式：f＝1/2π√K/m
其中，K为振子装置的弹性力系数，m为振子装置的质量。

由此
可见，固有频率的大小取决于系统中的K和m值。

为了更好地理解固有频率，我们可以以一个刚架为例。

刚架是机械学中最简单的系统之一，由一个悬置在两支支架上的质点构成，其位置受到变形合力的作用，因此可以完全利用来解释固有频率的概念。

如果假设悬移质点的质量既定，而弹性力系数也定，则根据上面的固有频率公式可求出这个系统的固有频率。

固有频率在日常生活中也有很多应用，比如，工程桥梁的抗震设计中，需要根据现有建筑的质量和弹性系数，来确定合理的固有频率，以便在震动作用下受力合理，以减小结构损坏可能性。

此外，船只在海上航行过程中，也需要确定其固有频率，防止船只在大浪作用下频繁震荡，产生不安全因素。

另外，固有频率也被广泛应用于影响电子系统的稳定性的研究中，这些电子系统也出现在我们的家居中，如家用电器、家庭影院和机器人等，如果它们不能在最佳状态下工作，就会影响整个电子系统的正常运行。

总之，固有频率在物理和电子学方面都有着重要的作用，而其固
有频率公式正是衡量它们性能的主要标准。

因此，熟悉固有频率公式，学习运用它，对于我们更好地理解固有频率必不可少。

第34卷第3期 2O 16年5月西安航空学院学报Journal of Xi7 an Aeronautical UniversityVol . 34 No . 3May . 2 O 1 6变质量悬臂转子轴结构固有频率计算分析张倩昀S 赵银燕2，向欢3(.西安航空学院电子工程学院，陕西西安71O O 77; 2.西安航空学院飞行器学院，陕西西安71O O 77;3.西北工业大学力学与土木建筑学院，陕西西安71O O 72)摘要：悬臂转子轴结构在工程机械中有着极大的应用，其固有频率的计算是设计工作的重要组成部分。

但由于悬 臂转子轴结构一般比较复杂，其质量，约束以及形状的变化都会直接影响到其固有频率，因而，其固有频率的计算也 是设计中的一个难点。

针对变质量条件下的悬臂转子轴结构，应用有限元计算软件AN S Y S ，通过对模型合理的简 化，提高计算效率，得到了悬臂转子轴结构符合实际的各阶固有频率，为整体设计和工况下的稳定运行提供了可靠的依据。

关键词：悬臂转子轴结构；变质量；AN S Y S ;模型简化；固有频率中图分类号：T H 113文献标识码：A文章编号：1O O 8-9233(2O 16)O 3-O O 38-O 4常大，而且转速高，极易发生共振问题，过大振动会 造成构件的疲劳破坏，直接影响卷绕头的使用寿 命，还会影响纺丝质量[]。

锭轴在运行过程中由于 丝饼变化引起的变质量问题，在不同工况条件下变 约束，变载荷问题等等，都使得锭轴固有频率计算 变的更为复杂，也更加关键。

锭轴工作过程中的丝饼质量不断变化，实际可看 作其质量不断变化的过程，直接影响了锭轴的刚度， 从而改变了锭轴的固有频率[]。

马晓晶等也对此类 问题进行了一定研究，并推导了质量慢变悬臂转子系 统的非线性动力学方程[]。

但对具有变质量的锭轴 结构的固有频率的计算较少。

本文通过对锭轴的复 杂结构简化建模，同时，将变质量离散化处理，借助于有限元软件ANSYS ，基于其强大的仿真能力，计算得 到了锭轴工作过程中的各阶固有频率，为后面锭轴结 构的设计提供了可靠依据，也为变质量悬臂转子轴结 构的固有频率计算奠定了基础。

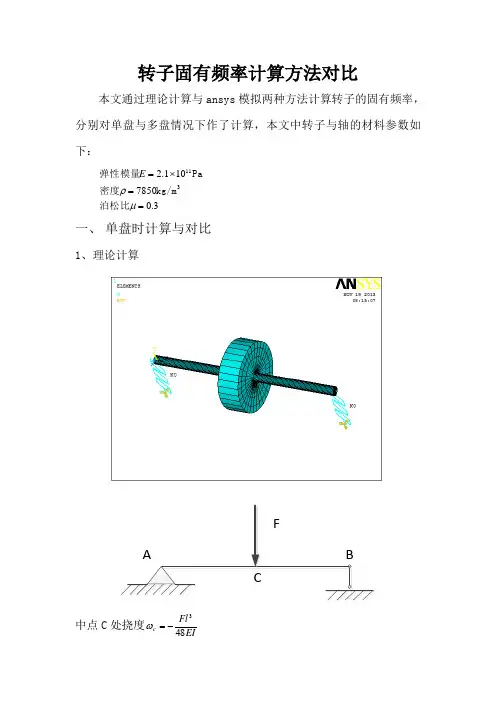
转子固有频率计算方法对比本文通过理论计算与ansys 模拟两种方法计算转子的固有频率，分别对单盘与多盘情况下作了计算，本文中转子与轴的材料参数如下：3.07850101.211==⨯=μρ泊松比kg/m 密度Pa 弹性模量3E一、 单盘时计算与对比1、理论计算ABFC中点C 处挠度EIFl c 483-=ω推出轴的刚度348l EIk =,其中l 为轴总长度，E 为弹性模量，I 为惯性矩，F 为外力644d I π=，d 为轴的轴径得：3443l d E k π=代入数据有： N/m 5341110342.4225.0401.014.3101.23⨯=⨯⨯⨯⨯⨯=k 质量kg 5.17850025.01.014.3414122=⨯⨯⨯⨯===ρπρa l D V mrad/s 5385.110342.45=⨯==m k n ωHZ 7.8528.65382===πωn f 2、ansys 模态计算固有频率约束方式：A 端铰支，即约束X 、Y 、Z 平动自由度，不约束转动自由度，B 端只约束Y 、Z 自由度用mass21单元：3、结论：1).不加集中质量结果偏差较大2).直接约束与用combin14和matrix27单元模拟与理论计算结果差不多二、多盘时计算与对比模型结构图考虑多个盘时对比较复杂，先画出本文结构如下图：理论推导示意图轴系统固有频率计算ANSYS 中模态分析直接得出固有频率通过柔度计算刚度，求固有频率根据轴挠度公式计算得柔度，得固有频率ANSYS 中静力分析求出柔度，推出固有频率1、理论推导其中：C 、D 两点为转盘所在位置，AC=CD=DB=l 31，l 为轴长，A 处铰支，B 处限制y 、z 方向自由度。

挠曲轴方程：⎪⎪⎩⎪⎪⎨⎧≤≤-+-≤≤+-=)()2(6)()0(),(622222l x a lx a x lEIx l Fa a x b l x lEIFbx ω将该系统视为两质量弹簧-阻尼系统，通过挠度公式推导柔度矩阵，继而推出刚度矩阵。

轴承固有频率计算轴承固有频率是指轴承在运转过程中固有的振动频率。

它是轴承设计和选择的重要参数之一，对于轴承寿命的预测和故障诊断具有重要意义。

轴承固有频率的计算是基于轴承的结构特性和材料性质。

首先，我们需要了解轴承的内外径、滚子或滚珠的直径、圆周、数量以及接触角等参数。

这些参数决定了轴承的结构，并直接影响轴承的固有频率。

其次，轴承的材料性质也会对固有频率产生影响。

常见的轴承材料有钢、铜、塑料等，它们的密度、弹性模量、泊松比等特性会对轴承的固有频率产生影响。

一般来说，材料的密度越大，固有频率越高；而材料的弹性模量越小，固有频率也越高。

在计算轴承固有频率时，我们可以借助数学公式和计算工具来简化计算过程。

其中，轴承的内外径、滚子或滚珠的直径、圆周、数量等参数可以通过测量或查找轴承产品资料得到；而轴承材料的密度、弹性模量等参数可以通过材料数据库或文献查询获得。

通过计算，我们可以得到轴承的轴向固有频率、径向固有频率和倾斜固有频率。

这些固有频率对于轴承设计和选择非常重要。

它们可以帮助工程师了解轴承的振动特性，避免频率与工作环境相匹配，从而减少振动噪音和故障的发生。

值得注意的是，轴承固有频率的计算结果仅为理论值，实际工作条件下还需要结合实际振动测试数据来进行验证。

因此，在轴承设计和选择过程中，工程师们需要综合考虑轴承的固有频率、工作环境的振动要求、静载荷和工作温度等因素，以确保轴承的正常运转和寿命。

总之，轴承固有频率是轴承设计和选择的重要参考参数。

通过计算轴承的固有频率，可以了解轴承的振动特性，预测轴承的寿命，并进行故障诊断。

然而，计算结果仅为理论值，在实际工作条件下需要结合振动测试数据进行验证。

因此，在轴承设计和选择过程中，工程师们需要综合考虑多种因素，以确保轴承的正常运转和寿命。