相似理论与模型试验例题集

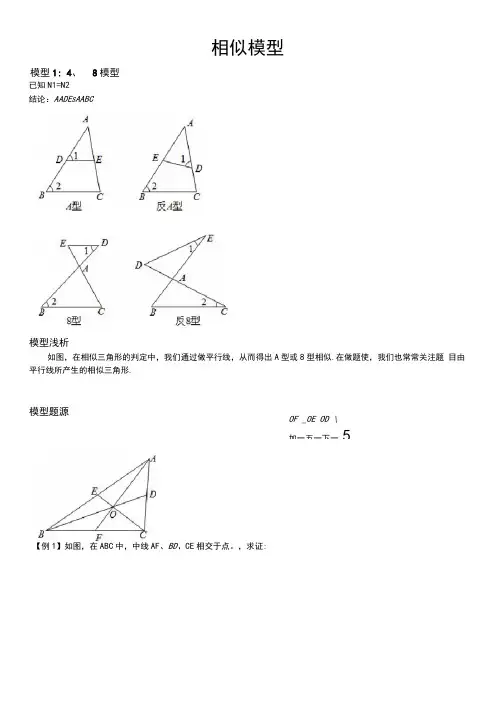
已知N1=N2 结论：AADE S AABC模型浅析如图，在相似三角形的判定中，我们通过做平行线，从而得出A 型或8型相似.在做题使，我们也常常关注题 目由平行线所产生的相似三角形.模型题源【例1】如图，在ABC 中，中线AF 、BD 、CE 相交于点。

，求证:模型1: 4、 8模型相似模型OF _OE OD \加一五一下一5DE 1证法一：如图①，连接。

£七是中点，，——=一.，DE//BCBC 2OF DF 1OF I•••△EODsacoB（8 模型）.••& = &!=2.同理：—=1OC BC 2 OA 2• OF _OE _OD _1GF BF 1 证法二：如图②，过尸作"V/AC 交8。

于点G, ••加是中点，； ------ =——=-AD BC 2QF 1•；AD=CD,:.——=一・•:FG"AD, •二△G 。

/（8 模型）AD 2OF GF 1 lXi OE 1 OD 1 . OF OE OD 1 OAAD 2 OC2OB2 OAOCOB2【例2】如图，点从厂分别在菱形A8C 。

的边AB 、AO 上，且AE=O 凡BF 交DE 于点、G,延长斯交C 。

的延长AF 线于H,若——=2,DF••市一无一方一天图②求器的值.解答：:四边形A8CQ是菱形，：.AB^=BC=CD=AD.设。

/=小则OF=AE=a, AF=EB=2a. 9：HD//AB, MHFDsABFAHD DF ■ —AB AF HFFB1=一,••HD = 1.5a, 2FHBH1=-93：.FH1= -BH 3■:HD”EB,：.△DGHs NGB,：-------- =GBHDEB\.5a2a_3=-9 4.BGHB4-7练习:1 .如图，D 、上分别是△ABC 的边AB 、8C 上的点，且DE 〃AC, AE,。

相交于点0,若S ：： S^COA =1： 25.则 S/.BD E 与Szxc 的比是.DE 1解答：VDE//AC, AADOE^ACOA,又 S SOE ： S^COA = 1： 25,； -------- -AC 52 .如图所示，在248CO 中，G 是8c 延长线上的一点，AG 与BD 交于点、E,与OC 交于点F,此图中的相似三 角形共有对.解：：四边形ABCD 是平行四边形，，AD 〃BC, AB//CD，(1) AABD^ACDB ： (2) AABE^AFDE ； (3) A AED ^A GEB ：(4) AABG^AFCG^AFDA,可以组成3对相似三角形.，图形中一共有6对相似三角形.3.如图，在aABC 中，中线8。

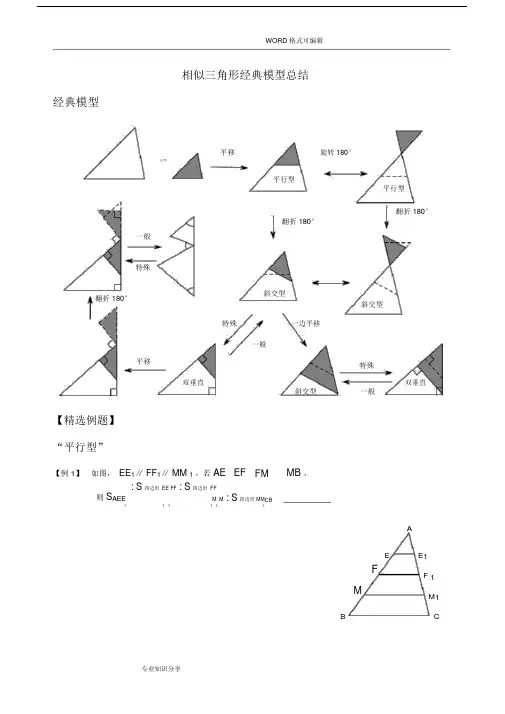
WORD 格式可编辑相似三角形经典模型总结经典模型平移旋转 180°∽平行型平行型翻折 180°翻折 180°一般特殊翻折 180°斜交型斜交型特殊一边平移一般平移特殊双垂直斜交型双垂直一般【精选例题】“平行型”【例 1】如图，EE1∥FF1∥MM1，若AE EF FM MB ，则S AEE : S四边形EE FF : S四边形FFM M : S四边形 MM C B _________1 1 1 1 1 1AE E1FF 1MM1B CWORD 格式可编辑【例 2】如图，AD∥EF∥MN∥BC，若AD 9，BC 18 ， AE:EM :MB 2:3:4,则EF _____ ， MN _____A DE FMNB C【例 3】已知，P为平行四边形ABCD 对角线， AC 上一点，过点P 的直线与 AD ， BC ， CD 的延长线， AB 的延长线分别相交于点 E ， F ， G ， H求证： PE PHPF PGG D CE PFA B H【例 4】已知：在ABC 中， D 为 AB 中点， E 为 AC 上一点，且AE2, BE、 CD相交于点 F ，求BF的值ECEF ADF EB C【例 5】已知：在ABC 中， AD 1AB，延长 BC到F ,使CF1BC,连接 FD交 AC于点 E 2 3求证：① DE EF ② AE 2CEADEB专业知识分享【例 6】已知：D，E为三角形ABC 中 AB 、BC 边上的点，连接 DE 并延长交 AC 的延长线于点 F ，BD: DE AB: AC求证：CEF 为等腰三角形ACDEB F【例7】如图，已知 AB / / EF / /CD ，若 AB a ， CD b ， EF c ，求证：11 1 .c a bACEB F D【例 8】如图，找出S ABD、 S BED、 S BCD之间的关系，并证明你的结论.CAEB F D【例 9】如图，四边形ABCD中，B D90M是AC上一点，ME AD于点EMF BC，，于点 F 求证：MFME 1AB CDDEMA CFB【例 10】如图，在ABC 中， D 是 AC 边的中点，过 D 作直线 EF 交 AB 于 E ,交 BC 的延长线于 F 求证： AE BF BE CFAEDBC F 【例 11】如图，在线段AB 上，取一点 C ，以 AC ， CB 为底在 AB 同侧作两个顶角相等的等腰三角形ADC 和CEB， AE交 CD于点 P， BD交 CE于点Q,求证： CP CQDEP QA C B【例 12】阅读并解答问题 .在给定的锐角三角形ABC 中，求作一个正方形DEFG，使 D， E落在 BC边上， F ， G分别落在AC , AB 边上，作法如下：ABC 两边上的正方形D'E'F 'G'如图，第一步：画一个有三个顶点落在第二步：连接 BF ' 并延长交 AC 于点 F第三步：过 F 点作 FE BC ,垂足为点 E第四步：过 F 点作 FG∥BC 交 AB 于点 G第五步：过 G 点作 GD BC ，垂足为点 D四边形 DEFG 即为所求作的正方形问题：⑴证明上述所作的四边形DEFG 为正方形⑵在 ABC 中，如果BC 6 3，ABC 45 , BAC 75 ,求上述正方形DEFG 的边长AG FG'F'E CWORD 格式可编辑“平行旋转型”图形梳理：E'F'AAAF'E'AEF'EFFFEE'FEF'BCBCBBCAEF 旋转到 AE ‘ F ’CAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’AEF 旋转到AE ‘F ’特殊情况： B 、 E'、 F '共线AAEF' EF'E'FE'FBC B CAEF 旋转到 AE ‘ F ’ AEF 旋转到 AE ‘ F ’C ， E'， F '共线E'AE'AEFEF'FF'BCBCAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’【例 13】已知梯形 ABCD ， AD ∥BC ，对角线AC 、 BD 互相垂直，则①证明： AD 2 BC 2AB 2 CD 2ADOB CWORD 格式可编辑【例 14】当AOD ，以点 O 为旋转中心，逆时针旋转度（090 ），问上面的结论是否成立，请说明理由DAOB C【例 15】（全国初中数学联赛武汉选拔赛试题）如图，四边形ABCD 和 BEFG 均为正方形，求AG : DF : CE_________.A DGFB CE“斜交型”【例 16】如图，ABC 中， D 在 AB 上，且 DE∥BC 交 AC 于 E ， F 在 AD 上，且 AD2AF AB ，求证：AEF :ACDAFD EB C【例 17】如图，等边三角形ABC中，D，E分别在BC，AB上，且CE BE ，AD ，CE 相交于 M ，求证 : EAM : ECAAEMB DC AGF BE【例 18】如图，四边形ABCD 的对角线相交于点O ，BAC CDB ,求证：DAC CBDADOB C【例 19】如图，设ABBCCA，则 1 2 吗？AD DE EAA1 DE2B C【例 20】在锐角三角形ABC 中， AD ， CE 分别为 BC ， AB 边上的高，ABC 和BDE 的面积分别等于 18和 2 ， DE 2，求 AC 边上的高AEB D C【例 21】如图，在等边ABC 的边 BC 上取点 D ，使BD 1，作CH AD，H为垂足，连结BH。

相似模型练习题相似模型练习题是数学中一类常见的题型，用于考察学生对相似模型的理解和应用能力。

相似模型是指形状相似的两个或多个物体，在比例尺不变的情况下，对应部分的长度比保持不变。

以下是几个相似模型练习题，每个题目都附有解析和具体步骤。

题目一：已知圆A的半径是5，圆B的半径是8，求圆A和圆B面积的比值。

解析：圆A的面积为π * 5^2 = 25π圆B的面积为π * 8^2 = 64π所以圆A和圆B面积的比值为25π / 64π = 25 / 64 ≈ 0.39题目二：一辆汽车行驶了180公里，行驶时间是2小时。

求相似模型下，汽车行驶100公里所需要的时间。

解析：根据题意，汽车行驶180公里用时2小时，即速度为180 / 2 = 90公里/小时。

所以相似模型下，汽车行驶100公里所需要的时间为100 / 90 ≈ 1.11小时。

题目三：两根长度分别为12cm和16cm的木棍相似模型下的比例尺是1:2，求这两根木棍相似模型下的长度比。

解析：根据题意，相似模型下的比例尺是1:2，即长度比为1/2。

所以这两根木棍相似模型下的长度比为12 * 1/2 : 16 * 1/2 = 6 : 8 = 3 : 4。

题目四：已知两个相似三角形的边长比是3:5，其中一个三角形的周长是24cm，求另一个三角形的周长。

解析：根据题意，三角形的边长比为3:5。

假设其中一个三角形的周长是24cm，则另一个三角形的周长为24 * (5/3) = 40cm。

通过以上四个例子，我们可以发现相似模型练习题的基本思路是根据已知条件，运用相似模型的定义和性质进行推导和计算。

在解答过程中，要善于运用比例关系，注意单位的换算，严谨而准确地进行计算。

相似模型题目的难易程度有所不同，需要灵活运用所学知识进行求解。

相似模型在数学中具有广泛的应用，不仅可以用于求解长度、面积、体积等几何问题，还可以用于解决实际生活中的比例关系和缩放问题。

在学习相似模型的过程中，要加强对相似形状的观察和判断能力，培养准确运用比例关系和相似模型求解问题的能力。

中考相似模型大全（附20道绝妙好题）
“射影定理”
“一线三等角相似”
“手拉手相似模型”
两相似，共顶点，等顶角，则必有手拉手相似（口诀）
“对角互补相似模型”
“三平行模型”
证明方法：
“内接矩形相似模型”
“线束模型”
以下为中考超纲内容，仅供有兴趣的同学研究
看了这么多，来几道好题热热身吧！第一题：A字相似模型的构造
第二题：相似三角形的性质与判定
第三题：8字相似模型的构造
第四题：线束模型的构造
（此题如果学过四点共圆的同学应该可以秒杀）第五题：内接矩形相似模型的构造
第六题：三平行模型
第七题：反A模型的构造
第十、十一题：斜射影模型
第十二题：射影模型应用
第十三题：射影模型应用
第十四题：射影模型的构造
第十五题：三垂直模型的应用
第十六题：一线三等角模型的构造
第十七题：手拉手相似模型的构造（1）
第十八题：手拉手相似模型的构造（2）
第十九题：对角互补类旋转相似应用
第二十题：对角互补类旋转相似的构造
本篇推文从定内容到选题、排版、编辑，耗时近十个小时，希望能对大家有所帮助，如有错误辛苦指正，欢迎大家一起探讨！。

万能解题模型1．(2019·遵义)如图，已知⊙O的半径为1，AB，AC是⊙O的两条弦，且AB＝AC，延长BO交AC于点D，连接OA，OC.若AD2＝AB·DC，则OD22．(2019·娄底)如图，点D 在以AB 为直径的⊙O 上，AD 平分∠BAC ，DC ⊥AC ，过点B 作⊙O 的切线交AD 的延长线于点E.求证：(1)直线CD 是⊙O 的切线； (2)CD·BE ＝AD·DE.证明：(1)连接OD. ∵AD 平分∠BAC ， ∴∠CAD ＝∠BAD.∵OA ＝OD ，∴∠BAD ＝∠ADO. ∴∠CAD ＝∠ADO.∴AC ∥OD. ∵CD ⊥AC ，∴CD ⊥OD. 又∵OD 为⊙O 的半径， ∴直线CD 是⊙O 的切线． (2)连接BD.∵BE 是⊙O 的切线，AB 为⊙O 的直径， ∴∠ABE ＝∠BDE ＝90°.∵CD ⊥AC ，∴∠C ＝∠BDE ＝90°. ∴∠CAD ＝∠BAE ＝∠DBE.∴△ACD ∽△BDE.∴CD DE ＝ADBE.∴CD·BE ＝AD·DE.3．(2018·巴中)如图，⊙O的两弦AB，CD相交于点P，连接AC，BD，得S△ACP∶S△DBP＝16∶9，则AC∶BD ＝4∶3．4．(2018·扬州)如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，CD与BE，AE分别交于点P，M.对于下列结论：①△BAE∽△CAD；②MP·MD＝MA·ME；③2CB2＝CP·CM.其中正确的是(A) A．①②③B．①C．①②D．②③相关结论：△ACD∽△ABC∽△CBD，CD2＝BD·AD，BC2＝BD·AB，AC2＝AD·AB.5．(2019·宜宾)如图，已知Rt △ABC 中，CD 是斜边AB 上的高，AC ＝4，BC ＝3，则AD ＝165．6．(2018·安顺)如图，点P 1，P 2，P 3，P 4均在坐标轴上，且P 1P 2⊥P 2P 3，P 2P 3⊥P 3P 4.若点P 1，P 2的坐标分别为(0，－1)，(－2，0)，则点P 4的坐标为(8，0)．7．(2019·南充)如图，在△ABC 中，以AC 为直径的⊙O 交AB 于点D ，连接CD ，∠BCD ＝∠A. (1)求证：BC 是⊙O 的切线；(2)若BC ＝5，BD ＝3，求点O 到CD 的距离．解：(1)证明：∵AC 是⊙O 的直径， ∴∠ADC ＝90°.∴∠A ＋∠ACD ＝90°. ∵∠BCD ＝∠A ，∴∠ACD ＋∠BCD ＝90°. ∴∠ACB ＝90°.又∵OC 是⊙O 的半径， ∴BC 是⊙O 的切线．(2)过点O 作OH ⊥CD 于点H. ∵∠ACB ＝∠BDC ＝90°，∠B ＝∠B ， ∴△ACB ∽△CDB. ∴BC BD ＝AB BC .∴53＝AB 5. ∴AB ＝253.∴AD ＝163.∵OH ⊥CD ，∴CH ＝DH.∵AO ＝OC ，∴OH ＝12AD ＝83.∴点O 到CD 的距离是83.(1)如图1，△CAP ∽△PBD(此图又叫做“三垂图”)； (2)如图2、图3，有以下结论： ①△CAP ∽△PBD ；②连接CD ，当点P 为AB 的中点时，△CAP ∽△PBD ∽△CPD.8．(2019·凉山州)如图，在正方形ABCD 中，AB ＝12，AE ＝14AB ，点P 在BC 上运动(不与B ，C 重合)，过点P 作PQ ⊥EP ，交CD 于点Q ，则CQ 的最大值为4．9．如图，在边长为9的等边△ABC 中，BD ＝3，∠ADE ＝60°，求AE 的长．解：∵△ABC是边长为9的等边三角形，∴∠B＝∠C＝60°，AB＝BC＝AC＝9.∴∠BAD＋∠ADB＝120°.∵∠ADE＝60°，∴∠CDE＋∠ADB＝120°.∴∠BAD＝∠CDE.∴△ABD∽△DCE.∴ABDC＝BDCE，即99－3＝3CE.∴CE＝2.∴AE＝9－2＝7.【变式】点D，E分别变到CB，AC的延长线上．如图，△ABC是等边三角形，点D，E分别在CB，AC的延长线上，∠ADE＝60°.求证：△ABD∽△DCE.证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°.∴∠ABD＝∠DCE＝120°.∵∠ABC＝∠DAB＋∠BDA，∠ADE＝∠EDC＋∠BDA，∠ABC＝∠ADE＝60°，∴∠DAB＝∠EDC.∴△ABD∽△DCE.10．如图，在矩形纸片ABCD中，将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM)，点A和点B都与点E 重合；再将△CQD沿DQ折叠，点C落在线段EQ上点F处．(1)判断△AMP，△BPQ，△CQD和△FDM中有哪几对相似三角形？(不需说明理由)(2)如果AM＝1，sin∠DMF＝35，求AB的长．基本模型5三角形内接矩形模型解：(1)有三对相似三角形：△AMP ∽△BPQ ∽△CQD.(2)设AP ＝x ，由折叠的性质，得BP ＝AP ＝EP ＝x.∴AB ＝DC ＝2x.由△AMP ∽△BPQ ，得AM BP ＝APBQ ，∴BQ ＝x 2.由△AMP ∽△CQD ，得AP CD ＝AMCQ，∴CQ ＝2.AD ＝BC ＝BQ ＋CQ ＝x 2＋2，MD ＝AD －AM ＝x 2＋2－1＝x 2＋1.在Rt △FDM 中，sin ∠DMF ＝35，DF ＝DC ＝2x ，∴2x x 2＋1＝35. 解得x 1＝3，x 2＝13(不合题意，舍去)．∴AB ＝2x ＝6.11.如图，已知正方形DEFG 的顶点D 、E 在△ABC 的边BC 上，顶点G 、F 分别在边AB 、AC 上．如果BC=4，△ABC 的面积是6，那么这个正方形的边长是 7．。

相似理论试题（硕士）
2011级硕士研究生相似理论试题
一、基本理论（30分）
1．几何相似、运动相似、动力相似的涵义是什么？
2．何谓相似准则？模型实验怎样选择相似准则？
3．怎样运用π定理建立物理方程？
4．何谓量纲？量纲和单位有何不同？
5．量纲分析方法的理论根据是什么？
二、有一轿车，高h=1.5m，在公路上行驶，设计时速v=108km/h，拟通过风洞中模型实验来确定此轿车在公路上以此速行驶时的空气阻力。

已知该风洞系低速全尺寸风洞(kl=2/3)，并假定风洞试验段内气流温度与轿车在公路上行驶时的温度相同，试求：风洞实验时，风洞实验段内的气流速度应安排多大？
（15分）
三、简述应用相似理论方法确定经验公式的试验过程（15分）
四、已知文丘里流量计喉管流速u与流量计压强差Δp、主管直径d1、喉管直径d2以及流体的密度ρ和运动粘度μ有关，试用π定理确定流速关系式。

（15分）
五、在苜蓿草薄层干燥实验过程中，影响苜蓿茎杆干燥速度因素有（包括量纲，
括号内为对应物理量的量纲或导出量纲符号）初始含水率Mo （无），样品质量G（M），干燥温度ta （ML2T - 2），介质流速V （LT-1），茎杆长度l（L），干燥常数k（T- 1），根据量纲齐次原理导出相似准则。

（25分）
两相似流动应几何相似、运动相似、动力相似，
几何相似：两流动的对应边长成同一比例，对应角相等。

运动相似：两流动的对应点上的流体速度矢成同一比例。

THANKS
致力为企业和个人提供合同协议，策划案计划书，学习课件等等
打造全网一站式需求
欢迎您的下载，资料仅供参考。

相似三角形八大模型归纳例题相似三角形，这可是个有趣的话题！大家好，今天我们就来聊聊这八大模型，轻松又幽默地让你了解它们，没问题吧？想象一下你在公园里散步，忽然看到两个小朋友，一个高一个矮，他们在玩搭积木。

高的小朋友把积木堆得高高的，矮的小朋友也不甘示弱，拼命地跟着学。

这不就是相似三角形的真实写照吗？他们的比例相同，但是大小却不一样，这样想就简单多了。

咱们得了解相似三角形的基本概念。

简单来说，相似三角形就像一对亲密无间的兄弟，虽然身高不一样，但长相、比例却是那么相似。

就好比你家猫咪和邻居的猫咪，虽然毛色不同，但总能一眼认出它们是亲戚。

这种相似可不光是外表，连角度都得一样。

没错，角度就像我们的性格，各有千秋但都能和谐共处。

我们来聊聊相似三角形的判定。

首先是AA判定，就是两个三角形的两个角相等，嘿，这简直像是两个人在合唱，和声完美，谁都不敢说不。

这一招，绝对是相似三角形的杀手锏。

然后就是SSS判定，三个边的比例相等，这可不简单，像极了团队合作，每个人都发挥了自己的作用，最终实现了目标。

SAS判定，两个边的比例相等，还有夹角相等。

这就像打麻将，牌虽然不一样，但搭配得当，赢的机会就大大增加了。

咱们再来看看实际应用。

比如，建筑师设计房子的时候，就得用到这些相似三角形的原理，保证建筑的稳定性和美观性。

你想想，如果房子的角度都乱了，那可就麻烦大了！还有航海测量，水手们通过相似三角形来测量距离，别小看这个，关键时刻可关乎生死，真是一不小心就得跳海了。

学习相似三角形不光是为了考试，生活中处处都能见到它的影子。

你去超市买东西，看到两瓶相同品牌的饮料，虽然瓶子大小不一样，但标签和设计却一模一样。

这样一来，你就能轻松判断哪瓶更划算。

这就像购物时遇到的“买一送一”，表面看似优惠，其实是相似三角形的另一种变相体现。

说到这里，可能有人会觉得相似三角形太抽象，不够有趣。

学数学就像是吃大餐，得慢慢品味，才能发现其中的美味。

想象一下，你在烧烤摊，烤肉时得掌握火候，太熟了或者太生了都不好，学数学也是如此，掌握了相似三角形的精髓，才能在考试时游刃有余。

相似三角形模型分析大全、相似三角形判定的基本模型认识（一）A字型、反A字型（斜A字型）C （平行）（二）8字型、反8字型（平行）（蝴蝶型）（不平行）（三）母子型母子型相似三角形例1 :如图，梯形 ABCD 中，AD // BC ,对角线 AC 、BD 交于点O , BE // CD 交CA 延长线于 E .2求证：OC 2 OA OE .例2 :已知：如图，△ ABC 中，点E 在中线AD 上，DEB ABC .求证：DB 2 DE DA ;相关练习：1、如图，已知 ADABC 的角平分线，EF 为AD 的垂直平分线.求证:谕=AD” BD 曲二HE •皿 BC 2= EA • RD2FD FB FC . 图1inS.SSDAD^AABC 的角平分线,EF 为AD 的垂晝平分竦求证FD=FB FC.解析连AF.则DF 二 AF.再由4ACF7日AF 对应边戚比例即可求证悦考网证明•连接AF.2、已知：AD 是Rt △ ABC 中/A 的平分线，/ C=90°, EF 是AD 的垂直平分线交 AD 于M 交于一点M证明2TEF 垂直曲AD .\ZMMA=ZNMD=90 二 ZDNM 十 ZADC=90/ZACB=90/.ZCAD+ZADC=90 .\ZDNM=ZCAD .\AAME<^AhJMD CAA)2、TEF 垂直平分AD/.NA=ND/.Z NAD -^NDATAD 平分 2BAC.\ZBAD=ZCADZNAD= ZNAC^ZCAD, ZNDA=ZB+ZBAD 〈三甬形AB 另卜角〉.\ZNAC=ZB■；ZANC=ZBNA 〔公共甬》.'.AANC^ABNA (AA).'.NA/NG^NB/NA/.NA^NC K NB.-.D^-NCxNB求证： ⑴△ AM 3A NMD; (2)ND 2 =NC- NBEF 、BC 的延长线3在ABC中，AB=AC高AD与BE交于H, EF BC，垂足为F,延长A［到G,使DG=EF M是AH的中点。