第七章 形式逻辑的基本规律

形式逻辑四大定律形式逻辑是逻辑学的一门分支，主要研究逻辑结构和形式规则的应用。

其中，四大定律是形式逻辑的重要基础，下面分别介绍这四大定律。

1.恒等律：P∧T ≡ P恒等律指的是，当并集P与永真式T交集时，得到的结果仍然是原集合P。

这表明了“真”与其他命题的关系，即“真”与任意命题取交集仍等于原命题。

2.排中律：P∨~P ≡ T排中律指的是，对于任意命题P，它与其否定~P的并集得到永真式T。

这表明了任意命题与其否定之间的关系，即二者只有其中一个可以为真。

3.否定律：P∧~P ≡ F否定律指的是，对于任意命题P，它与其否定~P的交集得到永假式F。

这表明了任意命题与其否定之间的关系，即二者不可能同时为真。

4.归谬律：{P, P→Q} ⊢ Q归谬律指的是，当前提中出现矛盾时，可以从中任选一命题进行否定，并将其作为新的命题，同时推导出与之相反的命题。

从而证明前提中的矛盾并推导出结论。

这表明了推理中如果出现了矛盾，可以通过否定其中一命题来达到推导目的。

以上四大定理是形式逻辑的基础，对于推理、证明、判断等都有极大的帮助。

熟练掌握四大定理是进行形式推理的重要前提。

形式逻辑是研究逻辑结构和形式规则的一门学科。

在形式逻辑中，最基本的概念是命题和联结词。

命题是一个陈述语句，联结词则是用于连接两个或多个命题，以形成更复杂命题的符号。

在联结词的使用中，需要遵循一定的规则，这些规则被称为“定律”，形式逻辑的四大定律即是其中最为基础的定律。

1. 恒等律：P∧T ≡ P恒等律是指当并集P与永真式T交集时，得到的结果仍然是原集合P。

这个定律表明，真值为“真”的命题与其他命题的关系，即真值为“真”的命题与任何其他命题取“且”的交集，结果仍然是原命题。

例如，假设P代表“今天是星期天”，那么“今天是星期天且猫是动物”与“今天是星期天”其实是等价的。

由于T代表着“真”，因此P∧T实际上就是P本身，模式就是P∧T ≡ P。

2. 排中律：P∨~P ≡ T排中律指的是，对于任意命题P，它与其否定~P的并集得到永真式T。

形式逻辑逻辑规律形式逻辑有四个模块，分别是概念、判断、推理和论证。

可是概念是怎么产生的呢？我们知道，宇宙是非常大的，一直在膨胀中，宇宙到底有多大呢？对于人类而言，仍然是未知的；可是，人类的认知是有限的，用有限的认知去认识无限的宇宙，这是很难做到的。

但是，有没有一种办法可以提高我们的效率呢？有。

我们的古人曾经说过，物以类聚人以群分。

注意，这8个字非常重要，道明了根本的认知方法，这也是分类的方法。

而古希腊人，也早早地明白了这个道理，古希腊的苏格拉底、柏拉图和亚里士多德，他们是师父、徒弟和徒孙的关系，其实这三个人都致力于一件事，那就是给各种概念下定义。

比如，勇气这个概念，它是什么意思？你怎么给这个概念下定义？苏格拉底用的方法就是辩证法，当然那时候的辩证法还是朴素的辩证法，通过不断的追问寻找概念的本质。

而柏拉图发明了理型论，认为事物的理型就是本质，而所有的概念都代表事物背后的那个理型；等到亚里士多德时，就开始用分类的方法，把事物按照种属进行不断的分类，最后用种差法给概念下定义。

这种方法与中国的古人不谋而合。

我们现在的伦理学、政治学、经济学、数学等学科，就是亚里士多德当年分类出来的，这些学科的概念一直沿用至今。

每个学科都有自己单独的研究领域，这完全是分类的结果，有了分类就有了各种各样的概念。

比如，母鸡，石头等……有了概念，就需要判断概念与概念之间的关系。

比如，母鸡和石头之间是什么关系呢？我们现在画一个圈，代表物体，中间画一个竖线将圆圈一分为二：左半边代表无生命的物体；右半边代表有生命的物体。

左边画个圈，代表无机，面里画个圈，代表石头；右边画个圈，代表动物，里面画个圈，代表母鸡。

这样，我们就能根据分类的方法，能清晰的构建出一幅概念图。

然后，我们能容易的判断出，原来母鸡和石头都是物体。

有了这个概念图，我们就可以推理，比如，现在有一个物体A，但它是什么我们不知道，但是我们能推理出，这个A要么是有生命的物体，要么是无生命的物体。

整理版逻辑学课后习题答案形式逻辑学练习（堂上训练部分）第⼀章绪论⼀、填空：1．普通形式逻辑研究的对象是：思维形式思维基本规律简单逻辑⽅法_。

2．在抽象思维、形象思维和灵感思维三者中，普通形式逻辑研究的思维属于_抽象思维__。

3．思维的逻辑形式⼜叫_ _思维的形式结构_____，指具有不同思维容的思维形式所共同具有的__共同联系⽅式___。

4．思维的形式结构是__由逻辑常项和逻辑变项结合⽽成__的符号系统。

5．思维形式结构中固定不变的部分叫__逻辑常项_，可以变化的部分叫__逻辑变项__。

⼆、指出下列命题的形式结构：1．这个学⽣是三好学⽣。

（这个S是P ）2．马克思主义不是教条，⽽是⾏动的指南。

（⾮p，但q）3．这节课或者你来讲，或者我来讲。

或p，或q4．如果不努⼒学习，就很难取得好成绩。

如果⾮p，那么，⾮q三、指出下列形式结构中的逻辑常项和逻辑变项：1．所有S是P逻辑常项：所有，是。

逻辑变项：S，P2．p←q逻辑常项：←，。

逻辑变项：p，q3．有S不是P逻辑常项：有，不是。

逻辑变项：S，P4．（p∧q）→r逻辑常项：∧，→逻辑变项：p，q，r5．直⾔命题的周延性，是指在直⾔命题中对主词、谓词外延数量的___断定情况___。

6．⽭盾关系是⼀种_____不可同真，也不可同假____的关系。

7．关系命题是断定___事物之间关系___的命题。

8．如果aRb，并且 bRc成⽴，那么aRc也⼀定成⽴，这种关系就是_传递关系__关系。

⼆、下列语句是否表达命题？为什么？1．解放思想，实事求是。

（表达命题。

因为这个述句具有命题的"有所述"和"有真假之分"的逻辑特征。

）2．我还有很多事情要办。

（表达命题。

因为该述句具有命题的两个逻辑特征。

）3．这部电脑为什么⽼出⽑病？（不表达命题。

这是⼀个⼀般的疑问句，它只是提出了⼀个问题，亦⽆所谓真假。

）4．⼈⾮圣贤，孰能⽆过？（表达命题。

形式逻辑推理规则
以下是 7 条形式逻辑推理规则：
1. 同一律呀，简单来说就是在同一个推理过程中，每个概念和判断都要保持自身的同一性。

比如说“小猫咪就是小猫咪，不能一会儿说小猫咪是小狗呀！”
2. 矛盾律呢，就是两个互相矛盾的判断不能同时为真。

就好像说“今天不能既是晴天又是雨天呀，这多矛盾！”
3. 排中律哦，两个互相矛盾的判断必定有一个是真的。

好比“这个人要么是好人，要么不是好人，没有中间情况呀！”
4. 充足理由律呀，任何判断都要有充足的理由来支持。

像“他说他病了，那得有真的不舒服的表现或者医生的诊断才可信呀！”
5. 三段论，“所有的猫都爱睡觉，这只动物是猫，所以这只动物也爱睡觉。

是不是很清楚呀！”
6. 演绎推理，从一般到特殊呀，比如“大家都知道人要吃饭，那具体的张三当然也要吃饭啦！”
7. 归纳推理，可以从个别事例中归纳出一般结论呢。

就像“这只鸟会飞，那只鸟会飞，好多鸟都会飞，那可以归纳出鸟一般都会飞呀！”
总之呢，形式逻辑推理规则就像是我们思考的指南针，帮助我们更准确、更有条理地理解和判断事物哟！。

【关键字】小学第七章普通形式逻辑的基本规律【堂上操练】一、填空题：1．普通形式逻辑的基本规律有_________、________和_________。

2．在同一思维过程中，三条基本规律都共同要求保持_______。

3．违反同一律的要求，就会出现"________"和"_______"的逻辑错误。

4．违反矛盾律的要求，就会出现"________"的逻辑错误。

5．违反排中律的要求，就会出现"_______"的逻辑错误。

二、下列各段文字是否符合同一律要求？如不符合，犯了什么逻辑错误？1．甲：今年你们厂的产值是多少？乙：今年原材料提了很多价，不亏本就算好了。

2．上面不是老说领导要多听群众意见？我是群众，可领导总是不听我的意见。

3．这门课程很难学，我花了很多时间还是学不好。

4．凡是你所没有丧失的，就是你有的；你没有丧失角，所以你有角。

5．唐代以后古体诗转韵的也不少，如白居易的《长恨歌》、《琵琶行》就是这样。

三、下列各段文字是否符合矛盾律和排中律的要求？如不符合，指出违反了哪条基本规律和犯了什么逻辑错误：1．这个公司今年做了差不多一百万元以上的生意。

2．张三考试作弊，一种意见是要处分，一种意见是不要处分，这两种意见我都不赞成，关键是做好张三的思想工作。

3．有的人死了，他还活着；有的人活着，他已经死了。

4．万里长城是我国劳动人民智慧的结晶，也是我国的天然屏障。

5．"鲁迅是一个乡土作家"是一种意见，"鲁迅不是一个乡土作家"也是一种意见，对这两种意见我很难表态。

如果一定要我表态的话。

我认为："如果鲁迅是一个乡土作家，那么，他就是一个乡土作家，如果鲁迅不是一个乡土作家，那么，他就不是一个乡土作家。

"6．既不能说这筒胶卷每张相片都照得很好，也不能说这筒胶卷每张相片都照得不好。

【课后作业】一、下列议论是否违反普通形式逻辑的基本规律？请加以简要分析：1．犯罪嫌疑人没有犯罪之故意，不是犯罪嫌疑人。

《形式逻辑》思维训练题第一章概述1. 一个猜帽子的游戏有甲乙丙三人，同向站立。

在三人不知道的情况下，主持人给三人各戴上一顶子：红帽或白帽。

三人都知道有三顶红帽和两顶白帽。

丙可看见甲和乙的帽子，乙可看见甲的帽子。

主持人问丙是否知道自己戴的是什么帽子，丙答不知道；又问乙是否知道，也答不知道；问甲是否知道，甲答知道了，是——。

问：甲是怎么知道的？他的推理过程是——。

2. “有角的”诡辩在古希腊，有一个“有角的”诡辩。

这个诡辩是这样说的：“你没有失去的东西，还在你那里；你没有失去角，所以，你有角。

”问：在这个诡辩中，诡辩家使用的诡辩手法是什么？要害在哪里？第二章概念1 .举例：“阎锡山登报征求下联”1937年，阎锡山经过无锡，游览了锡山，写了上联：阎锡山过无锡登锡山锡山无锡登报征求下联，当时无人能对。

你能对吗？请能对者在纸上写出下联交给我。

8年后，范长江随陈毅同志到天长县采访。

范对陈毅说：“阎锡山的绝句我对上了，是‘范长江到天长望长江长江天长’。

”陈毅连声赞道：“妙！妙！长江，才子也。

”2. 案例：浑水摸鱼——混淆概念的诡辩据报载，某人在家具商场看中了一件家具，按约定向商家交了200元订金，而商场却在相关票据上将“订金”改为“定金”。

后来这个人由于某种原因不打算购买这件家具了，便要求商场退还200元订金。

但商场却以《合同法》的有关规定为由，不予退款。

此时，这个人才意识到当初商场将“订金”改写为“定金”就是为了扣住这200元钱。

3. 实例：“客人的反驳”前不久，有客人来常德旅游。

主人对客人介绍说：“常德的最大特色是秀气。

山秀水秀人亦秀。

”客人反驳道：“那不见得，我看有些常德人并不秀。

”4. 分析下列句子：宣武区环卫局970多名居住在市区和近郊区的职工中，有26户家中养了鸡、鹅、兔、鸽等。

我父亲已去世一年，父亲在世的十几年中，经常教育我，要发扬艰苦朴素的优良作风。

他离开祖国定居巴黎四十年了，虽然加入了法国籍，但对故土很关心，是一位热爱祖国的华侨。

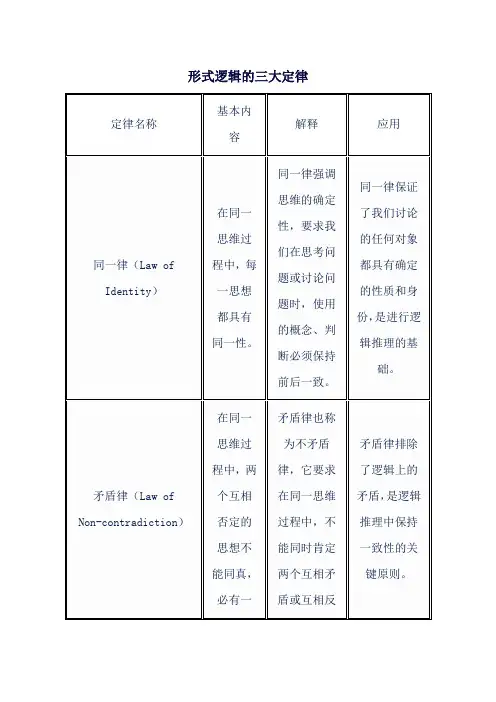
形式逻辑的基本规律形式逻辑的基本规律的概述形式逻辑的基本规律是各种思想逻辑形式的普遍规律，它包括同一律、矛盾律、排中律和充足理由律。

我们这里所说的基本规律就是相对于特定规律而言的。

我们以前曾经谈过许多逻辑规则，比如定义规则、分割规则、三段论规则等等。

这些逻辑规则相对于同一律、矛盾律、排中律和充裕理由律这四条逻辑规律来说，都具有特殊性。

它们只在特定的思想逻辑形式里有效率。

相对于这些逻辑规律来说，逻辑的基本规律则具有普遍性，就是对这些规则的进一步归纳。

因而它们广泛地适用于于各种思想形式，正是在这个意义上，形式逻辑把它们称作基本规律。

形式逻辑的基本规律存有以下几个特点：一、普遍有效性。

逻辑规律是思维活动中的基本准则，对一切思维过程都有制约作用。

任何正确的思想，无论是概念、命题还是推理，都必须具有确定性。

有确定的内容，确定地反映客观对象，这是逻辑思维的基本特征。

同一律、矛盾律和排中律正是从不同角度反映这一特征。

同一律明确提出任何思想与自身同一，矛盾律建议思想不自相矛盾，排中律则确定两个矛盾思想的中间可能性。

严格遵守这三条规律就是思想具备确定性的必要条件，违背了它们的建议，则势必犯下逻辑错误。

这从逻辑规律在思维中的促进作用说道的。

再者，充足理由律也是逻辑思维的必要条件，它是思想具有论证性的必要条件。

违反了它的要求，同样犯逻辑错误。

1二、客观必然性。

逻辑规律不是客观事物的规律，而是思维自身的规律，因此有其主观性。

但逻辑规律不是同客观事物毫无关系的纯思维的产物，它有其自身的客观基础，即一切客观事物在其存在时必须具有的规律。

因为一切事物在其存在时只能是该事物而非他物；一切事物在其存在时不能是虚无；一切事物要么存在，要么不存在，二者必居其一；一切事物的存在必有其存在的理由。

三、逻辑思维具备确定性和论证性的特征。

其中，思维的确定性又具体表现为思维的同一性、一贯性和明确性。

同一律、矛盾律、排中律就是有关思维具备确定性的规律，充裕理由律就是有关思维具备论证性的规律。

形式推理的基本规则形式推理是一种逻辑思维的方式，通过运用一定的规则和方法，从已知的前提中推导出新的结论。

它在数学、哲学、科学等领域中具有重要的应用价值。

本文将探讨形式推理的基本规则，帮助读者理解和运用这一思维方式。

一、假设与推理形式推理的基础是假设和推理。

假设是指在推理过程中所假定的前提条件，推理则是基于这些前提条件进行的逻辑推导。

在形式推理中，我们常常使用条件语句来表达假设和推理的关系，如“A则B”表示如果A成立，则B也成立。

通过合理的推理，我们可以从已知的前提中得出新的结论。

二、充分必要条件在形式推理中，充分必要条件是一种重要的推理方式。

充分必要条件是指两个命题之间既是充分条件又是必要条件的关系。

如果A是B的充分条件，那么B是A的必要条件。

例如，如果一个人是成年人，那么他必须年满18岁。

这里，成年人是年满18岁的充分条件，而年满18岁是成年人的必要条件。

三、假言推理假言推理是形式推理中常见的一种方法。

它通过对条件语句的推理，得出新的结论。

假言推理有两种形式：假设条件为真，然后推出结论；或者假设结论为假，然后推出条件的否定。

例如，如果A成立则B成立，我们可以通过假设A成立，然后推导出B成立的结论。

四、消解法消解法是一种常用的形式推理方法，尤其在数理逻辑中得到广泛应用。

它通过对命题的否定和合取范式的转化，将问题简化为更易解决的形式。

消解法的基本思想是通过对两个命题的否定进行合并，得出新的命题。

例如，如果我们已知“所有A都是B”和“所有B都是C”，我们可以通过消解法得出“所有A都是C”的结论。

五、归谬法归谬法是一种常用于推理论证中的方法，它通过推导出矛盾的结论来否定前提条件。

如果我们假设A成立，然后通过推理得出既是A又是非A的结论，那么我们可以推断出A是错误的。

归谬法在逻辑学中扮演着重要的角色，它帮助我们排除错误的推理和论证。

六、归纳与演绎形式推理中的归纳和演绎是两种不同的思维方式。

归纳是从特殊到一般的推理方式，通过观察和总结个别事实，得出普遍性的结论。

形式逻辑简明教程一、引言形式逻辑是一门研究命题和谓词之间关系的学科，它帮助我们理解和分析逻辑结构，提高我们的推理能力。

本文将为您介绍形式逻辑的基本概念和常见推理规则，帮助您快速入门。

二、命题逻辑命题逻辑是形式逻辑的基础，它研究命题之间的逻辑关系。

命题是陈述句，可以判断为真或假。

在命题逻辑中，我们用符号表示命题，如P、Q、R等。

逻辑连接词用来连接命题，如与、或、非等。

三、命题逻辑的逻辑连接词1. 与：用符号∧表示，表示两个命题都为真时，整个命题才为真。

2. 或：用符号∨表示，表示两个命题中至少有一个为真时，整个命题为真。

3. 非：用符号¬表示，表示命题的否定。

4. 条件：用符号→表示，表示如果前提为真，则结论也为真。

5. 反条件：用符号←表示，表示如果结论为真，则前提也为真。

6. 双条件：用符号↔表示，表示前提和结论相互依赖，要么都为真，要么都为假。

四、命题逻辑的推理规则1. 假言推理：如果前提为真，则结论也为真。

2. 拒取式：如果前提为假，则结论也为假。

3. 假言拒取式：如果结论为假，则前提也为假。

4. 析取三段论：如果两个命题中至少有一个为真，而另一个为假，则整个命题为真。

5. 假言三段论：如果前提和结论相互依赖，且前提为真，则结论也为真。

五、谓词逻辑谓词逻辑是形式逻辑的扩展，它研究谓词之间的逻辑关系。

谓词是描述性的陈述，可以用变量表示。

在谓词逻辑中，我们用量词来描述变量的范围，如∀（全称量词）和∃（存在量词）。

六、谓词逻辑的量词1. 全称量词∀：表示变量的所有值都满足命题。

2. 存在量词∃：表示变量存在一个值使命题为真。

七、谓词逻辑的推理规则1. 全称引入：从一个实例推出一个全称命题。

2. 全称消去：从一个全称命题推出一个实例。

3. 存在引入：从一个实例推出一个存在命题。

4. 存在消去：从一个存在命题推出一个实例。

八、结论形式逻辑是一门重要的学科，它帮助我们理解和分析逻辑结构，提高我们的推理能力。