广东省中山市普通高中高考数学一轮复习模拟试题01

考点01 集合1．若集合A＝{－1,0,1}，B＝{y|y＝x2，x∈A}，则A∩B＝( )A．{0} B．{1}C．{0,1} D．{0，－1}【答案】C【解析】因为B＝{y|y＝x2，x∈A}＝{0,1}，所以A∩B＝{0,1}．2．设集合，集合，则（）A． B． C． D．【答案】B【解析】集合=,集合,则。

故答案为：B.3．已知全集为整数集Z.若集合A＝{x|y＝1－x，x∈Z}，B＝{x|x2＋2x>0，x∈Z}，则A∩(∁Z B)＝( ) A．{－2} B．{－1}C．[－2,0] D．{－2，－1,0}【答案】D【解析】由题意可知，集合A＝{x|x≤1，x∈Z}，B＝{x|x>0或x<－2，x∈Z}，故A∩(∁Z B)＝{－2，－1,0}．故选D.4．已知集合A＝{x|0<x≤6}，B＝{x∈N|2x<33}，则集合A∩B中的元素个数为( )A．6 B．5C．4 D．3【答案】B【解析】集合A＝{x|0<x≤6}，B＝{x∈N|2x<33}＝{0,1,2,3,4,5}，∴A∩B＝{1,2,3,4,5}，∴A∩B中元素个数为5.故选B.5．已知集合，，则（）A． B． C． D．【答案】A【解析】因为集合，，所以A∩B={0,1}.故答案为：A.6．若集合M＝{x||x|≤1}，N＝{y|y＝x2，|x|≤1}，则( )A ．M ＝NB ．M ⊆NC ．M ∩N ＝∅D ．N ⊆M【答案】D【解析】∵M ＝{x ||x |≤1}＝{x |－1≤x ≤1}，N ＝{y |y ＝x 2，|x |≤1}＝{y |0≤y ≤1}，∴N ⊆M .故选D. 7．已知集合 ，，则（ ）A ．B ．C ．D ．【答案】C 【解析】由题意得，，.故选C.8．已知集合A ＝{1，a 2}，B ＝{2a ，－1}，若A ∩B ＝{4}，则实数a 等于( ) A ．－2 B ．0或－2 C ．0或2 D ．2【答案】D【解析】因为A ∩B ＝{4}，所以4∈A 且4∈B ，故⎩⎪⎨⎪⎧a 2＝4，2a ＝4，a ＝2.故选D.9．已知集合，，则集合（ ）A ．B ．C ．D ．【答案】D 【解析】已知集合，，∴A∩B 中的元素满足：解得： 则A∩B=. 故选D.10．设全集U ＝R ，已知集合A ＝{x ||x |≤1}，B ＝{x |log 2x ≤1}，则(∁U A )∩B ＝( ) A ．(0,1] B ．[－1,1] C ．(1,2]D ．(－∞，－1]∪[1,2]【答案】C【解析】因为A＝{x||x|≤1}＝{x|－1≤x≤1}，B＝{x|log2x≤1}＝{x|0<x≤2}，所以∁U A＝{x|x>1或x<－1}，则(∁U A)∩B＝(1,2]．11．已知全集U＝R，集合A＝{0,1,2,3,4}，B＝{x|x2－2x＞0}，则图中阴影部分表示的集合为( )A．{0,1,2} B．{1,2}C．{3,4} D．{0,3,4}【答案】A【解析】∵全集U＝R，集合A＝{0,1,2,3,4}，B＝{x|x2－2x＞0}＝{x|x＞2或x＜0}，∴∁U B＝{x|0≤x≤2}，∴图中阴影部分表示的集合为A∩(∁U B)＝{0,1,2}．故选A.12．设集合M＝{x|x<4}，集合N＝{x|x2－2x<0}，则下列关系中正确的是( )A．M∩N＝M B．M∪(∁R N)＝MC．N∪(∁R M)＝R D．M∩N＝N【答案】D【解析】由题意可得N＝(0,2)，M＝(－∞，4)，N⊆M.故选D.13．设集合A＝{x|y＝lg(－x2＋x＋2)}，B＝{x|x－a>0}．若A⊆B，则实数a的取值X围是( ) A．(－∞，－1) B．(－∞，－1]C．(－∞，－2) D．(－∞，－2]【答案】B【解析】集合A＝{x|y＝lg(－x2＋x＋2)}＝{x|－1<x<2}，B＝{x|x－a>0}＝{x|x>a}，因为A⊆B，所以a≤－1.14．已知，则（）A． B．C． D．【答案】C【解析】由题可得则故选C.15．已知集合A＝{x|x＜1}，B＝{x|x2－x－6＜0}，则( )A．A∩B＝{x|x＜1}B．A∪B＝RC．A∪B＝{x|x＜2}D．A∩B＝{x|－2＜x＜1}【答案】D【解析】集合A＝{x|x＜1}，B＝x{x|x2－x－6＜0}＝{x|－2＜x＜3}，则A∩B＝{x|－2＜x＜1}，A∪B＝{x|x ＜3}．故选D.16．设U＝R，已知集合A＝{x|x≥1}，B＝{x|x＞a}，且(∁U A)∪B＝R，则实数a的取值X围是( ) A．(－∞，1) B．(－∞，1]C．(1，＋∞)D．[1，＋∞)【答案】A【解析】∵U＝R，集合A＝{x|x≥1}＝[1，＋∞)，∴∁U A＝(－∞，1)，由B＝{x|x＞a}＝(a，＋∞)以及(∁U A)∪B＝R可知实数a的取值X围是(－∞，1)．故选A.17．已知集合，集合，则A． B． C． D．【答案】A【解析】由题得A={x|-2<x<3},所以={x|x≤-2或x≥3}，所以=.故答案为：A18．已知集合，，则∁A． B． C． D．【答案】A【解析】由，即，解得或，即，∁，解得，即，则∁，故选A.1．A ，B 为两个非空集合，定义集合A －B ＝{x |x ∈A 且x ∉B }，若A ＝{－2，－1,0,1,2}，B ＝{x |(x －1)(x ＋2)＜0}，则A －B ＝( ) A ．{2} B ．{1,2} C ．{－2,1,2} D ．{－2，－1,0}【答案】C【解析】∵A ，B 为两个非空集合，定义集合A －B ＝{x |x ∈A 且x ∉B }，A ＝{－2，－1,0,1,2}，B ＝{x |(x －1)(x ＋2)＜0}＝{x |－2＜x ＜1}，∴A －B ＝{－2,1,2}．故选C.20．对于任意两集合A ，B ，定义A －B ＝{x |x ∈A 且x ∉B }，A *B ＝(A －B )∪(B －A )，记A ＝{y |y ≥0}，B ＝{x |－3≤x ≤3}，则A *B ＝________. 【答案】[－3,0)∪(3，＋∞)【解析】由题意知A －B ＝{x |x >3}，B －A ＝{x |－3≤x <0}，所以A *B ＝[－3,0)∪(3，＋∞)． 21．设集合I ＝{x |－3<x <3，x ∈Z }，A ＝{1,2}，B ＝{－2，－1,2}，则A ∩(∁I B )＝________. 【答案】{1}【解析】∵集合I ＝{x |－3<x <3，x ∈Z }＝{－2，－1,0,1,2}，A ＝{1,2}，B ＝{－2，－1，2}，∴∁I B ＝{0,1}，则A ∩(∁I B )＝{1}．22．(2018某某红色七校联考)集合A ＝{x |x 2＋x －6≤0}，B ＝{y |y ＝x ，0≤x ≤4}，则A ∩(∁R B )＝________. 【答案】[－3,0)【解析】∵A ＝{x |x 2＋x －6≤0}＝{x |－3≤x ≤2}，B ＝{y |y ＝x ，0≤x ≤4}＝{y |0≤y ≤2}，∴∁R B ＝{y |y <0或y >2}，∴A ∩(∁R B )＝[－3,0)．23．已知集合A ＝{y |y 2－(a 2＋a ＋1)y ＋a (a 2＋1)>0}，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ⎪⎪⎪ y ＝12x 2－x ＋52，0≤x ≤3.若A ∩B ＝∅，则实数a 的取值X 围是________． 【答案】(－∞，－3]∪[3，2]【解析】由题意可得A ＝{y |y <a 或y >a 2＋1}，B ＝{y |2≤y ≤4}．当A ∩B ＝∅时，⎩⎪⎨⎪⎧a 2＋1≥4，a ≤2，∴3≤a ≤2或a ≤－3，∴a 的取值X 围是(－∞，－3]∪[3，2]． 24．已知集合，，则_________．【答案】【解析】因为，，所以，故{0,7}，故填. 25．已知集合，.（1）若A∩B=，某某数m的值；（2）若，某某数m的取值X围.【答案】（1）2；（2）【解析】由已知得:，.(1)因为,所以，故，所以.(2).因为,或，所以或.所以的取值X围为.。

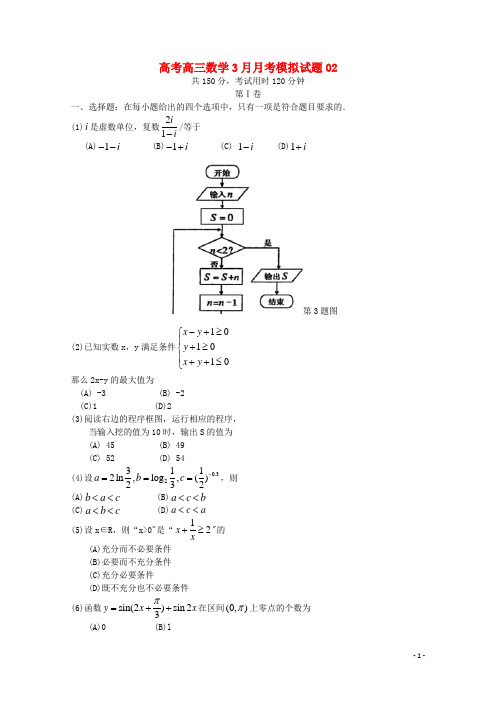
高考高三数学3月月考模拟试题02共150分，考试用时120分钟第Ⅰ卷一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．(1)i 是虚数单位，复数21ii-/等于 (A)1i -- (B)1i -+ (C) 1i - (D)1i +第3题图(2)已知实数x ，y 满足条件101010x y y x y -+≥⎧⎪+≥⎨⎪++≤⎩那么2x-y 的最大值为(A) -3 (B) -2 (C)1 (D)2(3)阅读右边的程序框图，运行相应的程序， 当输入挖的值为10时，输出S 的值为 (A) 45 (B) 49 (C) 52 (D) 54(4)设0.323112ln,log ,()232a b c -===，则 (A)b a c << (B)a c b << (C)a b c << (D)a c a <<(5)设x ∈R ，则“x>0"是“12x x+≥"的(A)充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件(D)既不充分也不必要条件 (6)函数sin(2)sin 23y x x π=++在区间(0,)π上零点的个数为(A)0 (B)l(C)2 (D)3(7)直角三角形ABC 中，90,2,1C AB AC ∠===，点D 在斜边AB 上，且AD AB λ=,R λ∈,若2CD CB ⋅=，则λ=(A)12(B)13）23(8)下列函数中，同时具有性质：①图象过点(0，1):②在区间(0,)+∞上是减函数； ③是偶函数。

这样的函数是(A)1()()2xf x = (B)()lg(2)f x x =+ (C)12()f x x = (D)()2xf x =第Ⅱ卷二、填空题：本大题共6小题，每小题5分，共30分． (9)已知集合{}|12,A x x =->{}|(5)0B x x x =-<, 则AB =________．11图(10)一个几何体的三视图如图所示（单位：m ）， 则该几何体的体积为_______2m ． (11)如图，ABC ∆内接于圆O ，过点C 的切线交 AB 的延长线于点D ，若10,6,9AB BC AC ===， 则切线DC 的长为____．(12)若(,)a b c c在圆221x y +=上，则直线0ax by c ++=与圆222x y +=相交所得弦的长为_____________。

2022年广东省中山市高考数学一模试卷注意事项：1.答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2.选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡的非答题区域均无效。

3、非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。

写在试卷、草稿纸和答题卡的非答题区域均无效。

4.考试结束后，请将本试卷和答题卡一并上交。

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设全集U 与集合M ，N 的关系如图所示，则图中阴影部分所表示的集合是（ ）A ．M ∩NB ．M ∪NC ．（∁U M ）∪ND ．（∁U M ）∩N2．（5分）平面向量a →与b →的夹角为60°，|a →|＝2，|b →|＝1，则|a →+2b →|＝（ ） A ．√3B ．12C ．4D ．2√33．（5分）已知{a n }为正项等比数列，且a 2a 4＝4，设T n 为该数列的前n 项积，则T 5＝（ ） A ．8B ．16C ．32D ．644．（5分）3男3女六位同学站成一排，则3位女生中有且只有两位女生相邻的不同排法种数是（ ） A ．576B ．432C ．388D ．2165．（5分）抛物线C ：y 2＝2px 上一点（1，y 0）到其焦点的距离为3．则抛物线C 的方程为（ ） A ．y 2＝4xB ．y 2＝8xC ．y 2＝12xD ．y 2＝16x6．（5分）已知函数f （x ）＝log a x （a ＞0，a ≠1），则y ＝f （|x |﹣1）的图象可能是（ ）A．B．C．D．7．（5分）已知如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，过A1B且与AC1平行的平面交B1C1于点P，则PC1＝（）A ．2B ．√3C ．√2D ．18．（5分）甲、乙两支田径队的体检结果为：甲队体重的平均数为60kg ，方差为200，乙队体重的平均数为70kg ，方差为300，又已知甲、乙两队的队员人数之比为1：4，那么甲、乙两队全部队员的平均体重和方差分别是（ ） A ．65，280B ．68，280C ．65，296D ．68，296二、选择题：本大题共4小题，每小题5分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．（多选）9．（5分）已知函数f （x ）＝A sin （ωx +φ）（A ＞0，ω＞0，|φ|＜π2）的部分图象如图所示，下列说法正确的是（ ）A ．函数y ＝f （x ）的图象关于点（−π6，0）对称 B ．函数y ＝f （x ）的图象关于直线x =−5π12对称C ．函数y ＝f （x ）在[−2π3，−π6]单调递减 D ．该图象向右平移π6个单位可得y ＝2sin2x 的图象（多选）10．（5分）已知a ＞0，b ＞0，a +b 2＝1，则下列选项中正确的是（ ） A ．3a﹣b的最大值为3B ．b √a 的最大值为12C ．√a +b 的最大值为√2D ．1a+1+1b 2的最小值为2（多选）11．（5分）已知函数f(x)=log 2(1+4x )−x ，则下列说法正确的是（ ） A ．函数f （x ）是偶函数 B ．函数f （x ）是奇函数C ．函数f （x ）在（﹣∞，0]上为增函数D ．函数f （x ）的值域为[1，+∞）（多选）12．（5分）已知球O 的半径为2，球心O 在大小为60°的二面角α﹣l ﹣β内，二面角α﹣l ﹣β的两个半平面分别截球面得两个圆O 1，O 2，若两圆O 1，O 2的公共弦AB 的长为2，E 为AB 的中点，四面体OAO 1O 2的体积为V ，则下列结论中正确的有（ ） A ．O ，E ，O 1，O 2四点共面B ．O 1O 2=√32C ．O 1O 2=32D ．V 的最大值为√316三、填空题：本大题共4小题，每小题5分，共20分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分． 13．（5分）若sin 2α=23，则cos2α＝ ．14．（5分）在数列{a n }中，a 1＝2，√a n+1=√a n +√2，则数列{a n }的通项公式为 ． 15．（5分）已知复数z 满足方程z 2﹣3z +9＝0，则|z |＝ ． 16．（5分）已知点M 为双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）在第一象限上一点，点F 为双曲线C 的右焦点，O 为坐标原点，4|MO |＝4|MF |＝7|OF |，则双曲线C 的离心率为 ；若MF ，MO 分别交双曲线C 于P ，Q 两点，记直线PM 与PQ 的斜率分别为k 1，k 2，则k 1k 2＝ ．四、解答题：本大题共6个小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）已知数列{a n }，{b n }满足b n ＝a n ﹣（﹣1）n n 2，a 1+b 1＝1，a 2+b 2＝8，且数列{b n }是等差数列．（1）求数列{a n }的通项公式；（2）设数列{a n }的前n 项和为S n ，若A ＝{n |n ≤110且S n ≤100}，求集合A 中所有元素的和S ．18．（12分）如图，已知圆锥AO的底面半径为2，母线长为2√10，点C为圆锥底面圆周上的一点，O为圆心，D是AB的中点，且∠BOC=π2．（1）求三棱锥D﹣OCB的表面积；（2）求A到平面OCD的距离．19．（12分）在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且a b=b+c a=sinA cosB．（1）求A ；（2）如图，已知AB ＝2，D 为AC 的中点，点P 在BD 上，且满足AP →⋅CP →=1，求△P AC 的面积．20．（12分）某科技公司组织技术人员进行某新项目研发，技术人员将独立地进行项目中不同类型的实验甲，乙，丙，已知实验甲、乙、丙成功的概率分别为34，23，12．（1）对实验甲、乙、丙各进行一次，求至少有一次成功的概率；（2）该项目研发流程如下：实验甲做一次，若成功，则奖励技术人员1万元并进行实验乙，否则技术人员不获得奖励且该项目终止；实验乙做两次，若两次都成功，则追加技术人员3万元奖励并进行实验丙，否则技术人员不追加奖励且该项目终止；实验丙做三次，若至少两次成功，则项目研发成功，再追加技术人员4万元奖励，否则不追加奖励且该项目终止．每次实验相互独立，用X （单位：万元）表示技术人员所获得奖励的数值，写出X 的分布列及数学期望．21．（12分）已知椭圆C ：x 2a 2+y 2b2=1(a ＞b ＞0)的右焦点为F ，离心率为12，直线l ：y ＝x被椭圆截得的弦长为4√427． （1）求椭圆C 的标准方程；（2）若P 是椭圆C 上一点，O 是坐标原点，过点F 与直线l 平行的直线与椭圆C 的两个交点为A ，B ，且OP →=λOA →+μOB →，求λμ的最大值．22．（12分）已知函数f（x）＝（x﹣2）e x﹣ax+alnx（a∈R）．（1）当a＝﹣1时，求函数f（x）的单调区间；（2）讨论f（x）的零点个数．2022年广东省中山市高考数学一模试卷参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设全集U 与集合M ，N 的关系如图所示，则图中阴影部分所表示的集合是（ ）A ．M ∩NB ．M ∪NC ．（∁U M ）∪ND ．（∁U M ）∩N【解答】解：由Venn 图，元素属于N 但不属于M ， 即阴影部分对应的集合为（∁U M ）∩N ， 故选：D ．2．（5分）平面向量a →与b →的夹角为60°，|a →|＝2，|b →|＝1，则|a →+2b →|＝（ ） A ．√3B ．12C ．4D ．2√3【解答】解：由题意可得|a →+2b →|=√(a →+2b →)2 =√a →2+4b →2+4a →⋅b →=√a →2+4b →2+4|a →||b →|cos60°=√22+4×12+4×2×1×12=2√3 故选：D ．3．（5分）已知{a n }为正项等比数列，且a 2a 4＝4，设T n 为该数列的前n 项积，则T 5＝（ ） A ．8B ．16C ．32D ．64【解答】解：根据等比数列性质得a 1a 5＝a 2a 4==a 32=4，又a 3＞0，∴a 3＝2，∴T 5=a 35=25＝32． 故选：C ．4．（5分）3男3女六位同学站成一排，则3位女生中有且只有两位女生相邻的不同排法种数是（）A．576B．432C．388D．216【解答】解：根据题意，分2步进行分析：①先将3名男生排好，有A33＝6种排法，排好后有4个空位，②将女生分为1﹣2的两组，有C31＝3种分组方法，安排到4个空位中，考虑2个女生一组的顺序，有2×A42＝12种情况，则有3×24＝72种排法，则有6×72＝432种不同排法，故选：B．5．（5分）抛物线C：y2＝2px上一点（1，y0）到其焦点的距离为3．则抛物线C的方程为（）A．y2＝4x B．y2＝8x C．y2＝12x D．y2＝16x【解答】解：抛物线C：y2＝2px的准线方程为：x=−p2，由抛物线的定义以及抛物线C：y2＝2px上一点（1，y0）到其焦点的距离为3，可得1﹣（−p2）＝3，解得p＝4，所以抛物线方程为：y2＝8x．故选：B．6．（5分）已知函数f（x）＝log a x（a＞0，a≠1），则y＝f（|x|﹣1）的图象可能是（）A．B．C．D．【解答】解：函数f（x）＝log a x（a＞0，a≠1），则y＝f（|x|﹣1）＝log a（|x|﹣1），因为y＝f（|x|﹣1）是偶函数，故图象关于y轴对称，则选项A，D错误；由选项B，C的图象可知，0＜a＜1，当x＝4时，y＝f（|4|﹣1）＝log a（|4|﹣1）＝log a3＜log a1＝0，故选项C错误，选项B正确．故选：B．7．（5分）已知如图，在棱长为2的正方体ABCD﹣A1B1C1D1中，过A1B且与AC1平行的平面交B1C1于点P，则PC1＝（）A．2B．√3C．√2D．1【解答】解：连接AB1，交BA1于E，取B1C1的中点为P，因为E是AB1的中点，所以EP∥AC1，所以PC1＝1．故选：D．8．（5分）甲、乙两支田径队的体检结果为：甲队体重的平均数为60kg，方差为200，乙队体重的平均数为70kg，方差为300，又已知甲、乙两队的队员人数之比为1：4，那么甲、乙两队全部队员的平均体重和方差分别是（）A．65，280B．68，280C．65，296D．68，296【解答】解：由题意可知甲队的平均数为60，乙队体重的平均数为70，甲队队员在所有队员中所占权重为11+4=1 5，乙队队员在所有队员中所占权重为41+4=4 5，则甲、乙两队全部队员的平均体重为x=15×60+45×70=68，甲、乙两队全部队员体重的方差为s2=15[200+(60−68)2]+45[300+(70−68)2]=296．故选：D．二、选择题：本大题共4小题，每小题5分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．（多选）9．（5分）已知函数f（x）＝A sin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分图象如图所示，下列说法正确的是（）A ．函数y ＝f （x ）的图象关于点（−π6，0）对称 B ．函数y ＝f （x ）的图象关于直线x =−5π12对称C ．函数y ＝f （x ）在[−2π3，−π6]单调递减 D ．该图象向右平移π6个单位可得y ＝2sin2x 的图象【解答】解：由函数的图象可得A ＝2，由14•2πω=π3−π12，解得ω＝2．再根据最值得2×π12+φ＝2k π+π2，k ∈Z ； 又|φ|＜π2，得φ=π3，得函数f （x ）＝2sin （2x +π3）， 当x =−π6时，f （x ）＝0，故A 正确；当x =−5π12时，f （x ）＝﹣2，是最值，故B 正确； x ∈[−2π3，−π6]，则2x +π3∈[﹣π，0]， 函数f （x ）＝2sin （2x +π3）不单调，故C 错误；函数f （x ）＝2sin （2x +π3）的图象向右平移π6个单位可得y ＝2sin （2x −π3+π3）＝2sin2x的图象，故D 正确． 故选：ABD ．（多选）10．（5分）已知a ＞0，b ＞0，a +b 2＝1，则下列选项中正确的是（ ） A ．3a﹣b的最大值为3B ．b √a 的最大值为12C ．√a +b 的最大值为√2D ．1a+1+1b 2的最小值为2【解答】解：由a ＞0，b ＞0，a +b 2＝1，得a ＝1﹣b 2＞0，所以0＜a ＜1，0＜b ＜1， 根据0＜b ＜1，得﹣1＜﹣b ＜0，所以﹣1＜a ﹣b ＜1，所以3a ﹣b ＞3﹣1=13，故选项A 错误；b √a =√1−a •√a ≤1−a+a 2=12，当且仅当√1−a =√a ，即a =12时等号成立， 所以b √a 的最大值为12，故选项B 正确；因为b =√1−a ，所以√a +b =√a +√1−a ≤2√(√a)2+(√1−a)22=√2， 当且仅当√a =√1−a ，即a =12时等号成立，故选项C 正确；由a+b2＝1，得b2＝1﹣a，即1b2=11−a，所以1a+1+1b2=1a+1+11−a=−2a2−1（a＞0），显然选项D错误．故选：BC．（多选）11．（5分）已知函数f(x)=log2(1+4x)−x，则下列说法正确的是（）A．函数f（x）是偶函数B．函数f（x）是奇函数C．函数f（x）在（﹣∞，0]上为增函数D．函数f（x）的值域为[1，+∞）【解答】解：根据题意，函数f(x)=log2(1+4x)−x，其定义域为R，有f(−x)=log2(1+14x)+x=log2(1+4x)−x=f(x)，所以函数f（x）是偶函数，则A正确，B错误，对于C，f(−1)=log252＞1=f(0)，f（x）不是增函数，C错误，对于D，f（x）＝log2（1+4x）﹣x＝log2（12x+2x），设t=12x+2x≥2，当且仅当x＝0时等号成立，则t的最小值为2，故f（x）≥log22＝1，即函数的值域为[1，+∞），D正确，故选：AD．（多选）12．（5分）已知球O的半径为2，球心O在大小为60°的二面角α﹣l﹣β内，二面角α﹣l﹣β的两个半平面分别截球面得两个圆O1，O2，若两圆O1，O2的公共弦AB 的长为2，E为AB的中点，四面体OAO1O2的体积为V，则下列结论中正确的有（）A．O，E，O1，O2四点共面B．O1O2=√32C．O1O2=32D．V的最大值为√316【解答】解：因为公共弦AB在棱l上，连结OE，O1E，O2E，O1O2，OA，则OE=√OA2−AE2=√3，因为二面角α﹣l﹣β的两个半平面分别截球面得两个圆O1，O2，O为球心，所以OO1⊥α，OO2⊥β，又O1E⊂平面α，O2E⊂平面β，所以OO1⊥O1E，OO2⊥O2E，故O，E，O1，O2四点共圆，故选项A正确；因为E为弦AB的中点，故O1E⊥AB，O2E⊥AB，故∠O1EO2即为二面角α﹣l﹣β的平面角，所以∠O1EO2＝60°，故O1O2＝OE sin60°=32，故选项B错误，选项C正确；设OO1＝d1，OO2＝d2，在△OO1O2中，由余弦定理可得，O1O22=94=d12+d22+d1d2≥3d1d2，所以d1d2≤34，故S△OO1O2≤3√316，所以V=13⋅AE⋅S△OO1O2≤√316，当且仅当d1＝d2时取等号，故选项D正确．故选：ACD．三、填空题：本大题共4小题，每小题5分，共20分．请将答案填在答题卡对应题号的位置上．答错位置，书写不清，模棱两可均不得分．13．（5分）若sin2α=23，则cos2α＝−13．【解答】解：若sin2α=23，则cos2α＝1﹣2sin2α＝1﹣2×23=−13．故答案为：−1 314．（5分）在数列{a n}中，a1＝2，√a n+1=√a n+√2，则数列{a n}的通项公式为a n=2n2．【解答】解：∵√a n+1=√a n+√2，a1＝2，∴数列{√a n}是首项为√2，公差为√2的等差数列，∴√a n=√2+√2(n−1)=√2n，∴a n=2n2，故答案为：a n=2n2．15．（5分）已知复数z 满足方程z 2﹣3z +9＝0，则|z |＝ 3 ． 【解答】解：设z ＝a +bi ，a ，b ∈R ， ∵z 2﹣3z +9＝0，∴a 2﹣b 2+2abi ﹣3a ﹣3bi +9＝0，∴{a 2−b 2−3a +9=02ab −3b =0，解得a =32，b =±3√32， ∴z =32±3√32， ∴|z|=(32)2+(±3√32)=3． 故答案为：3．16．（5分）已知点M 为双曲线C ：x 2a 2−y 2b 2=1（a ＞0，b ＞0）在第一象限上一点，点F 为双曲线C 的右焦点，O 为坐标原点，4|MO |＝4|MF |＝7|OF |，则双曲线C 的离心率为 4 ；若MF ，MO 分别交双曲线C 于P ，Q 两点，记直线PM 与PQ 的斜率分别为k 1，k 2，则k 1k 2＝ 15 ．【解答】解：设M （x 0，y 0），由已知可得，4|MO |＝4|MF |＝7|OF |＝7c ， 则x 0=c2，y 0=√|MO|2−(|OF|2)2=3√54c ，即M （c2，3√54c ），把M 代入双曲线方程，可得c 24a 2−45c 216b 2=1，即4b 2c 2﹣45a 2c 2＝16a 2b 2，又b 2＝c 2﹣a 2，代入上式可得4c 4﹣65a 2c 2+16a 4＝0， 即4e 4﹣65e 2+16＝0，解得e 2＝16或e 2=14（舍）， 所以双曲线C 的离心率e ＝4； 设P （x 1，y 1），则Q （﹣x 0，﹣y 0），所以k 1k 2=y 1−y 0x 1−x 0⋅y 1+y 0x 1+x 0=y 12−y 02x 12−x 02，把P 、M 的坐标分别代入双曲线方程，得{ x 12a 2−y 12b 2=1x 02a 2−y 02b 2=1， 两式作差，可得y 12−y 02x 12−x 02=b 2a 2，由e ＝4，得ca=4，即c 2＝a 2+b 2＝16a 2，所以b 2a 2=15．∴k 1k 2＝15．故答案为：4；15．四、解答题：本大题共6个小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）已知数列{a n}，{b n}满足b n＝a n﹣（﹣1）n n2，a1+b1＝1，a2+b2＝8，且数列{b n}是等差数列．（1）求数列{a n}的通项公式；（2）设数列{a n}的前n项和为S n，若A＝{n|n≤110且S n≤100}，求集合A中所有元素的和S．【解答】解：（1）b n＝a n﹣（﹣1）n n2，可得b1＝a1+1，b2＝a2﹣4，代入a1+b1＝1，a2+b2＝8中，可得b1＝1，b2＝2，而数列{b n}是等差数列，所以{b n}公差d＝b2﹣b1＝2﹣1＝1，所以数列{b n}的通项公式b n＝b1+（n﹣1）d＝1+（n﹣1）•1＝n，所以a n＝b n+（﹣1）n n2＝n+（﹣1）n n2；即{a n}的通项公式a n＝n+（﹣1）n n2；（2）由（1）可得a n＝n+（﹣1）n n2，a1＝0，所以a2n+a2n+1＝2n+（2n）2+2n+1﹣（2n+1）2＝0，可得S2n﹣1＝a1+（a2+a3）+.....+（a2n﹣2+a2n﹣1）＝0+0+....+0＝0，所以当n为奇数时，S n＝0，故1，3，5，....109都是集合A中的元素，由S2n＝S2n﹣1+a2n＝0+2n+（2n）2＝2n（2n+1），所以当n为偶数时S n＝n（n+1），A＝{n|n≤110且S n≤100}，所以n（n+1）≤100，可得n≤9，所以2，4，6，8为集合A中的元素，所以S＝（1+3+……+109）+（2+4+6+8）=55(1+109)2+20＝3045．18．（12分）如图，已知圆锥AO的底面半径为2，母线长为2√10，点C为圆锥底面圆周上的一点，O为圆心，D是AB的中点，且∠BOC=π2．（1）求三棱锥D﹣OCB的表面积；（2）求A到平面OCD的距离．【解答】解：（1）∵OC⊥OB，OC⊥OA，OB∩OA＝O，∴OC⊥平面OBA，∴∠COD=π2，∴三棱锥D﹣OCB的表面积等于S△OCB+S△OCD+S△ODB+S△CDB，∴S△OCB=12×2×2＝2，S△OCD=12×2×2√10=2√10，∵OA=√(2√10)2−22=6，∴S△ODB=12×12×2×6＝3，∵CB＝2√2，DB=√10，CD=√22+10=√14，∴cos∠DCB=2×2√2×√14=3√714，∴sin∠DCB=1−(3√714)2=√1928，∴S△CDB=12×√14×2√2×√1928=√19，∴三棱锥D﹣OCB的表面积为5+√10+√19；（2）∵D是AB的中点，∴A到平面OCD的距离即为点B到平面OCD的距离，过点B作BH⊥OD，垂足为H，∵OC⊥平面OCD，且OC⊂平面OCD，∴平面OBA⊥平面OCD，又BH ⊥OD ，平面OBA ∩平面OCD ＝OD ， ∴BH ⊥平面OCD ，∴线段BH 的长度即为点B 到平面OCD 的距离， ∴BH =2S △ODB OD =√10=3√105， 故A 到平面OCD 的距离为3√105．19．（12分）在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且ab =b+c a=sinA cosB．（1）求A ；（2）如图，已知AB ＝2，D 为AC 的中点，点P 在BD 上，且满足AP →⋅CP →=1，求△P AC 的面积．【解答】解：（1）由ab =sinA cosB，可得sin A cos B ＝sin B sin A ，又sin A ≠0，则tan B ＝1． 因为B ∈（0，π），所以B =π4． 由ab =b+c a，可得a 2＝b 2+bc ，即a 2+c 2−b 22ac=c+b 2a，所以c +b ＝2a cos B ．由正弦定理可得sin C +sin B ＝2sin A cos B ， 则sin （A +B ）+sin B ＝2sin A cos B ， 可得sin B ＝sin （A ﹣B ），则B ＝A ﹣B 或B +A ﹣B ＝π（舍去），所以A =2B =π2．（2）因为AP →⋅CP →=1，所以AP ⋅CP cos ∠APC ＝1．又因为AC 2＝AP 2+CP 2﹣2AP ⋅CP cos ∠APC ，所以AP 2+CP 2＝6．因为CP 2＝CD 2+DP 2﹣2CD ⋅DP cos ∠CDP ，AP 2＝AD 2+DP 2﹣2AD ⋅DP cos ∠ADP ， 两式相加可得CP 2+AP 2＝CD 2+AD 2+2DP 2，解得DP =√2．如图，过点P 作PE ⊥AC ，则S △PACS △ABC =EP AB =DP BD =√2√5=√105． 又因为S △ABC =12AB ⋅AC =2，所以S △PAC =2√105．20．（12分）某科技公司组织技术人员进行某新项目研发，技术人员将独立地进行项目中不同类型的实验甲，乙，丙，已知实验甲、乙、丙成功的概率分别为34，23，12． （1）对实验甲、乙、丙各进行一次，求至少有一次成功的概率；（2）该项目研发流程如下：实验甲做一次，若成功，则奖励技术人员1万元并进行实验乙，否则技术人员不获得奖励且该项目终止；实验乙做两次，若两次都成功，则追加技术人员3万元奖励并进行实验丙，否则技术人员不追加奖励且该项目终止；实验丙做三次，若至少两次成功，则项目研发成功，再追加技术人员4万元奖励，否则不追加奖励且该项目终止．每次实验相互独立，用X （单位：万元）表示技术人员所获得奖励的数值，写出X 的分布列及数学期望．【解答】解：（1）记实验甲，乙，丙成功分别为事件A ，B ，C ，且它们相互独立， 故实验甲、乙、丙各进行一次，至少有一次成功的概率P =1−P(ABC)=1−14×13×12=2324； （2）由题意可知，随机变量X 的可能取值为0，1，4，8，所以P （X ＝0）＝1−34=14，P （X ＝1）=34×[1−(23)2]=512，P （X ＝4）=34×(23)2[C 31(12)3+(12)3]=16， P （X ＝8）=34×(23)2[C 32(12)3+(12)3]=16， 所以X 的分布列为：X0 1 4 8 P14 512 16 16 故E （X ）＝0×14+1×512+4×16+8×16=2912万元． 21．（12分）已知椭圆C ：x 2a 2+y 2b 2=1(a ＞b ＞0)的右焦点为F ，离心率为12，直线l ：y ＝x 被椭圆截得的弦长为4√427． （1）求椭圆C 的标准方程；（2）若P 是椭圆C 上一点，O 是坐标原点，过点F 与直线l 平行的直线与椭圆C 的两个交点为A ，B ，且OP →=λOA →+μOB →，求λμ的最大值．【解答】解：（1）由题可知e =c a =12，则a 2＝4c 2，b 2＝3c 2①，联立{y =x x 2a 2+y 2b 2=1，解得x ＝±√a 2+b 2，所以y ＝±√a 2+b 2， 则弦长=√2•|x 1﹣x 2|=√2•√a 2+b 2=4√427②， 解得c 2＝1，a 2＝4，b 2＝3，所以椭圆C 的标准方程为x 24+y 23=1；（2）由（1）知F （1，0），则直线AB 的方程为y ＝x ﹣1，联立{y =x −1x 24+y 23=1，整理得7x 2﹣8x ﹣8＝0， 设A （x 1，y 1），B （x 2，y 2），则有x 1+x 2=87，x 1x 2=−87，同时3x 12+4y 12＝12，3x 22+4y 22＝12，设P （x ，y ），由OP →=λOA →+μOB →，得（x ，y ）＝λ（x 1，y 1）+μ（x 2，y 2）＝（λx 1+μx 2，λy 1+μy 2），所以{x =λx 1+μx 2y =λx 1+μy 2，又因为点P 在椭圆上， 所以3x 2+4y 2＝3（λx 1+μx 2）2+4（λy 1+μy 2）2＝λ2（3x 12+4y 12）+μ2（3x 22+4y 22）+2λμ（3x 1x 2+4y 1y 2）＝12λ2+12μ2+2λμ（3x 1x 2+4y 1y 2）＝12，又因为3x 1x 2+4y 1y 2＝3x 1x 2+4（x 1﹣1）（x 2﹣1）＝7x 1x 2﹣4（x 1+x 2）+4＝7×（−87）﹣4×87+4=−607，代入上式得12λ2+12μ2+2λμ×（−607）＝12， 即λ2+μ2−107λμ＝1， 则1＝λ2+μ2−107λμ≥2λμ−107λμ=47λμ，所以λμ≤74，当且仅当λ＝μ时取“＝”，则λμ的最大值为74． 22．（12分）已知函数f （x ）＝（x ﹣2）e x ﹣ax +alnx （a ∈R ）．（1）当a ＝﹣1时，求函数f （x ）的单调区间；（2）讨论f （x ）的零点个数．【解答】（1）解：当a ＝﹣1时，f （x ）＝（x ﹣2）e x +x ﹣lnx ，则f′(x)=(x −1)e x +1−1x =(x −1)(e x +1x )，因为x ∈（0，+∞），则e x +1x ＞0，所以x ＞1时，f '（x ）＞0，0＜x ＜1时，f '（x ）＜0，所以函数f （x ）在（0，1）上单调递减，在（1，+∞）上单调递增，故f （x ）的单调递减区间是（0，1），单调递增区间是（1，+∞）．（2）因为f （x ）＝（x ﹣2）e x ﹣ax +alnx ，则f′(x)=(x −1)e x −a +a x =(x −1)(e x −a x)． （i ）当a ＜0时，因为x ∈（0，+∞），则e x −a x ＞0，则x ＞1时，f '（x ）＞0，所以0＜x ＜1时，f '（x ）＜0，所以函数f （x ）在（0，1）上单调递减，在（1，+∞）上单调递增，f （1）＝﹣e ﹣a ．当f（1）＝﹣e﹣a＞0时，即a＜﹣e时，f（x）≥f（1）＞0，所以当a＜﹣e时，函数f（x）没有零点，即函数f（x）零点个数为0；当f（1）＝﹣e﹣a＝0，即a＝﹣e时，f（x）≥f（1）＝0，所以当a＝﹣e时，函数f（x）有且只有一个零点x＝1，即函数f（x）的零点个数为1；当f（1）＝﹣e﹣a＜0，即﹣e＜a＜0时，f（2）＝﹣a（2﹣ln2）＞0，则存在一个实数x1∈（1，2），使得f（x1）＝0，当x∈（0，1）时，（x﹣2）e x＞﹣e，﹣ax＞0，对任意的x∈（0，1），则f（x）＞﹣e+alnx，取x0=e 3a，因为a＜0，则0＜e3a＜1，则f(x0)＞−e+alne 3a=3−e＞0，则存在x2∈(e3a，1)，使得f（x2）＝0，即﹣e＜a＜0时，函数f（x）的零点个数为2．（ii）当a＝0时，令f（x）＝0，则（x﹣2）e x＝0，则x＝2，即函数f（x）有且只有一个零点x＝2；即函数f（x）的零点个数为1．（iii）当a＞0时，令g(x)=e x−ax，g′(x)=ex+ax2＞0，故g(x)=e x−ax在（0，+∞）上单调递增，令m=min{12，a2}，n＝max{1，a}，故g(m)≤√e−2＜0，g（n）≥e﹣1＞0，则一定存在x0∈（m，n），使得g（x0）＝0，所以x∈（0，x0）时，g（x）＜0，x∈（x0，+∞）时，g（x）＞0．因为f′(x)=(x−1)e x−a+ax=(x−1)(e x−a x)，当x0＝1，即a＝e时，f（x）＝（x﹣2）e x﹣ex+elnx，所以f′(x)=(x−1)(e x−ex )，所以x＞1时，f'（x）＞0，所以0＜x＜1时，f'（x）＞0，则f（x）在（0，+∞）上单调递增，且f（1）＝﹣2e＜0，f（3）＝e3﹣3e+eln3＞0，则存在x1∈（1，3），使得f（x1）＝0，所以函数f（x）有且只有一个零点x＝x1，即函数f（x）的零点个数为1．因为f′(x)=(x−1)e x−a+ax=(x−1)(e x−a x)，当x0＞1，x∈（0，1）时，f'（x）＞0，当x∈（1，x0）时，f'（x）＜0，当x∈（x0，+∞）时，f'（x）＞0，则f（x）在（0，1）上单调递增，在（1，x0）上单调递减，在（x0，+∞）上单调递增，当0＜x0＜1，x∈（0，x0）时，f'（x）＞0，当x∈（x0，1）时，f'（x）＜0，当x∈（1，+∞）时，f'（x）＞0，则f（x）在（0，x0）上单调递增，在（x0，1）上单调递减，在（1，+∞）上单调递增，因为x∈（0，1]时，（x﹣2）e x＜0，﹣ax＜0，alnx≤0，即f（x）＜0，所以f（x）在x∈（0，1]时没有零点，x∈（1，+∞）上f（x）至多有一个零点，而f（a+2）＝ae a+2﹣a（a+2）+aln（a+2）＝a（e a+2+ln（a+2）﹣（a+2）），令t＝a+2，h（t）＝e t+lnt﹣t（t＞2），则ℎ′(t)=e t+1t−1（t＞2），则h'（t）＞0，故h（t）在t∈（2，+∞）上单调递增，而h（2）＝e2+ln2﹣2＞0，即f（a+2）＞0，故存在一个，则存在x1∈（1，a+2），使得f（x1）＝0，所以函数f（x）有且只有一个零点x＝x1，即函数f（x）的零点个数为1，综上所述：当a＜﹣e时，函数f（x）的零点个数为0；当a＝﹣e或a≥0时，函数f（x）的零点个数为1；当﹣e＜a＜0时，函数f（x）的零点个数为2．。

广东省中山市（新版）2024高考数学统编版模拟(预测卷)完整试卷一、单选题：本题共8小题，每小题5分，共40分 (共8题)第(1)题已知函数，则的解集是（）A．B．C．D．第(2)题下列说法①将一组数据中的每一个数据都加上或减去同一个常数后，方差不变；②设有一个回归方程，变量增加1个单位时，平均增加5个单位；③线性回归方程必过点；④设具有相关关系的两个变量，的相关系数为，则越接近于0，，之间的线性相关程度越高；其中错误的个数是（）A．3B．2C．1D．0第(3)题如图位于西安大慈恩寺的大雁塔是我国现存最早､规模最大的唐代四方楼阁式砖塔，其最高处的塔刹可以近似地看成一个正四棱锥，已知正四棱锥的高为，其侧棱与底面的夹角为，则该正四棱锥的体积约为（）A．B．C．D．第(4)题某三棱柱的三视图如图所示，该三棱柱的体积为（）A．B．C．D．第(5)题已知函数，其中表示不超过的最大整数．设，定义函数：，，，，则下列说法正确的有个①的定义域为；②设，，则；③；④若集合，则中至少含有个元素．A．个B．个C．个D．个第(6)题记等差数列的前项和为，则（）A．14B．72C．36D．60第(7)题若复数满足.则（）A．B．C．D．第(8)题若函数在上单调递增，则的取值范围为（）A．B．C．D．二、多选题：本题共3小题，每小题6分，共18分 (共3题)第(1)题已知是两个虚数，则下列结论中正确的是（）A．若，则与均为实数B．若与均为实数，则C．若均为纯虚数，则为实数D．若为实数，则均为纯虚数第(2)题已知所有顶点在两个平行平面内的多面体叫作拟柱体，在这两个平面内的面叫作拟柱体的底面，其余各面叫作拟柱体的侧面，到上、下底面距离相等的截面叫作中截面．现有拟柱体，其中上、下底面均为边长为2的正方形，分别为底面和底面的中心，与两底面垂直，且，则（）A．拟柱体外接球的表面积为B．直线与平面所成角满足C．拟柱体的中截面面积的最大值为D．拟柱体的侧面为全等的三角形第(3)题已知在平面直角坐标系中，，，，，，P为该平面上一动点，记直线PD，PE的斜率分别为和，且，设点P运动形成曲线F，点M，N是曲线F上位于x轴上方的点，且，则下列说法正确的有（）A．动点P的轨迹方程为B．△PAB面积的最大值为C．的最大值为5D．的最小值为三、填空题：本题共3小题，每小题5分，共15分 (共3题)第(1)题已知，则______.第(2)题二项式（x+y）5的展开式中，含x2y3的项的系数是___（用数字作答）．第(3)题对于的展开式，含项的系数为________．四、解答题：本题共5小题，每小题15分，最后一题17分，共77分 (共5题)第(1)题已知抛物线的焦点为，直线与抛物线交于两点，其中两点的横坐标之积为．(1)求的值；(2)若在轴上存在一点，满足，求的值．第(2)题设函数在上有定义，实数和满足.若在区间上不存在最小值，则称在区间上具有性质P.（1）当，且在区间上具有性质P，求常数C的取值范围；（2）已知，且当时，，判别在区间上是否具有性质P；（3）若对于满足的任意实数和，在区间上具有性质P，且对于任意，当时，有：，证明：当时，.第(3)题设函数.(1)若最小值为，求的范围；(2)令，的图象上有一点列，若直线的斜率为，证明：.第(4)题在中,为的角平分线,且.(1)若,,求的面积;(2)若,求边的取值范围.第(5)题已知双曲线的焦距为10，且经过点．A，B为双曲线E的左、右顶点，P为直线上的动点，连接PA，PB交双曲线E于点C，D（不同于A，B）．(1)求双曲线E的标准方程．(2)直线CD是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．。

一轮复习数学模拟试题01满分150分.用时120分钟． 第一部分（选择题 满分50分）一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合}5,3,1{=A ，集合},,2{b a B =，若A ∩B {1,3}=，则b a +的值是( )．A.10B.9C.4D.7 2．如图在复平面内，复数21,z z 对应的向量分别是OB OA ,， 则复数21z z -的值是( )．A ．i 21+-B ．i 22--C ．i 21+D ．i 21- 3．若点),9(a 在函数x y 3log =的图象上，则6tanπa 的值为( )． A.0 B.33C.1D.3 4．若向量)1,1(),0,2(==b a ，则下列结论正确的是( )．A ．1=⋅ B.||||a = C ．b b a ⊥-)( D ．// 5．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量为n 的样本，其频率分布直方图如图所示，其 中支出在[50，60)元的同学有30人，则n 的值为( )．A.100B.1000C.90D.9006．如图正四棱锥（底面是正方形，顶点在底面的射影是底 面的中心）P-ABCD 的底面边长为6cm ，侧棱长为 5cm ，则它的侧视图的周长等于( )．A.17cmB.cm 5119+C.16cmD.14cm7．若实数x ，y 满足条件⎪⎩⎪⎨⎧≤≤≥+-≥+,1001,0x y x y x ，则目标函数|3|y x z -=的最大值为( )．A.6B.5C.4D.38．按如图所示的程序框图运行程序后，输出的结果是15，则判断框中的整数H=( )．A.3B.4C.5D.6 9．给出下面结论：①命题”“023,:0200≥+-∈∃x x R x p 的否定为 ”“023,:2<+-∈∀⌝x x R x p ②函数x x f x32)(+=的零点所在区间是（-1，0）； ③函数x y 2sin =的图象向左平移3π个单位后，得到函数)32sin(π+=x y 图象；④对于直线m ，n 和平面α，若n ,⊥⊥m m α，则α//n . 其中正确结论的个数是( )．A.1B.2C.3D.4 10.定义np p p n+++ 21为n 个正数n p p p ,,21的“均倒数”．若已知数列}{n a 的前n 项的“均倒数”为121+n ，又41+=n n a b ，则11103221111b b b b b b +++ =( )． A.111 B.109 C.1110 D.1211 第二部分 （非选择题 满分100分）二、填空题：本大题共4小题，每小题5分，满分20分．（一）必做题：第11、12、13题为必做题，每道试题考生都必须作答． 11.已知833833,322322=+=+， ,15441544=+，若t a t at a ,(,66=+ 均为正实数），类比以上等式，可推测a,t 的值，则t a -=_________. 12.已知：33)6cos(=-a π，则)65cos()6(sin 2a a +--ππ的值为________. 13.已知定义在R 上的奇函数)(x f 满足)()4(x f x f -=-，且]2,0[∈x 时，)1(log )(2+=x x f ， 甲、乙、丙、丁四位同学有下列结论：甲：1)3(=f ；乙：函数)(x f 在]2,6[--上是减函数；丙：函数)(x f 关于直线x=4对称；丁：若)1,0(∈m ，则关于x 的方程0)(=-m x f 在[0，6]上所有根之和为4．其中结论正确的同学是____．（二）选做题：第14、15题为选做题，考生只能选做一题，两题全答的，只计算前一题的得分．14.（几何证明选讲）如图，AB 是半圆O 的直径，点C 在半圆上，AB CD ⊥于点D ，且AD=3DB ，设θ=∠COD ，则2tan 2θ=________.15.（坐标系与参数方程）已知直线4sin cos :=-θρθρl ，圆θρcos 4:=C ，则直线l 与圆C 的位置关系是________.（相交或相切或相离？）三、解答题：本大题共6小题，满分80分，解答应写出文字说明、证明过程或演算步骤． 16.（本小题满分12分）某种零件按质量标准分为1，2，3，4，5五个等级，现从—批该零件中随机抽取20个，对其等级进行统计分析，得到频率分布表如下：等级 1 2 3 4 5 频率 0.05 m 0.15 0.35 n(1)在抽取的20个零件中，等级为5的恰有2个，求m ，n 的值；(2)在(1)的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级不相同的概率．17.（本小题满分12分）已知：函数x x x f ωω2sin 22sin 3)(-=的最小正周期为π3.(1)求函数)(x f 的解析式；(2)在ABC ∆中，若1)(=C f ，且)cos(cos sin 22C A B B -+=，求A sin 的值.18.（本小题满分14分）已知正项等差数列}{n a 中，11=a ，且9733,2,a a a +成等比数列． (1)求数列}{n a 的通项公式； (2)设}{n a 的前n 项和为1)18()(,++=n nn S n S n f S ，试问当n 为何值时，)(n f 最大，并求出)(n f 的最大值．19.（本小题满分14分）在如图所示的几何体中，平面⊥ACE 平面ABCD ，四边形ABCD 为平行四边形，2,//,90===∠BC AC BC EF ACB ，AE=EC=1.(1)求证：⊥AE 平面BCEF ； (2)求三棱锥D-ACF 的体积．20.（本小题满分14分）某种上市股票在30天内每股的交易价格P （元）、日交易量Q （万股）与时间t （天）的对应关系分别如下：[有序数对(t ，P)落在图甲中的折线上，日交易量Q （万股）与时间t （天）的部分数据如表乙所示．](1)根据图甲的图象，写出该种股票每股交易价格P （元）与时间t （天）所满足的函数关系式；(2)根据表中数据确定日交易量Q(万股)与时间t （天）的一次函数关系式；(3)用y （万元）表示该股票日交易额，写出y 关于t 的函数关系式，并求这30天中第几天日交易额最大，最大值为多少？（注：各函数关系式都要写出定义域．）21.（本小题满分14分）设函数a x a e a x x f x+-+-=)1()()(，R a ∈．（注：e 为自然对数的底数．） (1)当1=a 时，球的单调区间；(2)(i)设)(x g 是)(x f 的导函数，证明：当2>a 时，在),0(+∞上恰有—个0x 使得0)(0=x g (ii)求实数a 的取值范围，使得对任意的]2,0[∈x ，恒有0)(≤x f 成立．参考答案一．选择题： 题号 1 2 3 4 5 6 7 8 9 10 答案CBDCADBABC二．填空题： 11．-29. 12．332+． 13．甲、乙、丁. 14．31. 15．相交 解答过程分析：10．选D ．解析：由已知得12121+=+++n a a a n n n n S n n a a a =+=+++∴)12(21当2≥n 时，141-=-=-n S S a n n n 当1=n 时也成立，14-=∴n a n1111,411+-=⋅∴=+=∴+n n b b n a b n n n n11103221111b b b b b b +++∴)3121()211(-+-=1110)111101(=-++ . 11．填-29．解析：类比等式可推测35,6==t a ，则.29-=-t a12．填332+。

一轮复习数学模拟试题03一、选择题（本大题共10小题，每小题5分，满分50分.每小题给出的四个选项中，只有一项是符合题目要求.）1．在同一坐标系中，函数x y 2=与xy )21(=的图象之间的关系是（ ）．A ．关于y 轴对称B ．关于x 轴对称C ．关于原点对称D ．关于直线x y =对称 2．下列函数中，在区间),0(+∞上是增函数的是（ ）．A ．2x y -=B ． 22-=x yC ．xy )21(= D ．xy 1log 2= 3．下列函数中为偶函数的是（ ）．A ． 2()1f x x x =+-B ． ||)(x x x f =C ． 1()lg 1x f x x +=-D ． 22()2x xf x -+=4. 函数)0(||log 31≠∈=x R x x y 且 为（ ）．A ．奇函数且在)0,(-∞上是减函数B ．奇函数且在)0,(-∞上是增函数C ．偶函数且在),0(+∞上是减函数D ．偶函数且在),0(+∞上是增函数 5.函数33)(3--=x x x f 有零点的区间是( )A ．)0,1(-B ．)1,0(C ．)2,1(D ．)3,2(6．设0.5log 6.7a =，2log 4.3b =，2log 5.6c =，则c b a ,,的大小关系为（ ）．A ． a c b <<B ． b c a <<C ． c b a <<D ． a b c <<7. 设)(x f 是周期为2的函数，当10≤≤x 时，)1(2)(x x x f -=，则)25(f ＝( )A ．21-B ．41- C. 41 D. 218.一次函数b ax y +=与二次函数c bx ax y ++=2在同一坐标系中的图象大致是( )9. 如果函数c bx x y ++=2对任意的实数x ，都有)()1(x f x f -=+，那么( )A ．)2()0()2(f f f <<-B ．)2()2()0(f f f <-<C ．)2()0()2(-<<f f fD ．)2()2()0(-<<f f f10．《优化方案》系列丛书第三年的销量比第一年的销量增长了%44，若每年的平均增长率相同(设为x )，则以下结论正确的是( )A ．%22>xB ．%22<xC ．%22=xD ．x 的大小由第一年的销量确定二、填空题（本大题共4小题，每小题5分，满分20分.） 11. 计算25lg 41lg-＝ . 12. 已知关于x 的二次方程01222=+++m mx x ，若方程有两根，其中一根在区间)0,1(-内，另一根在区间)2,1(内，m 的范围是 ．13．设函数⎩⎨⎧>≤-=).0(),0()(2x x x x x f 若4)(=a f ，则实数=a ．14. 函数)0(≥-=x x x y 的值域为 ．三、解答题：本大题共6小题，满分80分.解答须写出文字说明、证明过程和演算步骤. 15. (12分)已知函数12)(-=x x f . （1）用函数的单调性的定义证明)(x f 在),1(+∞上是减函数．(8分) （2）求函数)(x f 在]6,2[上的最大值和最小值。

高考数学三轮复习冲刺模拟试题01集合一、选择题1 ．集合，，那么〔 〕A ．B ．C ．D ．2 ．设集合{1}A x x a x R =-<∈，，B={x|1<x<5,x ∈Ｒ}，假设A ⋂B=φ，那么实数a 的取值范围是 〔 〕A ．{a|0≤a ≤6}B ．{a|a ≤2，或a ≥4}C ．{a|a ≤0，或a ≥6}D ．{a|2≤a ≤4}3 ．集合2A={|log <1},B={x|0<<c}x x x ，假设=A B B ，那么c 的取值范围是 〔〕A ．(0,1]B ．[1,+)∞C ．(0,2]D ．[2,+)∞二、填空题4 ．假设不等式4+-2+1x m x ≥对一切非零实数x 均成立,记实数m 的取值范围为M .集合{}=A x x M ∈,集合{}2=--6<0B x R x x ∈,那么集合=A B ___________.5 ．设集合是A={32|()=83+6a f x x ax x -是(0，+∞)上的增函数}，5={|=,[-1,3]}+2B y y x x ∈，那么()R A B = ；6 ．试题〕己知集合222{|28},{|240}x x A x B x x mx -=<=+-<, 假设{|11},{|43}A B x x A B x x =-<<=-<<,那么实数m 等于__________ . 7 ．设集合{}1,R A x x a x =-<∈,{}15,R B x x x =<<∈,假设∅=B A ,那么实数a 取值范围是___________.三、解答题8 ．={()|1},B={()|3,0x 3}2A x,y y =-x +mx -x,y x+y =≤≤，假设A B ⋂是单元素集，求实数m的取值范围.参考答案一、选择题1. 【答案】B【解析】{(3)0}{03}P x x x x x =-<=<<,={2}{22}Q x x x x <=-<<，所以{02}(0,2)P Q x x =<<=, 选B. 2. 【答案】C【解析】{1}{11}A x x a x R x a x a =-<∈==-<<+，,因为=A B φ，所以有15a -≥或11a +≤，即6a ≥或0a ≤，选C.3. 【答案】D【解析】2{log 1}{01}A x x x x =<=<<.因为AB B =，所以A B ⊆.所以1c ≥，即[1,)+∞，选B.二、填空题4. {}-1<3x x ≤;5. 【答案】(,1)(4,)-∞+∞【解析】2()=2466f 'x x ax -+，要使函数在(0,)+∞上是增函数，那么2()=24660f 'x x ax -+>恒成立，即14a x x <+，因为144x x +≥=，所以4a ≤，即集合{4}A a a =≤.集合5={|=,[-1,3]}+2B y y x x ∈{15}y x =≤≤，所以{14}A B x x ⋂=≤≤，所以()=R A B (,1)(4,)-∞+∞.6. 【答案】32222{|28}{|230}{13}x x A x x x x x x -=<=--<=-<<，因为{|11},{|43}A B x x A B x x =-<<=-<<，所以由数轴可知{|41}B x x =-<<，即4,1-是方程2240x mx +-=的两个根，所以4123m -+=-=-，解得32m =。

高考高三数学3月模拟考试试题(一)一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的） 1．已知i 是虚数单位，则11i ii i ++=+（ ）A ．1322i -+ B ．1322i - C ．3122i + D ．3122i - 2．已知集合{|sin()sin ,(0,)},{|cos()cos ,2A k Z k Bk Z k ppq q q p q q q =?=??=?(0,)},()2z A B p = 则ð A ．{|2,}k k n n Z =? B ．{|21,}k k n n Z =-? C ．{|4,}k k n n Z =?D ．{|41,}k k n n Z =-?3．设P 为函数()sin()f x x p =的图象上的一个最高点，Q 为函数()cos()g x x p =的图象上的一个最低点，则|PQ|最小值是（ ）AB ．2 C．2D ．4．设直线：:(0)l y kx m m =+?，双曲线2222:1(0,0)x y C a b a b+=>>，则“b k a =-”是“直线l 与双曲线C 恰有一个公共点“的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分条件D ．既不充分也不必要条件5．若存在实数x ，y 使不等式组0320,60x y x y x y ì-?ïïï-+?íïï+-?ïïî与不等式20x y m -+?都成立，则实数m的取值范围是（ ） A ．m≥0B ． m≤3C ．m≥lD ．m≥36．设数列{a n }是首项为l 的等比数列，若11{}2n n a a ++是等差数列，则12231111()()22a a a a +++2012201311()2a a +++ 的值等于（ ） A ． 2012B ． 2013C ． 3018D ． 30197．已知双曲线2222:1(0,0)y x C a b a b+=>>，A ，B 是双曲线的两个顶点．P 是双曲线上的一点，且与点B 在双曲线的同一支上．P 关于y 轴的对称点是Q 若直线AP ，BQ 的斜率分别是k 1，k 2， 且k 1·k 2=45-，则双曲线的离心率是（ ） AB ．94C ．32D ．958．若函数()(1).x f x x e =+，则下列命题正确的是（ ）A ．对任意21m e<-，都存在x R Î,使得()f x m < B ．对任意21m e>-，都存在x R Î，使得()f x m < C ．对任意21m e <-，方程()f x m =只有一个实根 D ．对任意21m e>-，方程()f x m =总有两个实根 9．在直角坐标中，A （3，1），B （－3，－3），C （l ．4）．P 是AB 和AC夹角平分线上的一点，且AP =2，则AP的坐标是A．(-B．(-C．(-D (-10．如图，平面a 与平面b 交于直线l ，A ，C 是平面a 内 不同的两点，B ，D 是平面b 内不同的两点，且A ，B ．C ．D 不在直线l 上，M ，N 分别是线段AB ，CD 的中 点，下列判断正确的是（ ）A ．若AB 与CD 相交，且直线AC 平行于l 时，则直线BD与l 可能平行也有可能相交B ．若AB ，CD 是异面直线时，则直线MN 可能与l 平行C ．若存在异于AB ，CD 的直线同时与直线AC ，MN ，BD都相交，则AB ，CD 不可能是异面直线D ．M ，N 两点可能重合，但此时直线AC 与l 不可能相交 二、填空题（本大题共7小题，每小题4分，共28分） 11．已知2cos ()3x x R =?，则cos()3x p-= 。

2025年高考数学一轮复习讲义之滚动测试卷01（新高考专用）测试范围：集合与常用逻辑用语、不等式、函数与基本初等函数一、单选题(本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的)1．（2024·全国·高考真题）集合{}{}1,2,3,4,5,9,A B A ==，则()A A B ⋂=ð（）A ．{}1,4,9B ．{}3,4,9C ．{}1,2,3D ．{}2,3,52．（2024·江苏南通·三模）已知z 为复数，则“z z =”是“22z z =”的（）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．非充分非必要条件3．（2024·重庆·模拟预测）已知函数()(22)x x f x x -=-，则(2)(21)f x f x ->+的解集为（）A ．(,3)-∞-B ．()3,3-C ．13,3⎛⎫- ⎪⎝⎭D ．(3,)-+∞4．（2024·全国·高考真题）已知函数为22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩，在R 上单调递增，则a 取值的范围是（）A ．(,0]-∞B ．[1,0]-C ．[1,1]-D ．[0,)+∞5．（2024·安徽合肥·模拟预测）函数()()2e cos 2e e 1x xx f x =-（e 为自然函数的底数）的图像大致为（）A ．B ．C ．D ．6．（2024·福建福州·模拟预测）当药品A 注射到人体内，它在血液中的残余量会以每小时25%的速度减少，另一种药物B 注射到人体内，它在血液中的残余量会以每小时10%的速度减少．现同时给两位患者分别注射800mg 药品A 和500mg 药品B ，当两位患者体内药品的残余量恰好相等时，所经过的时间约为（）（参考数据：lg20.301,lg30.477≈≈）A ．0.57hB ．1.36hC ．2.58hD ．3.26h7．（2024·北京·高考真题）已知()11,x y ，()22,x y 是函数2x y =图象上不同的两点，则下列正确的是（）A ．12122log 22y y x x ++>B ．12122log 22y y x x ++<C ．12212log 2y y x x +>+D ．12212log 2y y x x +<+8．（2024·北京·三模）2024年1月17日我国自行研制的天舟七号货运飞船在发射3小时后成功对接于空间站天和核心舱后向端口，创造了自动交会对接的记录.某学校的航天科技活动小组为了探索运动物体追踪技术，设计了如下实验：目标P 在地面轨道上做匀速直线运动；在地面上相距7m 的A ，B 两点各放置一个传感器，分别实时记录A ，B 两点与物体P 的距离.科技小组的同学根据传感器的数据，绘制了“距离-时间”函数图像，分别如曲线a ，b 所示.1t 和2t 分别是两个函数的极小值点.曲线a 经过()()0110,,,r t r 和()20,t r ，曲线b 经过()22,t r .已知211212,4m,4s rt r t r t ===，并且从0=t 时刻到2=t t 时刻P 的运动轨迹与线段AB 相交.分析曲线数据可知，P 的运动轨迹与直线AB 所成夹角的正弦值以及P 的速度大小分别为（）A ．6m /s74B ．6m /s72C ．2m /s7D ．2/s7二、多选题(本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分)9．（2024·河南·三模）已知函数()()lg 1f x x =-，则（）A ．()f x 的定义域为(),1-∞B ．()f x 的值域为RC ．()()141f f -+-=D ．()2y f x =的单调递增区间为()0,110．（2024·江苏苏州·模拟预测）已知函数()1f x x =+，设1()()g x f x =，()()*1()()1,N n n g x f g x n n -=>∈．且关于x 的函数()2*1()N ni i y x g x n ==+∈∑．则（）A ．()n g x x n =+或()1n g x nx =+B ．22242n n n y x +⎛⎫=++ ⎪⎝⎭C ．当2n ≤时，存在关于x 的函数y 在区间(,1]-∞-上的最小值为6，0n =D ．当2n >时，存在关于x 的函数y 在区间(,1]-∞-上的最小值为6，4n =11．（2024·湖北·模拟预测）设定义在R 上的函数()f x 与()g x 的导函数分别为()f x '和()g x '.若()()42f x g x +=-+，()()2g x f x ='+'，且()2f x +为奇函数，则下列说法正确的是（）A ．函数()f x 的图象关于直线1x =对称B ．()()202320252g g +=-C ．()202310k f k ==∑D ．()20231k g k ==∑三、填空题(本大题共3小题，每小题5分，共15分，把答案填在题中的横线上)12．（2024·山东济宁·三模）已知函数410()2log 0xx f x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩，，，则12f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭.13．（2024·重庆·模拟预测）已知()22ln f x x x x=-+，若实数m ，n 满足()210f m f n⎛⎫+= ⎪⎝⎭，则214m n +的最小值为14．（2023·黑龙江哈尔滨·模拟预测）牛顿选代法又称牛顿——拉夫逊方法，它是牛顿在17世纪提出的一种在实数集上近似求解方程根的一种方法.具体步骤如下图示：设r 是函数()y f x =的一个零点，任意选取0x 作为r 的初始近似值，在点()()00,x f x 作曲线()y f x =的切线1l ，设与1l 轴x 交点的横坐标为1x ，并称1x 为r 的1次近似值；在点()()11,x f x 作曲线()y f x =的切线2l ，设与2l 轴x 交点的横坐标为2x ，称2x 为r 的2次近似值.一般地，在点()()(),N n n x f x n ∈作曲线()y f x =的切线1n l +，记1n l +与x 轴交点的横坐标为1n x +，并称1n x +为r 的1n +次近似值.设()()330f x x x x =+-≥的零点为r ，取00x =，则r 的1次近似值为；若nx 为r 的n 次近似值，设33323n nn n x x a x +=+，N n *∈，数列{}n a 的前n 项积为n T .若任意N n *∈，n T λ>恒成立，则整数λ的最大值为.四、解答题(本大题共5小题，共77分，解答应写出文字说明，证明过程或演算步骤)15.(13分)（22-23高一上·山东济南·期末）已知集合{A x x a =<或}2x a >+，{}139x B x -=≥.(1)当2a =时，求A B ⋃；(2)若“x A ∈”是“x B ∈”成立的必要不充分条件，求a 的取值范围.16.(15分)（23-24高三上·山东威海·期末）在ABC 中，角,,A B C 所对的边分别为a b c ,,,记ABC 的面积为S 2AB AC S ⋅=.(1)求角A 的大小；(2)若a =，求22b c +的最大值.17.(15分)（23-24高一下·广东汕头·期中）已知函数()212x x f x a+=+为奇函数．(1)求实数a 的值；(2)判断函数()f x 的单调性（不用证明）；(3)设函数22()log log 24x xg x m =⋅+，若对任意的1[2,8]x ∈，总存在2(0,1]x ∈，使得()()12g x f x =成立，求实数m 的取值范围．18.(17分)（2024·湖南长沙·模拟预测）设n 次多项式()121210()0n n n n n n P t a t a t a t a t a a --=+++++≠ ，若其满足(cos )cos n P x nx =，则称这些多项式()n P t 为切比雪夫多项式.例如：由cos cos θθ=可得切比雪夫多项式1()P x x =，由2cos 22cos 1θθ=-可得切比雪夫多项式22()21P x x =-.(1)若切比雪夫多项式323()P x ax bx cx d =+++，求实数a ，b ，c ，d 的值；(2)对于正整数3n 时，是否有()()()122n n n P x x P x P x --=⋅-成立？(3)已知函数3()861f x x x =--在区间()1,1-上有3个不同的零点，分别记为123,,x x x ，证明：1230x x x ++=.19.(17分)（2024·山东·模拟预测）法国数学家弗朗索瓦·韦达发现了一元二次方程的根与系数之间的关系，将其推广到高次方程，并在其著作《论方程的识别与订正》中正式发表，后来人们把这个关系称为韦达定理，即如果()123,,,,2n x x x x n ⋅⋅⋅≥是关于x 的实系数一元n 次方程()111000n n n n n a x a x a x a a --++⋅⋅⋅++=≠在复数集C 内的n 个根，则()123121311231242101231,2,3,,1.n n nn n n n n n n n n n n n a x x x x a a x x x x x x a a x x x x x x x x x a a x x x x a ----⎧+++⋅⋅⋅+=-⎪⎪⎪-++⋅⋅⋅+=⎪⎪⎪-⎨++⋅⋅⋅+=-⎪⎪⎪⎪⎪⋅⋅⋅⋅⋅=-⋅⎪⎩试运用韦达定理解决下列问题：(1)已知,,R a b c ∈，1a b c ++=，0ab bc ca ++=，求333a b c ++的最小值；(2)已知,R a b ∈，关于x 的方程()()32200x a x bx a a +-+-=>有三个实数根，其中至少有一个实效根在区间()0,a 内，求2a b -的最大值．。

一轮复习数学模拟试题02共150分，时间120分钟.第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设全集{x N x U *∈=＜}6，集合{}{}1,3,3,5A B ==，则()U C AB 等于A ．{}4,1B ．{}5,1C ．{}4,2D ．{}5,22．复数z 满足12i z i ⋅=-，则z ＝.2.2.12.12A iB iC iD i ---+-3．如图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的全面积为 A ．π4 B ．π2 C ．π3D ．23π4．已知等差数列{}n a 的公差0d ≠，它的第1、5、17公比是 A ．2B ．12C ．3D ．45．阅读右侧程序框图，为使输出的数据为31应填的数字为 A ．5 B ．4 C ．6 D ．76. 如右图所示为函数()()2sin f x x ωϕ=+(ω﹥0,2π﹤φ﹤π)的部分图像，其中,A B 两点之间的距离为5,那么()1f -= A ．2 BC．．2-7．直线20ax y a -+=与圆229x y +=的位置关系是A ．相离B ．相切C ．相交D ．不确定8．已知O 为坐标原点，点M 坐标为(2,1)-，在平面区域020x x y y ≥⎧⎪+≤⎨⎪≥⎩上取一点N ，则使MN 为最小值时点N 的坐标是A ．)0,0(B ．)1,0(C ．)2,0(D ．)0,2( 9．函数221ln )(x x x f -=的图象大致是A ．B ．C ．D ．10. 已知函数()2,f x x bx c =++其中04,04b c ≤≤≤≤.记函数满足()()21213f f ≤⎧⎪⎨-≤⎪⎩的事件为A ，则事件A 的概率为 A ．58 B ．12 C ．38 D ．14第Ⅱ卷（非选择题共100分）二、填空题：本大题共5小题，第14、15小题任选一题作答，多选的按第14小题给分，每小题5分，共20分．11. 不等式162-+x x ﹤0的解集是 .12．已知向量)4,(,)2,1(-==x ，若//，则⋅= . 13．已知函数()f x ，()g x 分别由下表给出则[(1)]f g的值为 ；满足[()][()]f g x g f x >的x 的值是14．（坐标系与参数方程选做题）若点) , 3(m P 在以点F 为焦点的抛物线⎩⎨⎧==ty t x 442(t 为参数)上，则=||PF ．15．（几何证明选讲选做题）如右图，O 是半圆的圆心， 直径62=AB ，PB 是圆的一条切线，割线PA 与 半圆交于点C ，4=AC ，则=PB ．三、解答题：本大题共6小题，共80分，解答应写出文字说明或演算步骤.16．（本小题满分12分） 已知函数2()sin cos2x f x x a =+，a 为常数，a R ∈，且2π=x 是方程0)(=x f 的解. （1）求函数()f x 的最小正周期； （2）当],0[π∈x 时，求函数)(x f 值域. 17．（本小题满分12分）某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[)50,40，[)60,50，…，[]100,90后得到如图4的频率分布直方图．（1）求图中实数a 的值；（2）若该校高一年级共有学生640人，试估计该校高一年级期中考试数学 成绩不低于60分的人数；（3）若从数学成绩在[)40,50与[]90,100两个分数段内的学生中随机选取两名学生，求这两名学生的数学成绩之差的绝对值不大于10的概率．图41A1B1CABDC18．（本小题满分14分）如右图, 在三棱柱111ABC A B C -中，3AC =，1CC ⊥平面ABC ，4BC =，5AB =,14AA =，点D 是AB 的中点， （1）求证：1AC BC ⊥； （2）求证：//1AC 平面1CDB ； （3）求三棱锥11C CDB -的体积.19．（本小题满分14分）已知二次函数()y f x =的图像经过坐标原点，其导函数为'()62f x x =-，数列{}n a 的前n 项和为n S ，点(,)()n n S n N *∈均在函数()y f x =的图像上. （1）求二次函数()y f x =的表达式； （2）求数列{}n a 的通项公式； （3）设13+=n n n a a b ，n T 是数列{}n b 的前n 项和，求使得20n m T <对所有n N *∈都成立的最小正整数m .20．（本小题满分14分）矩形ABCD 的两条对角线相交于点(20)M ，，AB 边所在直线的方程为360x y --=，点(11)T -，在AD 边所在直线上． （1）求AD 边所在直线的方程； （2）求矩形ABCD 外接圆的方程；（3）若动圆P 过点(20)N -，，且与矩形ABCD 的外接圆外切，求动圆P 的圆心的轨迹方程．21．（本小题满分14分）设函数()y f x =在(,)a b 上的导函数为()f x '，()f x '在(,)a b 上的导函数为()f x ''，若在(,)a b 上，()0f x ''<恒成立，则称函数()f x 在(,)a b 上为“凸函数”．已知432113()1262f x x mx x =--． （1）求()x f '、()x f ''；（2）若()f x 为区间(1,3)-上的“凸函数”，试确定实数m 的值；（3）若当实数m 满足||2m ≤时，函数()f x 在(,)a b 上总为“凸函数”，求b a -的最大值．参考答案18．解 ：（1）直三棱柱111ABC A B C -，底面三边长3AC =，4BC =，5AB =,222AB AC BC ∴=+，∴ AC BC ⊥，1,,CC ABC AC ABC ⊥⊂平面平面1AC CC ∴⊥，又1,BC CC C =1111,AC B BC BCC B ∴⊥⊂1平面BCC 平面，1A1B1CABDCE……………………………………………………9分故点P 的轨迹是以M N ，为焦点，实轴长为12分从而解得10x -<<． ………………………………………………………………13分。