方向导数和梯度

方向导数与梯度公式关系方向导数和梯度是微积分中两个常用的概念,它们之间的关系可以用以下公式表示:方向导数 = 梯度 / 权重其中,梯度是指目标函数对变量的导数,权重是指变量的系数。

具体来说,假设我们有一个线性回归模型$$y = x"beta + epsilon$$其中$y$是输出变量,$x$是输入变量,$beta$是模型的参数,$epsilon$是噪声。

那么,$beta$的梯度可以表示为:$$frac{partial}{partial beta}left(frac{y}{x"beta}ight) = frac{partial y}{partial beta}x" - frac{partial x"}{partial beta}frac{y}{x"beta} = frac{y"beta - x"betay}{x"beta}$$其中,$frac{partial y}{partial beta}$表示$beta$对$y$的导数,$frac{partial x"}{partial beta}$表示$x"beta$对$x$的导数。

现在,如果我们想要计算$beta$的方向导数,可以使用上述公式:$$frac{partial}{partial beta}left(frac{y}{x"beta}ight) = frac{y"beta - x"beta y}{x"beta} = frac{y"}{x"}beta - frac{x"}{x"}beta = frac{y-x"beta"}{x"}$$其中,$beta" = x"(beta)$。

因此,$beta$的方向导数可以通过计算它与其他变量的差来得到。

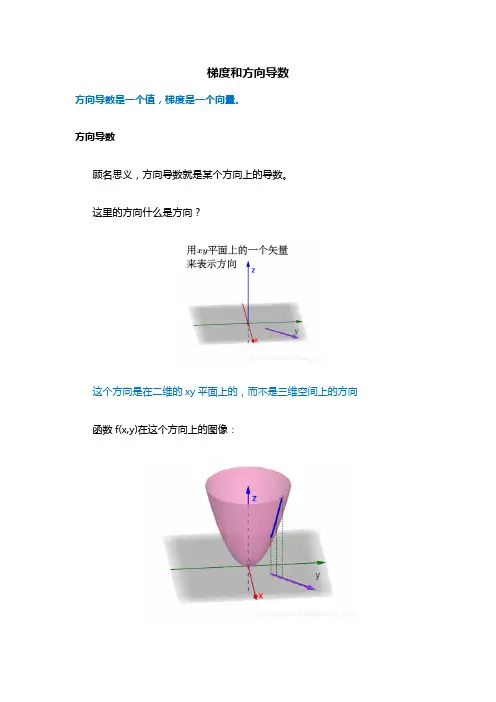
梯度和方向导数
方向导数是一个值，梯度是一个向量。

方向导数
顾名思义，方向导数就是某个方向上的导数。

这里的方向什么是方向？
这个方向是在二维的xy平面上的，而不是三维空间上的方向函数f(x,y)在这个方向上的图像：
我们知道：
函数f(x,y) 的A 点在这个方向上也是有切线的，其切线的斜率就是方向导数：
梯度
很显然，A 点不止一个方向，而是360°都有方向：
每个方向都是有方向导数的：
这就引出了梯度的定义：
梯度：是一个矢量，其方向上的方向导数最大，其大小正好是此最大方向导数。

方向导数与梯度在多变量微积分和优化理论中，方向导数和梯度是两个重要的概念。

它们提供了函数在某一点处关于不同方向的信息，以及函数在该点处的变化率和方向。

理解这两个概念对于解决各种实际问题，如最优控制、机器学习、图像处理等都至关重要。

方向导数是函数在某一点处沿特定方向的变化率。

给定一个函数f(x)在点x0，对于任意的方向v = (h1, h2,..., hn)，方向导数Df(x0)v 是f(x)在x0处沿v方向的变化率。

具体地，Df(x0)v = lim(h->0) [f(x0 + hv) - f(x0)] / h。

方向导数的重要性在于它提供了函数在某一点处对不同方向的敏感度。

例如，如果你在山峰上沿着不同的方向行走，方向导数可以告诉你哪个方向更容易攀登，哪个方向更困难。

梯度是函数在某一点处所有方向导数的向量。

给定一个函数f(x)在点x0，梯度gradf(x0)是一个向量，其方向是f(x)在x0处增加最快的方向，而其大小是f(x)在该方向的导数。

具体地，gradf(x0) = (f'(x01), f'(x02),..., f'(xn))。

梯度是一个非常重要的概念，因为它提供了函数在某一点处的最大变化率方向。

在很多实际问题中，找到这个最大变化率方向往往能够指引我们找到最优解。

例如，如果你在山峰上寻找攀登最快的方式，梯度可以告诉你应该沿着哪个方向前进。

梯度是方向导数的最大值。

换句话说，对于任意给定的方向v，方向导数Df(x0)v都不超过梯度的长度。

这是因为梯度是所有方向导数向量的范数，即||gradf(x0)|| = max{Df(x0)v : ||v|| = 1}。

这个性质表明，梯度不仅提供了函数在某一点处的最大变化率方向，还给出了沿这个方向的导数（即变化率）。

这使得梯度在优化问题中具有特别的重要性，因为它可以用来找到使函数值下降最快的方向。

方向导数和梯度是多变量微积分和优化理论中的重要概念。

方向导数与梯度
1. 基本概念
方向导数：是一个数；反映的是f(x,y)在P0点沿方向v 的变化率。

偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。

偏导函数：是一个函数；是一个关于点的偏导数的函数。

梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。

2. 方向导数
反映的是f(x,y)在P0点沿方向v的变化率。

例子如下：
2.0 方向导数计算公式
2.1 偏导数
2.2 二元函数偏导数的几何意义
2.3 偏导函数
偏导数与偏导函数的关系：
偏导数是偏导函数在指定点的函数值，因此在求偏导数时，也可先求出偏导函数，然后再将点代入偏导函数，从而求出函数在此点的偏导数。

3. 全微分
4. 梯度
梯度是一个向量；既有大小，也有方向。

4.1 几何意义
函数z=f(x,y)在点P0处的梯度方向是函数变化率(即方向导数)最大的方向。

梯度的方向就是函数f(x,y)在这点增长最快的方向，梯度的模为方向导数的最大值。

三维空间中的方向导数和梯度在物理和数学学科中，经常需要对函数在三维空间中的方向变化进行研究，方向导数和梯度就是两个比较重要的概念。

本文将从定义、意义、计算方法等角度详细介绍这两个概念。

一、方向导数1.1 定义方向导数是指函数$f(x,y,z)$在某一点$(x_0,y_0,z_0)$沿着某一方向$\vec{v}=(a,b,c)$的变化率。

记作$D_{\vec{v}}f(x_0,y_0,z_0)$。

1.2 意义方向导数能够衡量函数在某一点沿着某一方向的变化速度，这在实际应用中非常重要。

比如说，在工程领域中，需要对某一物体的某一点进行受力分析，这个时候就会用到方向导数。

同时，在最优化问题中，求解方向导数也是非常必要的。

1.3 计算方法计算方向导数之前，需要先求出函数的偏导数。

设函数$f(x,y,z)$的偏导数分别为$\dfrac{\partial f}{\partial x}$、$\dfrac{\partial f}{\partial y}$、$\dfrac{\partial f}{\partial z}$。

则函数在某一点$(x_0,y_0,z_0)$沿着方向$\vec{v}=(a,b,c)$的方向导数为：$$D_{\vec{v}}f(x_0,y_0,z_0)=\dfrac{\partial f}{\partialx}(x_0,y_0,z_0)a+\dfrac{\partial f}{\partialy}(x_0,y_0,z_0)b+\dfrac{\partial f}{\partial z}(x_0,y_0,z_0)c $$这个公式就是方向导数的定义式。

可以发现，它是一个点乘形式的表达式，非常容易计算。

二、梯度2.1 定义梯度是指函数$f(x,y,z)$在某一点$(x_0,y_0,z_0)$处的方向导数取得最大值的方向。

梯度的方向是函数在该点处变化最快的方向。

梯度的大小等于函数在该点处方向导数的大小。

方向导数与梯度的关系公式
方向导数和梯度是微积分中的两个重要概念。

它们之间存在着密切的关系。

首先，我们来介绍一下方向导数的概念。

方向导数是指函数在某一点沿着某一方向的变化率。

如果函数在该点可微分，那么它的方向导数可以用该点的梯度来表示。

接下来，我们来介绍一下梯度的概念。

梯度是一个向量，表示函数在某一点上的变化率最大的方向。

梯度的方向指向函数值增加的最快的方向，大小表示该方向的最大变化率。

梯度的计算方式是取该点的偏导数向量。

在同一点上，如果沿着梯度的方向进行变化，则函数值的变化率最大。

因此，方向导数沿着梯度的方向取得最大值，即方向导数等于梯度与该方向的点积值。

因此，可以得出方向导数和梯度的关系公式如下：
设函数f(x,y)在点P(x0,y0)可微分，向量v=(cosθ,sinθ)表示与x轴正向夹角为θ的方向，则f(x0,y0)在方向v上的方向导数为：
∂f/∂v = ▽f(x0,y0) ·v
其中▽f(x0,y0)表示f(x0,y0)的梯度向量。