方向导数与梯度教案

gradf
(
P0
)


f x
,
f , y
f . z P0
类似于二元函数，此梯度也是一个向量， 其方向与取得最大方向导数的方向一致，其模 为方向导数的最大值.
目录 上页 下页 返回 结束
类似地, 设曲面 f ( x, y, z) c 为函数 u f ( x, y, z)的等量面，此函数在点P( x, y, z)的 梯度的方向与过点 P 的等量面 f ( x, y, z) c 在这
求函数z f ( x, y)在点P( x, y)沿方向l的方向导数z :
1)

l (1, 0) (cos0,
cos )
l
2
f lim f ( x0 t, y0 ) f ( x0 , y0 )
l t0
t
f x ( x0 , y0 ) f x ( x0 , y0 ).
其方向余弦为 cos 1 , cos 1 ,
2
2
z e2 y 1;
x (1,0)
(1,0)
z 2xe2 y 2,
y (1,0)
(1,0)
故所求方向导数 z f cos f cos
l P x
y
P
1 2 1 2.
P0可微，l
), 则
是过点
P0
的任意一个方向，
f f cos f cos
l P0 x P0
f , f
y P0
{cos , cos }

x gradf
y P0 ( x0 , y0
)

el

gradf ( x0, y0 ) cos ,

z z z f f cos cos cos cos l x y x y
记： {
f f , } gradf ( x, y ) ~~~~ z f ( x, y ) 在 ( x, y ) 点 处 的 梯 度 向 量 ， 简 称 为 梯 度 ； 记 ： x y {cos , cos } e 是与 l 同方向的单位向量，则 z f f cos cos gradf ( x, y ) e | gradf ( x, y ) | | e | cos( gradf , e ) l x y z | gradf ( x, y ) | cos l （ ( gradf , e ) ）
2
⑵注意到曲线

y2 b
2
1 恰 好 是 曲 面 z 1 (

y2 b
2
) 当 z 0 时的一条等高线，而曲面 x2 a
2
z 1 (
x2 a
2

y2 b
是凸曲面； 从而曲线 2 ) 是开口向下的椭圆抛物面，

y2 b
2
1 在点 P0 (
a b , )处 2 2
的内法线方向恰好就是其梯度方向，因此就是要求在 P0 ( 已求得： gradf ( x, y ) {
1，
P0
u y
1，
P0
u z
1；
P0
1 3 1 3 l P0 P 9 4 3 4 ， l 0 l { , , } ，故 1 {3, 2, 3} ， l l 4 2 4
2
《高等数学》下册教案
第九章
多元函数微分学
刘伟庆
cos

第七讲 方向导数与梯度授课题目：§8. 7 方向导数与梯度教学目的与要求：了解方向导数与梯度的概念及其计算方法。

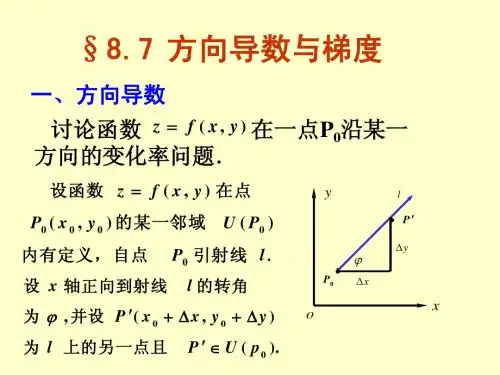
教学重点与难点：重点与难点：方向导数的概念及方向导数的计算讲授内容：一、 方向导数1、方向导数的概念回顾偏导数现在我们来讨论函数z =f (x , y )在一点P 沿某一方向的变化率问题. 设l 是xOy 平面上以P 0(x 0, y 0)为始点的一条射线, e l =(cos α, cos β)是与l 同方向的单位向量. 射线l 的参数方程为x =x 0+t cos α, y =y 0+t cos β (t ≥0).设函数z =f (x , y )在点P 0(x 0, y 0)的某一邻域U (P 0)内有定义, P (x 0+t cos α, y 0+t cos β)为l 上另一点, 且P ∈U (P 0). 如果函数增量f (x 0+t cos α, y 0+t cos β)-f (x 0, y 0)与P 到P 0的距离|PP 0|=t 的比值ty x f t y t x f ),()cos ,cos (0000-++βα 当P 沿着l 趋于P 0(即t →t 0+)时的极限存在, 则称此极限为函数f (x , y )在点P 0沿方向l 的方向导数, 记作),(00y x l f∂∂, 即),(00y x l f∂∂ty x f t y t x f t ),()cos ,cos (lim 00000-++=+→βα. 从方向导数的定义可知, 方向导数),(00y x l f∂∂就是函数f (x , y )在点P 0(x 0, y 0)处沿方向l 的变化率.注： ),(),(0000y x f y y x x f -∆+∆+))()((),(),(220000y x o y y x f x y x f y x ∆+∆+∆+∆=∆x =t cos α, ∆y =t cos β,t y x =∆+∆22)()(.2、方向导数的计算:定理 如果函数z =f (x , y )在点P 0(x 0, y 0)可微分, 那么函数在该点沿任一方向l 的方向导数都存在, 且有 ),(00y x l f∂∂βαcos ),(cos ),(0000y x f y x f y x +=,其中cos α, cos β是方向l 的方向余弦.简要证明: 设∆x =t cos α, ∆y =t cos β, 则f (x 0+t cos α, y 0+t cos β)-f (x 0, y 0)=f x (x 0, y 0)t cos α+f y (x 0, y 0)t cos β+o (t ). 所以ty x f t y t x f t ),()cos ,cos (lim 00000-+++→βαϕϕsin ),(cos ),(0000y x f y x f y x +=.这就证明了方向导数的存在, 且其值为),(00y x l f∂∂βαcos ),(cos ),(0000y x f y x f y x +=.讨论: 函数z =f (x , y )在点P 沿x 轴正向和负向, 沿y 轴正向和负向的方向导数如何?提示：沿x 轴正向时, cos α=1, cos β=0, xf l f ∂∂=∂∂; 沿x 轴负向时, cos α=-1, cos β=0, xf l f ∂∂-=∂∂. 沿y 轴正向时, cos α=0, cos β=1, yf l f ∂∂=∂∂;沿y 轴负向时, cos α=0, cos β=--1,yf l f ∂∂-=∂∂. 课堂练习：习题8-7：2，4 例1 求函数z =xe 2y 在点P (1, 0)沿从点P (1, 0)到点Q (2, -1)的方向的方向导数.解 这里方向l 即向量→)1 ,1(-=PQ 的方向, 与l 同向的单位向量为)21 ,21(-=l e . 因为函数可微分, 且1)0,1(2)0,1(==∂∂y e x z, 22)0,1(2)0,1(==∂∂y xe y z ,所以，所求方向导数为22)21(2211)0,1(-=-⋅+⋅=∂∂l z . 对于三元函数f (x , y , z )来说, 它在空间一点P 0(x 0, y 0, z 0)沿e l =(cos α , cos β , cos γ)的方向导数定义为),,(000z y x l f∂∂tz y x f t z t y t x f t ),,()cos ,cos ,cos (lim 0000000-+++=+→γβα. 如果函数f (x , y , z )在点(x 0, y 0, z 0)可微分, 则函数在该点沿着方向e l =(cos α , cos β , cos γ)的方向导数为),,(000z y x l f∂∂=f x (x 0, y 0, z 0)cos α+f y (x 0, y 0, z 0)cos β+f z (x 0, y 0, z 0)cos γ.例2 求f (x , y , z )=xy +yz +zx 在点(1, 1, 2)沿方向l 的方向导数, 其中l 的方向角分别为60︒, 45︒, 60︒.解 与l 同向的单位向量为e l =(cos60︒, cos 45︒, cos60︒))21 ,22,21(=. 因为函数可微分, 且f x (1, 1, 2)=(y +z )|(1, 1, 2)=3,f y (1, 1, 2)=(x +z )|(1, 1, 2)=3，,f z (1, 1, 2)=(y +x )|(1, 1)=2,所以)235(21212223213)2,1,1(+=⋅+⋅+⋅=∂∂lf. 二、梯度1、梯度的概念 设函数z =f (x , y )在平面区域D 内具有一阶连续偏导数, 则对于每一点P 0(x 0, y 0)∈D , 都可确定一个向量f x (x 0, y 0)i +f y (x 0, y 0)j ,这向量称为函数f (x , y )在点P 0(x 0, y 0)的梯度, 记作grad f (x 0, y 0), 即grad f (x 0, y 0)= f x (x 0, y 0)i +f y (x 0, y 0)j .2、梯度与方向导数的关系：如果函数f (x , y )在点P 0(x 0, y 0)可微分，e l =(cos α , cos β )是与方向l 同方向的单位向量, 则),(00y x l f∂∂βαcos ),(cos ),(0000y x f y x f y x +=,= grad f (x 0, y 0)⋅e l=| grad f (x 0, y 0)|⋅cos(grad f (x 0, y 0),^ e l ).这一关系式表明了函数在一点的梯度与函数在这点的方向导数间的关系. 特别, 当向量e l 与grad f (x 0, y 0)的夹角θ=0, 即沿梯度方向时, 方向导数),(00y x l f∂∂取得最大值, 这个最大值就是梯度的模|grad f (x 0, y 0)|. 这就是说: 函数在一点的梯度是个向量, 它的方向是函数在这点的方向导数取得最大值的方向, 它的模就等于方向导数的最大值.讨论: lf ∂∂的最大值; 结论: 函数在某点的梯度是这样一个向量, 它的方向与取得最大方向导数的方向一致, 而它的模为方向导数的最大值.3、梯度与等值线的关系：我们知道, 一般说来二元函数z =f (x , y )在几何上表示一个曲面, 这曲面被平面z =c (c 是常数)所截得的曲线L 的方程为⎩⎨⎧==c z y x f z ),(. 这条曲线L 在xOy 面上的投影是一条平面曲线L *, 它在xOy 平面上的方程为f (x , y )=c .对于曲线L *上的一切点, 已给函数的函数值都是c , 所以我们称平面曲线L *为函数z =f (x , y )的等值线.若f x , f y 不同时为零, 则等值线f (x , y )=c 上任一点P 0(x 0, y 0)处的一个单位法向量为)),(),,((),(),(10000002002y x f y x f y x f y x f y x y x +=n . 这表明梯度grad f (x 0, y 0)的方向与等值线上这点的一个法线方向相同, 而沿这个方向的方向导数nf ∂∂就等于|grad f (x 0, y 0)|, 于是 n nf y x f ∂∂=),(00grad . 这一关系式表明了函数在一点的梯度与过这点的等值线、方向导数间的关系. 这说是说: 函数在一点的梯度方向与等值线在这点的一个法线方向相同, 它的指向为从数值较低的等值线指向数值较高的等值线, 梯度的模就等于函数在这个法线方向的方向导数.梯度概念可以推广到三元函数的情形. 设函数f (x , y , z )在空间区域G 内具有一阶连续偏导数, 则对于每一点P 0(x 0, y 0, z 0)∈G , 都可定出一个向量f x (x 0, y 0, z 0)i +f y (x 0, y 0, z 0)j +f z (x 0, y 0, z 0)k ,这向量称为函数f (x , y , z )在点P 0(x 0, y 0, z 0)的梯度, 记为grad f (x 0, y 0, z 0), 即grad f (x 0, y 0, z 0)=f x (x 0, y 0, z 0)i +f y (x 0, y 0, z 0)j +f z (x 0, y 0, z 0)k .结论: 三元函数的梯度也是这样一个向量, 它的方向与取得最大方向导数的方向一致, 而它的模为方向导数的最大值.如果引进曲面f (x , y , z )=c为函数的等量面的概念, 则可得函数f (x , y , z )在点P 0(x 0, y 0, z 0)的梯度的方向与过点P 0的等量面 f (x , y , z )=c 在这点的法线的一个方向相同, 且从数值较低的等量面指向数值较高的等量面, 而梯度的模等于函数在这个法线方向的方向导数.例3 求221y x +grad . 解 这里221),(y x y x f +=. 因为 222)(2y x x x f +-=∂∂, 222)(2y x y y f +-=∂∂, 所以 221y x +grad j i 222222)(2)(2y x y y x x +-+-=. 例4 设f (x , y , z )=x 2+y 2+z 2, 求grad f (1, -1, 2).解 grad f =(f x , f y , f z )=(2x , 2y , 2z ),于是 grad f (1, -1, 2)=(2, -2, 4).数量场与向量场: 如果对于空间区域G 内的任一点M , 都有一个确定的数量f (M ), 则称在这空间区域G 内确定了一个数量场(例如温度场、密度场等). 一个数量场可用一个数量函数f (M )来确定, 如果与点M 相对应的是一个向量F (M ), 则称在这空间区域G 内确定了一个向量场(例如力场、速度场等). 一个向量场可用一个向量函数F (M )来确定, 而F (M )=P (M )i +Q (M )j +R (M )k ,其中P (M ), Q (M ), R (M )是点M 的数量函数.利用场的概念, 我们可以说向量函数grad f (M )确定了一个向量场——梯度场, 它是由数量场f (M )产生的. 通常称函数f (M )为这个向量场的势, 而这个向量场又称为势场. 必须注意, 任意一个向量场不一定是势场, 因为它不一定是某个数量函数的梯度场.例5 试求数量场rm 所产生的梯度场, 其中常数m >0,222z y x r ++=为原点O 与点M (x , y , z)间的距离.解 32)(rmx x r r mr m x -=∂∂-=∂∂, 同理 3)(r my r m y -=∂∂, 3)(r mzr m z -=∂∂. 从而 )(2k j i r z ry r x r m r m ++-=grad . 记k j i e rz r y r x r ++=, 它是与→OM 同方向的单位向量, 则r rm r m e 2-=grad . 上式右端在力学上可解释为, 位于原点O 而质量为m 质点对位于点M 而质量为l 的质点的引力. 这引力的大小与两质点的质量的乘积成正比、而与它们的距平方成反比, 这引力的方向由点M 指向原点. 因此数量场r m 的势场即梯度场grad r m 称为引力场, 而函数rm 称为引力势. 课外作业： P51-2,4。

π 方向导数达到最大值 2 ; 故 1）当α = 时， （ 4 5π π （2）当α = 时， 方向导数达到最小值− 2 ; 4 3π 7π π π （3）当α = 和α = 时，方向导数等于 0. 4 4
推广可得三元函数方向导数的定义
对于三元函数 u = f ( x, y, z )，它在空间一点 P( x0 , y0 , z0 ) 沿着方向 l = (cosα ,cos β ,cos γ ) 的方 向导数 ，可定义为 f ( x0 + ∆x, y0 + ∆y, z0 + ∆z ) − f ( x0 , y0 , z0 ) ∂f = lim ρ ∂l ρ →0
方向导数仍可理解 为曲线上一点处右 切线在新坐标系下 的斜率. 的斜率
y
t
P = ( x 0 , y0 )
v = (cos α ,sin α )
方向导数的物理意义：
设一质点 P 在三维空间的运动轨迹为 (时间t) 时间
x = x0 + t cos α , y = y0 + t sin α , z = f ( x0 + t cos α , y0 + t sin α )
y
l
• P′
•
•
ϕ
∆x
∆y
x
（如图） 如图）
ρ f ( x + ∆x , y + ∆y ) − f ( x , y ) 是否存在？ 是否存在？ lim ρ →0 ρ
上述极限若存在, 定义: 上述极限若存在 则称此极限为函数 f 在 P处沿方向 l 的方向导数 记为 方向导数, 处沿方向
∵ | PP ′ |= ρ = ( ∆x )2 + ( ∆y )2 , 且 ∆z = f ( x + ∆x , y + ∆y ) − f ( x , y ), ∆z 考虑 , 当 P′沿着 l 趋于 P时，

3 1 在 P0 ( , ,0) 处梯度为 0. 2 2
例题 6.
处的梯度 解:
函数
在点
2 (1, 2 , 2) 9
(92考研)
则 注意 x , y , z 具有轮换对称性
2 (1, 2 , 2) 9
3. 梯度的基本运算公式
(2) grad (C u ) C grad u (4) grad ( u v ) u grad v v grad u
令向量
f f f G , , x y z l 0 (cos , cos , cos )
问题 : 函数在点 P 沿哪一方向增加的速度 最快? f 0 max 当 l 与 G 方向一致时, 方向导数取最大值： l 方向：f 变化率最大的方向 这说明 G : 模 : f 的最大变化率之值
2. 梯度 • 三元函数
在点
处的梯度为
f f f grad f , , x y z
• 二元函数 3. 关系 在点 处的梯度为
grad f ( f x ( x, y ) , f y ( x, y ))
• 可微 方向导数存在
0
偏导数存在
f grad f l • l
2
2
例5
求函数 u x 2 2 y 2 3 z 2 3 x 2 y 在点 (1,1,2)处的梯度，并问在 哪些点处梯度为零？
解 由梯度计算公式得
u u u gradu( x , y , z ) i j k x y z
(2 x 3)i (4 y 2) j 6zk , 故 gradu(1,1,2) 5i 2 j 12k .
（1）当 时， 方向导数达到最大值 2 ; 4

1 4 3 , , ) l = ±( 26 26 26
0
例6.(填空) 函数 u = ln(x + y +z ) 在点 .(填空 填空)
2 2 2
处的梯度 解:
2 (1, 2, − 2) 9
(92考研 (92考研) 考研)
16
在点A 例7. (填空)函数 u = ln(x + y2 + z2 ) 在点A ( 1 , 0 , 1) (填空 填空) 处沿点A 指向 B( 3, －2 , 2) 方向的方向导数是 解:
(2,3)
x = x 已知曲线 的参数方程为 y = x2 − 1
r 它在点 P 的切向量为 (1, 2x) x=2= (1, 4) = l = r0 y 3 l P r0 ⋅l
8
∂z ∴ = o −1 2 x ∂l P
例3.设 n 是曲面 3.设 指向外侧 的法向量,求函数 的法向量, 方向 n 的方向导数. 方向导数. 解: grad
第七节 方向导数 与梯度
一、梯度 二、方向导数
1
一. 梯度 三元函数 f (x, y, z) 在点 P 处的梯度(gradient), 处的梯度 ∂f ∂f ∂f , ) grad = ( , ∂ x ∂ y ∂z 点的一个法 曲面 f (x , y , z)=0 在 P 点的一个法向量 二元函数 在点 P( x, y) 处的梯度 处的梯度
r n = ( fx ( x, y, z), f y ( x, y, z), fz ( x, y, z)) = grad f ( x, y, z)
grad
例如 的梯度 grad 的梯度 grad
2
二、方向导数 x =x0 + ρ cosα 射线 l 的起点为 P ,方向角为α , β , 0 P( x, y)为该射线上一点,| PP |= ρ (ρ ≥ 0) y = y0 + ρ cos β 为该射线上一点, 0

两边同除以 (即t ), 得到
f ( x t cos , y t sin ) f ( x , y ) t

f x
cos
f y
sin
o( ) t
故有方向导数为:
lim
t 0
f ( x t cos , y t sin ) f ( x , y )
f l
( x0 , y0 )
lim
t 0
f ( x0 t cos , y0 t sin ) f ( x0 , y0 ) t
y)在点P沿着x轴正向 i =(1,

.
依定义, 函数z=f(x, 0), y 轴正向 j =(0, 1)的方向导数分别为 fx, fy. 沿着x轴负向, y轴负向的方向导数分别为 -fx, -fy.
类似于二元函数，此梯度也是一个向量， 其方向与取得最大方向导数的方向一致，其模 为方向导数的最大值.
类 似 地 ,设 曲 面 f ( x , y , z ) c 为 函 数 u f ( x , y , z ) 的 等 量 面 ，此 函 数 在点 P ( x, y, z)的 梯 度 的 方 向 与 过 点 P 的 等 量 面 f ( x, y, z) c 在 这 点 的 法 线 的 一 个方向相同，且从数值较低的等量面指向数值较 高的等量面，而梯度的模等于函数在这个法线方 向的方向导数.
lim f ( x0 x , y0 y ) f ( x0 , y0 )
0

x x 0 t cos l: y y 0 t sin
是否存在？
(t 0)
l 的参数方程为:
P(x0+tcos, y0+tsin)为 l 上的另一点, 且PU(P).

微分学中的方向导数与梯度-教案一、引言1.1微分学的核心概念1.1.1微分学是数学分析的一个重要分支，主要研究函数的局部性质，如导数、微分等。

1.1.2微分学在物理学、工程学、经济学等领域有着广泛的应用，是现代科学技术发展的重要基础。

1.1.3方向导数与梯度是微分学中的重要概念，它们描述了函数在某一点沿特定方向的瞬时变化率。

1.1.4理解方向导数与梯度的概念和性质，对于深入掌握微分学具有重要意义。

1.2教学目标1.2.1使学生理解方向导数与梯度的定义及其物理意义。

1.2.2培养学生运用方向导数与梯度解决实际问题的能力。

1.2.3帮助学生建立微分学的整体观念，为后续课程学习打下基础。

1.2.4培养学生的逻辑思维能力和数学素养，提高学生分析和解决问题的能力。

1.3教学重点与难点1.3.1教学重点：方向导数与梯度的定义、计算方法和应用。

1.3.2教学难点：方向导数与梯度的物理意义、方向导数的计算公式。

二、知识点讲解2.1方向导数2.1.1定义：方向导数是函数在某一点沿特定方向的瞬时变化率。

2.1.2物理意义：方向导数可以描述物体在空间中沿某一方向的运动速度。

2.1.3计算方法：方向导数可以通过函数的偏导数和方向向量来计算。

2.1.4应用：方向导数在物理学、工程学等领域有着广泛的应用，如流体力学、电磁学等。

2.2梯度2.2.1定义：梯度是一个向量，其方向与函数在该点增长最快的方向一致，大小为该方向上的方向导数。

2.2.2物理意义：梯度可以描述函数在某一点的局部变化趋势。

2.2.3计算方法：梯度可以通过函数的偏导数来计算。

2.2.4应用：梯度在优化问题、图像处理等领域有着广泛的应用。

2.3方向导数与梯度的关系2.3.1方向导数与梯度的方向相同。

2.3.2梯度的大小等于方向导数的最大值。

2.3.3梯度的方向是函数增长最快的方向。

2.3.4方向导数与梯度的概念可以相互转化，用于解决实际问题。

三、教学内容3.1方向导数的计算3.1.1单变量函数的方向导数：单变量函数的方向导数可以通过函数的导数和方向向量来计算。

i =1 n
i =1 n
i =1
进一步可计算得： A = f aa = 2∑ xi2 > 0, B = f ab = 2∑ xi , C = f bb 2n ，
f (a + h, y + k ) − f (a, b) = Φ (1) − Φ (0)
3．Taylor 定理
定理 17.9 设 f ( x, y ) 在 P0 ( x0 , y 0 ) 的邻域 U ( P0 ) 内有 n + 1 阶连续偏 导，则 ∀P( x0 + h, y 0 + k ) ∈ U ( P0 ), ∃θ ∈ (0,1) ，使得
取得极大值，当 H f ( P0 ) 是不定矩阵时， f ( x, y ) 在 P0 ( x0 , y 0 ) 不取得极 值。 证明
f ( x, y ) − f ( x 0 , y 0 ) =
1 (∆x, ∆y ) H f ( P0 )(∆x, ∆y ) T + o(∆x 2 + ∆y 2 ) 2
注：若 P0 ( x0 , y 0 ) 是 f ( x, y ) 的稳定点，则定理 17.11 又可表述为比 较实用的形式： 记 A = f xx ( x0 , y 0 ), B = f xy ( x0 , y 0 ) = f yx ( x 0 , y 0 ), C = f yy ( x0 , y 0 )
{ f x ( P0 ), f y ( P0 ), f z ( P0 )} 为函数 f ( x, y, z ) 在点 P0 ( x0 , y 0 , z 0 ) 的梯度，记作 gradf = { f x ( P0 ), f y ( P0 ), f z ( P0 )}
作业：2，3，6，

故
对于三元函数 u = f ( x , y , z ) ,它在点
处沿方向
的方向导数定义为
如果 u = f ( x , y , z ) 在点
处可微，则
例3 设 是曲面
在点
处的指向外侧的法向量，求函数 在此处沿方向 的方向导数.
解： 令 则曲面上任意一点 P ( x , y , z ) 处的法向量可取为
（2）等值线与梯度 等值线在点 P ( x , y ) 处的一 个法向量可取为
梯度与等值线的关系：
梯度的概念可以推广到三元函数
三元函数 在空间区域G内具有一阶连续偏导数，则对于每一点
，都可定义一个向量(梯度)
类似于二元函数，此梯度也是一个向量， 其方向与取得最大方向导数的方向一致，其模 为方向导数的最大值.
一、问题的提出
考虑二元函数 z = f ( x , y ) 的偏导数
仅反映函数在水平方向 （横轴方向）上的变化率。 同理，偏导数 仅反映函数在垂直平方向 上的变化率。 在实际问题中，还需要考虑函数在斜方向上的变化 率问题，如冷热空气的流动，温度场的变化等。
实例：一块长方形的金属板，四个顶点的坐标是 (1,1)，(5,1)，(1,4)，(5,4)．在坐标原点处有一个 火焰，它使金属板受热．假定板上任意一点处的 温度与该点到原点的距离成反比．在(4,3)处有一 个蚂蚁，问这只蚂蚁应沿什么方向爬行才能最快 到达较凉快的地点？
解 由梯度计算公式得 故
例5：设在 xo y 平面上，各点的温度与点的位置关系为
解 故
例5：设在 xo y 平面上，各点的温度与点的位置关系为 解
例5：设在 xo y 平面上，各点的温度与点的位置关系为
解 （3）沿梯度方向温度变化率最大，最大值为

收稿日期：2019-01-14 基金项目：国家自然科学基金项目（11271206）；北京科技大学本科教育教学改革与研究项目（JG2018M38） 作者简介：赵金玲（1978-），女，辽宁沈阳人，副教授，博士，从事最优化计算方法研究．E-mail：jlzh1 问题引入——如何尽快爬到山顶
可以通过登山问题，引入方向导数和梯度概念．黄山素有“五岳归来不看山，黄山归来不看岳”之美
誉，怎样才能尽快地爬到山顶，将天都峰、莲花峰和鳌鱼峰的绝胜美景尽收眼底，这是一个非常有趣的问
（School of Mathematics and Physics，University of Science and Technology Beijing，Beijing 100083，China）
Abstract：Aiming at the characteristics of science and engineering students，designs a teaching process for easy and explicit understanding of the concepts from directional derivative to gradient．By introducing the vector explanations for partial derivative and directional derivative，and using a large number of graphics and animation demonstrations， shows the geometric meaning of gradients to the students simply．Then the effect of the motion picture is used to give students an intuitive impression of the relationship between gradient and directional derivative. At the same time, strict mathematical proof is given by theoretical deduction．Furthermore，the whole design follows the process of putting forward problems——analyzing problems——solving problems——expanding thinking to guide the students step by step，train their mathematical thinking，and develop their ability of analyzing and solving problems． Key words：directional derivative；gradient；partial derivative；vector；teaching design

高中数学备课教案多元函数的方向导数与梯度的应用高中数学备课教案多元函数的方向导数与梯度的应用在高中数学中，多元函数是一个重要的概念。

而方向导数和梯度则是研究多元函数的常用方法。

本教案将重点介绍多元函数的方向导数和梯度的应用。

一、方向导数的引入在一元函数中，导数表示函数在某点的变化率。

那么在多元函数中，如何描述函数在某点沿着一定方向的变化率呢？这就需要引入方向导数。

方向导数的定义：设函数z=f(x,y)在点P（x0,y0）的某邻域内有定义，若沿着单位向量$\boldsymbol{i} \cdot \cos \alpha+\boldsymbol{j} \cdot \cos \beta$ 方向，函数在点P的一个变化率$$\lim _{\rho \rightarrow 0} \frac{f\left(x_{0}+\rho \cos \alpha,y_{0}+\rho \cos \beta\right)-f\left(x_{0}, y_{0}\right)}{\rho}$$存在，则称此极限为函数f(x,y)在点P的方向导数，记作$D_\alphaf(x_0,y_0)$。

二、方向导数的计算公式方向导数的计算公式为：$$D_\alpha f(x_0,y_0)=\frac{\partial f}{\partial x} \cdot \cos\alpha+\frac{\partial f}{\partial y} \cdot \cos \beta$$其中，$\frac{\partial f}{\partial x}$和$\frac{\partial f}{\partial y}$分别表示函数f(x,y)对x和y的偏导数。

三、梯度的引入与性质梯度是用来描述多元函数的斜率的向量。

在二维平面上，梯度是一个二维向量。

在三维空间中，梯度是一个三维向量。

梯度的性质如下：1. 梯度的模表示函数在某点的最大变化率，即梯度的模为函数在某点的方向导数的最大值。

1 教学内容分析方向导数是研究多元函数在任意方向上的变化情况，梯度是刻画方向导数的几何意义的，该节内容是偏导数知识的拓广和深入，在研究函数性质方面起重要作用，具有不可忽视的地位。

本节课为概念教学课型，多元函数的方向导数的内涵、外延，与其它概念间的关系及运用概念是教学重点。

教学难点是方向导数与函数可微、函数连续、偏导数存在之间的关系。

2 教学目标设计根据教材的地位作用，本节课的教学知识目标是（1）掌握多元函数的方向导数的概念和多元函数梯度的概念；（2）掌握方向导数存在与函数可微、方向导数与函数连续、方向导数与偏导数的关系；（3）掌握方向导数与梯度的关系及计算。

在原有知识的基础上构建新的知识结构，实现概念的同化和顺应。

根据本节课的知识内容，在数学思想上要培养学生辩证的观点，理解数学现象之间的联系与区别，培养学生分析问题解决问题的能力，在探寻数学概念之间关系的过程中发展思维，灵活地运用思维，创新思维品质。

3 教学对象分析学生是在学习了多元函数可微和偏导数的概念的基础之上来学习的，绝大多数同学已经掌握了偏导数的概念及几何意义、多元函数可微的概念及几何意义，知识准备非常充分，因此学习本节内容并不困难，难在要辨析方向导数与函数可微、函数连续、偏导数之间的关系，学生要紧紧抓住概念的本质，辨析概念。

因方向导数和梯度具有方向性，所以学生也应具备向量的有关知识，如向量的内积、模等概念。

4 教学媒体设计用幻灯片制作的部分多媒体辅助课件，在教师主机上进行播放，包含本节教学的全部内容。

5 教学策略及教法设计5.1教学策略以目标教学为驱动，以问题教学为切入点，以计算机辅助教学为手段，通过师生互动，运用发展学生认知结构的策略，揭示概念内涵，层层推进，辨析方向导数概念与其它概念间的关系，从而达到掌握概念、运用概念的目的。

5.2教法设计以建构主义的教与学理论作指导，创设一个实际问题情境，从偏导数的复习入手，揭示偏导数刻画函数在坐标轴方向上的变化情况的特征，引出方向导数的概念，在教师的引导下，运用问题教学法，以师生对话的形式，揭示概念本质，启发学生思维，明晰概念，掌握概念。

| y | ( 0 , 0 ) lim y 0 y
z 同理： y
故两个偏导数均不存在.
沿任意方向l { x, y}的方向导数,
z l
( 0,0 )
lim
f ( x , y ) f (0,0)
0

( x ) 2 ( y ) 2 lim 1 2 2 0 ( x ) ( y )
显然f x , f y是f ( x , y )沿x , y轴的方向导数 沿x , y轴正向时为f x , f y ;负向时为 f x , f y .
f 2. 的存在定理 l 若z f ( x , y)在P ( x , y)可微,
则函数在该点沿任一方向 l 的方向导数存在，且 f f x cos f y cos , l 其中cos , cos 为方向l 的方向余弦. y Proof. z f ( x, y)可微, P y1 z f x x f y y o( ), P x z x y o( ) fx fy , o
u cos cos l (1,1)
此时

2
u 从而 2 cos( ) l (1,1) 4
u 显然当 时, 4 l (max)

2,
u 当 时, 0, 4 2 l


而gradu i j ,
即
r cos cos sin sin cos( ) l r r 且当 时, 1;当 时, 0. l 2 l
二. 梯度
定义 设函数 z f ( x , y ) 在平面区域 D 内具有 一阶连续偏导数，则对于每一点 P ( x , y ) D ，