梯度与方向导数

§3 方向导数与梯度在许多问题中，不仅要知道函数在坐标轴方向上的变化率（即偏导数），而且还要设法求得函数在其他特定方向上的变化率.这就是本节所要讨论的方向导数． 定义1 设三元函数f 在点),,(0000z y x P 的某邻域30)(R P ⊂ 内有定义，l 为从点0P 出发的射线，),,(z y x P 为l 上且含于 )(0P 内的任一点，以ρ表示P 与0P 两点间的距离。

若极限ρρρρf P f P f l ∆=-++→→000lim )()(lim存在，则称此极限为函数f 在点0P 沿方向l 的方向导数，记作)(,00P f l f l P ∂∂或).,,(000z y x f l 容易看到，若f 在点0P 存在关于x 的偏导数，则f 在点0P 沿轴正向的方向导数恰为 .00P P x f lf∂∂=∂∂ 当l 的方向为x 轴的负方向时，则有 .00P P x f l f∂∂-=∂∂ 沿任一方向的方向导数与偏导数的关系由下述定理给出．定理17.6 若函数f 在点),,(0000z y x P 可微，则f 在点0P 处沿任一方向l 的方向导数都存在，且,cos )(cos )(cos )()(0000γβαP f P f P f P f z y x ++= )1( 其中γβαcos ,cos ,cos 为方向l 的方向余弦．证 设),,(z y x P 为l 上任一点，于是（见图17－5）⎪⎭⎪⎬⎫=∆=-=∆=-=∆=-.cos ,cos ,cos 000γρβραρz z z y y y x x x ()2由假设f 在点0P 可微，则有 ()()=-0p f p f ()ρo z P f y P f x P f z y x .).()()(000+∆+∆+∆上式左、右两边皆除以ρ，并根据（2）式可得()ρρρρρρo z P f y P f x P f P f P f z y x +∆+∆+∆=-)()()()()(0000 ()ρργβαo P f P f P f z y x +++=cos )(cos )(cos )(000. 因为当0→ρ时，上式右边末项,0)(→ρρo ，于是左边极限存在且有()ρρ)()(lim 000P f P f P f l -=+→ .cos )(cos )(cos )(000γβαP f P f P f z y x ++= □对于二元函数),(y x f 来说，相应于)1(的结果是 (),cos ),(cos ),(00000βαy x f y x f P f y x l += 其中βα,是平面向量l 的方向角．例1 设,),,(32z y x z y x f ++=求f 在点0P )1,1,1(沿方向)1,2,2(:-l 的方向导数． 解 易见f 在点0P 可微.故由3)(,2)(,1)(000===P f P f P f z y x 及方向l 的方向余弦,321)2(22cos ,321)2(22cos 222222-=+-+-==+-+=βα grad ),3,3,1()(0--=P f g ra d .19)3()3(1222=-+-+=f □作业布置：Ｐ１２７ １；３．。

向量的梯度和方向导数向量是一个非常重要的数学概念，它在物理学、工程学和计算机科学等多个领域中都有广泛应用。

而向量的梯度和方向导数则是向量分析中的两个基本概念，掌握它们对于理解各种物理现象和计算机模型都非常有帮助。

一、向量的梯度向量的梯度是一个向量。

它描述了一个多元函数在每一点的变化率和方向。

在物理学和工程学中，向量的梯度被用来描述各种场的变化率和方向，例如电场、磁场和温度场等。

向量的梯度的定义如下：假设f(x,y,z)是定义在三维空间中的一个可微函数，则它在点P(x0,y0,z0)处的梯度记作grad f(x0,y0,z0)，它的值为：grad f(x0,y0,z0) = (∂f/∂x, ∂f/∂y, ∂f/∂z) |P其中∂f/∂x, ∂f/∂y, ∂f/∂z分别表示对于变量x、y和z的偏导数。

从上式可以看出，向量的梯度就是函数在每个方向上的变化率所构成的向量。

因此，向量的梯度的模长表示函数在该点处的最大变化率，而梯度的方向则表示函数在该点处增加最快的方向。

这个方向是沿着一个切平面的法线方向，可以用来指导分析区域最陡峭的部分。

二、方向导数方向导数是一个标量。

它描述了一个多元函数在某一点沿着给定方向的变化率。

在物理学和工程学中，方向导数被用来描述物体的运动和力学量的变化。

方向导数的定义如下：假设f(x,y,z)是定义在三维空间中的一个可微函数，而v=(v1,v2,v3)是一个非零向量，则函数f在点P(x0,y0,z0)沿着方向v 的方向导数记作Dvf(x0,y0,z0)，它的值为：Dvf(x0,y0,z0) = ∇f(x0,y0,z0)·v其中∇f(x,y,z)表示向量的梯度，·表示点积。

从上式可以看出，方向导数就是向量的梯度在给定方向上的投影所构成的标量。

因此，方向导数的值也可以表示为函数在该点处增加最快的速率。

三、应用举例下面我们通过一个应用举例来说明向量的梯度和方向导数的作用。

梯度和方向导数
方向导数是一个值，梯度是一个向量。

方向导数
顾名思义，方向导数就是某个方向上的导数。

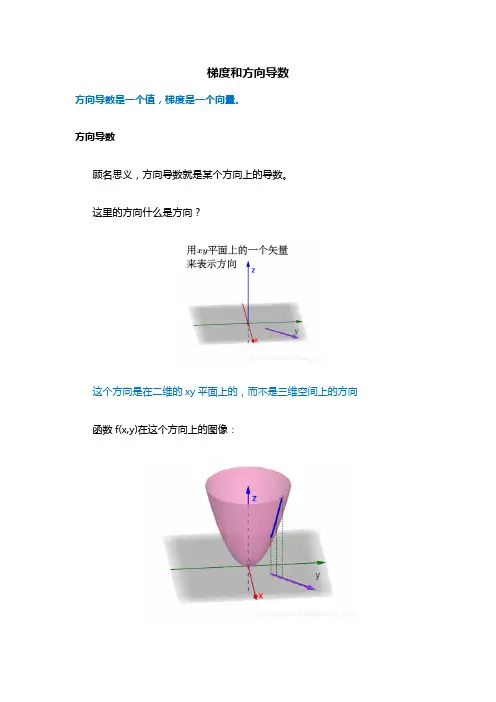
这里的方向什么是方向？
这个方向是在二维的xy平面上的，而不是三维空间上的方向函数f(x,y)在这个方向上的图像：
我们知道：
函数f(x,y) 的A 点在这个方向上也是有切线的，其切线的斜率就是方向导数：
梯度
很显然，A 点不止一个方向，而是360°都有方向：
每个方向都是有方向导数的：
这就引出了梯度的定义：
梯度：是一个矢量，其方向上的方向导数最大，其大小正好是此最大方向导数。

方向导数与梯度在多变量微积分和优化理论中，方向导数和梯度是两个重要的概念。

它们提供了函数在某一点处关于不同方向的信息，以及函数在该点处的变化率和方向。

理解这两个概念对于解决各种实际问题，如最优控制、机器学习、图像处理等都至关重要。

方向导数是函数在某一点处沿特定方向的变化率。

给定一个函数f(x)在点x0，对于任意的方向v = (h1, h2,..., hn)，方向导数Df(x0)v 是f(x)在x0处沿v方向的变化率。

具体地，Df(x0)v = lim(h->0) [f(x0 + hv) - f(x0)] / h。

方向导数的重要性在于它提供了函数在某一点处对不同方向的敏感度。

例如，如果你在山峰上沿着不同的方向行走，方向导数可以告诉你哪个方向更容易攀登，哪个方向更困难。

梯度是函数在某一点处所有方向导数的向量。

给定一个函数f(x)在点x0，梯度gradf(x0)是一个向量，其方向是f(x)在x0处增加最快的方向，而其大小是f(x)在该方向的导数。

具体地，gradf(x0) = (f'(x01), f'(x02),..., f'(xn))。

梯度是一个非常重要的概念，因为它提供了函数在某一点处的最大变化率方向。

在很多实际问题中，找到这个最大变化率方向往往能够指引我们找到最优解。

例如，如果你在山峰上寻找攀登最快的方式，梯度可以告诉你应该沿着哪个方向前进。

梯度是方向导数的最大值。

换句话说，对于任意给定的方向v，方向导数Df(x0)v都不超过梯度的长度。

这是因为梯度是所有方向导数向量的范数，即||gradf(x0)|| = max{Df(x0)v : ||v|| = 1}。

这个性质表明，梯度不仅提供了函数在某一点处的最大变化率方向，还给出了沿这个方向的导数（即变化率）。

这使得梯度在优化问题中具有特别的重要性，因为它可以用来找到使函数值下降最快的方向。

方向导数和梯度是多变量微积分和优化理论中的重要概念。

方向导数和梯度的关系公式方向导数和梯度是微积分中的重要概念，它们在多元函数的研究中起着重要作用。

方向导数描述了函数在某一给定方向上的变化率，而梯度则是方向导数的一种特殊情况。

本文将探讨方向导数和梯度之间的关系，并阐述它们的定义、性质和应用。

让我们来定义方向导数。

对于一个多元函数f(x, y, z)，在某一点P(x0, y0, z0)处，沿着一个与坐标轴夹角为θ的方向v=(cosθ, sinθ)的方向导数表示函数在该方向上的变化率。

方向导数的计算公式为：Dvf(x0, y0, z0) = ∇f(x0, y0, z0)·v其中，∇f(x0, y0, z0)是函数f在点P的梯度。

梯度是一个向量，其分量为函数在各个方向上的偏导数。

梯度的计算公式为：∇f(x0, y0, z0) = (∂f/∂x, ∂f/∂y, ∂f/∂z)可以看出，梯度是一个向量，方向导数是梯度与方向向量的点积。

因此，方向导数可以通过计算梯度和方向向量的点积来求得。

方向导数具有以下性质：1. 方向导数的值与方向向量的长度无关，只与方向向量的方向有关。

这意味着方向导数可以通过单位向量来表示。

2. 方向导数的最大值和最小值分别是函数在某一点上沿着梯度方向和负梯度方向的方向导数。

当方向向量与梯度方向相同时，方向导数达到最大值；当方向向量与负梯度方向相同时，方向导数达到最小值。

3. 方向导数为0的点是函数的临界点，即梯度为0的点。

梯度是方向导数的一种特殊情况。

当方向向量与梯度方向相同时，方向导数达到最大值，即梯度的模长为方向导数的最大值。

因此，梯度可以看作是方向导数的最大值和方向。

梯度在数学中具有重要的应用。

在优化问题中，梯度可以帮助我们找到函数的最大值或最小值。

当函数的梯度为0时，函数达到极值点。

因此，我们可以通过求解梯度为0的方程组来求解极值问题。

梯度还可以用于描述函数在空间中的变化趋势。

当梯度的模长越大时，函数在该点的变化趋势越明显；当梯度的模长趋近于0时，函数在该点的变化趋势越平缓。

第五节 方向导数和梯度一、方向导数前面我们学习的偏导数是函数在坐标轴方向上的变化率，下面我们讨论函数沿任一射线 方向的变化率。

以三元函数),,(z y x f u =为例我们给出如下定义：定义5.4 设三元函数),,(z y x f u =在点),,(0000z y x P 的一个邻域⊂)(0P U 3R 中有定义，任意方向向量l 的同向单位向量为e ，记}cos ,cos ,{cos γβα=e ，实数k 是使得两点),,(0000z y x P 和)cos ,cos cos (000γβαk z k y k x P k ++,+的连线段包含在邻域)(0P U 内的任意正数。

如果极限kz y x f k z k y k x f k ),,()cos ,cos cos (lim 0000000-++,++→γβα 存在，则称此极限为函数),,(z y x f u =在点),,(0000z y x P 沿方向或的方向导数，记为),0,00z y x ),0,00z y x e ∂。

特别地，沿x 轴、y 轴和z 轴的正向的方向分别为)0,0,1(1=e 、)0,1,0(2=e 和)1,0,0(3=e ，我们容易得到函数),,(z y x f 在点),,(0000z y x P 关于x （y 或z ）可求偏导的充分必要条件是),,(z y x f 沿方向1e 和1e -（2e 和2e -或3e 和3e -）的方向导数都存在且为相反数，并且这时成立：),(0,001z y x e f ∂∂=),(0,00z y x x f ∂∂（),(0,002z y x e f ∂∂=),(0,00z y x y f ∂∂或),(0,003z y x e f ∂∂=),(0,00z y x zf ∂∂）。

方向导数与偏导数有如下关系：定理 5.15 如果),,(z y x f u =在点),,(0000z y x P 可微，那么),,(z y x f 在点),,(0000z y x P 沿任意方向}cos ,cos ,{cos γβα=的方向导数存在，且γβαcos ),,(cos ),,(cos ),,(),,(000000000000z y x zf z y x y f z y x x f z y x e f ∂∂+∂∂+∂∂=∂∂证 因为),,(z y x f 在点),,(0000z y x P 可微，我们有kz y x f k z k y k x f z y x e f k ),,()cos ,cos cos (lim ),,(000000000-++,+=∂∂+→γβα kk k z y x z f k z y x y f k z y x x f k )(0cos ),,(cos ),,(cos ),,(lim 0000000000+∂∂+∂∂+∂∂=+→γβαγβαc o s ),,(c o s ),,(c o s ),,(000000000z y x zf z y x y f z y x x f ∂∂+∂∂+∂∂=类似地，我们可以对一般n 元函数给出方向导数的定义并且相应有上面定理。