方向导数与梯度

方向导数与梯度在许多问题中，不仅要知道函数在坐标轴方向上的变化率（即偏导数），而且还要设法求得函数在其他特定方向上的变化率。

这就是接下来要谈论的方向导数。

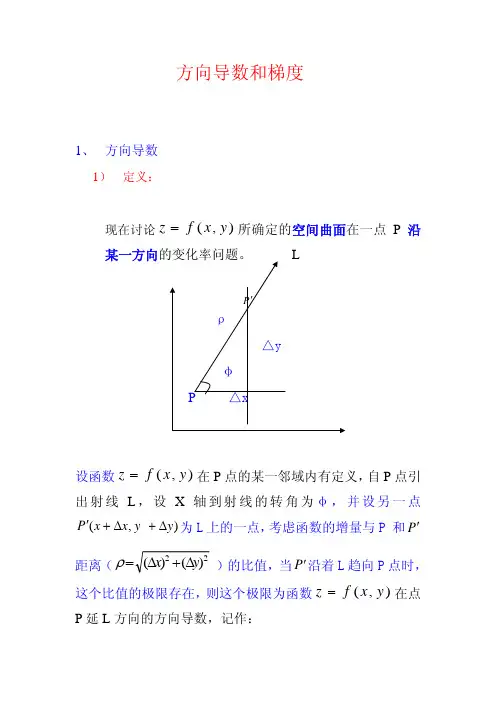
定义 1 设三元函数),,(z y x f 在点),,(0000z y x P 的某邻域30)(R P U ⊂内有定义，l 为从点0P 出发的射线，),,(z y x P 为l 上且含于)(0P U 内的任一点，以ρ表示P 与0P 两点间的距离，若极限ρρρρf P f P f 1000lim lim )()(∆=-++→→存在，则称此极限为函数f 在点0P 沿方向l 的方向导数，记作),,()(,|0000p 0z y x f p f l f l l 或。

沿任一方向的方向导数与偏导数的关系由下述定理给出。

定理 若函数f 在点),,(0000z y x P 可微，则f 在点0P 处沿任一方向l 的方向导数都存在，且γβαcos )(cos )(cos )()(0000P f P f P f P f z y x l ++=其中γβαcos ,cos ,cos 为方向l 的方向余弦。

注：最后会介绍方向余弦的知识例1 设32),,(z y x z y x f ++=，求f 在点)1,1,1(0P 沿方向)1,2,2(:-l 的方向导数。

解 易见f 在点)1,1,1(0P 可微。

故由3)(,2)(,1)(000===P f P f P f z y x 及方向l 的方向余弦311)2(21cos ,321)2(22cos ,321)2(22cos 222222222=+-+=-=+-+-==+-+=γβα 可按定理中的公式求得f 沿方向l 的方向导数为31313)32(2321)(0=⋅+-⋅+⋅=P f l .定义 2 若),,(z y x f 在),,(0000z y x P 存在所有自变量的偏导数，则称向量))(),(),((000P f P f P f z y x 为函数f 在点0P 的梯度，记作))(),(),(( 000P f P f P f f grad z y x =.向量 f grad 的长度（或模）为202020)()()( P f P f P f f grad z y x ++=.在上述定理的条件下，若记l 方向上的单位向量为)cos ,cos ,(cos 0γβα=l .于是方向导数公式又可以写成θcos )(00f grad l f grad P f l =∙=这里θ是梯度向量)( 0P f grad 与的夹角0l 。

梯度与方向导数
梯度与方向导数是微积分中的两个重要概念。

梯度是一个向量，它指向一个函数在某一点上增加最快的方向。

方向导数是一个标量，它描述了在某一点上沿着某个方向变化的速率。

梯度和方向导数都有广泛的应用，例如在优化问题中，可以使用梯度来找到函数的极大值或极小值，并使用方向导数来确定函数在某个方向上的渐近行为。

此外，梯度和方向导数还可以用于描述流体力学和电磁学中的物理现象，例如速度和电场的变化。

因此，深入理解梯度和方向导数的概念对于学习微积分和应用数学都是非常重要的。

- 1 -。

方向导数和梯度grad计算公式
方向导数和梯度grad是向量微积分中常用的概念，它们用于描述函数在某一点处的变化率和变化的方向。

方向导数是在某一点处沿着某一方向的变化率，而梯度则是函数在某一点处的最大变化方向。

下面是方向导数和梯度的计算公式：
1. 方向导数的计算公式：
设函数f(x,y,z)在点P(x0,y0,z0)处可微分，向量v=(a,b,c)是以P为起点的任意向量，则函数f在P点沿着v方向的方向导数为： Dvf(x0,y0,z0) = f(x0,y0,z0) · v
其中，f(x0,y0,z0)是函数f在点P(x0,y0,z0)处的梯度向量，即：
f(x0,y0,z0) = (fx(x0,y0,z0), fy(x0,y0,z0), fz(x0,y0,z0)) 其中，fx, fy, fz分别是函数f在点(x0,y0,z0)处的偏导数。

2. 梯度的计算公式：
设函数f(x,y,z)在点P(x0,y0,z0)处可微分，则函数f在P点处的梯度向量为：
f(x0,y0,z0) = (fx(x0,y0,z0), fy(x0,y0,z0), fz(x0,y0,z0)) 梯度向量的大小表示函数在该点处的最大变化率，方向表示函数在该点处变化最快的方向。

总之，方向导数和梯度是向量微积分中的重要概念，它们的计算公式可以帮助我们更好地理解和应用这些概念。

- 1 -。

梯度与方向导数的关系梯度与方向导数是微分学中两个重要概念，它们在多元函数的求导和优化中有着密切的联系。

首先，我们先来介绍一下梯度的概念。

对于一个多元函数，梯度是一个向量，它的方向指向函数在某一点处取得最大增加的方向，其模长表示增加的速率。

梯度通常用符号∇表示，如果函数f(x,y,z)在点P(x0,y0,z0)处可微分，则梯度定义为：∇f(x0,y0,z0) = (∂f/∂x, ∂f/∂y, ∂f/∂z)其中的∂f/∂x表示函数f对变量x求导的偏导数。

可以看出，梯度是一个向量，其分量分别对应于各个变量的偏导数值。

而方向导数，顾名思义，就是函数沿着某一给定方向上的导数。

对于一个函数f(x,y,z)，在点P(x0,y0,z0)处的方向向量为u=(u1,u2,u3)，方向导数定义为：Duf(x0,y0,z0) = ∇f(x0,y0,z0)·u其中的·表示向量的点积运算。

可以看出，方向导数是梯度和方向向量的点积，它表示了函数f在给定方向上的变化速率。

那么梯度与方向导数之间有什么联系呢？根据上述定义可以得知，梯度是一个向量，其方向与方向导数的方向相同，且梯度的模长表示了方向导数的大小。

换句话说，梯度可以看作是方向导数的一个特例。

具体来说，若给定一个向量u，如果f(x,y,z)在点P(x0,y0,z0)处可微分，则由方向导数的定义可知：Duf(x0,y0,z0) = ∇f(x0,y0,z0)·u =|∇f(x0,y0,z0)||u|cosθ其中的θ表示梯度向量∇f(x0,y0,z0)与方向向量u的夹角。

根据向量的点乘性质，可以得出：|∇f(x0,y0,z0)||u|cosθ = ∇f(x0,y0,z0)·u也就是说，梯度向量的模长和方向导数的大小是一样的。

当方向向量u与梯度向量的夹角为零时，即u与梯度的方向相同，方向导数取得最大值；当方向向量u与梯度向量的夹角为180°时，即u与梯度的方向相反，方向导数取得最小值。

方向导数与梯度的关系公式
方向导数和梯度是微积分中的两个重要概念。

它们之间存在着密切的关系。

首先，我们来介绍一下方向导数的概念。

方向导数是指函数在某一点沿着某一方向的变化率。

如果函数在该点可微分，那么它的方向导数可以用该点的梯度来表示。

接下来，我们来介绍一下梯度的概念。

梯度是一个向量，表示函数在某一点上的变化率最大的方向。

梯度的方向指向函数值增加的最快的方向，大小表示该方向的最大变化率。

梯度的计算方式是取该点的偏导数向量。

在同一点上，如果沿着梯度的方向进行变化，则函数值的变化率最大。

因此，方向导数沿着梯度的方向取得最大值，即方向导数等于梯度与该方向的点积值。

因此，可以得出方向导数和梯度的关系公式如下：
设函数f(x,y)在点P(x0,y0)可微分，向量v=(cosθ,sinθ)表示与x轴正向夹角为θ的方向，则f(x0,y0)在方向v上的方向导数为：
∂f/∂v = ▽f(x0,y0) ·v
其中▽f(x0,y0)表示f(x0,y0)的梯度向量。

方向导数与梯度在多变量微积分和优化理论中，方向导数和梯度是两个重要的概念。

它们提供了函数在某一点处关于不同方向的信息，以及函数在该点处的变化率和方向。

理解这两个概念对于解决各种实际问题，如最优控制、机器学习、图像处理等都至关重要。

方向导数是函数在某一点处沿特定方向的变化率。

给定一个函数f(x)在点x0，对于任意的方向v = (h1, h2,..., hn)，方向导数Df(x0)v 是f(x)在x0处沿v方向的变化率。

具体地，Df(x0)v = lim(h->0) [f(x0 + hv) - f(x0)] / h。

方向导数的重要性在于它提供了函数在某一点处对不同方向的敏感度。

例如，如果你在山峰上沿着不同的方向行走，方向导数可以告诉你哪个方向更容易攀登，哪个方向更困难。

梯度是函数在某一点处所有方向导数的向量。

给定一个函数f(x)在点x0，梯度gradf(x0)是一个向量，其方向是f(x)在x0处增加最快的方向，而其大小是f(x)在该方向的导数。

具体地，gradf(x0) = (f'(x01), f'(x02),..., f'(xn))。

梯度是一个非常重要的概念，因为它提供了函数在某一点处的最大变化率方向。

在很多实际问题中，找到这个最大变化率方向往往能够指引我们找到最优解。

例如，如果你在山峰上寻找攀登最快的方式，梯度可以告诉你应该沿着哪个方向前进。

梯度是方向导数的最大值。

换句话说，对于任意给定的方向v，方向导数Df(x0)v都不超过梯度的长度。

这是因为梯度是所有方向导数向量的范数，即||gradf(x0)|| = max{Df(x0)v : ||v|| = 1}。

这个性质表明，梯度不仅提供了函数在某一点处的最大变化率方向，还给出了沿这个方向的导数（即变化率）。

这使得梯度在优化问题中具有特别的重要性，因为它可以用来找到使函数值下降最快的方向。

方向导数和梯度是多变量微积分和优化理论中的重要概念。

方向导数与梯度
1. 基本概念
方向导数：是一个数；反映的是f(x,y)在P0点沿方向v 的变化率。

偏导数：是多个数（每元有一个）；是指多元函数沿坐标轴方向的方向导数，因此二元函数就有两个偏导数。

偏导函数：是一个函数；是一个关于点的偏导数的函数。

梯度：是一个向量；每个元素为函数对一元变量的偏导数；它既有大小（其大小为最大方向导数），也有方向。

2. 方向导数
反映的是f(x,y)在P0点沿方向v的变化率。

例子如下：
2.0 方向导数计算公式
2.1 偏导数
2.2 二元函数偏导数的几何意义
2.3 偏导函数
偏导数与偏导函数的关系：
偏导数是偏导函数在指定点的函数值，因此在求偏导数时，也可先求出偏导函数，然后再将点代入偏导函数，从而求出函数在此点的偏导数。

3. 全微分
4. 梯度
梯度是一个向量；既有大小，也有方向。

4.1 几何意义
函数z=f(x,y)在点P0处的梯度方向是函数变化率(即方向导数)最大的方向。

梯度的方向就是函数f(x,y)在这点增长最快的方向，梯度的模为方向导数的最大值。