2003年清北学堂国庆数学班讲义精选集
- 格式:pdf
- 大小:339.99 KB
- 文档页数:34



北京清北学堂数学竞赛导学材料几何特训一导学一、几个重要定理:1、梅涅劳斯定理:设',','C B A 分别是ΔABC 的三边BC ,CA ,AB 或其延长线上的点,若',','C B A 三点共线,则.1''''''=⋅⋅BC AC A B CB C A BA '''AC CB BA,C AP 2=AB 2•BC PC +AC 2•BCBP-BP•PC. 6、欧拉定理、欧拉公式:ΔABC 的外心O ,垂心H ,重心G 三点共线,且.21GH OG =设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则d 2=R 2-2Rr . 二、三角形的五心三角形的外心、重心、垂心、内心及旁心,统称为三角形的五心. 1. 重心:三角形的三条中线交于一点。
(1)设G 为△ABC 的重心,连结AG 并延长交BC 于D ,则D 为BC 的中点,且:2:1AG GD =;(2)重心坐标公式:设G 为△ABC 的重心,则(,)33A B C A B Cx x x y y y G ++++(3)设G 为△ABC 的重心,则ABC ACG BCG ABG S S S S ∆∆∆∆===31; (4)设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则(2)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍; (3)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上;(4)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆; (5)设O ,H 分别为△ABC 的外心和垂心,则HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,.(6)由三角形的垂心造成的四个等(外接)圆三角形,给我们解题提供了极大的便利. (7)垂线定理:2222BD BC AD AC CD AB -=-⇔⊥.高线长:C b B c A abcc p b p a p p ah a sin sin sin ))()((2===---=. 3. 内心:三角形的三条角分线的交点—内切圆圆心。


专题三:数列的概念序:本章注意培养:观察归纳思想、递推思想、等价转化思想、函数思想解决数列问题。
实例引入:①印度国王奖励象棋发明者时,对象棋各格子里放麦粒,各格子里的麦粒数按位置放置的先后排成一列数:234631,2,2,2,2,,2L ②正整数从小到大依次排成一列:1,2,3,4,5,6,L③正整数的倒数排成一列:111111,,,,,,23456L的精确到1,0.1,0.01,0.001,L 的不足近似值排成一列:1,1.4,1.41,1.414,L⑤1-的1次幂、2次幂、3次幂、4次幂、…,排成一列:1,1,1,1,1,1,1,1,----L⑥无穷多个1排成一列:1,1,1,1,1,1,L一、数列的概念1.数列的定义:___________________________________叫做数列。
(这列数可“有限”也可“无限”) 注意:①数列的一列数是有次序性的,注意“数列”与“数集”的区分! ②数列中的项:数列中的每个数。
③数列的项数:数列中项的序号。
如:Ⅰ)234631,2,2,2,2,,2L ; Ⅱ)111111,,,,,,23456L 。
2.函数观点下“数列”的定义:数列实质上可以看做一个定义域为_________________________的函数()f n ,当自变量n 从1开始从小到大依次取正整数值时对应的一列函数值(1),(2),(3),,(),f f f f n L L (或(1),(2),(3),,()f f f f n L )。
注意:数列视为正整数为自变量的函数值,与普通的函数有区别,它是离散的。
3.①数列的表示:123,,,,,n a a a a L L ,简记为{}n a 。
其中n a 叫数列的第n 项。
如数列:111111,,,,,,23456L ,简记为1n ⎧⎫⎨⎬⎩⎭。
n a ——数列{}n a 的第n 项(通项),n 为项数;{}n a ——数列123,,,,,n a a a a L L 。

清北学堂08国庆赠送试题答案数学1、 不等式<证法一>()21111x a a +-=41211221-+⎪⎭⎫ ⎝⎛-x a由柯西不等式: ⎪⎪⎭⎫⎝⎛+∑=n k k x a 12212≤()⎪⎪⎭⎫ ⎝⎛+∑=n k k k xa a 122⎪⎪⎭⎫ ⎝⎛∑=n k k a11≤()∑=+n k k k x a a 1222只需证:()()21112221121x a a x aa n k kk+-≤+∑= (1) 由于()2222xaa kk+<()22222kkka xaa -+=4121122-+⎪⎭⎫ ⎝⎛-x a k -4121122-+⎪⎭⎫ ⎝⎛+x a k2()∑∑==⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+⎪⎭⎫ ⎝⎛+--+⎪⎭⎫ ⎝⎛-<+n k k k nk kkx a x a x aa 1222212224121141211 由于a1<a2<…<an,且均为正整数 ∴21211-≤++k k a a ∴(1)式成立<证法二> 当()1112-≥a a x 由111≤∑=nk ka ,可设: 21221⎪⎪⎭⎫ ⎝⎛+∑=n k k x a ≤2121⎪⎪⎭⎫⎝⎛∑=n k k x a =212141⎪⎪⎭⎫ ⎝⎛∑=n k k a x ≤()2211212121x a a x +-≤ 当()1112-<a a x 时,显然,()12-<k k a a x ,由柯西不等式只需证:()()21112221121x a a xaa nk kk+-≤+∑= (1)由于()222222241k k k a x a xa -⎪⎭⎫ ⎝⎛++≥+()22222224122kk kkka x a a xaa -⎪⎭⎫ ⎝⎛++≤+∴=2222222221121121212x a x a x a x a a kk k k k +⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛-=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛- 由此可证:()()211221221122211214121121211212x a a x a x a x aa nk kk+-=-+⎪⎭⎫ ⎝⎛-<+⎪⎭⎫ ⎝⎛-<+∑= 二、平面几何如图1-3,连结MN ,BD ,CD ∵FM ⊥AB ,FN ⊥AC∴∠AMN+∠BAE=∠AFN+∠CAF=90°, ∴MN ⊥AD∵∠FMN=∠FAN=∠BAD=∠BCD ,∠FNM=∠DBC , ∴△MNF ∽△CBD ∴FM DC FN DB MN CB MN CB==,. 对圆内接四边形ABCD 用托勒密定理有 AB ·CD+AC ·BD=AD ·BC ∴···ABC AMDN S FM AB FN ACS MN AD+=△=··FM AB FN ACMN AD MN AD + =··DC AB DB ACCB AD CB AD +=···DC AB DB ACCB AD +=·1·AD BCCB AD= ∴SAMDN=S △ABC.3、数论 解: 因为22162544OP AD += 所以 224625AD OP += 同理,224625CD OQ += 对于方程224625x y +=2462512y y ≤⇒≤ y 为偶数(,)(7,12)(15,10)x y =或所以7151210AD CD OP OQ =⎧⎪=⎪⎨=⎪⎪=⎩或1571012AD CD OP OQ =⎧⎪=⎪⎨=⎪⎪=⎩求得20AC =,ABC ∆中,222cos 2AB BC AC B AB BC++=⨯求得2264005AB BC AB BC +-⨯= 设15AB a =,所以2211256400a BC a BC +-⨯=2211(3)16400BC a a -+=,所以2116400a ≤ 15a ≤ a 可能的值为1,2,3,4,5求得(,)(15,25)(25,15)AB BC =或(20,24)或取(20,24) C=664、组合计数解:分四种情形讨论: (1),用了6种颜色,将1种颜色染下底,则上底有5种染法,依照圆排列,其余4个侧面有3!种染法,共有5×3!=30种,(或6!64⨯) (2), 用5种颜色,选5种颜色有C 56种方式,再选一种染上下底有5种,固定一种颜色朝东,朝西的一面有3种共有C 56⨯56⨯=90种(3)用4种颜色,再选其中两种各染一对对面,有C 46⨯C 24种,将一对同色的面作为上底,下底,另一对同色的在东西两面,则南北相对两面的颜色互换后仍是同一染法,共有C 4624C ⨯=90种(4)用3种颜色,选三种颜色有36C 种方式,每种染相对两面,染出的都是同一种,共有36C =20种∴ 染色法有30+90+90+20=230种物理力学解:由水桶在离开水面的情形可知,重心上升距离为h,浮力2.3.4.5.化学一、解:PtNH 2CH 3I I II 2APt I BI NH 2CH 3PtI CNH 2CH 3PtI I H 3CH 2N INH 2CH 3Pt I DI NH 3NH 2CH 3 Pt O ENH 3O COH 2CC O由于AgI 的溶解度大大小于Ag 2CO 3,加入Ag 2CO 3后,能够使D 中的配体I -离开中心体而利于丙二酸根离子的配位。

专题三:排列与组合的综合选讲一、要点精析1.处理排列组合问题时,应遵循三大原则:先特殊后一般的原则、先取后排的原则、先分类后分步的原则。
2.掌握常见基本类型及方法:掌握排列组合中的“在”与“不在”、“含”与“不含”、“相邻”与“不相邻”、“不全”与“至少至多”等典型问题;会用“特殊元素法”、“特殊位置法”、“直接法”、“间接法”、“对称法”、“捆绑法”、“插空法”、“隔板法”和“递归法”等解决相关问题的应用题。
3.突出转化思想:把一些排列组合问题通过合理的分类或分步将其与基本类型相联系,从而将 这些问题转化为基本类型加以解决。
二、能力巩固1.(1)用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不 同,且1和2相邻,这样的六位数的个数是_______(用数字作答)。
40(2)由0到9这十个数字所组成的没有重复数字的五位数中,满足千位、百位、十位上的数字 成递增等差数列的五位数共有( )DA. 720个B. 684个C. 648个D.744个(3)先从数字0、1、2、3、4、5中每次取出3个成等差数列的不同数字,再把每一组的3个 数字组成三位数,则所有的三位数超过200的共有( )DA .22个B .18个C .36个D .26个(4)从0、1、2、3、4、5、6、7、8、9中任取三个数,组成没有重复数字的三位数,且满足 各位数字从左向右依此成等差数列,则这样的三位数有 个。
362.(1)将图中的正方体标上字母, 使其成为正方体1111ABCD A B C D , 不同的标字母方式共有( )BA .24种B .48种C .72种D .144种(2)如果一条直线与一个平面平行,那么称此直线与平面构成一个“平行线面组”,在一个长方 体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行线面组”的个数是( )BA .60B .48C .36D .24(3)在AOB ∠的边OA 上有1A 、2A 、3A 、4A 四点,OB 边上有1B 、2B 、3B 、4B ,5B 五点,共9个点,连结线段(14,15)i j ≤≤≤≤,如果其中两条线段不相交,则称之为一对“和睦线”,则共有_______________对。
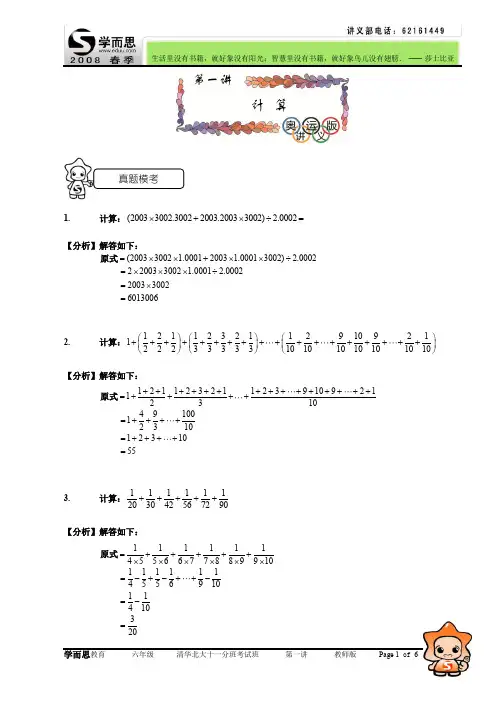
第一讲计 算1.计算:(20033002.30022003.20033002) 2.0002⨯+⨯÷=【分析】 解答如下:(20033002 1.00012003 1.00013002) 2.0002220033002 1.0001 2.0002200330026013006原式 =⨯⨯+⨯⨯÷=⨯⨯⨯÷=⨯=2. 计算:121123211291092112223333310101010101010⎛⎫⎛⎫⎛⎫++++++++++++++++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭【分析】 解答如下:121123211239109211231049100123101231055原式 +++++++++++++++=++++=++++=++++=3.计算:111111203042567290+++++【分析】 解答如下:1111114556677889910111111455691011410320原式 =+++++⨯⨯⨯⨯⨯⨯=-+-++-=-=4. 计算:11111111111111232004232005232005232004⎛⎫⎛⎫⎛⎫⎛⎫++++⨯+++-++++⨯+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭【分析】 设:111232004a +++=,111232005b +++= 1)(1)12005原式( a b b ab ab a abb a=+⨯-+⨯=+--=-=5.计算:2356235623562357÷【分析】 解答如下:23562357235623562357235723562356(23571)23572358原式 ⨯+=÷=⨯⨯+=6. 计算:9999222233333334⨯+⨯【分析】 解答如下:3333322223333333433336666333433331000033330000原式 () =⨯⨯+⨯=⨯+=⨯=7.按规律填数:261854________145813715_____63_____255511(1) 、、、、、、(2) 、、、、、、、、【分析】 (1)此串数列出现的规律为后数是前数三倍,填543162,1623486,48631458,⨯=⨯=⨯=.所以填162、486. (2)此串数列出现的规律为21n -的数,所以第五个是52131-=,第七个是721127-=.8.8.88.988.9988.99988.99998a a =++++,的整数部分是 .【分析】a 一定大于8.8544⨯=,一定小于8.99998544.9999⨯=,所以a 得整数部分只能是44. 9. 编辑一个运算程序:112,,(1)2m n k m n k δδδ==+=+则12005δ的输出结果为( ) A .4008 B .4006 C .4012 D .4010【分析】 解答如下:112,1(11)12224221(21)13426231(31)146282412005220054010δδδδδδδδ=+==+==⨯+==+==⨯+==+==⨯=⨯=10.某池塘中有A B C 、、三只游船,A 可乘坐3人,B 可乘坐2人,C 可乘坐1人,今有3个成人和2个儿童要乘坐这些游船,为了安全起见,有儿童乘坐的游船上必须至少有1个成人陪伴,那么他们5人乘坐这三条游船的所有安全乘坐方式有______种.【分析】 5320311221=++=++=++,当5320=++时,有2种;当5311=++时,有1种;当5221=++时,有1种,所以一共有2114++=种.【例1】 计算:253749517191334455÷+÷+÷【分析】 解答如下:513237143491545354759513271439154579314151123原式 ⨯+⨯+⨯+=⨯+⨯+⨯⨯+⨯+⨯+=++=++=【例2】 计算:1111111111111111()()()()5791179111357911137911+++⨯+++-++++⨯++【分析】 解答如下:设:1111111579117911a b +++=++=,11()()13131113131()1311135165原式 a b a b ab a ab ba b =⨯+-+⨯=+--=⨯-=⨯=【例3】 计算:1112112123123100++++++++++=______.【分析】 解答如下:222212239910010010111111112(1)2233410010112(1)101991101200101原式 =++++⨯⨯⨯⨯=⨯-+-+-++-=⨯-==【例4】 若200520062006200720072008,,200720082008200920092010a b c ⨯⨯⨯===⨯⨯⨯,则有( ). (A )a >b >c (B )a >c >b (C )a <c <b (D )a <b <c【分析】 解答如下: 200520062005200620072008200720082006200720062007200820092008200920072008200720082009201020092010a b c ⨯==⨯⨯⨯==⨯⨯⨯==⨯⨯ a >b ,b >c ,所以:a >b >c【例5】 对于任意的两个实数对(,)a b 和(,)c d ,规定(,)a b =(,)c d ,当且仅当,a c b d ==;运算“⊗”为:(,)a b ⊗(,)(,)c d ac bd bc ad =-+,运算“⊕”为:(,)a b ⊕(,)(,)c d a c b d =++.设,p q R ∈,若(1,2)⊗(,)p q =(5,0),则(1,2) ⊕(,)p q =( )A .(4,0)B .(2,0)C .(0,2)D .(0,4)-【分析】 ∵(1,2)⊗(,)(2,2)(5,0)p q p q p q =-+=∴25,20p q p q -=+= ∴1,2p q ==-∴(1,2) ⊕(,)(1,2)(11,22)(2,0)p q p q =++=+-=【例6】 从1到999这999个自然数中有( )个数的各位数字之和能被4整除.【分析】 一位数时有:48,,一共2个.两位数时有:4481216A B A B ++=能被整除,那么,,,, 13117222631354044485357,,,,,,,,,,,一共92220⨯+=个三位数时有:4481216,20,24A B C A B C ++++=能被整除,那么,,,,一共 318556043179++++=最后一共:220179201++=1.由012345,,,,,组成的没有重复数字的六位数,百位不是2的奇数有( )个.【分析】 分析:个位有1,3,5三种选择,百位有1,3,4,5四种选择,除去已经选择的个位的一个数字,那么还有三种选择.332313162⨯⨯⨯⨯⨯=2. 定义两种运算:“○”和“▲”,对于任意两个整数A B 、,已知:A ○B =1A B ++, A ▲B =1A B ⨯-.若X ○(X ▲4)=30,则X =_______.【分析】 X ○(X ▲4)=X ○(41)X -=(41)1530,6X X X X +-+===3.计算:5311631(42)684178+-⨯÷【分析】 解答如下:511631268178517168168173516163176原式 =+⨯÷=+⨯⨯=+= 4.计算:1111111111()()()()()234571014152830-+-+-+-+-【分析】 解答如下:1111111111()()247142835101530147421106321283011115415原式 =++++-++++++++++++=-=-=5. 计算:99999777783333366666⨯+⨯【分析】 解答如下:99999777783333332222299999777789999922222999997777822222999991000009999900000原式 () =⨯+⨯⨯=⨯+⨯=⨯+=⨯=。

2003年硕士研究生入学考试(数学一)试题及答案解析一、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)(1) )1ln(12)(cos lim x x x +→ =e1 .【分析】 ∞1型未定式,化为指数函数或利用公式)()(lim x g x f )1(∞=)()1)(lim(x g x f e -进行计算求极限均可.【详解1】 )1ln(12)(cos lim x x x +→=xx x ecos ln )1ln(1lim20+→,而 212c o s s i n lim cos ln lim )1ln(cos ln lim02020-=-==+→→→x x xx x x x x x x , 故 原式=.121ee=-【详解2】 因为 2121lim)1ln(1)1(cos lim 22020-=-=+⋅-→→x xx x x x , 所以 原式=.121ee=-【评注】 本题属常规题型(2) 曲面22y x z +=与平面042=-+z y x 平行的切平面的方程是542=-+z y x .【分析】 待求平面的法矢量为}1,4,2{-=n,因此只需确定切点坐标即可求出平面方程, 而切点坐标可根据曲面22y x z +=切平面的法矢量与}1,4,2{-=n平行确定.【详解】 令 22),,(y x z z y x F --=,则x F x 2-=',y F y 2-=', 1='z F .设切点坐标为),,(000z y x ,则切平面的法矢量为 }1,2,2{00y x --,其与已知平面042=-+z y x 平行,因此有11422200-=-=-y x , 可解得 2,100==y x ,相应地有 .520200=+=y x z故所求的切平面方程为0)5()2(4)1(2=---+-z y x ,即 542=-+z y x . 【评注】 本题属基本题型。

绝密★启用前2003年普通高等学校招生全国统一考试数 学(文史类)(北京卷)本试卷分第Ⅰ卷(选择题)第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟第Ⅰ卷(选择题 共50分)注意事项:1.答第Ⅰ卷前,考生务必将自己姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.3.考试结束,监考人将本试卷和答题卡一并收回. 参考公式:三角函数的积化和差公式: 正棱台、圆台的侧面积公式)]sin()[sin(21cos sin βαβαβα-++=⋅ l c c S )(21+'=台侧)]sin()[sin(21sin cos βαβαβα--+=⋅ 其中c '、c 分别表示上、下底面)]cos()[cos(21cos cos βαβαβα-++=⋅周长,l 表示斜高或母线长. )]cos()[cos(21sin sin βαβαβα--+-=⋅ 球体的体积公式:334R V π=球,其中R 表示球的半径.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合要求的. 1.设集合B A x x B x x A ⋂>=>-=则|},0log |{},01|{22等于 ( )A .}1|{>x xB .}0|{>x xC .}1|{-<x xD .}11|{>-<x x x 或2.设5.1344.029.01)21(,8,4-===y y y ,则( )A .y 3>y 1>y 2B .y 2>y 1>y 3C .y 1>y 2>y 3D .y 1>y 3>y 23.“232cos -=α”是“Z k k ∈+=,1252ππα”的 ( )A .必要非充分条件B .充分非必要条件C .充分必要条件D .既非充分又非必要条件 4.已知α,β是平面,m ,n 是直线.下列命题中不.正确的是 ( )A .若m ∥α,α∩β=n ,则m//nB .若m ∥n ,α∩β=n ,则n ⊥αC .若m ⊥α,m ⊥β,则α∥βD .若m ⊥α,β⊂m ,则α⊥β5.如图,直线022:=+-y x l 过椭圆的左焦点F 1和一个顶点B ,该椭圆的离心率为 ( )A .51 B .52C .55 D .552 6.若C z ∈且|22|,1|22|i z i z --=-+则的最小值是( )A .2B .3C .4D .57.如果圆台的母线与底面成60°角,那么这个圆台的侧面积与轴截面面积的比为 ( )A .π2B .π23C .π332 D .π218.若数列{}n a 的通项公式是 ,2,1,23)1(3=-+=--n a nn n n ,则)(lim 21n n a a a +++∞→ 等于( )A .241 B .81 C .61 D .21 9.从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上, 其中黄瓜必须种植,不同的种植方法共有 ( ) A .24种 B .18种 C .12种 D .6种10.某班试用电子投票系统选举班干部候选人.全班k 名同学都有选举权和被选举权,他们的编号分别为1,2,…,k ,规定:同意按“1”,不同意(含弃权)按“0”,令 ⎩⎨⎧=.,0.,1号同学当选号同学不同意第第号同学当选号同学同意第第j i j i a ij其中i =1,2,…,k ,且j =1,2,…,k ,则同时同意第1,2号同学当选的人数为( ) A .kk a a a a a a 2222111211+++++++B .2221212111k k a a a a a a +++++++C .2122211211k k a a a a a a +++D .k k a a a a a a 2122122111+++第Ⅱ卷(非选择题 共100分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.11.已知某球体的体积与其表面积的数值相等,则此球体的半径为12.函数x tg x h x x g x x f 2)(|,|2)(),1lg()(2=-=+=中, 是偶函数.13.以双曲线191622=-y x 右顶点为顶点,左焦点为焦点的抛物线的方程是 14.将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为三、解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13分)已知函数.sin cos sin 2cos )(44x x x x x f --= (Ⅰ)求)(x f 的最小正周期; (Ⅱ)求)(x f 的最大值、最小值. 16.(本小题满分13分)已知数列{}n a 是等差数列,且.12,23211=++=a a a a (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)令).(3R x a b nn n ∈=求数列{}n b 前n 项和的公式.17.(本小题满分15分)如图,正三棱柱ABC—A1B1C1中,D是BC的中点,AB=a.(Ⅰ)求证:直线A1D⊥B1C1;(Ⅱ)求点D到平面ACC1的距离;(Ⅲ)判断A1B与平面ADC的位置关系,并证明你的结论.CBC B118.(本小题满分15分)如图,A 1,A 为椭圆的两个顶点,F 1,F 2为椭圆的两个焦点. (Ⅰ)写出椭圆的方程及准线方程;(Ⅱ)过线段OA 上异于O ,A 的任一点K 作OA 的垂线,交椭圆于P ,P 1两点,直线 A 1P 与AP 1交于点M.求证:点M 在双曲线192522=-y x 上.19.(本小题满分14分)有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=13km,BC=10km.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)(Ⅰ)若希望点P到三镇距离的平方和为最小,点P应位于何处?(Ⅱ)若希望点P到三镇的最远距离为最小,点P应位于何处?20.(本小题满分14分)设)(x f y =是定义在区间]1,1[-上的函数,且满足条件: (i );0)1()1(==-f f(ii )对任意的.|||)()(|],1,1[,v u v f u f v u -≤--∈都有 (Ⅰ)证明:对任意的;1)(1],1,1[x x f x x -≤≤--∈都有 (Ⅱ)判断函数⎩⎨⎧∈--∈+=]1,0[,1)0,1[,1)(x x x x x g 是否满足题设条件;(Ⅲ)在区间[-1,1]上是否存在满足题设条件的函数)(x f y =,且使得对任意的 .|)()(|],1,1[,v u v f u f v u -=--∈都有若存在,请举一例:若不存在,请说明理由.绝密★启用前2003年普通高等学校招生全国统一考试 数学试题(文史类)(北京卷)参考解答一、选择题:本题考查基本知识和基本运算. 每小题5分,满分50分.1.A 2.D 3.A 4.A 5.D 6.B 7.C 8.B 9.B 10.C 二、填空题:本题考查基本知识和基本运算.每小题4分,满分16分.11.3 12.)();(x g x f 13.)4(362--=x y 14.44+π三、解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或演算步骤.15.本小题主要考查三角函数的倍角、和角公式,以及三角函数的性质等基本知识,考查运算能力,满分13分. (Ⅰ)解:因为x x x x x f 44sin cos sin 2cos )(--=)42cos(22sin 2cos 2sin )sin )(cos sin (cos 2222π+=-=--+=x x x x x x x x所以)(x f 的最小正周期.22ππ==T (Ⅱ)解:因为),42cos(2)(π+=x x f 所以)(x f 的最大值为2,最小值为-216.本小题主要考查等差、等比数列等基本知识,考查综合运用数学知识和方法解决问题的能力.满分13分. (Ⅰ)解:设数列}{n a 公差为d ,则,12331321=+=++d a a a a 又.2,21==d a所以.2n a n=(Ⅱ)解:由,323n n n nn a b ==得,323)22(343212n n n n n S ⋅+-+⋅+⋅=- ①.323)22(34323132+⋅+⋅-++⋅+⋅=n n n n n S ②将①式减去②式,得 .32)13(332)333(22112++⋅--=⋅-++-=-n n n n n n n S所以.32)31(31+⋅+-=n nnn S17.本小题主要考查直线与平面的位置关系,正棱柱的性质,棱锥的体积等基本知识,考查空间想象能力和逻辑推理能力.满分15分.(Ⅰ)证法一:∵点D 是正△ABC 中BC 边的中点,∴AD ⊥BC ,又A 1A ⊥底面ABC ,∴A 1D ⊥BC ,∵BC ∥B 1C 1,∴A 1D ⊥B 1C 1.证法二:连结A 1C 1,则A 1C=A 1B. ∵点D 是正△A 1CB 的底边中BC 的中点, ∴A 1D ⊥BC ,∵BC ∥B 1C 1,∴A 1D ⊥B 1C 1.(Ⅱ)解法一:作DE ⊥AC 于E , ∵平面ACC 1⊥平面ABC ,∴DE ⊥平面ACC 1于E ,即DE 的长为点D 到平面ACC 1的 距离. 在Rt △ADC 中,AC=2CD=.23,a AD a =∴所求的距离.43a AC AD CD DE =⋅=CC 1解法二:设点D 到平面ACC 1的距离为x , ∵体积111ACC D ACD C V V --= .21318331112x CC a CC a ⋅⋅⋅=⋅⋅∴,43a x =∴即点D 到平面ACC 1的距离为a 43. (Ⅲ)答:直线A 1B//平面ADC 1,证明如下:证法一:如图1,连结A 1C 交AC 1于F ,则F 为A 1C 的中点,∵D 是BC 的中点,∴DF ∥A 1B , 又DF ⊂ 平面ADC 1,A 1B ⊄平面ADC 1,∴A 1B ∥平面ADC 1. 证法二:如图2,取C 1B 1的中点D 1,则AD ∥A 1D 1,C 1D ∥D 1B ,∴AD ∥平面A 1D 1B ,且C 1D ∥平面A 1D 1B ,∴平面ADC 1∥平面A 1D 1B ,∵A 1B ⊂平面A 1D 1B ,∴A 1B ∥平面ADC 1.图(2)图(1)C 11C18.本小主要考查直线、椭圆和双曲线等基本知识,考查分析问题和解决问题的能力.满分15分. (Ⅰ)解:由图可知,.3a b ,4,522=-===c c a 所以该椭圆的方程为,192522=+y x准线方程为.425±=x(Ⅱ)证明:设K 点坐标)0,(0x ,点P 、P 1的坐标分别记为),(),,(0000y x y x -, 其中,500<<x 则,19252020=+y x ……① 直线A 1P ,P 1A 的方程分别为:),5()5(00+=+x y y x ……② ).5()5(00-=-x y y x ……③ ②式除以③式得,555500-+=-+x x x x 化简上式得,250x x =代入②式得,50x y y =于是,直线A 1P 与AP 1的交点M 的坐标为).5,25(0x y x 因为.1)251(2525)5(91)25(25120202020020=--=-x x x x y x所以,直线A 1P 与AP 1的交点M 在双曲线上192522=+y x .19.本小题主要考查函数,不等式等基本知识,考查运用数学知识分析问题和解决问题的能力.满分14分. (Ⅰ)解:设P 的坐标为(0,y ),则P 至三镇距离的平方和为 .146)4(3)12()25(2)(222+-=-++=y y y y f所以,当4=y 时,函数)(y f 取得最小值. 答:点P 的坐标是).4,0((Ⅱ)解法一:P 至三镇的最远距离为 ⎪⎩⎪⎨⎧-<+--≥++=.|12|25|,12||,12|25,25)(222y y y y y y x g 当当由|12|252y y -≥+解得,24119≥y 记,24119*=y 于是 ⎪⎩⎪⎨⎧<-≥+=.|,12|,,25)(**2y y y y y y x g 当当 因为225y +在[),*+∞y 上是增函数,而]y ,(-|12|*∞-在y 上是减函数. 所以*y y =时,函数)(y g 取得最小值. 答:点P 的坐标是);24119,0(解法二:P 至三镇的最远距离为 ⎪⎩⎪⎨⎧-<+--≥++=.|12|25|,12||,12|25,25)(222y y y y y y x g 当当 由|12|252y y -≥+解得,24119≥y 记,24119*=y 于是 ⎪⎩⎪⎨⎧<-≥+=.|,12|,,25)(**2y y y y y y x g 当当 函数)(y g x =的图象如图)(a ,因此,当*y y =时,函数)(y g 取得最小值.答:点P 的坐标是);24119,0(解法三:因为在△ABC 中,AB=AC=13,且,(b).,4,51222如图π=∠=>=-ACB OC OC AC 所以△ABC 的外心M 在线段AO 上,其坐标为)24119,0(, 且AM=BM=CM. 当P 在射线MA 上,记P 为P 1;当P 在射线MA 的反向延长线上,记P 为P 2,这时P 到A 、B 、C 三点的最远距离为P 1C 和P 2A ,且P 1C ≥MC ,P 2A ≥MA ,所以点P 与外心M重合时,P 到三镇的最远距离最小.答:点P 的坐标是);24119,0( 20.本小题考查函数、不等式等基本知识,考查综合运用数学知识分析问题和解决问题的能力.满分14分.(Ⅰ)证明:由题设条件可知,当]1,1[-∈x 时,有,1|1||)1()(||)(|x x f x f x f -=-≤-= 即.1)(1x x f x -≤≤-(Ⅱ)答:函数)(x g 满足题设条件.验证如下:).1(0)1(g g ==- 对任意的]1,1[,-∈v u ,当|;||)1()1(||)()(|,0,1][,u v u v u v g u g v -=---=-∈有时当|;||)()(|,,0]1-[,u v u v g u g v -=-∈同理有时 当0,u <⋅v不妨设],1,0(),0,1[∈-∈v u 有.|||||)1()1(||)()(|u v v u v u v g u g -≤+=--+=-所以,函数)(x g 满足题设条件.(Ⅲ)答:这样满足的函数不存在.理由如下:假设存在函数)(x f 满足条件,则由,0)1()1(==-f f 得,0|)1()1(|=--f f ①由于对任意的]1,1[,-∈v u ,都有.|||)()(|v u v f u f -=-所以,.2|)1(1||)1()1(|=--=--f f ② ①与②矛盾,因此假设不成立,即这样的函数不存在.。

第一学期第一次课第一章 代数学的经典课题§1 假设干准备知识1.1.1 代数系统的概念一个集合,如果在它里面存在一种或假设干种代数运算,这些运算满足一定的运算法那么,那么称这样的一个体系为一个代数系统。
1.1.2 数域的定义定义〔数域〕 设K 是某些复数所组成的集合。
如果K 中至少包含两个不同的复数,且K 对复数的加、减、乘、除四那么运算是封闭的,即对K 内任意两个数a 、b 〔a 可以等于b 〕,必有K b a b K ab K b a ∈≠∈∈±/0时,,且当,,那么称K 为一个数域。
典型的数域举例: 复数域C ;实数域R ;有理数域Q ;Gauss 数域:Q (i) = {b a +i |b a ,∈Q },其中i =1-。
命题 任意数域K 都包括有理数域Q 。
证明 设K 为任意一个数域。
由定义可知,存在一个元素0≠∈a K a ,且。
于是K aaK a a ∈=∈-=10,。
进而∈∀m Z 0>,K m ∈+⋯⋯++=111。
最后,∈∀n m ,Z 0>,K n m ∈,K nmn m ∈-=-0。
这就证明了Q ⊆K 。
证毕。
1.1.3 集合的运算,集合的映射〔像与原像、单射、满射、双射〕的概念定义(集合的交、并、差) 设S 是集合,A 与B 的公共元素所组成的集合成为A 与B 的交集,记作B A ⋂;把A 和B 中的元素合并在一起组成的集合成为A 与B 的并集,记做B A ⋃;从集合A 中去掉属于B 的那些元素之后剩下的元素组成的集合成为A 与B 的差集,记做B A \。
定义〔集合的映射〕 设A 、B 为集合。
如果存在法那么f ,使得A 中任意元素a 在法那么f 下对应B 中唯一确定的元素〔记做)(a f 〕,那么称f 是A 到B 的一个映射,记为).(,:a f a B A f →如果B b a f ∈=)(,那么b 称为a 在f 下的像,a 称为b 在f 下的原像。
目录第一讲逻辑推理初步 (2)第二讲循环小数化分数 (4)第三讲分数计算(一) (10)第四讲分数计算(二) (13)第五讲分数、百分数应用题(一) (17)第六讲分数、百分数应用题(二) (22)第七讲生活中的经济问题 (27)第八讲工程问题 (29)第九讲圆的周长与面积 (32)第十讲不定方程 (40)第一讲逻辑推理初步学习提示:本讲主要是逻辑推理问题,这类问题很少依赖数学概念、法则、公式进行计算,而主要是根据某些条件、结论以及它们之间的逻辑关系进行判断推理,最终找到问题的答案,像这样的问题我们称之为逻辑推理问题。
典型题解下面介绍一些逻辑推理问题以及逻辑推理的基本方法和基本技巧。
例1我国有“三山五岳”之说,其中五岳是指:东岳泰山,南岳衡山,西岳华山,北岳恒山和中岳嵩山。
一位老师拿出这五座山的图片,并在图片上标出数字,他让五位同学来辨别,每人说出两个。
学生回答如下:甲:2是泰山,3是华山乙:4是衡山,2是嵩山丙:1是衡山,5是恒山丁:4是恒山,3是嵩山戊:2是华山,5是泰山。
老师发现五个同学都只说对了一半,那么正确的说法是什么呢?例2甲乙丙三人对小强的藏书数目做了一个估计,甲说:“他至少有1000本书”。
乙说:“他的书不到1000本”。
丙说:“他至少有一本书”。
这三个估计只有一句是对的,那么小强究竟有多少本书?例3从前有三个和尚,一个讲真话,一个讲假话,另一个有时讲真话,有时讲假话。
一天,一位智者遇到这三个和尚,他问第一个和尚:“你后面是哪一个和尚?”和尚回答:“讲真话的”。
他又问第二位和尚:“你是哪一位?”得到的回答是:“有时讲真话,有时讲假话”。
他问第三位和尚:“你前面是哪位和尚?”第三位和尚回答说:“讲假话的”。
根据他们的回答,智者很快分清了他们各自是哪一位和尚,请你说出智者的答案。
例4桌上放了8张扑克牌,都背向上,牌放置的位置如图所示。
现已知:(1)每张都是A、K、Q、J中的一张;(2)这8张牌中至少有一张Q;(3)其中只有一张A;(4)所有的Q都夹在两张K之间;(5)至少有一张K夹在两张J之间;(6)J和Q互不相邻,A和K也互不相邻;(7)至少有两张K相邻。
清北学堂高中7+1课程09暑假数学特训班测试一试题解答一、选择题(满分36分,每一题6分)1. 给定公比为q (q ≠1)的等比数列{a n },设b 1=a 1+a 2+a 3, b 2=a 4+a 5+a 6,…, b n =a 3n -2+a 3n -1+a 3n ,…,则数列{b n } ( C ) (A )是等差数列 (B )是公比为q 的等比数列 (C )是公比为q 3的等比数列 (D )既非等差数列也非等比数2. 在某次乒乓球单打比赛中,原计划每两名选手恰比赛一场,但有3名选手各比赛了2( D ) (A )0 3. ABC 是( B )(A )4. (Db ax +2与解析:b 同号,而由C B ,中一次函数图象知b a ,异号,相矛盾,故舍去C B ,.又由b a >知,当0>>b a 时,1->-ab,此时与A 中图形不符,与D 中图形相符. 故选D 5.直线3-=mx y 与抛物线x m x y C m mx x y C )12(:,45:2221-+=-+=323:,3232--+=-+m mx x y C m 中至少有一条相交,则m 的取值范围是( B ) A 、283-≤≥m m 或 B 、211-≤-≥m m 或 C 、R m ∈ D 、以上均不正确解析:原命题可变为,求方程:m mx x mx 4532-+=-,3)12(322-+-+=-m x m x mx ,32332--+=-m mx x mx 中至少有一个方程有实数解,而此命题的反面是:“三个方程均无实数解”,于是,从全体实数中除去三个方程均无实数解的m 的值,使得所求.即变为解不等式组⎪⎩⎪⎨⎧<--<--<+--,0)2(44,04)1(,0)34(4)4(2222m m m m m m 得 13,故符合条件的m 取值范围是3或, 应选 6 A B C D 提示象P 二.填空题1. 的n 2. 已知点双曲线的两个焦点的距离的等差中项,那么,P 的横坐标是564-. 3. 已知直线ax +by +c =0中的a ,b ,c 是取自集合{-3,-2,-1,0,1,2,,3}中的3个不同的元素,并且该直线的倾斜角为锐角,那么,这样的直线的条数是_43 . 4. 如果1a b c ++=,23.5. 已知,,,,a b c d e 是满足8a b c d e ++++=,2222216a b c d e ++++=的实数解,试求e 最大值516.P R S6. 若[]x 表示不超过x 的最大整数(如[]11.31,234⎡⎤=-=-⎢⎥⎣⎦等等)则1111212323434200420032004⎡⎤⎡⎤⎡⎤⎡⎤++++⎢⎥⎢⎥⎢⎥⎢⎥-⨯-⨯-⨯-⨯⎣⎦⎣⎦⎣⎦⎣⎦=2003.提示: ⎥⎥⎦⎤⎢⎢⎣⎡+⨯-+)1(11n n n =⎥⎦⎤⎢⎣⎡-++)1(11n n n=⎥⎦⎤⎢⎣⎡+++11n n n = ⎥⎦⎤⎢⎣⎡++11n n = 1三.解答题(满分20分) 二次函数()2f x ax bx c =++,()0a <,()11f ≤,()22f ≤,()33f ≤,求:()4f 取最大时()f x 解析式解:()()()()()()()()()()()()11225322112324142339331323f a b c a f f f f a b c b f f f f a b c c f f f ⎧=+==-+⎧⎪⎪=++⇒=-+-⎨⎨⎪⎪=++=-+⎩⎩将其带入()()()()416413233f a b c f f f =++=-+()()()132331323316f f f ≤++≤+⨯+⨯=,取“=”,()11f =-,()22f =,()33f =-(由()0a <确定)4a ⇒=-,15b =,12c =-,此时()241512f x x x =-+-总结:未知和已知建立联系,a b a b a b -≤±≤+ 四. 解答题(满分20分)设二次函数的图象以y 轴为对称轴,已知,而且若点在的图象上,则点在函数的图象上。