第3章静定结构的

1、超静定结构的特性：与静定结构比较，超静定结构有如下特性：内力超静定，约束有多余，是超静定结构区别于静定结构的基本特点。

2、超静定次数的确定：结构的超静定次数为其多余约束的数目，因此上，结构的超静定次数等于将原结构变成静定结构所去掉多余约束的数目。

在超静定结构上去掉多余约束的基本方式，通常有如下几种：（1）断一根链杆、去掉一个支杆、将一刚接处改为单铰联接、将一固定端改为固定铰支座，相当于去掉一个约束。

举例（2）断一根弯杆、去掉一个固定端，相当于去掉三个约束。

举例（3）开一个单铰、去掉一个固定铰支座、去掉一个定向支座，相当于去掉两个约束。

举例返回顶部3、几点注意：①由图10-1结构的分析可得出结论：一个无铰闭合框有三个多余约束，其超静定次数等于三。

对于无铰闭合框结构其超静定次数=3×闭合框数。

如图10-2所示结构的超静定次数为3×5=15次；对于带铰闭合框结构其超静定次数=3×闭合框数－结构中的单铰数（复铰要折算成单铰）如图10-3所示结构的超静定次数为3×5-（1+1+3）=15次。

D点是连接四个刚片的复铰，相当于（4-1）=3个单铰。

②一结构的超静定次数是确定不变的，但去掉多余约束的方式是多种多样的。

如图10-1结构。

③在确定超静定次数时，要将内外多余约束全部去掉。

如图10-4结构外部1次超静定，内部6次超静定，结构的超静定次数是7。

④在支座解除一个约束，用一个相应的约束反力来代替，在结构内部解除约束，用作用力和反作用力一对力来代替。

如图10-1结构所示。

⑤只能去掉多余约束，不能去掉必要的约束，不能将原结构变成瞬变体系或可变体系。

如图10-4结构中A点的水平支杆不能作为多余约束去掉。

如图10-5结构中支杆a,b和链杆c不能作为多余约束去掉，否则就将原结构变成了瞬变体系。

返回顶部1、超静定结构的求解思路：欲求解超静定结构，先选取一个便于计算结构作为基本体系，然后让基本体系与原结构受力一致，变形一致即完全等价，通过这个等价条件去建立求解基本未知量的基本方程。

《材料力学》课程教案2（二）拉伸、压缩的超静定问题设教学安排 ● 新课引入如图所示的两杆组成的桁架结构受力，由于是平面汇交力系，可由静力平衡方程求出两杆内力。

如果为了提高构件安全性，再加一个杆，三杆内力还能由静力平衡方程求出吗？● 新课讲授一、 静定结构（一）提出问题1和2两杆组成桁架结构受力如图所示，角度已知，两杆抗拉刚度相同，2211A E A E =，求两杆中内力的大小。

（二）分析：求内力⇒截面法（1截2代3列平衡方程）⇒=∑0x 021=-ααSin F Sin F N N ⇒=∑0y 0321=-++F F Cos F Cos F N N N αα 两个方程，两个未知数，可以求解。

引出静定结构：约束反力(轴力）可以由静力平衡方程完全求出。

二、 超静定结构和超静定次数（一）继续提问在现实中为了增加构件的安全性，往往可以多加一个杆，在问题一的基础上在中间再加一个3杆，抗拉刚度为33A E ，如图所示，求3杆中内力的大小。

（二）分析：求内力⇒截面法（1截2代3列平衡方程） ①静平衡方程：平面汇交力系，只能列两个平衡方程⇒=∑0x21=-ααSin F Sin F N N⇒=∑0y 0321=-++F F Cos F Cos F N N N αα 两个方程，三个未知数，解不出。

引出超静定结构：约束反力(轴力）不能由静力平衡方程完全求出。

超静定次数：约束反力（轴力）多余平衡方程的个数。

上述问题属于一次超静定问题。

三、超静定结构的求解方法（一）继续提问，引导学生深入思考：超静定到底能不能求解？实际上F 一定，作用于每个杆上的力都是确定的。

还需再找一个补充方程，材料力学是变形体，受力会引起变形，力和力的关系看不出， 先把变形关系找到，再转化成力的关系。

（重点）②几何方程——变形协调方程：要找变形关系，关键是画变形图（难点）。

节点在中间杆上，左右两杆抗拉刚度相同，角度相同，即对称，因此中间杆仅沿竖直方向产生伸长，确定最终位置。

结构力学静定结构与超静定结构结构力学是研究结构承受外力后的力学性能的学科，它在建筑、机械、航空航天等领域都扮演着重要的角色。

在结构力学中，我们可以将结构分为两类：静定结构和超静定结构。

静定结构是指在确定边界条件下，结构的所有支反力以及结构内部的应力分布等参数都可以通过静力平衡方程唯一求解出来的结构。

在静定结构中，支反力的计算可以通过平衡方程解决，而应力的计算可以通过弹性力学理论求解。

以简支梁为例，简支梁的两端固定支承，中间用力作用时，通过平衡方程可以求解出支反力。

而根据梁的几何形状和荷载的大小，可以计算出梁内部的应力分布。

在静定结构中，支反力和应力可以通过简单的数学计算求解，因此设计和分析起来相对简单。

而超静定结构则相对复杂一些。

超静定结构是指在确定边界条件下，结构的参数无法通过静力平衡方程唯一求解出来的结构。

这意味着在求解超静定结构时，不仅需要静力平衡方程，还需要考虑结构的变形和材料的本构关系等。

以悬臂梁为例，悬臂梁的一端固定支承，另一端悬空。

在悬臂梁上增加一个附加支承，形成一个超静定结构。

在这种情况下，由于支承力未知，无法通过静力平衡方程唯一求解出来。

因此，我们需要考虑结构的变形情况，并将其作为一个未知数来求解。

在超静定结构中，我们通常采用的方法是引入截面变形理论和力法。

通过假设结构具有一定的变形形态，并利用力法求解出结构的变形、应力和支反力等参数。

通常情况下，超静定结构的计算需要较为复杂的数学方法和计算机仿真。

静定结构和超静定结构在工程实践中都有广泛的应用。

静定结构常常用于桥梁、楼房等普通建筑结构的设计与分析中，因其计算相对简单，容易掌握。

而超静定结构常常用于大跨度的特殊结构的设计与分析中，如悬索桥、曲线梁等。

虽然超静定结构计算较为复杂，但可以提供更多的设计自由度和结构优化的可能性。

总而言之，静定结构和超静定结构都是结构力学中的重要概念。

静定结构是可通过静力平衡方程求解出内部参数的结构，而超静定结构则需要额外的变形理论和力法求解。

第3章 静定梁和静定刚架（知识点小结）一、杆件内力分析方法1、内力分量轴力N F 是横截面上的应力沿截面法线方向的合力，一般以拉力为正，压力为负。

剪力S F 是横截面上的应力沿截面切线方向的合力，以绕截面处微段隔离体顺时针方向转动为正，反之为负。

弯矩M 是横截面上的应力对截面形心取矩的代数和，一般不规定正负号。

有时按习惯也可规定，在水平杆件中弯矩使杆件截面的下侧纤维受拉时为正，上侧受拉时为负。

2、截面法截面法是计算指定截面内力的基本方法，即沿指定截面假想将结构截开，切开后截面内力暴露为外力，取截面左侧（或右侧）作为隔离体，作隔离体受力图，建立平衡方程，从而可确定指定截面的内力。

由截面法可得截面上三个内力分量的运算规则如下：（1）轴力N F 等于截面左侧（或右侧）的所有外力（包括支座反力）沿截面法线方向的投影代数和；（2）剪力S F 等于截面左侧（或右侧）的所有外力（包括支座反力）沿截面切线方向的投影代数和；（3）弯矩M 等于截面左侧（或右侧）的所有外力（包括支座反力）对截面形心取矩的代数和。

3、内力图内力图表示结构上各截面的内力随横截面位置变化规律的图形，包括M 图、S F 图和N F 图。

内力图用平行于杆轴线方向的坐标表示横截面位置（又称基线），用垂直于杆轴线的坐标（又称竖标）表示相应截面的内力值。

轴力图、剪力图中，竖标正、负值分别画在杆件基线的两侧，要标明正负号；弯矩图画在杆件的受拉侧，不标正负。

内力图要画上竖标，标注某些控制截面处的竖标值，并写明图名和单位。

4、内力图的形状特征直杆段上内力图的形状特征归纳如表3-1所示。

熟练掌握内力图的这些形状特征，对于以后正确、迅速地绘制内力图、校核内力图是非常有帮助的。

5、区段叠加法作M图对承受横向荷载作用的任意结构中直杆段，都可采用区段叠加法作其弯矩图：先采用截面法求出该段两个杆端截面弯矩值并将其连以一虚线，然后以此虚线为基线，叠加相应简支梁在跨间相应荷载作用下的弯矩图，如图3-1所示。

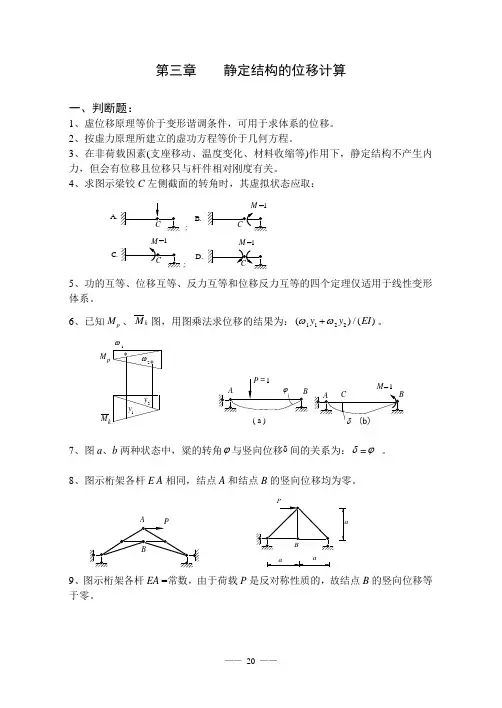
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;;B.D.C.M =1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M kM p21y 1y 2**ωω( a )M 17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q11、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数 ，a = 2m 。

10kN/m12、求图示结构E 点的竖向位移。

EI = 常数 。

ll l /32 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P14、求图示刚架B 端的竖向位移。

q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

E I = 常数。

qll l/l/2219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。

l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。

ll21、求图示结构B点的竖向位移，EI = 常数。

ll22、图示结构充满水后，求A 、B 两点的相对水平位移。

超静定结构的特性
超静定结构有下面几点主要特性
(一)同时满足超静定结构的平衡条件、变形协调条件和物理条件(力与变形的对应关系)的超静定结构内力的解是唯一真实的解。

力法和位移法的解题方法虽然不同，但在这两个基本方法中，却都综合应用了结构的平衡条件、几何条件和物理条件。

(二)超静定结构在荷载作用下的内力与各杆EI、EA的相对比值有关，而与各杆EI、EA的绝对值无关。

因此，在设计超静定结构之前，必须预先假定各杆的截面尺寸、选定材料的类别。

待内力求出后，再复核截面尺寸，若截面尺寸不合理，还要重复计算。

快把结构工程师站点加入收藏夹吧！
另外，也可以通过改变各杆刚度比值的办法来达到调整结构内力分布的目的。

(三)超静定结构在/考试大/非荷载因素(温度变化、杆件制造误差、支座位移等)作用下会产生内力(这种内力状态有时称为自内力状态)，且这种内力与各杆EI、EA的绝对值有关(成正比)。

因此，为了提高结构对温度变化、支座位移等因素的抵抗能力，增大结构截面尺寸并不是有效的措施，为了减小自内力的不利影响，可以采用设置温度缝、沉降缝等构造措施。

(四)超静定结构由于存在多余约束，故它与相应的静定结构比较而言，超静定结构的内力分布较为均匀，刚度和稳定性都有所提高。

静定和超静定的知识点梳理《静定和超静定的知识点梳理》嗨，小伙伴们！今天咱们来聊聊静定和超静定这两个听起来有点复杂，但是特别有趣的知识点哦。

我先来说说静定结构吧。

静定结构就像是搭积木一样，只要你知道了几个关键的部分，整个结构的情况就完全清楚啦。

比如说，一个简单的三角形的架子，就像我们在公园里看到的那种小亭子的框架，它是静定结构。

有三根杆件组成一个三角形，你只要知道这三根杆件的长度、材质这些基本信息，这个三角形架子的受力情况、能不能稳稳地立在那儿，你就都能搞明白。

这就好比你知道了做一个小蛋糕需要多少面粉、多少糖、多少鸡蛋，按照这个配方做出来的小蛋糕肯定不会出问题，对吧？在静定结构里，我们可以用一些简单的力学方法来分析。

就像我们在玩跷跷板的时候，你要是知道了两边人的重量，还有跷跷板的长度，就能算出两边是会平衡呢，还是会向哪一边倾斜。

这和分析静定结构里力的平衡是一个道理呀。

可是超静定结构就不一样喽。

超静定结构就像是一个神秘的大迷宫，光知道几个简单的信息可不够。

我给你们举个例子吧，像那种有好多柱子和横梁的大房子，它的结构就是超静定的。

为啥呢？因为它的杆件太多啦，你要是只知道几根柱子和横梁的信息，根本没法搞清楚整个房子的受力情况。

这就好像你要去一个超级大的游乐场，只知道一两个游乐设施的位置，你能说你了解整个游乐场吗？肯定不能呀！超静定结构比静定结构要复杂得多。

在超静定结构里，会有多余的约束。

这多余的约束是啥呢？就好比你本来已经把东西都固定得好好的了，但是你还非要再加上几个绳子或者夹子去固定它。

在超静定结构里，这些多余的约束会让力的分析变得超级复杂。

我问你们啊，如果有一堆乱七八糟的线缠在一起，你是不是觉得很难把它们分开？超静定结构里的力就像这些缠在一起的线一样，让人头疼。

我记得有一次，我和我的小伙伴们一起做一个小手工，是做一个小桥架模型。

我们最开始想做一个静定结构的桥架，就按照书上的简单方法，用几根小木棒搭起来。

超静定结构的特征：
超静定结构的特征主要包括以下几点：
1.具有多余约束：超静定结构相对于静定结构，具有多余的约束，这些多余约束不是维持体系几何
不变所必需的。

2.具有几何不变性：超静定结构在去掉多余约束后，仍然是一个几何不变体系，即受到外力作用时，
其整体和局部的形状和大小都不会发生变化。

3.受力状态复杂：超静定结构的支座反力和截面内力不能完全由静力平衡条件唯一确定，因此其受
力状态相对较为复杂。

4.结构形式多样：超静定结构的样式非常多样，包括连续梁、刚架、拱、薄壳等，这些结构都可以
通过添加多余约束来转化为超静定结构。

5.稳定性好：由于超静定结构的内力分布比较均匀，因此其稳定性较好，在受到外力作用时不易发
生失稳现象。

6.调整能力强：超静定结构的内力可以通过改变多余约束的约束力进行调节，因此其调整能力较强。

常见的超静定结构形式
1. 平衡树：平衡树是一种特殊的二叉查找树，它在每个节点左右子树的高度最多相差一，也就是说每个节点的子树中叶子节点分布平衡，它可以在O(logN)时间内完成插入，删除，查找操作。

2. AVL树：AVL树也是一种特殊的二叉查找树，它具有以下特性：1）每个节点的左右子树的高度最多相差1；2）每个节点的左右子树的高度最多相差1；3）它可以在O(logN)时间内完成插入，删除，查找操作。

3. 红黑树：红黑树也是一种特殊的二叉查找树，它具有以下特性：1）每个节点的左右子树的高度相等；2）每个节点的子节点不允许相互交叉；3）它可以在
O(logN)时间内完成插入，删除，查找操作。

4. 哈夫曼树：哈夫曼树是一种最优查找树，它的每个节点的权重符合最优性原理。

哈夫曼树的最坏情况的查找时间复杂度是O(logN)。

;。

三次超静定力法方程
三次超静定力法方程是一种结构力学中经常使用的求解问题的
方法。

该方法是在超静定的前提下，使用三次多项式的形式来表示结构的位移场，并且根据平衡条件和边界条件，推导出三次超静定力法方程，从而求解结构的内力和反力等问题。

三次超静定力法方程的推导可以分为以下几个步骤：
1. 建立位移场模型
首先，根据结构的几何形状和加载条件，建立结构的位移场模型。

在三次超静定力法中，通常使用三次多项式的形式来表示位移场，即：
u(x) = a0 + a1*x + a2*x^2 + a3*x^3
其中，u(x)表示结构在x处的位移，a0、a1、a2、a3是待定系数。

2. 推导内力和反力的表达式
然后，根据平衡条件和边界条件，推导出内力和反力的表达式。

平衡条件可以表示为：
d^2u(x)/dx^2 = q(x)
其中，q(x)表示结构的分布载荷。

边界条件可以表示为：
u(0) = u0, u(L) = uL, M(0) = M0, M(L) = ML
其中，u0、uL分别是结构两端的位移，M0、ML分别是结构两端的弯矩。

3. 求解待定系数
最后，将位移场模型和内力、反力的表达式代入边界条件中，得到一组方程组，通过求解待定系数，就可以得到结构的内力和反力等信息。

三次超静定力法方程的优点是相对简单易懂，适用于中小型结构的分析计算，尤其是在计算机不普及的年代，是一种非常有效的手算方法。

但随着计算机的广泛应用，更加复杂的结构分析问题或者超静定问题的求解，需要更加高级的数值方法和软件支持。