当前位置：文档之家 › 超静定结构的解法ppt课件

超静定结构的解法ppt课件

  • 格式：ppt
  • 大小：1.58 MB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

超静定结构解法力法.pptx

超静定结构解法力法.pptx

P
EI
EI
l
P
解:
X1
l
X1=1
Pl
P
1 0
11 X1 1P 0 11 l 3 / 3EI
1P Pl 3 / 2EI
X1 3P / 2()
M M1 X1 M P
l
M1
Pl
MP
第8页/共21页
3 Pl M 2
力法基本思路小结
解除多余约束，转化为静定结构。多余约 束代以多余未知力——基本未知力。
分析基本结构在单位基本未知力和外界因 素作用下的位移，建立位移协调条件——力 法方程。
从力法方程解得基本未知力，由叠加原理 获得结构内力。超静定结构分析通过转化为 静定结构获得了解决。
第9页/共21页
将未知问题转化为 已知问题，通过消除已 知问题和原问题的差别， 使未知问题得以解决。 这是科学研究的 基本方法之一。
X1
X2
X3
X1
X2
X3
去掉一个链杆或切断 一个链杆相当于去掉 一个约束
X1 X2
X3
第12页/共21页
X2 X1
X3
X3
X2 X1
X3 X1
X1 X2 X3
X2
去掉一个固定端支 座或切断一根弯曲 杆相当于去掉三个 约束.
将刚结点变成铰结 点或将固定端支座 变成固定铰支座相 当于去掉一个约束.
几何可变体系不能 X3 作为基本体系
M
1 0
1 11 1P 0
11 X1 11
力法 方程
11 X1 1P 0
1 11 l 3 / 3EI
1P ql 4 / 8EI
X1 3ql / 8() M M1 X1 M P

超静定结构的计算.ppt

超静定结构的计算.ppt
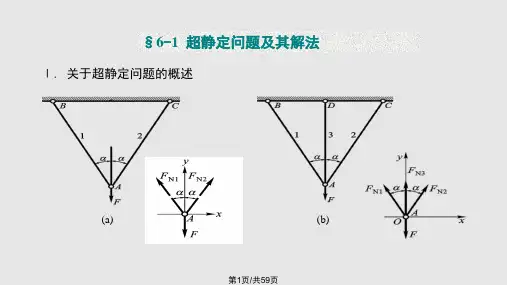
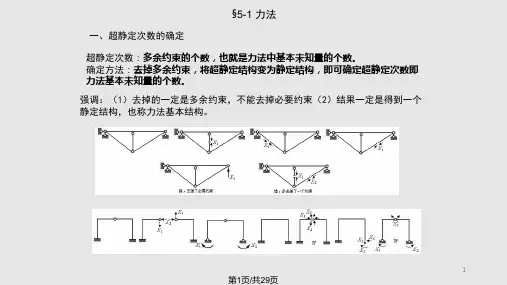
上一页 下一页 返回
第二节力法
若基第用本一△结个构下1q和在标△表X11示1作分位用别移处表发沿示生X荷1的方载地向、点产和与生多方的余向位未，移知第(力符二X号个1单△下独1q标和作表△用示1下1中引 起位移的原因)，则由叠加原理根据位移条件可得下列方程:
△1= △11+ △1q=0 是若上X1式=可1时以在写X成1方: 向产生的位移为11 ，则有 11 11X1，于
二、力法的典型方程 由力法基本原理可知，用力法计算超静定结构的关键在于
根据位移条件建立力法的基本方程，求解多余力。对于多次 超静定结构，其计算原理与一次超静定结构完全相同。下面 以一个三次超静定结构来说明力法解超静定结构的典型方程。 图15-12 (a)所示为一个三次超静定刚架，荷载作用下结构 的变形如图中虚线所示。这里我们取基本结构如图15-12 (b) 所X3示代，替去。掉固定支座C处的多余约束，用基本未知量X1、X2、 由于原结构C为固定支座，其线位移和转角位移都为零。 所X2以、，X3基方本向结的构位在移荷都载等及于X零1、，X即2、基X本3结共构同的作儿用何下位，移C点条沿件X为1、:
上一页 下一页 返回
第二节力法
第一式中△1q、△11、△12、△13分别为荷载q及多余未知力X1、 X2, X3分别作用在基本结构上沿X1方向产生的位移，如果
用结构11、上产12生、的1沿3 表X1示方单向位的力相X应1=位1移, X，2=如1,X图3=151-分12别(c作),(用d)于, (基c),本(d)


n nq n1X1 n2 X 2 n3 X 3 nn X n 0(15-4)
力法典型方程的物理意义是:基本结构在全部多余未知力和

超静定结构内力计算.pptx

超静定结构内力计算.pptx

μ
MBC= 0.429×(－24) = －10.3kNm
传递弯矩：
c MCB= 0
c
MAB= 0.5×(－13.7) = －6.85kNm
最后杆端弯矩：
MCB= 0
MAB= MFAB＋ MCAB = －66.85kNm
MBA= MFBA＋ MμBA = 46.3kNm
MBC= MFBC＋ MμBC = －46.3kNm
M
f AB
3 16
Pl
1 ql2 8
A
B
P A
3 Pl 16
B
M
f BA
3 16
Pl
1 ql2 8
A
B
M
f AB
1 8
ql 2
M
f BA
1 8
ql 2
第17页/共24页
1、计算各杆的固端 弯矩Mf
MfAB=0
M
f BA
1 8
ql 2=1/8×4×62=18
MfBC=-1/8PL=-1/8×30×6=-22.5 MfCB=1/8PL=1/8×30×6=22.5
所以，结点角位移的数目 等于该结构的刚结点数！
由于A、B、C为固定端支座，所以 其位移均已知为零，不需作为未知量； 而同一刚结点处各杆的杆端转角相等， 所以每个刚结点处只有一个独立的结 点转角未知量。故上图刚架只有一个 结点转角未知量。
第5页/共24页
2、独立结点线位移
在微弯状态下，假定受弯直杆两端之间距离在变形 前后保持不变，即杆长保持不变。
A
SAB = 3 i
B
A
SAB = i
θ =1
= B
A
B
当θ ≠ 1时: MAB = SAB θ

超静定问题PPT课件

超静定问题PPT课件

FN1 cos FN2 cos FN3 F 0
FN1
FN 3
EA cos2
E3 A3
FN3 1 2
F EA
cos2
E3 A3
FN1
FN 2
1 2cos
F
E
E3 A3
A cos2
第13页/共59页
B 1
1
Δl3
D
3
C 2
A
3 F2
A
Δl1A' NhomakorabeaFA A C
F
B FB
14
b
a
l
第六章 简单的超静定问题
例题2 求图a所示等直杆AB上,下端的约束力， 并求C截面的位移。杆的拉压刚度为EA。
解: 1. 列平衡方程 有两个未知约束力FA , FB(见图a)，但只有一个独 立的平衡方程
FA+FB-F=0 为一次超静定问题。
第14页/共59页
2. 取固定端B为“多余”约束。相应 的相当系统如图b，它应满足相容条件 ΔBF+ΔBB=0，参见图c，d。
MA 0
F a F 2a 0
A
B
P
FN1 a
A
FN2 a
FN3 B
P
第17页/共59页
变形协调方程：
ΔL 1
L1 L3 2(L2 L3 ) （2）
物理方程：
l1
FN 1l EA
l2
FN 2l EA
l3
FN 3l EA
（3）
联解（1）（2）（3）式得：
F 5P 6
F
2
1 3
P
F
3
1 6
D
由位移相容条

结构力学超静定结构的内力和位移计算PPT课件

结构力学超静定结构的内力和位移计算PPT课件
5
第5页/共29页
力法方程中的柔度系数与自由项，都是力法基本结构在已知力作用下的位 移，相应的计算公式为
dii
M
2 i
ds
EI
FN2i ds EA
kFS2i ds GA
dij d ji
MiM j ds EI
FNi FNj ds EA
kFSi FSj ds GA
FNitl
Dt h
M i ds
13
第13页/共29页
例题5-7. 图示刚架，外侧温度升高20oC，内侧温度升高30oC，试用力法求解并作出M图。已 知杆件横截面为矩形截面，高度h=l/10，EI=常数，材料线膨胀系数为。
原结构
力法基本结构
FN1
M1
M图
d11 X1 D1t 0
d11
1 EI
(1 l 2
d n1 X1 d n2 X 2 d nn X n DnP Dn 0
对于力法典型方程，应注意理解与掌握以下几点： (1) 力法典型方程的物理意义，是多余约束处的位移方程； (2) dij称为结构的柔度系数，其定义是j方向的单位力引起的i方向的位移，第1个下标表示 发生位移的位置，第2个下标表示产生位移的原因。位移互等定理，dij=dji。主柔度系数必 为正，即dii>0。副柔度系数dij可为正、负或0。柔度系数为结构的固有特性，与荷载等外 界因素无关； (3) 自由项DiP的物理意义是，荷载单独作用在力法基本结构上产生的沿Xi方向的位移，可 为正、负或0； (4) 力法方程也称为柔度方程，力法也称为柔度法；
D1P
X1 2d EA
FN
若将上弦杆DE去掉，其基本结构如示。此时，在X1与荷载共同作用下，D、E两点沿轴方向的相对线位移不

§8-7 超静定结构各类解法的比较和合理选用PPT教学课件

§8-7 超静定结构各类解法的比较和合理选用PPT教学课件
§8-7 超静定结构各类解法的比较和合理选用
1.超静定结构的解法
基本解法
力法 —— 未知量数为超静定次数 位移法—— 未知量数为结点位移数
由位移法派生
力矩分配法—— 解无移刚架
剪力分配法—— 解纯侧移刚架
技巧解法 —— 灵活应用刚、柔度概念和串并联技巧求解
4
2020/12/10
1
2. 各种解题方法的优势比较 （1）超静定桁架 —— 宜用力法 （2）两铰拱、无铰拱 —— 宜用力法 （3）连续梁 —— 宜用力矩分配法 （4）超静定刚架 —— 视结构情况具体分析
位移法： 未知量n＝4
力法： 未知量n＝1
2020/12/10
位移法： 未知量n＝1
力法： 未知量n＝6
2
Fp
EI1=
I
I
求作M图 —— 宜用剪力分配法
h 求侧移： —— 灵活应用刚、柔度概念 和串并联技巧求解
P
i3
i3
i2
i2
i1
i1
2020/12/10
求作M图 —— 宜用剪力分配法
求侧移： —— 灵活应用刚、柔度概念 和串并联技巧求解
3
PPT教学课件
谢谢观看
Thank You For Watching

力法求解超静定结构ppt课件

力法求解超静定结构ppt课件

2a


9a 3 EI
1P
23


1 EI
2ma 2a

4ma 2
EI
由 11 X1 1P 0 得
X1

4m 9a
RA

RC

4m 9a
mA

mB

m 逆时针
3
24
等截面平面框架的受力情况如图所示。试 求最大弯矩及其作用位置。
25
1P

0
得
X1

qa 16

XB

qa 16
,
YB
9qa 16

21
XA

qa ,
16
YA
7qa 16

等截面梁的受力情况如图所示。试求Ａ、 Ｂ、Ｃ三处的约束力。
22
M10 图
MP图
由反对称性知，B支座约束反力RB 0
11

1 EI
9a2 2
解除多余约束后得到的静定结构，称为原 静不定系统的静定基本系统，或相当系统。
（本章主要用力法解超静定结构）
4
补充-2 力法解超静定结构
在求解静不定结构时，一般先解除多余 约束，代之以多余约束力，得到基本静定系。 再根据变形协调条件得到关于多余约束力的补 充方程。这种以“力”为未知量，由变形协调
条件为基本方程的方法，称为力法。
X1

3qa 16

XC

3qa 16
，YC

0，M C

0
X A ()

X B ()

超静定结构的分析幻灯片PPT

超静定结构的分析幻灯片PPT

A
B
(c)
x2
A
B
(d)
x1
A
B
(e)
将各因素单独作用基本结构的位移
叠加，得：
1 11 21P1 21222P 2
(a)
引入位移影响系数,并代入位移条件， 式(a)写成：
1x 1112 x21p0
(b)
2x 1122 x22p0
式(b)既是两次超静定结构在荷载作 用下的力法方程。
2、次超静定结构的力法方程（力法 典型方程）
B A
L
(a)
解：
1)判定梁的超静定次数，并确定相应的力 法基本体系。见图(b)。
x1
x2
A
B
(b)基本体系
2)写力法方程。
1x 1112 x21p0
(a)
2x 1122 x22p0
3)求力法方程中的系数和自由项。
（1）作基本结构分别在各多余力及荷载作用 下的弯矩图。见图(c)、(d)、(e)。
使 11 = 11x1 式(b)改写成：
11x1 + 1P 0
=
(c)
力法基本方程，是基本结构上多余力 处沿多余力方向的位移与原结构一致 的条件。即位移条件。
例8-1-1 试用力法计算图(a)所示超静定梁， 并作梁的弯矩图。
q
A
B
(a)原结构
解： 1)取基本体系如图(b)。 q
A
B
x1
(b)基本体系
1
55 21 2 1.7 6
1 1 E [1 A 1 (3 ) 2 ( 6 ) 6 () 5 ] E (2 I 2 4 3 2 )EI
1 1 2 214 0 2 1 2.6 67 6
1 P E (2 I 2 44 0 3 2 3

1超静定结构的解法PPT课件

1超静定结构的解法PPT课件

(2) 三刚片法则（三角形法则）： 三刚片用不共线的三个铰两两相连 ，可组 成一个 无多余 约束的 几何不 变体系 。
(3) 二元体法则： 在一个体系上增加或拆除二元体， 不改变 原体系 的几何 组成性 质。
第16页/共35页
8.1 超静定结构及超静定次数的确定
判定下列结构的超静定次数：
课堂练习 ：
M
0 i
(
x)、M
0 j
(
x)——为单位力X
i
1、X
j
1单独作用时，静定基的弯矩;
M P (x)——荷载单独作用时，静定基的弯矩;
第27页/共35页
8.2 力法和典型方程
n次超静定结构：
d11X1 d12 X 2 d1n X n D1P 0 d21X1 d22 X 2 d2n X n D2P 0
4. 去掉一个固定端支座相当于解除3 个约束 ；
5. 切断一 根梁（ 杆）或 切开一 个闭合 框相当 于解除 3 个约束;
第13页/共35页
8.1 超静定结构及超静定次数的确定
判定下列结构的超静定次数：
课堂练习 ：
3
3
3 3
n 12
2 3 1
第14页/共35页
n6
8.1 超静定结构及超静定次数的确定
B
∆B=0
原结构:
B
X1
B
D1P
静定基:
∆11 +∆1P=∆B=0 3、建立方程：
q单独作用下: ∆1P
X1
单独作用下: ∆11
∆11 =δ11X1
D11
B
d11
X1
设δ11 ：单位多余力作用下，静定基 在去掉多余约束处的位移；

超静定结构内力计算不错讲义.pptx

超静定结构内力计算不错讲义.pptx
余未六知力、引超起静。 定结构的位移计算
超静定结构的力法计算的基本思想是利用静定的基本体系来计算多余未知力， 基本体系的内力、变形与原来超静定结构完全相同。因此，在求解超静定结构的位移
时，仍可以借助于基本体系，把已求出的多余力当作主动力来看待，采用前面的静定
结构求位移的方法即可以求出基本体系的位移，该位移也就是原来超静定结构中相应
X1
3EI l2
(
a) l
(3) 求内力。原超静定结构内力与基本体系相同，而支座移动在基本体系(静定结
构)中不引起内力，所以最后弯矩为：
M＝ M i X i
i
第15页/共52页
力法
原结构的弯矩图如图6.13(e)所示。 由此可以看出，计算超静定结构由于支座移动引起的内力时，其力法方程右端 项应等于原结构相应处的位移，而自由项为基本结构由于支座移动产生的与多余未知 力相应的位移。该两项可直接由基本结构中变形关系求出。结构的最后内力全部由多
力法
下面结合具体例子说明力法的运用。 【例6.2】 用力法计算如图6.10(a)所示的刚架，各杆的EI 相等且为常数，绘制内力图。
图6.10 超静定刚架
解 (1) 由几何组成分析知，该结构是二次超静定结构，去掉处的两个多余约束， 得到基本结构，如图6.10(b)所示。
第10页/共52页
力法
(2) 由已知点的位移条件，列出力法的典型方程：
第5页/共52页
力法
△1 ＝0 ，
△2＝0
图6.9 力法解二次超静定刚架
第6页/共52页
力法
设各单位未知力X1=1、X2=1 和荷载分别作用于基本结构上，A点沿X1 方向的位 移分别为δ11、 δ12、 △1P ；沿X2 方向的位移分别为δ21、 δ22、 △2P (如图6.9(c)、(d)、 (e))所示。根据叠加原理，上述位移条件可表示为：

超静定结构的解法PPT(力法)

超静定结构的解法PPT(力法)

C 11X1 1C 0 iC RiC
例. 求图示梁由于支座移动引起的
内力.
解：
12
0 0
11X1 12 X 2 1C 0 21X1 22 X 2 2C 0
12 21 0
11
l3 12 EI
22
l EI
l/2
EI
l
X1
X2 X1 1
l
1C 2
2C
M1
X1
6
EI l2
1C=0 2C=0 3C=0
X3 X1 X2
l
X1 1
11X1 12 X 2 13 X 3 1C 0 21X1 22 X 2 23 X 3 2C 0 31X1 32 X 2 33 X 3 3C 0
X3 X1 X2
1C [1 b (l ) ] l b
0
11
1
1
X2 1
0
0
X3 1
0 2C a
3C
0
支座移动时,结构中的位移以及 位移条件的校核公式如下:
i
Mi Mds EI
iC
Mi M造长了1cm,如何作弯矩图?
A
10m 10m
X3 X1 X2
第四章 超静定结构的解法
Methods of Analysis of Statically Indeterminate Structures
4.2 力法(Force Method)
一.力法的基本概念 二.力法的基本体系与基本未知量 三.荷载作用下超静定结构的计算 四.对称性 (Symmetry) 的利用 五.温度变化时超静定结构的计算
h
Mi
M
温度低的一侧受拉。
4.2 力法(Force Method)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
和杆件内力，这种结构称为超静定结构。
8.1 超静定结构及超静定次数的确定
超静定结构的特性：
1.超静定结构是具有多余约束的几何不变体系，求解内力 必须考虑变形条件。
2.超静定结构的内力与材料的物理性质和截面的几何性质有关。 （EI）
3.超静定结构在支座移动、温度改变等因素下，会产生内力。
4.超静定结构的局部位移和内力比静定结构小。
A
FB
C
A
FB
C
8.1 超静定结构及超静定次数的确定
超静定次数的确定：
超静定次数=多余约束的个数 确定方法：如果从原结构中去掉n个约束后，结构成为静 定结构，则原结构的超静定次数=n
B
B X1
n 1
A
A
X 1 ——多余约束力
静定基：超静定结构解除多余约束后得到的几何不变体，称 为该超静定结构的静定基。
力法的基本思路：
1. 解除多余约束，使之成为静定结构——静定基； 2. 在静定基上施加与多余约束相对应的多余力——基本
未知量； 3. 应用变形条件求解多余约束力。
8.2 力法和典型方程
力法的基本思路：
q
解: 1、确定静定基 2、分析位移条件:B点处
原结构
A
B
l
原结构: ∆B=0
q
静定基:
q单独作用下:∆1P
δ11 X1+∆1P=0 ——力法方程
原结构
A
静定基
A
q
A
l
B
l
5、解方程求X1
q
B
X1
X1
D1P
d11
3 ql 8
BБайду номын сангаас
6、求原结构的反力和内力
3 ql
反力:根据整体平衡求支座反力
8
ql2 / 8
内力:
M

M
0 1
X1

M
P
M图
ql2 / 8
M
A

l

3 8
ql

1 2
ql 2


1 8
ql2 (上拉）
力法的基本思路：
d11
A
B X1=1
M10图
l
M10图
l
X1=1 X1=1
q
B
A
D1P
ql2 / 2
MP图
M10图 l
X1=1
δ11 X1+∆1P=0 ——力法方程
δ11：系数
∆1P：自由项
4、求系数δ11 和自由项∆1P
d1设 在1 δ去1l1掉M：1多0单(余x位E) 约IM多束10余(处x力) d的作x位用移E1下I；，l22静定23l基
X1 X1
可变体系 X1
静定基不唯一
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况： 2. 在杆件内添加一个铰，相当于解除一个约束；
X3
X1
X2
也称：刚结点（刚性联结）变铰结点相当于解除一个约束；
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况： 3.去掉一个固定铰支座,或拆开一个单铰相当于解除 两个约束；
静定基
A A A
B
X1
q
B
D1P
D11
B X1
d11
X1单独作用下:∆11 ∆11 +∆1P=∆B=0 3、建立方程： ∆11 =δ11X1
设δ11 ：单位多余力作用下，静定基 在去掉多余约束处的位移；
δ11 X1+∆1P=0 ——力法方程
A
B X1=1
δ11：系数
∆1P：自由项
8.2 力法和典型方程
8.1 超静定结构及超静定次数的确定
课堂练习： 判定下列结构的超静定次数：
(a) 1次 (c) 1次
(b) 2次
(e) 1次
(f) 3次
(c) 4次
(g) 3次
(i) 4次
(h) 9次
8.2 力法和典型方程
8.2 力法和典型方程
力法：以力为未知数求解超静定问题的方法。
求解超静定问题的方法有多种，力法是最基本、也是历史最悠 久的一种。它是以多余约束力为未知数，列出变形补充方程求解 后，其他未知力和变形等就可按静定结构来计算。
8.1 超静定结构及超静定次数的确定
超静定次数的确定：
超静定次数=多余约束的个数 超静定结构根据解除约束的不同可以有多种静定基。
X1 X1 X2 X2 X3 X3
n3
n 3 X1 X1 X 2 X 2 X 3 X 3
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况： 1. 去掉一个支座链杆相当于解除一个约束。
8.2 力法和典型方程
力法的思路：
8.1 超静定结构及超静定次数的确定
课堂练习： 判定下列结构的超静定次数：
3
3
3
3
n 12
2
3
1
n6
8.1 超静定结构及超静定次数的确定
课堂练习： 判定下列结构的超静定次数：
1
1
1
n3
3 n3
8.1 超静定结构及超静定次数的确定
组成无多余约束几何不变体系的基本规则： (1) 两刚片法则： 两个刚片用三根不共点的链杆相连，或者，两刚片用 一铰和一不通过铰心的链杆相连，可组成一个无多余约束 的几何不变体系。 (2) 三刚片法则（三角形法则）： 三刚片用不共线的三个铰两两相连，可组成一个无多 余约束的几何不变体系。 (3) 二元体法则： 在一个体系上增加或拆除二元体，不改变原体系的几 何组成性质。
X2
X1
X1
X1
X2 X2
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况： 4.去掉一个固定端支座相当于解除三个约束；
X3
X1
X2
X1 X2 X3
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况：
5.切断一根梁相当于解除三个约束。
或：切开一个闭合框相当于解除三个约束。
X1
X1
X1
X1
X2 X2 X3
X3 X2
X3 X3 X2
8.1 超静定结构及超静定次数的确定
解除多余约束的几种情况： 1. 去掉一个支座链杆相当于解除1个约束。 2. 在杆件内添加一个铰，相当于解除1个约束； 3. 去掉一个固定铰支座,或拆开一个单铰相当于解除 2个约束； 4. 去掉一个固定端支座相当于解除3个约束； 5. 切断一根梁（杆）或切开一个闭合框相当于解除3 个约束;
第八章
0
第八章 主要内容
8-1 超静定结构及超静定次数的确定 8-2 力法和典型方程 8-3 对称性的利用
重点：力法
本节内容
8.1 超静定结构及超静定次数的确定 8.2 力法和典型方程
8.1 超静定结构 及超静定次数的确定
8.1 超静定结构及超静定次数的确定
超静定结构：几何不变体系，有多余约束。 不能利用静力平衡条件求出结构的全部支座反力
l3 3EI
δ11 =单位多余力产生的弯矩图自乘/EI；
D1P
M P (x) M10 (x) dx
l
EI


1 EI

1 3

l

ql 2 2

3l 4


ql 4 8EI
△1P =单位多余力产生的弯矩图乘外荷 载弯矩图/EI；
8.2 力法和典型方程
力法的基本思路：
q