流体的一些性质
- 格式:docx
- 大小:1.21 MB
- 文档页数:6







化工原理流体知识点总结一、流体的基本性质1. 流体的定义流体是指在受到作用力的情况下,能够流动的物质,包括液体和气体。
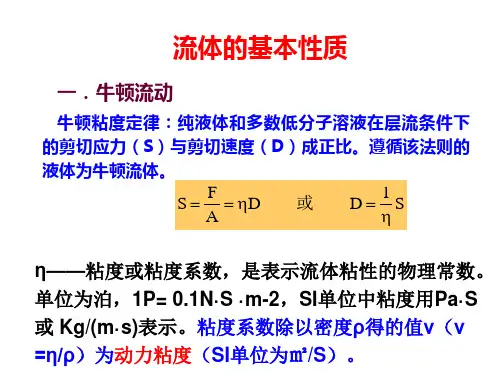
2. 流体的分类(1)牛顿流体:满足牛顿流体定律的流体,即剪切应力与剪切速率成正比。
(2)非牛顿流体:不满足牛顿流体定律的流体,如塑料、胶体等。
3. 流体的性质(1)密度:单位体积流体的质量,通常用ρ表示,单位kg/m³。
(2)粘度:流体流动时的内部摩擦阻力,通常用η表示,单位Pa·s或mPa·s。
(3)表观黏度:流体在管道中流动时表现出的粘度,通常用μ表示,单位Pa·s或mPa·s。
(4)流变性:流体在外力作用下的形变特性,包括剪切流变和延伸流变。
4. 流体的运动(1)层流:流体呈层状流动,流线平行且不交叉。
(2)湍流:流体呈旋涡形式混合流动,流线交叉且无规律。
二、流态力学1. 流体静压(1)静压力:流体在容器中受到的压力,通常用P表示,单位Pa。
(2)流体的压强:P = ρgh,其中ρ为流体密度,g为重力加速度,h为液面高度。
(3)帕斯卡定律:在静止流体中,内部任意一点的压力均相等。
2. 流体动压(1)动压力:流体在流动状态下受到的压力。
(2)动压公式:P = 0.5ρv²,其中ρ为流体密度,v为流体的流速。
3. 流体的质量守恒(1)连续方程:描述流体在流动中的质量守恒关系。
(2)连续方程公式:ρ1A1v1 = ρ2A2v2,其中ρ为流体密度,A为管道横截面积,v为流速。
4. 流体的动量守恒(1)牛顿第二定律:描述流体在流动中的动量守恒关系。
(2)牛顿第二定律公式:F = ρQ(v2 - v1),其中F为管道上流体受到的合力,Q为流体流量,v为流速。
三、流体的运动1. 流体的流动类型(1)层流:小阻力、流速较慢。
(2)湍流:大阻力、流速较快。
2. 流体的流动参数(1)雷诺数:描述流体流动状态的无量纲参数,Re = ρvD/η,其中D为管道直径。



流体力学11.1 流体的基本性质1)压缩性流体是液体与气体的总称。
从宏观上看,流体也可看成一种连续媒质。
与弹性体相似,流体也可发生形状的改变,所不同的是静止流体内部不存在剪切应力,这是因为如果流体内部有剪应力的话流体必定会流动,而对静止的流体来说流动是不存在的。
如前所述,作用在静止流体表面的压应力的变化会引起流体的体积应变,其大小可由胡克定律描述。
大量的实验表明,无论气体还是液体都是可以压缩的,但液体的可压缩量通常很小。
例如在500个大气压下,每增加一个大气压,水的体积减少量不到原体积的两万分之一。
同样的条件下,水银的体积减少量不到原体积的百万分之四。
因为液体的压缩量很小,通常可以不计液体的压缩性。
气体的可压缩性表现的十分明显,例如用不大的力推动活塞就可使气缸内的气体明显压缩。
但在可流动的情况下,有时也把气体视为不可压缩的,这是因为气体密度小在受压时体积还未来得与改变就已快速地流动并迅速达到密度均匀。
物理上常用马赫数M来判定可流动气体的压缩性,其定义为M=流速/声速,若M2<<1,可视气体为不可压缩的。
由此看出,当气流速度比声速小许多时可将空气视为不可压缩的,而当气流速度接近或超过声速时气体应视为可压缩的。
总之在实际问题中若不考虑流体的可压缩性时,可将流体抽象成不可压缩流体这一理想模型。
2)粘滞性为了解流动时流体内部的力学性质,设想如图10.1.1所示的实验。
在两个靠得很近的大平板之间放入流体,下板固定,在上板面施加一个沿流体表面切向的力F 。
此时上板面下的流体将受到一个平均剪应力F/A 的作用,式中A 是上板的面积。
实验表明,无论力F 多么小都能引起两板间的流体以某个速度流动,这正是流体的特征,当受到剪应力时会发生连续形变并开始流动。
通过观察可以发现,在流体与板面直接接触处的流体与板有相同的速度。
若图10.1.1中的上板以速度u 沿x 方向运动下板静止,那么中间各层流体的速度是从0(下板)到u (上板)的一种分布,流体内各层之间形成流速差或速度梯度。
流体的特点和流体的相关性质
流体的特点是:不像固体那样能单独保持一定的形状;而且具有流动性。
流体主要力学性质:
1、流体具有易流动性;
2、流体具有质量,有一定的密度;
3、流体受有重力作用;
4、流体具有粘性;
5、流体具有一定的压缩性和膨胀性;
6、流体具有一定的表面张力;
7、流体的连续介质模型:
任何流体都是由无数分子组成的,分子与分子间有空隙,所以微观上流体并不是连续分布的物质。
但是流体力学并不研究微观的分子运动,因此在研究流体宏观运动时,要对流体作力学模型假设。
流体复习整理资料第一章 流体及其物理性质1.流体的特征——流动性:在任意微小的剪切力作用下能产生连续剪切变形的物体称为流体。
也可以说能够流动的物质即为流体。
流体在静止时不能承受剪切力,不能抵抗剪切变形。
流体只有在运动状态下,当流体质点之间有相对运动时,才能抵抗剪切变形。
只要有剪切力的作用,流体就不会静止下来,将会发生连续变形而流动。
运动流体抵抗剪切变形的能力(产生剪切应力的大小)体现在变形的速率上,而不是变形的大小(与弹性体的不同之处)。
2.流体的重度:单位体积的流体所的受的重力,用γ表示。
g 一般计算中取9.8m /s 23.密度:=1000kg/,=1.2kg/,=13.6,常压常温下,空气的密度大约是水的1/8003. 当流体的压缩性对所研究的流动影响不大,可忽略不计时,这种流体称为不可压缩流体,反之称为可压缩流体。
通常液体和低速流动的气体(U<70m /s )可作为不可压缩流体处理。
4.压缩系数:弹性模数:21d /d pp E N m ρβρ==膨胀系数:)(K /1d d 1d /d TVV T V V t ==β5.流体的粘性:运动流体内存在内摩擦力的特性(有抵抗剪切变形的能力),这就是粘滞性。
流体的粘性就是阻止发生剪切变形的一种特性,而内摩擦力则是粘性的动力表现。
温度升高时,液体的粘性降低,气体粘性增加。
6.牛顿内摩擦定律: 单位面积上的摩擦力为:3/g N m γρ=p V V p V V p d d 1d /d -=-=β21d 1d /d d p V m NV p pρβρ=-=h U μτ=内摩擦力为: 此式即为牛顿内摩擦定律公式。
其中:μ为动力粘度,表征流体抵抗变形的能力,它和密度的比值称为流体的运动粘度ν τ值既能反映大小,又可表示方向,必须规定:公式中的τ是靠近坐标原点一侧(即t -t 线以下)的流体所受的内摩擦应力,其大小为μ du/dy ,方向由du/dy 的符号决定,为正时τ与u 同向,为负时τ与u 反向,显然,对下图所示的流动,τ>0, 即t —t 线以下的流体Ⅰ受上部流体Ⅱ拖动,而Ⅱ受Ⅰ的阻滞。
流体的一些性质流体的很多性质与固体中的定义相通的,比如密度、压力、温度等。
但也有其独特的属性,这里最典型的就是区分流体和固体的力学特性——粘性。
此外,液体有表面张力、气体具有易压缩性,这些都是流体特有的属性。
流体的粘性当流体收到外界的剪切力作用的时候,它会不断地变形下去,在这种连续的剪切变形作用下的流体内部会产生剪切应力,这种性质称为流体的粘性。
我们通常见到的液体和气体都有粘性,只有超流体可以认为是没有粘性的。
我们都知道蜂蜜的粘性要远大于水的粘性,现在来分析一下决定流体粘性力大小的因素。
仍然用固体之间的摩擦力做类比,对于沿斜面下滑的方块而言,摩擦力等于摩擦系数与它们相互挤压的力的乘积。
摩擦系数体现了两个物体的分子作用力大小及它们相接触的表面的粗糙程度,这比较容易理解。
但摩擦力为什么和挤压力呈正比呢?毕竟挤压力与摩擦力是垂直关系,应该没有沿摩擦力方向的分量才对。
原因是这样:挤压力越大,则两物体的接触面积就越大,这个接触面积与挤压力之间基本上是线性关系,因此摩擦力也与挤压力呈正比。
如果是分子级别光滑的两个物体相接触,则摩擦力就基本上与挤压力无关了。
固体的动摩擦系数与静摩擦系数一般并不相等,因为它们的产生机理不完全相同。
静摩擦完全是力的平衡,而动摩擦则还包含动能向内能的转化过程。
当两个固体靠在一起并相对滑动时,在摩擦面上不但发生跟静摩擦时类似的力的作用,还会发生两物体分子之间的键不断地被打破,同时又不断形成新的键,并且还伴随着分子和分子团从原物体上脱落等过程。
这些过程中会伴随着分子振动能量的变化以及分子运动方向性的混乱,所以摩擦过程一定是产生热量的。
图1-4显示了接触面上发生的3种典型的现象。
图1-4 固体动摩擦力的微观解释从上一节的分析我们知道,当流体与固体相接触时,紧挨着固体的流体分子会被吸附在固体上随之运动。
因此,所谓流体与固体之间的摩擦力其实也就是流体之间的摩擦力。
这也就是一般书籍中并不特别区分流体内部的摩擦力和流体与固体之间的摩擦力的原因。
液体与固体的接触是分子级别的全面接触,因此摩擦力应该与挤压力无关。
这个挤压力就是指流体内部的压力(本书中若非特别强调,压力都是指压强.即单位面积上的压力),这可以解释为什么液体的粘性力大小基本与压力无关。
但流体的粘性力大小与温度却有着极大的关系,我们都知道凉的糖浆较粘稠,加热后粘性降低,一般对于液体来说温度越高粘性力越小。
气体的粘性力较小,生活中一般较难察觉,但精密的实验已经证实,与液体相反,对于气体来说温度越高粘性力越大。
液体和气体粘性的这些特性与产生粘性的物理本质是直接相关的,既然这两者不同,就应该分别加以分析。
对于液体而言,如果两层之间的运动速度不同,上层速度快的分子在扫过下层速度慢的分子时,会通过吸引力和排斥力带动下层运动。
这种运动包含了平动和传动,下层分子平动速度的增加相当于是从上层获得了额外的动能,而下层分子转动速度的增加相当于是将一部分从上层分子获得的动能转化成内能了。
这个过程中分子的动量会减小,下层分子的动量会增加,动量传递靠的就是两层之间的摩擦力作用。
这个摩擦力对于包含上下层分子的整个体系来说是内力,所以总的动量应该是守恒的。
图1-5显示了上层液体比下层液体速度快时,对下层分子的拖动作用。
图1-5 液体内粘性力的微观解释上面讨论的由分子力引起摩擦力的作用与固体有些类似,实际上对与液体摩擦力来说还有一个不同于固体的作用,那就是液体分子并不会安分地分层流动,而是会相互扩散。
也就是说各层的分子会有与运动方向垂直的横向运动上层的分子会跑到下层去,下层的分子也会跑到上层去。
这样,上层的分子进入下层后就会推动下层的分子运动得快一些,而下层的分子跑到上层后会拖累上层分子使之速度减慢。
这种作用也可以解释为两层之间的动量传递,既然是沿运动方向的动量传递,就有沿这个方向的力,这个力就是摩擦力。
对于做层流运动的液体而言,这个作用远小于前述的分子吸引力和排斥力的作用,因此经常可以忽略,而认为液体的粘性就是由分子力造成的,其中吸引力经常是主要的。
我们之前曾经说过,液体的粉分子是随遇而安的,因此不会产生静摩擦力。
当运动时,液体上下层分子之间的引力又是如何产生了沿接触面方向的分量的呢?这其实与分子的形状和极性相关,如果要将缺分析,需要的是更深入的理论物理的知识,但我们这里至少可以进行一下定性的分析。
在我们的生活经验中,那些有机物的液体一般都具有较大的粘性,比如油漆、蜂蜜,血液等。
这些物质的分子较大,且形状不规则,具有极性,运动时自然不利索,分子之间容易纠缠不清。
以甘油为例,它的分子并不是很大,但形状较为不圆滑,且具有极性,当甘油分子通过粗糙表面时就很容易卡住,甘油分子之间也较容易纠缠,因此甘油的粘性较大。
汞的分子比甘油分子还大,但呈球形,而且没什么极性,因此汞的粘性虽然比水大得多,但比起相同相对分子质量的有机物来说还是很小的。
图1-5(b)显示了一种有机物分子的运动,其中用虚线包围起来表示的是一个分子,可以直观地看出,比起图1-5 (a)中的水分子来说,这种有机物的分子个头大,形状不规则,互相的纠缠必然大,粘性也就会比较大。
当液体的温度升高时,单个分子的振动加强,分子与分子之间的纠缠就更容易松脱,手机放在泥浆上面可以保持相当长的一段时间不沉下去,如果这时候恰巧来了电话手机振动起来的话,很快就会沉下去。
液体内部的粘性与此类似,因此温度升高时液体的粘性是减小的,并且通常分子之间纠缠越强的液体对温度越敏感浆的粘性随温度的升高迅速降低,而分子呈球形的汞的粘性随温度的变化就要小得多。
然而也不是所有的液体的粘性都是随温度的升高而降低的,这是由粘性产生的机理决定的。
比如,单一成分的润滑油的粘性随温度的升高降低很快,这给发动机这类工作作温度范围大的机械部件的润滑带来了很大的问题。
为了克服这一点,现代的润滑油里面添加了这样一种物质,当温度升高时,它的分子从球形伸展为长条状,这使得该物质的粘性是随温度的升高而增大的。
添加了这种物质后,润滑油的粘性就对温度不那么敏感了。
对于气体来说,分子之间几乎没有作用力—既没有吸引力也没有排斥力,其内部压力产生的机理是分子之间频繁的碰撞产生的动量传递。
这种碰撞不但可以产压力这样的正应力,也可以产生粘性力这样的剪切力。
当各层分子的宏观运动速度不同时,比如上层速度快,下层速度慢时,上层的分子在热运动的作用下不断地跳入下层中,推动低速的分子运动,下层的分子也会不断地跳入上层中,拖累上层的分子使其减速。
从宏观上看来,这种动量交换表现为上层和下层之间存在拖动作用,这就是气体的粘性作用。
前面我们说过,在液体中也存在这样的作用,但比起分子力来说可以忽略。
在气体中,分子间几乎没有吸引力,但分子很活跃,这种动量交换才是气体粘性的本质。
图1-6显示了气体粘性的这种机理,其中上层的分子运动快,下层的分子运动慢,但它们都同时还在进行着热运动,互相交换很频繁,粘性也就因此产了。
很显然,当温度升髙时,气体内部的分子热运动加剧,各层之间分子交换频率上升,就能产生更多的动量交换,这就是气体的粘性随温度升高而增大的原因。
跟液体一样,气体的粘性也基本上与压力无关,这又怎么解释呢?对于某种理想气体来说,压力由温度和密度两个因素决定,当温度不变时,压力的变化就对应了密度的变化,所以某一温度下气体的粘性与压力无关也就意味着气体的粘性与其密度无关。
这是很奇怪的,因为显然密度越大,分子碰撞的频率就越大,能传递的动量就更多,似乎密度越大粘性力也应该越大才对。
实际情况是这样的,我们来看图1-6,当密度增加时,确实单位时间内有更多的分子从上层跳到了下层。
但是由于分子自由程的减小,各层之间的宏观速度差,以及单个分子碰撞所传递的动量也减小了。
这种单次动量减小的比例是相同的,因此效果体现为总的动量的交换还是一样的,也就是说密度的改变并不影响粘性力的大小。
图1-6 气体内粘性力的微观解释以上这些基于分子运动论的分析只能是定性的,事实上迄今为止有关粘性的物理本质问题也没有完全搞清楚,因为说到底流体内的压力和粘性力都是电磁力,这方面的研究属于基础物理学的问题。
在经典力学方面最早对流体的粘性进行定量研究的是英国人牛顿(Isaac Newton, 1642—1727)。
他于1686年通过实验测量了液体的粘性,并建立了描述流体内部摩擦力的“牛顿内摩擦定律”。
牛顿的实验是基于图1-7所示的模型进行的,这是大概可以想到的最简单的测量粘性的流动模型了。
然而很不幸的是这样的模型在理论上很简单,实现起来并不容易,所以牛顿的实验效果其实并不好。
但凭借强大的理解能力,牛顿还是得到了理论上正确的结果,并在后来被泊肃叶(Jean Louis Marie Poiseuille, 1799—1869)的管流实验所证实。
图1-7 牛顿的流体粘性力实验图1-7中,下面的壁面保持静止,上面的平板以水平速度运动。
鉴于流体在与固体壁面接触的地方会依附在固体表面,与下壁面接触的流体保持静止,与上平板接触的流体以速度C/随之运动。
牛顿根据实验结果总结出的规律是:上平板所需的拖动力与其运动速度成正比,与两平板间的距离成反比,即式中,F为拖动平板的力;A为平板和流体的接触面积;U为上平板的运动速度;L为两平板间的距离。
鉴于实验时流体左侧和右侧的压力相同,因此平板给予流体的x向拖动力在各层流体之间都是相同的,这样就可以得到任意两层流体之间的切应力。
实验中还发现流体速度沿y方向呈线性分布,因此牛顿得到:平行流动中,任意两层流体之间的切应力可以写为式中,r为切应力;u为流体水平方向的速度;y为垂直方向的坐标;μ是一个描述流体粘性大小的系数,称为粘性系数,有时候称为动力粘性系数。
μ就是流体粘性大小的度量,不同流体的粘性系数差别很大,同一流体的粘性系数则基本上只随温度变化。
事实上并不是所有的流体都遵循式(1.1),牛顿实验所用的流体是满足这个关系的,这些流体被大家称为牛顿流体。
因为这种流体的应切力与速度梯度之间是线性关系,因此有时也成为线性流体。
自然界中也存在大量不满足式(1.1)的流体,这一类流体统称为非牛顿流体。
可以看出牛顿流体一般对应着大分子的液体,这些液体的分子在有速度梯度的流场中会相互纠缠,因此粘性力与与速度梯度都不是线性关系,有些非牛顿流体的剪切力不但与速度相关,还与作用时间长短相关。
参考文献《我所理解的流体力学》王洪伟著2016。