非均匀磁场测量实验

霍尔效应及其应用实验(FB510A 型霍尔效应组合实验仪)（亥姆霍兹线圈、螺线管线圈）实验讲义长春禹衡时代光电科技有限公司实验一 霍尔效应及其应用置于磁场中的载流体，如果电流方向与磁场垂直，则在垂直于电流和磁场的方向会产生一附加的横向电场，这个现象是霍普金斯大学研究生霍尔于1879年发现的，后被称为霍尔效应。

如今霍尔效应不但是测定半导体材料电学参数的主要手段，而且利用该效应制成的霍尔器件已广泛用于非电量的电测量、自动控制和信息处理等方面。

在工业生产要求自动检测和控制的今天，作为敏感元件之一的霍尔器件，将有更广泛的应用前景。

掌握这一富有实用性的实验，对日后的工作将有益处。

【实验目的】1．了解霍尔效应实验原理以及有关霍尔器件对材料要求的知识。

2．学习用“对称测量法”消除副效应的影响，测量试样的S H I ~V 和M H I ~V 曲线。

3．确定试样的导电类型。

【实验原理】1．霍尔效应：霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场方向上产生正负电荷的聚积，从而形成附加的横向电场，即霍尔电场H E 。

如图1所示的半导体试样，若在X 方向通以电流S I ，在Z 方向加磁场B ，则在Y 方向即试样A A '- 电极两侧就开始聚集异号电荷而产生相应的附加电场。

电场的指向取决于试样的导电类型。

对图1（a ）所示的N 型试样，霍尔电场逆Y 方向，（b ）的P 型试样则沿Y 方向。

即有)(P 0)Y (E )(N 0)Y (E H H 型型⇒>⇒<显然，霍尔电场H E 是阻止载流子继续向侧面偏移，当载流子所受的横向电场力HE e •与洛仑兹力B v e ••相等，样品两侧电荷的积累就达到动态平衡，故有B v e E e H ••=• （1）其中H E 为霍尔电场，v 是载流子在电流方向上的平均漂移速度。

上海电力学院大学物理实验备课教案实验名称：非均匀磁场的测定面向专业：电力热动信控实验室名称：物理实验室一、实验目的：测量圆形电流的磁场分布二、实验仪器、设备：三、原理摘要——测量公式、测量电路图、光路图或其它示意图：在圆形线圈中通以交流电，则在其周围产生一个交变的磁场。

用一个适当大小的探测线圈置于磁场中，由于磁场以一定的频率作周期性变化，那么通过探测线圈的磁感应通量也随之作周期性变化，在探测线圈中必定有感生电动势产生。

用晶体管毫伏表测量出感生电动势的大小，就可以计算出磁感应强度的大小。

磁场是矢量场，磁感应强度不仅有大小，而且有方向。

下面分别叙述如何测定磁感应强度的大小和方位。

1、计算磁感应强度的大小式中E0是在测量点处晶体管毫伏表指示的最大值，N是探测线圈的匝数，S为其有效面积，为交流电的频率。

2、确定B的方位在交变磁场中，磁场的方向也是作周期性变化，但是对于同一点磁感应强度的方位不变。

根据法拉第电磁感应定律，B的方位即是探测线圈在该测量点感应电动势达到极大值E0时，探测线圈的法线的方位线。

但在实验中，达到极大值时的方位不易测准，因而采用转动探测线圈的方向使晶体管毫伏表读数为最小，此时，即B的方位与的方位垂直。

参考讲义第88页图16-1和图16-2。

利用探测线圈T的正方形底座，可画出线圈T中心O处B的方位，它平行与AD。

四、实验内容与步骤：一、按右图接通电路。

调节低频信号发生器，使频率固定在70.0HZ，调节输出电流，使通过圆形线圈的激磁电流在0.100 A。

二、测出圆形电流的磁场沿轴线方向的分布1、将坐标纸放在磁场测量片面上，并确定坐标原点，使其和圆电流几何中心重合（纸面与圆电流所在平面垂直）。

2、从坐标原点开始，沿轴线每隔1厘米测量一次探测线中感应电动势大小，共测15个点，来回重复一次。

三、形象描绘圆形电流的磁场分布图沿轴线每隔2厘米测一次磁场方位（画0.5厘米长的短线）；由原点沿直径向边缘每隔2厘米，在测量平面上等间隔测量磁场方位，直到磁场方位线均匀分布在四分之一测量平面上。

实验3—9 磁场的描绘【实验目的】1．掌握感应法测量磁场的原理和方法。

2．研究载流圆线圈轴向磁场的分布。

3．描绘亥姆霍兹线圈的磁场均匀区。

【实验仪器】非均匀磁场测量仪，400H Z 交流电源，晶体管毫伏表，探测线圈等。

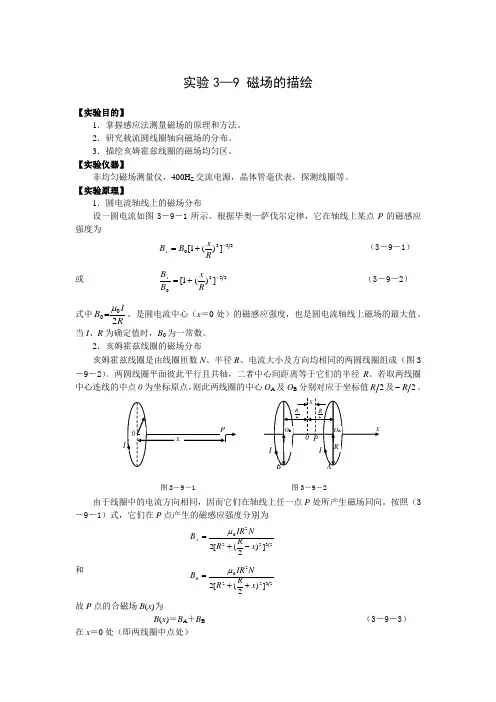
【实验原理】1．圆电流轴线上的磁场分布设一圆电流如图3－9－1所示。

根据毕奥—萨伐尔定律，它在轴线上某点P 的磁感应强度为320])(1[-+=R xB B x （3－9－1）或2320])(1[-+=RxB B x （3－9－2） 式中RIB 200μ=，是圆电流中心（x ＝0处）的磁感应强度，也是圆电流轴线上磁场的最大值。

当I 、R 为确定值时，B 0为一常数。

2．亥姆霍兹线圈的磁场分布亥姆霍兹线圈是由线圈匝数N 、半径R 、电流大小及方向均相同的两圆线圈组成（图3－9－2）。

两圆线圈平面彼此平行且共轴，二者中心间距离等于它们的半径R 。

若取两线圈中心连线的中点0为坐标原点，则此两线圈的中心O A 及O B 分别对应于坐标值2R 及2R -。

由于线圈中的电流方向相同，因而它们在轴线上任一点P 处所产生磁场同向。

按照（3－9－1）式，它们在P 点产生的磁感应强度分别为232220])2([2x RR N IR B A -+=μ和32220])2([2x RR N IR B B ++=μ故P 点的合磁场B (x )为B (x )＝B A ＋B B （3－9－3） 在x ＝0处（即两线圈中点处）523R计算表明，当)10(R x <时，B (x)和B (0)间相对差别约万分之一，因此亥姆霍兹线圈能产生比较均匀的磁场。

在生产和科研中，若所需磁场不太强时，常用这种方法来产生较均匀的磁场。

3．测量磁场的方法磁感应强度是一个矢量，因此磁场的测量不仅要测量磁场的大小且要测出它的方向。

测定磁场的方法很多，本实验采用感应法测量磁感应强度的大小和方向。

感应法是利用通过一个探测线圈（如图3－9－3）中磁通量变化所感应的电动势大小来测量磁场。

非均匀磁场的测量[目的]1.掌握感应法测磁场原理。

2.测量非均匀磁场分布。

3.测量亥姆霍兹线圈磁场分布，验证叠加原理。

[原理]测量磁场的方法很多，具体采用什么方法，要由被测磁场的类型和强弱来确定。

均匀磁场的测量在8.2实验中我们应用了物质在磁场中表现的磁特性而产生的霍耳效应法，而对于非均匀磁场的研究和测量，本实验采用感应法测磁场。

这种方法是以电磁感应定律 dtd ϕε−=为基础：当导线中通有变化电流时，其周围空间必然产生变化磁场。

处在变化磁场中的闭合回路，由于通过它的磁通量发生变化，回路中将有感应电动势产生。

通过测量此感应电动势的大小，就可以计算出磁场的量值，这就是感应法的实质。

这种方法既可测交变磁场，也可测恒定磁场。

对于不随时间变化的恒定磁场，可采用恒速转动测量线圈的方法来获得感应电动势，达到测量磁场的目的。

磁场是矢量场，因此磁场的测量就是要测出场中各点的磁感应强度大小与方向。

但实际上往往只能测出某一小区域的平均值，很难测得非均匀磁场中各点的磁感应强度矢量。

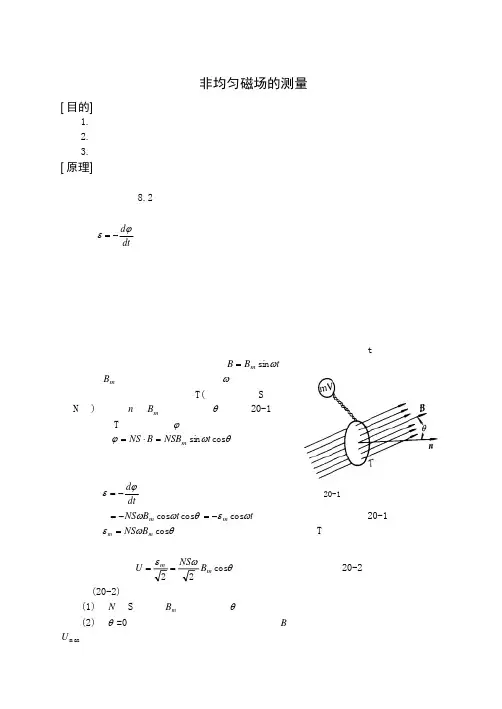
为叙述简单起见，先假定有一个均匀的交变磁场，其量值随时间t 按正弦规律变化t B B m ωsin =式中m B 为磁感应强度的峰值，ω为角频率。

再假定置于此磁场中探测线圈T(线圈面积为S ，共有N 匝)的法线n 与m B 之间夹角为θ，如图20-1所示。

则通过T 的总磁通量ϕ为θωϕcos sin t NSB B NS m =⋅=由于磁场是交变的，因此在线圈中会出现感应电动势，其值为 dt d ϕε−= θωωcos cos t B NS m −=t m ωεcos −= （20-1）式中θωεcos m m B NS =为感应电动势峰值。

将探测线圈T 的两条引线与一个交流毫伏表连接，则毫伏表指针会发生偏转。

注意读数为有效值，它与峰值的关系为θωεcos 22m m B NS U == （20-2） 由(20-2)式可知(1)当N 、S 、ω、m B 一定时，角θ越小，毫伏表读数越大，反之亦然。

大学物理实验习题汇编一、示波器的使用[预习题]1、简述示波器各个按纽的作用。

2、观察信号随时间的变化图形时必须加上锯齿波扫描信号，为什么？[作业题]1、如何在示波器屏幕上得到以下图形？（1）一个光点；（2）两条点线；（3）两个从左至右移动的亮点。

2、假定扫描信号是频率为f 的锯齿波，Y 轴输入信号为]2)(4sin[00ππ+-=t t f U V y ，试用作图法画出示波器屏幕上显示的图形。

二、电位差计的原理和使用[预习题]1、用电位差计测量电动势的原理、方法。

2、测量中，电流标准化后，强调变阻器R 1固定不变的原因和可变电阻R 2的作用？3、箱式电位差计的组成及各按纽的作用。

4、本实验要求及注意事项。

[作业题]1、按图4连接电路，接通K 1，将K 2倒向Es 或Ex 后，无论怎样调节活动端m 、n ，检流计指针总向一边偏转，试问有哪些可能的原因？三、全息照相[预习题]1、全息片的基本特点是什么？2、要想得到再现图像不重叠的全息片，在拍摄过程中应注意什么？3、物光与参考光的光程差一般为多少？为什么？4、冲洗全息底片时应注意什么？[作业题]1、为什么要求光路中物光与参考光的光程尽量相等？2、制作全息衍射光栅时，为什么到达感光片的两束光要接近于平行光？四、霍尔效应[预习题]1、什么是霍尔效应？霍尔电压是如何产生的？2、简述用霍尔效应测量磁场的原理。

3、如何消除副效应对实验的影响？[作业题]1、由V H-x 、V H-y 曲线讨论说明电磁铁缝隙中磁场的分布情况。

2、根据实验计算出载流子浓度n 及载流子迁移率μ。

五、等厚干涉[预习题]1、由于测微鼓轮中螺距间总有间隙存在，当测微鼓轮刚开始反向旋转时会发生空转，引起读数误差（称为空回误差），实验时应如何避免？2、在实验中，若叉丝中心没有通过牛顿环的中心，以叉丝中心对准暗环中央所测出的并不是牛顿环的直径，而是弦长，以弦长代替直径代入公式进行计算，仍能得到相同的结果，请从几何的角度证明之。

非均匀磁场的测量实验报告一、引言磁场是物质的一种特性，对于磁性材料和电流都会产生作用力。

在物理学中，磁场的测量是非常重要的实验之一。

本实验的目的是测量非均匀磁场的分布情况。

二、实验原理非均匀磁场是指在空间中磁场强度不均匀的情况。

为了测量非均匀磁场，我们通常使用霍尔效应。

霍尔效应是指当电流通过一块导体时，如果导体处于磁场中，那么导体的两侧会产生电压差。

利用这一现象，我们可以测量磁场的强度和方向。

三、实验步骤1. 准备工作：将霍尔元件固定在实验台上，并连接电源和电压测量仪器。

2. 测量磁场分布：将霍尔元件沿着特定的方向移动，记录不同位置的电压值。

根据霍尔效应的原理，电压值与磁场的强度成正比。

3. 绘制磁场分布图：根据测得的电压值，我们可以绘制出磁场的分布图。

通过观察分布图，我们可以得出磁场的强度分布情况。

四、实验结果与分析根据实验测得的数据，我们可以绘制出非均匀磁场的分布图。

通常情况下，非均匀磁场的分布图会呈现出一定的规律性。

例如，在一个磁场中心附近，磁场的强度会较大，而在磁场边缘部分，磁场的强度会逐渐减小。

五、实验误差分析在实验过程中，由于设备的精度限制以及外界因素的干扰，可能会导致实验结果出现一定的误差。

为了减小误差，我们可以采取以下措施：1. 提高测量仪器的精度：使用更加精确的电压测量仪器，可以提高实验的准确性。

2. 控制外界干扰：在实验过程中，尽量避免外界磁场和电流的干扰，以确保测量结果的准确性。

3. 重复实验：多次重复实验，取平均值，可以减小误差，提高实验结果的可靠性。

六、实验结论通过本次实验，我们成功地测量了非均匀磁场的分布情况。

根据实验结果，我们可以得出磁场强度在空间中不均匀分布的结论。

实验中，我们还发现了一些规律性的现象，这对于进一步研究和应用磁场有着重要的意义。

七、实验应用非均匀磁场的测量在工程和科学领域有着广泛的应用。

例如，在磁共振成像技术中，通过测量非均匀磁场的分布，可以得到物体内部的结构信息。

磁场测量灵敏度定义理论说明1. 引言1.1 概述磁场测量是一项重要的科学技术领域，广泛应用于物理、工程、医学等多个领域。

磁场测量灵敏度作为评价磁场测量仪器性能的重要指标，具有着对于精确测量和检测所需的能力以及对噪声信号干扰的抵抗能力。

1.2 文章结构本文将首先介绍磁场测量灵敏度的概念与意义，然后详细讨论磁场测量灵敏度的定义与计算方法。

接下来，通过介绍磁场理论基础知识，分析影响磁场测量灵敏度的因素，并提出提高磁场测量灵敏度的方法与技术。

最后，在实验方法与结果分析中，我们将设计实验并针对实验数据进行处理和分析。

最后总结得出结论。

1.3 目的本文旨在全面了解磁场测量灵敏度定义与理论原理，并探讨如何通过改进仪器设备和技术手段来提高磁场测量灵敏度。

通过这些内容的介绍和分析，读者能够更好地理解磁场测量领域中灵敏度的概念与意义，以及如何应用磁场测量灵敏度来提高磁场测量的精确性与可靠性。

2. 磁场测量灵敏度定义2.1 磁场测量概述磁场测量是指对磁场进行定量和定性的测量和分析。

在很多科学研究和工程应用领域，如地球物理学、电力工程、材料科学等，对磁场的准确测量具有重要意义。

2.2 灵敏度的概念与意义在磁场测量中，灵敏度是评价一种磁场传感器或仪器对磁场变化的响应能力的重要指标之一。

它可以反映出该传感器或仪器对微小磁场变化的探测能力以及对噪声的抑制能力。

灵敏度也被称为传感器输出信号与输入信号之间关系的导数。

换句话说，灵敏度是衡量单位输入信号引起单位输出信号变化的比例关系。

通常情况下，灵敏度值越大，代表着传感器或仪器更加敏感，能够更好地检测微小磁场变化。

在实际应用中，选择合适灵敏度的传感器非常重要。

如果灵敏度过低，则无法探测到微弱的磁场变化；而如果灵敏度过高，则容易受到噪声干扰，导致测量结果不准确。

2.3 磁场测量灵敏度的定义与计算方法磁场的灵敏度可以通过以下公式进行计算：灵敏度= ΔB/ΔV其中，ΔB表示单位磁场变化引起的传感器输出信号变化，ΔV表示传感器输出信号的变化。

实验21 非均匀磁场的测量一、实验目的（1）掌握感应法测量磁场的原理（2）测量赫姆霍兹线圈轴线上的磁场强度分布，并画出一条磁力线。

二、实验原理磁场的的测量方法有很多，具体采用什么方法决定于被测磁场的类型和强弱。

本实验中，我们采用感应法测量非均匀磁场，如图1所示。

这种方法是以电磁感应定律ε=−dφ为基础的：当导dt线中通有变化的电流，其周围会产生变化的磁场。

处在变化磁场中的闭合电路，由于通过它的磁通量发生变化，回路中会有感应电动势产生。

通过测量感应电动势的的大小便可测出磁场的量值。

磁场是矢量场，在测量磁场时既要测出其大小，还要测出其方向，但实际中，只能测出一小区域中的平均值，很难测出磁感应强度的矢量。

若假定有一均匀的交变磁场：B=B m sinωt公式（1）式中，B m是磁感应强度的峰值；ω为角频率。

置于磁场中探测线圈T(线圈的面积为S，共有N匝)的法线n与B m之间的夹角为θ，如图1所示。

则通过的总磁通量为φ=NS∙B=NSB m sinωt cosθ公式（2）由于磁场是交变的，在线圈中会会出现感应电动势：ε=−dφ=−NSωB m cos ωt cosθ=−εm cos ωt公式（3）dt式中，εm= NSωB m cosθ感应电动势的峰值。

将探测线圈T的两条引线接交流毫伏表，则毫伏表的示值将会发生变化，毫伏表显示的有效值与峰值的关系为：U=m√2=√2B m cosθ公式（4）由上式可知：1）当N、S、ω、B m一定时，角越小，毫伏表的示值越大，反之示值越小。

2）当θ=0时，探测线圈的法线方向与磁场的方向一致，毫伏表示值最大为U max,其值为：U max=√2m公式（5）则，B m=√2NSωU max公式（6）因此，可用毫伏表示值的最大值来确定磁场的大小。

3）当θ=π2时，毫伏表示数为零，即U=0,则εm=0由以上结论可知，用下述方法确定磁感应强度的大小和方向比较方便。

测量时，将探测线圈放在待测点，用手缓慢移动它，直到毫伏表值达到最大值U max，由公式（5）可知该处的磁场值B m。

非均匀磁场实验报告非均匀磁场实验报告引言磁场是物理学中一个重要的概念，它在我们日常生活中无处不在。

磁场的强弱和方向对于物体的运动和相互作用有着重要的影响。

本次实验旨在研究非均匀磁场的特性，并探索其在实际应用中的潜力。

实验目的1. 理解磁场的概念和特性；2. 探究非均匀磁场的形成原理；3. 研究非均匀磁场对物体的影响。

实验设备和材料1. 磁铁；2. 铁磁材料（如铁钉、铁片等）；3. 磁感应强度计；4. 直尺、卷尺等测量工具。

实验步骤及结果1. 实验一：磁场强度的测量将磁感应强度计放置在不同位置，测量磁场的强度。

结果显示，磁场强度随着距离磁铁的远近而减弱，呈现出非均匀分布的特点。

2. 实验二：磁场的形成原理通过观察铁磁材料在磁场中的行为，我们可以了解磁场的形成原理。

将铁磁材料放置在磁铁附近，观察其受力情况。

结果显示，铁磁材料会被磁铁吸引，并沿着磁场方向排列。

这表明磁场是由磁铁产生的，并且对铁磁材料有一定的作用力。

3. 实验三：非均匀磁场对物体的影响在一个非均匀磁场中，我们放置一个铁磁材料，并观察它的运动情况。

结果显示，铁磁材料会受到一个力的作用，使其沿着磁场的方向运动。

当铁磁材料离开磁场时，它的运动会减缓并最终停止。

这说明非均匀磁场对物体的运动有一定的影响。

讨论与分析通过以上实验，我们可以得出以下结论：1. 非均匀磁场的强度随距离的增加而减弱，这是由磁场的特性决定的。

2. 铁磁材料在磁场中会受到磁力的作用，这是由磁场对铁磁材料的吸引力决定的。

3. 非均匀磁场对物体的运动有一定的影响，这是由磁场对物体的作用力决定的。

结论通过本次实验，我们深入了解了非均匀磁场的特性和对物体的影响。

磁场在日常生活中有着广泛的应用，例如电动机、磁共振成像等。

通过进一步研究和实验，我们可以更好地利用磁场的特性，为科学技术的发展做出贡献。

参考文献：[1] 张三, 李四. 磁场的基本概念与特性[J]. 物理学报, 2010, 30(2): 123-135.[2] 王五, 赵六. 非均匀磁场对物体的影响研究[J]. 科学实验, 2015, 40(3): 234-246.。

1、前言和实验目的核磁共振是指受电磁波作用的原子核系统在外磁场中磁能级之间发生共振跃迁的现象。

本实验的样品在外磁场中，外磁场使样品核能级因核自旋不同的取向而分裂，在数千高斯外磁场下核能级的裂距一般在射频波段，样品在射频电磁波作用下，粒子吸收电磁波的能量，从而产生核能级的跃迁。

1932年发现中子后，才认识到核自旋是质子自旋和中子自旋之和，质子和中子都是自旋角动量为2 的费米子，只有质子数和中子数两者或其一为奇数时，核才有非零的核磁矩，正是这种磁性核才能产生核磁共振。

核磁共振信号可提供物质结构的丰富信息，如谱线的宽度、形状、面积、谱线在频率或磁场刻度上的准确位置、谱线的精细结构、超精细结构、弛豫时间等，加之是对样品的无损测量，广泛的应用于分子结构的确定、液相和固相的动力学研究、医用诊断、固体物理学、分析化学、分子生物学等领域，是确定物质结构、组成和性质的重要实验方法。

核磁共振还是磁场测量和校准磁强计的标准方法之一，其不确定度可达001.0±%。

实验目的：（1）掌握核磁共振的实验原理和方法（2）用核磁共振方法校准外磁场B ，测量氟核的F g 因子以及横向驰豫时间2T2、实验原理如原子处在磁场中会发生能级分裂一样，许多原子核处在磁场中也会发生能级的分裂，因为原子核也存在自旋现象。

质子和中子都是自旋角动量等于2 的费米子，当质子数和中子数都为偶数时原子核的磁矩为0，当其一为奇数时原子核磁矩为半整数，当两个都为奇数时核磁矩为整数。

只有具有核磁矩的原子核才有核磁共振现象。

我们知道在微观世界里物理量都只能取分立的值，即都是量子化的。

原子核的角动量也只能取分立的值 )1(+=I I p ,I 为自旋量子数，取分立的值。

对于本实验用到的H 1和F 19，自旋量子数I 都为1/2。

沿z 方向的角动量为 m p z =，在这里m 只能取1/2或-1/2。

而自旋角动量不为0的核具有核磁矩p m e gp 2F =，考虑沿z 轴方向则有N z pZ mgF p m eG F ==2，其中以 γ==p z m e F 2为原子核磁矩的基本单位，pm e2=γ。

核磁共振实验报告【实验目的】1. 了解核磁共振的实验基本原理2. 学习利用核磁共振校准磁场和测量g 因子的方法3.【实验原理】1. 核磁共振现象与共振条件原子的总磁矩j μ和总角动量j P 存在如下关系22B j j j j e e B e g P g P P m h e e m πμμγμγ=-==为朗德因子，、是电子电荷和质量，称为玻尔磁子，为原子的旋磁比 对于自旋不为零的原子核，核磁矩j μ和自旋角动量j P 也存在如下关系22N I N I N I I p e g P g P P m h πμμγ=-==按照量子理论，存在核自旋和核磁矩的量子力学体系，在外磁场0B 中能级将发生赛曼分裂，相邻能级间具有能量差E ∆，当有外界条件提供与E ∆相同的磁能时，将引起相邻赛曼能级之间的磁偶极跃迁，比如赛曼能级的能量差为02B h E γπ∆=的氢核发射能量为h ν的光子，当0=2B h h γνπ时，氢核将吸收这个光子由低塞曼能级跃迁到高塞曼能级，这种共振吸收跃迁现象称为“核磁共振”。

由上可知，核磁共振发生和条件是电磁波的圆频率为00B ωγ=2. 用扫场法产生核磁共振在实验中要使0=2B hh γνπ得到满足不是容易的，因为磁场不是容易控制，因此我们在一个永磁铁0B 上叠加一个低频交谈磁场sin m B B t ω=，使氢质子能级能量差()0sin 2m h B B t γωπ+有一个变化的区域，调节射频场的频率ν，使射频场的能量h ν能进入这个区域，这样在某一瞬间等式()0sin 2m h B B t γωπ+总能成立。

由图可知，当共振信号非等间距时共振点处()0sin 2m h B B t γωπ+，sin m B t ω未知，无法利用等式求出0B 的值。

调节射频场的频率ν使共振信号等间距时，共振点处sin =0m B t ω，0=2B hh γνπ，0B 的值便可求出。

【实验仪器用具】试验装置如图所示。

实验21非均匀磁场的测量(详)实验简介：本实验的目的是测量非均匀磁场的磁感应强度，利用螺线管接通电源引入的磁场对指南针的影响来测定，通过实验得出非均匀磁场的磁场线、磁场强度分布和磁场的梯度，以及验证磁场的叠加原理和电流对磁场的影响。

实验原理：在非均匀磁场中，磁感应强度与空间位置有关，即在空间中的不同位置，磁场的大小和方向都不相同。

在实验中，通过测量磁场在空间中的强度分布和方向变化，可以得到非均匀磁场的磁场线，以及计算磁场的梯度。

磁场梯度是指磁场强度在空间中的变化率，一般表示为B'，它是一个矢量，指向磁场强度增加的方向。

在实验中，利用螺线管接通直流电源，在非均匀磁场中感应出电流，然后通过测量电流的大小和方向来确定磁场的强度和方向。

此外，还通过测量实验用的材料的磁化曲线来确定磁感应强度B和磁场强度H之间的关系，从而得到磁场的线圈。

实验器材：1、电源：可变直流电源2、磁铁：堆叠在一起的 U 形磁铁，用于产生非均匀磁场3、磁感应计：用于测量非均匀磁场中的磁感应强度4、指南针：用于测量磁场的方向5、螺线管：用于感应非均匀磁场中的电流6、电流表：用于测量螺线管中的电流7、导线、垫片、卡尺等实验流程：1、设置磁铁和磁感应计首先，将磁铁放置在实验桌上，接通电源，调整电源输出电压，使磁感应计的指针指向零位，然后在磁感应计的X、Y方向上分别移动感应计，测量出非均匀磁场在空间中的强度分布和方向，并记录数据。

2、测量非均匀磁场的梯度在上一步的基础上，用卡尺测量磁感应计的横向位置，然后通过计算得出非均匀磁场在该位置处的梯度。

3、测量螺线管中的电流将螺线管放置到磁铁中央的非均匀磁场区域中，接通电流表，调整电流表的零位，在电源输出电压和电流表的读数之间建立电流关系，并记录数据。

4、测量螺线管中的磁场强度和确定磁化曲线在上一步的基础上，移动指南针，测量螺线管中电流引起的磁场强度和方向，并记录数据。

可以利用磁化曲线法，通过在外界变化磁场的情况下，测量材料磁感应强度，从而确定磁场强度和磁感应强度之间的关系。

实验十六 磁化率的测定1． 摘要磁化率的测定是一个经典的磁学测量方法。

1889年Gouy [1]建立了在均匀磁场中测量磁化率的古埃法，1964年Mulay [2]设计了在非均匀磁声中测定磁化率的Faraday 法。

摩尔磁化率定义为据κ的特点将物质分为三类：κ>0称顺磁性物质；κ<0称反磁性物质；另外有少数物质的κ值与外磁场H 有关，随外磁场强度的增加而急剧地增强，且伴有剩磁现象，称此为铁磁性物质（如铁、钴、镍等）。

凡原子分子中具有自旋未配对电子的物质都是存在固有磁矩的顺磁性物质。

这些原子分子的磁矩象小磁铁一样，在外磁场中总是趋向顺着磁场方向定向排列，但原子分子的热运动又使这些磁矩趋向混乱，在一定温度下这两个因素达成平衡，使原子分子磁矩部分顺着磁场方向定向排列而得以增强物质内部的磁场，显示顺磁性。

凡是原子分子中电子自旋已配对的物质，一般是反磁性的物质。

大部分物质属反磁性。

其原因是物质内部电子轨道运动受外磁场作用，感应出“分子电流”而产生与外磁场方向相反的诱导磁矩。

一般说来，原子分子中含电子数目较多电子活动范围较大时，其反磁化率就较大。

实际上顺磁物质的磁化率除了分子磁矩定向排列所产生的χ顺外，同时还包含有感应所产生的反磁化率χ反，即：χM =χ顺+χ反由于χ顺比χ反大1~3个数量级，因此顺磁性物质的反磁性被掩盖而表现出顺磁性。

在不很精确的计算中，可近似地视χ顺为χM 。

顺磁化率与分子磁矩的关系一般服从居里定律（2.16.2）式将物质的宏观性质χM 与物质的微观性质μ联系起来，因此可通过实验测定χM 来计算物质分子的永久磁矩μ。

实验表明，对自由基或其它具有未成对电子的分子和某些第一族过渡元素离子的磁矩μ与未成对电子数n 的关系为B n n μμ)2(+= （2.16.3）联系（2.16.2）和（2.16.3）两式，可直接得到n 的表达式 11)2(84.22-++=T n n n 顺χ （2.16.4）关键词：顺磁 反磁 分子磁矩 摩尔磁化率 古埃氏天平 2． 仪器药品磁化率的测定通常可用共振法或天平法。

实验目的：1：了解核磁共振的基本原理，包括：对核自旋、在外磁场中的能级分裂、受激跃迁的基本概念的理解，同时对实验的基本现象有一定认识。

2：学习利用核磁共振校准磁场和测量因子g的方法：了解实验设备的基本结构，掌握利用扫场法创造核磁共振条件的方法，学会利用示波器观察共振吸收信号。

实验简介：自旋不为零的粒子，如电子和质子，具有自旋磁矩。

如果我们把这样的粒子放入稳恒的外磁场中，粒子的磁矩就会和外磁场相互作用使粒子的能级产生分裂，分裂后两能级间的能量差为ΔE = γhB0 （1）其中：γ为旋磁比，h为约化普朗可常数，B0为稳恒外磁场。

如果此时再在稳恒外磁场的垂直方向加上一个交变电磁场，该电磁场的能量为hν（2）其中：ν为交变电磁场的频率。

当该能量等于粒子分裂后两能级间的能量差时，即：hν = γh B0（3）2πν = γ B0（4）低能极上的粒子就要吸收交变电磁场的能量产生跃迁，即所谓的磁共振。

实验设备a) 样品水：提供实验用的粒子，氢（1H）核。

b) 永磁铁：提供稳恒外磁场,中心磁感应强度B约为Bo（实验待求）。

c) 边限振荡器：产生射频场,提供一个垂直与稳恒外磁场的交变磁场，频率ν。

同时也将探测到的共振电信号放大后输出到示波器，边限振荡器的频率由频率计读出。

d) 绕在永铁外的磁感应线圈：其提供一个叠加在永磁铁上的扫场e) 调压变压器：为磁感应线圈提供50Hz 的扫场电压。

f) 频率计：读取射频场的频率。

g) 示波器：观察共振信号。

探测装置的工作原理:图一中绕在样品上的线圈是边限震荡器电路的一部分，在非磁共振状态下它处在边限震荡状态（即似振非振的状态），并把电磁能加在样品上,方向与外磁场垂直。

当磁共振发生时，样品中的粒子吸收了震荡电路提供的能量使振荡电路的Q 值发生变化，振荡电路产生显著的振荡，在示波器上产生共振信号。

二：实验原理，实验设计思想：在微观世界中物理量只能取分立数值的现象很普遍。

一般来说原子核自旋角动量也不能连续变化，只能取分立值即：其中I 称为自旋量子数，只能取0，1，2，3，… 等整数值或1/2，3/2，5/2，… 等半整数值)1I (I p +=[右图是在外磁场B 0中塞曼分裂图（半数以上的原子核具有自旋，旋转时产生一小磁场。

实验20 霍尔效应原理及其应用实验【实验目的】1、了解活儿效应实验原理以及有关霍尔器件对材料要求的知识。

2、学习用“对称测量法”消除副效应的影响。

3、确定试样的导电类型、载流子浓度以及迁移率。

【预习思考题】1、什么叫霍尔效应？为什么此效应在半导体中特别显著？答：霍尔效应在本质上讲是运动的粒子在磁场中受洛伦兹力作用而引起偏转，最终两极板间形成电势差，使粒子受电场力和洛伦兹力平衡的现象。

因为半导体的迁移率高，电阻率适中，从而较其他材料有更强的优势。

2、采用霍尔元件测量磁场时，具体要测量哪些量？实验中如何操作才能消除副效应的影响？I I，用对称测量法可以尽可能的消除副影响。

答：霍尔电压、两输出电流,M S3、列出计算霍尔系数、载流子浓度n、电导率σ及迁移率μ的计算公式，并注明单位。

答：=单位：; n=单位：σ单位：μ μ= σ单位：2/m V s【实验原理】霍尔效应从本质上讲是运动的电子在磁场中受到洛伦兹力作用而引起的偏转。

当带电粒子（电子或空穴）被约束在固体材料中，这种偏转就导致在垂直电流和磁场方向上产生正负电荷的积累，从而形成附加的横向电场，即霍尔电场。

如图1所示的半导体试样，若在X方向通以电流，在Z方向加磁场,则试样中的载流子（电子）将受到洛伦兹力的作用，其大小为公式（1）图1 样品示意图在的作用下，电子流发生偏转，聚集到薄片的横向端面上A上，而使横向端面出现了剩余电荷，由此在Y轴方向上形成了一个横向的附加电场，称为霍尔电场，对于N型试样，方向由指向A。

电场对载流子产生一个方向和相仿的静电力,其大小为公式（2）显然，该电场的作用是阻碍载流子的进一步堆积，当载流子所受到的电场力和洛伦兹力相等时，样品两侧电荷的积累就会达到静电平衡，故有：公式（3）其中，是载流子在电流方向上的平均飘逸速度。

设试样的宽度为b，厚度为d,载流子浓度为n, 则公式（4）这时，A和之间的霍尔电势差为:公式（5）由公式（4）、（5）可得：公式（6）即霍尔电压与成正比，与试样厚度称反比。