当前位置：文档之家 › 第7章 粘性流体动力学_下

第7章 粘性流体动力学_下

  • 格式：ppt
  • 大小：844.50 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

第七章粘性流体动力学

第七章粘性流体动力学

D
x
三边长为dx， ， ， 点坐标为 点坐标为（ 三边长为 ，dy，dz，A点坐标为（x,y,z） ） 对微小平面可以为其上面具有相同的应力 由于τ的存在 表面力不垂直表面， 的存在， 由于 的存在，表面力不垂直表面，为τ 的合力方向。 和p的合力方向。 的合力方向 外法线方向为正， 设p外法线方向为正，过A点三个平面上切 外法线方向为正 点三个平面上切 力方向与坐标轴相同。 力方向与坐标轴相同。 在直角坐标系下， 上的相关应力可以 在直角坐标系下，AC上的相关应力可以 分解为 pxx τ xy τ xz
N—S方程的说明： 方程的说明： 方程的说明 a. 对理想流体 对理想流体ν=0，N—S变成欧拉微分方 ， 变成欧拉微分方 对于静止流体， 程 。 对于静止流体 ， N—S方程中的惯性 方程中的惯性 力项为0，变为欧拉平衡方程。 力项为 ，变为欧拉平衡方程。 b. N—S方程适用于不可压缩流体 方程适用于不可压缩流体 c. N—S方程适用于牛顿流体 方程适用于牛顿流体 d. 对真实流体 对真实流体N—S适用于不同流态，对 适用于不同流态， 适用于不同流态 紊流时，转变为时均流场的雷诺方程。 紊流时，转变为时均流场的雷诺方程。 e. N—S方程有 p vx v y vz 四个未知量，补 四个未知量， 方程有 充连续方程理论上可以解
p yy τ yx τ yz AD面上的应力为 pzz τ zx τ zy 面上的应力为
AB面上的应力为 面上的应力为
τ，p下标中， 第一个表示与平面垂直的 ， 下标中 下标中， 坐标轴， 坐标轴， 第二个表示与应力作用线平行 的坐标轴，这样，六个面上有18个应力 的坐标轴 ， 这样 ， 六个面上有 个应力 将六面体向A点缩小 三个面上的9个 点缩小， 若 将六面体向 点缩小，三个面上的 个 应力就表示A点的应力 因此， 点的应力， 应力就表示 点的应力 ， 因此 ， 粘性流 体中任一点的应力由9个分量组成 个分量组成。 体中任一点的应力由 个分量组成。 以过六面体中心M及平行 轴的直线为准 以过六面体中心 及平行x轴的直线为准 及平行 ，对该直线取力矩 定义：逆时针力矩为正，顺时针为负， 定义：逆时针力矩为正，顺时针为负， 对该直线力矩和为

第7章 粘性流体动力学_6

第7章 粘性流体动力学_6

u i
粘性力做功的 扩散项
ui u j ui x x i x j j
粘性力做功的 耗散项
将 ui ui ui'
vi vi vi'
p p p'
带入再分解可分别得到时均的总能量方程和脉动的 总能量方程
1 ui u j sij 2 x j xi
1877年，Boussinesq根据雷诺应力与粘性应力的相似性，假设
' ij ui'u 'j A ij t ui x j u j xi
A
2 k 3 pt 2 k / 3
0
ui u j ui ui u j ui ( ) x j x j xi x j xi x j
( ui ui ) u u u u ( p h ) i i i j t 2 x j 2 xi x j ui u j ui x j xi x j u u j i ui x j xi
第七章 粘性流体运动
湍流运动方程的模式化
（1）Boussinesq 涡粘性假设和Prandtl混合长度理论 （零方程模型） Boussinesq 涡粘性（eddy viscosity)假设（1877）将雷诺应力与时均流 场联系起来。 Prandtl 混合长度理论 Prandtl mixing length theory was presented in 1925 by Prandt. It is an oldest and most important semi-empirical theory. (实际上混合长度的概念 是英国物理学家Taylor于1915年提出) 这些紊流模型只应用到紊流的时均方程，未引入任何脉动量的微 分方程，被称为零方程模型。

流体力学第七章不可压缩流体动力学基础

流体力学第七章不可压缩流体动力学基础

第七章不可压缩流体动力学基础在前面的章节中，我们学习了理想流体和粘性流体的流动分析，按照水力学的观点，求得平均量。

但是，很多问题需要求得更加详细的信息，如流速、压强等流动参数在二个或三个坐标轴方向上的分布情况。

本章的内容介绍流体运动的基本规律、基本方程、定解条件和解决流体问题的基本方法。

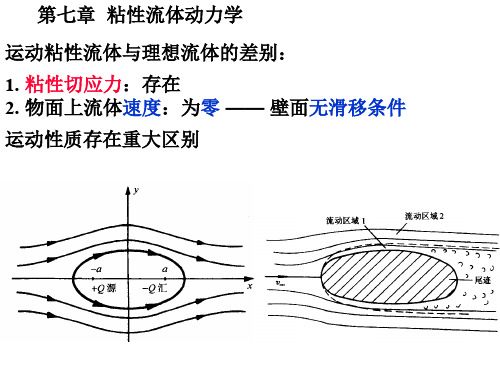
第一节流体微团的运动分析运动方式：①移动或单纯的位移（平移）②旋转③线性变形④角变形。

位移和旋转可以完全比拟于刚体运动，至于线性变形和脚变形有时统称为变形运动则是基于液体的易流动性而特有的运动形式，在刚体是没有的。

在直角坐标系中取微小立方体进行研究。

一、平移：如果图（a ）所示的基体各角点的质点速度向量完全相同时，则构成了液体基体的单纯位移，其移动速度为z y x u u u 、、。

基体在运动中可能沿直线也可能沿曲线运动，但其方位与形状都和原来一样（立方基体各边的长度保持不变）。

二、线变形：从图（b ）中可以看出，由于沿y 轴的速度分量，B 点和C 点都比A 点和D 点大了dy yu y ∂∂，而yu y ∂∂就代表1=dy 时液体基体运动时，在单位时间内沿y 轴方向的伸长率。

x u x ∂∂，y u y ∂∂，zuz ∂∂ 三、角变形（角变形速度）ddd DCABCDBAdt yu dy dt dy y u d x x ∂∂=⋅∂∂=α dt x udx dt dx x u d yy∂∂=⋅∂∂=β θβθα+=-d d 2βαθd d -=∴ 角变形： ⎪⎪⎭⎫⎝⎛∂∂+∂∂=+=-=x u y u d d d y x z 212βαθαθ ⎪⎭⎫⎝⎛∂∂+∂∂=x u z u z x y 21θ⎪⎪⎭⎫⎝⎛∂∂+∂∂=y u z u z y x 21θ 四、旋转（旋转角速度）⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=-=y u x u x y z 21θω ⎪⎪⎭⎫⎝⎛∂∂-∂∂=z u y u y zx 21ω 即， ⎪⎭⎫⎝⎛∂∂-∂∂=x u z u z x y 21ωzyxu u u z y x k ji ∂∂∂∂∂∂=21ω 那么，代入欧拉加速度表达式，得：z x x x x x x z y y z z y y y y y y y x z z x x z z z z z z z y x x y y x x y du u u u u u u u dt t xu u u u u u u u dt t y u u uu u u u u dt t z αθθωωαθθωωαθθωω∂∂⎫==++++-⎪∂∂⎪∂∂∂⎪==++++-⎬∂∂⎪⎪∂∂∂==++++-⎪∂∂⎭各项含义： （1） 平移速度（2）线变形运动所引起的速度增量（3）（4）角变形运动所引起的速度增量 （5）（6）微团的旋转运动所产生的速度增量流体微团的运动可分解为平移运动，旋转运动，线变形运动和角变形运动之和。

第7章_理想流体动力学基本方程

第7章_理想流体动力学基本方程

④列动量方程求解。
Fx p1A1 p2 A2 cos Rx Qv2x v1x
Fy p2 A2 sin Ry Q v2y v1y
Fx p1A1 p2 A2 cos Rx Qv2 cos v1
Fy p2 A2 sin Ry Qv2 sin 0
Rx p1A1 p2 A2 cos Qv2 cos v1
动量方程：反映了流体的动量变 化与外力之间的关系
粘性流体：实际流体都具有粘性。既有粘性切应力，又有法向压应力。
0
理想流体：理想流体可忽略粘性。即无粘性切应力，只有法向压应力。
0
粘性流体：
理想流体：
一、动量方程——流体的运动方程
1、积分形式的动量方程——流体的运动方程
质点系的动量定理：
系统的动量对时间的变化率等于作
第7章 理想流体动力学动量方程
粘性流体：实际流体都具有粘性，致使所研究的问题比较复杂。 理想流体：指粘性为零的流体，实际上并不存在，但在有些问题
中，粘性的影响很小，可以忽略不计，致使所研究的 问题简单化。 理想流体动力学规律可以应用于粘性的影响很小的实 际流体中，所以本章的研究具有实际意义。
主要内容
过流断面是均匀流或渐（缓）变流断面不可压缩流体
Fx Q(2v2x 1v1x ) Fy Q(2v2 y 1v1y ) Fz Q(2v2z 1v1z )
④当沿程有分流和汇流时：
Fx (3Q3v3x 2Q2v2x 1Q1v1x ) Fy (3Q3v3y 2Q2v2 y 1Q1v1y ) Fz (3Q3v3z 2Q2v2z 1Q1v1z )
对1-1，2-2断面列伯努利方程
p1 v12 p2 v22
g 2g g 2g
v1 1.42m / s v2 3.18m / s

粘性流体动力学

粘性流体动力学

§3 牛顿流体的本构关系z本构关系应力张量P和变形速率张量S之间的关系，这是与物质结构有关的，通常称为“本构方程”。

z本构关系建立的原则1. 坐标系不变性原则：本构关系必须不依赖于坐标系的选择，以张量形式来表示可确保这一原则得以满足。

2. 物质客观性原则：本构关系描述的是流体固有的力学性质，与流体本身的刚体运动或观察者的运动无关。

3. 材料元行为依赖原则：一个材料元的行为只依赖于材料元自身形变的历史，而与相邻材料元的状态无关。

§3 牛顿流体的本构关系Stokes关于应力与变形速率之间一般关系的三条假定：（1）应力与变形速率成线性关系；（2）应力与变形速率的关系在流体中各向同性；（3）在静止流体中，切应力为零，正应力的数值为静压强p。

§5 粘性流体运动的基本特征1. 机械能的耗散性1[()]1[()]P V p V P V ρφρ∇=−∇+∇ i i i i i ＋表面力作功：对流体作的可逆膨胀功用以增加流体宏观运动的动能粘性耗散功变成热能，使内能增加导致熵增。

2. 粘性流体运动的有旋性3. 粘性流体中旋涡的扩散性§6 关于N－S方程的求解途径可采用近似方法求解的主要有下列两种情况：小雷诺数Re情况：此时粘性力较惯性力大得多。

可以全部或部分地忽略惯性力得到简化的线性方程。

大雷诺数Re情况：在贴近物面很薄的一层“边界层”中，考虑粘性的影响，而在边界层外，仍可将粘性全部忽略。

边界层理论。

对于中等雷诺数Re的情况：惯性力和粘性力都必须保留，利用数值计算方法求N－S方程得到数值解。

§7 圆管中粘性不可压缩流体的定常层流流动（Hagen-Poiseuille 流动）1. 问题的提法zxy 12l p 1p 2无限长水平园管内的粘性不可压缩流体的定常层流流动，假定质量力可略去不计，已知园管直径为D ，轴向压力梯度为常值。

欲求速度分布剖面、流量及管道中的阻力系数。

《工程流体力学》第七章 粘性流体动力学

《工程流体力学》第七章 粘性流体动力学

x方向 ： 1)表面力：作用在左右两面上力的合力：
作用在上下两面上力的合力：
作用在前后两面上力的合力：
作用在整个六面体上表面力沿x轴方向的合力：
2) x方向质量力 ： 单位质量流体受到的质量力分量：X;
六面体受到的质量力： Xrdxdydz
牛顿第二定律：
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式：
应力：各向同性
运动粘性流体：存在法向、切向表面力 应力：各向异性
流体中：任一点c ：绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz：定义c上的应力
需要2个下标表示：9个应力分量
第1个下标i：应力作用方向 第2个下标j：作用面方向
第七章 粘性流体动力学
运动粘性流体与理想流体的差别： 1. 粘性切应力：存在 2. 物面上流体速度：为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力： 1.质量力：与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法：和理想流体相同
2. 表面力： 静止和运动理想流体：仅存在指向作用面法向表面力
由于外部无粘流：受到分离流的排挤 明显改变：其中压强分布 实际计算：用实测物面压力分布计算分离点前附面层流动 附面层分离：使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生：是工程上一个重要问 题
边界层分离后：形成尾涡区 尾涡区压强：基本上等于分离点压强 压强：上下对称 若将压强在圆柱面上积分：则得压差阻力
流体在y+l层时均速度：

《工程流体力学》第七章 粘性流体动力学

附面层厚度d：从外边界到物面的垂直距离
2.附面层位移厚度d*: 设物面P点附面层厚度d ，在垂直于纸面方向取单位宽度，
则该处通过附面层的质量流量：
通过同一面积理想流体流量：
ro, Vo —— 附面层外边界处理想
流体的密度和速度
以d*高度作一条线平行于物面，
使两块阴影处面积相同：
即在流量相等条件下将理想流体流动区从物面向外移动了
流体绕物体流动，整个流场分为三个区域：
1)附面层： 流速：由壁面上零值急剧增加到自由来流速度同数量级值 沿物面法线方向：速度梯度很大
即使流体粘性系数小：粘性应力仍可达到一定数值
由于速度梯度很大： 使得通过附面层物体 涡旋强度很大，流体 是有旋的
2)尾迹流： 附面层内流体：离开物体流入下游，在物体后形成尾迹流
各物理量都是统计平均值， \ 瞬时物理量＝平均物理量＋脉动物理量， 对整个方程进行时间平均的运算。
一、常用时均运算关系式：
时均运算规律：
推论：脉动量对空间坐标各阶导数的时均值=0。
二、连续方程：对二维流动，瞬态运动连续方程 进行时均运算：
\ 可压缩紊流运动连续方程：
进行时均运算： 上两式相减：
\ 附加法向应力
法向应力： l： 比例系数，与体积变化率有关
三个法向应力平均值的负值：为粘性流体在该点压强
最后得表面应力与变形率之间的关系：
第二节 粘性流体运动的基本方程
一、连续方程：
粘性流体运动：服从质量守恒定律 连续方程：不涉及力的作用 仍能得出与理想流体相同形式的方程
二、运动微分方程： 粘性流体中：微元六面体 微元六面体中心：c
三、雷诺方程： 二维不可压缩粘性流，不考虑质量力，N-S为：
对上式进行时均运算：

第7章 粘性流体动力学_3(N--S)


正方形截面
a
圆管内的定常层流运动
讨论速度分布、流量及阻力 。 dp
dx
r
：压力梯度；
置，截面上压力均布。 0
1. NS方程（柱坐标系（r,θ,z）中）：
v2 Dv r v 1 p 2 v fr 2 vr 2 r 2 Dt r r r r Dv v r v 1 p 2 v r v 2 f v 2 2 Dt r r r r Dv z 1 p 2 fz v z Dt z D 2 1 1 2 2 2 vr v vz 2 2 2 2 Dt t r r z r r r r z
边界条件：r 0 处 u 有限值，得 c1 0
r a
0
a 2 dp c2 4 dx
速度分布为
u
1 dp 2 a r2 4 dx


若 l 长度管道内压力降 速度
d p p p p1 p2 0 则 dx l
1 p 2 u a r2 4 l
dp d 2u d 2u 2 2 x dy dy
u y U
1 dp y 2 u Ay B x 2
y 0, u 0 y h, u U
y y y P 1 , h h h
h 2 dp 其中P 2U dx
——（Hagen-Poiseuille定律，1939）。
4 a 成正比， p Q 圆管内的流量 与压力降 、半径
而与粘性系数 及管长 l 成反比。
4.阻力及阻力系数（层流）
剪应力分布:
u p r r 2l 1 p 2 u a 管壁剪应力： 0 0 m 8 2l

粘性流体动力学的数值模拟与分析

粘性流体动力学的数值模拟与分析粘性流体动力学是涉及流体运动和其内部粘性的物理学领域。

在许多工程和科学领域中，对粘性流体的数值模拟与分析具有重要意义。

本文将介绍粘性流体动力学数值模拟的基本原理、常用数值方法以及分析结果的评估。

一、粘性流体动力学的基本原理粘性流体动力学研究的基础是纳维-斯托克斯方程（Navier-Stokes equations），它描述了粘性流体的流动。

纳维-斯托克斯方程由连续性方程和动量方程组成，在实际计算中，还需要考虑能量方程和相对运动的边界条件。

二、粘性流体动力学数值模拟的方法1. 有限差分法（Finite Difference Method）：有限差分法是最早被应用到计算流体力学的数值方法之一，它通过将连续性方程和动量方程分别离散化，将微分方程转化为差分方程，进而使用差分方程进行数值计算。

2. 有限体积法（Finite Volume Method）：有限体积法将流体域划分为小的控制体积，通过积分的方式得到物理方程的离散形式，然后通过迭代求解差分方程，得到流体的数值解。

3. 有限元法（Finite Element Method）：有限元法通常用于解决边界复杂的流体问题。

它将流体问题转化为边界值问题，并将流体区域离散化为无数小的单元，通过有限元方法求解流体的数值解。

4. 计算流体动力学方法（Computational Fluid Dynamics, CFD）：CFD是一种基于数值模拟的流体力学方法，通过将流体域划分为网格，将纳维尔-斯托克斯方程离散化数值求解，模拟流体在不同条件下的行为。

三、粘性流体动力学数值模拟的分析1. 利用数值模拟可以得到流体在不同条件下的速度场、压力场等相关参数。

通过分析这些数据，可以对流体的流动行为进行定量描述。

2. 可以通过数值模拟分析流体的粘性特性和流动特性，包括流体的粘滞性、阻力、湍流等。

这些分析结果对于工程设计和优化具有重要指导意义。

3. 数值模拟还可以用于研究流体流动中的复杂现象，如乱流、湍流、涡旋等。

粘性流体动力学基础

⎩
= τ xz
=
μ ( ∂vz
∂x
+
∂vx ) ∂z
=
2με zx
五、法向应力与变形速度的关系
在理想流体中，同一点各个方向的法向应力（压强）与作用的方位无
关而且相等，即： pxx = pyy = pzz = p 但在粘性流体中，流体微团除了发生角变形（角变形引起切应力）,同时
发生直线变形，使微团产生拉伸或压缩。
方程。 N-S 方程表示了质量力、表面力、粘性力、惯性力的平衡关系（∑ Fv = m av ）。
一、实际流体中的应力 在讨论理想流体（平衡流体）时，作用在流体微团表面上的力只有一
个与表面垂直的压应力，这个压应力称为理想流体的动压强（= 平衡流体 的静压强）。其特性为：1）方向沿作用面的内法线方向，2）大小与作用 面的方位无关。
对于实际流体，由于具有粘性，不仅在表面应力中存在切向应力，而 且在法线方向上也不再具有理想流体中的与方位无关的性质。
在实际流体中，一点处的三个方向的应力由于切应力的存在，不再 垂直于作用面，而与作用面斜交，即具有某一方向，应写成，
pvx ， pv y ， pvz 对任一面积，设作用在其上任一点的表面应力为 pv ，如图所示， pv 分解 为：
第七章 粘性流体动力学基础
实际流体都是有粘性的,粘性流体运动中不可避免地存在阻力、衰减 和扩散现象，运动时总是伴随着内摩擦和传热过程，发生能量损耗。
对于每一个具体的流动问题来讲，粘性所起的作用不一定相同。对于 某些问题，例如求解流体作用于被绕流物体上的升力、表面波的运动等， 粘性的作用并不是占支配地位，因而可以应用非粘性流体力学（理想流体 动力学）理论，可以获得较满意的结果。而对另一些问题，例如求解运动 流体中的粘性阻力、旋涡的扩散，以及能量的传递等，粘性的作用已占主 导地位，若忽略粘性的存在，将导致完全不符合实际的结果。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例7-2 输水管路系统
Given：
=0.5 H=5m =0.3 l3 =0.4
=2
d， e，li，H； ；
Find：流量 Q
=0.4
um1
A um2 l2
l1 B l4 =3 (对总流)
=1.5 (对总流)
f (Re,
e
d
)
Solution:
• 设阻力平方区湍流:
e
d 0.0163
u u p ij u iu j v u w u
湍流应力 Reynolds应力
是对称张量,六个独立量。它源于湍流脉动引起 的动量输运。因此，湍流应力 u iu j 是和平均流关联的。
pij p ji
0 const
If Rei < Re0
Re 2 u m 2 d 87600 Re 0
湍流运动方程组的封闭性：
方程数：4个
u 未知量： i , p , pij （6个）共10个 补充方程：湍流应力与平均速度之间的关系式——湍流模式。
7.6 Prandtl 混合长度理论（半经验）
基本思想：把湍流中微团的脉动与气体分子的运动相比拟。
层流：
l
du dy
（分子运动）
du dy
u 2.5 ln y 5.5,
( y 30 )
au
最大速度： 平均速度： 亏损定律：
u max u
2.5 ln

5.5
u m u max 3.75 u
u max u u
2.5 ln
a y
n
——水力光滑和水力粗糙管
n
u y u yu 指数定律： c n u u max a
总流量等于各支管流量之和。
Q Q1 Q 2 (节点条件 )
支管流量由支管阻力系数确定
例7-1
铸铁输水管路
Given： L、d、Q、h 滤水网1个 5.2 ，90弯头10个 ( 0.48 ) ，
( 0.08)
1.3mm 2 / s
e 1.3mm
求： 所需水泵压头。 解：出口2与水泵轴线在同一水平面上。 1和2截面能量方程：
u (u i u j ) p i 2 ui ( u iu j ) x j x i x j t
2 ui
——平均运动的粘性应力
u v v v w v u w v w w w
2g
z1 H T
p2

2
2g
z2 h
动能修正系数：
2 （层流） 1 (湍流）
扬程
流动损失
2 2
动力源的功率： N QH T
2.流动损失
h h f h
z 1 1 水泵 水池
沿程损失（管路粘性摩擦损失）
h f l u
2 m
d 2g
Re 0 6 10 4
=0.5
d， e，li，H； ；
=2 =0.4
H=5m
=0.3 l3 =0.4
um1
A um2
l1 B
0 0.045
Moody
l2
l4
=3 (对总流)
=1.5 (对总流)
• 水平支管能量方程：
2 2 l1 u m1 l2 u m 2 2 2 1 1 d1 i 2 g d 2 i 2 g
， f (Re,
e
d
) , Re
um d

o
局部损失（局部范围流动旋涡、转向或撞击引起）
h
2 um
2g
—局部损失系数
阀门
2 2
z 1 1
水泵 水池
o
3.管路计算
简单管路：——查到 ， 后应用能量方程
串联管路：直径或粗糙度不同的简单管路串在一起
2 2 l um um h h f h d 2 g 2 g i i i i i i
• 各种部件（弯头、阀门、突缩结构、
扩张结构和分叉等）。
三类问题：
• 给定管路尺寸和流量，确定管路压降（损失），选择动力头；
• 给定管路尺寸和压降（动力头），确定流量； • 根据给定的流量和压降，设计管路尺寸（管径）。
1. 能量方程
p1
u mi Q / Ai
轴线位置
2 um2

1
2 u m1
u m1 um2
0 .87
iteration
u m1 u m 2 u m
u m1 0.465 u m , u m 2 0.535 u m
um 2.05( m / s ), Q 10.3 (l / s )
• 整个管路能量方程： • 验算：
0
Re1 u m1d 76400 Re 0

d
Prandtl 近壁假设：核心区 0 常数， l ky
( t )
du dy l (
2
du dy
)2 0
对数定律：
u u

1 k
ln
yu

c
（Nikuradse实验） ——水力光滑管
y a
k 0 .4 ,
c 5 .5
2 m 2
um
速度分布公式
f (Re,
e
d
)
层流：解析解 光滑管或粗糙管湍流：理论方法、经验或半径公式（实验）。
五个区域——层流区、临界区、光滑管区、过渡区、完全湍 流粗糙区。
Nikuradse管流实验曲线：
f (Re, e
d )
人工粗糙度
1
1. 层流区 (Re 2300 )

17
Re 3.2 10
6
光滑管
Blasuis 1/7次方规律： u y ， Re 10 5 u max a
根据比值
um u max
测定管中最大流速求平均流速、流量。
管流速度剖面 层流：抛物型
Re=106
Re=104 Re<2000
湍流：指(对)数型（丰满）。Re愈大愈接近于平均速度。
4. 水力粗糙管湍流核心区速度分布
(
e u 60 )
Nikuradse实验：k=0.4 、c=8.5，得到
u u 2.5 ln y
e
a
8 .5
um u
2.5 ln
e
4.75
e
d
7.7.3 圆管中的摩擦阻力系数
u 0 u 8 8 um 1
并联管路：在某处分成几路，后汇合成一路。 分叉点处流动连续，各支管流动损失相等：
h1 h2 (环路条件 )
2 2 u m1 um2 l1 l2 1 d 1i 2 g 2 d 2 i 2 g i i 1 2
湍流核心区 过渡区 2 层流底层 d 340..875
d Re
e
e
d
——管壁的绝对粗糙度 ——相对粗糙度
e (a)
d
e (b)
d
7.7.2 圆管内的湍流速度分布(5个区域)
1.层流底层
u
(y d ):
yu

du dy

0
u y
0
（y从壁面算起）
HT h
2 um
2 2
2g
um d
h
um
5
Q
z
水泵 1 1 水池
d 4
2
3.18m / s
o
由
Re

4.9 10
e
d
0.0065
查Moody图得： 0.033
2 l um 500 3.18 2 h 5.2 10 0.48 2 0.08 0.033 47 .8m d i 2g 0 .2 2 9 .8 i 3.18 2 于是 H T 5 2 9.8 47 .8 53 .3m
64 Re
1次方阻力区
h f u m
2.过渡区 (2300 Re 4000 ) 流动不稳定，可能是层流，也可能是湍流。
3.流水力光滑区
4000 Re 105：
4000 Re 26.98 d e 8 7
（1.75次方阻力区）
1.75

0.3164 Re
0.25
h f u m
（1/7次方规律）
d 4000 Re 26.98 ： e
8 7
1

2.0 lg Re 0.8


(Karman-Prandtl公式)
26.98 d e 8 7 Re 4160 d 2e 0.85 4.湍流粗糙管过渡区
0 y
u u u ,
u u

yu
（ u
— 壁面剪应力速度）
记
y

，无因次速度分布：
y u 11 arctan 11

u y ( y 5)
2.过渡层(5 y 30 )

：
e u e 4, y 30 ) ： 3. 水力光滑管湍流核心区 (
连续方程