分数中的单位“1”的认识

分数中的单位“1”的认识1. 引言在数学中，分数是一个常见的概念。

在分数中，我们经常会遇到一个特殊的单位——“1”。

虽然它看似简单，但它在分数的表示和运算中却有着重要的作用。

本文将深入探讨分数中的单位“1”的认识，包括它的定义、常见形式及在运算中的应用。

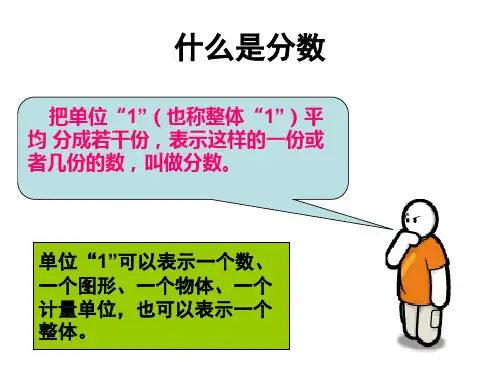
2. 分数中的单位“1”定义在分数中，单位“1”表示一个整体。

举个例子，当我们说“有1/2个苹果”的时候，实际上是指一个苹果被平均分成了2份，而“1”就代表了其中一份。

这种表示方法可以帮助我们更好地理解分数的概念，将整体分成若干等分。

3. 分数中的单位“1”常见形式在分数中，单位“1”的形式有很多种。

下面是一些常见的形式：•分数形式：比如1/2、1/4、1/10等，在这种形式中，“1”表示整体被等分成的份数之一。

•假分数形式：比如3 1/2、2 3/4等，在这种形式中，“1”表示整数部分所代表的整体，后面的分数部分表示剩余部分。

•百分数形式：比如100%、50%等，在这种形式中，“1”表示整体被平均分成100份，而百分数则表示所占的比例。

这些形式中的单位“1”在不同的情境下有着不同的含义，但总的来说，它们都表示一个整体。

4. 分数运算中的单位“1”应用在分数的加、减、乘、除等运算中，单位“1”起着重要的作用。

下面是一些示例：•加法：当我们将1/3和2/3进行相加时，实际上是将两个等分的整体合并在一起，得到的结果是3/3 = 1。

•减法：当我们将1/2从2/3中减去时，实际上是从两个等分的整体中减去一部分，得到的结果是1/6。

•乘法：当我们将1/4乘以2/3时，实际上是将一个等分的整体分成4份，并取其中的2份，得到的结果是2/12 = 1/6。

•除法：当我们将1/4除以1/8时，实际上是将一个等分的整体分成4份，并取其中的8份，得到的结果是8/4 = 2。

通过以上的例子，我们可以看到，在分数的运算过程中，单位“1”起到了将整体分成若干等分的作用，使得我们能够更好地描述和计算分数。

学生运用分数的有关知识，根据以上条件说出是以哪个数量为单位“1”的。在学生说话的过程中，很自然地复习了分数及单位“1”的有关知识，为学生进一步组合应用题及进行分数乘除法应用题的对比打下基础。并且使学生感受到数学就在自己身边，数学并不难。
二、导入新课
我们复习了分数乘、除法应用题的数量关系。通过上题发现，有很多题的叙述形式很相似，但解题方法却大不相同。为什么不相同呢？今天我们就来研究稍复杂的分数乘除法的应用题，对比、区别它们之间的异同点。（板书课题）
（1）观察讨论。
（2）全班交流。
（3）师生归纳。
这两道题都是把篮球看作单位“1”，而且单位“1”的量是未知的，因此要设单位“1”的量为，根据一个数乘以分数的意义找出等量关系列方程解答。熟练之后也可以直接列除法算式解答。
3、教师小结。
这是本节课的重点，也是本节课的难点。在这里，让学生通过小组讨论，自己进行对比，学生之间既要各抒己见，敢想敢说，敢于问出心中的疑惑；又要认真倾听对方的思路和想法，学会比较、分析。这样，数学课堂就成为全体学生之间进行交流、合作的活动中心。课堂上学生之间的交流与合作，是体现学生主体性的一个重要标志，也是形成信息多向交流和反馈的新型课堂教学结构的重要活动方式。就学习而言，已有认知结构是学生学习的出发点，每个学生总是以自己的认知方式和在已有经验的基础上进行学习的。因此，在数学课堂上学生与学生之间的交流与合作，既可使学生从多角度看问题，也可使学生通过对比发现自己存在的问题。合作与交流，能让所有的学生都体验到成功的喜悦。
三、学习新知
（一）出示例题。（板书在黑板上）
1、学校有20个足球，篮球比足球多，篮球有多少个？
2、学校有20个足球，篮球比足球少，篮球有多少个？
3、学校有20个足球，足球比篮球多，篮球有多少个？

什么是分数
把单位“1”（也称整体“1”）平 均 分成若干份，表示这样的一份或 者几份的数，叫做分数。
单位“1”可以表示一个数、 一个图形、一个物体、一个 计量单位，也可以表示一个 整体。
§一、单位“1”表示一个数
1
• 例：1的二分一是多少？（答：是 ）
2
以上问题表示的意义：即把数字“1”平均分成二份，每 份是多少。
这里把数字“1”看成了整体单位“1”。
如果问一个数的几分之几是多少？用乘法。即用这个数乘 以几分之几。
1
1
如上题：1× 2 ＝ 2
1 • 例2：28的四分一是多少？（答：是 7 ）
以上问题表示的意义：即把数字“28”平均分成 四份，每份是多少。
这里把数字“28”看成了整体单位“1”。
如果问一个数的几分之几是多少？用乘法。即 用这个数乘以几分之几。
注意：并不是所有的物体都可以 看作单位“1”。因为许多事物 是不能平均分的。
§四、单位“1”表示一个整体
例1：六（1）班有125人，平均 分成五组，每组多少人？
这里把六（1）班125人看成一个整
体。平均分成五份。
125
1
× 5 ＝ 25
把六（1）班125人 看成了一个整体。 分成五份。
我们16个可以看成整 体“1”。我们可以分
成四组玩。
把我们16个熊猫看 成了一个整体。分 成四份。
例1：
Байду номын сангаас
每份是 1
3
把一个图形圆平均分成三份。 这里把这个圆看成了整体“1”。
§二、单位“1”表示一个图形
例2：
每份是 1
4
∠A
把一个角平均分成四份。 这里把这个角看成了整体“1”。

如何找分数应用题中的单位"1"准确找出单位“1”，是解答分数应用题的关键。

每一道分数应用题中总是有关键句。

如何从关键句中找准单位“1”，下面方法仅供参考。

一、部分数和总数在同一整体中，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，即单位“1”。

例如：（1）我国人口约占世界人口的1/5，世界人口是总数，我国人口是部分数，所以，世界人口就是单位“1”。

（2）食堂买来100千克白菜，吃了2/5，吃了多少千克？在这里，食堂买来100千克白菜是总数，吃掉的是部分数，所以100千克白菜就是单位“1”。

二、比较两种数量关系分数应用题中，两种数量相比的关键字句非常多。

有的是“比”字句，有的则没有“比”字，在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。

例如：六（2）班男生比女生多1/2。

就是以女生人数为标准（单位“1”），男生比女生多的人数作为比较量。

在另外一种没有比字的两种量相比的时候，而是带指向性特征的“占”、“是”、“相当于”，看“占”谁的，“相当于”谁的，“是”谁的几分之几。

这个“占”，“相当于”，“是”后面的数量就是单位“1”。

例如，（1）一个长方形的宽是长的5/12。

它以长作为标准，宽和长相比较，“是”的后面也就是说长就是单位“1”。

（2）今年的产量相当于去年的4/5倍。

那么“相当于”后面的“去年的产量”就是标准量，也就是单位“1”。

三、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。

这类分数应用题的单位“1”比较难找。

例如，水结成冰后体积增加了1/10，冰融化成水后，体积减少了1/10。

象这样的水和冰两种数量到底谁作为单位“1”？两句关键句的单位“1”是否相同？用上面的两种方法不容易找出单位“1”。

因此我们只要看，原来的数量是谁，谁就是单位“1”，例如：水结成冰，原来的数量就是水，那么水就是单位“1”。

分数的意义和单位一分数的意义和单位一分数是数学中一种常见的表示方法，它代表了一个整体被分成多个部分的数量关系。

分数由两个数值组成，分母表示整体被分成的等份数量，分子表示其中的部分数量。

例如，1/4表示一个整体被分成4等分，其中有1份。

分数的意义在于它可以用于描述各种实际情况中的比例、比率和部分关系。

无论是商业活动中的利润分配、化学反应中的物质比例、物理运动中的速度比例，还是食谱中的原料配方，都可以通过分数来详细描述和解释。

分数中，分子和分母都有着重要的意义。

分子表示部分的数量，可以帮助我们理解整体中的具体部分有多少。

而分母表示等份的数量，可以帮助我们理解整体被分成了多少部分。

分子和分母之间的比值关系也是分数的重要组成部分，它帮助我们理解整体与部分之间的数量比例。

单位一是指分数中分母为1的情况。

当分母为1时，分数的意义更为简洁和明确，不再需要表示整体被分成多少等份，而只需要关注部分的数量。

单位一的分数可以更加直观地描述整体中的具体部分数量，并且能够更轻松地进行比较和计算。

在日常生活中，单位一的分数经常被用于描述百分比、概率、比率等情况。

例如，50%表示一个整体中的一部分，分数为1/2，表示整体被分成2等份，其中有1份。

在化学实验中，溶液的浓度常常用分数表示，如1mol/L表示1摩尔的溶质溶解在1升溶剂中。

使用单位一的分数可以使得数学计算更加方便和灵活。

当计算两个具有相同单位的分数时，只需对分子进行加减运算，分母保持不变。

当计算两个具有不同单位的分数时，只需将它们的分母相乘得到新的分母，再进行分子的加减运算。

这简化了计算过程，提高了计算的效率。

另外，单位一的分数还可以通过乘除法来实现数量的缩放。

例如，将一个单位一的分数乘以2，就相当于将部分的数量翻倍，即变成了2份。

同样地，将一个单位一的分数除以2，就相当于将部分的数量减半，即变成了1/2份。

这种数量缩放的特性为问题的解决提供了更多的可能性。

综上所述，分数作为一种表示比例、比率和部分关系的常见方法，具有重要的意义。

小学五年级数学教案：分数中的单位“1”的认识(1)1．进一步认识单位1，从而加深对分数意义的理解．2．渗透辩证唯物主义观点的启蒙教育．教学过程一、复习．分别说出下面各个分数所表示的意义．说明：一个物体、一个图形、一个计量单位，都可以看作单位1．二、新课．1．看图列式．＋＝＝1 ＋＋＝＝1说明：我们是把这堆小方块看作一个整体，即单位1表示由9个小方块组成的整体．2．练一练：看图填空．（1）把一堆皮球（9个）看作单位1．黑皮球占，白皮球占，花皮球占＋＋＝＝1（2）把一批书（11本）看作单位1．语文书占，数学书占，英语书占＋＋＝＝1小结：单位1不仅可以代表自然数1，代表一个物体、一个图形、一个计量单位，还可以表示由一群物体组成的一个整体．如：一堆苹果，一盒粉笔，一个班的人数，一个月的生产任务，一项工作等等．三、巩固练习．1．我校共有24个班，每班占全校班级数的几分之几？把什么看作单位1？2．把全班学生平均分成4个小组，每个小组占全班学生的几分之几？把什么看作单位1？教师说明：用单位1表示一个整体时，整体包含的数量可大可小，并初步知道部分和整体是相对而言，是可以转化的．3．把一盘苹果（4只）看作单位1，平均分成4份，每一份占这盘苹果的，有（）个苹果．4．（出示12只苹果）现在把（）个苹果看作单位1，这堆苹果的有（）个苹果．教师追问：同样是，为什么苹果的个数不一样？（因为单位1不同，所以它们的所表示的个数也不同）教师说明：在具体问题中，由于单位1包含的数量可大可小，所以同样的一个分数，所表示的具体数量是不一样的．5．看图回答问题．红色方块占总数的红色方块占总数的教师提问：红色方块同样是3块，为什么会出现两个不同的结果？若要使3块红色方块占总数的，应该怎么办？6．指出下面各题中是把什么看作单位1的，说说各分数表示的意义．（1）花皮球占这堆皮球的（2）语文书的本数占这批书的（3）男生人数是数学兴趣小组人数的（4）陆地面积占地球表面积的（5）空气中的氧气约占（6）的鸡是母鸡（7）一堆煤，运走了，烧去了吨（对比和吨）思考题：姐姐、妹妹和弟弟3人做一堆花，姐姐做5朵，妹妹做4朵，姐姐做的占这堆花的．弟弟做了多少朵？。

小学数学中关于单位1的解析一、关于单位1的理解目前，关于单位“1”的定义并不是很明确具体，它只是在分数学习中比较常见，总的来说，是一个算术概念。

单位“1”是指把一个整体的量当做一个整体、单位。

一段时间、一段距离、一块面积都可以当做整体“1”。

它既可以是一个用于计数的单位，也可以被当成相同计数共同构成的一个整体。

在小学数学中，它具有以下数学意义：第一，指的是原有量的一个单位。

即构成原有量的部分――更小量，例如一项任务要4个小时才能完成，而每个小时完成的任务量就代表了一项任务的单位。

也可以指的是能够变成比“1”还小的数的单位，即分数，是平均把整体一划分成几份或者无数份的分数。

第二，单位“1”可以用分数进行表示，是和原有量单位相同的其他量，是其他量的对应的一个分率。

原有量产生的分数，一般被当成切分法，其中的整体“1”是分数中的分子，而其他量中的产生分数，一般被当成量比法，其中的整体“1”是分数中的分母。

在数学中，单位“1”同与自然数1既相区别又相联系，教师在教学中应注意引导学生正确看待两者之间的差别与关系，才能促使学生答题。

单位“1”指的是一个量，而自然数的1只是文字符号的代表，前者能够用来等分，而后者不可以。

其次，单位“1”是一个尺度的标准，被确定于度量过程之前，是一个量。

因此，学生在学习数学时，要掌握定义上的不同，不能将其混淆，加大解题难度。

二、学生确定单位1的几点诀窍任何一个分数应用题都会有包含分率的语句，而其中包含分率的就是解决数学分数应用题的重点。

学生可以从以下几个方面进行学习，提高解题的技巧。

1.理清总数与部分数总数与部分数在处于同样的整体时，通常容易被比较，总数一般是标准量，部分数一般是比较量，这意味着总数就是学生要找的单位“1”。

学生在进行实际的解题时，应理清题目中的总数以及部分数，主要确定好总数，就找到了单位“1”。

例如，在以下这些题中：假设小明父母从蛋糕店买了一个蛋糕，总共有500克，吃了其中的■，那么总共吃了多少克？在这道题中，一共买的蛋糕是总数，吃完的属于部分数，因此题中的500克就是学生要找的单位“1”。

如何确定分数乘除法应用题中的单位1（只要找出关键字，关键字后面的就是单位1）正确找准单位“1”，是解答分数（百分数）应用题的关键，每一道分数应用题中总是有关键句（含有分率的句子）。

如何从关键句中找准单位“1”，我觉得可以从以下这些方面进行考虑。

一、部分数和总数在同一整体中，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，那么总数就是单位“1”。

例如我国人口约占世界人口的1/5，世界人口是总数，我国人口是部分数，所以，世界人口就是单位“1”。

再如，食堂买来100千克白菜，吃了2/5，吃了多少千克？在这里，食堂一共买来的白菜是总数，吃掉的是部分数，所以100千克白菜就是单位“1”。

解答这类分数应用题，只要找准总数和部分数，确定单位“1”就很容易了。

二、两种数量比较分数应用题中，两种数量相比的关键句非常多。

有的是“比”字句，有的则没有“比”字，而是带有指向性特征的“占”、“是”、“相当于”、“正好”。

在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。

例如：六（2）班男生比女生多1/2。

就是以女生人数为标准（单位“1”），男生比女生多的人数作为比较量。

在另外一种没有比字的两种量相比的时候，我们通常找到分率，看“占”谁的，“相当于”谁的，“是”谁的几分之几。

这个“占”，“相当于”，“是”后面的数量——谁就是单位“！”。

例如，一个长方形的宽是长的5/12。

在这关键句中，很明显是以长作为标准，宽和长相比较，也就是说长是单位“1”。

又如，今年的产量相当于去年的4/3倍。

那么相当于后面的去年的产量就是标准量，也就是单位“1”。

三、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。

这类分数应用题的单位“1”比较难找。

例如，水结成冰后体积增加了1/10，冰融化成水后，体积减少了1/12。

象这样的水和冰两种数量到底谁作为单位“1”？两句关键句的单位“1”是不是相同？用上面讲过的两种方法不容易找出单位“1”。

分数应用题解题技巧（一）——单位“1”的确定（含例题）我们知道，在分数乘、除法应用题中：分率对应的量＝单位“1”×分率单位“1”＝分率对应的量÷分率因此，在分数学习中，单位“1”是一个重要的问题。

从广泛的意义来讲，它可以是一个整体，比如一本书，一项工程，或者一条路等。

它也可以是两个或几个量中的一个。

打个比方，单位“1”就是一把尺子，我们把这把尺子看做自然数意义上的1，其它量都来与它作比较，比较出的结果就是其它量相对应的分率或分量。

判断单位“1”是分数解题的重要一步，除了理解它的意义，再进行判断之外，可总结以下方法。

第一，单位“1”是一个整体。

这种情况最容易判断，如一本书，一项工程，一条路，一桶水等等，题目中出现的只有这个整体，其它都是它的一部分，这个时候，单位“1”就是这个整体。

第二，题目中有多个量的，需要确定哪个量是单位“1”，我们从题目中找到如：去年的几分之几，比乙多几分之几，比一班少几分之几等这种与分量连在一起的量，这个量就是单位“1” 。

另外，有的题目中出现如，今年减产两成，打八折等，这种有省略的，我们可以把它补充完整再判断。

比如，今年减产两成，应该是今年比去年减产两成。

打八折，应该是原价打八折。

因为不可能说今年比今年减产两成，也不可能说卖出价打八折（这与折上折不同）。

可以判断，去年产量是单位“1”，原价是单位“1”。

在题目中出现有多个量的时候，单位“1”是可能变化的，例如：甲是乙的15，乙又是丙的13，在甲和乙的关系中，乙是单位“1”，在乙和丙的关系中，丙是单位“1”。

这时，要根据题目中给出的已知条件，例如题目中给出是的甲的量，那就先利用甲和乙的关系，先求乙，在利用求出来的乙，去求丙。

在确定了单位“1”之后，我们可根据公式；分率对应的量＝单位“1”×分率；单位“1”＝分率对应的量÷分率，得出；如果单位“1”已知，用乘法；如果要求单位“1”，用除法。

分数中的单位“1”的认识1. 前言在我们的日常生活中，分数是很常见的一个数学概念。

在初中数学课程中，分数的表示、比较、运算等都是重点难点。

而分数中的单位“1”则是一个特殊的概念，在初中数学中也属于必须要掌握的知识点之一。

因此，本文将对分数中的单位“1”的认识进行探讨，希望能够帮助初中生更好的掌握这一知识点。

2. 什么是分数中的单位“1”在分数的表示中，分子表示的是分割的数量，分母表示的是分割成几份。

而当分母中出现“1”时，就表示把整体分成了一份，也就是将整体作为一个单位。

这个单位就是分数中的单位“1”。

例如，1/3 中的分子表示分成了 1 份，分母表示分成了 3 份，也就是将整体分成了 3 份，每份的大小是 1/3。

而 1/1 中的分子表示分成了 1 份，分母表示分成了1 份，也就是整体不分割，作为一个单位。

因此，1 就是这个单位“1”。

3. 单位“1”的运用3.1 分数的简化当分数的分子和分母都可以同时除以一个数时，这个数就是它们的公约数。

例如，12/16 可以同时除以 4，得到 3/4；而 14/28 可以同时除以 2 和 7，得到 1/2。

此时，可以使用分数中的单位“1”来简化运算。

以 12/16 为例，我们可以先将分数写成 12/16 = （12÷4）/（16÷4）= 3/4。

这个过程中，我们用到了分数中的单位“1”：我们将原来的分子 12 分成了 3 份，每份大小为 4；将原来的分母 16 分成了 4 份，每份大小为 4。

这样一来，12/16 就被简化成了 3/4。

3.2 分数的通分通分是指将两个或两个以上的分数分母都改写成相同的数，分数的分子可以不变，这样才能进行加减运算。

而当两个分数中都含有分数中的单位“1”时，我们就可以使用它们来进行通分。

以 1/2 和 2/3 为例，我们希望将它们进行通分，那么我们可以将它们的分母都改写成 6，这样就可以进行加减运算。

但是，如果我们直接将分母 2 和分母 3 相乘得到 6，那么有可能计算过程中就需要使用较大的数。

新修订小学阶段原创精品配套教材数学教案－分数中的单位“1”的认识教材定制 / 提高课堂效率 /内容可修改Mathematics lesson plan-understanding of the unit "1" in fractions教师：风老师风顺第二小学编订：FoonShion教育数学教案－分数中的单位“1”的认识教学目标1．进一步认识单位“1”，从而加深对分数意义的理解．2．渗透辩证唯物主义观点的启蒙教育．教学过程一、复习．分别说出下面各个分数所表示的意义．说明：一个物体、一个图形、一个计量单位，都可以看作单位“1”．二、新课．1．看图列式．＋＝＝1 ＋＋＝＝1说明：我们是把这堆小方块看作一个整体，即单位“1”表示由9个小方块组成的整体．2．练一练：看图填空．（1）把“一堆皮球（9个）”看作单位“1”．黑皮球占，白皮球占，花皮球占＋＋＝＝1（2）把“一批书（11本）”看作单位“1”．语文书占，数学书占，英语书占＋＋＝＝1小结：单位“1”不仅可以代表自然数1，代表一个物体、一个图形、一个计量单位，还可以表示由一群物体组成的一个整体．如：一堆苹果，一盒粉笔，一个班的人数，一个月的生产任务，一项工作等等．三、巩固练习．1．我校共有24个班，每班占全校班级数的几分之几？把什么看作单位“1”？2．把全班学生平均分成4个小组，每个小组占全班学生的几分之几？把什么看作单位“1”？教师说明：用单位“1”表示一个整体时，整体包含的数量可大可小，并初步知道部分和整体是相对而言，是可以转化的．3．把一盘苹果（4只）看作单位“1”，平均分成4份，每一份占这盘苹果的，有（）个苹果．4．（出示12只苹果）现在把（）个苹果看作单位“1”，这堆苹果的有（）个苹果．教师追问：同样是，为什么苹果的个数不一样？（因为单位“1”不同，所以它们的所表示的个数也不同）教师说明：在具体问题中，由于单位“1”包含的数量可大可小，所以同样的一个分数，所表示的具体数量是不一样的．5．看图回答问题．红色方块占总数的红色方块占总数的教师提问：红色方块同样是3块，为什么会出现两个不同的结果？若要使3块红色方块占总数的，应该怎么办？6．指出下面各题中是把什么看作单位“1”的，说说各分数表示的意义．（1）花皮球占这堆皮球的（2）语文书的本数占这批书的（3）男生人数是数学兴趣小组人数的（4）陆地面积占地球表面积的（5）空气中的氧气约占（6）的鸡是母鸡（7）一堆煤，运走了，烧去了吨（对比和吨）思考题：姐姐、妹妹和弟弟3人做一堆花，姐姐做5朵，妹妹做4朵，姐姐做的占这堆花的．弟弟做了多少朵？FoonShion教育研究中心编制Prepared by foonshion Education Research Center。

(20)甲仓货物的重量相当于乙仓货物的8/9（）×（）=( )
(21)鹅只数的11/16是鸭的只数（）×（）=( )
二．判断。
1．3吨钢铁的1/4和1吨棉花的3/4同样重。（）
2．12×2/5就是求12的2/5是多少。（）
3．1.2×4/15的积小于被乘数。（）
4．大于4/9小于7/9的分数只有2个。（）
（2）油菜子的出油率是42％，一个榨油厂榨出菜子油2100千克，用油菜子多少千克？
（3）某工厂计划制造拖拉机550台，比原计划超额完成了50台，超额了百分之几？
五．应用题。
1．一桶油10千克，用去这桶油的4/5，用去了多少千克？
2．育民小学有男同学840人，女同学人数是男同学的4/7，这个学校有女同学多少人？
例2:一个长方形的宽是长的5/12。在这关键句中，很明显是以长作为标准，宽和长相比较，也就是说长是单位“1”。
例3:今年的产量相当于去年的4/3倍。那么相当于后面的去年的产量就是标准量，也就是单位“1”。
(三)、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。这类分数应用题的单位“1”比较难找。
巩固提高：
一．填空。
找出单位“1”，用波浪线划出，并完成数量关系式。
（1）男生人数占女生人数的4/5。（）
（2）甲的6/7相当于乙。（）
（3）乙的5/9与甲相等。（）
(4)鸡的只数是鸭的7/8（）×7/8=( )
(5)乙数是甲数的1/3（）×（）=( )
(6)大鸡只数的4/5相当于小鸡的只数。（）×（）=( )
例1:水结成冰后体积增加了1/10，冰融化成水后，体积减少了1/12。象这样的水和冰两种数量到底谁作为单位“1”？两句关键句的单位“1”是不是相同？用上面讲过的两种方法不容易找出单位“1”。其实我们只要看，原来的数量是谁？这个原来的数量就是单位“1”！比如水结成冰，原来的数量就是水，那么水就是单位“1冰融化成水，原来的数量是冰，所以冰的体积，就是单位“1”。

教学内容巩固提高:•填空。

找出单位“ 1”，用波浪线划出，并完成数量关系式。

(1)男生人数占女生人数的4/5。

((2)甲的6/7相当于乙。

(3)乙的5/9与甲相等。

(4)鸡的只数是鸭的7/8 X 7/8=((5)乙数是甲数的1/3 X( )=( )⑹大鸡只数的4/5相当于小鸡的只数。

( X( )=(⑺读了一本书的2/7 )X( )=((8)三好学生占全校人数的1/10 )X( )=((9)完成了计划工作量的3/4 )X( ) =( )(10)小军的体重是爸爸体重的3/8 )X( )=((11)苹果树的棵数占果树总棵数的2/5 )X( ) =( )(12)汽车速度相当于飞机速度的1/5 )X( )=((13)已经修了一条路的1/4 )X( )=((14)黑兔是白兔的3/7 )X( )=((15)黑兔的3/4相当于白兔)X( )=((16)甲数的5/6是乙数)X( )=((17)甲数是乙数的3/4 )X( )=((18)苹果树占果园面积的2/5 )X( )=((19)钢笔的价钱等于书的7/8 )X( )=((20)甲仓货物的重量相当于乙仓货物的8/9 )X( )=((21)鹅只数的11/16是鸭的只数)X( )=(.判断。

1. 3吨钢铁的1/4和1吨棉花的3/4同样重。

完整版本完整版本1•一桶油10千克，用去这桶油的4/5,用去了多少千克?2 •育民小学有男同学840人，女同学人数是男同学的4/7,这个学校有女同学多少人?3.—堆煤12吨，又运来它的1/4，又运来的煤是多少吨?4 •教师公寓有三居室180套，二居室的套数是三居室的2/3，一居室的套数是二居室的1/4。

教师公寓有一居室多少套？5 •阳光小学有男生750人，女生人数是男生的4/5 ,这个学校有女生多少人？一共有学生多少人?6.李庄共有小麦地320公亩，水稻地比小麦地多1/4，这个庄的水稻地比小麦地多多少公亩？有水稻地多少公亩？7.修一条公路，长1000米，甲队已经修了这条路的2/5 ,剩下的由乙队修，乙队修多少米?8•—辆汽车从甲地开往乙地，第一小时行了全程的，第二小时比第一小时多行了16千米，这时距离乙地还有94千米•甲、乙两地间的公路长多少千米？9.学校购进3600本儿童读物，其中1/81是经典名著，3/40是科普读物。

分数的意义单位1分数的意义单位1分数是数学中的一种表示方法，用来表示分割整体的部分。

它由两个数值组成，分别表示分子和分母。

分子表示分割后的部分数量，而分母表示整体被分割成几等份。

在分数中，分子位于斜线的上方，分母位于斜线的下方。

例如，1/2表示将整体分割成两份，取其中一份的部分。

在我们的日常生活中，分数的意义单位1有着广泛的应用。

下面将从几个方面说明分数的意义单位1的重要性。

首先，分数的意义单位1在分割整体时提供了准确的测量。

在实际问题中，我们经常需要将整体分割成部分，并且需要进一步确定每个部分的数量。

分数提供了一种准确的度量方式，可以精确地表示分割后的部分数量。

例如，当我们将一张披萨分割成八份时，我们可以用1/8表示每份的部分。

其次，分数的意义单位1可以帮助我们比较和计算不同部分之间的关系。

分数提供了一种相对比较的方式，可以将一个部分与整体进行比较。

例如，当我们说一个人吃了3/4的披萨时，我们可以清楚地知道它吃了较多的部分。

此外，分数还可以进行加减乘除的运算，使我们能够更方便地进行分数的计算。

第三，分数的意义单位1也有助于我们理解和解决实际问题。

在实际问题中，可以通过分数来描述和解决各种情况。

例如，在购物时，我们可以使用分数来计算折扣的比例；在做菜时，我们可以使用分数来确定食材的比例；在旅行中，我们可以使用分数来确定每个人的分摊费用等等。

通过理解和应用分数，我们能够更好地解决与实际生活相关的问题。

此外，分数的意义单位1还在其他学科中有着重要的应用。

在科学中，分数的意义单位1可以表示比例和概率。

在艺术和设计中，分数的意义单位1可以表示比例尺和设计比例。

在经济学中，分数的意义单位1可以表示成本和收益的比率。

分数的应用范围广泛，为各个学科提供了一种通用的表示和计算方式。

总结起来，分数的意义单位1是数学中一个重要且实用的概念。

它提供了一种准确的测量方式，帮助我们比较和计算不同部分之间的关系。

同时，分数的意义单位1也有助于我们理解和解决实际问题，并在其他学科中有着广泛的应用。

分数应用题找单位1的技巧《嘿，分数应用题找单位“1”的那些事儿》嘿，大家好呀！今天咱来说说分数应用题里找单位“1”的那些事儿。

咱每次碰到分数应用题，这找单位“1”就像是大海捞针，找不对可就容易错得一塌糊涂啦。

但是别怕，就像超级英雄有超能力一样，咱也有找单位“1”的技巧呢！首先啊，咱得眼睛亮，看到那些关键的字眼。

比如说“占”“是”“比”这些词，那后面跟着的很可能就是单位“1”哦。

就好像是游戏里的线索，得紧紧抓住才行。

有时候吧，这题目还挺狡猾，它不直接给咱提示。

别急，咱可以看看总量是啥，那总量通常就是单位“1”啦。

咱就像是侦探，得从蛛丝马迹中找到关键信息。

我记得有一次啊，我做一道题，那题目绕来绕去，差点把我给绕晕了。

我就拼命找呀找，终于找到了单位“1”，那一刻，我感觉自己就像是发现了宝藏一样兴奋！然后顺顺利利把题目给做出来了，那成就感，简直爆棚！还有哦，找单位“1”的时候咱可不能死脑筋，得灵活点儿。

要是一种方法不行，咱就换另一种试试。

别在一棵树上吊死嘛，多换几棵树说不定就找到答案了呢。

有时候也会出点小差错，找错了单位“1”，那就像是走在迷宫里走错了路。

不过没关系，咱赶紧迷途知返，重新找就是了。

总之啊，这找单位“1”就像是一场有趣的游戏，只要咱掌握了技巧，多练练，肯定能越来越厉害。

别把它想得那么难，就当成是和题目玩的一场游戏，咱得斗智斗勇，把单位“1”这个小调皮给揪出来。

大家在做分数应用题的时候可要记住这些小技巧哦，相信有了它们的帮忙，咱都能在这场游戏中取得胜利，让那些难题都乖乖投降！加油吧，小伙伴们！让我们一起在分数应用题的海洋里畅游，找到属于我们的解题宝藏！哈哈！。

如何确定分数乘除法应用题中的单位1（只要找出关键字，关键字后面的就是单位1）正确找准单位“1”，是解答分数（百分数）应用题的关键，每一道分数应用题中总是有关键句（含有分率的句子）。

如何从关键句中找准单位“1”，我觉得可以从以下这些方面进行考虑。

一、部分数和总数在同一整体中，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，那么总数就是单位“1”。

例如我国人口约占世界人口的1/5，世界人口是总数，我国人口是部分数，所以，世界人口就是单位“1”。

再如，食堂买来100千克白菜，吃了2/5，吃了多少千克？在这里，食堂一共买来的白菜是总数，吃掉的是部分数，所以100千克白菜就是单位“1”。

解答这类分数应用题，只要找准总数和部分数，确定单位“1”就很容易了。

二、两种数量比较分数应用题中，两种数量相比的关键句非常多。

有的是“比”字句，有的则没有“比”字，而是带有指向性特征的“占”、“是”、“相当于”、“正好”。

在含有“比”字的关键句中，比后面的那个数量通常就作为标准量，也就是单位“1”。

例如：六（2）班男生比女生多1/2。

就是以女生人数为标准（单位“1”），男生比女生多的人数作为比较量。

在另外一种没有比字的两种量相比的时候，我们通常找到分率，看“占”谁的，“相当于”谁的，“是”谁的几分之几。

这个“占”，“相当于”，“是”后面的数量——谁就是单位“！”。

例如，一个长方形的宽是长的5/12。

在这关键句中，很明显是以长作为标准，宽和长相比较，也就是说长是单位“1”。

又如，今年的产量相当于去年的4/3倍。

那么相当于后面的去年的产量就是标准量，也就是单位“1”。

三、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。

这类分数应用题的单位“1”比较难找。

例如，水结成冰后体积增加了1/10，冰融化成水后，体积减少了1/12。

象这样的水和冰两种数量到底谁作为单位“1”？两句关键句的单位“1”是不是相同？用上面讲过的两种方法不容易找出单位“1”。

【关键词 】分数乘除 ；应运 ；单位…１’的量
在 小学六年级上册数学教 学 中，分数 的应用贯 穿始 末 ， 在本 学年安 排 的八个 单 元 中 ，除 第一 单 元 位 置 、第 四单 元 圆 、第七单元数学 广角之外 ，其余 的五个 单元都 与分数 有着 不 可分割的关系．而如 何 寻找单 位 “１”，如何 理解 单 位 …１’ 是 关键 中的关键 ．通过近期 的观察 ，我 发现部分 学生 一遇到 分 数应用的题 目，乱写 一气 ，不是 乘 、就 是 除；不 是加 、就是 减 ；究其根本是他不 能真正意义上理 解什 么是分数 ，如何利 用 其中的分 数．我 认 为 要 解决 这 类 错 误 ，必须 从 单 位 “１” 人 手 ．
是在水中传播速度的÷，声音在水中传播的速度是多少？
…１ ’
在水中 ［二二二二工
．２１Ｏ ｋ
５
二 二］
在空气中 ［二二＝二］ 分 析 关 键 条 件 “声 音 在 空 气 中 的 传 播 速 度 是 在 水 中
传播速度的÷ ”，所以声音在水 中的传播速度是单位 “１”．
１１
１
而声音在空气的速度 干米恰恰是在水中的÷，这就说明
例 １ 六 年 一 班 男 生 有 ２８人 ，六 年 级 二 班 的 男 生 数 是
六年 级一班的÷ ，六年级二班有男 生多少 人？
六 一 班 男 生
六 二 班 男 生
分 析 关 键 条 件 “六 年 级 二 班 的 男 生 是 六 年 级 一 班 男 生 的ｉ＇－Ｉ－”，所 以 它 是 把 六 年 级 一 班 的男 生 人 数 看 成 一 个 整
相 等的 ３份 （每份 ４），取 其 中的 ２份 （４×２每份 ４，那 么两份