上海市曹杨二中2018-2019学年高二上学期期末数学试题

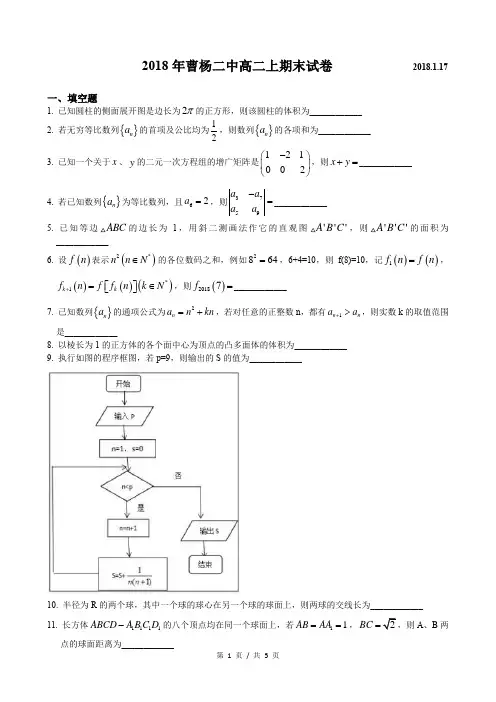
2018年曹杨二中高二上期末试卷 2018.1.17一、填空题1. 已知圆柱的侧面展开图是边长为2π的正方形，则该圆柱的体积为____________2. 若无穷等比数列{}n a 的首项及公比均为12，则数列{}n a 的各项和为____________ 3. 已知一个关于x 、y 的二元一次方程组的增广矩阵是121002-⎛⎫⎪⎝⎭，则x y +=____________4. 若已知数列{}n a 为等比数列，且62a =，则3759a a a a -=____________5. 已知等边ABC 的边长为1，用斜二测画法作它的直观图'''A B C ，则'''A B C 的面积为____________6. 设()f n 表示()2*n n N ∈的各位数码之和，例如2864=，6+4=10，则f(8)=10，记()()1f n f n =，()()()*1k k f n f f n k N +=∈⎡⎤⎣⎦，则()20187f =____________7. 已知数列{}n a 的通项公式为2n a n kn =+，若对任意的正整数n ，都有1n n a a +>，则实数k 的取值范围是____________8. 以棱长为1的正方体的各个面中心为顶点的凸多面体的体积为____________ 9. 执行如图的程序框图，若p=9，则输出的S 的值为____________10. 半径为R 的两个球，其中一个球的球心在另一个球的球面上，则两球的交线长为____________ 11. 长方体1111ABCD A B C D -的八个顶点均在同一个球面上，若11AB AA ==，BC =A 、B 两点的球面距离为____________12. 设集合{n M n =位纯小数0.{}()12|0,11,2,1,1}n i n a a a a i n a ∈=-=，n T 是n M 中元素的个数，n S 是n M 中所有元素的和，则limnn nS T →∞=____________二、选择题13. 设“1P 、2P 、3P 、4P 为空间中有三点在同一条直线上”是“1P 、2P 、3P 、4P 在同一个平面上”的（ ） A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件14. 在等差数列{}n a 中，10a >，且383a a =，设{}n a 的前n 项和为n S ，则数列{}n S 中的最大项是（ ） A. 5SB. 6SC. 10SD. 11S15. 将长度分别为2、3、5、6、9（单位：cm ）的五根木棒连接（所有木棒都要用到），组成长方体共顶点的条棱，则能够得到的长方体的最大表面积为（ ） A. 2582cmB. 4142cmC. 4162cmD. 4182cm16. 已知数列1234,,,a a a a 的各项均不等于零，此数列前n 项的和为n S ，且满足()2214n n n S a a n =+≤≤，则满足条件的数列个数为（ ） A. 4 B. 5C. 6D. 7三、解答题17. 如图，1111ABCD A B C D -是棱长为2的正方体，M 、N 分别是1BB ，CD 的中点. （1）求三棱锥B-AMN 的体积；（2）求异面直线MN 与1DD 所成的角的大小（用反三角函数值表示）.SO ，AB=4，P是母线SA的中点，C 18. 如图，已知AB是底面SO的底面直径，O是底面圆心，23是底面圆周上一点，∠AOC=60°.（1）求圆锥的侧面积；（2）求直线PC与底面所成的角的大小.19. 如图，在底面是棱形的四棱锥P-ABCD中，PA⊥底面ABCD，PA=AC=2，∠ABC=60°，点E在线段PD上，且PE:ED=2:1.（1）求二面角E-AC-D的大小；（2）在棱PC上是否存在一点F，使得BF//平面AEC?证明你的结论.20. 如图，四边形ABCD 和ABEF 均为边长为1的正方形，且二面角C-AB-E 的大小为3π. （1）证明：直线AE 和直线BD 是异面直线； （2）求点B 到平面ACE 的距离；（3）求异面直线AE 和BD 所成角的大小（结果用反三角函数值表 示）.21. 记{}1,2,3,,100U =，对数列{}()*n a n N ∈和U 的子集T ，若T=∅，定义0T S =；若{}123,,,k T t t t t =，定义12n t t t t S a a a =+++，例如：{}1,3,6T =时，136T S a a a =++.设数列{}()*n a n N ∈是公比为3的等比数列，且当{}2,4T =时，30T S =. （1）求数列{}n a 的通项公式；（2）对任意正整数()199k k ≤≤，若{}1,2,3,,T k ⊆，求证：1T k S a +<；（3）设C U ⊆，D U ⊆，C D S S ≥，求证：2C C D D S S S ⋂+≥.参考答案一、填空题1. 22π2. 13. 74. 85. 166. 167. ()3,-+∞8. 169. 25R 11.3π12.118二、选择题13. A 14. C 15. C 16. C三、解答题17.（1）23（2）arctan arcsin arccos 66== 18.（1）8π（2）4π19.（1）6π（2）F 为PC 的中点20.（1）证明略（2（3）1arccos 421.（1）13n n a -=（2）证明略（3）证明略。

2021-2022学年上海市曹杨第二中学高二上学期期末数学试题一、单选题1．已知点()1,1,2A -在平面α上，其法向量()2,1,2n =-，则下列点不在平面α上的是（ ） A ．()2,3,3 B ．()3,7,4 C ．()1,7,1-- D ．()2,0,1-【答案】D【分析】根据法向量的定义，利用向量垂直对四个选项一一验证即可. 【详解】()1,1,2A -对于A ：记()12,3,3A ,则()11,4,1AA =.因为()()11,4,12,1,22420AA n =-=-+=，所以点()12,3,3A 在平面α上 对于B ：记()3,7,4B ,则()2,8,2AB =.因为()()2,8,22,1,24840AB n =-=-+=，所以点()3,7,4B 在平面α上 对于C ：记()1,7,1C --,则()2,6,1AC =---.因为()()2,6,12,1,24620AC n =----=-+-=，所以点()1,7,1C --在平面α上 对于D ：记()2,0,1D -,则()3,1,1AD =--.因为()()3,1,12,1,26120AD n =---=---≠，所以点()2,0,1D -不在平面α上. 故选：D2．实数m n ≠且2sin cos 10m m θθ-+=，2sin cos 10n n θθ-+=，则连接()2,m m ，()2,n n两点的直线与圆C ：221x y +=的位置关系是（ ） A ．相离 B ．相切 C ．相交 D ．不能确定【答案】B【解析】由题意知，m ，n 是方程2sin cos 10x x θθ-+=的根,再根据两点式求出直线方程，利用圆心到直线的距离与半径之间的关系即可求解. 【详解】由题意知，m ，n 是方程2sin cos 10x x θθ-+=的根，cos sin m n θθ∴+=，1sin mn θ=m n ≠，∴过()2,m m ，()2,n n 两点的直线方程为：222y n x nm n m n--=--，()0m n x y mn ∴+--=∴圆心()0,0到直线的距离为：()211mnd m n ==++，故直线和圆相切，故选：B【点睛】本题考查了直线与圆的位置关系，考查了计算求解能力，属于基础题. 3．某学校随机抽取了部分学生，对他们每周使用手机的时间进行统计，得到如下的频率分布直方图.则下列说法：①0.03a =；②若抽取100人，则平均用时13.75小时；③若从每周使用时间在[)15,20，[)20,25，[)25,30三组内的学生中用分层抽样的方法选取8人进行访谈，则应从使用时间在[)20,25内的学生中选取的人数为3.其中正确的序号是（ ）A ．①②B ．①③C ．②③D ．①②③【答案】B【分析】根据频率分布直方图中小矩形的面积和为1可求出a ，再求出频率分布直方图的平均值，即为抽取100人的平均值的估计值，再利用分层抽样可确定出使用时间在[)20,25内的学生中选取的人数为3.【详解】(0.020.040.060.040.01)510.03a a +++++⨯=⇒=，故①正确； 根据频率分布直方图可估计出平均值为(0.02 2.50.047.50.0612.50.0417.50.0322.50.0127.5)513.75⨯+⨯+⨯+⨯+⨯+⨯⨯=，所以估计抽取100人的平均用时13.75小时，②的说法太绝对，故②错误；每周使用时间在[)15,20，[)20,25，[)25,30三组内的学生的比例为4:3:1，用分层抽样的方法选取8人进行访谈，则应从使用时间在[)20,25内的学生中选取的人数为3838⨯=，故③正确.故选：B.4．连掷一枚均匀的骰子两次，所得向上的点数分别为m ，n ，记t m n =+，则下列说法正确的是（ ） A ．事件“12t =”的概率为121B ．事件“t 是奇数”与“m n =”互为对立事件C ．事件“2t =”与“3t ≠”互为互斥事件D ．事件“8t >且32mn <”的概率为14【答案】D【分析】计算出事件“t ＝12”的概率可判断A ；根据对立事件的概念，可判断B ；根据互斥事件的概念，可判断C ；计算出事件“t ＞8且mn ＜32”的概率可判断D ； 【详解】连掷一枚均匀的骰子两次，所得向上的点数分别为m ，n ，则共有6636⨯=个基本事件， 记t ＝m ＋n ，则事件“t ＝12”必须两次都掷出6点，则事件“t ＝12”的概率为136，故A 错误； 事件“t 是奇数”与“m ＝n ”为互斥不对立事件,如事件m =3,n =5，故B 错误； 事件“t ＝2”与“t ≠3”不是互斥事件，故C 错误； 事件“t ＞8且mn ＜32”有344555666,,,,,,,,656456345m m m m m m m m m n n n n n n n n n =========⎧⎧⎧⎧⎧⎧⎧⎧⎧⎨⎨⎨⎨⎨⎨⎨⎨⎨=========⎩⎩⎩⎩⎩⎩⎩⎩⎩共9个基本事件， 故事件“t ＞8且mn ＜32”的概率为14，故D 正确；故选：D ． 二、填空题5y 10-+=的倾斜角为______． 【答案】3π 【分析】把直线方程化为斜截式，再利用斜率与倾斜角的关系即可得出．【详解】10y -+=的倾斜角为θ．10y -+=化为1y +，故tan θ= 又(]0,θπ∈，故3πθ=，故答案为3π． 【点睛】一般地，如果直线方程的一般式为()00Ax By C B ++=≠，那么直线的斜率为Ak B=-，且tan θk ，其中θ为直线的倾斜角，注意它的范围是(]0,π．6．数据：1，1，3，4，6的方差是______. 【答案】1853.6 【分析】先计算平均数，再计算方差. 【详解】该组数据的平均数为1134635++++=，方差为()222221182201355++++=故答案为：1857．已知三角形OAB 顶点()0,0O ，()2,4A ，()3,6B -，则过B 点的中线长为______.【答案】【分析】先求出OA 中点坐标，再由距离公式得出过B 点的中线长. 【详解】由中点坐标公式可得OA 中点()1,2C ，则过B 点的中线长为BC ==故答案为：8．用一个平面去截半径为5cm 的球，截面面积是29πcm .则球心到截面的距离为_______． 【答案】4cm【分析】根据圆的面积公式算出截面圆的半径3r cm =，利用球的截面圆性质与勾股定理算出球心到截面的距离． 【详解】解：设截面圆的半径为r ，截面的面积是29cm π，29r ππ∴=，可得3r cm =．又球的半径为5cm ，∴根据球的截面圆性质，可得截面到球心的距离为4d cm =．故答案为：4cm ．【点睛】本题主要考查了球的截面圆性质、勾股定理等知识，考查了空间想象能力，属于基础题．9．若圆心坐标为()2,1-的圆被直线10x y --=截得的弦长为______. 【答案】2【分析】利用垂径定理计算即可. 【详解】设圆的半径为r ，则2222112222r ⎛⎫⎛+-⎫=+ ⎪ ⎪ ⎪⎝⎭⎝⎭， 得2r =. 故答案为：2.10．如图是用斜二测画法画出的水平放置的正三角形ABC 的直观图，其中1O B O C ''''==，则三角形A B C '''的面积为______.【答案】64【分析】根据直观图和平面图的关系可求出O A ''，进而利用面积公式可得三角形A B C '''的面积【详解】由已知可得3132222O A ''=⨯⨯=则132622224A B C S '''=⨯⨯⨯=故答案为：64. 11．已知()y f x =是定义在R 上的奇函数，当0x ≥时()21x f x x =-+，则当0x <时()f x =___________.【答案】()21x f x x -=+-【分析】当0x <时，利用0x ->及()()f x f x =--求得函数的解析式. 【详解】当0x <时，0x ->，由于函数是奇函数，故()()2121x xf x f x x x --⎡⎤=--=---+=+-⎣⎦. 【点睛】本小题主要考查已知函数的奇偶性以及y 轴一侧的解析式，求另一侧的解析式，属于基础题.12．甲、乙两名运动员5场比赛得分的茎叶图如图所示，已知甲得分的极差为32，乙得分的平均值为24，则甲、乙两组数据的中位数是______.【答案】26【分析】先由极差以及平均数得出,x y ，进而得出中位数.【详解】由34632-<可得，30632x +-=，8x =，因为乙得分的平均值为24，所以122031131245,6y y +⨯+++=⨯=，所以甲、乙两组数据的中位数是2626262+=. 故答案为：2613．已知正三棱台111ABC A B C -上、下底面边长分别为1和2，高为1，则这个正三棱台的体积为______. 【答案】7312【分析】先计算两个底面的面积，再由体积公式计算即可.【详解】上底面的面积为1311sin 6024⨯⨯⨯︒=，下底面的面积为122sin 6032⨯⨯⨯︒=，则这个正三棱台的体积为1337333134412⎛⎫⎪⨯++⨯⨯= ⎪⎝⎭.故答案为：731214．如图，SD 是球O 的直径，A 、B 、C 是球O 表面上的三个不同的点，30ASD BSD CSD ∠=∠=∠=︒，当三棱锥S ABC -的底面是边长为3的正三角形时，则球O 的半径为______.【答案】2【分析】由三棱锥S ABC -是正三棱锥，利用正弦定理得出三角形ABC 外接圆的半径，进而求出AS ，再由余弦定理得出球O 的半径.【详解】因为30ASD BSD CSD ∠=∠=∠=︒，所以SD ⊥平面ABC ，三棱锥S ABC -是正三棱锥，设1O 为三角形ABC 外接圆的圆心，则1O 在SD 上，连接1AO ，AO ，由132sin 60AO ︒=得出13AO =123sin 30AO AS ︒==AOS △中，22223)2cos120R R R ︒=+-，即2123R =，解得2R =，则球O 的半径为2.故答案为：215．设在ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，从下列四个条件：①2a c =；②6C π=；③2cos B =④7b =ABC 存在且唯一的所有c 的值为______. 7227【分析】由①②结合正弦定理可求出sin A ，但是角A 不唯一，故所选条件中不能同时有①②，只能是①③④或②③④，若选①③④，结合余弦定理可求c ，若选②③④，结合正弦定理即可求解 【详解】由①②结合正弦定理sin sin a c A C =，所以2sin 2A C ==A 不唯一，所以故所选条件中不能同时有①②， 所以只能是①③④或②③④， 若选①③④，即2a c ，2cos B =7b = 由余弦定理可得22222c c =⋅7c =， 若选②③④，即6C π=，2cos B =，7b = 因为2cos B =,2B ππ⎛⎫∈ ⎪⎝⎭，所以2214sin 1cos 116B B =--=由正弦定理得sin sin b cB C=，17sin 22sin 14b Cc B ===，72 16．设数列{}n a 的前n 项和为n S ，且2n S 是6和n a 的等差中项，若对任意的*n N ∈，都有[]13,n nS s t S -∈，则t s -的最小值为________． 【答案】94【分析】先根据和项与通项关系得{}n a 通项公式，再根据等比数列求和公式得n S ，再根据函数单调性得13n nS S -取值范围，即得t s ，取值范围，解得结果. 【详解】因为2n S 是6和n a 的等差中项，所以46n n S a =+ 当2n ≥时，111114643n n n n n n n S a a a a a a ----=+∴=-∴=-当1n =时，11146=2S a a =+∴因此112[1()]13132()[1()]132313n n n n n a S ---=⨯-∴==--+ 当n 为偶数时，3143[1()][,)2332n n S =-∈当n 为奇数时，313[1()](,2]232n n S =+∈因此343(,2][,)232n S ∈因为13n n S S -在343(,2][,)232上单调递增， 所以[]113232*********,,4662244n n S s t t s S ⎡⎤-∈⋃⊆∴-≥-=⎢⎥⎣⎦）（， 故答案为：94【点睛】本题考查根据和项求通项、等比数列定义、等比数列求和公式、利用函数单调性求值域，考查综合分析求解能力，属较难题. 三、解答题17．已知圆C 经过(3,2)A 、(1,6)B 两点，且圆心在直线2y x =上． （1）求圆C 的方程；（2）若直线l 经过点(1,3)P -且与圆C 相切，求直线l 的方程． 【答案】（１）22(2)(4)5x y -+-= ；（２）250250x y x y -+=+-=或【解析】【详解】试题分析：（1）根据圆心在弦的垂直平分线上，先求出弦AB 的垂直平分线的方程与2y x =联立可求得圆心坐标，再用两点间的距离公式求得半径，进而求得圆的方程；（2）当直线l 斜率不存在时，与圆相切，方程为1x =-；当直线l 斜率存在时，设斜率为k ，写出其点斜式方程，利用圆心到直线的距离等于半径建立方程求解出k 的值.试题解析：（1）依题意知线段AB 的中点M 坐标是()2,4，直线AB 的斜率为62213-=--，故线段AB 的中垂线方程是()1422y x -=-即260x y -+=， 解方程组260{2x y y x -+==得2{4x y ==，即圆心C 的坐标为()2,4，圆C 的半径5r AC ==，故圆C 的方程是()()22245x y -+-=（2）若直线l 斜率不存在，则直线l 方程是1x =-，与圆C 相离，不合题意；若直线l 斜率存在，可设直线l 方程是()31y k x -=+，即30kx y k -++=，因为直线l 与圆C 相切，所以有224351k k k -++=+，解得2k =或12k =-．所以直线l 的方程是250x y -+=或250x y +-=.18．如图，几何体是圆柱的一部分，它是由矩形ABCD （及其内部）以AB 边所在直线为旋转轴旋转120︒得到的封闭图形.(1)设1BC =，2AB =，求这个几何体的表面积；(2)设G 是弧DF 的中点，设P 是弧CE 上的一点，且AP BE ⊥.求异面直线AG 与BP 所成角的大小. 【答案】(1)42π+ (2)6π【分析】（1）将几何体的表面积分成上下两个扇形、两个矩形和一个圆柱形侧面的一部分组成，分别求出后相加即可；（2）先根据条件得到BE ⊥面PAB ，通过平移将异面直线转化为同一个平面内的直线夹角即可 (1)上下两个扇形的面积之和为：212221233ππ⨯⨯⨯= 两个矩形面积之和为：4侧面圆弧段的面积为：24233ππ⨯= 故这个几何体的表面积为：2444233πππ++=+ (2)如下图，将直线AG 平移到下底面上为1BG由AP BE ⊥，且BE AB ⊥，AP AB A =，可得：BE ⊥面PAB则2PBE π∠=而G 是弧DF 的中点，则3FAG π∠=由于上下两个平面平行且全等，则直线AG 与直线BP 的夹角等于直线1BG 与直线BP 的夹角，即1PBG ∠为所求，则1236PBG πππ∠=-=则直线AG 与直线BP 的夹角为6π19．如图，水平桌面上放置一个棱长为4的正方体的水槽，水面高度恰为正方体棱长的一半，在该正方体侧面11CDD C 有一个小孔（小孔的大小忽略不计）E ，E 点到CD 的距离为3，若该正方体水槽绕CD 倾斜（CD 始终在桌面上）.(1)证明图2中的水面也是平行四边形；(2)当水恰好流出时，侧面11CDD C 与桌面所成的角的大小. 【答案】(1)证明见解析(2)【分析】（1）由水的体积得出1BN =，进而得出//NM PQ ，NM PQ =，从而证明图2中的水面也是平行四边形；（2）在平面11BCC B 内，过点1C 作1//C H NP ，交1BB 于H ，由四边形1NPC H 是平行四边形，得出侧面11CDD C 与桌面所成的角即侧面11CDD C 与水面MNPQ 所成的角，再由直角三角形的边角关系得出其夹角. (1)由题意知，水的体积为44232⨯⨯=，如图所示，设正方体水槽倾斜后，水面分别与棱1AA ，1BB ，1CC ，1DD 交于M ，N ，P ，Q ，则3PC =，水的体积为32BCPN S CD ⋅=，∴322+⋅⋅=BN CPBC CD ，即344322BN +⨯⨯=，1BN ∴=． 1AM ∴=，故四边形ABNM 为平行四边形，即//AB MN ，且4AB MN ==又CD PQ =，//CD PQ ，//NM PQ ∴，NM PQ =∴四边形NMQP 为平行四边形，即图2中的水面也是平行四边形； (2)在平面11BCC B 内，过点1C 作1//C H NP ，交1BB 于H ，则四边形1NPC H 是平行四边形，11NH C P ==，114112B H BB NH BN ∴=--=--=，1C H =侧面11CDD C 与桌面所成的角即侧面11CDD C 与水面MNPQ 所成的角，即侧面11CDD C 与平面11HC D 所成的角，1HC C ∴∠即为所求，而111HC C B HC ∠=∠，在11Rt B HC 中，1111cos H B B HC C H ∠=，∴侧面11CDD C 与桌面所成角的为20．已知数列{}n a 满足112a =，221321n n a a +=+，21n n b a =-，n 为正整数. (1)证明：数列{}n b 是等比数列，并求通项公式；(2)证明：数列{}n b 中的任意三项i b ，j b ，()k b i j k <<都不成等差数列；(3)若关于正整数n 的不等式n nb m >的解集中有且仅有三个元素，求实数m 的取值范围； 【答案】(1)证明见解析；132(),()43n n b n N -*=⋅∈(2)证明见解析 (3)3849m ≤< 【分析】（1）将所给等式221321n n a a +=+变形为2213(1)2(1)n n a a +-=-，根据等比数列的定义即可证明结论；（2）假设存在i b ，j b ，()k b i j k <<成等差数列，根据等差数列的性质可推出矛盾，故说明假设错误。

2018-2019学年上海市曹杨第二中学高二上学期期末复习（二）数学试题一、单选题1．下面是关于三棱锥的四个命题：①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥；②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥；③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥；④侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥。

其中真命题的编号是（）A.③④B.①②C.①③④D.①④【答案】D【解析】根据正三棱锥的定义，结合二面角判断①的正误；侧棱与底面所成的角判断④的正误；找出反例否定②，找出反例对选项③否定可得正确结论．【详解】解：①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥．可推出底面中心是棱锥顶点在底面的射影，所以是正确的．②显然不对，比如三条侧棱中仅有一条不与底面边长相等的情况，侧面都是等腰三角形的三棱锥但不是正三棱锥．③底面是等边三角形，侧面的面积都相等，说明顶点到底面三边的距离（斜高）相等，根据射影长的关系，可以得到顶点在底面的射影（垂足）到底面三边所在直线的距离也相等，由于在底面所在的平面内，到底面三边所在直线的距离相等的点有4个：内心（本题的中心）1个、旁心3个，因此不能保证三棱锥是正三棱锥．④侧棱与底面所成的角相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．是正确的．正确的为：①④故选：D【点睛】本题考查棱锥的结构特征，二面角及其度量，考查作图能力，是基础题．2．下列命题中，错误的是 ( )A ．一条直线与两个平行平面中的一个相交，则必与另一个平面相交B ．平行于同一平面的两个不同平面平行C ．如果平面不垂直平面，那么平面内一定不存在直线垂直于平面D ．若直线不平行平面，则在平面内不存在与平行的直线 【答案】D【解析】若直线与另外一个平面不相交，则直线与该平面平行，由此可得直线与该平面平行的平面也平行，矛盾，所以命题A 正确； 命题B 显然正确； 若存在有，则根据面面垂直判定可得，矛盾，所以命题C 正确；不平行于平面，则相交或。

上海中学2018-2019学年第一学期期末高二年级期末考数学试卷2019.01时间：120分；满分：100分一、填空题（本大题共12题，共36分） 1、抛物线x y =2的准线方程是__________.2、若复数z 满足i x 232-=，其中i 为虚数单位，则=z ________.3、点()0,1p 到曲线⎩⎨⎧==ty t x 22（其中参数R t ∈）上的点的最短距离为________.4、双曲线141222=-y x 的两条渐近线的夹角为________. 5、在平面直角坐标系xOy 中，焦点在x 轴上的椭圆13222=+my m x 的焦距为6，则=m _______. 6、已知复数θθcos sin 3i z +=（i 是虚数单位）且，5=z 则当θ为钝角时，=θtan ________. 7、若直线2+=kx y 与双曲线622=-y x 的右支交于不同的两点，则实数k 的取值范围是___. 8、设直线,3:,3:21x y l x y l -==点A 和点B 分别在直线1l 和2l 上运动，且2-=⋅OB OA ，其中O 为原点，则AB 的中点M 的轨迹方程为____________.9、已知椭圆()10122<<=+m y mx 上存在不同的两点B A ,关于直线1:+=x y l 对称，则m 的取值范围是________.10、双曲线2:22=-y x C 的右焦点为P F ，为其左支上任意一点，点A 的坐标为)1,1(-，则△APF 周长的最小值为________.11、椭圆134:221=+y x C ，抛物线x y C 4:22=，过抛物线2C 上一点P （异于原点O ）作不平行与x 轴的直线l ，使得直线l 与抛物线只有一个交点，且与椭圆1C 交于B A ,两点，则直线l 在x 轴上的截距的取值范围是_________.12、已知点n n B A ,在双曲线1=xy 上，且点n A 的横坐标为1+n n，点n B 的横坐标为()*1N n nn ∈+，记M 点的坐标为()1,1，()n n n y x P ,是△M B A n n 的外心，则=∞→n n x lim ________.二、选择题（本大题共4题，每题4分，共16分） 1、已知复数z 在复平面上对应的点为()1,2-z ，则（ ）A . i z 21+-=B . 5=z C. i z --=2 D . 2-z 是纯虚数2、下列以t 为参数方程所表示的曲线中，与1=xy 所表示的曲线完全一致的是（ ）A . ⎪⎩⎪⎨⎧==-2121t y t x B . ⎪⎩⎪⎨⎧==t y tx 1 C . ⎩⎨⎧==t y t x sec cos D . ⎩⎨⎧==ty tx cot tan 3、设双曲线()0,012222>>=-b a b y a x ，右焦点()20,=acc F ，，方程02=--c bx ax 的两个实数根分别为21,x x ，则点()21,x x P 与圆422=+y x 的位置关系是（ ）A . 点P 在圆外B . 点P 在圆上C . 点P 在圆内D . 不确定4、已知抛物线x y C 42=：的焦点为F ，对称轴与准线的交点为，T P 为抛物线C 上任意一点，当PTPF 取最小值时，∠=PTF （ ）A .3π B . 4π C . 5π D . 6π三、解答题（本大题共6题，共48分）1、（本题满分6分）若i z z z f 52)(-+=，i z f 36)(-=，试求z .2、（本题满分6分）已知曲线C 的参数方程为⎩⎨⎧==θθsin 4cos 6y x （θ为参数），在同一平面直角坐标系中，将曲线C 上的点按坐标变换⎪⎪⎩⎪⎪⎨⎧='='y y x x 4131得到曲线C '. （1）求曲线C '的普通方程；（2）若点A 在曲线C '上，点)3,1(D ，当点A 在曲线C '上运动时，若PD AP 2=，求P 点的轨迹方程.3、（本题满分7分）我边防局接到情报，在两个海标A 、B 所在直线的一侧M 处有走私团伙在进行交易活动，边防局迅速排出快艇前去搜捕. 如图，已知快艇出发位置在码头P 处，线段AB 布满暗礁，已知8=PA 公里，10=PB 公里， 60=∠APB ，且BM AM >.请建立适当的直角坐标系，求使快艇沿航线M A P →→或M B P →→的路程相等的点M 的轨迹方程，且画出轨迹的大致图形.4、（本题满分7分）已知关于x 的二次方程0)1()1(222=+++++i a x i a x i a 有实根，求实数a 的值及相应的实根.5、（本题满分10分）已知椭圆12222=+by a x （0>>b a ）经过点)21,26(P ，22=a c ，动点M 在直线2=x 上，O 为坐标原点. （1）求椭圆的标准方程；（2）设F 是椭圆的右焦点，过点F 作OM 的垂线与以OM 为直径的圆交于点N ，证明线段ON 的长为定值，并求出这个值.6、（本题满分12分）如图，点)0,3(-H ，动点P 在y 轴上，动点Q 在x 轴的非负半轴上，动点M满足0=⋅PM HP ，23-=，设动点M 的轨迹为曲线C ，过定点)0,(m D （0>m ）的直线l与曲线C 交于A 、B 两点.（1）求曲线C 的方程；（2）若点E 的坐标为)0,(m -，求证：BED AED ∠=∠；（3）是否存在实数a ，使得以AD 为直径的圆截直线a x l =':所得的弦长为定值？若存在， 求出实数a 的值；若不存在，说明理由.。

杨浦区第二中学2018-2019学年高二上学期数学期末模拟试卷含解析班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 点A 是椭圆上一点，F 1、F 2分别是椭圆的左、右焦点，I 是△AF 1F 2的内心．若，则该椭圆的离心率为（）A ．B ．C ．D ．2． 设a 是函数x 的零点，若x 0＞a ，则f （x 0）的值满足（）A ．f （x 0）=0B ．f （x 0）＜0C ．f （x 0）＞0D ．f （x 0）的符号不确定3． 已知是虚数单位，若复数（）的实部与虚部相等，则（ ）)(3i a i +-R a ∈=a A ．B ．C ．D ． 1-2-4． 已知一元二次不等式f （x ）＜0的解集为{x|x ＜﹣1或x ＞}，则f （10x ）＞0的解集为（ ）A ．{x|x ＜﹣1或x ＞﹣lg2}B ．{x|﹣1＜x ＜﹣lg2}C ．{x|x ＞﹣lg2}D ．{x|x ＜﹣lg2}5． 函数的定义域为（）A ．{x|1＜x ≤4}B ．{x|1＜x ≤4，且x ≠2}C ．{x|1≤x ≤4，且x ≠2}D ．{x|x ≥4}6． 已知向量=（1，），=（，x ）共线，则实数x 的值为（）A ．1B ．C ．tan35°D ．tan35°7． 设数列{a n }的前n 项和为S n ，若S n =n 2+2n （n ∈N *），则++…+=（）A ．B ．C ．D ．8． 设函数f （x ）=，则f （1）=（）A ．0B ．1C ．2D ．39． 已知 m 、n 是两条不重合的直线，α、β、γ是三个互不重合的平面，则下列命题中 正确的是（ ）A ．若 m ∥α，n ∥α，则 m ∥nB ．若α⊥γ，β⊥γ，则 α∥βC ．若m ⊥α，n ⊥α，则 m ∥nD ．若 m ∥α，m ∥β，则 α∥β10．若,则的值为（ ）()()()()2,106,10x x f x f f x x -≥⎧⎪=⎨+<⎡⎤⎪⎣⎦⎩()5f A ． B ． C.D ．1011121311．在二项式（x 3﹣）n （n ∈N *）的展开式中，常数项为28，则n 的值为（ ）A ．12B ．8C ．6D ．412．下列命题中正确的是（）A ．若命题p 为真命题，命题q 为假命题，则命题“p ∧q ”为真命题B ．命题“若xy=0，则x=0”的否命题为：“若xy=0，则x ≠0”C ．“”是“”的充分不必要条件D ．命题“∀x ∈R ，2x ＞0”的否定是“”二、填空题13．命题“∀x ∈R ，x 2﹣2x ﹣1＞0”的否定形式是 ．14．某种产品的加工需要 A ，B ，C ，D ，E 五道工艺，其中 A 必须在D 的前面完成（不一定相邻），其它工艺的顺序可以改变，但不能同时进行，为了节省加工时间，B 与C 必须相邻，那么完成加工该产品的不同工艺的排列顺序有 种．（用数字作答）15．已知函数f （x ）是定义在R 上的单调函数，且满足对任意的实数x 都有f[f （x ）﹣2x ]=6，则f （x ）+f （﹣x ）的最小值等于 ．　16．抛物线的焦点为，经过其准线与轴的交点的直线与抛物线切于点，则24x y =F y Q P FPQ ∆外接圆的标准方程为_________.17．已知x 是400和1600的等差中项，则x= ．18．将一张坐标纸折叠一次，使点与点重合，且点与点重合，则的()0,2()4,0()7,3(),m n m n +值是．三、解答题19．已知函数f （x ）=log a （x 2+2），若f （5）=3；（1）求a 的值； （2）求的值；（3）解不等式f （x ）＜f （x+2）．20．已知函数f（x）=ax3+bx2﹣3x在x=±1处取得极值．求函数f（x）的解析式．21．如图，四面体ABCD中，平面ABC⊥平面BCD，AC=AB，CB=CD，∠DCB=120°，点E在BD上，且CE=DE ．（Ⅰ）求证：AB⊥CE；（Ⅱ）若AC=CE，求二面角A﹣CD﹣B的余弦值．22．某滨海旅游公司今年年初用49万元购进一艘游艇，并立即投入使用，预计每年的收入为25万元，此外每年都要花费一定的维护费用，计划第一年维护费用4万元，从第二年起，每年的维修费用比上一年多2万元，设使用x年后游艇的盈利为y万元．（1）写出y与x之间的函数关系式；（2）此游艇使用多少年，可使年平均盈利额最大？23．设f（x）=ax2﹣（a+1）x+1（1）解关于x的不等式f（x）＞0；（2）若对任意的a∈[﹣1，1]，不等式f（x）＞0恒成立，求x的取值范围．24．如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E、F分别是AP、AD的中点，求证：（1）直线EF∥平面PCD；（2）平面BEF⊥平面PAD．杨浦区第二中学2018-2019学年高二上学期数学期末模拟试卷含解析（参考答案）一、选择题1．【答案】B【解析】解：设△AF1F2的内切圆半径为r，则S△IAF1=|AF1|r，S△IAF2=|AF2|r，S△IF1F2=|F1F2|r，∵，∴|AF1|r=2×|F1F2|r﹣|AF2|r，整理，得|AF1|+|AF2|=2|F1F2|．∴a=2，∴椭圆的离心率e===．故选：B．2．【答案】C【解析】解：作出y=2x和y=log x的函数图象，如图：由图象可知当x0＞a时，2＞log x0，∴f（x0）=2﹣log x0＞0．故选：C．3．【答案】A考点：复数运算．4．【答案】D【解析】解：由题意可知f（x）＞0的解集为{x|﹣1＜x＜}，故可得f（10x）＞0等价于﹣1＜10x＜，由指数函数的值域为（0，+∞）一定有10x＞﹣1，而10x＜可化为10x＜，即10x＜10﹣lg2，由指数函数的单调性可知：x＜﹣lg2故选：D5．【答案】B【解析】解：要使函数有意义，只须，即，解得1＜x≤4且x≠2，∴函数f（x）的定义域为{x|1＜x≤4且x≠2}．故选B6．【答案】B【解析】解：∵向量=（1，），=（，x）共线，∴x====，故选：B．【点评】本题考查了向量的共线的条件和三角函数的化简，属于基础题．7．【答案】D【解析】解：∵S n=n2+2n（n∈N*），∴当n=1时，a1=S1=3；当n≥2时，a n=S n﹣S n﹣1=（n2+2n）﹣[（n﹣1）2+2（n﹣1）]=2n+1．∴==，∴++…+=++…+==﹣．故选：D．【点评】本题考查了递推关系、“裂项求和”方法，考查了推理能力与计算能力，属于中档题．8．【答案】D【解析】解：∵f（x）=，f（1）=f[f（7）]=f（5）=3．故选：D．9．【答案】C【解析】解：对于A，若m∥α，n∥α，则m与n相交、平行或者异面；故A错误；对于B，若α⊥γ，β⊥γ，则α与β可能相交，如墙角；故B错误；对于C，若m⊥α，n⊥α，根据线面垂直的性质定理得到m∥n；故C正确；对于D，若m∥α，m∥β，则α与β可能相交；故D错误；故选C．【点评】本题考查了空间线线关系．面面关系的判断；熟练的运用相关的定理是关键．10．【答案】B【解析】考点：函数值的求解.11．【答案】B【解析】解：展开式通项公式为T r+1=•（﹣1）r•x3n﹣4r，则∵二项式（x3﹣）n（n∈N*）的展开式中，常数项为28，∴，∴n=8，r=6．故选：B．【点评】本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．12．【答案】D【解析】解：若命题p为真命题，命题q为假命题，则命题“p∧q”为假命题，故A不正确；命题“若xy=0，则x=0”的否命题为：“若xy≠0，则x≠0”，故B不正确；“”⇒“+2kπ，或，k∈Z”，“”⇒“”，故“”是“”的必要不充分条件，故C不正确；命题“∀x∈R，2x＞0”的否定是“”，故D正确．故选D．【点评】本题考查命题的真假判断，是基础题，解题时要认真审题，仔细解答．二、填空题13．【答案】 ．【解析】解：因为全称命题的否定是特称命题所以，命题“∀x∈R，x2﹣2x﹣1＞0”的否定形式是：．故答案为：．14．【答案】　24　【解析】解：由题意，B与C必须相邻，利用捆绑法，可得=48种方法，因为A必须在D的前面完成，所以完成加工该产品的不同工艺的排列顺序有48÷2=24种，故答案为：24．【点评】本题考查计数原理的应用，考查学生的计算能力，比较基础．　15．【答案】　6　．【解析】解：根据题意可知：f （x ）﹣2x 是一个固定的数，记为a ，则f （a ）=6，∴f （x ）﹣2x =a ，即f （x ）=a+2x ，∴当x=a 时，又∵a+2a =6，∴a=2，∴f （x ）=2+2x ，∴f （x ）+f （﹣x ）=2+2x +2+2﹣x =2x +2﹣x +4≥2+4=6，当且仅当x=0时成立，∴f （x ）+f （﹣x ）的最小值等于6，故答案为：6．【点评】本题考查函数的最值，考查运算求解能力，注意解题方法的积累，属于中档题．　16．【答案】或()2212x y -+=()2212x y ++=【解析】试题分析：由题意知，设，由，则切线方程为，代入()0,1F 2001,4P x x ⎛⎫ ⎪⎝⎭1'2y x =()20001142y x x x x -=-得，则，可得，则外接圆以为直径，则()0,1-02x =±()()2,1,2,1P -PF FQ ⊥FPQ ∆PQ ()2212x y -+=或.故本题答案填或．1()2212x y ++=()2212x y -+=()2212x y ++=考点：1.圆的标准方程；2.抛物线的标准方程与几何性质．17．【答案】　1000　．【解析】解：∵x 是400和1600的等差中项，∴x==1000．故答案为：1000．18．【答案】345【解析】考点：点关于直线对称；直线的点斜式方程.三、解答题19．【答案】【解析】解：（1）∵f（5）=3，∴，即log a27=3解锝：a=3…（2）由（1）得函数，则=…（3）不等式f（x）＜f（x+2），即为化简不等式得…∵函数y=log3x在（0，+∞）上为增函数，且的定义域为R．∴x2+2＜x2+4x+6…即4x＞﹣4，解得x＞﹣1，所以不等式的解集为：（﹣1，+∞）…20．【答案】【解析】解：（1）f'（x）=3ax2+2bx﹣3，依题意，f'（1）=f'（﹣1）=0，即，解得a=1，b=0．∴f（x）=x3﹣3x．【点评】本题考查了导数和函数极值的问题，属于基础题．21．【答案】【解析】解：（Ⅰ）证明：△BCD中，CB=CD，∠BCD=120°，∴∠CDB=30°，∵EC=DE，∴∠DCE=30°，∠BCE=90°，∴EC⊥BC，又∵平面ABC⊥平面BCD，平面ABC与平面BCD的交线为BC，∴EC⊥平面ABC，∴EC⊥AB．（Ⅱ）解：取BC的中点O，BE中点F，连结OA，OF，∵AC=AB，∴AO⊥BC，∵平面ABC⊥平面BCD，平面ABC∩平面BCD=BC，∴AO⊥平面BCD，∵O是BC中点，F是BE中点，∴OF⊥BC，以O为原点，OB为y轴，OA为z轴，建立空间直角坐标系，设DE=2，则A（0，0，1），B（0，，0），C（0，﹣，0），D（3，﹣2，0），∴=（0，﹣，﹣1），=（3，﹣，0），设平面ACD的法向量为=（x，y，z），则，取x=1，得=（1，，﹣3），又平面BCD的法向量=（0，0，1），∴cos＜＞==﹣，∴二面角A﹣CD﹣B的余弦值为．【点评】本小题主要考查立体几何的相关知识，具体涉及到线面以及面面的垂直关系、二面角的求法及空间向量在立体几何中的应用．本小题对考生的空间想象能力与运算求解能力有较高要求．22．【答案】【解析】解：（1）（x∈N*） (6)（2）盈利额为…当且仅当即x=7时，上式取到等号 (11)答：使用游艇平均7年的盈利额最大． (12)【点评】本题考查函数模型的构建，考查利用基本不等式求函数的最值，属于中档题．　23．【答案】【解析】解：（1）f（x）＞0，即为ax2﹣（a+1）x+1＞0，即有（ax﹣1）（x﹣1）＞0，当a=0时，即有1﹣x＞0，解得x＜1；当a＜0时，即有（x﹣1）（x﹣）＜0，由1＞可得＜x＜1；当a=1时，（x﹣1）2＞0，即有x∈R，x≠1；当a＞1时，1＞，可得x＞1或x＜；当0＜a＜1时，1＜，可得x＜1或x＞．综上可得，a=0时，解集为{x|x＜1}；a＜0时，解集为{x|＜x＜1}；a=1时，解集为{x|x∈R，x≠1}；a＞1时，解集为{x|x＞1或x＜}；0＜a＜1时，解集为{x|x＜1或x＞}．（2）对任意的a∈[﹣1，1]，不等式f（x）＞0恒成立，即为ax2﹣（a+1）x+1＞0，即a（x2﹣1）﹣x+1＞0，对任意的a∈[﹣1，1]恒成立．设g（a）=a（x2﹣1）﹣x+1，a∈[﹣1，1]．则g（﹣1）＞0，且g（1）＞0，即﹣（x2﹣1）﹣x+1＞0，且（x2﹣1）﹣x+1＞0，即（x﹣1）（x+2）＜0，且x（x﹣1）＞0，解得﹣2＜x＜1，且x＞1或x＜0．可得﹣2＜x＜0．故x的取值范围是（﹣2，0）．24．【答案】【解析】证明：（1）在△PAD中，因为E，F分别为AP，AD的中点，所以EF∥PD．又因为EF不在平面PCD中，PD⊂平面PCD所以直线EF∥平面PCD．（2）连接BD．因为AB=AD，∠BAD=60°．所以△ABD为正三角形．因为F是AD的中点，所以BF⊥AD．因为平面PAD⊥平面ABCD，BF⊂平面ABCD，平面PAD∩平面ABCD=AD，所以BF⊥平面PAD．又因为BF⊂平面EBF，所以平面BEF⊥平面PAD．【点评】本题是中档题，考查直线与平面平行，平面与平面的垂直的证明方法，考查空间想象能力，逻辑推理能力，常考题型．。

曹杨二中高二期末数学试卷2019.06一. 填空题1. 1-的平方根为2. 复数2i iz +=的虚部为 3. 抛物线2y x =的焦点到准线的距离为 4. 若复数z 满足||1z =，则|1i |z -+的最大值是5. 若双曲线的焦点在x 轴上，焦距为4，且过点(2,3)P ，则双曲线的标准方程为6. 用1，2，3，4，5，6组成没有重复数字的六位数，要求任意相邻两个数码的奇偶性都不同，则这样的六位数的个数是7. 已知直线1l ：10mx y +-=，2l ：(2)20m x my ++-=，若1l 与2l 平行，则实数m 的值为8. 已知方程220x x p -+=的两个虚根为α、β，且||4αβ-=，则实数p =9. 已知直线l 过点(0,5)，且它的一个方向向量为（1,2），则原点O 到直线l 的距离为10. 设6523001230(1)x x a a x a x a x ++=+++⋅⋅⋅+，其中01230,,,,a a a a ⋅⋅⋅是各项的系数，则在01230,,,,a a a a ⋅⋅⋅这31个系数中，值为零的个数为11. 在直角坐标系中，已知(1,0)A ，(4,0)B ，若直线10x my +-=上存在点P ，使得||2||PA PB =，则实数m 的取值范围是12. 从集合{,,,}U a b c d =的子集中选出2个不同的子集，需同时满足以下两个条件：①a 、b 都至少属于其中一个集合；②对选出的两个子集A 、B ，必有A B ⊆或B A ⊆，那么共有 种不同的选法二. 选择题13. 若12i +是关于x 的实系数一元二次方程20x bx c ++=的一个根，则（ ）A. 2b =, 5c =B. 2b =-,5c =C. 2b =-,3c =-D. 2b =,1c =-14. 若m 是小于10的正整数，则(15)(16)(20)m m m --⋅⋅⋅-等于（ ）A. 515m P -B. 1520m m P --C. 520m P -D. 620m P -15. 已知曲线C :421x y +=，给出下列命题：①曲线C 关于x 轴对称；②曲线C 关于y 轴对称；③曲线C 关于原点对称；④曲线C 关于直线y x =对称；⑤曲线C 关于直线y x =-对称，其中正确命题的个数是（ ）A. 1B. 2C. 3D. 416. 在复数列{}n z 中，1816i z =+，1i 2n n z z +=⋅()n *∈N ，设n z 在复平面上对应的点为n Z ， 则（ ） A. 存在点M ，对任意的正整数n ，都满足||10n MZ ≤B. 不存在点M ，对任意的正整数n ，都满足||55n MZ ≤C. 存在无数个点M ，对任意的正整数n ，都满足||65n MZ ≤D. 存在唯一的点M ，对任意的正整数n ，都满足||85n MZ ≤三. 解答题17. （1）已知2||()i 32i z z z ++=-，求复数z ；（2）已知复数z 满足2z z -为纯虚数，且|i |1z -=，求复数z .18. 已知41(2)n x x+的展开式的二项式系数之和为1024.（1）求展开式中的常数项；（2）求展开式中系数最大的项.19. 如图所示是竖直平面内的一个“通道游戏”，图中竖直线段和斜线都表示通道，并且在交点处相遇，若有一条竖直线段的为第一层，有二条竖直线段的为第二层，以此类推，现有一颗小球从第一层的通道向下运动，在通道的交叉处，小球可以落入左右两个通道中的任意一个，记小球落入第n 层的第m 个竖直通道（从左向右计）的不同路径数为(,)A n m .（1）求(2,1)A ，(3,1)A ，(4,2)A 的值；（2）猜想(,)A n m 的表达式（不必证明），并求不等式(9,)28A m ≤的解集.20. 已知复数z 满足|1||1|z z -++=z 在复平面上对应点的轨迹为C ，A 、B 分别 是曲线C 的上、下顶点，M 是曲线C 上异于A 、B 的一点.（1）求曲线C 的方程；（2）若M 在第一象限，且||OM =，求M 的坐标； （3）过点M 作斜率为1的直线分别交曲线C 于另一点N ，交y 轴于点D ，求证：存在常数λ，使得||||||||DM DN DA DB λ⋅=⋅恒成立，并求出λ的值.21. 已知抛物线Γ：24y x =，F 为其焦点，过F 的直线l 与抛物线Γ交于A 、B 两点.（1）若2AF FB =u u u r u u u r ，求B 点的坐标；（2）若线段AB 的中垂线l '交x 轴于M 点，求证：||||AB FM 为定值； （3）设(1,2)P ，直线PA 、PB 分别与抛物线的准线交于点S 、T ，试判断以线段ST 为直径的圆是否过定点？若是，求出定点的坐标；若不是，请说明理由.参考答案一. 填空题1.i ±2.2-3.12 4. 1+5.2213y x -= 6. 72 7.1- 8. 510. 10 11. (,)-∞+∞U 12. 32二. 选择题13. B 14. D 15. C 16. D三. 解答题17.（1）1-±；（2）2i z =，1i z =-+，1i z =+.18.（1）180；（2）2515360x .19.（1）(2,1)1A =，(3,1)1A =，(4,2)3A =；（2）11m n C --，{1,2,3,7,8,9}.20.（1）2212x y +=；（2）；（3）43. 21.（1）1(,1)4±；（2）2；（3）(0,0)，(2,0)-.。

上海市曹杨第二中学高二上学期期末复习（一）数学试题一、单选题1．设1234P P P P 、、、为空间中的四个不同点，则“1234P P P P 、、、中有三点在同一条直线上”是“1234P P P P 、、、在同一个平面上”的（ ）A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件【答案】A【解析】由公理2的推论()()12即可得到答案.【详解】由公理2的推论:过一条直线和直线外一点,有且只有一个平面,可得1234P P P P 、、、在同一平面,故充分条件成立;由公理2的推论：过两条平行直线,有且只有一个平面,可得,当11213242,P l P l P l P l ∈∈∈∈、、、12l l P 时,1234P P P P 、、、在同一个平面上, 但1234P P P P 、、、中无三点共线,故必要条件不成立;故选:A【点睛】本题考查点线面的位置关系和充分必要条件的判断,重点考查公理2及其推论;属于中档题;公理2的三个推论：()1经过一条直线和直线外一点,有且只有一个平面;()2经过两条平行直线,有且只有一个平面;()3经过两条相交直线,有且只有一个平面;2．已知正方体''''ABCD A B C D -记过点A 且与三直线AB AD 、 、'AA 所成的角都相等的直线的条数为m ,过点A 与三个平面'',,AB AC AD 所成角都相等的直线的条数为n ，则（ ）A.11m n ==，B.41m n ==，C.34m n ==，D.44m n ==，【答案】D【解析】根据正方体的结构特征、空间中线线角、线面角定义,即可得到答案.【详解】作图如下:过点A 与三条直线'AB AD AA 、、所成角都相等的直线有：'AC ,过A 作'BD 的平行线,过A 作'A C 的平行线，过A 作'B D 的平行线,共4条,故4m =；过点A 与三个平面'',,AB AC AD 所成角都相等的直线分两类：第一类：通过点A 位于三条棱之间的直线有一条体对角线'AC ;第二类：在图形外部和每面所成角和另两个面所成角相等,有3条；故4n =.故选：D【点睛】本题考查空间直线与平面所成角和直线与直线所成角;结合正方体的结构特征,准确找出符合题意的线线角和线面角是求解本题的关键;注重考查学生的空间想象能力;本题属于抽象型、难度大型试题.3．已知正三棱柱111ABC A B C -的底面边长为2，高为1，过顶点A 作一平面α与侧面11BCC B 交于EF ，且EF ∥BC ，若平面α与底面ABC 所成二面角的大小为06x x π⎛⎫≤ ⎪⎝⎭＜，四边形BCEF 面积为y ，则函数()y f x =的图像大致是（ ） A. B. C. D.【答案】C【解析】先作出平面α与底面ABC 所成的二面角的平面角为x ，如图为GAH ∠,在直角三角形AGH 中用x ,及3AH =表示出GH ,再利用四边形BCEF 面积为y BC GH =⨯求出()f x ,根据解析式，作出简图，即可得到答案.【详解】作图如下：过A 作AM BC P ,,H G 分别是,BC EF 中点,则AH BC ⊥,所以AH AM ⊥,在等腰三角形AEF ∆中,AG EF ⊥，//EF BC Q ,AG AM ∴⊥,所以GAH ∠是平面α与底面ABC 所成角的平面角.GAH x ∴∠=,tan GH x AH =, 3tan GH x ∴=,所以四边形BCEF 面积为： ()y f x =BC GH =⨯23tan x =根据正切函数图象可知C 符合.故选:C【点睛】本题主要考查空间中两面所成二面角的平面角的求解及性质;利用线线平行、线线垂直证明GAH ∠是平面α与底面ABC 所成的二面角的平面角是求解本题的关键;本题属于难度较大型试题.4．如图,在棱长为1的正方体1111ABCD A B C D -中,点P 在截面1A DB 上,则线段AP 的最小值为（ ）A.13B.12 3 D.22【答案】C【解析】由已知可得,1AC ⊥平面1A DB ,可得P 为1AC 与截面1A DB 的垂足时线段AP 最小,然后利用等体积法求解即可.【详解】如图所示:连接1AC 交截面1A DB 于P ,由1CC ⊥底面ABCD ,可得,1CC BD ⊥,由AC BD ⊥,可得,BD ⊥面11A ACC ,则1AC BD ⊥.同理可得,11AC A B ⊥,1AC ∴⊥面1A DB ,此时线段AP 最小.由棱长为1,可得等边三角形1A BD 2,116322A BD S ∆∴==由11-ABD A A A BD V V -=,可得,1113111323AP ⨯⨯⨯⨯=， 可得3AP =. 故选:C【点睛】本题考查点、线、面间距离的计算和线面垂直的判定;利用等体积法间接地求出AP 的距离是求解本题的关键;属于中档题;二、填空题5．直线l 和平面α相交于点A ,用集合符号表示_________.【答案】l A α=I【解析】由点、线、面位置关系的符号表示即可得解.【详解】由题意可得,答案为：l A α=I【点睛】本题考查直线与平面相交的符号表示,属于基础题,解题时注意符号的合理运用. 6．ABC ∆所在平面α外一点P 到三角形三个顶点距离相等,那么点P 在平面α内的射影一定是ABC ∆的_______.【答案】外心【解析】由ABC ∆所在平面α外一点P 到三角形三个顶点距离相等可得,斜线,,PA PB PC 在底面的射影相等;由三角形外心的性质可得是ABC ∆的外心.【详解】作图如下:由题意可得,PA PB PC ==,PO ⊥面ABC ,,,PO OA PO OB PO OC ∴⊥⊥⊥,故POA POB POC ∆≅∆≅∆,OA OB OC ∴==,故答案为:外心【点睛】本题主要考查线面垂直的性质及三角形外心的定义;属于中档题；三角形外心是三角形外接圆的圆心,亦是三角形三边垂直平分线的交点;其性质:到三角形三个顶点的距离相等.7．半径为2的球的表面积为________.【答案】16π【解析】代入球的表面积公式:2=4S R π表即可求得.【详解】 2R =Q ，∴由球的表面积2=4S R π表公式可得,2=42=16S ππ⨯⨯球表,故答案为:16π【点睛】本题考查球的表面积公式;属于基础题.8．已知圆锥的底面半径为3，体积是12π，则圆锥侧面积等于___________.【答案】15π【解析】试题分析：求圆锥侧面积必须先求圆锥母线，既然已知体积，那么可先求出圆锥的高，再利用圆锥的性质(圆锥的高，底面半径，母线组成直角三角形)可得母线，221131233V r h h πππ==⋅⋅=，4h =，5l ==，15S rl 侧ππ==． 【考点】圆锥的体积与面积公式，圆锥的性质．9．已知地球的半径为R ，在北纬45︒东经30︒有一座城市A ，在北纬45︒西经60︒有一座城市B ，则坐飞机从城市A 飞到B 的最短距离是 ．(飞机的飞行高度忽略不计) 【答案】3R π【解析】欲求坐飞机从A 城市飞到B 城市的最短距离，即求出地球上这两点间的球面距离即可．A 、B 两地在同一纬度圈上，计算经度差，求出AB 弦长，以及球心角，然后求出球面距离．即可得到答案．【详解】解：由已知地球半径为R ，则北纬45°，又∵两座城市的经度分别为东经30°和西经60°，故连接两座城市的弦长L 2=R =R ， 则A ，B 两地与地球球心O 连线的夹角∠AOB 3π=， 则A 、B 两地之间的距离是3R π． 故答案为：3R π．【点睛】 本题考查球面距离及其他计算，考查空间想象能力，是基础题．10．设α表示平面,a b 、表示直线,给定下列四个命题：①a a b b αα⊥⇒P P ，；②a b a b αα⊥⇒⊥P ，；③a a b b αα⊥⊥⇒P ，；④.a b a b αα⊥⊥⇒P ，其中正确的命题是___________(填序号).【答案】②④【解析】利用线面垂直的判定方法、线面垂直的性质定理及线面平行的判断方法、性质,对已知中的四个结论逐一进行分析,即可得到答案.【详解】对于①,,a a b α⊥⇒P b 与α平行、相交或b α⊂，故①错误;对于②,a b a α⊥∥，,由直线与平面垂直的性质：两条直线平行,其中一条直线垂直与一个平面,则另外一条直线也垂直此平面.b α∴⊥.故②正确;对于③,,α⊥⊥a a b ,由线面垂直的性质可得,b αP ，或b α⊂,故③错误;对于④,,a b αα⊥⊥，由垂直于同一平面的两直线平行,a b ∴∥，故④正确;故答案为: ②④【点睛】本题考查立体几何中的线面垂直的判定、线面垂直的性质和线面平行的判定、线面平行的性质;线面垂直性质的应用是求解本题的关键;属于中档题;11．已知点P 是棱长为1的正方体1111ABCD A B C D -的底面1111D C B A 上一点(包括边界)，则PA PC ⋅u u u r u u u r 的取值范围是_________. 【答案】1,12⎡⎤⎢⎥⎣⎦【解析】建立空间直角坐标系,设(),,0P x y ,[](),0,1x y ∈.可得,()()22111111222PA PC x x y y x y ⎛⎫⎛⎫⋅=----+=-+-+ ⎪ ⎪⎝⎭⎝⎭u u u v u u u v ，即可得出答案. 【详解】如图所示：建立空间直角坐标系.则()()()10,0,0,0,0,1,1,1,1A A C . 设(),,0P x y ，[](),0,1x y ∈.则(),,1PA x y =--u u u v ，()1,1,1PC x y =--u u u v .()()111PA PC x x y y ∴⋅=----+u u u v u u u v22111222x y ⎛⎫⎛⎫=-+-+ ⎪ ⎪⎝⎭⎝⎭. [],0,1x y ∈Q ,∴当11,22x y ==时, PA PC ⋅u u u v u u u v 有最小值12. 当点P 取()()()()0,0,0,1,0,0,1,1,0,0,1,0时,PA PC ⋅u u u v u u u v 有最大值1.故答案为:1,12⎡⎤⎢⎥⎣⎦【点睛】 本题考在空间直角坐标系中两向量数量积的坐标表示:121212+a b x x y y z z ⋅=+v v 及其取值范围的求解;建立合适的空间直角坐标系是求解本题的关键;着重考查学生的运算能力和知识迁移能力; 属于中档题.12．半径为R 的两个球,其中一个球的球心在另一个球的球面上,则两球的交线长为_____. 3R π【解析】将两球的相交情形,转化为考虑球的两个大圆的相交情形,容易求得CD 的长为3R.从而求得其周长即可.【详解】将两球的相交情形,转化为考虑球的两个大圆的相交情形,如图所示:由题意得,,AB R AC R==，故22232RCD R R⎛⎫=-=⎪⎝⎭.所以两球交线所在圆面的半径为3r R =,所以所求的交线长为3232l R Rππ=⋅=.故答案为:3Rπ【点睛】本题考查球与球的位置关系和圆的周长公式;重点考查学生的空间想象能力;把空间立体几何中球的问题转化为平面几何中圆的问题是求解本题的关键;属于难度大型试题. 13．已知正四棱锥P ABCD-的棱长都相等，侧棱PB、PD的中点分别为M、N，则截面AMN与底面ABCD所成的二面角的余弦值是________．【答案】25【解析】如图，正四棱锥P﹣ABCD中，O为正方形ABCD的两对角线的交点，则PO⊥面ABCD，PO交MN 于E ，则PE=EO ， 又BD ⊥AC ，∴BD ⊥面PAC ，过A 作直线l ∥BD ，则l ⊥EA ，l ⊥AO ， ∴∠EAO 为所求二面角的平面角． 又EO=12AO=24a ，AO=22a ，∴AE=104a ∴cos ∠EAO=255． ∴截面AMN 与底面ABCD 所成的二面角的余弦值是255． 14．如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为________．【答案】43【解析】分析：先分析组合体的构成，再确定锥体的高，最后利用锥体体积公式求结果. 详解：由图可知，该多面体为两个全等正四棱锥的组合体，正四棱锥的高为1，底面正方形的边长等于2，，所以该多面体的体积为21421(2).33⨯⨯⨯=点睛：解决本类题目的关键是准确理解几何体的定义，真正把握几何体的结构特征，可以根据条件构建几何模型，在几何模型中进行判断；求一些不规则几何体的体积时，常用割补法转化成已知体积公式的几何体进行解决． 15．有两个相同的直三棱柱，高为，底面三角形的三边长分别为。

上海市曹杨第二中学2022学年度第一学期高二年级总结性评价数学试卷命题人：黄坪校对人：郭天翔试卷共4页1张考生注意：1、答卷前，考生务必将姓名、班级、学号等在指定位置填写清楚.2、本试卷共有21道试卷，满分150分，评价时间120分钟.请同学们将选择题答案直接点击在智学网上，非选择题用黑色水笔将答案写在答题卷上，并按要求拍照上传至智学网相关位置.一、填空题：（共12题，满分54分，前6题每题4分，后6题每题5分）1.半径为1cm 的球的体积是___________3cm .2.设正四面体的棱长为1，则该正四面体的高为______.3.两条平行直线3410x y -+=与3420x y --=之间的距离为______.4.若直线l的一个法向量为(-，则过原点的直线l 的方程为______.5.如图是用斜二测画法画出的水平放置的正三角形ABC 的直观图，其中1O B O C ''''==，则三角形A B C '''的面积为______.6.如果圆锥的底面圆半径为1，母线长为2，则该圆锥的侧面积为___．7.一个椭圆的长轴长是短轴长的2倍，则该椭圆的离心率为________.8.已知直线:cos 10l x y θ+-=，R θ∈，则直线l 的倾斜角的取值范围是______.9.已知正三棱台111ABC A B C -上、下底面边长分别为1和2，高为1，则这个正三棱台的体积为______.10.已知圆22:16C x y +=，直线()():20l a b x b a y a -+--=（a 、b 不同时为0），当a 、b 变化时，圆C 被直线l 截得的弦长的最小值为______.11.在棱长为2的正方体1111ABCD A B C D -，M ，N ，Q ，P 分别为棱11A B ，11B C ，1BB ，1CC 的中点，三棱锥M PQN-的顶点在同一个球面上，则该球的表面积为___________.12.如图，已知F 是椭圆22143x y +=的左焦点，A 为椭圆的下顶点，点P 是椭圆上任意一点，以PF 为直径作圆N ，射线ON 与圆N 交于点Q ，则AQ的取值范围为______.二、选择题：（共4题，满分18分，前2题每题4分，后2题每题5分）13.设1234P P P P 、、、为空间中的四个不同点，则“1234P P P P 、、、中有三点在同一条直线上”是“1234P P P P 、、、在同一个平面上”的（）A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件14.若点O 和点F 分别为椭圆2212x y +=的中心和右焦点，点P 为椭圆上的任意一点，则OP FP ⋅ 的最小值为A.22- B.12C.22D.115.已知曲线C ：()3222216x yx y +=，命题p ：曲线C 仅过一个横坐标与纵坐标都是整数的点；命题q ：曲线C上的点到原点的最大距离是2.则下列说法正确的是（）A.p 、q 都是真命题B.p 是真命题，q 是假命题C.p 是假命题，q 是真命题D.p 、q 都是假命题16.四面体ABCD 的所有棱长都为1，棱AB 平面α，则四面体上的所有点在平面α内的射影构成的图形面积的取值范围是（）A.21,22⎤⎢⎥⎣⎦ B.31,42⎤⎥⎣⎦C.21,42⎤⎥⎣⎦D.23,44⎣⎦三、解答题：（共5题，满分78分，前3题每题14分，其中第1问6分，第2问8分；后2题每题18分，其中第1问4分，第2问6分，第3问8分）17.已知圆C 经过(3,2)A 、(1,6)B 两点，且圆心在直线2y x =上．（1）求圆C 的方程；（2）若直线l 经过点(1,3)P -且与圆C 相切，求直线l 的方程．18.如图，在三棱锥D ABC -中，平面ACD ⊥平面ABC ，AD AC ⊥，AB BC ⊥，E 、F 分别为棱BC 、CD 的中点.（1）求证：直线//EF 平面ABD ；（2）若直线CD 与平面ABC 所成的角为45°，直线CD 与平面ABD 所成角为30°，求二面角B AD C --的大小.19.如图，A 、B 是海岸线OM 、ON 上的两个码头，海中小岛有码头Q 到海岸线OM 、ON 的距离分别为2km 、710km 5.测得tan 3MON ∠=-，6km OA =.以点O 为坐标原点，射线OM 为x 轴的正半轴，建立如图所示的直角坐标系.码头Q 在第一象限，且三个码头A 、B 、Q 均在一条航线上.（1）求码头Q 点的坐标；（2）海中有一处景点P （设点P 在平面xOy 内，PQ OM ⊥，且6km PQ =），游轮无法靠近.求游轮在水上沿旅游线AB 航行时离景点P 最近的点C 的坐标.20.如图，在长方体1111ABCD A B C D -中，11DD DA ==，2AB =，点E 在棱AB 上运动.（1）证明：11B C D E ⊥；（2）设E 为棱AB 的中点，在棱1CC 上是否存在一点F ，使得//BF 平面1DEC ，若存在，求1CFCC 的值，若不存在，说明理由；（3）求直线AB 与平面1DEC 所成角的取值范围.21.已知椭圆22:142x y C +=，过动点()()0,0M m m >的直线l 交x 轴于点N ，交C 于点A 、P （P 在第一象限），且M 是线段PN 的中点，过点P 作x 轴的垂线交C 于另一点Q ，延长QM 交C 于点B .设()11,A x y 、()22,B x y.（1）若点N的坐标为()，求PNQ V 的周长；（2）设直线PM 的斜率为k ，QM 的斜率为k '，证明：k k'为定值；（3）求直线AB 倾斜角的最小值.上海市曹杨第二中学2022学年度第一学期高二年级总结性评价数学试卷命题人：黄坪校对人：郭天翔试卷共4页1张考生注意：1、答卷前，考生务必将姓名、班级、学号等在指定位置填写清楚.2、本试卷共有21道试卷，满分150分，评价时间120分钟.请同学们将选择题答案直接点击在智学网上，非选择题用黑色水笔将答案写在答题卷上，并按要求拍照上传至智学网相关位置.一、填空题：（共12题，满分54分，前6题每题4分，后6题每题5分）1.半径为1cm 的球的体积是___________3cm .【答案】4π3【分析】根据球体积公式计算．【详解】由题意球体积为()3344π1πcm 33V =⨯=．故答案为：4π3．2.设正四面体的棱长为1，则该正四面体的高为______.【答案】63【分析】设正四面体为A BCD -，过A 作AO ⊥底面BCD ，可知O 为底面正三角形的中心，然后求解直角三角形得答案．【详解】如图，设正四面体为A BCD -，过A 作AO ⊥底面BCD ，垂足为O ，四面体为正四面体，∴O 为底面正三角形的中心，连接CO 并延长交BD 于G ，则G 为BD 中点，底面边长为1，323CO CG ∴==，63AO ∴==，∴该正四面体的高为3．故答案为：3．3.两条平行直线3410x y -+=与3420x y --=之间的距离为______.【答案】35##0.6【分析】根据两平行直线间的距离公式求得正确答案.【详解】两条平行直线3410x y -+=与3420x y --=之间的距离为：35=.故答案为：35.4.若直线l的一个法向量为(-，则过原点的直线l 的方程为______.【答案】0x -=【分析】根据直线法向量，可设出直线方程，由直线过原点，求出未知系数.【详解】若直线l的一个法向量为(-，可设直线方程为0x c -++=，由直线过原点，∴0c =，故所求直线方程为0x -=，即0x -=.故答案为：0x -=5.如图是用斜二测画法画出的水平放置的正三角形ABC 的直观图，其中1O B O C ''''==，则三角形A B C '''的面积为______.【答案】4【分析】根据直观图和平面图的关系可求出O A ''，进而利用面积公式可得三角形A B C '''的面积【详解】由已知可得12222O A ''=⨯⨯=则132622224A B C S '''=⨯⨯=故答案为：64.6.如果圆锥的底面圆半径为1，母线长为2，则该圆锥的侧面积为___．【答案】2π【分析】由圆锥的侧面积公式即可求解．【详解】由题意，圆锥底面周长为2π×1=2π，又母线长为2，所以圆锥的侧面积12222S ππ=⨯⨯=．故答案为：2π.7.一个椭圆的长轴长是短轴长的2倍，则该椭圆的离心率为________.【答案】2【分析】根据已知可知：2a b =，再代入离心率公式e =即可.【详解】由题知：222a b =⨯，即2a b =.32c e a =====.故答案为：2【点睛】本题主要考查离心率的求法，根据题意找到关系式为解题的关键，属于简单题.8.已知直线:cos 10l x y θ+-=，R θ∈，则直线l 的倾斜角的取值范围是______.【答案】π3π[0,[,π)44⋃【分析】由题意可得直线l 的斜率cos [1,1]k θ=-∈-，设直线l 的倾斜角为β，则有tan [1,1]β∈-，[0,π)β∈，再根据正切函数的性质即可求得答案.【详解】解：因为直线:cos 10l x y θ+-=，R θ∈，所以直线l 的斜率cos k θ=-，所以[1,1]k ∈-，设直线l 的倾斜角为β，则有tan [1,1]k β=∈-，又因为[0,π)β∈，所以π3π[0,][,π)44β∈⋃.故答案为：π3π[0,[,π)44⋃9.已知正三棱台111ABC A B C -上、下底面边长分别为1和2，高为1，则这个正三棱台的体积为______.【答案】12【分析】先计算两个底面的面积，再由体积公式计算即可.【详解】上底面的面积为1311sin 6024⨯⨯⨯︒=，下底面的面积为122sin 602⨯⨯⨯︒=积为113412⎛⨯+⨯= ⎝.故答案为：731210.已知圆22:16C x y +=，直线()():20l a b x b a y a -+--=（a 、b 不同时为0），当a 、b 变化时，圆C 被直线l 截得的弦长的最小值为______.【答案】【分析】由题意知直线l 恒过定点(1,1)--，当圆心到直线距离取最大值时，此时圆C 被直线l 截得的弦长为最小值，即可求出答案.【详解】把直线()():20l a b x b a y a -+--=化为(21)()0a x y b x y --+-+=，210101x y x x y y --==-⎧⎧⇒⎨⎨-+==-⎩⎩，恒过定点(1,1)--，当圆C 被直线l 截得的弦长的最小值时，圆心(0,0)到定点(1,1)--=，圆心到直线()():20l a b x b a y a -+--=距离最大值时即为，此时直线弦长为最小值=故答案为：.11.在棱长为2的正方体1111ABCD A B C D -，M ，N ，Q ，P 分别为棱11A B ，11B C ，1BB ，1CC 的中点，三棱锥M PQN -的顶点在同一个球面上，则该球的表面积为___________.【答案】8π【分析】由正方体性质确定三棱锥M NPQ -的性质，从而确定其外接球球心O 所在位置，然后由直角梯形和直角三角形求出半径得表面积．【详解】如图，取PQ 中点K ，11A D AD H = ，由正方体性质知HK ⊥平面11BCC B ，由已知NPQ △是等腰直角三角形，PQ 是斜边，则三棱锥M NPQ -的外接球球心O 在HK 上，连接,OM OP ，由HK ⊥平面11BCC B 知1,HK KB HK PQ ⊥⊥，同理111A B B K ⊥，1OKB M 是直角梯形，11MB =，1B K =，1KP =，设外接球半径为R ，则1OK =在直角三角形OPK 中，222(11R =+，解得R =．所以球表面积为248S R ππ==．故答案为：8π．【点睛】关键点点睛：本题考查求三棱锥外接球的表面积，解题关键是找到外接球的球心，一般外接球球心必在过三棱锥各面外心且与此面垂直的直线上．确定球心位置后通过直角梯形与直角三角形求得半径．12.如图，已知F 是椭圆22143x y +=的左焦点，A 为椭圆的下顶点，点P 是椭圆上任意一点，以PF 为直径作圆N ，射线ON 与圆N 交于点Q ，则AQ 的取值范围为______.【答案】23,23⎡⎤+⎣⎦【分析】由题意求得点Q 轨迹，根据轨迹判断计算AQ 的取值范围.【详解】F '为椭圆右焦点，连接PF '，如图所示：,O N 分别为,FF FP '的中点，12ON PF '=，PF 为直径，12NQ PF =，()1112222OQ ON NQ PF PF PF PF ''=+=+=+=，所以点Q 轨迹是以O 为圆心2为半径的圆，(0,3A -在圆内，所以AQ 的最小值为23-，最大值为23+，即AQ 的取值范围为23,23⎡⎤-+⎣⎦.故答案为：23,23⎡⎤-+⎣⎦二、选择题：（共4题，满分18分，前2题每题4分，后2题每题5分）13.设1234P P P P 、、、为空间中的四个不同点，则“1234P P P P 、、、中有三点在同一条直线上”是“1234P P P P 、、、在同一个平面上”的（）A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件【答案】A【分析】由公理2的推论()()12即可得到答案.【详解】由公理2的推论:过一条直线和直线外一点,有且只有一个平面,可得1234P P P P 、、、在同一平面,故充分条件成立;由公理2的推论：过两条平行直线,有且只有一个平面,可得,当11213242,P l P l P l P l ∈∈∈∈、、、12l l 时,1234P P P P 、、、在同一个平面上,但1234P P P P 、、、中无三点共线,故必要条件不成立;故选:A【点睛】本题考查点线面的位置关系和充分必要条件的判断,重点考查公理2及其推论;属于中档题;公理2的三个推论：()1经过一条直线和直线外一点,有且只有一个平面;()2经过两条平行直线,有且只有一个平面;()3经过两条相交直线,有且只有一个平面;14.若点O 和点F 分别为椭圆2212x y +=的中心和右焦点，点P 为椭圆上的任意一点，则OP FP ⋅ 的最小值为A.22-B.12C.22+ D.1【答案】B【详解】试卷分析：设点，所以，由此可得(,)(1,)OP FP x y x y ⋅=⋅-，[2,2]x ∈，所以OP FP ⋅的最小值为12.考点：向量数量积以及二次函数最值．15.已知曲线C ：()3222216x y x y +=，命题p ：曲线C 仅过一个横坐标与纵坐标都是整数的点；命题q ：曲线C上的点到原点的最大距离是2.则下列说法正确的是（）A.p 、q 都是真命题B.p 是真命题，q 是假命题C.p 是假命题，q 是真命题D.p 、q 都是假命题【答案】A【分析】结合均值不等式得到当且仅当22x y =时，等号成立，以及224x y +≤，从而可判断命题q 的真假性，检验点()()()()()()()()()0,0,1,1,1,1,1,1,1,1,2,0,2,0,0,2,0,2------是否在曲线上即可判断命题p 的真假性.【详解】因为()2223222216162x y x y x y ⎛⎫++=≤ ⎪⎝⎭，当且仅当22x y =时，等号成立，所以224x y +≤，因此曲线C 所围成的区域的在圆224x y +=2£，故曲线C 上的点到原点的最大距离是2，因此命题q 为真命题，圆224x y +=上以及内部横坐标与纵坐标都是整数的点有()()()()()()()()()0,0,1,1,1,1,1,1,1,1,2,0,2,0,0,2,0,2------，其中点()0,0显然在曲线C 上，但是()()()()()()()()1,1,1,1,1,1,1,1,2,0,2,0,0,2,0,2------不在曲线上，故曲线C 仅过一个横坐标与纵坐标都是整数的点，因此命题p 为真命题，故选：A.16.四面体ABCD 的所有棱长都为1，棱AB 平面α，则四面体上的所有点在平面α内的射影构成的图形面积的取值范围是（）A.1,22⎤⎢⎥⎣⎦ B.31,42⎤⎥⎣⎦ C.21,42⎤⎥⎣⎦ D.23,44⎣⎦【答案】D【分析】设A 、B 、C 、D 在平面α内的射影依次为1111A B C D 、、、，分别讨论11C D 、在11A B 两侧、11C D 、其中一点在11A B 上、11C D 、在11A B 同侧时的投影图形，其中11C D 、在11A B 同侧时，CD α⊥时面积最小、平面ABD α 时面积最大，结合正四面体的几何性质及投影性质即可求面积.【详解】四面体ABCD 的所有棱长都为1，则为正四面体，由正四面体的性质可知AB CD ⊥,正四面体的侧面上的高为2h ¢==，正四面体的高3h ==.∵棱AB 平面α，设A 、B 、C 、D 在平面α内的射影依次为1111A B C D 、、、，则111A B AB ==，i.当11C D 、在11A B 两侧时，构成的图形即为四边形1111A C B D ，此时1111A B C D ^，11h C D CD <£，即11613C D <£，则所求面积即11111111161,262A B C D S A B C D ú=ú棼；ii.当11C D 、在11A B 同侧或其中一点在11A B 上时，构成的图形即为111A B C △，1D 在111A B C △的高1C E 上（或1C 在111A B D 的高上，由对称性，只研究其中一种即可），其中①当平面ABD α^时，163C E h ==；②当平面ABD α 时，132C E h ¢==；③当CD α⊥时，1C E 为CD 到面α的距离，即12C E ==.故12322C E ＃，则所求面积即111111123,244A B C S A B C E 犏=鬃犏臌.综上，四面体上的所有点在平面α内的射影构成的图形面积的取值范围是,44⎣⎦.故选：D三、解答题：（共5题，满分78分，前3题每题14分，其中第1问6分，第2问8分；后2题每题18分，其中第1问4分，第2问6分，第3问8分）17.已知圆C 经过(3,2)A 、(1,6)B 两点，且圆心在直线2y x =上．（1）求圆C 的方程；（2）若直线l 经过点(1,3)P -且与圆C 相切，求直线l 的方程．【答案】（１）22(2)(4)5x y -+-=；（２）250250x y x y -+=+-=或【详解】试卷分析：（1）根据圆心在弦的垂直平分线上，先求出弦AB 的垂直平分线的方程与2y x =联立可求得圆心坐标，再用两点间的距离公式求得半径，进而求得圆的方程；（2）当直线l 斜率不存在时，与圆相切，方程为=1x -；当直线l 斜率存在时，设斜率为k ，写出其点斜式方程，利用圆心到直线的距离等于半径建立方程求解出k 的值.试卷解析：（1）依题意知线段AB 的中点M 坐标是()2,4，直线AB 的斜率为62213-=--，故线段AB 的中垂线方程是()1422y x -=-即260x y -+=，解方程组260{2x y y x -+==得2{4x y ==，即圆心C 的坐标为()2,4，圆C的半径r AC ==，故圆C 的方程是()()22245x y -+-=（2）若直线l 斜率不存在，则直线l 方程是1x =-，与圆C 相离，不合题意；若直线l 斜率存在，可设直线l 方程是()31y k x -=+，即30kx y k -++=，因为直线l 与圆C=解得2k =或12k =-．所以直线l 的方程是250x y -+=或250x y +-=.18.如图，在三棱锥D ABC -中，平面ACD ⊥平面ABC ，AD AC ⊥，AB BC ⊥，E 、F 分别为棱BC 、CD 的中点.（1）求证：直线//EF 平面ABD ；（2）若直线CD 与平面ABC 所成的角为45°，直线CD 与平面ABD 所成角为30°，求二面角B AD C --的大小.【答案】（1）证明见解析；（2）45【分析】（1）根据//EF BD 即可证明；（2）证明AD ⊥平面ABC ，BC ⊥平面ABD ，进而结合已知条件证明ABC 为等腰直角三角形，45BAC ∠= ，再根据二面角的概念求解即可.【小问1详解】证明：因为E 、F 分别为棱BC 、CD 的中点.所以，在BCD △中，//EF BD ，因为EF ⊄平面ABD ，BD ⊂平面ABD ，所以，直线EF P 平面ABD 【小问2详解】解：因为平面ACD ⊥平面ABC ，平面ACD 平面ABC AC =，AD ⊂平面ACD AD AC ⊥,所以AD ⊥平面ABC ，所以，DCA ∠是直线CD 与平面ABC 所成的角，因为直线CD 与平面ABC 所成的角为45°，所以，45DCA ∠= ，所以AD AC=因为AD ⊥平面ABC ，,AB BC ⊂平面ABC ，所以AD BC ⊥，AD AB ⊥，因为AB BC ⊥，AB AD A ⋂=，,AB AD ⊂平面ABD ，所以BC ⊥平面ABD ，所以，BDC ∠是直线CD 与平面ABD 所成角，因为直线CD 与平面ABD 所成角为30°，所以30BDC ∠=o ，所以1,2BC CD BD ==，不妨设1BC =，则2,1CD BD AD AC AB =====，所以，ABC 为等腰直角三角形，45BAC ∠= 因为AD AB ⊥，AD AC ⊥，所以BAC ∠是二面角B AD C --的平面角，所以二面角B AD C --的大小为4519.如图，A 、B 是海岸线OM 、ON 上的两个码头，海中小岛有码头Q 到海岸线OM 、ON 的距离分别为2km 、km 5.测得tan 3MON ∠=-，6km OA =.以点O 为坐标原点，射线OM 为x 轴的正半轴，建立如图所示的直角坐标系.码头Q 在第一象限，且三个码头A 、B 、Q 均在一条航线上.（1）求码头Q 点的坐标；（2）海中有一处景点P （设点P 在平面xOy 内，PQ OM ⊥，且6km PQ =），游轮无法靠近.求游轮在水上沿旅游线AB 航行时离景点P 最近的点C 的坐标.【答案】（1）()42Q ，（2）(1,5)C 【分析】（1）根据已知条件，写出直线ON 方程，再求解Q 点坐标.（2）由直线AQ 的方程求解B 点坐标，进而求解AB 的直线方程.由（1）知C 为垂足，可联立直线AB 与PC 方程，即可求解C 点坐标.【小问1详解】由已知得，(6,0)A ，直线ON 方程：3y x =-设00(,2)(0)Q x x >，由5=及图，得04x =，()42Q ∴，.【小问2详解】直线AQ 的方程为(6)y x =--即60x y +-=由360y x x y =-⎧⎨+-=⎩，解得39x y =-⎧⎨=⎩，即(3,9)B -则直线AB 方程60x y +-=，点P 到直线AB 的垂直距离最近，则垂足为C ，因为PQ OM ⊥，且6km PQ =，()42Q ，，(4,8)P ∴，则直线PC 方程为40x y -+=联立6040x y x y +-=⎧⎨-+=⎩，解得15x y =⎧⎨=⎩轮在水上沿旅游线AB 航行时离景点P 最近的点C 的坐标为(1,5).20.如图，在长方体1111ABCD A B C D -中，11DD DA ==，2AB =，点E 在棱AB 上运动.（1）证明：11B C D E ⊥；（2）设E 为棱AB 的中点，在棱1CC 上是否存在一点F ，使得//BF 平面1DEC ，若存在，求1CFCC 的值，若不存在，说明理由；（3）求直线AB 与平面1DEC 所成角的取值范围.【答案】（1）证明详见解析（2）存在，且112CF CC =（3）15arcsin ,arcsin35⎡⎢⎣⎦【分析】（1）建立空间直角坐标系，利用向量法证得11B C D E ⊥.（2）根据向量法列方程，从而求得1CFCC .（3）利用向量法求得直线AB 与平面1DEC 所成角的正弦值，结合不等式的性质求得所成角的取值范围.【小问1详解】建立如图所示空间直角坐标系，()()()()1110,0,1,1,2,1,0,2,0,1,0,1D B C B C =--，设()1,,0,02E t t ≤≤，则()11,,1D E t =-，111010D E B C ⋅=-++=，所以11B C D E ⊥.【小问2详解】若E 是AB 的中点，则()1,1,0E ，()10,2,1C ，设平面1DEC 的法向量为()111,,x n y z =，则11111020n DE x y n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ ，故可设()1,1,2n =-- ，设()0,2,,01F λλ≤≤，()()1,2,0,1,0,B BF λ=-，若//BF 平面1DEC ，BF ⊄平面1DEC ，则1120,2n BF λλ⋅=-== ，所以F 是1CC 的中点，所以112CF CC =.【小问3详解】()0,2,0AB =，设()1,,0,02E t t ≤≤，设平面1DEC 的法向量为()222,,m x y z =，则22122020m DE x ty m DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ ，故可设(),1,2m t =-- ，设直线AB 与平面1DEC 所成角为π,02θθ≤≤，则sin m AB m AB θ⋅==⋅由于2202,04,559,3t t t ≤≤≤≤≤+≤，所以1sin ,35θ⎡=⎢⎣⎦，所以15arcsin ,arcsin35θ⎡∈⎢⎣⎦.21.已知椭圆22:142x y C +=，过动点()()0,0M m m >的直线l 交x 轴于点N ，交C 于点A 、P （P 在第一象限），且M 是线段PN 的中点，过点P 作x 轴的垂线交C 于另一点Q ，延长QM 交C 于点B .设()11,A x y 、()22,B x y .（1）若点N 的坐标为()2,0-，求PNQ V 的周长；（2）设直线PM 的斜率为k ，QM 的斜率为k '，证明：k k'为定值；（3）求直线AB 倾斜角的最小值.【答案】（1）8（2）证明见解析（3）直线AB 倾斜角的最小值为6arctan2【分析】（1）利用椭圆C 的标准方程和点N 的坐标，结合题中条件可得PNQ V 为焦点三角形，周长为4a ；（2）设0000(,)(0,0)P x y x y >>，由(0,)(0)M m m >，可得02(),P x m ，0,2()Q x m -，求出直线PM 的斜率，QM 的斜率，推出k k'为定值．（3）设1(A x ，1)y ，2(B x ，2)y ．直线PA 的方程为y kx m =+直线QB 的方程为3y kx m =-+，联立方程椭圆与椭圆方程，利用韦达定理，求解AB 坐标，然后求解AB 的斜率的表达式，利用基本不等式求解斜率的最小值，即可得到直线AB 倾斜角的最小值．【小问1详解】椭圆22:142x y C +=，由方程可知，椭圆两焦点坐标为()2,0，若点N 的坐标为()2,0-，点N 为左焦点，点()0,M m 是线段PN 的中点，故点P 的坐标为)2,2m ，PQ 垂直于x 轴，则PQ 与x 轴交点为椭圆右焦点，可得PNQ V 的周长为点P 到两焦点距离之和加上点Q 到两焦点距离之和，,P Q 都在椭圆上，所以PNQ V 的周长为8.【小问2详解】证明：设0000(,)(0,0)P x y x y >>，由(0,)(0)M m m >，可得02(),P x m ，0,2()Q x m -，所以直线PM 的斜率002m m m k x x -==，QM 的斜率0023m m m k x x '--==-，所以033mk x m kx -'==-，所以k k'为定值．【小问3详解】设11(,)A x y ，22(,)B x y ，直线PA 的方程为y kx m =+，直线QB 的方程为3y kx m =-+，联立方程2224y kx mx y =+⎧⎨+=⎩，整理得222(21)4240k x mkx m +++-=，根据根与系数可得20122421m x x k -=+，可得21202(2)(21)m x k x -=+，所以211202(2)(21)k m y kx m m k x -=+=++，同理222222002(2)6(2),(181)(181)m k m x y m k x k x ---==+++，所以22222122220002(2)2(2)32(2)(181)(21)(181)(21)m m k m x x k x k x k k x -----=-=++++，22222122220006(2)2(2)8(61)(2)(181)(21)(181)(21)k m k m k k m y y m m k x k x k k x ----+--=+--=++++，所以221216111644ABy y k k k x x k k -+⎛⎫===+ ⎪-⎝⎭．由0m >，00x >，可得0k >，所以16k k +≥16k k =，即66k =时，取得等号，6=，解得147m =，所以直线AB斜率的最小值为2，直线AB 倾斜角的最小值为6arctan 2．。

2019-2020学年曹杨二中高二上期末数学试卷一、填空题1.三个平面最多把空间分割成 个部分． 【答案】 8 【解析】试题分析：两个平面相交把空间分成四部分，第三个平面从中间截开，把每一部分一分为二，故可把空间分成八部分． 考点：空间两个平面的位置关系．2.若线性方程组的增广矩阵是121234c c ⎛⎫ ⎪⎝⎭，解为02x y =⎧⎨=⎩，则12c c +=_______； 【答案】12 【解析】 【分析】根据增广矩阵还原出相应的线性方程组，然后将02x y =⎧⎨=⎩代入线性方程组即可得到12,c c 的值，即可得答案．【详解】由题意，此增广矩阵对应的线性方程组为：122,34,x y c x y c +=⎧⎨+=⎩将02x y =⎧⎨=⎩代入方程组得：12,4,8c c == ∴1212c c +=. 故答案为：12.【点睛】本题主要考查线性方程组与增广矩阵的对应关系，以及根据线性方程组的解求参数，属于基础题.3.若行列式31227314k--中元素1-的代数余子式的值为5，则k =______；【答案】4- 【解析】 【分析】由题意可知求得122(23)31kA k =--=-+，代入即可求得k 的值． 【详解】由题意可知求得122(23)31kA k =--=-+，∴(23)54k k -+=⇒=-. 故答案为：4-.【点睛】本题考查三阶行列式的代数余子式的定义及行列式的运算，考查计算能力，属于基础题．4.已知一个圆锥的轴截面是等边三角形，侧面积为6π，则该圆锥的体积等于____． 【答案】3π 【解析】 【分析】分别求得底面积和高，利用圆锥的体积公式求解即可.【详解】设圆锥的底面半径为R ，因为轴截面是等边三角形，所以母线长为2R ，高为3R ，侧面积S ＝12262R R ππ⨯⨯=，解得：R ＝3， 所以，圆锥的体积为：V ＝21(3)33π⨯⨯⨯＝3π.故答案为3π.【点睛】本题主要考查了圆锥的体积的计算，属于基础题. 5.．四面体ABCD 的外接球球心在CD 上，且2CD =，，在外接球面上A B ，两点间的球面距离是 ． 【答案】【解析】【详解】因为四面体ABCD 的外接球球心在CD 上，且2CD =，，所以在外接球面上A B ，两点间的球面距离是23π. 6.在正方体ABCD ﹣A 1B 1C 1D 1，二面角A ﹣BD ﹣A 1的大小为_____．【答案】3rccos a 【解析】 【分析】连接,AC BD ，交于O ，连1A O ，可得1A OA ∠是二面角A ﹣BD ﹣A 1的平面角，在直角三角形1A OA 中可求得结果.【详解】连接,AC BD ，交于O ，连1A O ， 如图所示：因为BD AC ⊥，且1A O 在底面ABCD 内的射影是AO ，所以由三垂线定理可得1BD AO ⊥， 所以1A OA ∠是二面角A ﹣BD ﹣A 1的平面角，设正方体的棱长为1，则2AO =，22211261()22AO A A AO =+=+=，所以11232cos 36AO AOA AO ∠===， 因为102AOA π<∠<，所以13rccos 3AOA a ∠=. 故答案为：3rccos3a . 【点睛】本题考查了三垂线定理，考查了求二面角，关键是作出二面角的平面角，属于基础题.7.若正四棱锥的底面边长为3，高为2.则这个正四棱锥的全面积为______； 【答案】24 【解析】 【分析】由题意画出图形，求出正四棱锥的斜高，再由正方形及三角形面积公式求解． 【详解】如图所示，四棱锥P ABCD -为正四棱锥，高2OP =，底面边长3AB =． 过O 作OG BC ⊥，垂足为G ，连接PG ，则斜高22352()22PG =+=．∴正四棱锥的全面积是1533432422S =⨯+⨯⨯⨯=．故答案为：24.【点睛】本题考查正四棱锥的全面积求法，考查计算能力，是基础题．8.已知ABCD 是棱长为a 的正四面体.则异面直线AB 与CD 间的距离为_______；【答案】2 a【解析】【分析】连结AF、BF，推导出EF AB⊥，EF CD⊥，由此能证明线段EF是异面直线AB与CD 的公垂线段．在Rt AEF∆中，求出EF的长度即可.【详解】如图，取E为AB 的中，F为CD的中点，连结AF、BF，由ACD∆、BCD∆为等边三角形，AF BF∴=，EF AB∴⊥．同理，EF CD⊥．又EF与AB、CD都相交，故线段EF是异面直线AB与CD的公垂线段．在Rt AEF∆中，31,2AF a AE a==，∴2EF a=，故异面直线AB与CD的距离为22a．【点睛】本题考查两条异面直线的公垂线长的求解，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想．9.若数列{}n a满足112a=，212323n na a a na n a++++=，*n N∈，则20a=______；【答案】35【解析】【分析】根据递推关系，少递推一项再相减，从而得到11(2)nna nna n--=≥，再利用累乘法求得答案.【详解】∵212323n na a a na n a++++=，∴21231123(1)(1)n na a a n a n a--++++-=-，两式相减得：222211(1)()(1)n n n n n na n a n a n n a n a --=--⇒-=-，∴11(2)n n a n n a n--=≥， ∴3202121912192320a a a a a a ⋅⋅=⋅⋅， ∴20123205a ==. 故答案为：35.【点睛】本题考查数列的递推关系求通项，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意累乘法的运用.10.某几何体的一条棱在主视图、左视图和俯视图中的长分别1，2，3，则这条棱的长为______； 【解析】 【分析】由棱和它在三视图中的投影扩展为长方体，利用三视图中的三个投影是三个面上的对角线， 即可求出棱长的值． 【详解】如图所示，由棱和它在三视图中的投影扩展为长方体， 则三视图中的三个投影，是三个面上的对角线，设这个长方体的长、宽、高分别是x 、y 、z ，对角线长为a ， 则221x z +=，224y z +=，229x y +=，22214972x y z ++∴++==， 22227a x y z ∴=++=，a ∴=．【点睛】本题考查棱的三视图，考查空间想象能力和运算求解能力，求解时注意构造长方体模型进行求解.11.对于实数x ，用{}x 表示其小数部分，例如{}10=，{}3.140.14=，若1233n n na ⎧⎫=⋅⎨⎬⎩⎭，*n N ∈，则数列{}n a 的各项和为______；【答案】724【解析】 【分析】根据{}x 的定义得数列1233n n na ⎧⎫=⋅⎨⎬⎩⎭的特点，再利用无穷递减等比数列的求和公式，进行求和.【详解】根据{}x 的定义得：2133n ⎧⎫=⎨⎬⎩⎭或2233n ⎧⎫=⎨⎬⎩⎭，∴123456S a a a a a a =++++++12341211121133333333=⋅+⋅+⋅+⋅+ 324211111()()333333=+++++ 2221172173327118332411339=+==--.故答案为：724.【点睛】本题考查无穷递减等比数列求各公式，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意将所有项的和分成奇数项和与偶数项的和. 12.下图是一座山的示意图.山呈圆锥形.圆锥的底面半径为10公里.侧棱长为40公里.B 是SA 上一点，且10AB =公里.为了发展旅游业，要建设一条最短的从A 绕山一周到B 的观光铁路这条铁路从A 出发到B 的最短距离为_______公里；【答案】50 【解析】 【分析】将圆锥的侧面展开，求得其展开图的扇形的圆心角为2π，利用勾股定理可求得AB 的长度. 【详解】如图所示为圆锥的侧展图， ∵210402ππ⋅=，∴2ASB π∠=， ∴22||403050AB =+=. 故答案为：50.【点睛】本题考查圆锥的侧展图、弧度计算、勾股定理，考查函数与方程思想、转化与化归思想，考查空间想象能力和运算求解能力. 二、选择题13.在学习等差数列时，我们由110a a d =+，211a a d =+.312a a d =+，……，得到等差数列{}n a 的通项公式是()11n a a n d +-=.像这样由特殊到一般的推理方法叫做（ ）A. 不完全归纳法B. 完全归纳法C. 数学归纳法D. 分析法【答案】A 【解析】 【分析】本题由题干可知由特殊到一般性的推理属于归纳推理．【详解】本题由前三项的规律猜想出一般项的特点属于不完全归纳法， 但本题并不是数学归纳法， 故选：A ．【点睛】本题主要考查归纳法的特点，以及数学归纳法与不完全归纳法的区别． 14.执行如图所示的程序框图.则输出的S 的值为（ ）A. 4B. 8C. 14D. 18【答案】B 【解析】 【分析】根据程序框图进行模拟计算即可．【详解】第一次，2i =，20218S =-=，不满足条件5i >， 第二次，4i =，18416S =-=，不满足条件5i >，第三次，8i =，1688S =-=，满足条件5i >， 输出8S =， 故选：B ．【点睛】本题主要考查程序框图的识别和应用，根据条件进行模拟计算是解决本题的关键． 15.设三棱锥V ABC -的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P AC B --的平面角为γ，则（ ） A. ,βγαγ<< B. ,βαβγ<< C. ,βαγα<< D. ,αβγβ<<【答案】B 【解析】 【分析】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半.【详解】方法1：如图G 为AC 中点，V 在底面ABC 的投影为O ，则P 在底面投影D 在线段AO 上，过D 作DE 垂直AE ，易得//PE VG ，过P 作//PF AC 交VG 于F ，过D 作//DH AC ，交BG 于H ，则,,BPF PBD PED α=∠β=∠γ=∠，则cos cos PF EG DH BD PB PB PB PB α===<=β，即αβ>，tan tan PD PDED BDγ=>=β，即y >β，综上所述，答案为B.方法2：由最小角定理βα<，记V AB C --的平面角为γ'（显然γ'=γ）由最大角定理β<γ'=γ，故选B.方法3：（特殊位置）取V ABC -为正四面体，P 为VA 中点，易得cos sin sin α=⇒α=β=γ=，故选B. 【点睛】常规解法下易出现的错误有，不能正确作图得出各种角.未能想到利用“特殊位置法”，寻求简便解法.16.已知平面α与β互相垂直，α与β交于l ，m 和n 分别是平面α，β上的直线.若m ，n 均与l 既不平行.也不垂直，则m 与n 的位置关系是（ ） A. 可能垂直，但不可能平行 B. 可能平行，但不可能垂直 C. 可能垂直，也可能平行 D. 既不可能垂直，也不可能平行【答案】D 【解析】 【分析】利用反证法，结合线面平行、垂直的判定定理与性质定理推导出与题设的矛盾，从而证明结论．【详解】①假设m n ⊥，n 与l 既不垂直，也不平行，n l O ∴⋂=，过O 在β内作直线c l ⊥，αβ⊥，c α∴⊥，m α⊂，c m ∴⊥，又m n ⊥，c n O ⋂=，m β∴⊥，l β⊂，m l∴⊥这与m 与l 既不垂直，也不平行矛盾，m ∴不可能垂直于n ， 同理：n 也不可能垂直于m ； ②假设//m n ，则//m β，m α⊂，l αβ=，//m l ∴这与m 和n 与l 既不垂直，也不平行矛盾，故m 、n 不平行． 故选：D ．【点睛】本题考查空间中线面平行与垂直的判定及性质，考查转化与化归思想，考查空间想象能力． 三、解答题17.如图，某公司制造一种海上用的“浮球”，它是由两个半球和一个圆柱筒组成，其中圆柱筒的高h 为2米，球的半径r 为0.5米.（1）求“浮球”的体积（结果精确到0.1立方米）；（2）假设该“浮球”的建造费用仅与其表面积有关，已知圆锥形部分每平方米建造费用为20元，半球形部分每平方米建造费用为30元，求该“浮球”的建造费用（结果精确到1元）. 【答案】（1）32.1m ；（2）220元 【解析】 【分析】（1）根据球的半径得到上下两个半球的体积之和，再由柱体体积公式算出圆柱筒的体积，相加即得该“浮球”的体积大小；（2）计算球的表面积公式和圆柱侧面积公式，结合条件，即可得到结论． 【详解】（1）球的半径r 为0.5米，∴两个半球的体积之和为3441133386V r m πππ==⋅=球，圆柱的高为2米，3112242V r h m πππ∴=⋅=⨯⨯=圆柱，∴该“浮球”的体积是：322.13V V V m π=+=≈球圆柱；（2）圆柱筒的表面积为222rh m ππ=；两个半球的表面积为224r m ππ=， 圆柱形部分每平方米建造费用为20元，半球形部分每平方米建造费用为30元，∴该“浮球”的建造费用为2203070220πππ⨯+⨯=≈元．【点睛】本题给出由两个半球和一个圆柱筒接成的“浮球”，计算了它的表面积和体积，着重考查了球、圆柱的表面积公式和体积公式等知识，属于中档题．18.如图.在四棱锥P ABCD -中，PA ⊥平面ABCD ，且2AB =，3AD =，3PA =//AD BC ，AB BC ⊥，45ADC ∠=︒.（1）求异面直线PC 与AD 所成角的大小； （2）求点A 到平面PCD 的距离. 【答案】（1）2arccos 4；（2）355； 【解析】 【分析】（1）以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立空间直角坐标系，利用向量法能求出异面直线PC 与AD 所成角大小．（2）求出平面PCD 的一个法向量，利用向量法能求出点A 到平面PCD 的距离.【详解】（1）以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立如图所示空间直角坐标系，则3)P ，(2,1,0)C ，(0,3,0)D ，∴(2,1,3)PC =-，(0,3,0)AD =，设异面直线PC 与AD 所成角为θ， 则||2cos 4||||89PC AD PC AD θ⋅===⋅，所以异面直线PC 与AD 所成角大小为2arccos4. （2）设平面PCD 的一个法向量为(n x =，y ，)z ，(2,1,3)PC =，(2,2,0)CD =-，(2,1,0)AC =则·230,·220,n PC x y z n CD x y ⎧=+-=⎪⎨=-+=⎪⎩，取1x =，得(1,1,3)n =，∴点A 到平面PCD 的距离||35||5n AC d n ⋅===.【点睛】本题考查异面直线所成角的余弦值的求法，考查点到直线的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．19.已知数列{}n a 的前n 项和为n S ，且461n n S n a =--，*n N ∈. （1）求证：数列{}1n a -是等比数列；（2）求当n 为何值时，n S 取最小值，并说明理由. 【答案】（1）见解析；（2）12； 【解析】 【分析】（1）根据递推关系，多递推一项再相减，得1541n n a a -=+，再利用定义证明数列为等比数列；（2）由（1）得n S 关于n 的表达式，再判断n S 的单调性，即可得答案. 【详解】（1）∵461n n S n a =--，∴11(1)461n n S n a --=---， 两式相减得：1541n n a a -=+，2n ≥，∴111441455115n n n n a a a a -----==--， ∴数列{}1n a -是等比数列.（2）由（1）得：数列{}1n a -以11a -为首项，以45为公比的等比数列， ∵1111146112S a a a =--=⇒=-，∴14112()5n n a --=-⋅，∴14614(1)6548654()5n n n n S n a n a n -=--=---=+⋅-，∴1148654()5n n S n +=++⋅-，∴11144()(()0148148555)15n n n n S S -+--=+⋅-=<-12n ⇒<， ∴1211121314S S S S S S >>>><<，∴12n =时，n S 取最小值.【点睛】本题考查利用数列的递推关系证明等比数列、数列的单调性判断，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意不等式的求解. 20.如图，在三棱柱111ABC A B C -中，112,AC BC AB AB ===⊥平面ABC ，1AC ⊥AC ，,D E 分别是11AC B C ，的中点.（Ⅰ）证明：11AC B C ⊥；（Ⅱ）证明：//DE 平面11AA B B ；（Ⅲ）求DE 与平面11BB C C 所成角的正弦值.【答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析；（Ⅲ）3【解析】【详解】分析：（Ⅰ）先证明AC ⊥平面11AB C ，再证明11AC B C ⊥.( Ⅱ) 取11A B 的中点M ，连接MA 、ME ．先证明DE ∥AM ，再证明DE //平面11AA B B .( Ⅲ)利用向量法直线DE 与平面11BB C C 所成角的正弦值.详解：（Ⅰ）因为1AB ⊥平面ABC ，AC ⊂平面ABC ，所以1AB AC ⊥． 因为1AC AC ⊥，11AB AC A =，1AB ，1AC ⊂平面11AB C ，所以AC ⊥平面11AB C ． 因为11B C ⊂平面11AB C ，所以11AC B C ⊥．（Ⅱ）取11A B 的中点M ，连接MA 、ME ． 因为E 、M 分别是11B C 、11A B 中点，所以ME ∥11A C ，且ME 1112A C =． 在三棱柱111ABC A B C -中，11AD A C ，且1112AD AC =， 所以ME ∥AD ，且ME =AD ， 所以四边形ADEM 是平行四边形，所以DE ∥AM ．又AM ⊂平面11AA B B ，DE ⊄平面11AA B B ， 所以//DE 平面1AA BB ．（Ⅲ）在三棱柱111ABC A B C -中，11//BC B C ， 因为11AC B C ⊥，所以AC BC ⊥． 在平面1ACB 内，过点C 作1//Cz AB ， 因为，1AB ⊥平面ABC ， 所以，Cz ⊥平面ABC ．建立空间直角坐标系C -xyz ，如图．则()0,0,0C ,()2,0,0B ,()10,2,2B ,()12,2,2C -,()0,1,0D ,()1,2,2E -. ()1,1,2DE =-，()2,0,0CB =，()10,2,2CB =．设平面11BB C C 的法向量为(),,n x y z =，则100n CB n CB ⎧⋅=⎪⎨⋅=⎪⎩，即20220x y z =⎧⎨+=⎩， 得0x =，令1y =，得1z =-，故()0,1,1n =-． 设直线DE 与平面11BB C C 所成的角为θ，则sin θ＝cos ,DE n DE n DE n⋅=⋅=， 所以直线DE 与平面11BB C C 所成角的正弦值为点睛：本题主要考查空间位置关系的证明和线面角的向量求法，意在考查空间位置关系证明中的转化能力和运算能力.21.给定整数n (4n ≥)，设集合12{,,,}n A a a a =，记集合{|,,1}i j i j B a a a a A i j n =+∈≤≤≤．（1）若{}3,0,1,2A =-，求集合B ； （2）若12,,,n a a a 构成以1a 为首项，d (0d >)为公差的等差数列，求证：集合B 中的元素个数为21n -； （3）若12,,,n a a a 构成以3为首项，3为公比的等比数列，求集合B 中元素的个数及所有元素之和．【答案】（1）{}6,3,2,1,0,1,2,3,4B =----（2）见解析（3）()()231312n nn C n +-+，【解析】 【分析】（1）由新定义和集合的列举法，可得所求集合；（2）运用等差数列为递增数列，以及性质，即可得到所求个数； （3）由等比数列的通项公式和性质，结合新定义计算可得所求结论． 【详解】（1）因{|,,1}i j i j B a a a a A i j n =+∈≤≤≤，当{}3,0,1,2A =-时，632101234i j a a +=----，，，，，，，，，∴{}6,3,2,1,0,1,2,3,4B =----． (2) 因为12,,,n a a a 构成以1a 为首项，d (0d >)为公差的等差数列，所以有11i n i n a a a a --+=+(22i n ≤≤-)，以及112i i i a a a -+=+(21i n ≤≤-)．此时，集合B 中的元素有以下大小关系：11213123122n n n n n n a a a a a a a a a a a a a a -<+<+<<+<+<+<<+<．因此，集合B 中含有21n -个元素．(3)由题设，3nn a =．设集合1{|,,1}i j i j B a a a a A i j n =+∈≤<≤，2{2|,1,2,,}i i B a a A i n =∈=．①先证1B 中的元素个数为2n C ，即从集合A 中任取两个元素，它们的和互不相同． 不妨设1i j k l ≤<<<，于是33333i j k l ≤<<<． 显然3333i j k l +<+．假设3333i l j k +=+，可得1333l i j i k i ---+=+，即()()133333311j i k i l i j i k j l k ------=+-=⋅-⋅-+．因为3k j -，33l k -≥，所以()33115k jl k ---⋅-+≤-，又30j i ->，于是()()333110j i k j l k ---⋅-⋅-+<，等式3333i l j k +=+不成立．因此，3333i l j k +≠+． 同理可证3333i k j l +≠+． ②再证12B B ⋂=∅．不妨设1i j k ≤<<，于是3333i j k ≤<<． 显然2333i j k ⨯<+，3323i j k +<⨯．假设2333j i k ⨯=+，可得2313j i k i --⨯=+，即()1233323j ik i j i k j ----=⨯-=⋅-，因为33k j -≥，所以230k j --<，又30j i ->，于是()3230j ik j --⋅-<，等式2333j i k⨯=+不成立．因此，2333j i k ⨯≠+．由①②，得12B B B =⋃，且12B B ⋂=∅．此时，集合B 中的元素个数为2n C n +．集合B中所有元素的和为()()()()2313113332nn nn+-++++=．【点睛】本题考查新定义的理解和运用，考查等差数列和等比数列的通项公式及求和公式的运用，考查运算能力，属于中档题．。

2018-2019学年曹二高二上期末数学试卷2019.1一、填空题：1、在空间中，若直线与无公共点，则直线的位值关系是________；a b ,a b 答案：平行或异面2、若两个球的体积之比为8：27，则这两个球的表面积之比为____；答案：4:93、若正方体中，异面直线和所成角的大小为_____；''''ABCD A B C D -AC 'BD 答案：2π4、若圆柱的轴截面面积为2，则其侧面积为___；答案：2π5、正四棱锥底面边长为4，侧棱长为3，则其体积为_____；答案：1636、若增广矩阵对应的线性方程组为无穷多紹，则实数的值为________；1111a a -⎛⎫⎪-⎝⎭a 答案：-17、有一列正方体，它们的棱长组成以1位首项，为公比的等比数列，设它们的体积依次为，1212,,,n V V V 则=__________；()12lim n n V V V →∞+++ 答案：878、已知，用斜二测画法作它的直观图，若是斜边平行于铀的等腰直角三角形，ABC ∆'''A B C ∆'''A B C ∆'x 则是________三角形（填“锐角”、“直角”、“钝角”）.ABC ∆答案：直角9、在北纬45°圈上有甲、乙两地，它们的经度差90°，则甲乙两地的球面距离与地球半径的比值为________；答案：3π10的正四面体的体积，可以看成一个棱长为1的正方体截去四个角后得到，类比2这种方法，一个相对棱长都相等的四面体，其三组对棱长分别为ABCD ，则此四面体的体积为_______；5,13,10AB CD AD BC AC BD ======答案：211、已知平面截一球面得圆，过圆的圆心且与平面呈45°二面角的平面截该球面得圆，若αM M M αβN 球的半径为4，圆的面积为12，则圆的面积为__________；M πN 答案：14π12、如图，棱长为3的正方体的顶点在平面上，三条棱都在平面的同侧，如顶点到A α,,AB AC AD α,B C 平面的距离分别为，则顶点到平面的距离为___________；α2D α二、选择题13、“直线垂直于的边’’是“直线垂直于的边”的（）l ABC ∆,AB AC l ABC ∆BC A 、充分非必要条件B 、必要非充分条件C 、充要条件D 、既不充分又不必要条件答案：A14、如果三棱锥的底面不是等比三角形，网组对棱互相垂直，且顶点在底面的射影在内，S ABC -S O ABC ∆那么是的（）O ABC ∆A 、外心B 、内心C 、垂心D 、重心答案：B15、底面是正三角形，且每个侧面是等腰三角形的三棱锥（）A 、一点时增三棱锥B 、一定是正四面体C 、不是斜三棱锥D 、可能是斜三棱锥答案：D16、在正方体中，点（异于点）是棱长一点，则满足与，所成的角为45°的点1111ABCD A B C D -P B BP 1AC 的个数为（）P A.0B.3C.4D.6答案：B 三、解答题：17、如图，在棱长为的正方体中，是棱的中点.a 1111ABCD A B C D -E 1DD （1）求三棱锥的体积；1D A BE -（2）求异面直线与所成角大小.BE 1CC解：（1）因为，，并且，11D A BE B A DE V V --=121224A DEa a S a ==1AB A DE ⊥平面所以11231133412D A BEA DE a a V a S a -=⋅==（2）因为，所以异面直线与所成角为直线与直线11//CC DD BE 1CC BE 1DD 所成角，即，因为，，所以BED ∠2a BE =222BD a a a =+=，所以，所以32a BE ==12332aCOS BED a ∠==，所以异面直线与所成角为.1arccos(3BED ∠=BE 1CC 1arccos(318、如图，某甜品创作一种冰淇淋，其上半部分呈半球形，下半部分呈圆锥形，现把半径为的圆形蛋10cm 皮等分成5个扇形，用一个扇形蛋皮固成圆锥的侧面（蛋皮厚度忽略不计）。

2019-2020学年上海市普陀区曹杨二中高二（上）期末数学试卷一、单选题（本大题共4小题，共12.0分）1.在学习等差数列时，我们由a1=a1+0d，a2=a1+1d，a3=a1+2d，……，得到等差数列{a n}的通项公式是a n=a1+(n−1)d，像这样由特殊到一般的推理方法叫做()A. 不完全归纳法B. 数学归纳法C. 综合法D. 分析法2.执行如图所示的程序框图，则输出的S的值为()A. 8B. 6C. 14D. 183.设三棱锥V−ABC的底面是正三角形，侧棱长均相等，P是棱VA上的点(不含端点)，记直线PB与直线AC所成角为α，直线PB与平面ABC所成角为β，二面角P−AC−B 的平面角为γ，则()A. β<γ，α<γB. β<α，β<γC. β<α，γ<αD. α<β，γ<β4.已知平面α与β互相垂直，α与β交于l，m和n分别是平面α，β上的直线.若m，n均与l既不平行.也不垂直，则m与n的位置关系是()A. 可能垂直，但不可能平行B. 可能平行，但不可能垂直C. 可能垂直，也可能平行D. 既不可能垂直，也不可能平行二、单空题（本大题共12小题，共36.0分） 5. 三个平面最多把空间分割成______ 个部分．6. 若线性方程组的增广矩阵是(12c 134c 2)，解为{x =0y =2，则c 1+c 2=______．7. 若行列式∣∣∣∣3−1227−314k ∣∣∣∣中元素−1的代数余子式的值为5，则k =______．8. 已知一个圆锥的轴截面是等边三角形，侧面积为6π，则该圆锥的体积等于______． 9. 四面体ABCD 的外接球球心在CD 上，且CD =2，AB =√3，则外接球面上两点A ，B间的球面距离是______．10. 在正方体ABCD −A 1B 1C 1D 1，二面角A −BD −A 1的大小为______11. 若正四棱锥的地面边长为3，高为2，则这个正四棱锥的全面积为______． 12. 已知ABCD 是棱长为a 的正四面体，则异面直线AB 与CD 间的距离为______． 13. 若数列{a n }满足a 1=12，a 1+2a 2+3a 3+⋅⋅⋅+na n =n 2a n ，n ∈N ∗，则a 20=______．14. 某几何体的一条棱在主视图、左视图和俯视图中的长分别为1、2、3，则这条棱的长为______．15. 对于实数x ，用{x}表示其小数部分，例如{1}=0，{3.14}=0.14，若a n =13n⋅{2n3}，n ∈N ∗，则数列{a n }的各项和为______．16. 如图是一座山的示意图，山呈圆锥形，圆锥的底面半径为10公里，母线长为40公里，B 是母线SA 上一点，且AB =10公里.为了发展旅游业，要建设一条最短的从A 绕山一周到B 的观光铁路.这条铁路从A 出发后首先上坡，随后下坡，则下坡段铁路的长度为______ 公里．三、解答题（本大题共5小题，共60.0分）17.如图，某公司制造一种海上用的“浮球”，它是由两个半球和一个圆柱筒组成．其中圆柱的高为2米，球的半径r为0.5米．(1)这种“浮球”的体积是多少立方米(结果精确到0.1m3)？(2)假设该“浮球”的建造费用仅与其表面积有关．已知圆柱形部分每平方米建造费用为20元，半球形部分每平方米建造费用为30元．求该“浮球”的建造费用(结果精确到1元)．18.如图，在四棱锥P−ABCD中，PA⊥平面ABCD，且AB=2，AD=3，PA=√3，AD//BC，AB⊥BC，∠ADC=45°．(1)求异面直线PC与AD所成角的大小；(2)求点A到平面PCD的距离．19.已知数列{a n}的前n项和为S n，且S n=n−5a n−85，n∈N∗(1)证明：{a n−1}是等比数列；(2)求数列{S n}的通项公式．请指出n为何值时，S n取得最小值，并说明理由15=−14.85)(参考数据log5620.如图，在三棱柱ABC−A1B1C1中，AC=BC=AB1=2，AB1⊥平面ABC，AC1⊥AC，D、E分别是AC、B1C1的中点．(1)求证：AC⊥B1C1；(2)求证：DE//平面AA1B1B；(3)求直线DE与平面BB1C1C所成角的正弦值的大小．21.给定整数n(n≥4)，设集合A={a1,a2,…,a n}.记集合B={a i+a j|a i,a j∈A,1≤i≤j≤n}．(1)若A={−3,0,1,2}，求集合B；(2)若a1，a2，…a n构成以a1为首项，d(d>0)为公差的等差数列，求证：集合B中的元素个数为2n−1；(3)若a1，a2，…，a n构成以3为首项，3为公比的等比数列，求集合B中元素的个数及所有元素之和．答案和解析1.【答案】A【解析】【分析】本题主要考查归纳法的特点，以及数学归纳法与不完全归纳法的区别，属于基础题．本题由题干可知由特殊到一般性的推理属于归纳推理，而本题并不是用数学归纳法进行的推理证明，可得到结果．【解答】解：本题由前三项的规律猜想出一般项的特点属于归纳法，但本题并不是数学归纳法，故选：A．2.【答案】B【解析】解：模拟程序的运行，可得S=20，i=1执行循环体，i=2，S=18不满足i>5，执行循环体，i=4，S=14不满足i>5，执行循环体，i=8，S=6此时，满足i>5，退出循环，输出S的值为6．故选：B．由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，是基础题．3.【答案】B【解析】【分析】本题考查空间三种角的求法，考查以三棱锥为载体，常规解法下易出现的错误的有：不能正确作出各种角，未能想到利用“特殊位置法”，寻求简单解法，为拔高题．综合考查异面直线所成角、直线和平面所成角和二倍角的概念和计算，解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小，充分运用图象，则可事半功倍．【解答】解：方法一、如图G为AC的中点，V在底面的射影为O，则P在底面上的射影D在线段AO上，作DE⊥AC于E，易得PE//VG，过P作PF//AC于F，过D作DH//AC，交BG于H，则α=∠BPF，β=∠PBD，γ=∠PED，则cosα=PFPB =EGPB=DHPB <BDPB=cosβ，可得β<α；tanγ=PDED >PDBD=tanβ，可得β<γ，方法二、由最小值定理可得β<α，记V−AC−B的平面角为γ′(显然γ′=γ)，由最大角定理可得β<γ′=γ；方法三、(特殊图形法)设三棱锥V−ABC为棱长为2的正四面体，P为VA的中点，易得cosα=12√3=√36，可得sinα=√336，sinβ=√63√3=√23，sinγ=√63√32=2√23，当AP=23时，由余弦定理可得PB=√4+49−2×2×23×12=2√73，cosα=289+169−2892×2√73×43=√7，sinα=√6√7，可得α<γ，故C错误．故选：B．4.【答案】D【解析】解：①假设m⊥n，因为n与l既不垂直，也不平行，所以n∩l=O，过O在β内作直线c⊥l，如图所示，因为α⊥β，所以c⊥α，又因为m⊂α，所以c⊥m，又因为m⊥n，c∩n=O，所以m⊥β，l⊂β，所以m⊥l，这与m与l既不垂直，也不平行矛盾，故假设不成立，所以m与n不垂直，同理n与m也不垂直；②假设m//n，则m//β，m⊂α，α∩β=l，所以m//l，这与m和n与l既不垂直，也不平行矛盾，故假设不成立，所以m与n不平行．综上所述，m与n的位置关系是既不可能垂直，也不可能平行．故选：D．假设m⊥n，然后利用已知条件推理，得到m⊥l，这与m与l既不垂直，也不平行矛盾，故假设不成立；假设m//n，利用线面平行的性质定理进行推导，得到m//l，这与m和n 与l既不垂直，也不平行矛盾，故假设不成立，从而得到答案．本题考查空间中线、面位置关系的判断与应用，考查了反证法的应用，考查了逻辑推理能力与空间想象能力，属于中档题．5.【答案】8【解析】解：三个平面两两平行时，可以把空间分成4部分，三个平面有两个平行，第三个与他们相交时，可以把空间分成6部分，三个平面交于同一直线时，可以把空间分成6部分，三个平面两两相交，交线相互平行时，可以把空间分成7部分，当两个平面相交，第三个平面同时与两个平面相交时，把空间分成8部分．所以空间中的三个平面最多能把空间分成8部分．故答案为：8．分别讨论三个平面的位置关系，根据它们位置关系的不同，确定平面把空间分成的部分数目．本题考查平面的基本性质及推论，要讨论三个平面不同的位置关系．6.【答案】12【解析】解：由题意，增广矩阵是(12c 134c 2)，对应的线性方程组为：{x +2y =c 13x +4y =c 2，方程组的解为{x =0y =2，代入可得c 1=4，c 2=8，所以c 1+c 2=12．故答案为：12．利用增广矩阵还原线性方程组，结合方程组的解，求解c 1+c 2即可．本题考查增广矩阵与线性方程组的关系，方程组的解法，考查计算能力，是基础题．7.【答案】−4【解析】解：∵行列式∣∣∣∣3−1227−314k ∣∣∣∣中元素−1的代数余子式的值为5，∴(−1)3∣∣∣2−31k ∣∣∣=−(2k +3)=5，解得k =−4． 故答案为：−4．利用行列式的代数余子式的性质直接求解．本题考查实数值的求法，考查代数余子式的性质等基础知识，考查运算求解能力，是基础题．8.【答案】3π【解析】 【分析】本题考查圆锥体积的求法，考查空间想象能力和思维能力，是中档题．由题意画出图形，设圆锥的底面半径为r ，则母线长为2r ，由侧面面积求得r ，再由圆锥体积公式求解． 【解答】 解：如图，设圆锥的底面半径为r ，则母线长为2r ， 高为√4r 2−r 2=√3r ．则其侧面积S =2πr 2=6π，解得r =√3． ∴圆锥的高为3．其体积V =13×π×3×3=3π， 故答案为：3π．9.【答案】2π3【解析】解：球心到四个顶点距离相等，故球心O 在CD 中点，则OA =OB =OC =OD =1 再由AB =√3，在△A0B 中，利用余弦定理cos∠AOB =OA 2+OB 2−AB 22⋅OA⋅OB=−12则∠AOB =120°，则弧AB =120°360∘⋅2π⋅1=2π3故答案为：2π3根据球心到四个顶点距离相等可推断出O 为CD 的中点，且OA =OB =OC =OD ，进而在△A0B 中，利用余弦定理求得cos∠AOB 的值，则∠AOB 可求，进而根据弧长的计算方法求得答案．本题主要考查了余弦定理的应用．四面体外接球的性质等．考查了学生观察分析和基本的运算能力．10.【答案】arctan √2【解析】解：连接AC ，AC ∩BD =O ，连接A 1O ，则∠A 1OA 为二面角A −BD −A 1的平面角 设正方体ABCD −A 1B 1C 1D 1的棱长为a ， ∴AO =√22a ， ∴tan∠A 1OA =a√22a=√2；所以∠A 1OA =arctan √2． 故答案为：arctan √2．连接AC ，AC ∩BD =O ，连接A 1O ，则∠A 1OA 为二面角A −BD −A 1的平面角； 本题考查面面角与线面角，解题的关键是确定线面角与面面角，属于基础题．11.【答案】24【解析】解：正四棱锥P −ABCD ，的底面边长为AB =BC =CD =AD =3，高为PO =2， 如图所示：所以PE =√22+(32)2=52，故S 表=4×12×3×52+3×3=24． 故答案为：24．直接利用四棱锥的性质求出PE 的长和四棱锥体的表面积．本题考查的知识要点：四棱锥的表面积，主要考查学生的运算能力和数学思维能力，属于基础题．12.【答案】√22a【解析】解：取AB 中点E ，CD 中点F ，连接AF 、BF 、CE 、DE 、EF ，则AF =BF =CE =DE =√a 2−(a2)2=√32a ， ∴EF ⊥AB ，EF ⊥CD ， ∴异面直线AB 与CD 间的距离为：EF=√(√32a)2−(a2)2=√22a．故答案为：√22a．取AB中点E，CD中点F，连接AF、BF、CE、DE、EF，求出AF=BF=CE=DE=√32a，从而EF⊥AB，EF⊥CD，进而异面直线AB与CD间的距离为EF，由此能求出结果．本题考查两异面直线间的距离的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是基础题．13.【答案】35【解析】解：∵a1+2a2+3a3+⋯+na n=n2a n，∴a1+2a2+3a3+⋯+(n−1)a n−1=(n−1)2a n−1，两式相減得：na n=n2a n−(n−1)2a n−1⇒(n2−n)a n=(n−1)2a n−1，∴a na n−1=n−1n(n≥2)，∴a2a1⋅a3a2⋯⋯a20a19=12⋅23⋯1920，∴a20a1=120，a20=1220=35．故答案为：35．根据递推关系，少递推一项再相减，从而得到a na n−1=n−1n(n≥2)，再利用累乘法求得答案．本题考㚗数列的递推关系求通项，考㚗函数与方程思想、转化与化归思想，考査逻辑推理能力和运算能力，属于中档题．14.【答案】√7【解析】解：如图所示，由棱和它在三视图中的投影扩展为长方体， 则三视图中的三个投影，是三个面上的对角线，设这个长方体的长、宽、高分别是x 、y 、z ，对角线长为a ， 则x 2+z 2=1，y 2+z 2=4，x 2+y 2=9， ∴x 2+y 2+z 2=1+4+92=7，∴a 2=x 2+y 2+z 2=7， ∴a =√7． 故答案为：√7．由棱和它在三视图中的投影扩展为长方体，利用三视图中的三个投影是三个面上的对角线，即可求出棱长的值．本题主要考查空间几何体的结构特征，属于基础题．15.【答案】724【解析】解：由于2n =(3−1)n =3n +C n 1⋅3n−1(−1)+...+C n n−13⋅(−1)n−1+(−1)n ，(∗)所以当n 为奇数时，(∗)的右边的最后一项为−1， 可得{2n3}=23；当n 为偶数时，(∗)的右边的最后一项为1， 可得{2n3}=13． 所以{a n }的奇数项是首项为29，公比为19的等比数列； 偶数项是首项为127，公比为19的等比数列．则数列{a n }的各项和为291−19+1271−19=14+124=724．故答案为：724．运用二项式定理求得当n 为奇数时，{2n3}=23；当n 为偶数时，{2n3}=13.再由无缺等比数列的求和公式，计算可得所求和．本题考查等比数列的通项公式和无穷递缩等比数列的求和公式，考查分类讨论思想和运算能力，属于中档题．16.【答案】18【解析】解：如图，展开圆锥的侧面，过点S 作A′B 的垂线，垂足为H ， 记点P 为A′B 上任意一点，联结PS ，A′A⏜=∠A′OA ⋅SA =2π⋅10⇒∠A′OA =π2， 由两点之间线段最短，知观光铁路为图中的A′B ，A′B =√SA′2+SB 2=50，上坡即P 到山顶S 的距离PS 越来越小，下坡即P 到山顶S 的 距离PS 越来越大，∴下坡段的铁路，即图中的HB ， 由Rt △SA′B∽Rt △HSB ， 可得：SBHB =A′BSB ，可求出HB =SB 2A′B=30×3050=18．即下坡段铁路的长度为18公里． 故答案为：18．根据题意，画出展开图，结合图形转化为求HB ，结合三角形相似即可求解． 本题考查了圆锥的展开图应用问题，也考查了运算求解能力，是基础题．17.【答案】解：(1)∵球的半径r 为0.5米，∴两个半球的体积之和为V 球=43πr3=43π⋅18=16πm 3， ∵圆柱的高为2米，∴V 圆柱=πr2⋅ℎ=π×14×2=12πm 3，∴该“浮球”的体积是：V =V 球+V 圆柱=23π≈2.1m 3；(2)圆柱筒的表面积为2πrℎ=2πm 2；两个半球的表面积为4πr 2=πm 2， ∵圆柱形部分每平方米建造费用为20元，半球形部分每平方米建造费用为30元， ∴该“浮球”的建造费用为2π×20+π×30=70π≈220元．【解析】(1)根据球的半径得到上下两个半球的体积之和，再由柱体体积公式算出圆柱筒的体积，相加即得该“浮球”的体积大小；(2)计算球的表面积公式和圆柱侧面积公式，结合条件，即可得到结论．本题给出由两个半球和一个圆柱筒接成的“浮球”，计算了它的表面积和体积，着重考查了球、圆柱的表面积公式和体积公式等知识，属于中档题．18.【答案】解：(1)以A 为原点，AB 、AD 、AP 所在的直线分别为x 、y 、z 轴，建立如图所示的空间直角坐标系，则A(0,0,0)，P(0,0,√3)，C(2,1,0)，D(0,3,0)， ∴PC ⃗⃗⃗⃗⃗ =(2,1,−√3)，AD ⃗⃗⃗⃗⃗⃗ =(0,3,0)， 设异面直线PC 与AD 所成角为θ， 则cosθ=|PC⃗⃗⃗⃗⃗ ⋅AD ⃗⃗⃗⃗⃗⃗ ||PC⃗⃗⃗⃗⃗ ||AD ⃗⃗⃗⃗⃗⃗ |=32√2×3=√24， 故异面直线PC 与AD 所成角的大小为arccos √24；(2)由(1)知，PC ⃗⃗⃗⃗⃗ =(2,1,−√3)，CD ⃗⃗⃗⃗⃗ =(−2,2,0)，AC⃗⃗⃗⃗⃗ =(2,1,0)， 设平面PCD 的一个法向量为n⃗ =(x,y,z)， 则{n⃗ ⋅PC ⃗⃗⃗⃗⃗ =2x +y −√3z =0n ⃗ ⋅CD ⃗⃗⃗⃗⃗ =−2x +2y =0，令x =1，则y =1，z =√3，∴n ⃗ =(1,1,√3)， ∴点A 到平面PCD 的距离d =|n ⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ ||n ⃗⃗ |=3√5=3√55．【解析】(1)以A 为原点，AB 、AD 、AP 所在的直线分别为x 、y 、z 轴，建立空间直角坐标系，写出A 、P 、C 、D 的坐标，设异面直线PC 与AD 所成角为θ，由数量积求夹角公式求解；(2)根据法向量的性质求得平面PCD 的法向量n ⃗ ，再由公式d =|n ⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ ||n ⃗⃗ |求解．本题考查空间向量在立体几何中的应用，掌握利用空间向量处理异面直线夹角和点到平面距离的方法是解题的关键，考查学生的空间立体感、逻辑推理能力和运算能力，属于中档题．19.【答案】证明：(1)当n =1时，a 1=S 1=1−5a 1−85，解得a 1=−14，则a 1−1=−15．∵当n ≥2时，S n−1=(n −1)−5a n−1−85，∴a n =S n −S n−1=1−5a n +5a n−1，∴6a n =5a n−1+1， 即a n −1=56(a n−1−1)，∴{a n −1}是首项为−15，公比为56的等比数列． 解：(2)∵a n −1=−15⋅(56)n−1，∴S n =n −5[1−15⋅(56)n−1]−85=n +75⋅(56)n−1−90．由a n =1−15⋅(56)n−1>0，即15⋅(56)n−1<1，解得n >log 56115+1≈15.85． ∴当n ≤15时，a n <0；当n ≥16时，a n >0． 故n =15时，S n 取得最小值．【解析】(1)当n =1时，a 1=S 1=1−5a 1−85，求出a 1−1=−15，当n ≥2时，a n =S n −S n−1=1−5a n +5a n−1，从而6a n =5a n−1+1，由此能证明{a n −1}是首项为−15，公比为56的等比数列．(2)由a n −1=−15⋅(56)n−1，得S n =n +75⋅(56)n−1−90.由此能求出n =15时，S n 取得最小值．本题考查等比数列的证明，考查数列的前n 项和的求法，考查前n 项和取最小值时项数n 的求法，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．20.【答案】证明：(1)因为AB 1⊥平面ABC ，AC ⊂平面ABC ，所以AB 1⊥AC ，因为AC 1⊥AC ，AB 1∩AC 1=A ，AB 1，AC 1⊂平面AB 1C 1， 所以AC ⊥平面AB 1C 1， 因为B 1C ⊂C 平面AB 1C 1， 所以AC ⊥B 1C 1；(2)取A 1B 1的中点M ，连接MA ，ME ，因为E，M分别是B1C1，A1B1的中点，A1C1，所以ME//A1C，且ME=12A1C1，在三棱柱ABC−A1B1C1中，AD//A1C1，且AD=12所以ME//AD，且ME=AD，所以四边形ADEM是平行四边形，所以DE//AM，又AM⊂平面AA1B1B，DE⊄平面AA1B1B，所以DE//平面AA1B1B；(3)在三棱柱ABC−A1B1C1中，BC//B1C1，因为AC⊥B1C1，所以AC⊥BC，在平面ACB1内，过点C作Cz//AB1，因为AB1⊥平面ABC，所以Cz⊥平面ABC，建立空间直角坐标系C−xyz，如图，则C(0,0,0)，B(2,0,0)，B1(0,2,2)，C1(一2，2，2)，D(0,1,0)，E(−1,2,2)，设BB 1C 1C 的法向量为n⃗ =(x,y,z)， 则{n ⃗ ⋅CB⃗⃗⃗⃗⃗ =0n ⃗ ⋅CB 1⃗⃗⃗⃗⃗⃗⃗ =0，即{2x =02y +2z =0，得x =0，令y =1，得z =−1， 故n⃗ =(0,1,−1)， 设直线DE 与平面BB 1C 1C 所成的角为θ， 则sinθ=|cos〈DE ⃗⃗⃗⃗⃗⃗ ,n ⃗ 〉|=|DE ⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ ||DE ⃗⃗⃗⃗⃗⃗ |⋅|n ⃗⃗ |=√36， 所以直线DE 与平面BB 1C 1C 所成角的正弦值为√36．【解析】(1)通过条件证明AC ⊥平面AB 1C 1，进而可证AC ⊥B 1C 1；(2)取A 1B 1的中点M ，连接MA ，ME ，通过造就平行四边形证明DE//AM ，然后利用线面平行的定理证明结论；(3)建立空间直角坐标系，将线面角的问题转化为向量夹角运算．本题考查了两直线的垂直、线面平行的证明，线面角的求法，属于中档题．21.【答案】解：(1)A ={−3,0,1,2}，由题意可得集合B ={−6,−3,−2,−1,0,1,2,3,4}；(2)证明：若a 1，a 2，…a n 构成以a 1为首项，d(d >0)为公差的等差数列， 可得等差数列{a n }为递增数列，由等差数列的性质a m +a n =a p +a q ，可得B 中的元素个数为n +n(n−1)2−(n−1)(n−2)2=2n −1；(3)a 1，a 2，…，a n 构成以3为首项，3为公比的等比数列，可得a n =3n ，由3n 为奇数，即有3m +3n =2⋅3k ，m.n ，k 为不相等的正整数，则方程无实数解， 3m +3n =3l +3k ，m.n ，k ，l 为不相等的正整数，则方程无实数解， 若a i ，a j 相等，可得a 1，a 2，…，a n 中取两个相等的，和为n 个；若a i ，a j 不相等，可得a 1，a 2，…，a n 中取两个，和为C n2=n(n−1)2个；B 中的元素个数为n +n(n−1)2=n 2+n 2个；则B 中元素的和为2(3+32+⋯+3n )+(n −1)(3+32+⋯+3n )=(n +1)(3+32+⋯+3n ) =(n +1)⋅3(1−3n )1−3=3(n+1)(3n −1)2．【解析】(1)由新定义和集合的列举法，可得所求集合；(2)运用等差数列为递增数列，以及性质，即可得到所求个数；(3)由等比数列的通项公式和性质，结合新定义计算可得所求结论．本题考查新定义的理解和运用，考查等差数列和等比数列的通项公式和求和公式的运用，考查运算能力，属于中档题．。

曹杨二中2018学年第一学期期终考试数学试卷一、填空题1、函数()sin cos f x x x =的最小正周期为_________2、2lim 12n P n→∞++K =_________3、函数()()()3log 212x f x x =-≥的反函数()1f x -_________4、在62x x ⎛⎫- ⎪⎝⎭的二项式展开式中，常数项为___________5、一直一组数据为2,11,9,8,10，则这组数据的方差为_________6、双曲线221x y -=的一条渐近线被圆()2224x y -+=截得线段长为________ 7、已知数列{}n a 的首项12a =，且满足()*22n n n a a n N +=∈，则20a =________ 8、已知函数()f x 是奇函数，()112f =，且()()()()22f x f x f x R +=+∈，则()5f =________ 9、将一颗均匀的骰子掷两次，第一次得到的点数记为a ，第一次得到的点数记为b ，则方程组322ax by x y +=⎧⎨+=⎩有唯一解的概率是___________10、已知等差数列{}n a 的前n 项和为n S ，若1313,615a S ≤≤≤≤，则21a a 的取值范围是__________11、设函数()3,1,1x a x f x x a x ⎧-<=⎨-≥⎩，若()f x 有且仅有1个零点，则实数a 的取值范围是___________12、定义全集U 的子集M 的特征函数()10M U x Mf x x C M ∈⎧=⎨∈⎩，对于两个集合,M N ，定义集合()(){}*1M N M N x f x f x =+=，已知集合{}{}2,4,6,8,10,1,2,4,8,16A B ==，并用S 表示有限集S 的元素个数，则对于任意有限集,**M M A M B +的最小值为________二、选择题13、若i 为虚数单位）是关于x 的实系数一元二次方程20z bz c ++=的一个复数根，则（） A. 2,3b c ==B. 2,1b c ==-C. 2,3b c =-=D. 2,1b c =-=-14、已知,,x y z 为正实数，且230x y -+=，则2y xz的最小值为（）A.1B.2C.3D.615、设平面α和平面β相交于直线m ，直线a 在平面α上，直线b 在平面β上，且b m ⊥，则“αβ⊥”是“a b ⊥”的（） A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件16、在ABC ∆中，若623AC AB AB BC BC CA ⋅=⋅=⋅u u u r u u u r u u u r u u u r u u u r u u u r，则A ∠=（）A.45°B.60°C.120°D.135°二、解答题17、在ABC ∆中，角,,A B C 的对边分别为,,a b c ，已知2,6a C π==，且ABC ∆（1）求c ；（2）若F 为边AC 上一点，且CF =，求sin BFC ∠18、如图，某甜品创作一种冰淇淋，其上半部分呈半球形，下半部分呈圆锥形，现把半径为10cm 的圆形蛋皮等分成5个扇形，用一个扇形蛋皮固成圆锥的侧面（蛋皮厚度忽略不计）。