上海市曹杨二中2020-2021学年高二下学期开学摸底考数学试题

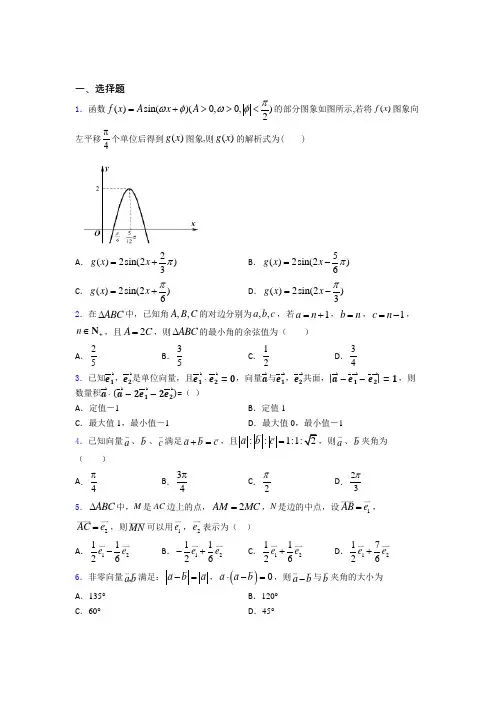
一、选择题1．函数()sin()(0,0,)2f x A x A πωφωφ=+>><的部分图象如图所示,若将()f x 图象向左平移4π个单位后得到()g x 图象,则()g x 的解析式为( )A ．2()2sin(2)3g x x π=+ B ．5()2sin(2)6g x x π=- C ．()2sin(2)6g x x π=+D ．()2sin(2)3g x x π=-2．在ABC ∆中，已知角,,A B C 的对边分别为,,a b c ，若1a n =+，b n =，1c n =-，n ∈+N ，且2A C =，则ABC ∆的最小角的余弦值为（ ）A ．25B ．35C ．12D ．343．已知e 1⃑⃑⃑ ，e 2⃑⃑⃑ 是单位向量，且e 1⃑⃑⃑ ⋅e 2⃑⃑⃑ =0，向量a ⃑ 与e 1⃑⃑⃑ ，e 2⃑⃑⃑ 共面，|a ⃑ −e 1⃑⃑⃑ −e 2⃑⃑⃑ |=1，则数量积a ⃑ ⋅(a ⃑ −2e 1⃑⃑⃑ −2e 2⃑⃑⃑ )=（ ）A ．定值－1B ．定值1C ．最大值1，最小值－1D ．最大值0，最小值－14．已知向量a 、b 、c 满足a b c +=，且::1:1:2a b c =a 、b 夹角为（ ） A ．4π B ．34π C ．2π D ．23π 5．ABC ∆中，M 是AC 边上的点，2AM MC =，N 是边的中点，设1AB e =，2AC e =，则MN 可以用1e ，2e 表示为（ ）A ．121126e e - B ．121126e e -+ C ．121126e e + D ．121726e e + 6．非零向量a b ，满足：a b a -=，()0a a b ⋅-=，则a b -与b 夹角的大小为 A ．135° B ．120° C ．60°D ．45°7．已知π(,π)2α∈，π1tan()47α+=，则sin cos αα+= （ ） A ．17-B ．25-C ．15-D ．158．已知角α的终边过点()4,3(0)P m m m -<,则2sin cos αα+的值是A ．1B ．25 C ．2 5- D ．-1 9．在平面直角坐标系中，角α的顶点与原点重合，始边与x 轴的非负半轴重合，终边过点(3,1)P --，则sin(2)2πα-=（ ）A ．32B ．32-C ．12D ．12-10．在中，,,A B C ∠∠∠所对的边长分别是,,a b c ，若sin sin()sin 2C B A A +-=，则的形状为A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形11．下列函数中，最小正周期为π且图象关于原点对称的函数是（ ） A ．cos 22y x π⎛⎫=+⎪⎝⎭B ．sin 22y x π⎛⎫=+⎪⎝⎭C ．sin2cos2y x x =+D ．sin cos y x x =+12．已知a ，b 是平面内两个互相垂直的单位向量，若向量c 满足()()0a c b c -⋅-=，则c 的最大值是( ) A ．1B ．2C ．D ．13．已知()()f x sin x ωθ=+（其中()()12120,0,,''0,2f x f x x x πωθ⎛⎫>∈==- ⎪⎝⎭，的最小值为(),23f x f x ππ⎛⎫=- ⎪⎝⎭，将()f x 的图象向左平移6π个单位得()g x ，则()g x 的单调递减区间是（ ） A ．(),2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦B ．()2,63k k k ππ⎡⎤π+π+∈⎢⎥⎣⎦Z C ．()5,36k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D ．()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦14．设sin1+=43πθ（），则sin 2θ=（ ）A ．79-B ．19-C ．19D ．7915．在ABC ∆中，a b c 、、分别是内角A B C 、、所对的边，若2224ABCa b c S ∆+-=（其中)ABC S ABC ∆∆表示的面积,且0,AB AC BC AB AC ⎛⎫⎪+⋅= ⎪⎝⎭则ABC ∆的形状是（ ） A ．有一个角为30的等腰三角形 B ．正三角形 C ．直角三角形D ．等腰直角三角形二、填空题16．已知向量()1,1a =，()3,2b =-，若2ka b -与a 垂直，则实数k =__________． 17．已知函数()sin()(,0,0,0)2f x A x x R A πωϕωϕ=+∈>><<的图象与x 轴的交点中，相邻两个交点之间的距离为2π，且图象上一个最低点为2(,2)3M π-.则()f x 的解析式为________． 18．已知θ为钝角，1sin()43πθ+=，则cos2θ=______. 19．已知1tan 43πα⎛⎫-=- ⎪⎝⎭，则2sin sin()cos()απαπα--+的值为__________. 202cos821sin8+-的化简结果是_________.21．已知向量a ，b 满足1a =，且()2a a b b -==，则向量a 与b 的夹角是__________．22．已知角θ的终边上的一点P 的坐标为()3,4，则cos 21sin 2θθ=+________________．23．在平行四边形ABCD 中，E 为线段BC 的中点，若AB AE AD λμ=+，则λμ+=__________．24．若sincos022αα<<，则角α的终边落在第________象限.25．已知()()2,1,,3a b λ=-=，若a 与b 的夹角为钝角，则λ的取值范围是___________．（用集合表示）三、解答题26．已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+ （Ⅰ）求函数()f x 的最小正周期和图象的对称轴方程（Ⅱ）求函数()f x 在区间[,]122ππ-上的值域 27．已知ABC ∆的三个内角A ，B ，C 的对边分别为a ，b ，c ，函数()()2sin cos sin f x x A x A =-+，且当512x π=时，()f x 取最大值. （1）若关于x 的方程()f x t =，0,2x π⎛⎫∈ ⎪⎝⎭有解，求实数t 的取值范围；（2）若5a =，且43sin sin 5B C +=，求ABC ∆的面积. 28．已知函数()44f x sin x asinx cosx cos x.=+⋅+(Ⅰ)当a 1=时，求()f x 的值域；(Ⅱ)若方程()f x 2=有解，求实数a 的取值范围．29．如图所示,函数()2cos (,0.0)2y x x R πωθωθ=+∈>≤≤的图象与y 轴交于点()0,3,且该函数的最小正周期为π.(1)求θ和ω的值； (2)已知点πA ,02⎛⎫⎪⎝⎭,点P 是该函数图象上一点,点00(,)Q x y 是PA 的中点,当003,,22y x ππ⎡⎤=∈⎢⎥⎣⎦时，求0x 的值.30．已知函数44()cos 2sin cos sin f x x x x x =--. （1）求()f x 的最小正周期； （2）当0,2x π⎡⎤∈⎢⎥⎣⎦时，求()f x 的最小值以及取得最小值是x 的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1．C2．D3．A4．C5．A6．A7．C8．C9．D10．D11．A12．C13．A14．A15．D二、填空题16．-1【解析】【分析】由题意结合向量垂直的充分必要条件得到关于k的方程解方程即可求得实数k的值【详解】由平面向量的坐标运算可得：与垂直则即：解得：【点睛】本题主要考查向量的坐标运算向量垂直的充分必要条17．【解析】【分析】根据函数周期为求出再由图象的最低点得到振幅及【详解】因为图象与两个交点之间的距离为所以所以由于图象的最低点则所以当时因为所以故填：【点睛】本题考查正弦型函数的图象与性质考查数形结合思18．【解析】【分析】将改写成的形式利用二倍角公式计算的值代入相关数值【详解】因为所以；因为且为钝角所以是第二象限角则故【点睛】（1）常见的二倍角公式：；（2）常用的角的配凑：；19．【解析】【分析】先根据已知求出最后化简代入的值得解【详解】由题得由题得=故答案为【点睛】本题主要考查差角的正切和同角的商数关系平方关系意在考查学生对这些知识的理解掌握水平和分析推理能力20．【解析】原式因为所以且所以原式21．【解析】【分析】先根据条件得再根据向量夹角公式求结果【详解】因为且所以因此【点睛】求平面向量夹角方法：一是夹角公式；二是坐标公式；三是几何方法从图形判断角的大小22．【解析】分析：由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解：角的终边上的一点的坐标为那么故答案为点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求23．【解析】分析：先根据三角形法则化为再根据分解唯一性求即得详解：因为所以因为不共线所以点睛：利用向量基本定理中唯一性可求参数：即若为不共线向量则24．二【解析】由题意结合三角函数的性质可得：则据此可得角的终边落在第二象限25．【解析】∵向量与的夹角为钝角∴即；解得即的取值范围是故答案为三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题 1．C 解析：C 【解析】 【分析】根据函数的图象求出函数()f x 的解析式，再根据图象的平移变换得到()g x 的解析式即可. 【详解】 由图象可知，A =2,541264T πππ=-=, 2T ππω∴==, 2ω∴=,又当512x π=时，52sin(2)212πφ⨯+=， 即5sin()16πφ+=， 2πφ<，3πφ∴=-，故()sin()f x x π=-223，将()f x 图象向左平移4π个单位后得到()g x ， ∴ ()2sin[2()]2sin(2)436g x x x πππ=+-=+，故选：C 【点睛】本题主要考查了正弦型函数的图象与性质，图象的变换，属于中档题.2．D解析：D 【解析】 【分析】利用余弦定理求出cos A 和cos C 的表达式，由2A C =，结合正弦定理sin sin c aC A=2sin cos aC C =得出cos C 的表达式，利用余弦定理得出cos C 的表达式，可解出n 的值， 于此确定ABC ∆三边长，再利用大边对大角定理得出C 为最小角，从而求出cos C ． 【详解】2A C =，由正弦定理sin sin c a C A=，即sin sin 22sin cos c a aC C C C ==， ()1cos 221a n C c n +∴==-， ()()()()222222114cos 22121n n n a b c n C ab n n n ++--+-+===++，()()142121n n n n ++∴=-+， 解得5n =，由大边对大角定理可知角C 是最小角，所以，63cos 244C ==⨯，故选D ． 【点睛】本题考查正弦定理和余弦定理的应用，考查大边对大角定理，在解题时，要充分结合题中的已知条件选择正弦定理和余弦定理进行求解，考查计算能力，属于中等题．3．A解析：A 【解析】 【分析】由题意可设e 1⃑⃑⃑ =(1,0),e 2⃑⃑⃑ =(0,1)，a ⃑ =(x,y)，再表示向量的模长与数量积， 【详解】由题意设e 1⃑⃑⃑ =(1,0),e 2⃑⃑⃑ =(0,1)，则向量a ⃑ =xe 1⃑⃑⃑ +ye 2⃑⃑⃑ =(x,y)，且|a ⃑ −e 1⃑⃑⃑ −e 2⃑⃑⃑ |=1， 所以a ⃑ −e 1⃑⃑⃑ −e 2⃑⃑⃑ =(x −1,y −1)， 所以(x −1)2+(y −1)2=1， 又a ⃑ −2e 1⃑⃑⃑ −2e 2⃑⃑⃑ =(x −2,y −2)，所以数量积a ⃑ ⋅(a ⃑ −2e 1⃑⃑⃑ −2e 2⃑⃑⃑ )=x(x −2)+y(y −2)=(x −1)2+(y −1)2−2=1−2=−1， 故选：A ． 【点睛】本题考查平面向量基本定理以及模长问题，用解析法，设出向量的坐标，用坐标运算会更加方便。

上海市曹杨第二中学高二数学理月考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 设m、n是不同的直线，α、β、γ是不同的平的，有以下四个命题：①若α∥β，α∥γ，则β∥γ②若α⊥β，m∥α，则m⊥β③若m∥n，n?α，则m∥α④若m⊥α，m∥β，则α⊥β其中正确命题的序号是（）A．①③B．①④C．②③D．②④参考答案：B【考点】空间中直线与平面之间的位置关系．【专题】定义法；空间位置关系与距离；简易逻辑．【分析】①根据面面平行的性质进行判断，②根据线面垂直和面面垂直的性质和判定定理进行判断，③根据线面平行的判定定理进行判断，④根据线面垂直，线面平行和面面垂直的性质进行判断．【解答】解：①若α∥β，α∥γ，则β∥γ，成立，故①正确，②若α⊥β，m∥α，则m⊥β或m∥β或m?β，故②错误，③若m∥n，n?α，则m∥α或m?α，故③错误，④若m⊥α，m∥β，则α⊥β成立，故④正确，故正确是①④，故选：B．【点评】本题主要考查与空间直线和平面平行或垂直的命题的真假的判断，要求熟练掌握空间线面，面面平行或垂直的性质定理和判定定理．2. i是虚数单位，则1+i3等于（）A.iB.-iC.1+iD.1-i参考答案：D略3. 某单位安排甲、乙、丙三人在某月1日至12日值班，每人4天．甲说：我在1日和3日都有值班;乙说：我在8日和9日都有值班；丙说：我们三人各自值班的日期之和相等．据此可判断丙必定值班的日期是( )A、2日和5日B、5日和6日C、6日和11日D、2日和11日参考答案：C提示：1~12日期之和为78，三人各自值班的日期之和相等，故每人值班四天的日期之和是26，甲在1日和3日都有值班，故甲余下的两天只能是10号和12号；而乙在8日和9日都有值班，8+9=17，所以11号只能是丙去值班了。

余下还有2号、4号、5号、6号、7号五天，显然，6号只可能是丙去值班了。

上海市曹杨第二中学2021届高三下学期3月月考数学试题学校:___________姓名：___________班级：___________考号：___________一、填空题1．21lim1n n n →∞+=-_____2．不等式01xx <-的解集为_____．3．已知复数z 满足234i(i z =+为虚数单位），则||z =_____．4．某校调查了200名学生每周的自习时间（单位:小时），制成了如图所示的的频率分布直方图，根据直方图，这200名学生中每周的自习时间不少于22.5小时的人数为：_____．5．若,x y 满足020x y x y y -≥⎧⎪+≤⎨⎪≥⎩，则目标函数2z x y =+的最大值是________．6．从1,2,3,4这四个数中一次随机地抽取两个数，则其中一个数是另一个数的两倍的概率是_____．（结果用数值表示）7．621(1)x x x ⎛⎫-- ⎪⎝⎭的展开式中常数项为_____．8．已知,a b R +∈，若直线()1210a x y -+-=与直线70x by ++=互相垂直，则ab 的最大值等于___________.9．若3sin()cos cos()sin 5x y x x y x ---=，则tan 2y 的值为________10．已知函数()2lg(100)x g x x =++，定义在(1,1)-上的函数()f x 满足()()()2f x g x g x =--+，则关于x 的不等式()()314f x f x ++>的解集为_____．11．设双曲线22214x y b-=（0b >）的左右焦点分别为12,F F ，过1F 的直线l 分别与双曲线左，右两支交于M ，N 两点，且2222,F M F N F M F N ⊥=，则双曲线的半焦距c =_____．12．已知平面向量1e 、2e 是不共线的单位向量，记1e 、2e 的夹角为θ，若平面向量a 满足12a = ，且对于任意的正实数k ，1214a e ke -+≥ 恒成立，则cos θ的最大值为___________.二、单选题13．直线121x ty t=+⎧⎨=+⎩，（t 为参数）的倾斜角为（）A ．π6B ．π3C ．1arctan 2D ．arctan 214．已知直线l 和两个不同的平面,αβ，则下列结论正确的为（）A ．若//,//l l αβ，则//αβB ．若,l αβα⊥⊥，则l β⊥C ．若//,l l αβ⊥，则αβ⊥D ．若,//l αβα⊥，则l β⊥15．定义在R 上的函数()f x ，若()(||)|()|g x f x f x =-，有下列两个结论：①若()f x 是偶函数，则()g x 是奇函数;②若()f x 是偶函数,则()g x 是偶函数，则（）A ．①②均正确B ．①②均错误C ．①对②错D ．①错②对16．已知数列{}n a 满足2112,n n n a a a a +==+，设1212333111m m m a a a S a a a =++++++ ，若2020m S <，则正整数m 的最大值为（）A ．672B ．673C ．674D ．675三、解答题17．如图，四边形ABCD 是正方形，PA ⊥平面ABCD ，//EB PA ，4AB PA ==，2EB =，F 为PD 的中点.(1)求证:AF PC ⊥;(2)求二面角D PC E --的大小.18．已知0a >且1a ≠，函数()()1log (1),log 1a a f x x g x x=+=-，记()()()2F x f x g x =+.（1）求函数()F x 的定义域D 及其零点；（2）若关于x 的方程()0F x m -=在区间[0,1)内仅有一解，求实数m 的取值范围.19．如图所示，经过村庄A 有两条夹角为60 的公路,AB AC ，根据规划要在两条公路之间的区域内修建一工厂P ，分别在两条公路边上建两个仓库,M N （异于村庄A ），要求2PM PN MN ===（单位：千米），记AMN θ∠=.（1）将,AN AM 用含θ的关系式表示出来；（2）如何设计（即,AN AM 为多长时），使得工厂产生的噪声对居民影响最小（即工厂与村庄的距离AP 最大）？20．已知椭圆22:184x y C +=，过点(0,4)P 作关于y 轴对称的两条直线12,l l ，且1l 与椭圆交于不同两点2,,A B l 与椭圆交于不同两点D ，C .(1)已知1l 经过椭圆的左焦点，求1l 的方程；(2)证明：直线AC 与直线BD 交于点(0,1)Q ;(3)求线段AC 长的取值范围.21．已知数列{}n a ，n S 为其前n 项的和，满足()12n n n S +=.（1）求数列{}n a 的通项公式；（2）设数列1n a 禳镲睚镲铪的前n 项和为n T ，数列{}n T 的前n 项和为n R ，求证：当2n ≥，*n ∈N 时()11n n R n T -=-；（3）已知当*n ∈N ，且6n ≥时有1132nmm n ⎛⎫⎛⎫-< ⎪ ⎪+⎝⎭⎝⎭，其中1,2,,m n = ，求满足()()3423n nan n n n a ++++=+L 的所有n 的值.参考答案：1．2【详解】122120lim lim 2.11101n n n n n n→+∞→+∞+++===---2．(0,1)【分析】将不等式01xx <-化为()10x x -<，即可得答案.【详解】由题意得不等式01xx <-即()()10,0,1x x x -<∴∈，即不等式01xx <-的解集为(0,1)，故答案为：(0,1)3【分析】根据复数的乘法运算求解即可.【详解】设i(,R)z a b a b =+∈，则2222i 34i z a b ab =-+=+，所以22324a b ab ⎧-=⎨=⎩解得21a b =⎧⎨=⎩或21a b =-⎧⎨=-⎩，所以2i z =+或2i z =--，所以||z ==故答案为:4．140【分析】求出这200名学生中每周的自习时间不少于22.5小时的频率，即可求得答案.【详解】由频率分布直方图得：这200名学生中每周的自习时间不少于22.5小时的频率为:(0.020.10) 2.50.71+⨯-=,这200名学生中每周的自习时间不少于22.5小时的人数为：2000.7140⨯=，故答案为：140.5．3；【详解】画出可行域,如下图阴影部分,其中(1,1),(1,0),A B 令0z =，则20x y +=,为经过坐标原点得到直线,将此直线向右上方平移,当经过点(1,1)A 时,2z x y =+有最大值3.6．13【分析】列举出四个数中一次随机地抽取两个数的所有可能情况，确定其中一个数是另一个数的两倍的情况有几种，根据古典概型的概率公式即可求得答案.【详解】从1,2,3,4这四个数中一次随机取两个数,有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)共6种情况,其中其中一个数是另一个的两倍的有两种，即(1,2)，(2,4),则其概率为2163=,故答案为：13.7．15-【分析】求出二项式621x x ⎛⎫- ⎪⎝⎭的展开式的通项公式，根据题意可得相应方程，求得r 的值，可得答案.【详解】621x x ⎛⎫- ⎪⎝⎭的展开式的通项公式()621231661C (1)C ,0,1,,6rrrr r rr T x xx r --+⎛⎫=-==- ⎪⎝⎭,令1231r -=-，解得133r =（舍）；令1230r -=，解得4r =，621(1)x x x ⎛⎫∴-- ⎪⎝⎭的展开式中常数项为46C 15-=-，故答案为：15-8．18【分析】先根据两直线互相垂直，得到21a b +=，再根据基本不等式即可求解.【详解】解： 直线()1210a x y -+-=与直线70x by ++=互相垂直，()1120a b ∴-⨯+=，即21a b +=，又,a b R +∈ ，由基本不等式得：222112224a b ab +⎛⎫⎛⎫≤== ⎪ ⎪⎝⎭⎝⎭，即18ab ≤，当且仅当2a b =，即11,24a b ==时等号成立.故答案为：18.9．247±【详解】由已知有()3sin 5x y x ⎡⎤--=⎣⎦3sin 5y =-，y ∴为第三或第四象限的角当y 为第三象限的角时，3tan 4y =，则22tan 24tan 217y y tan y ==-当y 为第四象限的角时，3tan 4y =-，则22tan 24tan 217y y tan y ==--24tan 27y ∴=±10．1(,0)4-【分析】根据给定条件，判断函数()g x 的单调性，函数()f x 的单调性及奇偶性，再利用性质求解不等式作答.【详解】函数()2lg(100)x g x x =++在(100,)-+∞上单调递增，()g x -在(1,1)-上单调递减，因此函数()()g x g x --在(1,1)-上单调递增，令()()2()()h x f x g x g x =-=--，当(1,1)x ∈-时，()()()()h x g x g x h x -=--=-，则()h x 为(1,1)-上的奇函数，且为增函数，不等式(31)()4(0)2()231f f f x x f x x ++>-+-⇔>+，有(31)()0h x h x ++>，即(31)()()h x h x h x +>-=-，于是得1311x x -<-<+<，解得104x -<<，所以所求不等式的解集为1(,0)4-.故答案为：1(,0)4-11．【分析】利用双曲线的定义结合余弦定理即可求解.【详解】设22F M F N t ==，由22F M F N ⊥，可得||MN =，由双曲线的定义可得1224F M F M a t =-=-，1224F N F N a t =+=+，11||8MN F N F M =-==，解得=t ，在12NF F △中，1212124,8,2,45F N F N F F c F NF ︒=+==∠=，则22248(428(4cos 45c ︒=++-⨯⨯+，解得c =故答案为:12．4【解析】由已知可得出1234e ke -≥ 或1214e ke -≤ 对任意正实数k 恒成立，在对应的不等式两边平方，利用参变量分离法结合基本不等式可求得cos θ的取值范围，进而可求得结果.【详解】12a = 且()1214a e ke --≥ 恒成立，则1214a e ke --≥ ，可得到1234e ke -≥ 或1214e ke -≤ ，①若1234e ke -≥对任意正实数k 恒成立，在不等式1234e ke -≥ 两边平方可得2912cos 16k k θ+-≥，所以17cos 216k k θ⎛⎫≤+ ⎪⎝⎭，由于0k >，由基本不等式可得17121624k k ⎛⎫+≥⨯ ⎪⎝⎭，当且仅当4k =时，等号成立，此时，cos 4θ≤；②若1214e ke -≤ 对任意正实数k 恒成立，在不等式1214e ke -≤两边同时平方可得2112cos 16k k θ+-≤，所以115cos 216k k θ⎛⎫≥+ ⎪⎝⎭，由于15216k k ⎛⎫+ ⎪⎝⎭没有最大值，所以1214e ke -≤不恒成立.综上所述，cos 4θ≤，即cos θ的最大值为4.故答案为：4.【点睛】思路点睛：由向量模的三角不等式可得出1214a e ke --≥，利用绝对值不等式得出1234e ke -≥ 或1214e ke -≤ ，在求参数的最值或取值范围时，可利用参变量分离法结合基本不等式求解.13．C【分析】将直线的参数方程化为普通方程，确定其斜率，即可得答案.【详解】直线直线121x ty t =+⎧⎨=+⎩，（t 为参数）的普通方程为210x y -+=，所以直线的斜率为12，故倾斜角为锐角，即1arctan 2α=，故选：C.14．C【分析】根据条件作出相应图形，结合图形证明或举出反例即可求解.【详解】对于A ，如下图，//,//l m l n ，则//,//l l αβ，满足题中条件，但α与β相交，故A 错误;对于B ，若,l αβα⊥⊥，当l 在β内且与,αβ的交线垂直时，符合题中条件，但不满足结论，故B 错误;对于C ，设过l 的平面γ与α相交于直线m ，则m α⊂，且//m l，由l β⊥，则m β⊥，由面面垂直的判定定理可得：αβ⊥，故C 正确;对于D ，若,//l αβα⊥，则l 与β可能平行，如下图中1l，也可能l 在β内，如图中2l ，故D 错误.故选：C.15．D【分析】根据函数奇偶性的定义分别去判断①②，即可得答案.【详解】对于①,()f x 是偶函数时，有()()f x f x -=，则()(||)|()|(||)|()|g x f x f x f x f x -=---=-(),()g x g x =是偶函数，故①错误;对于②，()f x 是偶函数时，()()f x f x -=，则()(||)|()|(||)|()|g x f x f x f x f x -=---=-(),()g x g x =是偶函数，故②正确，故选：D 16．B【分析】根据数列的递推式可得()116n n n a a a +=+≥，从而得11111n n n a a a +=-+，由此化简1212333111m m m a a a S a a a =++++++ 得13332m m a +-+，于是可得不等式结合2020m S <，即可求得答案.【详解】由题意数列{}n a 满足2112,n n n a a a a +==+，可知0n a >，又210n n n a a a +-=>，故数列{}n a 为递增数列，由2223226,6642a a =+==+=，可知()116n n n a a a +=+≥，()111111111,111n n n n n n n n a a a a a a a a ++∴==-∴=-+++，12121223133311111133111m m m m m a a a S m a a a a a a a a a +⎛⎫=+++=--+-++- ⎪+++⎝⎭ 111133313333312222m m m m m m a a ++⎛⎫=--=-+≤-+=- ⎝⎭，因为2020m S <，所以2312020,6733m m -<∴<+，故正整数m 的最大值为673，故选:B17．(1)证明见解析；(2)5π6.【分析】(1)利用空间向量的坐标运算证明；(2)利用空间向量的坐标运算求二面角的大小.【详解】（1）依题意，PA ⊥平面ABCD ，如图，以A 为原点，分别以,,AD AB AP的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系.依题意，可得(0,0,0),(0,4,0),(4,4,0)A B C ，(4,0,0),(0,0,4),(0,4,2),(2,0,2)D P E F ，(2,0,2),(4,4,4)AF PC ==-，80(8)0AF PC ∴⋅=++-= ，AF PC ∴⊥即AF PC ⊥；（2）∵AD AP =，F 为PD 的中点，∴,AF PD ⊥,AF PC PD PC P ⊥⋂= ，,PD PC ⊂平面PCD ,AF ∴⊥平面PCD ，故(2,0,2)AF =为平面PCD 的一个法向量.设平面PCE 的法向量为(,,)n x y z =，(4,4,4),(0,4,2)PC PE =-=-，00n PC n PE ⎧⋅=⎪∴⎨⋅=⎪⎩即4440420x y z y z +-=⎧⎨-=⎩，令1y =，得1,2x z ==，故(1,1,2)n =.cos ,AF n AF n AF n ⋅∴<>==⋅，由图可得二面角D PC E --为钝角，∴二面角D PC E --的余弦值为，则二面角D PC E --的大小为5π6.18．（Ⅰ）(11)D =-，，零点是0；（Ⅱ）当1a >时，0m ；当01a <<时，0m ．【详解】试题分析：（Ⅰ）先由对数函数中真数大于零建立不等式组求得定义域，再令()0F x =解出函数零点；（Ⅱ）把关于的方程化为，则设，然后利用函数的性质求解．试题解析：（Ⅰ）1()2log (1)log (01)1a aF x x a x=++<≠-，由，解得，所以函数的定义域为．令，则（*）方程变为，，即，解得，（舍）．综上函数的定义域(11)D =-，，零点是0．（Ⅱ）142log (1)log log (14)(01)11a aa m x x x x x=++=-+-<-- ，则，在[01)，上是单调函数，设，则函数在区间上是减函数，当时，此时，，所以．所以当，则，方程有解；②当，则，方程有解．考点：1、函数的定义域与零点；2、函数的单调性．19．（1）θAN ，()120θ︒-AM ；（2）2==AN AM .【分析】（1）根据正弦定理，得到()sin 60sin sin 120θθ︒︒==-MNANAM，进而可求出结果；（2）由余弦定理，得到2222cos =+-⋅⋅∠AP AM MP AM MP AMP ，结合题中数据，得到()22016sin 215033θ︒=-+AP ，2AP 取最大值时，噪声对居民影响最小，即可得出结果.【详解】（1）因为AMN θ∠=，在AMN ∆中，由正弦定理可得：()sin 60sin sin 120θθ︒︒==-MNANAM，所以θ=AN ，()120θ︒=-AM ；（2）由题意60θ︒∠=+AMP ，由余弦定理可得：()()()2222162cos sin 1204120cos 603θθθ︒︒=+-⋅⋅∠=-+--+ AP AM MP AM MP AMP()()()()()2168sin 60460cos 601cos 21204212033θθθθθ︒︒︒︒⎡⎤=++-++=-++-+⎣⎦ ()()()82020162120cos 2120sin 21503333θθθ︒︒︒⎤=-++++=-+⎦，又由（1）可得0120θ︒︒<<，所以()2150150,390θ︒︒︒+∈，当且仅当2150270θ︒︒+=，即60θ︒=时，2AP 取得最大值，工厂产生的噪声对居民影响最小，此时2==AN AM .【点睛】本题主要考查正弦定理与余弦定理的应用，熟记正弦定理与余弦定理即可，属于常考题型.20．(1)240x y -+=；(2)证明见解析(3)4AC <<【分析】（1）根据直线的截距式方程即可求得答案.（2）设直线()()11122:4,,,,l y kx A x y B x y =+，则()()1122,,,D x y C x y --，联立直线和椭圆方程，可得根与系数关系式，化简BQ DQ k k -，可证明直线BD 经过点(0,1)Q ，同理可证直线AC 经过点(0,1)Q ，即可证明结论.（3）表示出线段AC 的长，结合根与系数的关系式化简并采用换元法，可得29161168AC t t ⎛⎫⎪=+ ⎪++⎝⎭，利用函数的单调性，可求得答案.【详解】（1）22:184x y C +=的左焦点为(2,0)-，当1l 过左焦点时，1l 的方程为124x y +=-，即240x y -+=.（2）由题意知1l 斜率存在，设直线()()11122:4,,,,l y kx A x y B x y =+，则()()1122,,,D x y C x y --，联立221844x y y kx ⎧+=⎪⎨⎪=+⎩，消y 得()221216240k x kx +++=，需满足2225696(12)0k k ∆=-+>，即2230k ->，1212221624,1212k x x x x k k -∴+=⋅=++，又212111,BQDQ y y k k x x --==-，212121211133BQ DQ y y kx kx k k x x x x --++∴-=-+-，()21212248312222202412kx x k k k k k x x k -++=+=+=-=+，BQ DQ k k ∴=，故点B ，D ，Q 三点共线，即直线BD 经过点(0,1)Q ，同理可证AQ CQ k k =,即点A ，C ，Q 三点共线，即直线AC 经过点(0,1)Q ，故直线AC 与直线BD 交于点(0,1)Q ;（3）由（2）可知()()()()22222212121212AC x x y y x x k x x =++-=++-()()2221212124x x k x x x x ⎡⎤=+++-⋅⎣⎦()()22222222221616244121212k k k k k k ⎡⎤⋅⋅⎢⎥=+-⨯⎢⎥+++⎣⎦42242424106116161441441k k k k k k k ⎡⎤⋅+-=⨯=⨯+⎢⎥++++⎣⎦令261t k =-，则216t k +=，又由()22216424120k k ∆=-⨯⨯+>得232k >，所以8t >，2221699161611611681611844166t t AC t t t t t t ⎛⎫ ⎪⎛⎫∴=+=+=+ ⎪ ⎪++⎝⎭++⎛⎫ ⎪+++⨯+ ⎪⎝⎭⎝⎭，设216168,()()1h t h t t t t'==-++，(8,)t ∈+∞时，()0h t '>恒成立，168t t ∴++在(8,)t ∈+∞上单调递增，16818t t∴++>，9101628t t ∴<<++，93111628t t∴<+<++，21624AC ∴<<，4AC ∴<<【点睛】方法点睛：（1）证明直线AC 与直线BD 交于点(0,1)Q 时，采用证明0BQ DQ k k =-的方法，从而证明点B ，D ，Q 三点共线，即直线BD 经过点(0,1)Q ，同理可证直线AC 经过点(0,1)Q ，即可证明结论；（2）求解线段AC 长的取值范围时，利用两点间距离公式可表示其长，解答时要结合换元法以及函数的单调性进行解答.21．（1）n a n =；（2）证明见解析；（3）2n =或者3n =.【分析】（1）利用递推关系，1n n n a S S -=-，2n ≥，单独求111a S ==，即可得出；（2）法一：直接计算化简即可证明；法二：利用数学归纳法即可证明；（3）利用“累加求和”方法、不等式的性质、分类讨论即可得出.【详解】（1）解：当2n ≥时，1n n n a S S -=-=()()1122n n n n n +--=，又111a S == ，n a n ∴=.（2）证明：（法一）：11n a n =，1112n T n∴=+++ ，1111111223n R -⎛⎫⎛⎫∴=++++++ ⎪ ⎪⎝⎭⎝⎭L 11121n ⎛⎫++++=⎪-⎝⎭L ()()11122n n -⋅+-⋅+()113131n n -⋅++⋅-L 111111231n n n ⎛⎫=++++-+=⎪-⎝⎭L 111111231n n n ⎛⎫+++++ ⎪-⎝⎭L ()()12n n T n =-≥.（法二）：数学归纳法：①2n =时，11111R T a ===，()2121121211T a a ⎛⎫-=+-= ⎪⎝⎭，②假设n k =（2k ≥，*k ∈N ）时有()11k k R k T -=-，当1n k =+时，1k k k R R T -=+=()()11k k k k T T k T k -+=+-()1111k k k T ka ++⎛⎫=+-- ⎝⎭()111111k k T k k +⎛⎫=+-+-- ⎪+⎝⎭()()111k k T +=+-，1n k ∴=+是原式成立由①②可知当2n ≥，*n ∈N 时()11n n R n T -=-.（3）解：1132nmm n ⎛⎫⎛⎫-< ⎪ ⎪+⎝⎭⎝⎭Q ，1,2,,m n = .211,32nn m n +⎛⎫=<⎪+⎝⎭2112,32nn m n +⎛⎫⎛⎫=< ⎪ ⎪+⎝⎭⎝⎭313,32n n m n ⎛⎫⎛⎫=< ⎪ ⎪+⎝⎭⎝⎭L1411,32nn m n n -⎛⎫⎛⎫=-< ⎪ ⎪+⎝⎭⎝⎭31,32n nm n n ⎛⎫⎛⎫=< ⎪ ⎪+⎝⎭⎝⎭相加得：21433333nnnnn n n n n n ++⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭⎝⎭L 2311111122222n n-⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭L ，2311111122222n n -⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭Q L 1112n⎛⎫=-< ⎪⎝⎭，即214313333nnnnn n n n n n ++⎛⎫⎛⎫⎛⎫⎛⎫++++< ⎪ ⎪ ⎪++++⎝⎭⎝⎭⎝⎭⎝⎭L ，两边同时乘以()3n n +，()()3423nnn n n n <∴+++++L ，6n ∴≥时，()()3423nnn n n n =∴+++++L 无解，又当1n =时；34<，2n =时，222345+=；3n =时，33333456++=，4n =时，44443456+++为偶数，而47为奇数，不符合5n =时，5555534567++++为奇数，而58为偶数，不符合.综上所述2n =或者3n =.【点睛】本题考查了递推关系、学归纳法、“累加求和”方法、不等式的性质、分类讨论方法，考查了推理能力与计算能力，属于难题.。

某某市普陀区曹杨第二中学2020-2021学年高二数学下学期期末考试试题（含解析）一、填空题（共12小题）.1．已知复数z＝1﹣i（i为虚数单位），则Imz＝．2．若直线l上有三点A、B、C到平面α的距离均为1，则直线l与平面α的位置关系为．3．如果圆锥的底面积为π，母线长为2，那么该圆锥的侧面积为．4．方程的解是5．在长方体ABCD﹣A1B1C1D1中，AA1＝3，AB＝5，AD＝2，则异面直线AB1和DD1的距离为．6．若复数（i为虚数单位）是纯虚数，则实数k的值为．7．设空间向量＝（﹣1，2，m），＝（2，n，﹣4），若∥，则|﹣|＝．8．已知空间四边形ABCD，AB＝CD＝2，且AB与CD所成的角为，设E、F分别是BC、AD 的中点，则EF的长度为．9．已知正四棱柱ABCD﹣A1B1C1D1内接于半径为2的球，且A、B两点的球面距离为，则该正四棱柱的体积为．10．在复数X围内方程z2+2|z|﹣1＝0的解集为．11．在空间直角坐标系中，正四面体P1P2P3P4的顶点的坐标为P i（x i，y i，z i）（i＝1，2，3，4）．设集合A＝{z i|i＝1，2，3，4}，则集合A的元素个数可能为（写出所有可能的值）．12．在三棱锥A﹣BCD中，AB、AC、AD两两垂直且长度均为6，定长为l（l＜4）的线段MN 的一个端点M在棱AB上运动，另一个端点N在△ACD内运动（含边界），若线段MN的中点P的轨迹的面积为，则l的值为．二、选择题13．已知直线l和两个不同的平面α，β，则下列结论正确的是（）A．若l∥α，l⊥β，则α⊥βB．若α⊥β，l⊥α，则l⊥βC．若l∥α，l∥β，则α∥βD．若α⊥β，l∥α，则l⊥β14．设z1，z2，z3为复数，z1≠0．下列命题中正确的是（）A．若|z2|＝|z3|，则z2＝±z3B．若z1z2＝z1z3，则z2＝z3C．若＝z3，则|z1z2|＝|z1z3|D．若z1z2＝|z1|2，则z1＝z215．将6个相同的小球放入3个不同的盒子中，每个盒子至多可以放3个小球，且允许有空盒子，则不同的放法共有（）种A．10B．16C．22D．2816．在如图所示的棱长为20的正方体ABCD﹣A1B1C1D1中，点M为CD的中点，点P在侧面ADD1A1上，且到A1D1的距离为6，到AA1的距离为5，则过点P且与A1M垂直的正方体截面的形状是（）A．三角形B．四边形C．五边形D．六边形三、解答题17．有8名学生排成一排照相，求满足下列要求的排法的种数．（只需列式并计算结果）（1）甲、乙两人相邻；（2）丙、丁两人不相邻；（3）甲站在丙、丁两人的中间（未必相邻）．18．如图，AB是圆柱OO1的一条母线，BC是底面的一条直径，D是圆O上一点，且AB＝BC ＝5，CD＝3．（1）求直线AC与平面ABD所成角的大小；（2）求点B到平面ACD的距离．19．已知m∈R，α、β是关于x的方程x2+4x+m＝0（x∈C）的两根．（1）若α为虚数，且|α|＝3，某某数m的值；（2）若|α﹣β|＝2，某某数m的值．20．如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°，AB＝BC＝4，AD＝2，E、F分别是AB、CD的中点，沿EF将梯形AEFD翻折至A′EFD’，使得平面A′EFD′⊥平面BEFC．（1）求证：A′E⊥BE；（2）设G为EF上的动点，当A'G+GC取最小值时，求异面直线BD′与CG所成角的大小；（3）求多面体A′BCD′EF的体积．21．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA＝AD＝4，E为PD中点，F在PC上，且＝．（1）求证：AE⊥平面PCD；（2）求二面角F﹣AE﹣P的大小．（3）设平面AEF与直线PB交于点G，求的值．参考答案一、填空题1．已知复数z＝1﹣i（i为虚数单位），则Imz＝﹣1 ．解：因为z＝1﹣i，故Imz＝﹣1．故答案为：﹣1．2．若直线l上有三点A、B、C到平面α的距离均为1，则直线l与平面α的位置关系为平行．解：若直线l上有三点A、B、C到平面α的距离均为1，则直线l与平面α平行，不可能相交，因为三点A，B，C共线．．故答案为：平行．3．如果圆锥的底面积为π，母线长为2，那么该圆锥的侧面积为2π．解：设圆锥的底面积半径r，则底面半径为πr2＝π，解得r＝1；由母线长为l＝2，则该圆锥的侧面积为S侧＝πrl＝π×1×2＝2π．故答案为：2π．4．方程的解是x＝3或x＝7解：∵，∴x＝2x﹣3或x+2x﹣3＝18，解得x＝3或x＝7．∴方程的解是x＝3或x＝7．故答案为：x＝3或x＝7．5．在长方体ABCD﹣A1B1C1D1中，AA1＝3，AB＝5，AD＝2，则异面直线AB1和DD1的距离为 2 ．解：如图，在长方体体ABCD﹣A1B1C1D1中，因为AD⊥平面DD1C1C，且DD1⊂平面DD1C1C，所以AD⊥DD1，同理可证AD⊥AB1故AD是异面直线AB1和DD1的公垂线段，因此AB1和DD1的距离为AD＝2．故答案为：2．6．若复数（i为虚数单位）是纯虚数，则实数k的值为 1 ．解：因为＝为纯虚数，所以k﹣1＝0且k+1≠0，解得k＝1．故答案为：1．7．设空间向量＝（﹣1，2，m），＝（2，n，﹣4），若∥，则|﹣|＝9 ．解：因为空间向量＝（﹣1，2，m），＝（2，n，﹣4），且∥，所以，即（2，n，﹣4）＝λ（﹣1，2，m），可得，解得m＝2，n＝﹣4，所以＝（﹣1，2，2），＝（2，﹣4，﹣4），则﹣＝（﹣3，6，6），所以．故答案为：9．8．已知空间四边形ABCD，AB＝CD＝2，且AB与CD所成的角为，设E、F分别是BC、AD 的中点，则EF的长度为1或．解：如图，取BD中点M，连结FM，EM，由题可知，MF∥AB，ME∥CD，MF＝，ME＝，∵AB与CD所成的角为，∴或者＝，当时，△FME为等边三角形，∴EF＝1，当时，由余弦定理可知，EF2＝EM2+MF2﹣2EM•MF•cos∠FME＝，∴EF＝，综上，EF＝1或EF＝，故答案为：1或．9．已知正四棱柱ABCD﹣A1B1C1D1内接于半径为2的球，且A、B两点的球面距离为，则该正四棱柱的体积为8．解：设球的球心为O，正四棱柱的高为h，因为球的半径为2，且A、B两点的球面距离为，则有∠AOB•2＝，所以∠AOB＝，又OA＝OB＝2，所以AB＝2，即正四棱柱ABCD﹣A1B1C1D1的底面正方形的边长为2，又正四棱柱的体对角线为外接球的直径，则，解得h＝，所以该正四棱柱的体积为＝8．故答案为：8．10．在复数X围内方程z2+2|z|﹣1＝0的解集为{1+，，﹣i，i} ．解：设z＝x+yi（x，y∈R），则原方程化为，则，由②可知，y＝0或x＝0，故原方程有实根或纯虚数根，①若y＝0，则z＝x，故|x|2+2|x|﹣1＝0，解得x＝1+或x＝；②若x＝0，则z＝yi，则有|y|＝±1，所以z＝±i．综上所述，z＝1+或z＝或z＝±i．故答案为：{1+，，﹣i，i}．11．在空间直角坐标系中，正四面体P1P2P3P4的顶点的坐标为P i（x i，y i，z i）（i＝1，2，3，4）．设集合A＝{z i|i＝1，2，3，4}，则集合A的元素个数可能为2或3或4 （写出所有可能的值）．解：若集合A中只有一个元素，则P1P2P3P4在同一个垂直于z轴的平面内，故不可能，当正四面体P1P2P3P4的底面在坐标平面xoy内时，集合A中有2个元素，当正四面体P1P2P3P4的一面与x或y轴平行，集合A有3个元素，当正四面体P1P2P3P4的各面，各边都不与x或y或z轴平行，集合中有4个元素，故集合A的元素可能为2或3或4．故答案为：2或3或4．12．在三棱锥A﹣BCD中，AB、AC、AD两两垂直且长度均为6，定长为l（l＜4）的线段MN 的一个端点M在棱AB上运动，另一个端点N在△ACD内运动（含边界），若线段MN的中点P的轨迹的面积为，则l的值为 2 ．解：由题意可知，∠MAN＝90°，在Rt△AMN中，AP＝，线段MN的中点P的轨迹是以A为球心，为半径的球面的，所以线段MN的中点P的轨迹的面积为，则l＝2．故答案为：2．二、选择题13．已知直线l和两个不同的平面α，β，则下列结论正确的是（）A．若l∥α，l⊥β，则α⊥βB．若α⊥β，l⊥α，则l⊥βC．若l∥α，l∥β，则α∥βD．若α⊥β，l∥α，则l⊥β解：设m⊂α，且m∥l，由l⊥β，则m⊥β，由面面垂直的判定定理可得：α⊥β，即选项A正确，故选：A．14．设z1，z2，z3为复数，z1≠0．下列命题中正确的是（）A．若|z2|＝|z3|，则z2＝±z3B．若z1z2＝z1z3，则z2＝z3C．若＝z3，则|z1z2|＝|z1z3|D．若z1z2＝|z1|2，则z1＝z2解：由复数的形式可知，选项A错误；当z1z2＝z1z3时，有z1z2﹣z1z3＝z1（z2﹣z3）＝0，又z1≠0，所以z2＝z3，故选项B正确；当＝z3时，则，所以＝，故选项C正确；当z1z2＝|z1|2时，则，可得，所以，故选项D错误．故选：BC．15．将6个相同的小球放入3个不同的盒子中，每个盒子至多可以放3个小球，且允许有空盒子，则不同的放法共有（）种A．10B．16C．22D．28解：根据题意，分3种情况讨论：①2个盒子各放3个小球，一个盒子是空的，有C32＝3种放法，②若每个盒子放2个小球，有1种放法，③若1个盒子放1个小球，1个盒子放2个小球，最后一个放3个小球，有A32＝6种放法，则有3+1+6＝10种放法，故选：A．16．在如图所示的棱长为20的正方体ABCD﹣A1B1C1D1中，点M为CD的中点，点P在侧面ADD1A1上，且到A1D1的距离为6，到AA1的距离为5，则过点P且与A1M垂直的正方体截面的形状是（）A．三角形B．四边形C．五边形D．六边形解：截面形状草图，如图所示：由图可知，截面为六边形，故选：D．三、解答题17．有8名学生排成一排照相，求满足下列要求的排法的种数．（只需列式并计算结果）（1）甲、乙两人相邻；（2）丙、丁两人不相邻；（3）甲站在丙、丁两人的中间（未必相邻）．解：（1）根据题意，将甲乙看成一个整体，与其他6人全排列即可，有A22A77＝10080种排法；（2）根据题意，将8人全排列，有A88种排法，其中丙、丁相邻的排法有A22A77＝10080种，则丙、丁两人不相邻的排法有A88﹣A22A77＝30240种；（3）根据题意，将8人全排列，有A88种排法，甲乙丙三人的排法有A33＝6种，其中甲站在丙、丁两人的中间有2种，则有甲站在丙、丁两人的中间有＝13440种．18．如图，AB是圆柱OO1的一条母线，BC是底面的一条直径，D是圆O上一点，且AB＝BC ＝5，CD＝3．（1）求直线AC与平面ABD所成角的大小；（2）求点B到平面ACD的距离．解：（1）∵AB⊥平面BCD，CD⊂平面BCD，∴AB⊥CD，∵BC是圆O的直径，∴BD⊥CD，又BD⊂平面ABD，AB⊂平面ABD，AB∩BDE＝B，∴CD⊥平面ABD．∴∠CAD是AC与平面ABD所成的角．∵AB＝BC＝5，∴AC＝5，∴sin∠CAD＝＝．∴直线AC与平面ABD所成角的大小为arcsin．（2）过B作BM⊥AD，垂足为M，由（1）得CD⊥平面ABD，CD⊂平面ACD，∴平面ABD⊥平面ACD，又平面ABD∩平面ACD＝AD，BM⊂平面ABD，BM⊥AD，∴BM⊥平面ACD．∵BD＝＝4，∴AD＝＝．∴BM＝＝．即B到平面ACD的距离为．19．已知m∈R，α、β是关于x的方程x2+4x+m＝0（x∈C）的两根．（1）若α为虚数，且|α|＝3，某某数m的值；（2）若|α﹣β|＝2，某某数m的值．解：（1）因为α、β是关于x的方程x2+4x+m＝0（x∈C）的两根，因为α为虚数，设α＝a+bi，则β＝a﹣bi，又|α|＝3，则a2+b2＝9，解得，因为aβ＝（a+bi）（a﹣bi）＝a2+b2＝9＝m，所以m＝9；（2）①当△＝16﹣4m＜0时，由（1）可知，a+bi+a﹣bi＝﹣4，解得a＝﹣2，又aβ＝（a+bi）（a﹣bi）＝a2+b2＝m，因为|α﹣β|＝2，所以|2bi|＝2，解得b＝±1，故m＝5；②当△＝16﹣4m≥0时，则α+β＝﹣4，αβ＝m，所以|α﹣β|＝2，即，解得m＝3．综上所述，m＝3或m＝5．20．如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°，AB＝BC＝4，AD＝2，E、F分别是AB、CD的中点，沿EF将梯形AEFD翻折至A′EFD’，使得平面A′EFD′⊥平面BEFC．（1）求证：A′E⊥BE；（2）设G为EF上的动点，当A'G+GC取最小值时，求异面直线BD′与CG所成角的大小；（3）求多面体A′BCD′EF的体积．【解答】（1）证明：因为平面A′EFD′⊥平面BEFC，EF⊥BE，EF⊥A′E，所以∠A′EB是二面角A′﹣EF﹣B的平面角，所以∠A′EB＝90°，所以A′E⊥BE；（2）解：设G为EF上的动点，当A'G+GC取最小值时，EG＝2，建立空间直角坐标系，如图所示：A（0，0，2），B（2，0，0），C（2，4，0），D′（0，2，2），G（0，2，0），所以＝（﹣2，2，2），＝（﹣2，﹣2，0），设异面直线BD′与CG所成角为θ，则cosθ＝＝＝0，所以θ＝90°；（3）解：多面体A′BCD′EF的体积为：V A′BCD′EF＝+V D′﹣EBCF＝S△BEA′•EE1+•DE1＝×2×2×2+××2×2＝6．21．如图，在四棱锥P﹣ABCD中，底面ABCD为正方形，PA⊥平面ABCD，PA＝AD＝4，E为PD中点，F在PC上，且＝．（1）求证：AE⊥平面PCD；（2）求二面角F﹣AE﹣P的大小．（3）设平面AEF与直线PB交于点G，求的值．解：（1）因为PA⊥平面ABCD，所以PA⊥CD，因为底面ABCD为正方形，所以CD⊥AD，又AD，PD⊂平面PAD，AD∩PD＝D，所以CD⊥平面PAD，又AE⊂平面PAD，所以CD⊥AE，因为PA＝AD＝4，则△PAD是等腰三角形，又E是PD的中点，所以AE⊥PD，又PD，CD⊂平面PCD，PD∩CD＝D，所以AE⊥平面PCD．（2）如图所示分别以AB，AD，AP所在直线为x，y，z轴建立坐标系，则A（0，0，0），D（0，4，0），E（0，2，2），F（1，1，3），P（0，0，4），C（4，4，0）则，设平面AEF的一个法向量为，所以⇒，取c＝1，解得b＝﹣1，a＝2，所以．是平面AEF的一个法向量，设二面角F﹣AE﹣P的平面角为θ，则．（3）平面AEF与直线PB交于点G，设，则，设G（a，b，c），则，⇒（a，b，c﹣4）＝λ（4，0，﹣4）⇒a＝4λ，b＝0＝m⇒⇒﹣8λ+0+4﹣4λ＝0⇒，所以．。

上海市曹杨二中2020-2021学年高二下学期期末数学试题 学校:___________姓名：___________班级：___________考号：___________一、填空题1．已知复数1z =，则z =______.2．如果复数()2(1)++m i mi 是实数，则实数m =________．3．若a 、b R ∈，且()a i i b i +=+，则a b +=______.4．直线110l x y -+=：与直线250l x y -+=：之间的距离是______．5．若复数z 同时满足2i z z -=，iz z =，则z =__________．6．若抛物线24y x =上一点M 到焦点的距离等于2，则M 到坐标原点O 的距离等于______.7．若方程220x y x y m -++=+表示一个圆，则实数m 的取值范围是______. 8．过点()3,2P -且与直线210x y ++=垂直的直线方程是______.9．已知点M 0)，椭圆22+14x y =与直线y ＝k (x 交于点A ，B ，则△ABM 的周长为________.10．设()1,2A ，()3,1B -，若直线2y kx =-与线段AB 有公共点，则实数k 的取值范围是______.11．已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =，120F B F B ⋅=，则C 的离心率为____________．12．曲线C 是平面内与两个定点()11,0F -和()21,0F 的距离的积等于常数()21a a >的点的轨.给出下列四个结论：①曲线C 过坐标原点；②曲线C 关于坐标原点对称；③若点P 在曲线C 上，则122PF PF a +<；④若点P 在曲线C 上，则12F PF △的面积212S a ≤.其中，所有正确的序号是______.二、单选题13．已知直角坐标系xOy 平面上的直线1x y a b +=经过第一、第二和第四象限，则,a b 满足（ ）A ．0,0a b >>B ．0a >，0b <C ．0a <，0b <D ．0a <，0b <14．复数(),z a bi a b R =+∈，()m z z b =+，n z z =⋅，2p z =，则（ ）A ．m 、n 、p 三数都不能比较大小B ．m 、n 、p 三数的大小关系不能确定C ．m n p ≤=D ．m n p ≥=15．设复数()0,0z a bi a b =+>≠是实系数方程20x px q ++=的根，又3z 为实数，则点(),p q 的轨迹在一条曲线上，这条曲线是（ ）A ．圆B ．椭圆C ．双曲线D ．抛物线16．已知a 、b 、e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430b e b -⋅+=，则a b -的最小值是（ ）A 1-B ．1C ．2D ．2-三、解答题17．设,αβ分别是方程220x x a ++=()a R ∈的两个虚数根.（1）求a 的取值范围及αβ+的值；（2）若4αβ-=，求a 的值.18．已知ABC ∆的三个顶点(),A m n 、()2,1B 、()2,3C -.（1）求BC 边所在直线的方程； （2）BC 边上中线AD 的方程为2360x y -+=，且7ABC S ∆=，求点A 的坐标. 19．已知直线:l y x m =+，m R ∈.（1）若以点()2,0M 为圆心的圆与直线l 相切于点P ，且点P 在y 轴上，求该圆的方程；（2）若直线l 与抛物线2:4C x y =有且仅有一个公共点，求m 的取值范围. 20．已知椭圆222:1x C y m+=（常数1m >），点P 是C 上的动点，M 是右顶点，定点A 的坐标为(2,0)．⑴若M 与A 重合，求C 的焦点坐标；⑵若3m =，求PA 的最大值与最小值；⑶若PA 的最小值为MA ，求m 的取值范围．21．已知直线1:l y x =及直线2:l y x =-.平面上动点(),M x y ，且x y >，记M 到直线1l 、2l 的距离分别为1d 、2d ，满足：()21202a d d a ⋅=>. （1）求动点M 的轨迹Γ的方程；（2）若直线l 的方向向量为()1,2，过),0的直线l 与曲线Γ交于A 、B 两点，问以AB 为直径的圆是否恰过原点O ？若是，求a 的值；若不是，判断原点在圆内还是圆外，并说明理由？（3）若过原点O 作斜率为k 的直线n 交曲线Γ于M 、N 两点，设()0,1P ，求PMN 的面积S 关于k 的函数解析式，并求S 的取值范围.参考答案1【分析】利用复数模的求法：z =. 【详解】由复数1z =，则z ==【点睛】本题考查了复数模的求法，考查了基本运算求解能力，属于基础题.2．1-【分析】利用复数的四则运算法则将()2(1)++m i mi 化简为a bi +的形式，结合实数的定义即可求解.【详解】由题意可得，()223(1)(1)m i mi m m m i ++=-++，因为复数()2(1)++m i mi 是实数，所以310m +=，解得1m =-.故答案为：-1【点睛】本题主要考查复数的四则运算及复数的概念与分类，属于基础题.3．0【分析】利用复数的乘法法则和复数相等可得出关于a 、b 的方程组，解出a 、b 的值，进而可求得+a b 的值.【详解】()1b i a i i ai +=+=-+，所以11a b =⎧⎨=-⎩，因此，0a b +=. 故答案为：0.【点睛】本题考查利用复数的乘法法则和复数相等求参数，考查计算能力，属于基础题.4．【分析】根据两条平行线间的距离公式，可直接求出结果.【详解】直线110l x y -+=：与直线250l x y -+=：之间的距离==故答案为：【点睛】本题主要考查两平行线间的距离，熟记公式即可，属于常考题型.5．1i -+【分析】 消去z 后，根据复数的乘除法运算法则，计算可得答案.【详解】 因为2i z z -=，iz z =，所以2z iz i -=， 所以21i z i =-2(1)(1)(1)i i i i +=-+2212i i -+==-+. 故答案为：1i -+【点睛】本题考查了复数的乘法、除法运算法则，属于基础题.6【分析】根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等，进而利用点到直线的距离求得x 的值，代入抛物线方程求得y 值，即可得到所求点的坐标，从而求得其到原点的距离．【详解】 解：抛物线方程为24y x =， ∴焦点为(1,0)F ，准线为:1l x =-抛物线24y x =上一点P 到焦点的距离等于2， ∴根据抛物线定义可知P 到准线的距离等于2，即12x +=，解之得1x =，代入抛物线方程求得2y =±，∴点P 坐标为：(1,2)±=【点睛】本题主要考查了抛物线的简单性质．在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决，属于基础题．7．1,2⎛⎫-∞ ⎪⎝⎭【分析】根据题意，由圆的一般方程的形式分析可得1140m +-⨯>，解可得m 的取值范围，即可得答案．【详解】解：根据题意，方程220x y x y m -++=+表示一个圆，则有1140m +-⨯>，解的12m <，即m 的取值范围为1,2⎛⎫-∞ ⎪⎝⎭； 故答案为：1,2⎛⎫-∞ ⎪⎝⎭． 【点睛】本题考查二元二次方程表示圆的条件，涉及圆的一般方程，属于基础题．8．270x y --=【分析】根据直线的垂直关系，设出所求直线方程，将()3,2P -代入方程，即可求解.【详解】所求直线与直线210x y ++=垂直，设该直线方程为20x y c -+=，()3,2P -代入上式方程得7c =-，所以所求的直线方程为270x y --=.故答案为：270x y --=.【点睛】本题考查直线的位置关系求方程，利用直线的位置关系合理设方程是解题的关键，属于容易题.9．8【解析】【分析】直线y=k （过定点N （），确定椭圆的几何量，再利用椭圆的定义，即可求△ABM 的周长.【详解】直线y=k （过定点N （），由题设知M 、N 是椭圆的焦点，由椭圆定义知： AN+AM=2a=4，BM+BN=2a=4．△ABM 的周长为AB+BM+AM=（AN+BN ）+BM+AM=（AN+AM ）+（BN+BM ）=8， 故答案为：8．【点睛】本题考查椭圆的定义，直线过定点问题和利用椭圆的定义是解题的关键．10．(][),14,-∞-+∞【分析】画出图象求出定点与A 、B 两点连线的斜率，即可求出实数k 的取值范围．【详解】 解：直线2y kx =-恒过定点()0,2-，由题意平面内两点()1,2A ，()3,1B -，直线2y kx =-与线段AB 恒有公共点，如图求出定点与A 、B 两点连线的斜率，()122410k --==-．()212130k --==---， 所以直线2y kx =-与线段AB 恒有公共点，则实数k 的取值范围是(][),14,-∞-+∞， 故答案为：(][),14,-∞-+∞【点睛】本题考查直线斜率的求法，考查数形结合的思想的应用，考查计算能力．11．2.【分析】通过向量关系得到1F A AB =和1OA F A ⊥，得到1AOB AOF ∠=∠，结合双曲线的渐近线可得21,BOF AOF ∠=∠02160,BOF AOF BOA ∠=∠=∠=从而由0tan 60b a==离心率.【详解】如图，由1,F A AB =得1.F A AB =又12,OF OF =得OA 是三角形12F F B 的中位线，即22//,2.BF OA BF OA =由120F B F B =，得121,,F B F B OA F A ⊥⊥则1OB OF =有1AOB AOF ∠=∠，又OA 与OB 都是渐近线，得21,BOF AOF ∠=∠又21BOF AOB AOF π∠+∠+∠=，得02160,BOF AOF BOA ∠=∠=∠=．又渐近线OB 的斜率为0tan 60b a ==所以该双曲线的离心率为2c e a ====． 【点睛】 本题考查平面向量结合双曲线的渐进线和离心率，渗透了逻辑推理、直观想象和数学运算素养．采取几何法，利用数形结合思想解题．12．②④【分析】由题意曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >，利用直接法，设动点坐标为(,)x y ，及可得到动点的轨迹方程，然后由方程特点即可加以判断．【详解】解：对于①，由题意设动点坐标为(,)x y ，则利用题意及两点间的距离公式的得：22224[(1)][(1)]x y x y a ++-+=，将原点代入验证，此方程不过原点，所以①错；对于②，把方程中的x 被x -代换，y 被y - 代换，方程不变，故此曲线关于原点对称，故②正确；对于③，221y x =--，22211y x a ∴+=--，P ∴到原点的距离，当P 在y 轴时取等号，此时12PF PF a ==，122PF PF a +=故③对于④，由题意知点P 在曲线C 上，则△12F PF 的面积12122F PF Sy y =⨯⨯=，由①知221y x =--或221y x =--t ，则2424t a x -=，24442211(2)4444t a a a y t t -∴=--+=--+，1222212F PF S y a ∴=，故④正确．故答案为：②④． 【点睛】本题考查了利用直接法求出动点的轨迹方程，并化简，利用方程判断曲线的对称性及利用解析式选择换元法求出值域． 13．A 【分析】求出直线与坐标轴的交点，即可得出答案. 【详解】令0x =，则y b =；令0y =，则x a = 所以(0,),(,0)b a 在直线1x ya b+=上 因为直线1x ya b+=经过第一、第二和第四象限 所以0,0a b >> 故选：A 【点睛】本题主要考查了由直线所过象限求参数范围，属于基础题. 14．C 【分析】根据复数的四则运算，结合基本不等式，即可得出结论. 【详解】z a bi =-，()2m a bi a bi b ab =++-=，22()()n a bi a bi a b =+-=+，22p a b =+222a b ab +，当且仅当a b =时，取等号m n p ∴≤=故选：C本题主要考查了复数的四则运算，涉及了基本不等式的应用，属于中档题. 15．D 【分析】由3z 为实数，求出,a b 关系，实系数方程有虚数根，∆<0，且两根互为共轭，由韦达定理，求出,p q 与,a b 关系，结合,a b 关系，即可得出,p q 的关系式，得出结论. 【详解】()3220,0,(2)()z a bi a b z a b abi a bi =+>≠=-++，其虚部为22222()2(3)a b b a b b a b -+=-，又3z 为实数，所以2222(3)0,0,30b a b b b a -=≠=≠， 复数()0,0z a bi a b =+>≠是实系数方程20x px q ++=的根，()0,0z a bi a b =->≠也是实系数方程20x px q ++=的根，所以222240,2,40p q z z a p zz a b a q ∆=-<+==-=+==>， 所以2,0p q p =<，此时30q ∆=-<，即点(),p q 的轨迹在抛物线2y x 上.故选：D . 【点睛】本题考查实系数一元二次方程根的关系、复数的基本概念，韦达定理的应用是解题的关键，考查计算求解能力，属于中档题. 16．A 【分析】先确定向量a 、b 所表示的点的轨迹，一个为直线，一个为圆，再根据直线与圆的位置关系求最小值. 【详解】设()()(),,1,0,,a x y e b m n ===，则由π,3a e =得πcos ,3a e e x y a ⋅=⋅=∴=， 由2430b e b -⋅+=得()2222430,21,m n m m n +-+=-+=因此，a b -的最小值为圆心()2,0到直线y =1，为1.选A.【点睛】以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系，是解决这类问题的一般方法.17．（1）1a >，（2）5. 【分析】（1）由条件可得440a ∆=-<，得出a 的取值范围，根据求根公式可求得方程虚数根,αβ，代入αβ+，可得到答案.（2）由（1）可得αβ-==. 【详解】（1）由方程220x x a ++=()a R ∈有两个虚数根 所以440a ∆=-<，解得1a >由,αβ是方程220x x a ++=()a R ∈的两个虚数根.可得,αβ，不妨设1α==-,1β==-所以αβ+=（2）由（1）可得αβ-==根据4αβ-=，即4=，解得5a = 【点睛】本题考查实系数一元二次方程有虚数根的条件以及求根公式的应用，属于中档题.18．（1）240x y +-=；（2）点A 坐标为()3,4、()3,0- 【分析】（1）利用两点式求得BC 边所在直线方程；（2）利用点到直线的距离公式求得A 到直线BC 的距离，根据面积7ABC S ∆=以及点A 在直线2360x y -+=上列方程组，解方程组求得A 点的坐标. 【详解】（1）由()2,1B 、()2,3C -得BC 边所在直线方程为123122y x --=---，即240x y +-=. （2）BC ==A 到BC 边所在直线240x y +-=的距离为d =A 在直线2360x y -+=上，故1722360ABC S BC d m n ∆⎧=⋅⋅=⎪⎨⎪-+=⎩，即2472360m n m n ⎧+-=⎨-+=⎩，解得()3,4A 或()30A -,. 【点睛】本小题主要考查利用两点式求直线方程，考查点到直线的距离公式，考查三角形面积公式，属于基础题.19．（1）()2228x y -+=；（2）1m =-. 【分析】（1）利用待定系数法求本题中圆的方程是解决本题的关键，利用直线与圆相切的数学关系列出关于圆的半径的方程，通过求解方程确定出所求圆的半径，进而写出所求圆的方程； （2）联立直线与抛物线方程、消元，由0∆=计算可得； 【详解】解：（1）设所求圆的半径为r ，则圆的方程可设为222(2)x y r -+=．由题意，所求圆与直线:l y x m =+相切于点(0,)P m ，则有224m r r ⎧+==，解得2m r =⎧⎪⎨=⎪⎩，所以圆的方程为22(2)8x y -+=．（2）因为直线:l y x m =+与抛物线2:4C x y =有且仅有一个公共点，联立方程得24y x m x y=+⎧⎨=⎩消元得2440x x m --=，所以()()24440m ∆=--⨯-=解得1m =-【点睛】本题考查直线与圆的位置关系，直线与抛物线的位置关系，考查学生的方程思想和运算化简能力，属于基础题．20．（1）(（2）min ||2PA =max||5PA =（3）11m <≤+【解析】解：⑴2m =，椭圆方程为2214x y +=，c ==∴ 左、右焦点坐标为(．⑵3m =，椭圆方程为2219x y +=，设(,)P x y ，则222222891||(2)(2)1()(33)9942x PA x y x x x =-+=-+-=-+-≤≤∴94x =时min ||2PA =；3x =-时max ||5PA =． ⑶设动点(,)P x y ，则222222222222124||(2)(2)1()5()11x m m m PA x y x x m x m m m m m -=-+=-+-=--+-≤≤-- ∵ 当x m =时，PA 取最小值，且2210m m ->，∴2221mm m ≥-且1m >解得11m <≤21．(1) ()2220x y aa -=> (2) 以AB 为直径的圆不过原点O ，点O 在圆外(3)S a =, S 的取值范围是S a ≥ 【分析】（1）由条件有2221222x y a d d -⋅===，得出答案. （2）设()()1122,,,A x y B x y ，根据条件可设直线l的方程为：()2y x =，与曲线Γ的方程联立，得到12x x +=，2123x x a ⋅=，由1212OA OB x x y y ⋅=+的符号可得出答案.（3）由题意直线n 的方程为y kx =，与曲线Γ的方程联立，可得M （或N ）的点的横坐标，根据条件可得k的范围，122N S OP x a =⨯⨯⨯=，然后求出范围. 【详解】（1）由(),M x y 到直线1l 、2l 的距离分别为1d 、2d ，且2122a d d ⋅=则2221222x y a d d -⋅===，又x y > 所以22222222x y x y a --==，即222x y a -= 则动点M 的轨迹Γ的方程；()2220x y aa -=>（2）由直线l 的方向向量为()1,2，则直线l 的斜率为2k =. 又直线l过),0，则直线l的方程为：()2y x =设()()1122,,,A x y B x y，由()2222y x x y a⎧=⎪⎨-=⎪⎩得22390x a -+=则12x x +=，2123x x a ⋅=所以()()()212121212442y y x xx x x x a ⎡⎤⋅=⨯=⨯-++⎣⎦22244323a a a ⎛⎫=⨯+=- ⎪ ⎪⎝⎭2221212453033a a OA OB x x y y a ⋅=+=-=>所以以AB 为直径的圆不过原点O ，由0OA OB ⋅>，所以点O 在圆外. （3）直线n 的方程为y kx =由222y kx x y a=⎧⎨-=⎩得2222x k x a -=， 由直线n 交曲线Γ于M 、N 两点，则210k ->，则201k ≤<则2221a x k=-122N S OP x a =⨯⨯⨯=由201k ≤<，得2011k <-≤a a ≥所以PMN 的面积S 关于k 的函数解析式为S a =，PMN 的面积S 的取值范围是S a ≥.【点睛】本题考查求轨迹的方程，利用数量积研究点与圆的位置关系，求三角形的面积，属于中档题.。

（曹杨二中）2021年重点高中摸底考数学仿真模拟卷（上海专用）考试范围：入学摸底；考试时间：120分钟注意事项：1．本试卷满分150分，考试时间120分钟．2．答卷前，务必用钢笔或圆珠笔在正面清楚地填写姓名、准考证号码等相关信息．一、填空题(共58分)1．(本题4分)已知角0,x213x π⎛⎫-= ⎪⎝⎭，则角x 为________．【答案】4π或34π【分析】根据正切函数值求解． 【详解】213x π⎛⎫-= ⎪⎝⎭，tan 233x π⎛⎫-= ⎪⎝⎭，236x k πππ-=+，42k x ππ=+，k Z ∈，又因为0,x，所以4x π=，34π． 故答案为：4π或34π．2．(本题4分)ABC 的内角,,A B C 的对边分别为,,a b c ．若sin 2A =，2226b c a +=+，则ABC 的面积为______．【答案】2【分析】 先求出1cos 2A =±，再根据2226b c a +=+求出6bc =，即得解. 【详解】因为sin 2A =，所以1cos 2A =±.原创精品资源学科网独家享有版权，侵权必究！2由题得22212cos 6,cos 0,2662b c a bc A A bc bc -+==∴>⨯=∴=，. 所以ABC 的面积为113633222⨯=. 33【点睛】本题主要考查余弦定理解三角形和三角形面积的计算，意在考查学生对这些知识的理解掌握水平，属于基础题.3．(本题5分)已知向量()23,6a k =-，()2,1b =，且a b ⊥，则实数k =______． 【答案】0 【分析】利用向量垂直的性质直接求解． 【详解】 解：向量()23,6a k =-，()2,1b =，且a b ⊥，∴()223160a b k =⨯-+⨯=，解得0k =． 故答案为：0． 【点睛】本题考查实数值的求法，是基础题，解题时要认真审题，注意向量垂直的性质的合理运用．4．(本题5分)已知公差d 不为0的等差数列{}n a 的前n 项和为,n S 且32231,,S S a a 成等差数列，则10S =_____. 【答案】55d 【分析】由等差中项的性质有322321S S a a =+，可得1a d =，进而根据等差数列前n 项和公式写出10S .【详解】 由题意知：322321S S a a =+，即123122322()a a a a a a a +++=，结合等差数列通项公式， 整理得：21a d d =，又0d ≠，有1a d =，∴1101010()552a a S d +==，故答案为：55d5．(本题5分)设S n 为数列{a n }的前n 项和，若S n ＝na n ﹣3n （n ﹣1）（n ∈N *），且a 2＝11，则S 20的值为_____． 【答案】1240 【分析】先求得a 1＝5，转化条件得131n n S S n n --=-，可得n S n ⎧⎫⎨⎬⎩⎭是首项151S =，公差为3的等差数列，利用等差数列的通项公式即可得解. 【详解】由S 2＝a 1+a 2＝2a 2﹣3×2（2﹣1），a 2＝11，可得a 1＝5．当n ≥2时，由S n ＝na n ﹣3n （n ﹣1）＝n （S n ﹣S n ﹣1）﹣3n （n ﹣1）， 可得（n ﹣1）S n ﹣nS n ﹣1＝3n （n ﹣1）， ∴131n n S S n n --=-，∴数列n S n ⎧⎫⎨⎬⎩⎭是首项151S =，公差为3的等差数列， ∴2020S =5+3×19＝62， ∴S 20＝1240. 故答案为：1240. 【点睛】本题考查了数列11,1,2n nn S n a S S n -=⎧=⎨-≥⎩公式的应用和等差数列通项公式的应用，属于中档题.6．(本题5分)22sin sin 36x x ππ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭________．【答案】1 【分析】原创精品资源学科网独家享有版权，侵权必究！4观察已知的角有“362x x πππ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭”的关系，根据诱导公式转化，再利用同角三角函数关系：22sin cos 1αα+=得解. 【详解】222222sin sin sin sin sin cos 13632333x x x x x x πππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-++=-+--=-+-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦．故：填1 ． 【点睛】本题关键在于能不能发现“362x x πππ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭”，再利用诱导公式进行转换求值，属于基础题.7．(本题5分)若等比数列{a n }中，a 1=1，a n =－512，前n 项和为S n =－341，则n 的值是________. 【答案】10 【解析】很明显数列的公比1q ≠，则：S n =11n a a q q--，∴－341=15121qq +-，∴q =－2，又∴a n =a 1q n －1，∴－512=(－2)n －1，∴n =10.8．(本题5分)已知P 是边长为2的正六边形ABCDEF 内的一点，则AP AB ⋅的取值范围是__________. 【答案】()2,6- 【分析】画出图形，结合图形，利用平面向量的数量积的几何意义判断求解即可． 【详解】 画出图形如图，||||cos ,AP AB AP AB AP AB =<>，它的几何意义是AB 的长度与AP 在AB 向量的投影的乘积，由图可知，P 在C 处时，取得最大值，1||cos ||||32AC CAB AB AB ∠=+=，此时，可得||||cos ,236AP AB AP AB AP AB =<>=⨯=，即最大值为6，在F 处取得最小值，此时1·cos ,2222AP AB AP AB AP AB ⎛⎫==⨯⨯-=- ⎪⎝⎭， 最小值为2-，因为P 是边长为2的正六边形ABCDEF 内的一点，取不到临界值， 所以·AP AB 的取值范围是()2,6-． 故答案为：()2,6-．【点睛】本题考查向量的数量积的几何意义及其应用，考查了向量在几何中的应用，同时考查了数形结合思想的应用，是中档题．9．(本题5分)()sin()(0,0)f x x ωϕωϕπ=+>≤≤是R 上的偶函数，其图像关于点2,03M π⎛⎫ ⎪⎝⎭对称，且在0,2π⎡⎤⎢⎥⎣⎦上是单调函数，则ω的值为______【答案】34【分析】由()sin()f x x ωϕ=+是R 上的偶函数，可得2ϕπ=，即()cos f x x ω=，由函数图像关于点2,03M π⎛⎫ ⎪⎝⎭对称，可得3324k ω=+，k Z ∈，再结合函数的单调性可得02ω<≤，综合条件即可得解. 【详解】解：由()sin()f x x ωφ=+是R 上的偶函数，则,2k k Z πϕπ=+∈，又0φπ≤≤，则2ϕπ=，即()cos f x x ω=， 令2x k πωπ=+，则23x π=为此方程的解，则3324k ω=+，k Z ∈，原创精品资源学科网独家享有版权，侵权必究！6由()cos f x x ω=在0,2π⎡⎤⎢⎥⎣⎦上是单调函数，则2πωπ⨯≤，即02ω<≤，则34ω=， 故答案为34. 【点睛】本题考查了三角函数的奇偶性、对称性及单调性，重点考查了三角函数性质的应用，属中档题.10．(本题5分)在数列{}n a 中，14a =，132n n a a +=-，若对于任意的*n ∈N ，()125n k a n -≥-恒成立，则实数k 的最小值为__________．【答案】127【分析】利用待定系数法得出13nn a -=，然后由参变量分离法得出253nn k -≥，并利用单调性的定义分析数列253nn -⎧⎫⎨⎬⎩⎭，求出该数列的最大项的值，从而可得出实数k 的取值范围. 【详解】由132n n a a +=-有()1131n n a a +-=-，故数列{}1n a -为首项为3，公比为3的等比数列，可得13nn a -=.不等式()125n k a n -≥-可化为253nn k -≥， 令()()*253nn f n n -=∈N ，当12n ≤≤时()0f n <；当3n ≥时，()0f n >. 故当3n ≥时，()()()1143232510333n n n n n n f n f n ++---+-=-=≤，故()()1327f n f ≤=， 127k ∴≤，因此，实数k 的最小值是127. 故答案为127. 【点睛】本题考查利用待定系数法求数列通项，同时也考查了数列不等式的解法，在解题时一般利用参变量分离法转化为数列的最值来求解，考查分析问题和解决问题的能力，属于中等题.11．(本题5分)设{}n a 为等差数列，n S 为数列{}n a 前n 项和，若10a >，且1520S S =，则当n =____时，n S 取得最大值； 【答案】17或18 【分析】根据等差数列1520S S =,可求得180a =,结合10a >可判断出等差数列为递减数列,进而可得n S 取得最大值时n 的值. 【详解】因为{}n a 为等差数列,且1520S S = 所以16171819200a a a a a ++++=根据等差中项的性质可得180a =因为10a >所以等差数列{}n a 为递减数列,180a =,从第19项开始为负数所以当17n =或18n =时, n S 取得最大值 故答案为:17或18 【点睛】本题考查了等差数列前n 项和的性质,等差数列单调性的综合应用,等差中项的简单应用,属于中档题.12．(本题5分)若等差数列{}n a 满足()248912224a a a a =--，则19S 的最大值为__________．【答案】【分析】设数列{}n a 的公差为d ，由等差数列通项公式及性质化简，结合所给条件等式可化简得22488a a +=，根据等差数列前n 项和公式，可表示出4a ，代入等式即可得方程22819819212410801919a S a S -+-=，由方程由解可知0∆≥，即可求得19S 的最大值.原创精品资源学科网独家享有版权，侵权必究！8 【详解】数列{}n a 是等差数列，设公差为d ，因为9126121262a a a a a a -=+-=，所以248624a a a =-，因为6482a a a =+，所以()24861242a a a =-， 所以()2484828a a a a =+-，所以22488a a +=．因为()()11919819192422a a S a d +==+，所以19824219d S a =-，所以22819823819a S a ⎛⎫-+= ⎪⎝⎭，所以22819819212410801919a S a S -+-=，因为方程有解，所以22191922144440801919S S ⎛⎫∆=--≥ ⎪⎝⎭， 所以22191920S ≤⨯，则19S 的最大值为5故答案为：5 【点睛】本题考查等差数列通项公式及前n 项和公式的综合应用，等差数列性质及一元二次方程有解的应用，化简过程较为繁琐，属于难题.二、单选题(共20分)13．(本题5分)将函数()2sin(2)6f x x π=+的图象向左平移12π个单位，得到函数()g x 的图象，所得函数()g x 的一条对称轴为（ ）A ．12x π=B ．6x π=C ．512x π=D ．56x π=【答案】A 【分析】利用图象平移变换法则将()f x 的解析式中x 换成+12x π，得到()g x 的图象，利用正弦函数对称性由232x k πππ+=+，k Z ∈求得所有对称轴方程，再比较作出判定.【详解】将函数()2sin(2)6f x x π=+的图象向左平移12π个单位，得到函数()g x 的图象，则()2sin[2()]2sin(2)1263g x x x πππ=++=+， 由232x k πππ+=+，得26x k ππ=+，即212k x ππ=+，k Z ∈， 则当0k =时，对称轴为12x π=，故选A. 【点睛】本题考查结合三角函数的图像变换求三角函数的性质，先做变换，注意“左加右减”，再将变换后的函数解析式中的x ωϕ+当成一个整体X ,根据sin X 的对称轴求出所有对称轴，再作出判定.14．(本题5分)若2(23n a n tn t =++为常数）*n N ∈，且数列{}n a 为单调递增数列，则实数t 的取值范围为（ ） A ．2t <- B ．2t >- C ．6t <- D ．6t >-【答案】D 【分析】先判断1n n a a +>在*n N ∈时恒成立，代入化简得42t n >--在在*n N ∈时恒成立，再计算()max 42n --，即得结果. 【详解】因为数列{}n a 为单调递增数列，所以1n n a a +>，在*n N ∈时恒成立.所以()()()221211323420n n n a a a n t n n tn n t +⎡⎤-==++++-++=++>⎣⎦， 即42t n >--在在*n N ∈时恒成立，而1n =时，()max 426n --=-， 所以6t >-. 故选：D.15．(本题5分)如果，是平面E 内两个不共线的向量，那么下列说法中不正确的是 ∈可以表示平面E 内的所有向量；原创精品资源学科网独家享有版权，侵权必究！10∈对于平面E 内任一向量2，使的实数对有无穷多个； ∈若向量与共线，则有且只有一个实数，使得；∈若存在实数使得，则.A ．∈∈B ．∈∈C ．∈∈D ．∈【答案】B 【详解】由平面向量基本定理可知，∴∴是正确的．对于∴，由平面向量基本定理可知，一旦一个平面的基底确定，那么任意一个向量在此基底下的实数对是唯一的． 对于∴，当两向量的系数均为零，即时，这样的有无数个，故选B.考点：平面向量基本定理.16．(本题5分)设a 、b R ∈，[)0,2c π∈，若对于任意实数x 都有()2sin 3sin 3x a bx c π⎛⎫-=+ ⎪⎝⎭，则满足条件的有序实数组(),,a b c 的组数为（ ）A ．2组B ．4组C ．5组D ．6组【答案】B 【分析】由题意得出3b =，2=a ，然后对a 、b 的取值进行分类讨论，结合题中等式求出c 的值，即可得出正确选项. 【详解】由题意知，函数2sin 33y x π⎛⎫=- ⎪⎝⎭与函数()sin y a bx c =+的最大值相等，最小值也相等，则2=a . 函数2sin 33y x π⎛⎫=-⎪⎝⎭与函数()sin y a bx c =+的最小正周期相等，则3b =.当2a =，3b =时，由于()2sin 32sin 33x x c π⎛⎫-=+ ⎪⎝⎭，则()23c k k Z ππ=-+∈，由于02c π≤<，此时，53c π=； 当2a =，3b =-时，()()2sin 32sin 32sin 33x x c x c ππ⎛⎫-=-+=-+ ⎪⎝⎭，则()23c k k Z πππ-=-∈，得()423c k k Z ππ=-∈，02c π≤<，此时，43c π=； 当2a =-，3b =时，()()2sin 32sin 32sin 33x x c x c ππ⎛⎫-=-+=++ ⎪⎝⎭， 则()23c k k Z πππ+=-∈，得()()213c k k Z ππ=--∈，02c π≤<，则23c π=； 当2a =-，3b =-时，()()2sin 32sin 32sin 33x x c x c π⎛⎫-=--+=- ⎪⎝⎭， 则()23c k k Z ππ-=-∈，得()23c k k Z ππ=-∈，02c π≤<，则3c π=.因此，满足条件的有序实数组(),,a b c 的组数为4组. 故选B. 【点睛】本题考查利用三角函数解析式相等，求参数的值，解题时要从三角函数的基本性质和诱导公式进行计算，考查运算求解能力，属于中等题.三、解答题(共72分)17．(本题16分)我们知道如果点(),P x y 是角α终边OP 上任意一点（0OP r =>），则根据三角比的定义：sin y r α=，cos xrα=，因此点P 的坐标也可以表示为()cos ,sin P r r αα．（1）将OP 绕坐标原点O 逆时针旋转3π至'OP ，求点P'的坐标()','x y ．（即分别把'x 、'y 用x 、y 表示出来）（2）将OP 绕坐标原点O 逆时针旋转ϕ角度至'OP ，求点P'的坐标()','x y ．（即分原创精品资源学科网独家享有版权，侵权必究！12 别把'x 、'y 用x 、y 、ϕ表示出来） （3）把函数()10y x x =>的图像绕坐标原点逆时针旋转4π后，可以得到函数___________的图像．（写出解析式和定义域） 【答案】（1）13'2x x y =-；31'2y x y =+；（2）co in 's s x x y ϕϕ=-；'cos sin y y x ϕϕ=+；（3）)21y x x R =+∈．【分析】（1）利用相应角的三角函数表示点P '的坐标，利用两角和的余弦公式和正弦公式展开代入即得； （2）同（1）；（3）根据（2）的结论，取4πϕ=，得到旋转前后的曲线上的对应点的坐标之间关系，进而求得. 【详解】'OP OP r ==，（1）'cos 3x r πα⎛⎫=+⎪⎝⎭1313cos sin '2222r r x x y αα=-⇒=-； 同理，31'sin 32y r x y πα⎛⎫=+=+ ⎪⎝⎭； （2）'cos()cos cos sin sin x r r r αϕαϕαϕ=+=-， 故co in 's s x x y ϕϕ=-；同理，'sin()cos sin y r y x αϕϕϕ=+=+； （3）在（2）中令4πϕ=得'cossin44x x y ππ=-，可得1')22x x y x x ⎫=-=-⎪⎭，同理，1'y x x ⎫=+⎪⎭，因此，22''1y x -=，所以，函数为)y x R =∈．18．(本题18分)已知ABC ∆的周长为10，且sin sin 4sin B C A +=． （1）求边长的值；（2）若16bc =，求角A 的余弦值． 【答案】(1)2a = (2)7cos 8A = 【解析】试题分析：（∴）由正弦定理将条件转化为边的关系，结合周长即可求出； （∴）将条件16bc =代入余弦定理，即可求出A 的余弦值. 试题解析：（∴）根据正弦定理，sin sin 4sin B C A +=可化为4b c a +=联立方程组10,4a b c b c a ++=⎧⎨+=⎩解得 2.a = 所以，边长 2.a =（∴）由16,bc =又由（∴）得8,b c +=得4,b c ==222cos 2b c a A bc+-∴= =2224427.2448+-=⨯⨯点睛：解决三角形中的角边问题时，要根据条件选择正余弦定理，将问题转化统一为边的问题或角的问题，利用三角中两角和差等公式处理，特别注意内角和定理的运用，涉及三角形面积最值问题时，注意均值不等式的利用，特别求角的时候，要注意分析角的范围，才能写出角的大小.19．(本题18分)某同学用“五点法”画函数()()sin (00)2f x A x k A πωφωφ=++>><，，在一个周期内的图象，列表并填入数据得到下表：原创精品资源学科网独家享有版权，侵权必究！14 x ωφ+2π π32π 2π()f x1y 32y1-3y（1）求函数()f x 的解析式；（2）三角形ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若()2f B =，4b =，22cos cos 622C Aa c +=，求三角形ABC 的面积. 【答案】（1）()2sin 216f x x π⎛⎫=++ ⎪⎝⎭；（2）43 【分析】（1）由三角函数的图象与性质逐步计算出A 、k 、ω、φ，即可得解； （2）先计算出3B π=，利用降幂公式结合余弦定理可转化条件得12a b c ++=，再由余弦定理可得16ac =，结合三角形面积公式即可得解. 【详解】（1）由题意可得31A k A k +=⎧⎨-+=-⎩，解得21A k =⎧⎨=⎩，函数()f x 的最小正周期T 满足22362T πππ=-=，所以22T πω==，又2sin 1363f ππφ⎛⎫⎛⎫=++= ⎪ ⎪⎝⎭⎝⎭，所以sin 13πφ⎛⎫+= ⎪⎝⎭， 所以2,32k k Z ππφπ+=+∈，即2,6k k Z πφπ=+∈，由2πφ<可得6πφ=，所以()2sin 216f x x π⎛⎫=++ ⎪⎝⎭； （2）由题意，()2sin 2126f B B π⎛⎫=++= ⎪⎝⎭，所以1sin 262B π⎛⎫+= ⎪⎝⎭，由()0,B π∈可得132,666B πππ⎛⎫+∈ ⎪⎝⎭，所以5266B ππ+=，即3B π=， 又221cos 1cos coscos 62222C A C Aa c a c +++=⋅+⋅=， 所以cos cos 12a c a C c A +++=，即2222221222a b c b c a a c a c ab bc+-+-++⋅+⋅=，化简得12a b c ++=， 又4b =，所以8a c +=，由余弦定理得()22222cos 3b a c ac B a c ac =+-=+-，即22483ac =-， 所以16ac =，所以11sin 1622ABC S ac B ==⨯=△ 【点睛】关键点点睛：解决本题的关键是熟练掌握三角函数的图象与性质及三角恒等变换、余弦定理的应用，细心运算即可得解.20．(本题20分)已知数列{}n a 满足11a =，1nn n a a p +-=，n *∈N .（1）若1p =，写出4a 所有可能的值；（2）若数列{}n a 是递增数列，且1a 、23a 、35a 成等差数列，求p 的值； （3）若12p =，且{}21n a -是递增数列，{}2n a 是递减数列，求数列{}n a 的通项公式. 【答案】（1）2-、0、2、4；（2）15；（3）1411332n n a -⎛⎫=-⨯- ⎪⎝⎭.【分析】（1）由11a =，11nn n a a p +-==，n *∈N ，分别取1n =、2、3即可得出4a 的所有可能取值；（2）由数列{}n a 是递增数列，得出1nn n a a p +-=，且有0p >，得出2a 、3a 关于p 的表达式，然后利用1a 、23a 、35a 成等差数列得出关于p 的方程，解出即可； （3）由数列{}21n a -是递增数列得出21210n n a a +-->，可得()()2122210n n n n a a a a +--+->，但2211122n n -<，可得出212221n n n n a a a a +--<-，可得出()221221211122nn n n n a a ----⎛⎫-==⎪⎝⎭，由数列{}2n a 为递减数列，同理可得原创精品资源学科网独家享有版权，侵权必究！16 2120n n a a +-<，进而得到()1112n n nna a ++--=，再利用累加法可求出数列{}n a 的通项公式. 【详解】（1）当1p =时，11n n a a +-=，则11n n a a +-=±，11a =，20a ∴=或2.当31a =时，40a =或2；当31a =-时，40a =或2-；当33a =时，42a =或4. 因此，4a 的所有可能取值有2-、0、2、4； （2）数列{}n a 是递增数列，则10n n a a +->，则1nn n a a p +-=，21a a p ∴-=，211a a p p ∴=+=+，同理得22321a a p p p =+=++，由于1a 、23a 、35a 成等差数列，则21365a a a =+，即()()261151p p p +=+++，整理得250p p -=，0p >，解得15p =； （3）数列{}21n a -是递增数列，所以21210n n a a +-->，即()()2122210n n n n a a a a +--+->∴， 但2211122n n -<，所以212221n n n n a a a a +--<-∴， 由∴∴知，2210n n a a -->，所以()221221211122nn n n n a a ----⎛⎫-==⎪⎝⎭∴.数列{}2n a 是递减数列，同理可得2120n n a a +-<， 所以()21221221122n nn n na a ++-⎛⎫-=-=⎪⎝⎭∴，由∴∴知，()111122n nn n na a ++-⎛⎫-==-- ⎪⎝⎭.由累加法得()()()121321nn n a a a a a a a a -=+-+-++-12111112211111111112223212n n n ---⎡⎤⎛⎫-⨯--⎢⎥ ⎪⎡⎤⎝⎭⎢⎥⎛⎫⎛⎫⎛⎫⎛⎫⎣⎦=-------=-=+--⎢⎥⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦+1411332n -⎛⎫=-⨯- ⎪⎝⎭.【点睛】本题考查等比数列的通项公式与求和公式、数列的递推关系、绝对值的性质、不等式的性质，同时也考查了利用累加法求数列通项，考查推理能力与运算求解能力，属于难题.。

上海市曹杨二中2020-2021学年高三上学期第一次月考数学试题学校:___________姓名：___________班级：___________考号：___________一、填空题1．已知集合{}2|230A x x x =--≤，{||2|2}B x x =-<，则AB =________； 2．已知1sin 23πα⎛⎫+= ⎪⎝⎭，则()cos πα-=___________. 3．若()()12n x n N *+∈展开式中各项系数和为243，则n =___________. 4．满足方程2lg lg 1121x x -=的实数解x =____________.5．若x ∈R ，则不等式()10x x +>的解集是_______________.6．函数y =1−2x 1+2x的值域为 7．若线性方程组()3305(3)30a x y x a y ⎧++-=⎨-+-+=⎩有解，则实数a 的取值范围是_____________. 8．若函数()221f x ax x =-+在[]0,1x ∈上存在唯一零点，则实数a 的取值范围是_______.9．过球面上A ，B ，C 三点的截面和球心的距离等于球半径的一半，且3AB BC CA ===，则球的体积为________．10．从{}1,2,3,4,5中随机选取一个数a ，从{}1,2,3中随机选取一个数b ，则关于x 的方程2220x ax b ++=有两个虚根的概率是______________.11．已知121122sin 2sin 2αα+=++，其中1α，2R α∈，则1210παα--的最小值为_____.12．已知数列{}n a 的通项公式为52n n a -=，数列{}n b 的通项公式为n b n k =+ ， 设,(),()n n n n n n n b a b c a a b ≤⎧=⎨>⎩，若在数列{}n c 中，5n c c ≤对任意*n N ∈恒成立，则实数k 的取值范围是_____;二、单选题13．已知a b 、为实数，则22a b >是22log log a b >的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件14．数列{}n a 的通项22cos sin 33n n n a n ππ⎛⎫=- ⎪⎝⎭，其前n 项和为n S ，则10S 为（ ） A ．0B ．1-C ．12D ．12- 15．已知集合(){},log log 0a a A x y x y =+>，(){},B x y x y a =+<，若A B =∅，则a 的取值范围是（ ）A ．∅B ．0a >且1a ≠C ．02a <≤且1a ≠D ．12a <≤16．已知函数()()1x f x x R x=∈+时，则下列结论：①()f x 是R 上的偶函数；②()f x 是R 上的增函数；③不等式()1f x <在R 上恒成立；④函数()()g x f x x =-在R 上有三个零点.其中错误的个数是（ ）A ．1B ．2C ．3D ．4三、解答题17．在ABC ∆中，,,a b c 分别为内角,,A B C 所对的边，且满足)2cos cos cos b A c A a C =+.（1）求A 的大小；（2）若2,23a c ==，且b c >，求ABC ∆的面积.18．如图，在四棱锥P ABCD -中，底面为直角梯形，//,90AD BC BAD ∠=，PA 垂直于底面ABCD ,22PA AD AB BC ====,,M N 分别为,PC PB 的中点.（1）求证：,,,M N A D 四点共面，并证明PB MD ⊥;（2）求直线PC 与平面MNAD 所成角的大小.（用反三角函数值表示）19．已知直线1y kx =+与双曲线2231x y -=相交于,A B 两点，O 为坐标原点. （1）若0OA OB ⋅=，求实数k 的值；（2）是否存在实数k ，使得,A B 两点关于12y x =对称?若存在，求k 的值；若不存在，说明理由.20．已知点列()()()()11221,,1,,....,,...n n B y B y B n y n N *∈为函数()1xy a a =>图像上的点，点列()()()()1122,0,,0,...,,0,...n n A x A x A x n N *∈顺次为x 轴上的点，其中1(01)x m m =<<，对任意n *∈N ，点1n n n A B A +、、构成以n B 为顶点的等腰三角形. （1）证明：数列{}n y 是等比数列；（2）若数列{}n y 中任意连续三项能构成三角形的三边，求a 的取值范围；（3）求证：对任意n *∈N ，2n n x x +-是常数，并求数列{}n x 的通项公式.21．设定义在R 上的函数()f x 满足：对任意的12x x R ∈、，当12x x <时，都有()()12f x f x ≤.（1）若()31f x ax =+，求实数a 的取值范围； （2）若()f x 为周期函数，证明：()f x 是常值函数；（3）若()()()()100,11,52x f f x f x f f x ⎛⎫=+-== ⎪⎝⎭ ①记()15n n a f n N *⎛⎫=∈ ⎪⎝⎭，求数列{}n a 的通项公式；②求12017f⎛⎫⎪⎝⎭的值.参考答案1．(0,3]【解析】【分析】分别利用二次不等式与绝对值不等式的求解方法解出,A B 再计算A B 即可.【详解】 {}{}{}2|230|(3)(1)0|13A x x x x x x x x =--≤=-+≤=-≤≤{||2|2}{|222}{|04}B x x x x x x =-<=-<-<=<<,所以130304x x x -≤≤⎧⇒<≤⎨<<⎩,故(0,3]A B =； 故答案为：(0,3]【点睛】本题主要考查了二次不等式与绝对值不等式的求解方法与交集的运算,属于基础题型. 2．13-【分析】由条件利用诱导公式求得cos α的值，可得要求式子的值．【详解】 解：已知1sin()cos 23παα+==，则1cos()cos 3παα-=-=-， 故答案为：13-．【点睛】本题主要考查利用诱导公式进行化简求值，属于基础题．3．5【分析】在(12)n x +展开式中，令1x =求得各项系数和，从而求得n 的值． 【详解】解：在*(12)()n x n N +∈展开式中，令1x =，得各项系数和为3243n =，解得5n =．故答案为：5．【点睛】本题考查了利用赋值法求二项式展开式系数和的问题，属于基础题．4．10【分析】先根据二阶行列式的运算法则进行化简，然后解对数方程即可求出所求．【详解】 解：2lg lg 1121x x -=22(1)1lg x lgx ∴--=即2210lg x lgx -+=1lgx ∴=解得：10x =故答案为：10【点睛】本题主要考查了二阶行列式的运算法则，以及对数方程，属于基础题．5．()()1,00,-+∞【分析】通过讨论x 的范围，得到关于x 的不等式组，解出即可．【详解】解：||(1)0x x +>， ∴010x x >⎧⎨+>⎩或010x x <⎧⎨+>⎩， 解得：0x >或10x -<<，故不等式的解集是()()1,00,x ∈-+∞， 故答案为：()()1,00,-+∞．【点睛】本题考查了解绝对值不等式问题，考查分类讨论思想，属于基础题．6．(−1,1)【分析】分离常数，结合指数函数的值域可得结果.【详解】y =1−2x 1+2x =−(1+2x )+22x +1−1+22x +1因为2x +1>1∴0<22x +1<2 ∴y =1−2x1+2x y ∈(−1,1) 故答案为:(−1,1).【点睛】本题主要考查函数的值域以及指数函数的性质，意在考查运用所学知识解答问题的能力，属于中档题.7．()(),22,-∞--+∞ 【分析】令两直线平行得出a 的值，从而得出两直线不平行的条件，得出a 的范围．【详解】解：若方程组(3)305(3)30a x y x a y ++-=⎧⎨-+-+=⎩无解， 则直线(3)30a x y ++-=与直线5(3)30x a y -+-+=平行，30a ∴+≠且30a -≠， 故而3153a a +=--，解得2a =±． 当2a =-时，直线30x y +-=与直线5530x y --+=平行，当2a =时，直线530x y +-=与直线530x y --+=重合，方程组有无数解；∴当2a ≠-时，直线(3)30a x y ++-=与直线5(3)30x a y -+-+=相交或重合，即方程组(3)305(3)30a x y x a y ++-=⎧⎨-+-+=⎩有解， 即()(),22,a ∈-∞--+∞故答案为：()(),22,-∞--+∞． 【点睛】本题考查了直线与直线的位置关系，属于中档题．8．[]0,1【分析】由题意知，函数()f x 在区间[]0,1x ∈内有一个零点，利用对称轴与区间的关系，得出不等式组，解出即可．【详解】解：当0a =时，函数的零点为12，满足题意； 当0a ≠时，0x =时，(0)10=>f ，当函数的对称轴不在区间内时，函数2()21f x ax x =-+在[0x ∈，1]上存在唯一零点，()110f a =-<，可得1a <，且0a ≠， 函数2()21f x ax x =-+它的对称轴为1x a=， 函数的对称轴在区间[0，1]内，可得：1011()0a f a⎧⎪⎪⎨⎪=⎪⎩即： 11210a a a⎧⎪⎨-+=⎪⎩， 解得1a =．函数2()21f x ax x =-+在[0x ∈，1]上存在唯一零点，则实数a 的取值范围是：(-∞，1]．故答案为：(-∞，1]．【点睛】此题主要考查函数的零点以及二次函数的性质问题，容易得出答案，属于中档题． 9．323π 【分析】根据正弦定理求出ABC △外接圆的半径，根据题意结合勾股定理计算出球的半径R ，即可求出球的体积.【详解】ABC △的外接圆半径为r则由正弦定理得：32sin 60r =︒, r = 设球的半径为R,截面和球心的距离等于球半径的一半, 则：22212R R r ⎛⎫=+ ⎪⎝⎭，解得2R = 所以球的体积为343233R V ππ==,故答案为323π. 【点睛】本题主要考查了球的体积公式，确定ABC △的外接圆半径时，采用正弦定理是解题的关键. 10．15【分析】关于x 的方程2220x ax b ++=有两个虚根，即∆<0，即a b <．所有的(,)a b 共有53⨯个，而用列举法求得满足a b < 的(,)a b 共有3个，从而求得关于x 的方程2220x ax b ++=有两个虚根的概率．【详解】 解：关于x 的方程2220x ax b ++=有两个虚根，∴22440a b ∆=-<，a b ∴<． 所有的(,)a b 共有5315⨯=个，而满足a b < 的(,)a b 共有(1,2)、(1,3)、(2,3)，共计3个，故关于x 的方程2220x ax b ++=有两个虚根的概率是31155=，故答案为：15． 【点睛】 本题考主要查古典概型问题，可以列举出试验发生包含的事件和满足条件的事件，列举法，是解决古典概型问题的一种重要的解题方法，属于中档题．11．4π 【分析】根据正弦函数的范围可得12sin sin 21αα==-，从而得出1α，2α的值，从而可得出结论．【详解】解：11sin 1α-， ∴111132sin α+，同理：211132sin 2α+， 又121122sin 2sin 2αα+=++， ∴121112sin 2sin 2αα==++， 12sin sin 21αα∴==-，1122k παπ∴=-+，224k παπ=-+，1k ，2k Z ∈．()12121233|10||102||102|44k k k k πππααπππππ∴-+--=--=--， ∴当1229k k +=时，12|10|παα∴--取得最小值4π． 故答案为：4π． 【点睛】 本题考查了正弦函数的性质，考查了正弦型函数的有界性，属于中档题．12．[]5,3--.【解析】试题分析：数列n c 是取n a 和n b 中的最大值，据题意5c 是数列{}n c 的最小项，由于函数52n y -=是减函数，函数y n k =+是增函数，所以556b a b ≤≤或554a b a ≤≤，即55526k k -+≤≤+或5554252k --≤+≤，解得54k -≤≤-或43k -≤≤-，所以53k -≤≤-．考点：分段函数与数列的通项公式，数列的最小项问题． 13．B 【分析】分别解出22a b >，22log log a b >中a ，b 的关系，然后根据a ，b 的范围，确定充分条件，还是必要条件． 【详解】 解：22a b >，a b ∴>当0a <或0b <时，不能得到22log log a b >，反之由22log log a b >即：0a b >>可得22a b >成立． 故22a b >是22log log a b >的必要不充分条件 故选：B ． 【点睛】本题考查对数函数的单调性与特殊点，必要条件、充分条件与充要条件的判断，是基础题． 14．D 【分析】由数列{}n a 的通项22cos sin 33n n n a n ππ⎛⎫=- ⎪⎝⎭，利用二倍角公式化简，分别求解数列的各项，从而可得答案． 【详解】 解：数列{}n a 的通项222cos sin cos 333n n n n a n n πππ⎛⎫=-= ⎪⎝⎭， 1211cos32a π∴==-； 242cos13a π==-； 33cos23a π==；12332a a a ∴++=；同理可得，42a =-， 51055cos32a π==- 66cos46a π==；∴45632a a a ++= 71477cos 32a π==- 8168cos43a π==- 99cos69a π==；78932a a a ∴++=102010cos53a π==-． 10313522S ∴=⨯-=-故选：D ． 【点睛】本题考查数列的求和，求得数列的各个项的值，然后求和考查运算与推理能力，属于中档题． 15．D 【分析】利用对数的运算性质化简集合A ，然后画出图形，数形结合求得使A B =∅的a 的取值范围 【详解】log log log 0log 1a a a a x y xy +=>=，当1a >时，有1xy，1y x∴>当01a <<时，有01xy <<，1y x∴< (1)当01a <<时，1y x=与y x a +<的区域始终由公共点，01a ∴<<应舍去(2)当1a >时，要使AB =∅，需有x y a +=刚切过(1,1)时，即2a =时成立，将此直线向左下平移也成立，12a ∴<≤，故选：D 【点睛】本题考查简单的线性规划，交集及其运算，体现了数形结合的数学思想方法，数学转化思想方法，属于中档题 16．B 【分析】由函数奇偶性的定义判断①；利用导数研究单调性判断②；求出|()|f x 的范围判断③；由函数零点的判定判断④． 【详解】解：函数()f x 的定义域是实数集，且()()f x f x -=-，∴函数()f x 是奇函数，故①错误；当0x >时，()1xf x x=+，21()0(1)f x x '=>+，()f x 在(0,)+∞上为增函数，又()f x 为奇函数且在0x =处连续，()f x ∴是R 上的增函数，故②正确；|||()|1||1x f x x =<+，∴不等式|()|1f x <在R 上恒成立，故③正确； 当0x >时，函数2()()011x x g x f x x x x x-=-=-=<++，0x ∴>时，函数()()g x f x x =-无零点，由对称性可知，0x <时，函数()()g x f x x =-无零点，∴函数()()g x f x x =-在R 上有一个零点0，故④错误． ∴四个命题中错误的个数是2．故选：B ． 【点睛】本题考查命题的真假判断与应用，考查函数的奇偶性、单调性，函数值域及函数的零点，属于中档题．17．（1）=6A π；（2）【分析】（1）由2cos cos cos )b A c A a C =+利用正弦定理得2sin cos )B A A C B =+=，从而可求cos A 进一步可求A 的值；（2）由已知及（1）中的A 考虑利用余弦定理：22222cos 680a b c bc A b b =+-⇒-+=，结合b c >可求b ，然后代入面积公式1sin 2S bc A =； 【详解】解：（1）由2cos cos cos )b A c A a C =+，利用正弦定理得：2sin cos cos sin cos )B A C A A C =+，即：2sin cos )B A A C B =+=，所以cos A =6A π=，（2）由余弦定理：2222cos a b c bc A =+-，2680b b ∴-+=，又b c >，得4b =，所以111sin 4222S bc A ==⨯⨯=【点睛】三角形是研究三角函数的重要载体，在与三角形有关的试题中，正弦定理与余弦定理的应用已经成为高考命题的热点，解决此类问题，要善于抓住三角形边与角之间的关系，要学会将问题转化为三角恒等变形问题来处理．18．（1）证明见解析； （2）； 【分析】（1）可得////MN BC AD ，M ，N ，A ，D 四点共面，由已知可得AN PB ⊥．再由线面垂直的性质及底面为直角梯形得AD ⊥平面PAB ，从而得到AD PB ⊥，由线面垂直的判定可得PB ⊥平面ADMN ，则PB DM ⊥；（2）由（1）得PB ⊥平面ADMN ，即PMN ∠就是直线PC 与平面MNAD 所成角．，在Rt NPM ∆中，1122MN BC ==，tan PNPMN MN∠==，即可． 【详解】 （1）证明：M ，N 分别为PC ，PB 的中点，////MN BC AD ∴，M ∴，N ，A ，D 四点共面．N 是PB 的中点，PA AB =，AN PB ∴⊥．由PA ⊥底面ABCD ，得PA AD ⊥，又90BAD ∠=︒，即BA AD ⊥，AD ∴⊥平面PAB ，又PB ⊂平面PAB ，AD PB ∴⊥，AD ⊂平面ADMN ，AN ⊂平面ADMN ，又ADAN A =，PB ∴⊥平面ADMN ，则PB DM ⊥；（2）解：由（1）得PB ⊥平面ADMN ，PMN ∴∠就是直线PC 与平面MNAD 所成角．在Rt APB ∆中，2AP AB ==，12PN PB ∴==，在Rt NPM ∆中，1122MN BC ==，tan PNPMN MN∴∠=∴直线PC 与平面MNAD 所成角的大小为；【点睛】本题考查了异面直线垂直的判定，线面角的求解，属于中档题． 19．（1）1k =±；（2）不存在，理由见解析【分析】（1）将直线的方程代入双曲线方程，利用韦达定理及向量数量积的坐标运算即可求得k 的值；（2）假设存在实数k ，根据直线的斜率关系求得k 的值，由（1）求得124x x +=，利用中点坐标公式，即可求得AB 的中点坐标，验证中点是否在直线12y x =上． 【详解】解：（1）直线:1l y kx =+与双曲线22:31C x y -=联立，消去y 得22(3)220k x kx ---=①，由>0∆，且230k -≠，得k <k ≠；设1(A x ，1)y 、2(B x ，2)y ， 由·0OAOB =，所以12120x x y y +=，又12223k x x k -+=-，12223x x k -=-， 212121212(1)(1)()1y y kx kx k x x k x x ∴=++=+++， 2121212()10k x x k x x x x ∴++++=， 即222222210333k kk k k k ---+++=---， ∴22103k -+=-，解得1k =±． 经检验，1k =±满足题目条件，∴·0OAOB =，求实数k 的值±1；（2）假设存在实数k ，使A 、B 关于12y x =对称，则直线1y kx =+与12y x =垂直，2k ∴=-．∴直线l 的方程为21y x =-+．将2k =-代入③得124x x +=，AB ∴中点横坐标为2，纵坐标为2213y =-⨯+=-．但AB 中点(2,3)-不在直线12y x =上， 即不存在实数k ，使得A 、B 关于直线12y x =对称． 【点睛】本题考查直线与双曲线的位置关系，韦达定理与向量的坐标运算综合应用，考查转化思想，属于中档题．20．（1）证明见解析； （2）11,2⎛⎫⎪ ⎪⎝⎭； （3）证明见解析；1n n m n x n mn +-⎧=⎨-⎩当为奇数当为偶数 【分析】（1）因为()nn y a n N +=∈()1a >，所以1n ny a y +=，得到{}n y 为等比数列； （2）要使数列{}n y 中任意连续三项能构成三角形的三边，根据三角形三边关系得到不等式，解得.（3）因为12n n x x +-=为常数，所以1x ，3x ，5x ，21n x -及2x ，4x ，6x ，2n x 都是公差为2的等差数列，分别求出通项公式即可； 【详解】 解：（1）()n n y a n N +=∈，1n ny a y +=∴，{}n y ∴是以1y a =为首项，a 为公比的等比数列 （2）由（1）知n n y a =，要使数列{}n y 中任意连续三项能构成三角形的三边， 即n n y a =，11n n y a ++=，22n n y a ++=1a >所以需满足12n n n a a a +++>即2101a a a ⎧--<⎨>⎩解得1a <<即a ⎛∈ ⎝⎭（3）依题意，122x x +=，234x x +=，346x x +=，⋯⋯，12n n x x n ++= 312x x ∴-=，422x x -=，532x x -=，⋯⋯，12n n x x +-=为常数 1x ∴，3x ，5x ，⋯，21n x -及2x ，4x ，6x ，2n x 都是公差为2的等差数列， 2112(1)22n x x n n m -∴=+-=-+，222(1)2222n x x n m n n m =+-=-+-=-，1n n m n x n mn +-⎧∴=⎨-⎩当为奇数当为偶数【点睛】考查学生求等差数列通项公式的能力，灵活运用等差数列性质的能力，以及利用数列递推式求数列通项的能力．21．（1）0a ≥ ；（2）证明见解析；（3）①12n na =；②11201732f ⎛⎫= ⎪⎝⎭ 【分析】（1）直接由12()()0f x f x -求得a 的取值范围；（2）若()f x 是周期函数，记其周期为k T ，任取0x R ∈，则有00()()k f x f x T =+，证明对任意0[x x ∈，0]k x T +，00()()()k f x f x f x T +，可得00()()k f x f x nT =+，n Z ∈，再由0[3k x T ⋯-，002][2k k x T x T --，00][k k x T x T --，00][x x ，00][k k x T x T ++，02]k x T R +⋯=，可得对任意x ∈R ，0()()f x f x C ==，为常数；（3）依题意，可求得f （1）1=，11()22f f =（1）12=，再分别利用1()()52x f f x =，即可求得答案． 【详解】（1）解：由12()()f x f x ，得331212()()()0f x f x a x x -=-， 12x x <，33120x x ∴-<，得0a ．故a 的范围是[0，)+∞；（2）证明：若()f x 是周期函数，记其周期为k T ，任取0x R ∈，则有 00()()k f x f x T =+，由题意，对任意0[x x ∈，0]k x T +，00()()()k f x f x f x T +， 00()()()k f x f x f x T ∴==+．又00()()k f x f x nT =+，n Z ∈，并且 0[3k x T ⋯-，002][2k k x T x T --，00][k k x T x T --，00][x x ，00][k k x T x T ++，02]k x T R +⋯=，∴对任意x ∈R ，0()()f x f x C ==，为常数；（3）解：①(0)0f =，()(1)1f x f x +-=，()11f ∴=，由11()(1)122f f +-=，11()22f ∴=，1()()52x f f x =， 令1x =时，可得11()52f f =（1）12=，21111()()()25252f f ==， 11()()52n n f ∴=， *1()()5n n a f n N =∈， 12n na ∴=②44111()625216a f ===，55111()3125232a f ===． ()(1)1f x f x +-=，令12x =，则11()22f =， 由1()()52xf f x =，可得1111()()10224f f ==，于是11()508f =，11()25016f =，11()125032f =， 由111()()()312520171250f f f 11()201732f ∴= 【点睛】本题考查抽象函数及其应用，考查逻辑思维能力与理论运算能力考查分类讨论的数学思想方法，题目设置难度过大．。

上海市曹杨第二中学2020-2021学年高三下学期3月月考数学试题学校:___________姓名：___________班级：___________考号：___________一、填空题1．函数lg y x =的定义域是{}110，，则该函数的值域是_______. 2．二项式()61x +的展开式中的第三项为_________. 3．若向量a 、b 满足a ＝1，b ＝2，且a 与b 的夹角为3π，则a b +＝_________. 4．已知()sin 3cos απα-=，则()tan πα-=________.5．某工厂生产,,A B C 三种不同型号的产品,产品数量之比依次为2:3:5，现用分层抽样方法抽出一个容量为n 的样本,样本中A 种型号产品有16件,那么此样本的容量n = 6．已知()y f x =是奇函数. 若()()2g x f x =+且(1)1g =，则(1)g -= .7．已知22x x a +≥在[]03x ∈，上有解，则实数a 的取值范围是________. 8．在平面直角坐标系中，从六个点：A(0,0)、B(2,0)、C(1,1)、D(0,2)、E(2,2)、F(3,3)中任取三个，这三点能构成三角形的概率是 （结果用分数表示）.9．如图，在直三棱柱ABC －A 1B 1C 1中，点M 为棱AA 1的中点，记三棱锥A 1－MBC 的体积为V 1，四棱锥A 1－BB 1C 1C 的体积为V 2，则12V V 的值是__.10．设m R ∈，若z 是关于x 的方程2210x mx m ++-=的一个虚根，则z 的取值范围是____.11．在等比数列{}n a 中，已知()()14234a a a a +-+=，若()*1n n a a n N +>∈，则65a a -的最小值是________.12．若存在实数a b 、，对任意实数[]04x ∈，m ax b m ≤+≤恒成立，则实数m 的取值范围为________.二、单选题13．关于实数m n 、，“0mn <”是方程“221mx ny +=对应的曲线是椭圆”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件14．设有不同的直线a b 、和不同的平面αβγ、、，给出下列三个命题： ①若////a b αα，，则//a b ； ②若////a a αβ，，则//αβ； ③若αγβγ⊥⊥，，则.αβ⊥ 其中正确的个数是（ ） A ．0个B ．1个C ．2个D ．3个15．设(),n n n x y P 是直线21n x y n -=+（n *∈N ）与圆222x y +=在第一象限的交点，则极限1lim 1n n n y x →∞-=-（ ） A ．1-B ．12-C ．1D ．216．我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题：将1，2，3，4，5，6，7，8，9分别填入3×3的方格中，使得每一行，每一列及对角线上的三个数的和都相等(如图所示)，我们规定：只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同，就称为不同的幻方，那么不同的三阶幻方的个数是（ ）A ．9B ．8C ．6D ．4三、解答题17．已知圆锥的顶点为P ，底面圆心为O ，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设4PO =，OA 、OB 是底面半径，且90AOB ∠=︒，M 为线段AB 的中点，如图．求异面直线PM 与OB 所成的角的大小． 18．设常数R a ∈，函数()2sin22cos f x a x x =+．（1）若()f x 为偶函数，求a 的值；（2）若π14f ⎛⎫=⎪⎝⎭，求方程()1f x =[]ππ-，上的解． 19．某足球俱乐部对“一线队引援”和“青训”投入分别规划如下：2021年，该俱乐部在“一线队引援”投入资金为16000万元，“青训”投入资金为1000万元.计划每年“一线队引援”投入比上一年减少一半，“青训”投入比上一年增加一倍. （1）请问哪一年该俱乐部“一线队引援”和“青训”投入总和最少?（2）从2021年起（包括2021年）该俱乐部从哪一年开始“一线队引援”和“青训”总投入之和不低于62000万元?（总投入是指各年投入之和）20．给定椭圆()2222:10x y C a b a b+=>>，称圆心在坐标原点O 的圆是椭圆C 的“伴随圆”，已知椭圆C 的两个焦点分别是())12,F F .（1）若椭圆C 上一动点1M 满足11124M F M F +=，求椭圆C 及其“伴随圆”的方程； （2）在（1）的条件下，过点()()0,0P t t <作直线l 与椭圆C 只有一个交点，且截椭圆C 的“伴随圆”所得弦长为P 点的坐标； （3）已知()()cos 3,,0,sin sin m n mn m n θθπθθ+=-=-≠∈，是否存在a ，b ，使椭圆C 的“伴随圆”上的点到过两点()()22,,,m mn n 的直线的最短距离mindb =.若存在，求出a ，b 的值；若不存在，请说明理由.21．已知函数()f x 的定义域为[]01，，同时满足：对任意[]01x ∈，，总有()()2,13f x f ≥=，对定义域内的12x x 、，若满足121x x +≤，恒有()()()12122f x x f x f x ++-≥成立，则函数()f x 称为“Γ函数”.（1）判断函数()21xf x =+在区间[]01，上是否为“Γ函数”，并说明理由；（2）当()g x 为“Γ函数”时，求()g x 的最大值和最小值； （3）已知()h x 为“Γ函数”： ①证明：()*11222n n h n N ⎛⎫≤+∈⎪⎝⎭； ②证明：对一切(]01x ∈，，都有()2 2.h x x <+参考答案1．{}01，【解析】 【分析】由题意，将x =1和x =10分别代入解析式即可求得结果. 【详解】依题意，当x =1时，y =lg1=0，当x =10时，y =lg10=1，则该函数的值域是{}01，. 故答案为：{}01，.【点睛】本题考查函数的概念和对数函数的基本知识，要求学生必须掌握已知函数定义域，求函数值域的基本题型，属基础题. 2．415x 【分析】由二项式定理及二项式展开式的通项公式得：616r rr T C x -+=，令r +1=3，得r =2，从而由通项公式求得结果. 【详解】由二项式()61x +的展开式的通项公式得616r rr T C x -+=，令 r +1=3，得r =2，则二项式()61x +的展开式中的第三项为2626C x-，即415x ，故答案为415x . 【点睛】本题考查二项式定理的应用，解题的关键在于正确写出二项式展开式的通项公式，属基础题.3 【分析】由1,2,,a b a b ==夹角为3π，利用平面向量数量积公式，求得a b +平方的值，从而可得结果.1,2,,a b a b ==夹角为3π，所以2222a ba b a b +=++⋅142cos 3a b π=++152125272=+⨯⨯⨯=+=所以7a b +=，故答案为. . 4．3 【分析】根据诱导公式和同角三角函数的基本关系先求出tan α，从而求出()tan πα-. 【详解】由()sin sin απα-=-可得，sin 3cos αα-=，即tan 3α=-， 则()tan tan 3παα-=-=. 故答案为3. 【点睛】本题考查三角函数的诱导公式和同角三角函数的基本关系，准确运用公式是解题的关键，属基础题. 5．80． 【详解】解：A 种型号产品所占的比例为2/ (2+3+5) =2 /10 ，16÷2/10 =80， 故样本容量n=80， 6．3 【详解】()y f x =是奇函数，则(1)(1)f f -=-，(1)(1)(1)(1)44g g f f +-=+-+=,所以(1)4(1)3g g -=-=.【分析】令2()2g x x x =+，依题意，[0,3]x ∃∈，使()g x a ≥成立，转化为求max ()g x a ≥，从而利用一元二次函数的性质即可求得结果. 【详解】令2()2g x x x =+，依题意，[0,3]x ∃∈，使()g x a ≥成立，即max ()g x a ≥，又22()2(1)1g x x x x =+=+-，则2()2g x x x =+在[0,3]上单调递增，所以max ()(3)15g x g ==，所以15a ≤. 故答案为：15a ≤. 【点睛】本题考查存在性问题和一元二次函数的性质，也考查了学生转化与化归的能力，存在性问题通常转化为求函数最值问题，属中档题. 8．34【详解】已知A C E F B C D 、、、共线；、、共线；六个点任取三个不同取法总数为：36C ；可构成三角形的个数为：33364315C C C --=，所以所求概率为：3336433634C C C C --=. 9．141x = 【分析】首先设出该棱柱的底面积和高，之后根据椎体的体积公式求得1V 和2V 的值，进而求得其比值，得到结果. 【详解】设ABC ∆的面积为S ，三棱柱的高为h ， 则11111113326A MBC A ABC M ABC V V V V Sh S h Sh ---==-=-⨯=，111111121233A BBC C ABC A B C A ABC V V V V Sh Sh Sh ---==-=-=，所以1231624V Sh V Sh =⨯=， 故答案是14. 【点睛】该题考查的是有关椎体的体积的问题，熟记公式是正确解题的关键.10．3⎛⎫∞ ⎪ ⎪⎝⎭【解析】 【分析】设z =a +bi ，(a ,b ∈R )，则z a bi =-也是此方程的一个虚根，由方程有虚根可知，判别式为负数，据此可求出m的范围，再利用根与系数的关系可得||z =. 【详解】设z =a +bi ，(a ,b ∈R )，则z a bi =-也是此方程的一个虚根，z 是关于x 的方程x 2+mx +m 2−1=0的一个虚根，可得()22410m m ∆=--<，即243m >， 则由根与系数的关系，2221z z a b m ⋅=+=-，则||3z =>， 所以z的取值范围是：⎫∞⎪⎪⎝⎭.故答案为⎫∞⎪⎪⎝⎭.【点睛】本题考查实系数多项式虚根成对定理，以及复数的模的求解，属中档题. 11．16 【分析】将()()14234a a a a +-+=化简变形可得2124=1a a q --，则44652124()1q a a q a a q -=-=-，将该式变形成2244(1)81q q -++-，并利用基本不等式求出最小值，从而得到结果. 【详解】设数列{}n a 的公比为q ，()()1423a a a a +-+()()4321a a a a =--- ()()22121q a a a a =--- ()221(1)4q a a =--=，由()*1n n a a n N +>∈，2124=01a q a ->-，即210q ->， 则44652124()1q a a q a a q -=-=-，即444222222444444444(1)811111q q q q q q q q q -+-==+=-++-----，又2244(1)821q q -++≥-， 当且仅当2244(1)=1q q --，即2=2q 时，取等号. 所以65a a -的最小值是16. 故答案为：16. 【点睛】本题考查等比数列的性质和基本不等式的应用，考查了学生的计算能力，综合性较强，属难题. 12．14m ≥【分析】m ax b m ≤+≤可化为不等式|ax b m +≤，等价于存在实数a ，b ，对任意[0,4]x ∈，不等式|ax b m +≤成立，等价于存在实数a ，b ，不等式max |ax b m +≤成立，分别讨论14a ≤，11,42a ⎡⎤∈⎢⎥⎣⎦，1,2a ⎛⎫∈+∞ ⎪⎝⎭的情况，注意由任意性和存在性可知需先求出max |ax b +，再求()maxmin|ax b +即可解决.【详解】m ax b m ≤+≤可化为不等式|ax b m +≤，原题等价于存在实数a ，b ，对任意[0,4]x ∈，不等式|ax b m +≤成立，等价于存在实数a ，b，不等式max |ax b m +≤成立，令y ax b =+y a '=，（1）在[0,4]x ∈上，当0y '≤，即14a ≤时，函数单调递减， 此时42a b y b +-≤≤，当12b a ≤-时，42a b b +-≤-，且420a b +-<，则max ||42y a b =--+， 当12b a >-时，42a b b +->-，且0b >，则max ||y b =， 从而当14a ≤时，设max 42,12()||,12a b b a g b y b b a --+≤-⎧==⎨>-⎩，则()g b 在(,12)a -∞-单调递减，在(12,)a -+∞单调递增， 所以12b a =-时，()g b 取最小值，最小值为1(12)122g a a -=-≥； （2）当14a >时，由0y a '=-<可得，y 在210,4a ⎡⎫⎪⎢⎣⎭上单调递减，在21,44a ⎡⎤⎢⎥⎣⎦上单调递增，①在11,42a ⎡⎤∈⎢⎥⎣⎦时，42b a b ≥+-，则14b y b a -≤≤， 同理可得，当11,42a ⎡⎤∈⎢⎥⎣⎦时，max 11,48()||1,8b b a ag b y b b a ⎧-≤⎪⎪==⎨⎪>⎪⎩，则()g b 在1(,)8a -∞单调递减，在1(,)8a +∞单调递增，故当18b a =时，()g b 取最小值，最小值为111()884g a a =≥； ②在1,2a ⎛⎫∈+∞⎪⎝⎭时，42b a b <+-，则1424b y a b a -≤≤+-，同理可得，当1,2a ⎛⎫∈+∞ ⎪⎝⎭时，max 11,1248()||142,128b b a a ag b y a b b a a ⎧-≤-+⎪⎪==⎨⎪+->-+⎪⎩，则()g b 在1(,12)8a a -∞-+单调递减，在1(12,)8a a -++∞单调递增， 故当1128b a a =-+时，()g b 取最小值，最小值为11(12)2188g a a a a-+=+-， 根据对勾函数的性质可得，111(12)21884g a a a a -+=+->. 综上所述，1()4g b ≥，即min 1()4g b =，14m ∴≥.故答案为14m ≥.【点睛】本题考查函数综合，考查了函数任意性和存在性问题的综合，难度较大，关键在于根据任意性先对a进行讨论求出max ||ax b +，再对b 进行分段得到分段函数()g b ，结合单调性和存在性的特点求出()g b 的最小值，属难题. 13．D 【分析】分别从充分性和必要性推导即可求得结果. 【详解】充分性：“0mn <”时，221mx ny +=对应的曲线是双曲线，不是椭圆，故充分性不成立； 必要性：已知“221mx ny +=对应的曲线是椭圆”，所以,0m n >且m n ≠，故必要性不成立.综上所述，“0mn <”是方程“221mx my +=对应的曲线是椭圆”的既不充分也不必要条件.故选：D. 【点睛】本题主要考查充分条件与必要条件和椭圆及其标准方程，熟练掌握椭圆方程的特点是解题的关键，属基础题. 14．A 【分析】根据线线平行的定义和性质、平面与平面平行或垂直的性质与判定，逐项判断即可得出结论. 【详解】①若////a b αα，，当a ，b 共面时，满足//a b 或a 与b 相交；当a ，b 不共面时，a 和b 为异面直线，所以a 和b 的关系是平行、相交或异面，故不正确； ②若////a a αβ，，则//αβ或α与β相交，故不正确； ③若αγβγ⊥⊥，，则//αβ或α与β相交，故不正确. 故选A. 【点睛】本题主要考查空间直线与直线，平面与平面的位置关系的判断，掌握线线平行的定义和性质、平面与平面平行或垂直的性质与判定是解决本题的关键，属基础题. 15．A 【解析】由题意得：因为21x y -=与圆222x y +=在第一象限的交点为1,1（），所以lim =1lim =1n n n n x y →∞→∞，，1limlim 1n n n n n ny y x x →∞→∞'-='∴-，又由222n n x y +=得220n nn n n n n n y x x x y y x y +=⇒=-''''lim 1lim lim lim() 1.1lim n n n n n n n n n n n nn x y y x x x y y →∞→∞→∞→∞→∞-∴='=-=-=--'选A.考点：极限 16．B 【分析】首先如题设分析，每行每列的所有书的和都是15，然后列举所有3个数的和为15的组合情况，含5的有5个，所以5放中间，含2，4，6，8的都3个，所以放在四个角处，并且456，258分占两条对角线，再用列举法即可得到结论. 【详解】 因为所有数的和为9(19)452⨯+=，45153=，所以每行每列，以及对角线的和都是15，采用列举法：492、357、816；276、951、438；294、753、618；438、951、276；816、357、492；618、753、294；672、159、834；834、159、672.共8种排法，则不同的三阶幻方的个数是8. 故选：B. 【点睛】高考已说明加强数学史等知识的考查，所以对于数学史书的数学问题，也会是高考的热点，本题考了计数问题，审题要清楚，并且能抽象为一个什么数学问题，当解决问题时，计算要准确，属中档题.17．arccos 6. 【分析】（1）由圆锥的顶点为P ，底面圆心为O ，半径为2，圆锥的母线长为4能求出圆锥的体积． （2）以O 为原点，OA 为x 轴，OB 为y 轴，OP 为z 轴，建立空间直角坐标系，利用向量法能求出异面直线PM 与OB 所成的角． 【详解】（1）∵圆锥的顶点为P ，底面圆心为O ，半径为2，圆锥的母线长为4，∴圆锥的体积2211ππ233V r h =⨯⨯⨯=⨯⨯3=． （2）∵4PO =，OA ，OB 是底面半径，且90AOB ∠=︒，M 为线段AB 的中点，∴以O 为原点，OA 为x 轴，OB 为y 轴，OP 为z 轴， 建立空间直角坐标系，()004P ，，，()200A ，，，()020B ，，， ()110M ，，，()000O ，，，()114PM =-，，，()020OB =，，，设异面直线PM 与OB 所成的角为θ，则2cos 618PM OB PM OBθ⋅===⋅．∴2arccos6θ=． ∴异面直线PM 与OB 所成的角的为arccos 6． 【点睛】求空间两条异面直线所成角的大小是立体几何中最为常见的基本题型之一。

2021-2022学年上海市曹杨第二中学高二下学期期末数学试题一、单选题1．用数学归纳法证明：“为正整数”，在到111111111(234212122nn n n n n -+-++-=+++-++ n k =时的证明中，（ ）1n k =+A ．左边增加的项为B ．左边增加的项为121k +122k -+C ．右边增加的项为D ．右边增加的项为112122k k +++112122k k -++【答案】D【分析】根据式子的结构特征，求出当n ＝k 时，等式的左边，再求出n ＝k +1 时，等式的左边，比较可得所求．【详解】当n ＝k 时，等式的左边为，111111234212k k -+-++-- 当n ＝k +1 时，等式的左边为，111111112342122122k k k k -+-++-+--++ 故从“n ＝k 到n ＝k +1”，左边所要添加的项是．112122k k -++故选：D ．2．已知正态分布的正态密度曲线如图所示，，则下列选项中，不能表示图中()21,N σ()21,x N σ-阴影部分面积的是（ ）A ．B ．()102P X -≤()122P X -≥C ．D ．()1122P X -≤≤()()112022P X P X ≤-≤【答案】C【分析】由正态密度曲线的对称性逐一分析四个选项即可得答案.【详解】解：由正态分布的正态密度曲线关于直线对称，()21,N σ1x =对A ：由对称性可得图中阴影部分可表示为，()()()()1011002P X P X P X P X ≤≤=≤-≤=-≤故选项A 不符合题意；对B ：由对称性可得，所以图中阴影部分可表示为()()02P X P X ≤=≥，故选项B 不符合题意；()()()10102212P X P X P X -≤=-≤=≥≤对C ：由对称性可得，故选项C 符合题意；()()()112022P X P X P X -≤≤=≤=≥对D ：由对称性可得，所以图中阴影部分可表示为()()0112P X P X ≤≤=≤≤，故选项D 不符合题意.()()()201201P X P X P X ≤≤≤=-≤⎡⎤⎣⎦故选：C.3．某地区气象台统计，该地区下雨的概率是，刮风的概率为，在下雨天里，刮风的概率为，41521538则既刮风又下雨的概率为（ ）A ．B ．C ．D ．3435110120【答案】C【分析】利用条件概率的计算公式求解即可【详解】记“下雨”，“刮风”，“刮风又下雨”，A =B =AB =则，()()()423,,15158P A P B P B A ===所以.()()()43115810P AB P A P B A ==⨯=故选：C4．已知函数有两个零点，对于下列结论：①；②()ln 1f x x ax =+-()1212,x x x x <01a <<；则（ ）122x x a +<A ．①②均对B ．①②均错C ．①对②错D ．①错②对【答案】C【分析】函数有两个零点，则有两个根，即，()ln 1f x x ax =-+()1212,x x x x <ln 10x ax -+=ln 1x a x +=设，利用导数法研究即可()()ln 10x g x x x +=>【详解】因为函数有两个零点，()ln 1f x x ax =-+()1212,x x x x <所以有两个根，即，ln 10x ax -+=ln 1x a x +=设，，()()ln 10x g x x x +=>()2ln x g x x =-'当时，解得，函数单调递增；()0g x '>01x <<()g x 当时，解得，函数单调递减，()0g x '<1x >()g x ，()max ()11g x g ==当趋向于正无穷时，趋向于0，当趋向于0时，趋向于负无穷，x ()g x x ()g x 所以当时，与有两个交点，故①正确；01a <<y a =ln 1x y x +=由此可知，1211e x x <<<因为，11122212ln 10ln ln 2ln 10x ax x x a x ax x x -+=⎧++⇒=⎨-+=+⎩若，即.122x x a +<122a x x <+即证，()1212121212ln ln 22ln 01x x x x x x x x x x ++<⇒<⇒<++当趋向于正无穷时，不成立，故②不正确.2x 故选：C二、填空题5．抛物线的准线方程是_______24y x =【答案】=1x -【分析】根据抛物线的标准方程形式求出，再根据开口方向，写出其准线方程.p 【详解】对于抛物线，，，24y x =24p = 2p ∴=又抛物线开口向右，准线方程为. ∴=1x -故答案为：.=1x -6．方程的解集是______.3055C C x -=【答案】{}2,3-【分析】由组合数的性质求解即可【详解】因为，3055C C x -=所以或，30x -=35x -=解得或，3x =2x =-所以方程的解集是，3055C C x -={}2,3-故答案为：{}2,3-7．的展开式中常数项是______.6x ⎛- ⎝【答案】15【分析】由二项式定理求出通项公式，得到，从而求出常数项.4r =【详解】的展开式的通项公式为：，6x ⎛ ⎝()136622166C 1C rr r r r r r T x x x ---+⎛⎫=-=- ⎪⎝⎭令，解得：，3602r -=4r =故.()44561C 15T =-=故答案为：158．已知随机变量，则______.1~5,2X B ⎛⎫⎪⎝⎭()2P X ==【答案】516【分析】根据二项分布的概率公式求即可.()2P X =【详解】由题意知：，()232511522216P X C ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭故答案为：.5169．在3双鞋子中任意抽取两只，恰为一双鞋子的概率是______.【答案】##150.2【分析】分别求解总的情况数与满足一双鞋子的情况数，进而可得概率.【详解】在3双鞋子中任意抽取两只，共种情况，其中满足一双鞋子的情况有3种，故在2615C =3双鞋子中任意抽取两只，恰为一双鞋子的概率是.31155=故答案为：1510．已知向量，，与的夹角为______.(1,a = ||3b = a b ⋅= a b 【答案】##6π30︒【分析】首先求出，设向量与的夹角为，再根据计算可得；a a bθcos ||||a b a b θ⋅=【详解】解：因为(1,a ==设向量与的夹角为，因为，所以.a b θcos ||||a b a b θ⋅=== []0,θπ∈6πθ=故答案为：6π11．已知是奇函数，且当时，，则______.()f x 0x ≥()()R f x x a a =+∈()2f -=【答案】2-【分析】由奇函数的定义和性质求解即可【详解】因为是奇函数，且，()f x ()00f a ==所以当时，，0x ≥()f x x=所以，()()222f f -=-=-故答案为：2-12．某天有10名工人生产同一零部件，生产的件数分别是：15、17、14、10、15、17、17、16、14、12，设其平均数为a ，中位数为b ，众数为c ，则a 、b 、c 从小到大的关系依次是________【答案】.a b c <<【详解】分析：将数据由小到大排列好，根据众数，中位数，平均数的概念得到相应的数据即可.详解：根据提干得到中位数为b=15，众数为c=17，平均数为=a.10+12+28+30+16+51=14.710故 .a b c <<故答案为.a b c <<点睛：这个题目考查了中位数，众数，平均数的概念和计算，较为基础,众数即出现次数最多的数据，中位数即最中间的数据，平均数即将所有数据加到一起，除以数据个数.13．函数的图像在点处的切线的倾斜角为______.()cos 2f x x =π12⎛ ⎝【答案】##3π4135︒【分析】先求导，再由导数的几何意义可得，再结合倾斜角的范围求解即可.tan θ=112f π⎛⎫'=- ⎪⎝⎭【详解】因为，所以，()cos 2f x x=()2sin 2f x x'=-则，ππ2sin 211212f ⎛⎫⎛⎫'=-⨯=- ⎪ ⎪⎝⎭⎝⎭设直线的倾斜角为，则，θ[)0,πθ∈又，tan 1θ=-所以，3π4θ=故答案为：.3π414．方程在上有三个不同的实根，则实数的取值范围是______.330x x a -+=[)2,x ∈-+∞a 【答案】()2,2-【分析】方程在上有三个不同的实根，则与有3个不330x x a -+=[)2,x ∈-+∞y a =()33g x x x =-+同的交点，利用导数研究函数的单调性，作出图象，即可求解()33g x x x=-+【详解】由得，330x x a -+=33a x x =-+令，()33g x x x=-+则 ，()233g x x '=-+令，解得，()0g x '>11x -<<令，解得或，()0g x '<1x <-1x >所以在上递减，在上递增，在上递减，()g x (),1-∞-()1,1-()1,+∞所以在处取得极小值，且为；=1x -()12g -=-在处取得极大值，且为；1x =()12g =画出的大致图像如下：()g x方程在上有三个不同的实根，330x x a -+=[)2,x ∈-+∞则与有3个不同的交点，y a =()33g x x x =-+由图象可知实数的取值范围是a ()2,2-故答案为：()2,2-15．口袋中放有大小相等的2个白球和1个黑球，有放回地每次摸取1个球，定义数列：若第{}n a 次摸到白球，；若第次摸到黑球，.设为数列的前项和，则的概率n 1n a =-n 1n a =n S {}n a n 73S =为______.【答案】28729【分析】题意说明共摸球七次，只有两次摸到白球，利用独立事件的概率公式求解即可73S =【详解】由题意说明共摸球七次，只有两次摸到白球，73S =因为每次摸球的结果之间没有影响，摸到白球的概率是，摸到黑球的概率为，2313所以只有两次摸到白球的概率为，52271228C 33729⎛⎫⎛⎫⋅=⎪⎪⎝⎭⎝⎭故答案为：2872916．已知､是椭圆的左､右焦点，点是椭圆上任意一点，以为直径作圆1F 2F 2221(3x y a a +=>P 1PF ，直线与圆交于点（点不在椭圆内部），则______.N ON N Q Q 12QF QF ⋅=【答案】3【分析】利用向量的数量积运算可得，利用，进一步利()()22121QF QF QO OF ⋅=- ||QO QN NO =+用椭圆的定义可转化为，进而得解.22a c -【详解】解：连接,设椭圆的半焦距为，半虚轴为，122,,QF QF PF c b ,()()()()2112221QF QF QO Q OF OF QO O O F ⋅=+⋅+=- .()221222222322PF PF QN NO c c a c b ⎛⎫=+-=+-=-== ⎪⎝⎭故答案为：3.三、解答题17．已知曲线和.31:C y x =22:2,(R)C y ax x a =+-∈(1)若曲线､在处的切线互相垂直，求的值；1C 2C 1x =a (2)若与曲线､在处都相切的直线的斜率大于3，求的取值范围.1C 2C 0x x =a 【答案】(1)23a =-(2)或1a >1a <-【分析】（1）根据切线垂直可得在处导数值的乘积为求解；1x =1-（2）利用导数计算切线斜率，再由斜率大于3求解即可.【详解】（1）由可得，3y x =23y x '=由可得，22,(R)y ax x a =+-∈21y ax '=+因为曲线､在处的切线互相垂直，1C 2C 1x =所以，解得.212(31)(21)1k k a ⋅=⨯⨯+=-23a =-（2）由题意，切线的斜率，2003213k x ax ==+>可得，且或，200312x ax -=01x >01x <-所以，00123a x x =-令，则函数在和上是增函数，1()3h x x x =-(1,)+∞(,1)-∞-所以或，()(1)2h x h >=()(1)2h x h <-=-即或，解得或.22a >22a <-1a >1a <-18．在数列中，为正整数.{}n a 1n a n +=(1)若数列为常数列，求的通项；{}n a {}n a (2)若，用数学归纳法证明：.10a =πcos2n n a =【答案】(1)；1n a =(2)见解析.【分析】（1）根据数列为常数列及所给递推关系，平方后即可得解；（2）根据数学归纳法的证明步骤，结合余弦的降幂公式即可得证.【详解】（1），10n a +=≥ ，又数列为常数列，2+1210n n a a ∴--={}n a ，2210n n a a ∴--=解得或（舍去）1na =12n a =-的通项公式为.∴{}n a 1n a =（2）当时，，成立；1n =1πcos 02a ==假设时成立，即，(2)n k n =≥πcos 2k ka =当时，（为锐角），1n k =+11πcos 2k k a ++====1π2k +即时，成立，1n k =+综上，对任意，都有.N n *∈πcos2n n a =19．某市为调研本市学生体质情况，采用按性别分层抽样的方法进行调查，得到体质测试样本的统计数据（单位：人）如表：优秀良好及格不及格男生100200780120女生120200520120(1)根据所给数据，完成下面列联表，并据此判断：能否有的把握认为该市学生体质测试是22⨯95%否达标与性别有关.（注：体质测试成绩为优秀､良好或及格则体质达标，否则不达标）达标不达标合计男生女生合计其中；()222(), 3.8410.05()()()()n ad bc P a b c d a c b d χχ-=≥≈++++(2)体质测试成绩为优秀或良好则称体质测试成绩为优良，以样本数据中男､女生体质测试成绩优良的频率视为该市男､女生体质测试成绩优良的概率，在该市学生中随机选取1名男生，1名女生，设所选2人中体质测试成绩优良人数为，求的分布列，数学期望与方差.X X 【答案】(1)列联表见解析，没有的把握认为该市学生体质达标与性别有关95%(2)分布列见解析，，()712E X =()59144D X =【分析】（1）直接列出列联表，计算，由独立性检验的思想求解即可；22⨯2χ（2）写出的可能取值，并求出相应的概率，即可求解X 【详解】（1）由题得列联表如下：22⨯达标不达标合计男生10801201200女生840120960合计19202402160()222160108012084012027 3.375 3.841192024096012008χ⨯-⨯===<⨯⨯⨯所以没有的把握认为该市学生体质达标与性别有关.95%（2）由题意男生体质测试优良率，女生体质测试优良率.114P =213P =的所有可能取值为.X 0,1,2()()()321123151110,1,24324343124312P X P X P X ==⨯===⨯+⨯===⨯=所以的分布列为X X012P 12512112，()15170122121212E X =⨯+⨯+⨯=()2227175715901212212121212144D X ⎛⎫⎛⎫⎛⎫=-⨯+-⨯+-⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭20．已知双曲线，直线，与交于、两点，为()222:10y x b b Γ-=>():0l y kx m km =+≠l ΓP Q P '关于轴的对称点，直线与轴交于点；P y P Q 'y ()0,N n (1)若点是的一个焦点，求的渐近线方程；()2,0ΓΓ(2)若，点的坐标为，且，求的值；1b =P ()1,0-32NP P Q ''= k (3)若，求关于的表达式．=2m n b 【答案】(1)y =(2)12±(3)22b n =-【分析】（1）由双曲线，点是的一个焦点，求出，，由此能求()222:10y x b b Γ-=>()2,0Γ=2c =1a 出的标准方程，从而能求出的渐近线方程.ΓΓ（2）双曲线为：，由定比分点坐标公式，结合已知条件能求出的值.Γ221x y -=k （3）设，，，则，，由，得()11,P x y ()22,Q x y 0P Q k k '=()11,P x y '-0:P Q l y k x n '=+222=+2=1y kx y x b -⎧⎪⎨⎪⎩，由，得，由此利用韦达定理，()2222440﹣＝b k x kx b ---0222=+=1y k x n y x b -⎧⎪⎨⎪⎩()222220020﹣＝b k x nk x n b ---结合已知条件能求出关于的表达式.n b 【详解】（1）∵双曲线，点是的一个焦点，()222:10y x b b Γ-=>()2,0Γ，，，2c ∴==1a 222413b c a ∴=-=-=的标准方程为：，∴Γ2213y x -=的渐近线方程为.Γy =（2），双曲线为：，，，1b = ∴Γ221x y -=()1,0P -()1,0P '，设，32NP P Q ''= ()22,Q x y 则由定比分点坐标公式，得：，解得，2230+21=31+23+20=31+2x n y ⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩253x =又∵，，22221x y -= 243y ∴=±则，()212140135213y y k x x ±--===±---所以的值为.k 12±（3）设，，，则，，()11,P x y ()22,Q x y 0P Q k k '=()11,P x y '-0:P Q l y k x n '=+由，得，222=+2=1y kx y x b -⎧⎪⎨⎪⎩()2222440﹣＝b k x kx b ---，，12224k x x b k ∴+=-212224b x x b k --=-由，得0222=+=1y k x n y x b -⎧⎪⎨⎪⎩()222220020﹣＝b k x nk x n b ---，，0122202k n x x b k ∴-+=-2212220n b x x b k ---=-，即，22212222204n b b x x b k b k +--==--222202224b k n b b k b -+=---又，2122222202121222210021002221042224y y kb k x x x x k k k n b b k y y k n k x x k n b k k n b x x b k ---++-====⋅=⋅-----+-化简得，()2222420n n b b +++=解得，222或b n n =-=-当时，由，得，2n =-222202224b k n b b k b -+=---22202b k k =+由，得，0=2=+2y k x y kx -⎧⎨⎩0004=2+2=x k k k k y k k --⎧⎪⎪⎨⎪⎪⎩即，代入000224,k k Q k k k k ⎛⎫+ ⎪--⎝⎭2221y x b -=化简得：，解得，()4200440b kk b kk -++=2204或b b kk ==当时，满足，24b =22b n =-当时，由，得（舍去），20b kk =22202b k k =+0k k =综上，得.22b n =-21．已知函数.21()ln (,R)2f x ax x x b a b =-+∈(1)已知时函数的极值为3，求和的值；1x =()y f x =a b (2)已知在上是严格增函数，求的取值范围；()y f x =(e,)+∞a (3)设，是否存在，使得函数的最小值为2？若存在，求出的值；若不()(),(0,e]g x f x x ='∈a ()g x a 存在，说明理由.【答案】(1)51,2a b ==(2)2,e ⎡⎫+∞⎪⎢⎣⎭(3)存在，2e a =【分析】（1）时函数的极值为3，有，可解和的值；1x =()y f x =(1)3(1)0f f =⎧⎨='⎩a b （2）在上是严格增函数，则在上恒成立，分离常数求的取值范()y f x =(e,)+∞()0f x ¢>(e,)+∞a 围；（3）分类讨论的单调性，计算最小值，看是否存在使得函数的最小值为2.()g x a ()g x 【详解】（1），，21()ln 2f x ax x x b =-+()ln 1f x ax x =--'依题意有：，解得；1(1)32(1)10f a b f a ⎧=+=⎪⎨⎪=-=⎩'51,2a b ==（2），在上是严格增函数，21()ln 2f x ax x x b =-+()y f x =(e,)+∞∴在上恒成立，即在上恒成立，()ln 10f x ax x =-->'(e,)+∞ln 1x a x +>(e,)+∞因为，所以是上的严格减函数，2ln 1ln 0x x x x '+-⎛⎫=< ⎪⎝⎭ln 1x y x +=()e,+∞当时，，故，的取值范围为.e x =ln 12e x x+=2e a ≥a 2,e ⎡⎫+∞⎪⎢⎣⎭（3），，()()ln 1,(0,e]g x f x ax x x =∈'=--()1g x a x '=-①当时，，是上的严格减函数，最小值为，不合题意；0a ≤()0g x '<()g x (]0,e ()e e 20g a =-<②当时，，是上的严格减函数，最小值为10e a <≤()110e g x a a x =-≤-≤'()g x (]0,e ，不合题意；()e e 20g a =-<③当时，在上，，严格减，在上，严格增，1e >a 10,a ⎛⎤ ⎥⎝⎦()0g x '<()g x 1,e a ⎡⎤⎢⎥⎣⎦()0g x '>()g x ，即，所以当时，存在.12g a ⎛⎫= ⎪⎝⎭ln 2a =2e a =min ()2g x =。