2019-2020学年上海市曹杨二中高二下学期期末考试数学试题 word版

上海第二中学2019-2020学年高二下学期数学期末测试时间：90分钟一、 填空题（本大题共10题，每题6分，共60分）1.将三份录取通知书投入四个邮筒共有_______种不同的投递方式。

2. 已知球的体积为36π，则该球的大圆的面积为3. 已知向量(0,2,1)a =，(1,1,2)b =-，则a 与b 的夹角为4.在6(2x展开式中，常数项为_______。

（用数字作答） 5. 高三某位同学参加物理、化学、政治科目的等级考，已知这位同学在物理、化学、政治科目考试中达A 的概率分别为56、78、34，这三门科目考试成绩的结果互不影响，则这位考生至少得1个A 的概率为6. 一个袋子中装有8个球，其中2个红球，6个黑球，若从袋中拿出两个球，记下颜色，则两个球中至少有一个是红球的概率是 （用数字表示）7.若在1()n x x-展开式中，若奇数项的系数之和为32，则含4x 的系数是______。

8. 点P 是棱长为1的正方体1111ABCD A B C D -的底面1111A B C D 上一点，则1PA PC ⋅的取值范围为9. 两个圆锥有等长的母线，它们的侧面展开图恰好拼成一个圆，若它们的侧面积之比为1:2，则它们的体积比是10．已知,x y 满足组合数方程21717x yC C =，则xy 的最大值是_______二、选择题（本大题共4题，每题5分，共20分）11. 在空间中，“直线m ⊥平面α”是“直线m 与平面α内无穷多条直线都垂直”的（ ）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 非充分非必要条件 12. 某样本平均数为a ，总体平均数为m ，那么（ ）A. a m =B. a m >C. a m <D. a 是m 的估计值 13．一个空间几何体的三视图如图所示，则该几何体的体积为（ ）A．2π+B．4π+C．2π+D．43π+14. 如图，梯形ABCD 中，AD ∥BC ，1AD AB ==，AD AB ⊥，45BCD ∠=︒，将△ABD 沿对角线BD 折起，设折起后点A 的位置为A '，使二面角A BD C '--为直二面角，给出下面四个命题：① A D BC '⊥；② 三棱锥A BCD '-的体积为6；③ CD ⊥平面 A BD '；④ 平面A BC '⊥平面A DC '；其中正确命题的个数是（ ）A. 1B. 2C. 3D. 4三、解答题（本大题4题，共70分）15. （本题满分14分）本题共有2个小题，第1小题6分，第2小题8分。

同步练习一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知函数()cos f x x m x =+，其图象关于直线3x π=对称，为了得到函数()g x x=的图象，只需将函数()f x 的图象上的所有点（ ） A ．先向左平移6π个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变 B ．先向右平移6π个单位长度，再把所得各点横坐标缩短为原来的12，纵坐标保持不变 C ．先向右平移3π个单位长度，再把所得各点横坐标伸长为原来的2倍，纵坐标保持不变 D ．先向左平移3π个单位长度，再把所得各点横坐标缩短为原来的12，纵坐标保持不变 2．在复平面内，复数221z i i=+-+所对应的点在第几象限（ ） A ．第一象限 B ．第二象限 C ．第三象限D ．第四象限3．若不等式2xln x≥－x 2＋ax －3对x∈(0，＋∞)恒成立，则实数a 的取值范围是( ) A ．(－∞，0)B ．(－∞，4]C ．(0，＋∞)D ．[4，＋∞)4．已知()23()f x x x R =+∈，若|()1|f x a -<的必要条件是|1|(,0)x b a b +<>，则a ，b 之间的关系是（ ） A ．2a bB ．2a b <C ．2b aD ．2b a >5．设函数()x f x xe =，则（ ） A ．1x =为()f x 的极大值点 B ．1x =为()f x 的极小值点 C ．1x =-为()f x 的极大值点D ．1x =-为()f x 的极小值点6．已知复数z 满足(1i)2z ⋅+=，则z =（ ）A ．1BC ．2D ．37．已知函数22()1x f x e ax bx =-+-，其中,a b ∈R ，e 为自然对数的底数，若(1)0f =，'()f x 是()f x 的导函数，函数'()f x 在区间(0,1)内有两个零点，则a 的取值范围是（ ）A ．22(3,1)e e -+B ．2(3,)e -+∞C ．2(,22)e -∞+D ．22(26,22)e e -+8．设集合{}1,2,4A =，{}240B x x x m =-+=．若{}1A B ⋂=，则B = ( )A ．{}1,3-B ．{}1,0C ．{}1,3D ．{}1,59．已知二项式2(*)nx n N x ⎛-∈ ⎪⎝⎭的展开式中第2项与第3项的二项式系数之比是2︰5，则3x 的系数为（ ） A ．14B ．14-C ．240D ．240-10．复数22cos sin 33z i ππ=+在复平面内对应的点在( ) A ．第一象限B ．第二象限C ．第三象限D ．第四象限11．平面内平行于同一直线的两直线平行，由类比思维，我们可以得到（ ） A ．空间中平行于同一直线的两直线平行 B ．空间中平行于同一平面的两直线平行 C ．空间中平行于同一直线的两平面平行 D ．空间中平行于同一平面的两平面平行 12．若()()()()9290129111x a a a x a x a x +=+++++++，若684a =，则实数a 的值为（ ）A ．1B ．2C ．2-D ．3-二、填空题：本题共4小题 13．已知函数()f x 的导函数为'()f x ，且满足()2'()ln f x xf e x =+，则()f e =__________．14．《左传.僖公十四年》有记载:“皮之不存,毛将焉附?"”这句话的意思是说皮都没有了,毛往哪里依附呢?比喻事物失去了借以生存的基础,就不能存在.皮之不存,毛将焉附?则“有毛”是“有皮”的__________条件(将正确的序号填入空格处).①充分条件②必要条件③充要 条件④既不充分也不必要条件15．已知33210n n A A =，那么n =__________．16．已知函数1y x =的图象的对称中心为()0,0，函数111y x x =++的图象的对称中心为1,02⎛⎫- ⎪⎝⎭，函数11112y x x x =++++的图象的对称中心为()1,0-.由此推测，函数12202012019x x x y x x x +++=+++++的图象的对称中心为________.三、解答题：解答应写出文字说明、证明过程或演算步骤。

2019学年上海市高二下学期期末考试数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________题号一二三总分得分一、填空题1. 已知，则________________________ ．2. 若正方体的体对角线长是4，则正方体的体积是______________________________ ．3. 经过抛物线的焦点，且以为方向向量的直线的方程是____________________________ ．4. 在二项式的展开式中，含的项的系数是______________________________ ．（用数字作答）5. 若双曲线的渐近线方程为，它的一个焦点与抛物线的焦点重合，则双曲线的标准方程为．6. 设<a href=""> 分别是双曲线<ahref=""> 的左、右焦点，若点<ahref=""> 在双曲线上，且，则_________________________________ ．7. 若五个人排成一排，则甲乙两人之间仅有一人的概率是____________________________ ．（结果用数值表示）8. 已知，，若直线与射线（为端点）有交点，则实数的取值范围是______________________________________ ．9. 圆锥的侧面展开图为扇形，若其弧长为 cm，半径为 cm，则该圆锥的体积为 ________ ．10. 在一个密闭的容积为1的透明正方体容器内装有部分液体，如果任意转动该正方体，液面的形状都不可能是三角形，那么液体体积的取值范围是______________________________ ．11. 在一个水平放置的底面半径为<a href="/"> cm的圆柱形量杯中装有适量的水，现放入一个半径为<a href="/"> cm 的实心铁球，球完全浸没于水中且无水溢出，若水面高度恰好上升<ahref="/"> cm，则<a href="/">___ ____cm ．12. 如图，中，，在三角形内挖去半圆，圆心在边AC上，半圆与BC、AB相切于点C、M ，与AC交于点N，则图中阴影部分绕直线AC旋转一周所得旋转体的体积为____________________ ．13. 已知抛物线，过定点作两条互相垂直的直线，与抛物线交于两点，与抛物线交于两点，设的斜率为．若某同学已正确求得弦的中垂线在y轴上的截距为，则弦MN的中垂线在y轴上的截距为_________________________________ ．14. 半径为的球的直径垂直于平面，垂足为，是平面内边长为的正三角形，线段、分别与球面交于点M，N，那么M、N两点间的球面距离是_________________________________ ．二、选择题15. 四位好朋友在一次聚会上，他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯，如下图所示，盛满酒后他们约定：先各自饮杯中酒的一半．设剩余酒的高度从左到右依次为，，，，则它们的大小关系正确的是（）A ．_________B ．_________C ．D ．16. 已知直线平面，直线在平面内，给出下列四个命题：①　；②　；③　；④　，其中真命题的个数是（）A ．①②____________________________B ．①④____________________________C ．②③______________________________D ．②④17. 方程的图象表示曲线C，则以下命题中甲：曲线C为椭圆 , 则1< t<4 ；乙：若曲线C为双曲线 , 则 t > 4 或 t<1 ；丙：曲线C不可能是圆； ________________________丁：曲线C表示椭圆,且长轴在 x 轴上 , 则．正确的有（）A ． 1个____________________________B ． 2个____________________________C ． 3个____________________________D ． 4个18. 将正整数n表示成k个正整数的和（不计较各数的次序），称为将正整数n分成k个部分的一个划分，一个划分中的各加数与另一个划分的各加数不全相同，则称为不同的划分，将正整数n划分成k个部分的不同划分的个数记为P （ n,k ），则P（ 10,3 ）的值为（）A ． 12______________________________B ． 10_________________________________C ． 8______________________________D ． 6三、解答题19. （本题满分 1 2分）如图，直线平面，为正方形，，求直线与所成角的大小．20. （本题满分 1 4分）本题共有2个小题，第 1 小题满分6分，第 2 小题满分8分．在二项式的展开式中：（1）若第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项；（2）若所有项的二项式系数和等于4096，求展开式中系数最大的项．21. （本题满分 1 4分）本题共有2个小题，第 1 小题满分6分，第2小题满分8分．已知圆．（1）求过点的圆C的切线的方程；（2）如图，为圆C上一动点，点P在AM上，点N在CM上，且满足求的轨迹．22. （本题满分 1 6分）本题共有3个小题，第 1 小题满分4分，第2小题满分6分，第3小题满分6分．如图，圆锥的轴截面为等腰直角三角形，为底面圆周上一点．（1）如果的中点为，，求证：平面；（2）如果 , ，求此圆锥的体积；（ 3 ）如果二面角大小为，求的大小．23. （本题满分 1 8分）本题共有3个小题，第 1 小题满分5分，第 2 小题满分8分，第3小题满分5分．定义：由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”．如果两个椭圆的“特征三角形”是相似的，则称这两个椭圆是“相似椭圆”，并将三角形的相似比称为椭圆的相似比．已知椭圆．（1）若椭圆，判断与是否相似？如果相似，求出与的相似比；如果不相似，请说明理由；（2）写出与椭圆相似且焦点在轴上、短半轴长为的椭圆的标准方程；若在椭圆上存在两点、关于直线对称，求实数的取值范围；（3）如图：直线与两个“相似椭圆”　和分别交于点和点，试在椭圆和椭圆上分别作出点和点（非椭圆顶点），使和组成以为相似比的两个相似三角形，写出具体作法．（不必证明）参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】。

2019-2020学年上海市曹杨二中高二下学期期末数学试题一、单选题1．已知直角坐标系xOy 平面上的直线1x ya b+=经过第一、第二和第四象限，则,a b 满足（ ） A ．0,0a b >> B ．0a >，0b < C ．0a <，0b < D ．0a <，0b <【答案】A【解析】求出直线与坐标轴的交点，即可得出答案. 【详解】令0x =，则y b =；令0y =，则x a = 所以(0,),(,0)b a 在直线1x ya b+=上 因为直线1x ya b+=经过第一、第二和第四象限 所以0,0a b >> 故选：A 【点睛】本题主要考查了由直线所过象限求参数范围，属于基础题.2．复数(),z a bi a b R =+∈，()m z z b =+，n z z =⋅，2p z =，则（ ）A ．m 、n 、p 三数都不能比较大小B ．m 、n 、p 三数的大小关系不能确定C ．m n p ≤=D ．m n p ≥=【答案】C【解析】根据复数的四则运算，结合基本不等式，即可得出结论. 【详解】z a bi =-，()2m a bi a bi b ab =++-=，22()()n a bi a bi a b =+-=+，22p a b =+222a b ab +，当且仅当a b =时，取等号m n p ∴≤=故选：C 【点睛】本题主要考查了复数的四则运算，涉及了基本不等式的应用，属于中档题.3．设复数()0,0z a bi a b =+>≠是实系数方程20x px q ++=的根，又3z 为实数，则点(),p q 的轨迹在一条曲线上，这条曲线是（ ） A ．圆 B ．椭圆C ．双曲线D ．抛物线【答案】D【解析】由3z 为实数，求出,a b 关系，实系数方程有虚数根，∆<0，且两根互为共轭，由韦达定理，求出,p q 与,a b 关系，结合,a b 关系，即可得出,p q 的关系式，得出结论. 【详解】()3220,0,(2)()z a bi a b z a b abi a bi =+>≠=-++，其虚部为22222()2(3)a b b a b b a b -+=-，又3z 为实数，所以2222(3)0,0,30b a b b b a -=≠=≠， 复数()0,0z a bi a b =+>≠是实系数方程20x px q ++=的根，()0,0z a bi a b =->≠也是实系数方程20x px q ++=的根，所以222240,2,40p q z z a p zz a b a q ∆=-<+==-=+==>， 所以2,0p q p =<，此时30q ∆=-<，即点(),p q 的轨迹在抛物线2y x 上.故选：D . 【点睛】本题考查实系数一元二次方程根的关系、复数的基本概念，韦达定理的应用是解题的关键，考查计算求解能力，属于中档题.4．已知a 、b 、e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430b e b -⋅+=，则a b -的最小值是（ ）A ．1-B ．1C ．2D ．2-【答案】A【解析】先确定向量a 、b 所表示的点的轨迹，一个为直线，一个为圆，再根据直线与圆的位置关系求最小值. 【详解】设()()(),,1,0,,a x y e b m n ===，则由π,3a e =得πcos ,3a e e x y a ⋅=⋅=∴=， 由2430b e b -⋅+=得()2222430,21,m n m m n +-+=-+=因此，a b -的最小值为圆心()2,0到直线y =1，为1.选A.【点睛】以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系，是解决这类问题的一般方法.二、填空题5．已知复数1z =-，则z =______.【解析】利用复数模的求法：z =.【详解】由复数1z =，则z ==，【点睛】本题考查了复数模的求法，考查了基本运算求解能力，属于基础题. 6．如果复数()2(1)++m i mi 是实数，则实数m =________． 【答案】1-【解析】利用复数的四则运算法则将()2(1)++m i mi 化简为a bi +的形式，结合实数的定义即可求解. 【详解】由题意可得，()223(1)(1)m i mi m m m i ++=-++，因为复数()2(1)++m i mi 是实数，所以310m +=，解得1m =-. 故答案为：-1本题主要考查复数的四则运算及复数的概念与分类，属于基础题. 7．若a 、b R ∈，且()a i i b i +=+，则a b +=______. 【答案】0【解析】利用复数的乘法法则和复数相等可得出关于a 、b 的方程组，解出a 、b 的值，进而可求得+a b 的值. 【详解】()1b i a i i ai +=+=-+，所以11a b =⎧⎨=-⎩，因此，0a b +=.故答案为：0. 【点睛】本题考查利用复数的乘法法则和复数相等求参数，考查计算能力，属于基础题. 8．直线110l x y -+=：与直线250l x y -+=：之间的距离是______．【答案】【解析】根据两条平行线间的距离公式，可直接求出结果. 【详解】直线110l x y -+=：与直线250l x y -+=：之间的距离==故答案为：【点睛】本题主要考查两平行线间的距离，熟记公式即可，属于常考题型. 9．若复数z 同时满足2i z z -=，iz z =，则z =__________． 【答案】1i -+【解析】消去z 后，根据复数的乘除法运算法则，计算可得答案. 【详解】因为2i z z -=，iz z =， 所以2z iz i -=， 所以21i z i=-2(1)(1)(1)i i i i +=-+2212i i -+==-+. 故答案为：1i -+本题考查了复数的乘法、除法运算法则，属于基础题.10．若抛物线24y x =上一点M 到焦点的距离等于2，则M 到坐标原点O 的距离等于______.【解析】根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等，进而利用点到直线的距离求得x 的值，代入抛物线方程求得y 值，即可得到所求点的坐标，从而求得其到原点的距离． 【详解】 解：抛物线方程为24y x =，∴焦点为(1,0)F ，准线为:1l x =-抛物线24y x =上一点P 到焦点的距离等于2，∴根据抛物线定义可知P 到准线的距离等于2，即12x +=，解之得1x =， 代入抛物线方程求得2y =±，∴点P 坐标为：(1,2)±=【点睛】本题主要考查了抛物线的简单性质．在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决，属于基础题．11．若方程220x y x y m -++=+表示一个圆，则实数m 的取值范围是______. 【答案】1,2⎛⎫-∞ ⎪⎝⎭【解析】根据题意，由圆的一般方程的形式分析可得1140m +-⨯>，解可得m 的取值范围，即可得答案． 【详解】解：根据题意，方程220x y x y m -++=+表示一个圆， 则有1140m +-⨯>，解的12m <，即m 的取值范围为1,2⎛⎫-∞ ⎪⎝⎭；故答案为：1,2⎛⎫-∞ ⎪⎝⎭． 【点睛】本题考查二元二次方程表示圆的条件，涉及圆的一般方程，属于基础题． 12．过点()3,2P -且与直线210x y ++=垂直的直线方程是______. 【答案】270x y --=【解析】根据直线的垂直关系，设出所求直线方程，将()3,2P -代入方程，即可求解. 【详解】所求直线与直线210x y ++=垂直， 设该直线方程为20x y c -+=，()3,2P -代入上式方程得7c =-，所以所求的直线方程为270x y --=. 故答案为：270x y --=. 【点睛】本题考查直线的位置关系求方程，利用直线的位置关系合理设方程是解题的关键，属于容易题.13．已知点M ，0)，椭圆22+14x y =与直线y ＝k (x 交于点A ，B ，则△ABM的周长为________. 【答案】8【解析】直线y=k （过定点N （），确定椭圆的几何量，再利用椭圆的定义，即可求△ABM 的周长. 【详解】直线y=k （过定点N （），由题设知M 、N 是椭圆的焦点，由椭圆定义知： AN+AM=2a=4，BM+BN=2a=4．△ABM 的周长为AB+BM+AM=（AN+BN ）+BM+AM=（AN+AM ）+（BN+BM ）=8， 故答案为：8．【点睛】本题考查椭圆的定义，直线过定点问题和利用椭圆的定义是解题的关键．14．设()1,2A ，()3,1B -，若直线2y kx =-与线段AB 有公共点，则实数k 的取值范围是______. 【答案】(][),14,-∞-+∞【解析】画出图象求出定点与A 、B 两点连线的斜率，即可求出实数k 的取值范围． 【详解】解：直线2y kx =-恒过定点()0,2-，由题意平面内两点()1,2A ，()3,1B -，直线2y kx =-与线段AB 恒有公共点，如图求出定点与A 、B 两点连线的斜率，()122410k --==-．()212130k --==---，所以直线2y kx =-与线段AB 恒有公共点，则实数k 的取值范围是(][),14,-∞-+∞，故答案为：(][),14,-∞-+∞【点睛】本题考查直线斜率的求法，考查数形结合的思想的应用，考查计算能力．15．已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F ，2F ，过1F 的直线与C 的两条渐近线分别交于A 、B 两点，若1F A AB =，120F B F B ⋅=，则C 的渐近线方程为__________. 【答案】3y x =±【解析】结合题意画出图形，结合已知条件可得1F B OA ⊥， 又A 为1F B 的中点，可得123FOA BOA F OB π∠=∠=∠=，得到结果.【详解】如图，1F A AB =，120F B F B ⋅=，121F B F B F B OA ∴⊥⊥，，又A 为1F B 的中点，∴1FOA BOA ∠=∠， 而直线OA ，OB 为两条渐近线，∴12FOA F OB ∠=∠， ∴123FOA BOA F OB π∠=∠=∠=，∴2tan F OB ∠=3ba= ∴C 的渐近线方程为3y x =故答案为：3y x = 【点睛】本题考查双曲线的几何性质，数形结合的思想方法，计算能力，属于中档题16．曲线C 是平面内与两个定点()11,0F -和()21,0F 的距离的积等于常数()21a a >的点的轨.给出下列四个结论：①曲线C 过坐标原点；②曲线C 关于坐标原点对称；③若点P 在曲线C 上，则122PF PF a +<；④若点P 在曲线C 上，则12F PF △的面积212S a ≤.其中，所有正确的序号是______. 【答案】②④【解析】由题意曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >，利用直接法，设动点坐标为(,)x y ，及可得到动点的轨迹方程，然后由方程特点即可加以判断． 【详解】解：对于①，由题意设动点坐标为(,)x y ，则利用题意及两点间的距离公式的得：22224[(1)][(1)]x y x y a ++-+=，将原点代入验证，此方程不过原点，所以①错； 对于②，把方程中的x 被x -代换，y 被y - 代换，方程不变，故此曲线关于原点对称，故②正确；对于③，221y x =--，22211y x a ∴+=-+-，P ∴到原点的，当P 在y 轴时取等号，此时12PF PF a ==，122PF PF a +=故③错误；对于④，由题意知点P 在曲线C 上，则△12F PF 的面积12122F PF Sy y =⨯⨯=，由①知221y x =--+或221y x =---t =，则2424t a x -=，24442211(2)4444t a a a y t t -∴=--+=--+，1222212F PF S y a ∴=，故④正确．故答案为：②④． 【点睛】本题考查了利用直接法求出动点的轨迹方程，并化简，利用方程判断曲线的对称性及利用解析式选择换元法求出值域．三、解答题17．设,αβ分别是方程220x x a ++=()a R ∈的两个虚数根. （1）求a 的取值范围及αβ+的值； （2）若4αβ-=，求a 的值.【答案】（1）1a >，（2）5.【解析】（1）由条件可得440a ∆=-<，得出a 的取值范围，根据求根公式可求得方程虚数根,αβ，代入αβ+，可得到答案.（2）由（1）可得αβ-==. 【详解】（1）由方程220x x a ++=()a R ∈有两个虚数根 所以440a ∆=-<，解得1a >由,αβ是方程220x x a ++=()a R ∈的两个虚数根. 可得,αβ，不妨设1α==-+,1β==--所以αβ+=（2）由（1）可得αβ-==根据4αβ-=，即4=，解得5a = 【点睛】本题考查实系数一元二次方程有虚数根的条件以及求根公式的应用，属于中档题. 18．已知ABC ∆的三个顶点(),A m n 、()2,1B 、()2,3C -. （1）求BC 边所在直线的方程；（2）BC 边上中线AD 的方程为2360x y -+=，且7ABC S ∆=，求点A 的坐标. 【答案】（1）240x y +-=；（2）点A 坐标为()3,4、()3,0- 【解析】（1）利用两点式求得BC 边所在直线方程；（2）利用点到直线的距离公式求得A 到直线BC 的距离，根据面积7ABC S ∆=以及点A 在直线2360x y -+=上列方程组，解方程组求得A 点的坐标. 【详解】（1）由()2,1B 、()2,3C -得BC 边所在直线方程为123122y x --=---，即240x y +-=.（2）BC ==，A 到BC 边所在直线240x y +-=的距离为d =A 在直线2360x y -+=上，故1722360ABC S BC d m n ∆⎧=⋅⋅=⎪⎨⎪-+=⎩，即2472360m n m n ⎧+-=⎨-+=⎩，解得()3,4A 或()30A -,. 【点睛】本小题主要考查利用两点式求直线方程，考查点到直线的距离公式，考查三角形面积公式，属于基础题.19．已知直线:l y x m =+，m R ∈.（1）若以点()2,0M 为圆心的圆与直线l 相切于点P ，且点P 在y 轴上，求该圆的方程；（2）若直线l 与抛物线2:4C x y =有且仅有一个公共点，求m 的取值范围.【答案】（1）()2228x y -+=；（2）1m =-.【解析】（1）利用待定系数法求本题中圆的方程是解决本题的关键，利用直线与圆相切的数学关系列出关于圆的半径的方程，通过求解方程确定出所求圆的半径，进而写出所求圆的方程；（2）联立直线与抛物线方程、消元，由0∆=计算可得； 【详解】解：（1）设所求圆的半径为r ，则圆的方程可设为222(2)x y r -+=．由题意，所求圆与直线:l y x m =+相切于点(0,)P m ，则有224m r r ⎧+==，解得2m r =⎧⎪⎨=⎪⎩，所以圆的方程为22(2)8x y -+=． （2）因为直线:l y x m =+与抛物线2:4C x y =有且仅有一个公共点，联立方程得24y x m x y=+⎧⎨=⎩消元得2440x x m --=，所以()()24440m ∆=--⨯-=解得1m =-【点睛】本题考查直线与圆的位置关系，直线与抛物线的位置关系，考查学生的方程思想和运算化简能力，属于基础题．20．已知椭圆222:1x C y m+=（常数1m >），点P 是C 上的动点，M 是右顶点，定点A 的坐标为(2,0)．⑴若M 与A 重合，求C 的焦点坐标； ⑵若3m =，求PA 的最大值与最小值； ⑶若PA 的最小值为MA ，求m 的取值范围．【答案】（1）(（2）min ||PA =max||5PA =（3）11m <≤+【解析】解：⑴2m =，椭圆方程为2214x y +=，c ==∴ 左、右焦点坐标为(．⑵3m =，椭圆方程为2219x y +=，设(,)P x y ，则222222891||(2)(2)1()(33)9942x PA x y x x x =-+=-+-=-+-≤≤∴94x =时min ||2PA =；3x =-时max ||5PA =． ⑶设动点(,)P x y ，则222222222222124||(2)(2)1()5()11x m m m PA x y x x m x m m m m m -=-+=-+-=--+-≤≤--∵ 当x m =时，PA 取最小值，且2210m m ->，∴2221mm m ≥-且1m >解得11m <≤+21．已知直线1:l y x =及直线2:l y x =-.平面上动点(),M x y ，且x y >，记M 到直线1l 、2l 的距离分别为1d 、2d ，满足：()21202a d d a ⋅=>.（1）求动点M 的轨迹Γ的方程；（2）若直线l 的方向向量为()1,2，过),0的直线l 与曲线Γ交于A 、B 两点，问以AB 为直径的圆是否恰过原点O ？若是，求a 的值；若不是，判断原点在圆内还是圆外，并说明理由？（3）若过原点O 作斜率为k 的直线n 交曲线Γ于M 、N 两点，设()0,1P ，求PMN 的面积S 关于k 的函数解析式，并求S 的取值范围. 【答案】(1) ()2220x y aa -=> (2) 以AB 为直径的圆不过原点O ，点O 在圆外(3)S a =, S 的取值范围是S a ≥ 【解析】（1）由条件有2221222x y a d d -⋅===，得出答案. （2）设()()1122,,,A x y B x y ，根据条件可设直线l的方程为：()2y x =，与曲线Γ的方程联立，得到123x x +=，2123x x a ⋅=，由1212OA OB x x y y ⋅=+的符号可得出答案.（3）由题意直线n 的方程为y kx =，与曲线Γ的方程联立，可得M （或N ）的点的横坐标，根据条件可得k的范围，122N S OP x a =⨯⨯⨯=，然后求出范围. 【详解】（1）由(),M x y 到直线1l 、2l 的距离分别为1d 、2d ，且2122a d d ⋅=则2221222x y a d d -⋅===，又x y > 所以22222222x y x y a --==，即222x y a -= 则动点M 的轨迹Γ的方程；()2220x y aa -=>（2）由直线l 的方向向量为()1,2，则直线l 的斜率为2k =. 又直线l过),0，则直线l的方程为：()2y x =设()()1122,,,A x y B x y，由()2222y x x y a⎧=-⎪⎨-=⎪⎩得22390x a -+=则123x x +=，2123x x a ⋅=所以()()()2121212124224222y y x axa x x a x x a ⎡⎤⋅=⨯--=⨯-++⎣⎦222824432233a a a a a ⎛⎫=⨯-⋅+=- ⎪ ⎪⎝⎭2221212453033a a OA OB x x y y a ⋅=+=-=>所以以AB 为直径的圆不过原点O ，由0OA OB ⋅>，所以点O 在圆外. （3）直线n 的方程为y kx =由222y kx x y a=⎧⎨-=⎩得2222x k x a -=， 由直线n 交曲线Γ于M 、N 两点，则210k ->，则201k ≤<则2221a x k=- 211221N S OP x a k =⨯⨯⨯=⋅-由201k ≤<，得2011k <-≤，所以211a a k⋅≥- 所以PMN 的面积S 关于k 的函数解析式为211S a k =⋅-，PMN 的面积S 的取值范围是S a ≥.【点睛】本题考查求轨迹的方程，利用数量积研究点与圆的位置关系，求三角形的面积，属于中档题.。

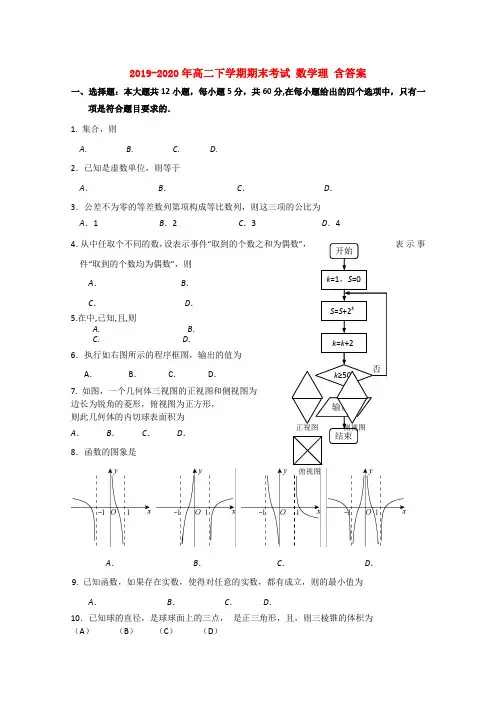
2019-2020年高二下学期期末考试数学理含答案一、选择题：本大题共12小题，每小题5分，共60分,在每小题给出的四个选项中，只有一项是符合题目要求的．1. 集合，则A. B. C. D.2．已知是虚数单位，则等于A．B．C．D．3．公差不为零的等差数列第项构成等比数列，则这三项的公比为A．1 B．2 C．3 D．44．从中任取个不同的数，设表示事件“表示事件“取到的个数均为偶数”，则A．B．C．D．5.在中,已知,且,则A.B.C. D.6．执行如右图所示的程序框图，输出的值为A．B．C．D．7. 如图，一个几何体三视图的正视图和侧视图为边长为锐角的菱形，俯视图为正方形，则此几何体的内切球表面积为A．B．C．D．8．函数的图象是A．B．C．D．9. 已知函数，如果存在实数，使得对任意的实数，都有成立，则的最小值为A．B．C．D．10．已知球的直径，是球球面上的三点，是正三角形，且，则三棱锥的体积为（A）（B）（C）（D）俯视图11. 过双曲线的左焦点，作圆：的切线，切点为，延长交双曲线右支于点，若，则双曲线的离心率为A. B. C. D.12．已知函数的两个极值点分别为且，记分别以为横、纵坐标的点表示的平面区域为，若函数的图象上存在区域D内的点，则实数的取值范围为A．B．C．D．试卷Ⅱ（共90 分）二、填空题：本大题共4小题，每小题5分, 共20分．13．某市有A、B、C三所学校共有高二理科学生1500人，且A、B、C三所学校的高二理科学生人数成等差数列，在三月进行全市联考后，准备用分层抽样的方法从所有高二理科学生中抽取容量为120的样本进行成绩分析，则应从B校学生中抽取_____人.14．过抛物线的焦点的直线与抛物线在第一象限的交点为A，直线l与抛物线的准线的交点为B，点A在抛物线的准线上的射影为C，若，，则抛物线的方程为.15. 设曲线在点处的切线与轴的交点的横坐标为，令，则的值为．16．观察下列算式：，若某数按上述规律展开后，发现等式右边含有“”这个数，则．三、解答题:本大题共6小题，共70分，解答应写出文字说明．证明过程或演算步骤.17. （本题满分12分）已知中，角所对的边分别是，且（Ⅰ）求；（Ⅱ）若，求面积的最大值．18.（本小题满分12分）在某大学自主招生考试中，所有选报II 类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A ,B ,C ,D ,E 五个等级. 某考场考生两科的考试成绩的数据统计如下图所示，其中“数学与逻辑”科目的成绩为的考生有人.（Ⅰ）求该考场考生中“阅读与表达”科目中成绩为A 的人数； （Ⅱ）若等级A ，B ，C ，D ，E 分别对应5分，4分，3分，2分，1分. （i ）求该考场考生“数学与逻辑”科目的平均分；(ii)若该考场共有10人得分大于7分，其中有2人10分，2人9分，6人8分. 从这人中随机抽取两人，求两人成绩之和的分布列和数学期望.19. (本小题满分12分）在三棱柱中，侧面为矩形，为 中点，与交于点，丄面．(Ⅰ )证明：(Ⅱ)若求二面角的余弦值.20．（本小题满分12分）已知椭圆的离心率且经过点，抛物线的焦点与椭圆的一个焦点重合．（Ⅰ）过的直线与抛物线交于两点，过分别作抛物线的切线，求直线的交点的轨迹方程； （Ⅱ）从圆上任意一点作椭圆的两条切线，切点分别为，试问的大小是否为定值，若是定值，求出这个定值；若不是定值，请说明理由。

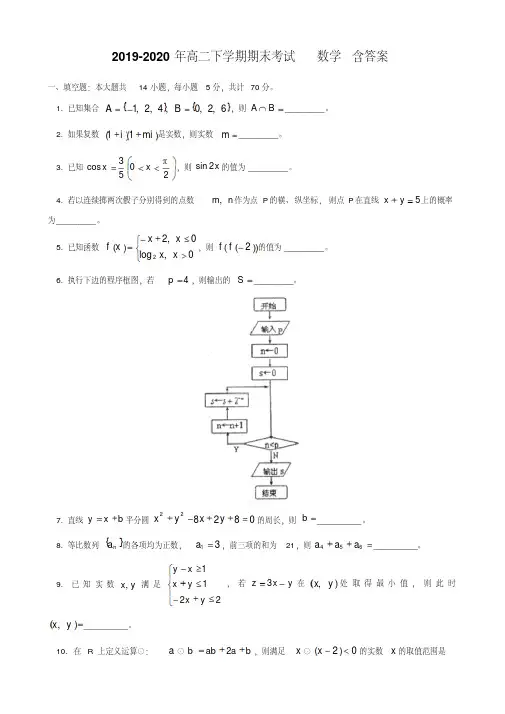
2019-2020年高二下学期期末考试数学含答案一、填空题：本大题共14小题，每小题5分，共计70分。

1. 已知集合6,2,0,4,2,1B A ，则B A _________。

2. 如果复数mi i 11是实数，则实数m _________。

3. 已知2053cos x x ，则x 2sin 的值为_________。

4. 若以连续掷两次骰子分别得到的点数n m,作为点P 的横、纵坐标，则点P 在直线5y x 上的概率为_________。

5. 已知函数0,log 0,22xx x x x f ，则2f f 的值为_________。

6. 执行下边的程序框图，若4p ，则输出的S _________。

7. 直线b x y平分圆082822y x y x 的周长，则b __________。

8. 等比数列n a 的各项均为正数，31a ，前三项的和为21，则654a a a __________。

9. 已知实数y x,满足2211y x y x xy ，若y x z 3在y x,处取得最小值，则此时y x,__________。

10. 在R 上定义运算⊙：a ⊙b b a ab 2，则满足x ⊙02x 的实数x 的取值范围是__________。

11. 在△ABC 中，∠BAC=90°，AB=6，D 为斜边BC 的中点，则AD AB 的值为__________。

12. 已知函数2,0,6sin 2x x x f ，则该函数的值域为__________。

13. 把数列n 21的所有项按照从大到小，左大右小的原则写成如图所示的数表，第k 行有12k 个数，第k 行的第s 个数（从左数起）记为s k,，则20121可记为__________。

14. 如图放置的边长为1的正三角形PAB 沿x 轴滚动，设顶点y x P ,的纵坐标与横坐标的函数关系式是x f y ，x f y 在其两个相邻零点间的图象与x 轴所围区域的面积记为S ，则S=__________。

2019-2020年高二下学期期末考试数学试题 含答案一、选择题（共12小题，共60分） 1．设，则下列不等式一定成立的是（ ） (A) (B) (C) (D)2．已知实数x ，y 满足，则z ＝4x ＋y 的最大值为( ) A 、10 B 、8 C 、2 D 、03．若不等式组0220x y x y y x y a-≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩，表示的平面区域是一个三角形区域，则的取值范围是（ ）A. B. C. D.或4．等差数列99637419,27,39,}{S a a a a a a a n 项和则前已知中=++=++的值为（ ） A ．66 B ．99 C ．144 D ．2975．已知，则“”是“成立”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件6．等差数列99637419,27,39,}{S a a a a a a a n 项和则前已知中=++=++的值为（ ） A ．66 B ．99 C ．144 D ．297 7．已知，则“”是“成立”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件 8．已知变量x,y 满足约束条件 则的取值范围是( ) A ． B ． C ． D ．(3,6] 9．当时，的最小值为（ ）A ．10B ．12C ．14D ．16 10．已知实数满足，则目标函数的最大值为（ ） A ． B ． C ． D ． 11．在中，内角的对边分别为，若,,,则等于( )A ．1B ．C ．D ．2 12．已知数列是公比为2的等比数列，若，则= ( )A ．1B ．2C ．3D ．4第II 卷（非选择题）二、填空题（4小题，共20分）13．已知向量，若⊥，则16x +4y 的最小值为 ．14．在锐角中,，三角形的面积等于，则的长为___________. 15．已知数列中，，，则=___________. 16．不等式的解是___________. 三、解答题（8小题，共70分）17．已知等比数列{a n }满足：a 1=2，a 2•a 4=a 6． （1）求数列{a n }的通项公式；（2）记数列b n =，求该数列{b n }的前n 项和S n ．18．已知数列的各项均为正数，是数列的前n 项和，且． （1）求数列的通项公式；（2）n n n nn b a b a b a T b +++== 2211,2求已知的值．19．在中，已知内角，边.设内角,面积为. (1)若，求边的长； (2)求的最大值. 20．等差数列中，，（），是数列的前n 项和. （1）求；（2）设数列满足（），求的前项和．21．已知的三个内角成等差数列，它们的对边分别为，且满足，． （1）求；（2）求的面积．22．已知函数，且的解集为． （1）求的值；（2）若，且，求证：． 23．已知数列满足首项为，，．设，数列满足． （1）求证：数列是等差数列； （2）求数列的前项和． 24．已知正实数、、满足条件， （1）求证：；（2）若，求的最大值．参考答案 1．D 【解析】试题分析：本题主要考查不等式的性质，在不等式的性质中，与乘除相关的性质中有条件“均为正数”，否则不等式不一定成立，如本题中当都是负数时，都不成立，当然只能选D ，事实上由于函数是增函数，故是正确的． 考点：不等式的性质． 2．B 【解析】试题分析：画出可行域，根据图形可知，当目标函数经过A(2，0)点时，z ＝4x ＋y 取得最大值为8考点：线性规划. 3．D【解析】根据0220x y x y y -≥⎧⎪+≤⎪⎨≥⎪⎪⎩画出平面区域（如图1所示），由于直线斜率为，纵截距为，自直线经过原点起，向上平移，当时，0220x y x y y x y a -≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩表示的平面区域是一个三角形区域（如图2所示）；当时，0220x y x y y x y a -≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩表示的平面区域是一个四边形区域（如图3所示），当时，220x y x y y x y a-≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩表示的平面区域是一个三角形区域（如图1所示），故选D.图1 图2 图3 考点：平面区域与简单线性规划. 4．B【解析】由已知及等差数列的性质得， 所以，19464699(a a )9(a a )13,9,S 99,22a a ++=====选B. 考点：等差数列及其性质，等差数列的求和公式.5．B【解析】解得其解集，解得， 因为，所以，”是“成立”的必要不充分条件，选. 考点：充要条件，一元二次不等式的解法. 6．B【解析】由已知及等差数列的性质得， 所以，19464699(a a )9(a a )13,9,S 99,22a a ++=====选B. 考点：等差数列及其性质，等差数列的求和公式.7．B【解析】解得其解集，解得， 因为，所以，”是“成立”的必要不充分条件，选. 考点：充要条件，一元二次不等式的解法. 8．A 【解析】试题分析：画出可行域，可理解为可行域中一点到原点的直线的斜率,可知可行域的边界交点为临界点（），（）则可知k ＝的范围是. 考点：线性规划，斜率. 9．D 【解析】试题分析：因为所以＝16.考点：基本不等式的应用.10．C【解析】试题分析：作出可行域如图：再作出目标函数线，并平移使之经过可行域，当目标函数线过点时纵截距最小但最大，此时.故C正确.考点：线性规划问题.11．A【解析】试题分析：由正弦定理得，即。

曹杨二中高二期末数学试卷2019.06一. 填空题1. 1-的平方根为2. 复数2i iz +=的虚部为 3. 抛物线2y x =的焦点到准线的距离为 4. 若复数z 满足||1z =，则|1i |z -+的最大值是5. 若双曲线的焦点在x 轴上，焦距为4，且过点(2,3)P ，则双曲线的标准方程为6. 用1，2，3，4，5，6组成没有重复数字的六位数，要求任意相邻两个数码的奇偶性都不同，则这样的六位数的个数是7. 已知直线1l ：10mx y +-=，2l ：(2)20m x my ++-=，若1l 与2l 平行，则实数m 的值为8. 已知方程220x x p -+=的两个虚根为α、β，且||4αβ-=，则实数p =9. 已知直线l 过点(0,5)，且它的一个方向向量为（1,2），则原点O 到直线l 的距离为10. 设6523001230(1)x x a a x a x a x ++=+++⋅⋅⋅+，其中01230,,,,a a a a ⋅⋅⋅是各项的系数，则在01230,,,,a a a a ⋅⋅⋅这31个系数中，值为零的个数为11. 在直角坐标系中，已知(1,0)A ，(4,0)B ，若直线10x my +-=上存在点P ，使得||2||PA PB =，则实数m 的取值范围是12. 从集合{,,,}U a b c d =的子集中选出2个不同的子集，需同时满足以下两个条件：①a 、b 都至少属于其中一个集合；②对选出的两个子集A 、B ，必有A B ⊆或B A ⊆，那么共有 种不同的选法二. 选择题13. 若12i +是关于x 的实系数一元二次方程20x bx c ++=的一个根，则（ ）A. 2b =, 5c =B. 2b =-,5c =C. 2b =-,3c =-D. 2b =,1c =-14. 若m 是小于10的正整数，则(15)(16)(20)m m m --⋅⋅⋅-等于（ ）A. 515m P -B. 1520m m P --C. 520m P -D. 620m P -15. 已知曲线C :421x y +=，给出下列命题：①曲线C 关于x 轴对称；②曲线C 关于y 轴对称；③曲线C 关于原点对称；④曲线C 关于直线y x =对称；⑤曲线C 关于直线y x =-对称，其中正确命题的个数是（ ）A. 1B. 2C. 3D. 416. 在复数列{}n z 中，1816i z =+，1i 2n n z z +=⋅()n *∈N ，设n z 在复平面上对应的点为n Z ， 则（ ） A. 存在点M ，对任意的正整数n ，都满足||10n MZ ≤B. 不存在点M ，对任意的正整数n ，都满足||55n MZ ≤C. 存在无数个点M ，对任意的正整数n ，都满足||65n MZ ≤D. 存在唯一的点M ，对任意的正整数n ，都满足||85n MZ ≤三. 解答题17. （1）已知2||()i 32i z z z ++=-，求复数z ；（2）已知复数z 满足2z z -为纯虚数，且|i |1z -=，求复数z .18. 已知41(2)n x x+的展开式的二项式系数之和为1024.（1）求展开式中的常数项；（2）求展开式中系数最大的项.19. 如图所示是竖直平面内的一个“通道游戏”，图中竖直线段和斜线都表示通道，并且在交点处相遇，若有一条竖直线段的为第一层，有二条竖直线段的为第二层，以此类推，现有一颗小球从第一层的通道向下运动，在通道的交叉处，小球可以落入左右两个通道中的任意一个，记小球落入第n 层的第m 个竖直通道（从左向右计）的不同路径数为(,)A n m .（1）求(2,1)A ，(3,1)A ，(4,2)A 的值；（2）猜想(,)A n m 的表达式（不必证明），并求不等式(9,)28A m ≤的解集.20. 已知复数z 满足|1||1|z z -++=z 在复平面上对应点的轨迹为C ，A 、B 分别 是曲线C 的上、下顶点，M 是曲线C 上异于A 、B 的一点.（1）求曲线C 的方程；（2）若M 在第一象限，且||OM =，求M 的坐标； （3）过点M 作斜率为1的直线分别交曲线C 于另一点N ，交y 轴于点D ，求证：存在常数λ，使得||||||||DM DN DA DB λ⋅=⋅恒成立，并求出λ的值.21. 已知抛物线Γ：24y x =，F 为其焦点，过F 的直线l 与抛物线Γ交于A 、B 两点.（1）若2AF FB =u u u r u u u r ，求B 点的坐标；（2）若线段AB 的中垂线l '交x 轴于M 点，求证：||||AB FM 为定值； （3）设(1,2)P ，直线PA 、PB 分别与抛物线的准线交于点S 、T ，试判断以线段ST 为直径的圆是否过定点？若是，求出定点的坐标；若不是，请说明理由.参考答案一. 填空题1.i ±2.2-3.12 4. 1+5.2213y x -= 6. 72 7.1- 8. 510. 10 11. (,)-∞+∞U 12. 32二. 选择题13. B 14. D 15. C 16. D三. 解答题17.（1）1-±；（2）2i z =，1i z =-+，1i z =+.18.（1）180；（2）2515360x .19.（1）(2,1)1A =，(3,1)1A =，(4,2)3A =；（2）11m n C --，{1,2,3,7,8,9}.20.（1）2212x y +=；（2）；（3）43. 21.（1）1(,1)4±；（2）2；（3）(0,0)，(2,0)-.。

2019-2020学年上海市中学高二期末数学试题及答案一、单选题1．已知平面直角坐标系内的两个向量(1,2),(,32)a b m m ==-,且平面内的任一向量c 都可以唯一表示成c a b λμ=+(,λμ为实数),则实数m 的取值范围是( ) A ．(,2)-∞ B ．(2,)+∞ C ．(,)-∞+∞D ．(,2)(2,)-∞⋃+∞【答案】D【解析】根据平面向量基本定理只需,a b 不共线即可. 【详解】由题意得,平面内的任一向量c 都可以唯一表示成c a b λμ=+(,λμ为实数),则,a b 一定不共线,所以1(32)2m m ⨯-≠⨯,解得2m ≠, 所以m 的取值范围是(,2)(2,)-∞⋃+∞. 故选：D. 【点睛】此题考查平面向量基本定理的辨析，平面内一组基底必须不共线，求解参数只需考虑根据平面向量共线的坐标运算求出参数即可得解.2．椭圆22:1169x y C +=与直线:(21)(1)74,l m x m y m m R +++=+∈的交点情况是（ ）A ．没有交点B ．有一个交点C ．有两个交点 D ．由m 的取值而确定【答案】C【解析】先将(21)(1)74,+++=+m x m y m 转化为：()2730x y m x y +-++-=，令30,270xy x y +-=+-=，解出直线过定点()3,1A ，再将()3,1A 代入22:1169x y C +=，判断点与椭圆的位置关系. 【详解】已知(21)(1)74,+++=+m x m y m 可转化为：()2740x y m x y +-++-= ，令+-=+-=40,270xy x y ，解得3,1x y ==，所以直线过定点()3,1A ，将()3,1A 代入22:1169x y C += 可得911169+<，所以点()3,1A 在椭圆的内部， 所以直线与椭圆必相交， 所以必有两个交点. 故选：C 【点睛】本题主要考查了点与椭圆，直线与椭圆的位置关系，还考查了转化化归的思想和运算求解的能力，属于基础题.3．过点(1,1)P 作直线与双曲线2212yx -=交于,A B 两点，使点P为AB 的中点，则这样的直线（ ）A ．存在一条，且方程为210x y --=B ．存在无数条C ．存在两条，且方程为2(1)0x y ±+=D ．不存在 【答案】D【解析】分当直线的斜率不存在时，将直线方程为1x = 代入2212y x -=，得0y =，与双曲线只有一个交点，不符合题意；当直线的斜率存在时，设直线方程为()11y k x -=-代入2212y x -=，得()()222221320k x k k x k k ----+-=，分220k -=和22k -≠0两种情况讨论求解.【详解】当直线的斜率不存在时，直线方程为1x = 代入2212y x -=，得0y = ，与双曲线只有一个交点，不符合题意. 当直线的斜率存在时，设直线方程为()11y k x -=-，代入2212y x -=，得()()222221320k x k k x k k ----+-=，当220k -=时，直线()11y x -=-与双曲线只有一个交点，不符合题意.当22k -≠0时，因为点P 为AB 的中点， 由韦达定理得()1222122k k x x k-+==- ，解得2k = 而当2k =时，222[2(1)]4(2)(32)24160k k k k k k ∆=----+-=-<，所以直线与双曲线不相交. 故选：D 【点睛】本题主要考查了直线与双曲线的位置关系，还考查了分类讨论的思想方法，属于中档题.4．已知圆心为O ，半径为1的圆上有不同的三个点,,A B C ，其中0OA OB ⋅=，存在实数,λμ满足0OC OA uOB λ++=，则实数,λμ的关系为A ．221λμ+=B ．111λμ+= C ．1λμ= D ．1λμ+=【答案】A【解析】由题意得1OA OB OC ===，且0OA OB ⋅=.因为0OC OA uOB λ++=，即OC OA uOB λ=--.平方得：221λμ+=. 故选A.二、填空题5．直线l 的倾斜角范围是__________； 【答案】0,【解析】由直线的倾斜角定义来确定. 【详解】由直线倾斜角的定义：x 轴正向与直线向上方向之间所成的角叫直线的倾斜角.特别地，当直线与x 轴平行或重合时，我们规定它的倾斜角为0度.范围：倾斜角的取值范围是0°≤α＜180°. 故答案为：0,【点睛】本题主要考查了直线倾斜角的定义及范围，还考查了理解辨析的能力，属于基础题.6．方程2214x y m+=表示焦点在y 轴上的椭圆，其焦点坐标是_________；【答案】(0,【解析】根据方程2214x y m +=表示焦点在y 轴上的椭圆，确定22,4a m b ==，再由,,a b c 的关系求出c ，写出坐标即可.【详解】因为方程2214x y m +=表示焦点在y 轴上的椭圆，所以22,4a m b == ，所以c==所以焦点坐标为：(0,.故答案为：(0,.【点睛】本题主要考查了椭圆的几何性质，还考查了理解辨析的能力，属于基础题.7．抛物线()20y ax a =<的焦点坐标为____________.【答案】10,4a ⎛⎫⎪⎝⎭【解析】将抛物线的方程化为标准方程，可得出该抛物线的焦点坐标. 【详解】抛物线的标准方程为21x y a=，因此，该抛物线的焦点坐标为10,4a ⎛⎫⎪⎝⎭. 故答案为：10,4a ⎛⎫⎪⎝⎭. 【点睛】本题考查抛物线焦点坐标的求解，解题的关键就是要将抛物线的方程表示为标准形式，考查计算能力，属于基础题. 8i -对应点的直线的倾斜角为_________； 【答案】56π【解析】先利用复数的几何意义，i -对应点的坐标，直线又经过原点()0,0，根据斜率公式求得斜率，再根据斜率与倾斜角的关系求解. 【详解】i -对应点)1- ，直线又经过原点()0,0 ，所以斜率103k ==-，所以tan α= ，又因为[0,)απ∈ ， 所以56πα=.故答案为：56π.【点睛】本题主要考查了直线的斜率，倾斜角及其关系，还考查了运算求解的能力，属于基础题.9．下面四个命题：①,a b 是两个相等的实数，则()()a b a b i -++是纯虚数；②任何两个负数不能比较大小；③12,z z C ∈，且22120z z +=，则120z z ==；④两个共轭虚数的差为纯虚数.其中正确的序号为_________； 【答案】④【解析】①采用特殊值法，当,a b 都是零时来判断.②通过负数也是实数来判断.③采用特殊值法，当121,z z i ==时来判断.④根据题意，是两个共轭虚数，则虚部不为零来判断. 【详解】 当0ab 时，则()()0a b a b i -++=，不是纯虚数，故错误.②因为负数是实数，实数可以比较大小，故错误. ③当121,z z i ==时，符合12,z z C ∈，且22120z z +=，而120z z ==不成立，故错误.④因为是两个共轭虚数，所以设()0z a bi b =+≠ ，其共轭复数是()0za bib =-≠，则()20z z bi b -=≠所以是纯虚数，故正确. 故答案为：④ 【点睛】本题主要考查了复数的概念，还考查了理解辨析的能力，属于中档题.10．已知点A 为双曲线221x y -=的左顶点，点B 和点在C 双曲线的右支上，ABC ∆是等边三角形，则ABC ∆的面积为_________； 【答案】【解析】根据题意得()1,0A -，再根据双曲线和等边三角形的对称性，得到AB k =AB 的方程，求出点(B ，从而可求ABC ∆的面积. 【详解】由题意得，()1,0A - ，因为点B 和C 在双曲线的右分支上，ABC ∆是等边三角形，根据对称性得，AB k =，所以直线AB 的方程是)1y x =+ ，代入双曲线方程，得220x x --= ， 解得2x = 或1x =- （舍去），所以(B ， 所以1233332∆ABCS .故答案为：【点睛】本题主要考查双曲线的几何性质和三角形面积的计算，还考查了分析解决问题的能力，属于基础题.11．直线l 经过点()2,1P -，且点()1,2--A 到l 的距离为1，则直线l 的方程为______． 【答案】2x =-或4350x y ++=【解析】当直线l 斜率存在时，设出点斜式并利用点到直线的距离公式算出l 的方程为4350x y ++=；当直线与x 轴垂直时，l 方程为2x =-也符合题意．由此即可得到此直线l 的方程． 【详解】设直线l 的方程为()12y k x -=+，即210kx y k -++= ∵点()1,2--A 到l 的距离为1，1=，解之得43k =-， 得l 的方程为4350x y ++=．当直线与x 轴垂直时，方程为2x =-，点()1,2--A 到l 的距离为1，∴直线l 的方程为2x =-或4350x y ++=． 故答案为：2x =-或4350x y ++= 【点睛】本题主要考查求经过定点，且到定点的距离等于定长的直线l 方程，着重考查了直线的方程、点到直线的距离公式等知识，属于基础题． 12．直线2y k =与曲线2222918(,0)k x y k x k R k +=∈≠的公共点的个数为_________； 【答案】4个【解析】将直线方程2y k =与曲线方程2222918+=k x y k x联立得，291840xx -+= ，根据方程根的个数来判断.【详解】将直线方程2y k =与曲线方程2222918+=kx y k x 联立得，291840x x -+=，解得13x =-或13x =+，所以13x=-或13x =-或13x =+或13x=--，故直线与曲线的公共点有4个. 故答案为：4 【点睛】本题主要考查了直线与曲线的位置关系，还考查了运算求解的能力，属于基础题.13．当实数,a b 变化时，两直线1:(2)()()0l a b x a b y a b ++++-=与22:20l m x y n ++=都通过一个定点，则点(,)m n 所在曲线的方程为_________； 【答案】226n m =-【解析】将(2)()()0++++-=a b x a b y a b 变形为()()(2)()()2110++++-=++++-=a b x a b y a b x y a x y b ，令210x y ++=且10x y +-=，求得定点坐标，再代入直线2l 的方程求解. 【详解】因为()()(2)()()2110++++-=++++-=a b x a b y a b x y a x y b ，对任意的实数,a b 都成立，所以21010x y x y ++=⎧⎨+-=⎩，解得23x y =-⎧⎨=⎩，所以直线1:(2)()()0l a b x a b y a b ++++-=过定点()2,3-， 因为 2l 也通过定点()2,3-， 将()2,3-代入220++=m x y n ， 得226n m =-. 故答案为：226n m =- 【点睛】本题主要考查了直线系及其应用，还考查了分析，解决问题的能力，属于基础题.14．动点P 到点(1,0)F -的距离比到它到y 轴的距离大1，动点P 的轨迹方程是_________；【答案】20,04,0x y x x >⎧=⎨-≤⎩【解析】设(),P x y 1x =+，两边平方化简，再去绝对值求解. 【详解】 设(),P x y ，1x =+， 两边平方化简整理得222y x x=- ，当0x > 时，20y =， 当0x ≤ 时，24y x =-，综上：20,04,0x y x x >⎧=⎨-≤⎩.故答案为：20,04,0x y x x >⎧=⎨-≤⎩【点睛】本题主要考查了动点轨迹方程的求解，还考查了运算求解的能力，属于中档题.15．椭圆2214x y +=的一个焦点是F ，动点P 是椭圆上的点，以线段PF 为直径的圆始终与一定圆相切，则定圆的方程是_________； 【答案】224x y +=【解析】先设1F 是椭圆的另一个焦点，M 是线段PF 的中点，根据三角形的中位线及椭圆的定义可得1111||||(2||)||222MO PF a PF a PF ==-=- ，再根据两圆的位置关系得到结论. 【详解】设1F 是椭圆的另一个焦点，M是线段PF 的中点，根据题意得，1111||||(2||)||222MO PF a PF a PF ==-=-，即以长轴长为直径的圆与以线段PF 为直径的圆相内切， 所以定圆的圆心是()0,0O ，半径r a 2== ，所以定圆的方程为224x y +=， 故答案为：224x y += 【点睛】本题主要考查了椭圆的定义及两圆的位置关系，还考查了数形结合的思想方法，属于中档题. 16．若实数x 、y 满足42x y x y -=-，则x 的取值范围是______.【答案】{}0[4,20]⋃ 【解析】【详解】 令(),0y a x y b a b =-=≥、，此时，()22x y x y a b =+-=+，且题设等式化为2242a b a b +-=. 于是，a b 、满足方程()()()222150a b a b -+-=≥、.如图，在aOb 平面内，点(),a b 的轨迹是以()1,2D 为圆心、5为半径的圆在0a b ≥、的部分，即点O 与弧ACB 并集. 故{}2202,25a b ⎡⎤+∈⋃⎣⎦.从而，{}[]2204,20x ab =+∈⋃.三、解答题17．已知x ∈R ，设22log (3)log (3)z x i x =++-，当x 为何值时： （1）在复平面上z 对应的点在第二象限？ （2）在复平面上z 对应的点在直线20x y +-=上. 【答案】（1）32x -<<-；（2）5x =【解析】（1）由复平面上z 对应的点在第二象限，根据复数的几何意义，则有22log (3)0log (3)0x x +<⎧⎨->⎩求解.（2）由复平面上z 对应的点在直线20x y +-=上.，则复数对应点的坐标()22log (3),log (3)+-x x 在直线上，代入直线方程求解即可. 【详解】（1）因为复平面上z 对应的点在第二象限，所以22log (3)0log (3)0x x +<⎧⎨->⎩，所以03131x x <+<⎧⎨->⎩，解得32x -<<-.（2）因为在复平面上z 对应的点在直线20x y +-=上， 所以22log (3)(3)l 4og +-=x x ，所以3030(3)(3)4x x x x +>⎧⎪->⎨⎪+-=⎩，解得x =.【点睛】本题主要考查了复数的几何意义及对数方程和对数不等式的解法，还考查了运算求解的能力，属于中档题. 18．已知直线与抛物线交于两点.（1）求证：若直线l 过抛物线的焦点，则212y y p ⋅=-； （2）写出（1）的逆命题，判断真假，并证明你的判断. 【答案】（1）证明见解析；（2）逆命题：若212y y p =-，则直线过抛物线的焦点；真命题.见解析【解析】（1）不妨设抛物线方程为22y px = ，则焦点坐标为,02p ⎛⎫⎪⎝⎭，当直线的斜率不存在时，直线方程为2px =代入22y px =，验证.当直线的斜率存在时，设直线方程为()2py k x =- 代入22y px =，得2220ky py kp --=，再由韦达定理验证.（2）逆命题：直线l 过抛物线的焦点. 是真命题.证明：当直线的斜率不存在时，设直线方程为(),0xm m =>代入22y px =，解得12y y == ，再由212y y p ⋅=-，求解.当直线的斜率存在时，设直线方程为y kx b =+ 代入22y px =，得2220ky py pb -+= ，由韦达定理得122pby y k⋅=再由212y y p ⋅=-，求得k 与b 的关系现求解.【详解】（1）设抛物线方程为22y px = ，则焦点坐标为,02p ⎛⎫⎪⎝⎭， 两个交点()()1122,,,A x y B x y ，当直线的斜率不存在时，直线方程为2px =，代入22y px =，得1,2y p y p==- ，所以212y y p ⋅=-.当直线的斜率存在时，设直线方程为()2py k x =-， 代入22y px =， 得2220ky py kp --= ，由韦达定理得 212y y p ⋅=-.所以若直线l 过抛物线的焦点时，则212y y p ⋅=-.（2）逆命题：若212y y p ⋅=-，则直线l 过抛物线的焦点. 是真命题证明：当直线的斜率不存在时，设直线方程为(),0x m m =>代入22y px =得12y y ==因为212y y p ⋅=-，所以22p -=-，解得2pm =，所以直线过抛物线的焦点.当直线的斜率存在时，设直线方程为y kx b =+， 代入22y px =， 得2220ky py pb -+=，由韦达定理得122pby y k⋅=，又因为212y y p ⋅=-， 所以2pkb =-，所以直线的方程2p y kx b k x ⎛⎫=+=- ⎪⎝⎭， 所以直线过定点,02p ⎛⎫ ⎪⎝⎭即直线过抛物线的焦点. 【点睛】本题主要考查了直线与抛物线的位置关系，还考查了运算求解的能力，属于中档题.19．（1）若圆C 的方程是222x y r +=，求证：过圆C 上一点00(,)M x y 的切线方程为200x x y y r +=.（2）若圆C 的方程是222()()x a y b r -+-=，则过圆C 上一点00(,)M x y 的切线方程为_______，并证明你的结论.【答案】（1）证明见解析；（2）200()()()()x a x a y b y b r --+--=；证明见解析；【解析】（1）设(),P x y 为切线上任一点，则()()0000,,,PM x x y y CM x y =--=，再由点00(,)M x y 为圆上的切点，则有PM CM⊥ ，即有0PM CM ⋅=求解即可.（2）设(),P x y 为切线上任一点，则()()0000,,,PM x x y y CM x a y b =--=--由点00(,)M x y 为圆上的切点，则有PM CM⊥ ，即有0PM CM ⋅=求解即可.【详解】（1）设(),P x y 为切线上任一点， 有()()0000,,,PMx x y y CM x y =--= ，因为PM CM⊥ ，所以0PM CM ⋅= ， 即()()0000,,0x x y y x y --⋅=，又点00(,)M x y 在圆上， 所以22200+=x y r 整理得200x x y y r +=.（2）设(),P x y 为切线上任一点， 则()()0000,,,PMx x y y CM x a y b =--=--，因为PMCM⊥ ，所以0PM CM ⋅= ， 即()()0000,,0x x y y x a y b --⋅--=，又点00(,)M x y 在圆上， 所以22200()()-+-=xa yb r .整理得200()()()()x a x a y b y b r --+--=. 【点睛】本题主要考查了圆的切线方程问题，还考查推理论证的能力，属于中档题.20．已知双曲线2212x y -=的两焦点为12,F F ，P 为动点，若124PF PF +=.（1）求动点P 的轨迹E 方程；（2）若12(2,0),(2,0)(1,0)A A M -，设直线l 过点M ，且与轨迹E 交于R Q 、两点，直线1A R 与2A Q 交于S 点.试问：当直线l 在变化时，点S 是否恒在一条定直线上？若是，请写出这条定直线方程，并证明你的结论；若不是，请说明理由.【答案】（1）2214x y +=；（2）是，4x =【解析】（1）根据124PF PF +=，且124F F >，由椭圆的定义可知，动点P 的轨迹是以12,F F 为焦点的椭圆，再求出,a b ，写出方程.（2）先设直线的方程为1x my =+，如果存在，则对任意m 都成立，首先取特殊情况，当0m =时，探究出该直线为:4l x =，再通过一般性的证明即可. 【详解】（1）双曲线2212x y -=的两焦点为())12,F F ，设动点P (),x y ， 因为124PF PF +=，且124F F > ，所以动点P 的轨迹E 是以12,F F 为焦点的椭圆.因为22,1ac b ===，所以的轨迹E 方程；2214x y +=.（2）由题意设直线的方程为1x my =+，取0m =，得,1,22R Q ⎛⎛- ⎪ ⎪⎝⎭⎝⎭， 直线1A R的方程是63y x =+，直线2A Q的方程是2y x =-交点为(1S .若1,,R Q ⎛⎛- ⎝⎭⎝⎭，由对称性可知：交点为(24,S .若点S 在同一条直线上，则该直线只能为:4l x =. 以下证明 对任意的m ，直线1A R 与2A Q 交点S 均在直线:4l x =上.由22114x my x y =+⎧⎪⎨+=⎪⎩得()224230m y my ++-= ，设()()1122,,,R x y Q x y ，由韦达定理得：12122223,44m y y y y m m +=-⋅=-++ 设直线1A R 与l 交点为()004,s y ，由011422y y x =++ ，得10162y y x =+.设直线1A R 与l 交点为()004,s y '' ， 由022422y y x '=-- ，得20222y y x '=-，因为()()()12121200121246622222my y y y y y y y x x x x -+'-=-=+-+-，()()2212121244022m m m m x x ---++==+- .所以()004,s y 与()004,s y ''重合.所以当直线l 在变化时，点S 恒在直线:4l x =上. 【点睛】本题主要考查了椭圆的定义及直线与椭圆的位置关系，还考查了特殊与一般的思想，运算求解的能力，属于难题. 21．已知椭圆E 两焦点12(1,0),(1,0)F F -，并经过点. （1）求椭圆E 的标准方程；（2）设,M N 为椭圆E 上关于x 轴对称的不同两点，12(,0),(,0)A x B x 为x 轴上两点，且122x x =，证明：直线,AM NB 的交点P 仍在椭圆E 上；（3）你能否将（2）推广到一般椭圆中？写出你的结论即可.【答案】（1）2212x y +=；（2）证明见解析；（3）若椭圆22221x y a b +=，若212x x a =，则直线,AM NB 的交点P 仍在椭圆E 上； 【解析】（1）已知焦点12(1,0),(1,0)F F -，利用椭圆的定义，求得椭圆的长轴长，再求得2b ，写出方程即可.（2）设()(),,,M m n N m n -，得到直线AM 的方程为()11n y xx m x =--，直线BN的方程为()22n y x x X m=--，设设交点()00,P x y ，分别代入直线AM ，BN 的方程得()0100yn x my nx -=- ，()0200y n x my nx +=+，两式化简得到220022x y +=，说明交点在椭圆上.（3）根据（2）的论证过程，推知规律是212x x a =. 【详解】根据题意，椭圆的长轴长：2a =+，解得22a = ， 又2211b a =-=，所以椭圆的方程是2212x y +=.（2）设()(),,,M m n N m n - ，则直线AM 的方程为()11n y x x m x =--①，直线BN的方程为()22ny xx X m=--②设交点()00,P x y ，代入①②得()0100y n x my nx -=-③，()0200yn x my nx +=+④，③与④两边分别相乘得()22222201200yn x x m y n x -=-，又因为2212m n +=，122x x =，所以220022x y +=，所以直线,AM NB 的交点P 的坐标适合椭圆的方程， 所以直线,AM NB 的交点P 仍在椭圆E 上.（3）若椭圆22221x y a b +=，若212x x a =，则直线,AM NB 的交点P 仍在椭圆E 上； 【点睛】本题主要考查了椭圆方程的求法，以及点与椭圆的位置关系，还考查了推理论证，运算求解的能力，属于难题.。

上海市曹杨二中2020-2021学年高二下学期期末数学试题 学校:___________姓名：___________班级：___________考号：___________一、填空题1．已知复数1z =，则z =______.2．如果复数()2(1)++m i mi 是实数，则实数m =________．3．若a 、b R ∈，且()a i i b i +=+，则a b +=______.4．直线110l x y -+=：与直线250l x y -+=：之间的距离是______．5．若复数z 同时满足2i z z -=，iz z =，则z =__________．6．若抛物线24y x =上一点M 到焦点的距离等于2，则M 到坐标原点O 的距离等于______.7．若方程220x y x y m -++=+表示一个圆，则实数m 的取值范围是______. 8．过点()3,2P -且与直线210x y ++=垂直的直线方程是______.9．已知点M 0)，椭圆22+14x y =与直线y ＝k (x 交于点A ，B ，则△ABM 的周长为________.10．设()1,2A ，()3,1B -，若直线2y kx =-与线段AB 有公共点，则实数k 的取值范围是______.11．已知双曲线C ：22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1，F 2，过F 1的直线与C 的两条渐近线分别交于A ，B 两点．若1F A AB =，120F B F B ⋅=，则C 的离心率为____________．12．曲线C 是平面内与两个定点()11,0F -和()21,0F 的距离的积等于常数()21a a >的点的轨.给出下列四个结论：①曲线C 过坐标原点；②曲线C 关于坐标原点对称；③若点P 在曲线C 上，则122PF PF a +<；④若点P 在曲线C 上，则12F PF △的面积212S a ≤.其中，所有正确的序号是______.二、单选题13．已知直角坐标系xOy 平面上的直线1x y a b +=经过第一、第二和第四象限，则,a b 满足（ ）A ．0,0a b >>B ．0a >，0b <C ．0a <，0b <D ．0a <，0b <14．复数(),z a bi a b R =+∈，()m z z b =+，n z z =⋅，2p z =，则（ ）A ．m 、n 、p 三数都不能比较大小B ．m 、n 、p 三数的大小关系不能确定C ．m n p ≤=D ．m n p ≥=15．设复数()0,0z a bi a b =+>≠是实系数方程20x px q ++=的根，又3z 为实数，则点(),p q 的轨迹在一条曲线上，这条曲线是（ ）A ．圆B ．椭圆C ．双曲线D ．抛物线16．已知a 、b 、e 是平面向量，e 是单位向量．若非零向量a 与e 的夹角为3π，向量b 满足2430b e b -⋅+=，则a b -的最小值是（ ）A 1-B ．1C ．2D ．2-三、解答题17．设,αβ分别是方程220x x a ++=()a R ∈的两个虚数根.（1）求a 的取值范围及αβ+的值；（2）若4αβ-=，求a 的值.18．已知ABC ∆的三个顶点(),A m n 、()2,1B 、()2,3C -.（1）求BC 边所在直线的方程； （2）BC 边上中线AD 的方程为2360x y -+=，且7ABC S ∆=，求点A 的坐标. 19．已知直线:l y x m =+，m R ∈.（1）若以点()2,0M 为圆心的圆与直线l 相切于点P ，且点P 在y 轴上，求该圆的方程；（2）若直线l 与抛物线2:4C x y =有且仅有一个公共点，求m 的取值范围. 20．已知椭圆222:1x C y m+=（常数1m >），点P 是C 上的动点，M 是右顶点，定点A 的坐标为(2,0)．⑴若M 与A 重合，求C 的焦点坐标；⑵若3m =，求PA 的最大值与最小值；⑶若PA 的最小值为MA ，求m 的取值范围．21．已知直线1:l y x =及直线2:l y x =-.平面上动点(),M x y ，且x y >，记M 到直线1l 、2l 的距离分别为1d 、2d ，满足：()21202a d d a ⋅=>. （1）求动点M 的轨迹Γ的方程；（2）若直线l 的方向向量为()1,2，过),0的直线l 与曲线Γ交于A 、B 两点，问以AB 为直径的圆是否恰过原点O ？若是，求a 的值；若不是，判断原点在圆内还是圆外，并说明理由？（3）若过原点O 作斜率为k 的直线n 交曲线Γ于M 、N 两点，设()0,1P ，求PMN 的面积S 关于k 的函数解析式，并求S 的取值范围.参考答案1【分析】利用复数模的求法：z =. 【详解】由复数1z =，则z ==【点睛】本题考查了复数模的求法，考查了基本运算求解能力，属于基础题.2．1-【分析】利用复数的四则运算法则将()2(1)++m i mi 化简为a bi +的形式，结合实数的定义即可求解.【详解】由题意可得，()223(1)(1)m i mi m m m i ++=-++，因为复数()2(1)++m i mi 是实数，所以310m +=，解得1m =-.故答案为：-1【点睛】本题主要考查复数的四则运算及复数的概念与分类，属于基础题.3．0【分析】利用复数的乘法法则和复数相等可得出关于a 、b 的方程组，解出a 、b 的值，进而可求得+a b 的值.【详解】()1b i a i i ai +=+=-+，所以11a b =⎧⎨=-⎩，因此，0a b +=. 故答案为：0.【点睛】本题考查利用复数的乘法法则和复数相等求参数，考查计算能力，属于基础题.4．【分析】根据两条平行线间的距离公式，可直接求出结果.【详解】直线110l x y -+=：与直线250l x y -+=：之间的距离==故答案为：【点睛】本题主要考查两平行线间的距离，熟记公式即可，属于常考题型.5．1i -+【分析】 消去z 后，根据复数的乘除法运算法则，计算可得答案.【详解】 因为2i z z -=，iz z =，所以2z iz i -=， 所以21i z i =-2(1)(1)(1)i i i i +=-+2212i i -+==-+. 故答案为：1i -+【点睛】本题考查了复数的乘法、除法运算法则，属于基础题.6【分析】根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等，进而利用点到直线的距离求得x 的值，代入抛物线方程求得y 值，即可得到所求点的坐标，从而求得其到原点的距离．【详解】 解：抛物线方程为24y x =， ∴焦点为(1,0)F ，准线为:1l x =-抛物线24y x =上一点P 到焦点的距离等于2， ∴根据抛物线定义可知P 到准线的距离等于2，即12x +=，解之得1x =，代入抛物线方程求得2y =±，∴点P 坐标为：(1,2)±=【点睛】本题主要考查了抛物线的简单性质．在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决，属于基础题．7．1,2⎛⎫-∞ ⎪⎝⎭【分析】根据题意，由圆的一般方程的形式分析可得1140m +-⨯>，解可得m 的取值范围，即可得答案．【详解】解：根据题意，方程220x y x y m -++=+表示一个圆，则有1140m +-⨯>，解的12m <，即m 的取值范围为1,2⎛⎫-∞ ⎪⎝⎭； 故答案为：1,2⎛⎫-∞ ⎪⎝⎭． 【点睛】本题考查二元二次方程表示圆的条件，涉及圆的一般方程，属于基础题．8．270x y --=【分析】根据直线的垂直关系，设出所求直线方程，将()3,2P -代入方程，即可求解.【详解】所求直线与直线210x y ++=垂直，设该直线方程为20x y c -+=，()3,2P -代入上式方程得7c =-，所以所求的直线方程为270x y --=.故答案为：270x y --=.【点睛】本题考查直线的位置关系求方程，利用直线的位置关系合理设方程是解题的关键，属于容易题.9．8【解析】【分析】直线y=k （过定点N （），确定椭圆的几何量，再利用椭圆的定义，即可求△ABM 的周长.【详解】直线y=k （过定点N （），由题设知M 、N 是椭圆的焦点，由椭圆定义知： AN+AM=2a=4，BM+BN=2a=4．△ABM 的周长为AB+BM+AM=（AN+BN ）+BM+AM=（AN+AM ）+（BN+BM ）=8， 故答案为：8．【点睛】本题考查椭圆的定义，直线过定点问题和利用椭圆的定义是解题的关键．10．(][),14,-∞-+∞【分析】画出图象求出定点与A 、B 两点连线的斜率，即可求出实数k 的取值范围．【详解】 解：直线2y kx =-恒过定点()0,2-，由题意平面内两点()1,2A ，()3,1B -，直线2y kx =-与线段AB 恒有公共点，如图求出定点与A 、B 两点连线的斜率，()122410k --==-．()212130k --==---， 所以直线2y kx =-与线段AB 恒有公共点，则实数k 的取值范围是(][),14,-∞-+∞， 故答案为：(][),14,-∞-+∞【点睛】本题考查直线斜率的求法，考查数形结合的思想的应用，考查计算能力．11．2.【分析】通过向量关系得到1F A AB =和1OA F A ⊥，得到1AOB AOF ∠=∠，结合双曲线的渐近线可得21,BOF AOF ∠=∠02160,BOF AOF BOA ∠=∠=∠=从而由0tan 60b a==离心率.【详解】如图，由1,F A AB =得1.F A AB =又12,OF OF =得OA 是三角形12F F B 的中位线，即22//,2.BF OA BF OA =由120F B F B =，得121,,F B F B OA F A ⊥⊥则1OB OF =有1AOB AOF ∠=∠，又OA 与OB 都是渐近线，得21,BOF AOF ∠=∠又21BOF AOB AOF π∠+∠+∠=，得02160,BOF AOF BOA ∠=∠=∠=．又渐近线OB 的斜率为0tan 60b a ==所以该双曲线的离心率为2c e a ====． 【点睛】 本题考查平面向量结合双曲线的渐进线和离心率，渗透了逻辑推理、直观想象和数学运算素养．采取几何法，利用数形结合思想解题．12．②④【分析】由题意曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >，利用直接法，设动点坐标为(,)x y ，及可得到动点的轨迹方程，然后由方程特点即可加以判断．【详解】解：对于①，由题意设动点坐标为(,)x y ，则利用题意及两点间的距离公式的得：22224[(1)][(1)]x y x y a ++-+=，将原点代入验证，此方程不过原点，所以①错；对于②，把方程中的x 被x -代换，y 被y - 代换，方程不变，故此曲线关于原点对称，故②正确；对于③，221y x =--，22211y x a ∴+=--，P ∴到原点的距离，当P 在y 轴时取等号，此时12PF PF a ==，122PF PF a +=故③对于④，由题意知点P 在曲线C 上，则△12F PF 的面积12122F PF Sy y =⨯⨯=，由①知221y x =--或221y x =--t ，则2424t a x -=，24442211(2)4444t a a a y t t -∴=--+=--+，1222212F PF S y a ∴=，故④正确．故答案为：②④． 【点睛】本题考查了利用直接法求出动点的轨迹方程，并化简，利用方程判断曲线的对称性及利用解析式选择换元法求出值域． 13．A 【分析】求出直线与坐标轴的交点，即可得出答案. 【详解】令0x =，则y b =；令0y =，则x a = 所以(0,),(,0)b a 在直线1x ya b+=上 因为直线1x ya b+=经过第一、第二和第四象限 所以0,0a b >> 故选：A 【点睛】本题主要考查了由直线所过象限求参数范围，属于基础题. 14．C 【分析】根据复数的四则运算，结合基本不等式，即可得出结论. 【详解】z a bi =-，()2m a bi a bi b ab =++-=，22()()n a bi a bi a b =+-=+，22p a b =+222a b ab +，当且仅当a b =时，取等号m n p ∴≤=故选：C本题主要考查了复数的四则运算，涉及了基本不等式的应用，属于中档题. 15．D 【分析】由3z 为实数，求出,a b 关系，实系数方程有虚数根，∆<0，且两根互为共轭，由韦达定理，求出,p q 与,a b 关系，结合,a b 关系，即可得出,p q 的关系式，得出结论. 【详解】()3220,0,(2)()z a bi a b z a b abi a bi =+>≠=-++，其虚部为22222()2(3)a b b a b b a b -+=-，又3z 为实数，所以2222(3)0,0,30b a b b b a -=≠=≠， 复数()0,0z a bi a b =+>≠是实系数方程20x px q ++=的根，()0,0z a bi a b =->≠也是实系数方程20x px q ++=的根，所以222240,2,40p q z z a p zz a b a q ∆=-<+==-=+==>， 所以2,0p q p =<，此时30q ∆=-<，即点(),p q 的轨迹在抛物线2y x 上.故选：D . 【点睛】本题考查实系数一元二次方程根的关系、复数的基本概念，韦达定理的应用是解题的关键，考查计算求解能力，属于中档题. 16．A 【分析】先确定向量a 、b 所表示的点的轨迹，一个为直线，一个为圆，再根据直线与圆的位置关系求最小值. 【详解】设()()(),,1,0,,a x y e b m n ===，则由π,3a e =得πcos ,3a e e x y a ⋅=⋅=∴=， 由2430b e b -⋅+=得()2222430,21,m n m m n +-+=-+=因此，a b -的最小值为圆心()2,0到直线y =1，为1.选A.【点睛】以向量为载体求相关变量的取值范围，是向量与函数、不等式、三角函数、曲线方程等相结合的一类综合问题.通过向量的坐标运算，将问题转化为解方程、解不等式、求函数值域或直线与曲线的位置关系，是解决这类问题的一般方法.17．（1）1a >，（2）5. 【分析】（1）由条件可得440a ∆=-<，得出a 的取值范围，根据求根公式可求得方程虚数根,αβ，代入αβ+，可得到答案.（2）由（1）可得αβ-==. 【详解】（1）由方程220x x a ++=()a R ∈有两个虚数根 所以440a ∆=-<，解得1a >由,αβ是方程220x x a ++=()a R ∈的两个虚数根.可得,αβ，不妨设1α==-,1β==-所以αβ+=（2）由（1）可得αβ-==根据4αβ-=，即4=，解得5a = 【点睛】本题考查实系数一元二次方程有虚数根的条件以及求根公式的应用，属于中档题.18．（1）240x y +-=；（2）点A 坐标为()3,4、()3,0- 【分析】（1）利用两点式求得BC 边所在直线方程；（2）利用点到直线的距离公式求得A 到直线BC 的距离，根据面积7ABC S ∆=以及点A 在直线2360x y -+=上列方程组，解方程组求得A 点的坐标. 【详解】（1）由()2,1B 、()2,3C -得BC 边所在直线方程为123122y x --=---，即240x y +-=. （2）BC ==A 到BC 边所在直线240x y +-=的距离为d =A 在直线2360x y -+=上，故1722360ABC S BC d m n ∆⎧=⋅⋅=⎪⎨⎪-+=⎩，即2472360m n m n ⎧+-=⎨-+=⎩，解得()3,4A 或()30A -,. 【点睛】本小题主要考查利用两点式求直线方程，考查点到直线的距离公式，考查三角形面积公式，属于基础题.19．（1）()2228x y -+=；（2）1m =-. 【分析】（1）利用待定系数法求本题中圆的方程是解决本题的关键，利用直线与圆相切的数学关系列出关于圆的半径的方程，通过求解方程确定出所求圆的半径，进而写出所求圆的方程； （2）联立直线与抛物线方程、消元，由0∆=计算可得； 【详解】解：（1）设所求圆的半径为r ，则圆的方程可设为222(2)x y r -+=．由题意，所求圆与直线:l y x m =+相切于点(0,)P m ，则有224m r r ⎧+==，解得2m r =⎧⎪⎨=⎪⎩，所以圆的方程为22(2)8x y -+=．（2）因为直线:l y x m =+与抛物线2:4C x y =有且仅有一个公共点，联立方程得24y x m x y=+⎧⎨=⎩消元得2440x x m --=，所以()()24440m ∆=--⨯-=解得1m =-【点睛】本题考查直线与圆的位置关系，直线与抛物线的位置关系，考查学生的方程思想和运算化简能力，属于基础题．20．（1）(（2）min ||2PA =max||5PA =（3）11m <≤+【解析】解：⑴2m =，椭圆方程为2214x y +=，c ==∴ 左、右焦点坐标为(．⑵3m =，椭圆方程为2219x y +=，设(,)P x y ，则222222891||(2)(2)1()(33)9942x PA x y x x x =-+=-+-=-+-≤≤∴94x =时min ||2PA =；3x =-时max ||5PA =． ⑶设动点(,)P x y ，则222222222222124||(2)(2)1()5()11x m m m PA x y x x m x m m m m m -=-+=-+-=--+-≤≤-- ∵ 当x m =时，PA 取最小值，且2210m m ->，∴2221mm m ≥-且1m >解得11m <≤21．(1) ()2220x y aa -=> (2) 以AB 为直径的圆不过原点O ，点O 在圆外(3)S a =, S 的取值范围是S a ≥ 【分析】（1）由条件有2221222x y a d d -⋅===，得出答案. （2）设()()1122,,,A x y B x y ，根据条件可设直线l的方程为：()2y x =，与曲线Γ的方程联立，得到12x x +=，2123x x a ⋅=，由1212OA OB x x y y ⋅=+的符号可得出答案.（3）由题意直线n 的方程为y kx =，与曲线Γ的方程联立，可得M （或N ）的点的横坐标，根据条件可得k的范围，122N S OP x a =⨯⨯⨯=，然后求出范围. 【详解】（1）由(),M x y 到直线1l 、2l 的距离分别为1d 、2d ，且2122a d d ⋅=则2221222x y a d d -⋅===，又x y > 所以22222222x y x y a --==，即222x y a -= 则动点M 的轨迹Γ的方程；()2220x y aa -=>（2）由直线l 的方向向量为()1,2，则直线l 的斜率为2k =. 又直线l过),0，则直线l的方程为：()2y x =设()()1122,,,A x y B x y，由()2222y x x y a⎧=⎪⎨-=⎪⎩得22390x a -+=则12x x +=，2123x x a ⋅=所以()()()212121212442y y x xx x x x a ⎡⎤⋅=⨯=⨯-++⎣⎦22244323a a a ⎛⎫=⨯+=- ⎪ ⎪⎝⎭2221212453033a a OA OB x x y y a ⋅=+=-=>所以以AB 为直径的圆不过原点O ，由0OA OB ⋅>，所以点O 在圆外. （3）直线n 的方程为y kx =由222y kx x y a=⎧⎨-=⎩得2222x k x a -=， 由直线n 交曲线Γ于M 、N 两点，则210k ->，则201k ≤<则2221a x k=-122N S OP x a =⨯⨯⨯=由201k ≤<，得2011k <-≤a a ≥所以PMN 的面积S 关于k 的函数解析式为S a =，PMN 的面积S 的取值范围是S a ≥.【点睛】本题考查求轨迹的方程，利用数量积研究点与圆的位置关系，求三角形的面积，属于中档题.。

2019-2020学年上海市第二中学高二下学期期末数学试题一、单选题1．在空间中，“直线m ⊥平面α”是“直线m 与平面α内无穷多条直线都垂直 ”的（ ）A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．非充分非必要条件【答案】A【解析】若“直线m ⊥平面α”则“直线m 与平面α内无穷多条直线都垂直 ”，正确；反之，若“直线m 与平面α内无穷多条直线都垂直 ”则“直线m ⊥平面α”是错误的，故直线m ⊥平面α”是“直线m 与平面α内无穷多条直线都垂直 ”的充分非必要条件. 故选A.2．某样本平均数为a ，总体平均数为m ，那么（ ） A ．a m = B ．a m >C ．a m <D ．a 是m 的估计值 【答案】D【分析】统计学中利用样本数据估计总体数据，可知样本平均数是总体平均数的估计值. 【详解】解：样本平均数为a ，总体平均数为m ， 统计学中，利用样本数据估计总体数据， ∴样本平均数a 是总体平均数m 的估计值. 故选：D.【点睛】本题考查了利用样本数据估计总体数据的应用问题，是基础题. 3．若某空间几何体的三视图如图所示，则该几何体的体积为( )A ．2π＋3B ．4π＋3C ．2π＋23D ．4π＋23【答案】C【详解】试题分析：由三视图知几何体是一个简单的组合体，上面是一个四棱锥，四棱锥的底面是一个正方形，对角线长是2，侧棱长2，高是2213-=，下面是一个圆柱，圆柱的底面直径是2，高是2，所以组合体的体积是2112322312232ππ⨯⨯⨯⨯+⨯⨯=+，故选C. 【解析】几何体的三视图及体积的计算. 【方法点晴】本题主要考查了几何体的三视图及其体积的计算，着重考查了推理和运算能力及空间想象能力，属于中档试题，解答此类问题的关键是根据三视图的规则“长对正、宽相等、高平齐”的原则，还原出原几何体的形状，本题的解答中根据三视图得出上面一个四棱锥、下面是一个圆柱组成的组合体，得到几何体的数量关系是解答的关键，属于基础题.4．如图，梯形ABCD 中，AD ∥BC ，AD ＝AB ＝1，AD ⊥AB ，∠BCD ＝45°，将△ABD 沿对角线BD 折起，设折起后点A 的位置为A ′，使二面角A ′—BD —C 为直二面角，给出下面四个命题：①A ′D ⊥BC ；②三棱锥A ′—BCD 的体积为2；③CD ⊥平面A ′BD ；④平面A ′BC ⊥平面A ′D C ．其中正确命题的个数是（ ）A ．1B ．2C ．3D ．4【答案】C【分析】根据//AD BC ，1AD AB ==，AD AB ⊥，45BCD ︒∠=， 易得 CD BD ⊥，再根据，平面A BD '⊥平面BCD ，得CD ⊥平面A BD '，可判断③的正误；由二面角A BD C '--为直二面角，可得A H '⊥平面BCD ，则可求出A BDC V '-，进而可判断②的正误；根据CD ⊥平面A BD '，有CD A B '⊥，,A B A D ''⊥得A B '⊥平面CDA '，④利用面面垂直的判定定理判断④的正误；根据CD ⊥平面A BD '，有CD A D '⊥，若A D BC '⊥，则可证A D '⊥平面BCD ，则得到A D BD '⊥，与已知矛盾，进而可判断①的正误.【详解】由题意，取BD 中点H ，连接A H '，则折叠后的图形如图所示：由二面角A BD C '--为直二面角，可得A H '⊥平面BCD ，则A H CD '⊥，∴A BDC V '-＝1221326⨯⨯=，②正确， ∵CD BD ⊥，A H CD '⊥，且A H BD H '=，∴CD ⊥平面A BD '，故③正确，∵1A B '=，由几何关系可得3A C '=，2BC =， ∴2222132A B A C BC ''+=+==，∴A B A C ''⊥， 由CD ⊥平面A BD '，得CD A B '⊥，又A C CD C '=∴A B '⊥平面A DC '，∵A B '⊂平面A BC '， ∴ 平面A BC '⊥平面A DC '，④正确，CD ⊥平面A BD '，CD A D '∴⊥，若A D BC '⊥，则可证A D '⊥平面BCD ，则得到A D BD '⊥，与已知矛盾，所以①错误. 故选C .【点睛】本题通过折叠性问题，考查了面面垂直的性质，面面垂直的判定，考查了体积的计算，解题关键是利用好直线与平面，平面与平面垂直关系的转化关系，属于中档题.二、填空题5．将三封录取通知书投入四个邮筒共有_____________种不同的投递方式. 【答案】64【分析】每封录取通知书放入邮筒有4种不同的投递方式，然后利用分步乘法计数原理可得出结果.【详解】由题意知，每封录取通知书放入邮筒有4种不同的投递方式，由分步乘法计数原理可知，将三封录取通知书投入四个邮筒共有3464=种不同的投递方式. 故答案为64.【点睛】本题考查分步乘法计数原理的应用，考查计算能力，属于基础题. 6．已知球的体积为36π，则该球大圆的面积等于______. 【答案】9π【分析】由球的体积，得到球的半径，进而可得出大圆的面积. 【详解】因为球的体积为36π，设球的半径为r ， 则34363r ππ=，解得：3r =， 因为球的大圆即是过球心的截面圆， 因此大圆的面积为29S r ππ==. 故答案为：9π.【点睛】本题主要考查球的相关计算，熟记球的体积公式，以及圆的面积公式即可，属于基础题型.7．已知向量(0,2,1)a =，(1,1,2)b =-，则a 与b 的夹角为________【答案】 【分析】利用空间向量的坐标运算求解即可.【详解】解：由已知224a b ⋅=+=，41a =+=11b =++=cos ,56a b a b a b⋅===⋅⋅，则a 与b 的夹角为.故答案为：. 【点睛】本题考查空间向量夹角的求解，是基础题.8．在62x⎛⎝二项式展开式中，常数项为__________.【答案】60【分析】求得二项式展开式的通项为12362162r rr r T C x--+=⋅，令4r =，即可求解，得到答案.【详解】由题意，二项式62x⎛⎝展开式的通项为123662166(2)2rrrr r rr T C x C x ---+==⋅， 令4r =，可得2456241560T C =⋅=⨯=，即展开式的常数项为60.故答案为：60.【点睛】本题主要考查了二项式定理的应用，其中解答中熟记二项展开式的通项，合理赋值是解答的关键，着重考查了推理与计算能力..9．高三某位同学参加物理、化学、政治科目的等级考，已知这位同学在物理、化学、政治科目考试中达A 的概率分别为56、78、34，这三门科目考试成绩的结果互不影响，则这位考生至少得1个A 的概率为____ 【答案】191192【分析】先求对立事件概率：三门科目考试成绩都不是A ，再根据对立事件概率关系求结果.【详解】这位考生三门科目考试成绩都不是A 的概率为5731(1)(1)(1)684192---=， 所以这位考生至少得1个A 的概率为11911192192-= 故答案为：191192【点睛】本题考查利用对立事件求概率，考查基本分析求解能力，属基础题.10．一个袋子中装有8个球，其中2个红球，6个黑球，若从袋中拿出两个球，记下颜色，则两个球中至少有一个是红球的概率是________（用数字表示） 【答案】1328【分析】根据题意，袋中有２个红球和６个黑球，由组合数公式可得从中取出2个的情况数目，若两个球中至少有一个是红球，即一红一黑，或者两红，由分步计数原理可得其情况数目，由等可能事件的概率，计算可得答案.【详解】解：根据题意，袋中有２个红球和６个黑球，共８个球，从中取出2个，有2828C =种情况，两个球中至少有一个是红球，即一红一黑，或者两红的情况有11226213C C C +=种，则两个球中至少有一个是红球的概率为1328P =， 故答案为：1328. 【点睛】本题考查等可能事件的概率的计算，是简单题，关键在于正确应用排列、组合公式.11．若在1()nx x-展开式中，若奇数项的系数之和为32，则含4x 的系数是______. 【答案】-6【分析】由题意可知，奇数项的系数之和为1232n -=，求出6n =，然后求出展开式的通项，利用x 的指数为4，求出参数的值，然后将参数的值代入通项，即可求出含4x 项的系数.【详解】1n x x ⎛⎫- ⎪⎝⎭展开式的通项为()211kk k n k kn k n n C x C x x --⎛⎫⋅⋅-=⋅-⋅ ⎪⎝⎭，奇数项的系数为0241232n n n n C C C -+++==，解得6n =，61x x ⎛⎫- ⎪⎝⎭展开式的通项为()6626611kk k k kk C x C x x --⎛⎫⋅⋅-=⋅-⋅ ⎪⎝⎭， 令624k -=，得1k =，因此，展开式中含4x 的系数为()11616C ⋅-=-.故答案为：6-.【点睛】关键点点睛：二项式问题通常先求通项，由通项确定所求量，然后再写出关系式计算.12．点P 是棱长为1的正方体ABCD ﹣A 1B 1C 1D 1的底面A 1B 1C 1D 1上一点，则1PA PC ⋅的取值范围是__. 【答案】[﹣12，0] 【分析】建立空间直角坐标系，设出点P 的坐标为（x ，y ，z ），则由题意可得0≤x ≤1，0≤y ≤1，z ＝1，计算PA •1PC =x 2﹣x ，利用二次函数的性质求得它的值域即可．【详解】解：以点D 为原点，以DA 所在的直线为x 轴，以DC 所在的直线为y 轴，以DD 1所在的直线为z 轴，建立空间直角坐标系，如图所示； 则点A （1，0，0），C 1（0，1，1），设点P 的坐标为（x ，y ，z ），由题意可得 0≤x ≤1，0≤y ≤1，z ＝1；∴PA =（1﹣x ，﹣y ，﹣1），1PC =（﹣x ，1﹣y ，0），∴PA •1PC =-x （1﹣x ）﹣y （1﹣y ）+0＝x 2﹣x +y 2﹣y 22111222x y ⎛⎫⎛⎫=-+-- ⎪ ⎪⎝⎭⎝⎭，由二次函数的性质可得，当x ＝y 12=时，PA •1PC 取得最小值为12-；当x ＝0或1，且y ＝0或1时，PA •1PC 取得最大值为0， 则PA •1PC 的取值范围是[12-，0]． 故答案为：[12-，0]．【点睛】本题主要考查了向量在几何中的应用与向量的数量积运算问题，是综合性题目． 13．两个圆锥有等长的母线，它们的侧面展开图恰好拼成一个圆，若它们的侧面积之比为1:2，则它们的体积比是_____________． 【答案】10【分析】设圆锥母线长为l ，小圆锥半径为r 、高为h ，大圆锥半径为R ，高为H ，根据侧面积之比可得2R r =，再由圆锥侧面展开扇形圆心角的公式得到3l r =，利用勾股定理得到,h H 关于r 的式子，从而将两个圆锥的体积都表示成r 的式子，，求出它们的比值.【详解】设圆锥母线长为l ，侧面积较小的圆锥半径为r ， 侧面积较大的圆锥半径为R ，它们的高分别为,h H ， 则:1:2rl Rl ππ=，得2R r =， 两圆锥的侧面展开图恰好拼成一个圆，22r Rlππ+∴=⨯，得3l r =，再由勾股定理，得h ==，同理可得，H =，∴两个圆锥的体积之比为2211:433r r ππ⎛⎫⎛⎫⋅⋅⋅= ⎪ ⎪⎝⎭⎝⎭故答案为【点睛】本题主要考查圆锥的性质与侧面积，意在考查对基础知识的掌握与应用，属于中档题.14．已知x 、y 满足组合数方程21717x yC C =，则xy 的最大值是_____________.【答案】128【分析】由组合数的性质得出()208y x x =≤≤或217x y +=，然后利用二次函数的性质或基本不等式求出xy 的最大值，并比较大小可得出结论.【详解】x 、y 满足组合数方程21717x yC C =，()208y x x ∴=≤≤或217x y +=，当2y x =时，则[]220,128xy x =∈；当217x y +=时，222172892224x y xy +⎛⎫⎛⎫≤== ⎪ ⎪⎝⎭⎝⎭. 因此，当216x y ==时，xy 取得最大值128. 故答案为128.【点睛】本题考查组合数基本性质的应用，同时也考查了两数乘积最大值的计算，考查了二次函数的基本性质的应用以及基本不等式的应用，考查运算求解能力，属于中等题.三、解答题15．若一圆锥的底面半径为4，体积是16π. （1）求该圆锥的母线长；（2）已知该圆锥的顶点为O ，并且OA 、OB 为圆锥的两个母线，求线段AB 长度为何值时，△OAB 的面积取得最大值？【答案】（1）5；（2）【分析】（1）先根据体积求高，再根据母线与高的关系求结果；（2）先确定△OAB 的面积最大值何时取得，再根据勾股定理求AB 长度. 【详解】（1）因为圆锥的底面半径为4，体积是16π，所以2116433h h ππ=⋅⋅∴=； （2）△OAB 的面积125sin sin 22S OA OB AOB AOB =⋅⋅∠=∠ 因为3(0,2arcsin ]5AOB ∠∈，所以当2AOB π∠=时，△OAB的面积取最大值，此时AB 【点睛】本题考查圆锥的体积以及截面积，考查基本分析求解能力，属基础题.16．21(2)nx x+的展开式一共有13项.（1）求展开式中二项式系数之和； （2）求展开式中的常数项 【答案】（1）122；（2）7920【分析】先由21(2)nx x+的展开式一共有13项得12n =，则直接可得（1）的结果，（2）根据展开式的通项122431122r rr r T C x --+=⋅⋅，令2430r -=，即可求出常数项. 【详解】解：由21(2)nx x+的展开式一共有13项得12n =，（1）由2121(2)x x+得展开式中二项式系数之和为122；（2）由2121(2)x x+得展开式的通项为()1221224311212122rrrr r r r T C x C x x ---+⎛⎫=⋅=⋅⋅ ⎪⎝⎭， 令2430r -=，得8r =， 所以展开式中的常数项为81281227920C -⋅=.【点睛】本题考查二项式定理及其应用，其中()na b +的展开式通项1C r n r rr n T a b -+=的熟练运用是关键，是基础题.17．已知二项式n的展开式中，前三项系数的绝对值成等差数列. （1）求正整数n 的值；（2）求展开式中二项式系数最大的项； （3）求展开式中系数最大的项. 【答案】（1）8；（2）358；（3）437x . 【分析】（1）根据等差中项的性质列方程可得出n 的值；（2）根据二项式系数的对称性和单调性可得出二项式系数最大的项；（3）由1188118811221122r rr rr rr rC CC C++--⎧⎛⎫⎛⎫⋅≥⋅⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎨⎛⎫⎛⎫⎪⋅≥⋅⎪ ⎪⎪⎝⎭⎝⎭⎩，求出r的取值范围，即可得出系数最大项对应的项的序数.【详解】（1）二项式n展开式的通项为2312r r n rn rr rn nC C x--⎛⎫⋅⋅=⋅⋅⎪⎝⎭，由于展开式系数的绝对值成等差数列，则10211224n n nC C C⋅=+⋅，即()118n nn-=+，整理得2980n n-+=，2n ≥，解得8n=；（2）第1r+项的二项式系数为8rC，因此，第5项的二项式系数最大，此时，4r=；（3）由1188118811221122r rr rr rr rC CC C++--⎧⎛⎫⎛⎫⋅≥⋅⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎨⎛⎫⎛⎫⎪⋅≥⋅⎪ ⎪⎪⎝⎭⎝⎭⎩，得()()()()()()28!8!!81!7!8!28!!81!9!r r r rr r r r⨯⎧≥⎪-+-⎪⎨⨯⎪≥⎪---⎩！！，整理得22892r rr r+≥-⎧⎨-≥⎩，解得23r≤≤，所以当2r或3时，项的系数最大.因此，展开式中系数最大的项为2442338172C x x⎛⎫⋅⋅=⎪⎝⎭.【点睛】本题考查二项式定理的应用，二项式系数的定义和基本性质，同时也考查了项的系数最大项的求解，考查运算求解能力，属于中等题.18．已知数列{}n a（*n∈N）的通项公式为1na n=-（*n∈N）.（1）分别求11(1)ax-的二项展开式中的二项式系数之和与系数之和；（2）求201(12)ax+的二项展开式中的系数最大的项；（3）记1245kakd+=⨯（*k∈N），求集合1{|,}k kx d x d x+<<∈Z的元素个数（写出具体的表达式）.【答案】（1）102，0；（2）133133200(2)C x，134134200(2)C x；（3）164(1)5k k+⋅+-.【分析】（1）根据二项展开式()na b+直接得二项式系数之和为2n，利用赋值法求二项第 11 页 共 11 页 展开式中的系数之和；（2）根据二项展开式通项公式得系数，再列方程组解得系数最大的项；（3）先根据二项式定理将k d 展开成整数与小数，再根据k 奇偶性分类讨论元素个数，最后根据符号数列合并通项.【详解】（1）1110(1)(1)a x x -=-∴二项展开式中的二项式系数之和为102， 令1x =得二项展开式中的系数之和为10(11)=0-；（2）2012001200(12)(12)2a r r r r x x T C x ++=+∴=⋅设二项展开式中的系数最大的项数为1,[0,200],r r r N +∈∈则112002001120020012(200)22133134133,1342(201)22r r r r r r r r r r C C r r r r C C ++--⎧+≥-⋅≥⋅⎧∴∴≤≤∴=⎨⎨-≥⋅≥⋅⎩⎩， 因此二项展开式中的系数最大的项为133133200(2)C x ，134134200(2)C x （3）1224455k a k k d Z +=⨯=⨯∉ 1111222(51)(555(1))(1)555k k k k k k k k k d C C ---=⨯-=⨯-++⨯⨯-+- 1121122[55(1)](1)5k k k k k k k C C ----=-++⨯-+- 所以当k 为偶数时，集合1{|,}k k x d x d x +<<∈Z 的元素个数为1111211112[55(1)]2[55(1)]1k k k k k k k k k k k k C C C C -----++=-++⨯---++⨯--12261[(51)1][(51)1]145555k k k +=-+----=⋅- 当k 为奇数时，集合1{|,}k k x d x d x +<<∈Z 的元素个数为1111211112[55(1)]2[55(1)]1k k k k k k k k k k k k C C C C -----++=-++⨯---++⨯-+12261[(51)1][(51)1]145555k k k +=----++=⋅+ 综上，元素个数为164(1)5k k +⋅+- 【点睛】本题考查二项式系数之和、二项式展开式各项系数之和、二项式展开式中系数最大项以及利用二项式展开式计数，考查综合分析求解与应用能力，属较难题.。

一、选择题1．已知函数()()sin f x A x ωϕ=+(A 、ω、ϕ均为正的常数)的最小正周期为π，当23x π=时，函数()f x 取得最小值，则下列结论正确的是（ ）A ．()()()220f f f -<<B ．()()()220f f f <-<C ．()()()202f f f -<<D ．()()()022f f f <-<2．已知函数()()π2sin 06f x x ωω⎛⎫=+> ⎪⎝⎭的周期为π，则下列选项正确的是 A ．函数()f x 的图象关于点π,06⎛⎫ ⎪⎝⎭对称 B ．函数()f x 的图象关于点π,012⎛⎫-⎪⎝⎭对称 C ．函数()f x 的图象关于直线π3x =对称 D ．函数()f x 的图象关于直线π12x =-对称 3．已知π(,π)2α∈，π1tan()47α+=，则sin cos αα+= （ ） A ．17-B ．25-C ．15-D ．154．将函数sin y x =图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），再将所得图象上所有的点向左平移π4个单位长度，则所得图象对应的函数解析式为（ ） A ．sin(2)4y x π=+B ．sin()24x y π=+C ．cos 2x y =D ．cos 2y x =5．在锐角ABC 中，4sin 3cos 5,4cos 3sin A B A B +=+=C 等于（ ）A ．150B ．120C ．60D ．306．已知a R ∈，则“cos 02πα⎛⎫+> ⎪⎝⎭”是“α是第三象限角”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件7．已知是12,e e ，夹角为60︒的两个单位向量，则12a e e =+与122b e e =-的夹角是( ) A ．60︒B ．120︒C ．30D ．90︒8．若O 为ABC ∆所在平面内一点，()()20OB OC OB OC OA -⋅+-=，则ABC ∆形状是（ ）． A ．等腰三角形 B ．直角三角形 C ．正三角形 D ．以上答案均错9．扇形OAB 的半径为1，圆心角为120°，P 是弧AB 上的动点，则AP BP ⋅的最小值为（ ） A ．12B ．0C ．12-D ．2- 10．若()2sin sinsin777n n S n N πππ︒=+++∈，则在中，正数的个数是（ ） A ．16B ．72C ．86D ．10011．已知()()f x sin x ωθ=+（其中()()12120,0,,''0,2f x f x x x πωθ⎛⎫>∈==- ⎪⎝⎭，的最小值为(),23f x f x ππ⎛⎫=- ⎪⎝⎭，将()f x 的图象向左平移6π个单位得()g x ，则()g x 的单调递减区间是（ ） A ．(),2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦B ．()2,63k k k ππ⎡⎤π+π+∈⎢⎥⎣⎦Z C ．()5,36k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D ．()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦12．在平面直角坐标系中，,,,AB CD EF GH 是圆221x y +=上的四段弧（如图），点P 在其中一段上，角α以O x 为始边，OP 为终边，若tan cos sin ααα<<，则P 所在的圆弧是A ．AB B ．CDC ．EFD ．GH13．如图，在ABC ∆中，23AD AC =，13BP BD =，若AP AB AC λμ=+，则=λμ( )A ．3-B ．3C ．2D ．2-14．设000020132tan151cos50cos 2sin 2,,221tan 152a b c -=-==+，则有（ ） A ．c a b <<B ．a b c <<C ．b c a <<D ．a c b <<15．已知函数()sin(2)3f x x π=+，将其图象向右平移(0)ϕϕ>个单位长度后得到函数()g x 的图象，若函数()g x 为偶函数，则ϕ的最小值为（ ）A ．12πB ．512π C ．6π D ．56π 二、填空题16．设函数()sin()f x A x ωϕ=+（A ，ω，ϕ为常数，且0A >，0>ω，0ϕπ<<）的部分图象如图所示，则(0)f =_____.17．在ABC 中，已知1tan 2tan tan A B A-=，则cos(2)A B -的值为________. 18．设F 为抛物线x 2=8y 的焦点，点A ，B ，C 在此抛物线上，若FA FB FC 0++=，则FA FB FC ++=______．19．仔细阅读下面三个函数性质：（1）对任意实数x ∈R ，存在常数(0)p p ≠，使得1()2f x p f x p ⎛⎫-=+ ⎪⎝⎭． （2）对任意实数x ∈R ，存在常数(0)M M >，使得|()|f x M ≤． （3）对任意实数x ∈R ，存在常数，使得()()0f a x f a x -++=．请写出能同时满足以上三个性质的函数（不能为常函数）的解析式__________．（写出一个即可） 20．函数1ππ()sin ()cos ()536f x x x =++-的最大值为___________. 21．函数()211sinsin (0)222x f x x ωωω=+->，若函数()f x 在区间x ∈(),2ππ内没有零点，则实数ω的取值范围是_____22．已知两个单位向量a 、b 的夹角为60，(1)c ta t b =+-，若b c ⊥，则实数t ＝__________. 23．函数2sin 24y x π⎛⎫=-⎪⎝⎭的单调增区间是________. 24．已知函数()tan 0y x ωω=>的图像与y m =（m 为常数）的图像相交的相邻两交点间的距离为2π，则=ω__________． 25．已知()1tan 2αβ+=，()tan 1αβ-=-，则sin 2sin 2αβ的值为__________．三、解答题26．在ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且2cos (cos cos )C a B b A c +=.（1）求C ；（2）若c =，ABC 的面积为ABC 的周长.27．已知函数()2sin()1(0)6f x x πωω=-->的周期是π.（1）求()f x 的单调递增区间； （2）求()f x 在[0,]2π上的最值及其对应的x 的值.28．已知函数f (x )2=sin2x +cos 2x . （1）求函数f (x )的最小正周期和最大值； （2）求函数f (x )的单调递增区间. 29．已知函数()2sin 22cos 6f x x x π⎛⎫=-- ⎪⎝⎭. （1）求函数()f x 的单调增区间； （2）求函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域. 30．已知(1,2),(2,2),(1,5)a b c ==-=-．若a b λ-与b c +平行，求实数λ的值．【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1．B2．B3．C4．D5．D6．B7．B8．A9．C10．C11．A12．C13．B14．A15．B二、填空题16．【解析】【分析】由图像可以计算出的值即可得到三角函数表达式然后计算出结果【详解】由图可知：由得从而将点代入得即又所以得所以【点睛】本题考查了由函数图像求三角函数的表达式熟练掌握图像是解题关键较为基础17．0【解析】【分析】通过展开然后利用已知可得于是整理化简即可得到答案【详解】由于因此所以即所以则故答案为0【点睛】本题主要考查三角函数诱导公式的运用意在考查学生的基础知识难度中等18．6【解析】【分析】由题意可得焦点F（02）准线为y＝﹣2由条件可得F是三角形ABC 的重心可得2由抛物线的定义可得【详解】由题意可得p＝4焦点F（02）准线为y＝﹣2由于故F是三角形ABC的重心设AB19．【解析】分析：由（1）得周期由（2）得最值（有界）由（3）得对称中心因此可选三角函数详解：由题目约束条件可得到的不同解析式由（1）得周期由（2）得最值（有界）由（3）得对称中心因此可选三角函数点睛：20．【解析】分析：利用诱导公式化简函数的解析式通过正弦函数的最值求解即可详解：函数故答案为点睛：本题考查诱导公式的应用三角函数的最值正弦函数的有界性考查计算能力21．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K取其它整数时无解同22．【解析】由题意得即解得t=2；故答案为223．【解析】即单调增区间是【点睛】函数的性质(1)(2)周期(3)由求对称轴(4)由求增区间;由求减区间;24．【解析】由题意得25．【解析】∵(α+β)+(α−β)=2α(α+β)−(α−β)=2β∴====故答案为：点睛：三角函数式的化简要遵循三看原则:一看角这是重要一环通过看角之间的差别与联系把角进行合理的拆分从而正确使用公三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题 1．B 解析：B 【解析】依题意得，函数f （x ）的周期为π， ∵ω＞0，∴ω=2ππ=2．又∵当x=23π 时，函数f （x ）取得最小值， ∴2×23π +φ=2kπ+32π ，k ∈Z ，可解得：φ=2kπ+6π，k ∈Z ， ∴f （x ）=Asin （2x+2kπ+6π）=Asin （2x+6π）． ∴f （﹣2）=Asin （﹣4+6π）=Asin （6π﹣4+2π）＞0． f （2）=Asin （4+6π）＜0， f （0）=Asin 6π=Asin 56π＞0， 又∵32π＞6π﹣4+2π＞56π＞2π，而f （x ）=Asinx 在区间（2π，32π）是单调递减的，∴f （2）＜f （﹣2）＜f （0）． 故选：B ．2．B解析：B 【解析】 【分析】根据函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭的周期为π，求解ω可得解析式，对各选项逐一考察即可． 【详解】函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π，则 即22T ππωω=∴=＝， ，则()2sin 26f x x π⎛⎫=+ ⎪⎝⎭，由对称轴方程：262x k k Z πππ+=+∈，（）得：126x k ππ=+，（k∈Z） 经考查C ，D 选项不对．由对称中心的横坐标：26x k k Z ππ+=∈，（），得：1212x k k Z ππ=-∈，（） 当k=0时，可得图象的对称中心坐标为,012π⎛⎫- ⎪⎝⎭． 故选B ． 【点睛】本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用，求出解析式是解决本题的关键．属于中档题．3．C解析：C 【解析】 【分析】由两角和的正切公式得出3sin cos 4αα=-，结合平方关系求出43cos ,sin 55αα=-=，即可得出sin cos αα+的值. 【详解】1tan 1tan 41tan 7πααα+⎛⎫+== ⎪-⎝⎭3tan 4α∴=-，即3sin cos 4αα=-由平方关系得出223cos cos 14αα⎛⎫-+= ⎪⎝⎭，解得：43cos ,sin 55αα=-=341sin cos 555αα+=-=-故选：C 【点睛】本题主要考查了两角和的正切公式，平方关系，属于中档题.4．D解析：D 【解析】 【分析】由正弦函数的周期变换以及平移变换即可得出正确答案. 【详解】函数sin y x =图象上所有点的横坐标缩短到原来的12倍（纵坐标不变）得到sin 2y x =，再将所得图象上所有的点向左平移π4个单位长度，得到sin 2sin 2cos 242y x x x ππ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭故选：D 【点睛】本题主要考查了正弦函数的周期变换以及平移变换，属于中档题.5．D解析：D 【解析】 【分析】由题：()()224sin 3cos 25,4cos 3sin 12A B A B +=+=，两式相加即可求出sin()A B +，进而求出A B +，角C 得解.【详解】由题：()()224sin 3cos 25,4cos 3sin 12A B A B +=+=，2216sin 24sin cos 9cos 25A A B B ++=，2216cos 24cos sin 9sin 12A A B B ++=，两式相加得：()1624sin cos cos sin 937A B A B +++=，1sin()2A B +=，所以1sin sin(())2C A B π=-+=，且C 为锐角， 所以30C =. 故选：D 【点睛】此题考查同角三角函数基本关系与三角恒等变换综合应用，考查对基本公式的掌握和常见问题的处理方法.6．B解析：B 【解析】 【分析】 先化简“cos 02πα⎛⎫+> ⎪⎝⎭”，再利用充要条件的定义判断. 【详解】因为cos 02πα⎛⎫+> ⎪⎝⎭，所以-sin 0,sin 0,ααα>∴<∴是第三、四象限和y 轴负半轴上的角.α是第三、四象限和y 轴负半轴上的角不能推出α是第三象限角，α是第三象限角一定能推出α是第三、四象限和y 轴负半轴上的角，所以“cos 02πα⎛⎫+>⎪⎝⎭”是“α是第三象限角”的必要非充分条件. 故答案为：B. 【点睛】(1)本题主要考查充要条件的判断和诱导公式，考查三角函数的值的符号，意在考查学生对这些知识的掌握水平和分析推理能力.(2) 判定充要条件常用的方法有定义法、集合法、转化法.7．B解析：B 【解析】 【分析】求出||,||,a b a b ⋅，根据向量夹角公式，即可求解. 【详解】22222121122||()2a a e e e e e e ==+=+⋅+ 022cos 603,||3a =+⨯=∴=22222121122||(2)44b b e e e e e e ==-=-⋅+ 054cos 603,||3b =-⨯==，1212()(2)a b e e e e ⋅=+⋅-2201122321cos602e e e e =-⋅-=--=-，设,a b 的夹角为1,cos 2||||a b a b θθ⋅==-，20,3πθπθ≤≤∴=. 故选:B, 【点睛】本题考查向量的夹角、向量的模长、向量的数量积，考查计算能力，属于中档题.8．A解析：A 【解析】 【分析】根据向量的减法运算可化简已知等式为()0CB AB AC ⋅+=，从而得到三角形的中线和底边垂直，从而得到三角形形状. 【详解】()()()20OB OC OB OC OA CB AB AC -⋅+-=⋅+= ()CB AB AC ∴⊥+∴三角形的中线和底边垂直 ABC ∆∴是等腰三角形本题正确选项：A 【点睛】本题考查求解三角形形状的问题，关键是能够通过向量的线性运算得到数量积关系，根据数量积为零求得垂直关系.9．C解析：C 【解析】 【分析】首先以OA 与OB 作为一组向量基底来表示AP 和BP ，然后可得()12AP BP OP OA OB ⋅=-⋅+，讨论OP 与OA OB +共线同向时，()OP OA OB ⋅+有最大值为1，进一步可得AP BP ⋅有最小值12-.【详解】 由题意得AP OP OA =-, BP OP OB =-，所以()()()()2AP BP OP OA OP OB OP OA OB OP OA OB ⋅=-⋅-=+⋅-⋅+()()11122OP OA OB OP OA OB =--⋅+=-⋅+因为圆心角为120°，所以由平行四边形法则易得1OA OB +=，所以当OP 与OA OB +共线同向时，()OP OA OB ⋅+有最大值为1，此时()12AP BP OP OA OB ⋅=-⋅+有最小值12-. 故选：C. 【点睛】本题主要考查平面向量的数量积，选择合适的基底表示相关的向量是求解的关键，侧重考查数学运算的核心素养.10．C解析：C 【解析】 【分析】【详解】 令7πα=，则7n n πα=，当1≤n≤14时，画出角序列n α终边如图，其终边两两关于x 轴对称，故有均为正数，而，由周期性可知，当14k-13≤n≤14k 时，Sn>0， 而，其中k=1,2,…,7，所以在中有14个为0，其余都是正数，即正数共有100－14＝86个，故选C.11．A解析：A 【解析】 【分析】利用正弦函数的周期性以及图象的对称性求得f （x ）的解析式，利用函数y ＝A sin （ωx +φ）的图象变换规律求得G （x ）的解析式，利用余弦函数的单调性求得则G （x ） 的单调递减区间． 【详解】∵f （x ）＝sin （ωx +θ），其中ω＞0，θ∈（0，2π），f '（x 1）＝f '（x 2）＝0，|x 2﹣x 1|min 2π=，∴12•T 2ππω==， ∴ω＝2，∴f （x ）＝sin （2x +θ）． 又f （x ）＝f （3π-x ）， ∴f （x ）的图象的对称轴为x 6π=，∴2•6π+θ＝k π2π+，k ∈Z ，又02πθ⎛⎫∈ ⎪⎝⎭，， ∴θ6π=，f （x ）＝sin （2x 6π+）．将f （x ）的图象向左平移6π个单位得G （x ）＝sin （2x 36ππ++）＝cos2x 的图象， 令2k π≤2x ≤2k π+π，求得k π≤x ≤k π2π+，则G （x ）＝cos2x 的单调递减区间是[k π，k π2π+]，故选A ． 【点睛】本题主要考查正弦函数的周期性以及图象的对称性，函数y ＝A sin （ωx +φ）的图象变换规律，余弦函数的单调性，属于中档题．12．C解析：C 【解析】分析：逐个分析A 、B 、C 、D 四个选项，利用三角函数的三角函数线可得正确结论. 详解：由下图可得：有向线段OM 为余弦线，有向线段MP 为正弦线，有向线段AT 为正切线.A 选项：当点P 在AB 上时，cos ,sin x y αα==，cos sin αα∴>，故A 选项错误；B 选项：当点P 在CD 上时，cos ,sin x y αα==，tan y xα=， tan sin cos ααα∴>>，故B 选项错误；C 选项：当点P 在EF 上时，cos ,sin x y αα==，tan y xα=， sin cos tan ααα∴>>，故C 选项正确；D 选项：点P 在GH 上且GH 在第三象限，tan 0,sin 0,cos 0ααα><<，故D 选项错误.综上，故选C.点睛：此题考查三角函数的定义，解题的关键是能够利用数形结合思想，作出图形，找到sin ,cos ,tan ααα所对应的三角函数线进行比较.13．B解析：B 【解析】 ∵21,33AD AC BP BD =∴=121()393AD AB AC AB -=- ∴2239AP AB BP AB AC =+=+ 又AP AB AC λμ=+，∴22,,339λλμμ=== 故选B.14．A解析：A 【解析】 【分析】利用两角差的正弦公式化简a ，分子分母同乘以2cos 15结合二倍角的正弦公式化简b ，利用降幂公式化简c ，从而可得结果. 【详解】()sin 302sin28a =︒-︒=︒ ，222sin15cos15sin 30cos 15cos 15b ==+sin28a >=sin25sin28,c a b a c ==︒<︒=∴>>，故选A.【点睛】本题主要考查二倍角的正弦公式、二倍角的余弦公式，两角差的正弦公式，意在考查综合运用所学知识解答问题的能力，属于中档题.15．B解析：B 【解析】 【分析】由平移变换得到()sin(22)3g x x πϕ=-+，由偶函数的性质得到sin(22)13x πϕ-+=±，从而求min 512πϕ=. 【详解】由题意得：()sin[2())]sin(22)33g x x x ππϕϕ=-+=-+， 因为()g x 为偶函数，所以函数()g x 的图象关于0x =对称，所以当0x =时，函数()g x 取得最大值或最小值，所以sin(2)13πϕ-+=±，所以2,32k k Z ππϕπ-+=+∈，解得：1,22k k Z ππϕ=--∈， 因为0ϕ>，所以当1k =-时，min 512πϕ=，故选B. 【点睛】平移变换、伸缩变换都是针对自变量x 而言的，所以函数()f x 向右平移(0)ϕϕ>个单位长度后得到函数()g x ，不能错误地得到()sin (2)3g x x x πϕ=+-.二、填空题16．【解析】【分析】由图像可以计算出的值即可得到三角函数表达式然后计算出结果【详解】由图可知：由得从而将点代入得即又所以得所以【点睛】本题考查了由函数图像求三角函数的表达式熟练掌握图像是解题关键较为基础解析：32【解析】 【分析】由图像可以计算出A ，ω，ϕ的值，即可得到三角函数表达式，然后计算出结果 【详解】由图可知：A =由741234T πππ=-=，得T π=，从而22T πω==.将点7,12π⎛ ⎝7212πϕ⎛⎫⨯+= ⎪⎝⎭ 即7sin 16πϕ⎛⎫+=-⎪⎝⎭，又0ϕπ<<，所以7362ππϕ+=，得3πϕ=.所以3(0)22f ϕ===. 【点睛】本题考查了由函数图像求三角函数的表达式，熟练掌握图像是解题关键，较为基础17．0【解析】【分析】通过展开然后利用已知可得于是整理化简即可得到答案【详解】由于因此所以即所以则故答案为0【点睛】本题主要考查三角函数诱导公式的运用意在考查学生的基础知识难度中等解析：0 【解析】 【分析】通过展开cos(2)A B -，然后利用已知可得2tan 12tan tan A B A -=，于是整理化简即可得到答案.【详解】 由于1tan 2tan tan A B A-=，因此2tan 12tan tan A B A -=，所以22tan 1tan 2=1tan tan A A A B=--，即tan 2tan 1A B ⋅=-，所以sin 2sin cos2cos A B A B ⋅=-⋅,则cos(2)cos 2cos sin 2sin =0A B A B A B -=+，故答案为0. 【点睛】本题主要考查三角函数诱导公式的运用，意在考查学生的基础知识，难度中等.18．6【解析】【分析】由题意可得焦点F （02）准线为y ＝﹣2由条件可得F 是三角形ABC 的重心可得2由抛物线的定义可得【详解】由题意可得p ＝4焦点F （02）准线为y ＝﹣2由于故F 是三角形ABC 的重心设AB解析：6 【解析】 【分析】由题意可得 焦点F （0，2），准线为 y ＝﹣2，由条件可得F 是三角形ABC 的重心，可得21233y y y ++=， 由抛物线的定义可得 结果． 【详解】由题意可得 p ＝4，焦点F （0，2），准线为 y ＝﹣2，由于 0FA FB FC ++=， 故F 是三角形ABC 的重心，设 A 、B 、C 的纵坐标分别为 y 1，y 2，y 3， ∴21233y y y ++=，∴y 1+y 2+y 3＝6． 由抛物线的定义可得 FA FB FC ++=（y 1+2）+（y 2+2）+（y 3+2）＝12． 故答案为12． 【点睛】本题考查抛物线的定义、标准方程，以及简单性质的应用，得到 y 1+y 2+y 3＝6，是解题的关键．19．【解析】分析：由（1）得周期由（2）得最值（有界）由（3）得对称中心因此可选三角函数详解：由题目约束条件可得到的不同解析式由（1）得周期由（2）得最值（有界）由（3）得对称中心因此可选三角函数点睛：解析：4()sin π3f x ⎛⎫= ⎪⎝⎭【解析】分析：由（1）得周期，由（2）得最值（有界），由（3）得对称中心，因此可选三角函数. 详解：由题目约束条件可得到()f x 的不同解析式．由（1）得周期，由（2）得最值（有界），由（3）得对称中心，因此可选三角函数()4sin π3f x ⎛⎫=⎪⎝⎭. 点睛：正余弦函数是周期有界函数，既有对称轴也有对称中心，是一类有特色得函数.20．【解析】分析：利用诱导公式化简函数的解析式通过正弦函数的最值求解即可详解：函数故答案为点睛：本题考查诱导公式的应用三角函数的最值正弦函数的有界性考查计算能力 解析：65【解析】分析：利用诱导公式化简函数的解析式，通过正弦函数的最值求解即可． 详解：函数()1ππ1πsin cos 353656fx x x sin x cos x π⎛⎫⎛⎫=++-=++-+ ⎪ ⎪⎝⎭⎝⎭（）（） 1ππ6π6533535sin x sin x sin x =+++=+≤（）（）（）． 故答案为65． 点睛：本题考查诱导公式的应用，三角函数的最值，正弦函数的有界性，考查计算能力．21．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w 的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K 取其它整数时无解同解析：][1150,,848⎛⎤⋃ ⎥⎝⎦ 【解析】分析：先化简函数f(x) )24wx π=-,再求得(,2),444wx w w πππππ-∈--再根据函数()f x 在区间x ∈ (),2ππ内没有零点得到不等式组，最后解不等式组即得w 的范围.详解：由题得f(x)=1cos 1111sin sin cos )222224wx wx wx wx wx π-+-=-=-, 因为x ∈ (),2ππ，所以(,2),444wx w w πππππ-∈--当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，由前一式得24,224k w w k πππππππ⎧≤-⎪⎪⎨⎪-≤+⎪⎩即152,48k w k +≤≤+由k=0得1548w ≤≤， K 取其它整数时无解，同理，由后一式，解得1(0,]8w ∈， 综上，w 的取值范围是][1150,,848⎛⎤⋃ ⎥⎝⎦. 点睛：（1）本题主要考查三角恒等变换，考查三角函数的图像和性质，考查三角函数的零点问题，意在考查学生对这些知识的掌握水平和分析推理能力数形结合的思想方法.(2)解答本题的关键有两点，其一是分析得到当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，其二是进一步转化得到不等式组解不等式组. 22．【解析】由题意得即解得t=2；故答案为2 解析：12【解析】由题意得,1cos602a b a b ⋅=⨯⨯=， 0b c ⋅=,即()()()2111111022b ta t b ta b t b t t t ⎡⎤⋅+-=⋅+-=+-=-=⎣⎦， 解得t =2； 故答案为2.23．【解析】即单调增区间是【点睛】函数的性质(1)(2)周期(3)由求对称轴(4)由求增区间;由求减区间;解析：()37,88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦【解析】πππ3π2sin(2)2π22π()4242y x k x k k =--∴+≤-≤+∈Z3π7πππ()88k x k k +≤≤+∈Z ，即单调增区间是()37,88k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦【点睛】函数sin()(0,0)y A x B A ωϕω=++>>的性质(1)max min =+y A B y A B =-，.(2)周期2π.T ω=(3)由 ππ()2x k k ωϕ+=+∈Z 求对称轴 (4)由ππ2π2π()22k x k k ωϕ-+≤+≤+∈Z 求增区间; 由π3π2π2π()22k x k k ωϕ+≤+≤+∈Z 求减区间; 24．【解析】由题意得解析：12【解析】 由题意得π12π2π2T ω=⇒== 25．【解析】∵(α+β)+(α−β)=2α(α+β)−(α−β)=2β∴====故答案为：点睛：三角函数式的化简要遵循三看原则:一看角这是重要一环通过看角之间的差别与联系把角进行合理的拆分从而正确使用公解析：13-【解析】 ∵()1tan 2αβ+=，()tan 1αβ-=-， (α+β)+(α−β)=2α,(α+β)−(α−β)=2β，∴sin2sin2αβ=()()()()sin αβαβsin αβαβ⎡⎤++-⎣⎦⎡⎤+--⎣⎦=()()()()()()()()sin αβcos αβcos αβsin αβsin cos cos sin αβαβαβαβ+-++-+--+- =()()()()tan αβtan αβtan tan αβαβ++-+-- =13-.故答案为：13-.点睛：三角函数式的化简要遵循“三看”原则:一看角，这是重要一环，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式 ；二看函数名称，看函数名称之间的差异，从而确定使用的公式，常见的有切化弦；三看结构特征，分析结构特征，可以帮助我们找到变形的方向，如遇到分式要通分等.三、解答题 26．（1）3C π=（2）7+【解析】 【分析】（1）利用正弦定理，将2cos (cos cos )C a B b A c +=，转化为2cos (sin cos sin cos )sin C A B B A C +=，再利用两角和与差的三角的三角函数得到sin (2cos 1)0C C -=求解.（2）根据ABC 的面积为1sin 2ab C =12ab =，再利用余弦定理得()23a b ab =+-，求得+a b 即可. 【详解】（1）因为2cos (cos cos )C a B b A c +=， 所以2cos (sin cos sin cos )sin C A B B A C +=， 所以()2cos sin sin C A B C +=， 所以sin (2cos 1)0C C -=， 所以1cos 2C =， 又因为()0,C π∈， 所以3C π=.（2）因为ABC 的面积为所以1sin 2ab C = 所以12ab =.由余弦定理得：若2222cos c a b ab C =+-，()23a b ab =+- 所以7a b +=所以ABC 的周长7【点睛】本题主要考查正弦定理、余弦定理和两角和与差的三角函数的应用，还考查了转化化归的思想和运算求解的能力，属于中档题.27．（1）(),63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦；（2）当0x =时，()min 2f x =-；当3x π=时，()max 1f x =.【解析】【分析】（1）先由周期为π求出2ω=,再根据222262k x k πππππ-+≤-≤+,k Z ∈进行求解即可；（2）先求出52666x πππ-≤-≤,可得12sin 226x π⎛⎫-≤-≤ ⎪⎝⎭,进而求解即可 【详解】（1）解：∵2T ππω==,∴2ω=,又∵0>ω,∴2ω=,∴()2sin 216f x x π⎛⎫=-- ⎪⎝⎭, ∵222262k x k πππππ-+≤-≤+,k Z ∈, ∴222233k x k ππππ-+≤≤+,k Z ∈, ∴63k x k ππππ-+≤≤+,k Z ∈, ∴()f x 的单调递增区间为(),63k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦ （2）解：∵02x π≤≤,∴02x ≤≤π,∴52666x πππ-≤-≤, ∴1sin 2126x π⎛⎫-≤-≤ ⎪⎝⎭, ∴12sin 226x π⎛⎫-≤-≤ ⎪⎝⎭, ∴22sin 2116x π⎛⎫-≤--≤ ⎪⎝⎭, 当0x =时,()min 2f x =-, 当226x ππ-=,即3x π=时,()max 1f x = 【点睛】 本题考查求正弦型函数的单调区间,考查正弦型函数的最值问题,属于基础题28．（1）T =π，最大值32（2）,,36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦【解析】【分析】利用降次公式和辅助角公式化简()f x 表达式，（1）根据()f x 表达式求得()f x 的最小正周期和最大值.（2）根据三角函数单调区间的求法，求得()f x 的单调递增区间.【详解】21cos 2()2cos sin 2222x f x x x x +=+=+1112cos 2sin 22262x x x π⎛⎫=++=++ ⎪⎝⎭ （1）所以()f x 的最小正周期22T ππ==，最大值为13122+=. （2）令222262k x k πππππ-+≤+≤+，解得,36k x k k Z ππππ-+≤≤+∈，所以()f x 的单调递增区间为,,36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦. 【点睛】本小题主要考查三角函数降次公式、辅助角公式，考查三角函数最小正周期、最值和单调区间的求法，属于基础题.29．（1）()π5ππ,π1212k k k Z ⎡⎤-+∈⎢⎥⎣⎦；（2）512⎡⎤-⎢⎥⎣⎦. 【解析】【分析】化简()f x 解析式.（1）根据三角函数单调区间的求法，求得函数()f x 的单调增区间；（2）根据三角函数值域的求法，求得函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域. 【详解】依题意()()ππsin 2cos cos 2sin 1cos 266f x x x x =--+32cos 212x x =--π213x ⎛⎫=-- ⎪⎝⎭. （1）由πππ2π22π232k x k -+≤-≤+，解得π5πππ1212k x k -≤≤+，所以()f x 的单调增区间为()π5ππ,π1212k k k Z ⎡⎤-+∈⎢⎥⎣⎦.（2）由于π02x ≤≤，所以ππ2π2333x -≤-≤π521132x ⎛⎫⎡⎤--∈- ⎪⎢⎥⎝⎭⎣⎦.所以()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域为512⎡⎤-⎢⎥⎣⎦. 【点睛】 本小题主要考查三角恒等变换，考查三角函数单调区间的求法，考查三角函数值域的求法，考查运算求解能力，属于基础题.30．18【解析】【分析】a b λ-与b c +用坐标表示，根据向量的平行坐标关系，即可求解.【详解】解：由题意得(12,22)a b λλλ-=-+，(1,3)b c +=，因为a b λ-与b c +平行，所以(12)3(22)1λλ-⋅=+⋅， 解得18λ=． 因此所求实数λ的值等于18． 【点睛】 本题考查平行向量的坐标关系，属于基础题.。

上海市曹杨二中高二下学期期末数学试题一、单选题1．若12i +是关于x 的实系数一元二次方程20x bx c ++=的一个根，则（ ） A.2b =，5c = B.2b =-，5c = C.2b =-，5c =- D.2b =，1c =-【答案】B【解析】由题意可知，关于x 的实系数一元二次方程20x bx c ++=的两个虚根分别为12i +和12i -，然后利用韦达定理可求出实数b 与c 的值.【详解】由题意可知，关于x 的实系数一元二次方程20x bx c ++=的两个虚根分别为12i +和12i -，由韦达定理得()()()()12121212b i i c i i ⎧-=++-⎪⎨=+⋅-⎪⎩，解得25b c =-⎧⎨=⎩. 故选：B. 【点睛】本题考查利用实系数方程的虚根求参数，解题时充分利用实系数方程的两个虚根互为共轭复数这一性质，并结合韦达定理求解，也可以将虚根代入方程，利用复数相等来求解，考查运算求解能力，属于中等题.2．若m 是小于10的正整数，则()()()151620m m m ---L 等于（ ） A.515m P - B.1520mm P --C.520m P -D.620m P -【答案】D【解析】利用排列数的定义可得出正确选项. 【详解】()()()()()()()()()()1231415162020!1516201231414!m m m m m m m m m m ⋅⋅--------==⋅⋅--L L Q L L ()()20!206!m m -=--⎡⎤⎣⎦，由排列数的定义可得()()()620151620m m m m P ----=L . 故选：D. 【点睛】本题考查排列数的表示，解题的关键就是依据排列数的定义将代数式表示为阶乘的形式，考查分析问题和解决问题的能力，属于中等题.3．已知曲线42:1C x y +=，给出下列命题：①曲线C 关于x 轴对称；②曲线C 关于y 轴对称；③曲线C 关于原点对称；④曲线C 关于直线y x =对称；⑤曲线C 关于直线y x =-对称，其中正确命题的个数是（ ）A.1B.2C.3D.4【答案】C【解析】根据定义或取特殊值对曲线C 的对称性进行验证，可得出题中正确命题的个数. 【详解】在曲线C 上任取一点(),x y ，该点关于x 轴的对称点的坐标为(),x y -，且()24421x y x y +-=+=，则曲线C 关于x 轴对称，命题①正确；点(),x y 关于y 轴的对称点的坐标为(),x y -，且()42421x y x y -+=+=，则曲线C 关于y 轴对称，命题②正确；点(),x y 关于原点的对称点的坐标为(),x y --，且()()42421x y x y -+-=+=，则曲线C 关于原点对称，命题③正确；在曲线C 上取点35⎫⎪⎪⎝⎭，该点关于直线y x =的对称点坐标为35⎛ ⎝⎭，由于2432915525⎛⎛⎫+=≠ ⎪ ⎝⎭⎝⎭，则曲线C 不关于直线y x =对称，命题④错误；在曲线C 上取点35⎫⎪⎪⎝⎭，该点关于直线y x =-的对称点的坐标为3,5⎛- ⎝⎭，由于243291525⎛⎛⎫-+=≠ ⎪ ⎝⎭⎝⎭，则曲线C 不关于直线y x =-对称，命题⑤错误. 综上所述，正确命题的个数为3. 故选：C. 【点睛】本题考查曲线对称性的判定，一般利用对称性的定义以及特殊值法进行判断，考查推理能力，属于中等题.4．在复数列{}n z 中，1816z i =+，()12n n iz z n *+=⋅∈N ，设n z 在复平面上对应的点为n Z ，则（ ）A.存在点M ，对任意的正整数n ，都满足10n MZ ≤B.不存在点M ，对任意的正整数n ，都满足n MZ ≤C.存在无数个点M ，对任意的正整数n ，都满足n MZ ≤D.存在唯一的点M ，对任意的正整数n ，都满足n MZ ≤ 【答案】D 【解析】由()12n n i z z n N *+=⋅∈，由复数模的性质可得出112n n z z +=，可得出数列{}n z 是等比数列，且得出1n z z ≤=再由n n n MZ OZ OM OZ OM =-≤+uuuu r uuur uuu r uuur uuu r，结合向量的三角不等式可得出正确选项. 【详解】1816z i =+Q ，1z ∴==()12n n iz z n *+=⋅∈N Q ，1122n n n i z z z +∴==，所以数列{}n z 是以以12为公比的等比数列，且n n OZ z =≤uuur O 为坐标原点），由向量模的三角不等式可得n n n MZ OZ OM OZ OM OM =-≤+≤uuuu r uuur uuu r uuur uuu r uuu r ，当点M 与坐标原点O 重合时，n MZ ≤uuuu r，因此，存在唯一的点M ，对任意的正整数n ，都满足n MZ ≤ 故选：D. 【点睛】本题考查复数的几何意义，同时也考查了复数模的性质和等比数列的综合应用，解题的关键就是利用向量模的三角不等式构建不等关系进行验证，考查推理能力，属于难题.二、填空题5．1-的平方根为______． 【答案】i ±【解析】根据()21i ±=-可得出1-的平方根. 【详解】()21i ±=-Q ，因此，1-的平方根为i ±.故答案为：i ±. 【点睛】本题考查负数的平方根的求解，要熟悉21i =-的应用，考查计算能力，属于基础题. 6．复数2iz i+=的虚部为______． 【答案】2-【解析】利用复数的除法将复数z 表示为一般形式，可得出该复数的虚部. 【详解】由复数的除法法则得212iz i i+==-，因此，复数z 的虚部为2-. 故答案为：2-. 【点睛】本题考查复数虚部的求解，一般利用复数四则运算法则将复数表示为一般形式即可，考查计算能力，属于基础题.7．抛物线2y x = 的焦点到准线的距离为________． 【答案】12【解析】21p = ，所以12p =，所以抛物线的焦点到准线的距离为12 .8．若复数z 满足1z =，则1z i -+的最大值是______．【答案】1【解析】利用复数模的三角不等式可得出()111z i z i z i -+=--≤+-可得出1z i -+的最大值.【详解】由复数模的三角不等式可得()11111z i z i z i -+=--≤+-=+=因此，1z i -+的最大值是1+故答案为：1+【点睛】本题考查复数模的最值的计算，可将问题转化为复平面内复数对应的点的轨迹，利用数形结合思想求解，同时也可以利用复数模的三角不等式进行计算，考查分析问题和解决问题的能力，属于中等题.9．若双曲线的焦点在x 轴上，焦距为4，且过点()2,3P ，则双曲线的标准方程为______．【答案】2213y x -=【解析】设双曲线的标准方程为()222210,0x y a b a b-=>>，利用双曲线的定义求出a 的值，结合焦距求出b 的值，从而可得出双曲线的标准方程. 【详解】设双曲线的标准方程为()222210,0x y a b a b-=>>，由题意知，该双曲线的左、右焦点分别为()12,0F -、()22,0F ，由双曲线的定义可得1222a PF PF =-==，1a \=，则b ==2213y x -=.故答案为：2213y x -=.【点睛】本题考查过点求双曲线的方程，在双曲线的焦点已知的前提下，可以利用定义来求双曲线的标准方程，也可以利用待定系数法求解，考查运算求解能力，属于中等题. 10．用1、2、3、4、5、6组成没有重复数字的六位数，要求任何相邻两个数字的奇偶性不同，这样的六位数的个数是_________（用数字作答）. 【答案】72【解析】先排奇数（或偶数），然后从排好的三个数形成的四个空中选择相邻的三个再排剩下的偶数（或奇数），由此可得结果． 【详解】先排三个奇数，共有336A =种结果，然后再从形成的四个空中选择前三个或后三个空排入三个偶数，共有33212A =种结果．由分步乘法计数原理可得这样的六位数共有3333272A A =个．故答案为：72． 【点睛】对于排列问题，一般情况下要从受到限制的特殊元素开始考虑，有时也从特殊的位置开始讨论．对于相邻问题常用“捆绑法”；对于不相邻问题常用“插空法”；对于“在与不在”的问题，常使用“直接法”或“排除法”．11．已知直线1:10l mx y +-=，()2:220l m x my ++-=，若1l 与2l 平行，则实数m 的值为______． 【答案】1-【解析】根据两直线平行，列出有关m 的等式和不等式，即可求出实数m 的值. 【详解】由于1l 与2l 平行，则()2222m m m m ⎧=+⎪⎨-≠-+⎪⎩，即2202m m m ⎧--=⎨≠⎩，解得1m =-.故答案为：1-. 【点睛】本题考查利用两直线平行求参数，解题时要熟悉两直线平行的等价条件，并根据条件列式求解，考查运算求解能力，属于基础题.12．已知方程220x x p -+=的两个虚根为α、β，且4αβ-=，则实数p =______． 【答案】5【解析】根据题意得出∆<0，然后求出方程220x x p -+=的两个虚根，再利用复数的求模公式结合等式4αβ-=可求出实数p 的值. 【详解】由题意可知，440p ∆=-<，得1p >.解方程220x x p -+=，即()211x p -=-，解得1i α=，1i β=.所以，4i αβ-===，解得5p =. 故答案为：5. 【点睛】本题考查实系数方程虚根的求解，同时也考查了复数模长公式的应用，考查运算求解能力，属于中等题.13．已知直线l 过点()0,5，且它的一个方向向量为()1,2，则原点O 到直线l 的距离为______．【解析】求出直线l 的方程，然后利用点到直线的距离公式可求出原点O 到直线l 的距离. 【详解】由于直线l 的一个方向向量为()1,2，则直线l 的斜率为2，所以，直线l 的方程为25y x =+，即250x y -+=，因此，原点O 到直线l=.【点睛】本题考查点到直线距离的计算，同时也考查了直线方向向量的应用，解题时要根据题中条件得出直线的斜率，并写出直线的方程，考查计算能力，属于中等题. 14．设()56230012501x x a a x a x a x ++=++++L ，其中0a 、1a 、2a 、L 、30a 是各项的系数，则在0a 、1a 、2a 、L 、30a 这31个系数中，值为零的个数为______． 【答案】10【解析】求出()61x x ++的展开式通项为3061,15r k k rr k r T C C x+-++=⋅⋅，列举出306k r+-在()05,k r k r N ≤≤≤∈的所有可能取值，从而可得出0a 、1a 、2a 、L 、30a 这31个系数中值为零的个数. 【详解】()()()()556665111rr r x x x x C x x -⎡⎤++=++=⋅⋅+⎣⎦Q ，而()1rx +的展开式通项为k k r C x ⋅.所以，()61x x ++的展开式通项为3061,15r k k rr k r T C C x+-++=⋅⋅，当()05,k r k r N ≤≤≤∈时，306k r +-的可能取值有：30、24、25、18、19、20、12、13、14、15、6、7、8、9、10、0、1、2、3、4、5，共21个，因此，在0a 、1a 、2a 、L 、30a 这31个系数中，值为零的个数为10. 故答案为：10. 【点睛】本题考查二项展开式中项的系数为零的个数，解题的关键就是借助二项展开通项，将项的指数可取的全都列举出来，考查分析问题和解决问题的能力，属于中等题.15．在直角坐标系中，已知()1,0A ，()4,0B ，若直线10x my +-=上存在点P ，使得2PA PB =，则实数m 的取值范围是______．【答案】(),-∞⋃+∞【解析】设点P 的坐标为(),x y ，根据条件2PA PB =求出动点P 的轨迹方程，可得知动点P 的轨迹为圆，然后将问题转化为直线10x my +-=与动点P 的轨迹圆有公共点，转化为圆心到直线的距离不大于半径，从而列出关于实数m 的不等式，即可求出实数m 的值. 【详解】设点P 的坐标为(),x y ，2PA PB =Q =化简得()2254x y -+=，则动点P 的轨迹是以()5,0为圆心，半径为2的圆， 由题意可知，直线10x my +-=与圆()2254x y -+=有公共点，2≤，解得m ≤或m ≥因此，实数m 的取值范围是(),-∞⋃+∞.故答案为：(),-∞⋃+∞.【点睛】本题考查动点的轨迹方程，同时也考查了利用直线与圆的位置关系求参数，解题的关键就是利用距离公式求出动点的轨迹方程，考查化归与转化思想的应用，属于中等题. 16．从集合{},,,U a b c d =的子集中选出2个不同的子集，需同时满足以下两个条件：①a 、b 都至少属于其中一个集合；②对选出的两个子集A 、B ，必有A B ⊆或B A ⊆．那么，共有______种不同的选法．【答案】32【解析】由题意可知，集合A 和B 可以互换，只需考查A B Ü，由题意可知{},a b B ⊆，分B 为二元集、三元集和四元集三种情况，利用真子集的个数公式可得出对应的集合A 的个数，然后利用分类计数原理可得出答案. 【详解】由于A B ⊆或B A ⊆，集合A 和B 可以互换，现考查A B ⊆，且A B ≠，则A B Ü，由题意知，{},a b B ⊆.①当B 为二元集时，{},B a b =，A B Q Ü，则集合A 的个数为2213-=； ②当B 为三元集时，若{},,B a b c =，A B Q Ü，则集合A 的个数为3217-=； 若{},,B a b d =，同理可知符合条件的集合A 也有7个；③若B 为四元集时，{},,,B a b c d =，A B Q Ü，则集合A 的个数为42115-=. 综上所述，共有3771532+++=种. 故答案为：32. 【点睛】本题考查了集合的化简与运算以及集合真子集个数的求法，同时也考查了分类讨论思想的应用，属于难题.三、解答题17．（1）已知()232z z z i i ++=-，求复数z ； （2）已知复数z 满足2z z-为纯虚数，且1z i -=，求复数z ． 【答案】（1）1-±；（2）2z i =或1z i =-+或1z i =+.【解析】（1）设复数(),z a bi a b R =+∈，根据复数的运算法则和复数相等得出关于a 、b 的方程组，解出这两个未知数，即可得出复数z ；（2）设复数(),z a bi a b R =+∈，根据2z z-为纯虚数和1z i -=列出关于a 、b 的方程组，解出这两个未知数，可得出复数z . 【详解】（1）设复数(),z a bi a b R =+∈，由()232z z z i i ++=-，得()22232ab ai i ++=-，根据复数相等得22322a b a ⎧+=⎨=-⎩，解得1a b =-⎧⎪⎨=⎪⎩1z =-±；（2）设复数(),z a bi a b R =+∈， 则()()()222222222a bi a b z a bi a bi a b i z a bi a bi a bi a b a b -⎛⎫⎛⎫-=+-=+-=-++ ⎪ ⎪++-++⎝⎭⎝⎭，由题意可得2220a a a b -=+，2220bb a b +≠+. ()11z i a b i -=+-=1=，所以有()()()2222222222202011a a b a b b a b a ba b ⎧+-⎪=+⎪⎪++⎪≠⎨+⎪⎪+-=⎪⎪⎩，解得02a b =⎧⎨=⎩或11a b =±⎧⎨=⎩. 因此，2z i =或1z i =-+或1z i =+. 【点睛】本题考查复数的求解，常将复数设为一般形式，根据复数的相关运算列举出方程组进行求解，考查运算求解能力，属于中等题.18．已知412nx x ⎛⎫+ ⎪⎝⎭的展开式的二项式系数之和为1024．（1）求展开式中的常数项； （2）求展开式中的系数最大的项． 【答案】（1）180；（2）2515360x .【解析】（1）根据二项式系数和为21024n =，求出n 的值，然后写出二项展开式的通项，令x 的指数为零，求出参数的值，再代入通项可得出展开式中的常数项；（2）设10102k kk a C -=⋅，利用作商法求出k a 的最大值，以及对应的k 值，再将k 的值代入展开式通项可得出所求的项. 【详解】（1）412nx x ⎛⎫+ ⎪⎝⎭的展开式的二项式系数之和为21024n =，得10n =.412nx x ⎛⎫+ ⎪⎝⎭Q 的展开式的通项为()1041040511010122kk k kk k k T C x C x x ---+⎛⎫=⋅⋅=⋅⋅ ⎪⎝⎭.令4050k -=，解得8k =，因此，412nx x ⎛⎫+ ⎪⎝⎭的展开式中的常数项为82102180C ⋅=；（2）设10102k kk a C -=⋅，则()()()()()1011110101010!1!9!210210!221!10!k k k k kk k k a C k a C k k k -+++-+-⋅-===⨯⋅+-.当02k ≤≤时，11k ka a +>，则有0123a a a a <<<； 当310k ≤≤时，11k ka a +<，则有3410a a a >>>L . 所以，当3k =时，k a 最大，因此，展开式中的系数最大的项为37252510215360C x x ⋅⋅=.【点睛】本题考查二项展开式常数项的求解，同时也考查了二项式系数和以及系数最大项的求解，一般要利用项的系数的单调性来求解，考查计算能力，属于中等题.19．如图所示是竖直平面内的一个“通道游戏”，图中竖直线段和斜线都表示通道，并且在交点处相遇．若有一条竖直线段的为第一层，第二条竖直线段的为第二层，以此类推，现有一颗小球从第一层的通道向下运动，在通道的交叉处，小球可以落入左右两个通道中的任意一个，记小球落入第n 层的第m 个竖直通道（从左向右计）的不同路径数为(),A n m ．（1）求()2,1A ，()3,1A ，()4,2A 的值；（2）猜想(),A n m 的表达式（不必证明），并求不等式()9,28A m ≤的解集． 【答案】（1）()2,11A =，()3,11A =，()4,23A =；（2）()11,m n A n m C --=，不等式的解集为{}1,2,3,7,8,9.【解析】（1）根据题意得出(),11A n =，(),1A n n =，且()()(),1,11,A n m A n m A n m =--+-可求出()2,1A ，()3,1A ，以及()()()()()()4,23,13,23,12,12,2A A A A A A =+=++；（2）根据()()(),1,11,A n m A n m A n m =--+-可得出()11,m n A n m C --=，然后得出()189,m A m C -=的表达式，从而得出不等式()9,28A m ≤的解集.【详解】（1）由题意可得(),11A n =，(),1A n n =，且()()(),1,11,A n m A n m A n m =--+-.()()2,13,11A A ∴==，()()()()()()4,23,13,23,12,12,23A A A A A A =+=++=；（2）由()()(),1,11,A n m A n m A n m =--+-可推得()11,m n A n m C --=，不等式()9,28A m ≤即为1828m C -≤，08881C C ==Q ，17888C C ==，268828C C ==，358856C C ==，4870C =. 解不等式1828m C -≤，可得1m -的可能取值有0、1、2、6、7、8.所以，不等式()9,28A m ≤的解集为{}1,2,3,7,8,9. 【点睛】本题考查杨辉三角性质的应用，考查组合数的应用以及组合不等式的求解，解题的关键就是要找出递推公式，逐项计算即可，考查运算求解能力，属于中等题.20．已知复数z 满足11z z -++=，z 在复平面上对应点的轨迹为C ，A 、B 分别是曲线C 的上、下顶点，M 是曲线C 上异于A 、B 的一点． （1）求曲线C 的方程；（2）若M 在第一象限，且2OM =，求M 的坐标； （3）过点M 作斜率为1的直线分别交曲线C 于另一点N ，交y 轴于点D ．求证：存在常数λ，使得DM DN DA DB λ⋅=⋅恒成立，并求出λ的值．【答案】（1）2212x y +=；（2）1,2⎛ ⎝⎭；（3）证明见解析，43λ=. 【解析】（1）根据复数模的几何意义以及椭圆的定义可得出曲线C 为椭圆，并设曲线C的方程为()222210x y a b a b+=>>，求出a 、b 的值，可得出曲线C 的方程；（2）设点M 的坐标为()()0000,0,0x y x y >>，根据OM =以及220012x y +=得出关于0x 、0y 的方程组，解出这两个未知数，即可得出点M 的坐标；（3）设直线MN 的方程为y x m =+，设点()11,M x y 、()22,N x y ，将直线MN 的方程与曲线C 的方程联立，并列出韦达定理，求出点D 的坐标，并求出DM 、DN 、DA 、DB 的表达式，结合韦达定理可求出λ的值.【详解】（1）设复数(),z x yi x y R =+∈，由11z z -++=可知，复平面内的动点(),P x y 到点()11,0F -、()21,0F的距离之和为122F F =<，所以，曲线C 是以点()11,0F -、()21,0F 为左、右焦点的椭圆， 设曲线C 的方程为()222210x y a b a b+=>>，则2a =，a ∴=1b ==.因此，曲线C 的方程为2212x y +=；（2）设点M 的坐标为()()0000,0,0x y x y >>，则OM ==， 又点M 在曲线C 上，所以22022000032120,0x y x y x y ⎧+=⎪⎪⎪+=⎨⎪>>⎪⎪⎩，解得0012x y =⎧⎪⎨=⎪⎩，因此，点M的坐标为⎛ ⎝⎭；（3）设直线MN 的方程为y x m =+，点()11,M x y 、()22,N x y ，由于M为第一象限内的点，则1m <<，直线MN 交y 轴于点()0,D m ，将直线MN 的方程与曲线C 的方程联立得2212y x mx y =+⎧⎪⎨+=⎪⎩， 消去y ，得2234220x mx m ++-=，由韦达定理得1243m x x +=-，212223m x x -=. 1DM ∴=，2DN =，2124123m DM DN x x -∴⋅==，2111DA DB m m m ⋅=-⋅+=-，因此，22414331m DM DN DA DBm λ-⋅===⋅-. 【点睛】本题考查椭圆的轨迹方程、椭圆上的点的坐标的求解以及直线与椭圆中线段长度比的问题，一般利用将直线方程与椭圆方程联立，利用韦达定理设而不求法求解，考查运算求解能力，属于中等题.21．已知抛物线2:4y x Γ=，F 为其焦点，过F 的直线l 与抛物线Γ交于A 、B 两点． （1）若2AF FB =u u u r u u u r，求B 点的坐标；（2）若线段AB 的中垂线l '交x 轴于M 点，求证：ABFM为定值； （3）设()1,2P ，直线PA 、PB 分别与抛物线的准线交于点S 、T ，试判断以线段ST 为直径的圆是否过定点？若是，求出定点的坐标；若不是，请说明理由．【答案】（1）12⎛⎝或1,2⎛ ⎝；（2）证明见解析；（3）以线段ST 为直径的圆过定点,定点的坐标()3,0-或()1,0.【解析】（1）设点()11,A x y 、()22,B x y ，设直线l 的方程为1x my =+，将直线l 的方程与抛物线Γ的方程联立，列出韦达定理，由2AF FB =u u u r u u u r，可得出122y y =-，代入韦达定理可求出2y 的值，由此可得出点B 的坐标；（2）求出线段AB 的中垂线l '的方程，求出点M 的坐标，求出AB 、FM 的表达式，即可证明出ABFM为定值；（3）根据对称性知，以线段ST 为直径的圆过x 轴上的定点，设定点为(),0Qq ，求出点S 、T 的坐标，由题意得出0TQ SQ ⋅=u u r u u r，利用平面向量数量积的坐标运算并代入韦达定理，可求出q 的值，从而得出定点的坐标. 【详解】（1）设点()11,A x y 、()22,B x y ，设直线l 的方程为1x my =+，易知点()1,0F ，()111,AF x y =--uu u r ，()221,FB x y =-u u u r ，由2AF FB =u u u r u u u r可得122y y -=，得122y y =-. 将直线l 的方程与抛物线Γ的方程联立214x my y x=+⎧⎨=⎩，消去x 得，2440y my --=，由韦达定理得124y y m +=，124y y =-，122y y =-Q ，212224y y y ∴=-=-，得2y =此时，222142yx==，因此，点B的坐标为1,22⎛⎫⎪⎝⎭或1,22⎛⎫-⎪⎝⎭；（2）易知0m≠，1222y ym+=，()1221212122m y yx xm++=+=+，所以，线段AB的中点坐标为()221,2m m+，则直线l'的方程为()2221y m m x m-=---，即223y mx m m=-++，在该直线方程中，令0y=，得223x m=+，则点()223,0M m+.()()222212121211441AB m x x m x x x x m=+⋅-=+⋅+-=+，()2223121FM m m=+-=+，因此，()()2241221mABFM m+==+（定值）；（3）如下图所示：抛物线Γ的准线方程为1x=-，设点()1,S s-、()1,T t-.()211111,21,24yPA x y y⎛⎫=--=--⎪⎝⎭uu r，()2,2PS s=--uu r，PQ、A、S三点共线，则//PA PSuu r uu r，则()()21121224ys y⎛⎫--=--⎪⎝⎭，得11242ysy-=+，则点11241,2ySy⎛⎫-- ⎪+⎝⎭，同理可知点22241,2yTy⎛⎫-- ⎪+⎝⎭.由对称性可知，以线段ST为直径的圆过x轴上的定点(),0Q q，则0TQ SQ⋅=u u r u u r.11241,2y TQ q y ⎛⎫-=+ ⎪+⎝⎭uu r ，22241,2y SQ q y ⎛⎫-=+ ⎪+⎝⎭uu r .()()()()()()()()2212121212121224244816112224y y y y y y TQ SQ q q y y y y y y ---++⋅=++=+++++++uu r uu r ()()()2244841611404244m q q m ⨯--⨯+=++=+-=-+⨯+，解得3q =-或1.因此，以线段ST 为直径的圆过定点()3,0-和()1,0. 【点睛】本题考查抛物线中的向量成比例问题、线段长度的比值问题以及圆过定点问题，一般将直线方程与抛物线方程联立，利用韦达定理设而不求法进行求解，考查运算求解能力，属于难题.。

同步练习一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知一个几何体的三视图如图所示，且该几何体的体积为433，则a 的值为（ ）A 3B 233C ．23D 32． “杨辉三角”又称“贾宪三角”，是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算，而杨辉在公元1261年所著的《详解九章算法》一书中，记录了贾宪三角形数表，并称之为“开方作法本源”图．下列数表的构造思路就源于“杨辉三角”．该表由若干行数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数是 （ ）2017 2016 2015 2014……6 5 4 3 2 14033 4031 4029…………11 9 7 5 38064 8060………………20 16 12 816124……………………36 28 20………………………A ．201620172⨯B ．201501822⨯C ．201520172⨯D ．201601822⨯3．若离散型随机变量X 的分布如下：则X 的方差()D X =（ ） X0 1 Pm 0.6 A ．0.6B ．0.4C ．0.24D ．1 4．已知函数31()42f x x ax =++ ，则“0a > ”是“()f x 在R 上单调递增”的( ) A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件5．曲线2()(1)x f x e x x =--在点(0,(0))f 处的切线方程是( )A ．10x y ++=B ．10x y -+=C ．210x y -+=D ．210x y ++=6．已知复数2017i 12i z =-，则复数z 的虚部为 （ ） A ．25- B ．1i 5 C ．15 D ．15- 7．在区间[1,2]-上随机取一个数k ，使直线(4)y k x =-与圆224x y +=相交的概率为（ ） A ．33 B ．32 C ．239 D ．368．一个几何体的三视图如图所示，若主视图是上底为2，下底为4，高为1的等腰梯形，左视图是底边为2的等腰三角形，则该几何体的体积为（ ）A ．103B ．113C ．2D ．49．某快递公司的四个快递点,,,A B C D 呈环形分布（如图所示），每个快递点均已配备快递车辆10辆．因业务发展需要，需将,,,A B C D 四个快递点的快递车辆分别调整为5,7,14,14辆，要求调整只能在相邻的两个快递点间进行，且每次只能调整1辆快递车辆，则A ．最少需要8次调整，相应的可行方案有1种B ．最少需要8次调整，相应的可行方案有2种C ．最少需要9次调整，相应的可行方案有1种D ．最少需要9次调整，相应的可行方案有2种10．把编号分别为1，2，3，4，5的五张电影票全部分给甲、乙、丙三个人，每人至少一张，若分得的电影票超过一张，则必须是连号，那么不同分法的种数为（ ）A ．36B ．40C ．42D ．4811．下列运算正确的为（ ）A ．'1C =（C 为常数）B ．211()'x x =C ．()'x x e e =D ．(sin )cos x 'x =-12．已知点(0,1)M -在抛物线2:2(0)C x py p =>的准线上，F 为C 的焦点，过M 点的直线与C 相切于点N ，则FMN ∆的面积为（ ）A ．1B ．2C ．12D ．4二、填空题：本题共4小题13．计算123452!3!4!5!6!++++=____． 14．如图，在Rt ABC ∆中，1AB BC ==，D 和E 分别是边BC 和AC 上一点，DE BC ⊥，将CDE ∆沿DE 折起到点P 位置，则该四棱锥P ABDE -体积的最大值为_______．15．观察下列等式：11=，3211=123+=，332123+=1236++=，33321236++=……可以推测3333123n +++⋅⋅⋅+=____（*n N ∈，用含有n 的代数式表示）．16．若函数2243,0(),0x x x f x ax bx c x ⎧-+≥=⎨++<⎩为偶函数，则(1)'(1)f f -+-的值为______． 三、解答题：解答应写出文字说明、证明过程或演算步骤。