基本体的相贯线(V17版).

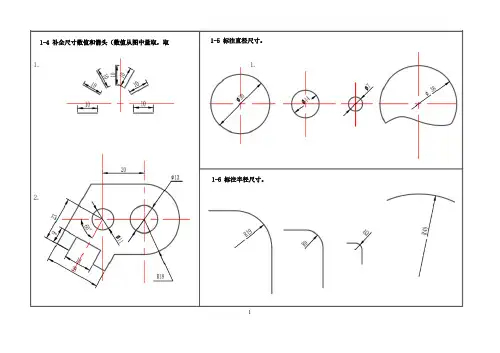
11-6 标注半径尺寸。

1-5 标注直径尺寸。

1-4 补全尺寸数值和箭头（数值从图中量取，取1-7 补画箭头并填写线性尺寸和角度尺寸数字（量取整数）。

1-8 根据尺寸注法的规定，标注各图形的尺寸(量取整数）。

2模块二投影基础2-1根据立体轴测图及其在三投影面体系中所处的位置，画出它的三视图并回答问题。

123452-6 已知A(25，10，20) 、B(10，20，10)两点坐标,求2-7已知点的二面投影，求其第三面投影。

作两点的三面投影,并判断两点的相对位置。

62-8 填空2-9 根据A、B两点的直观图作出其三面投影图（尺寸从图中量取）。

2-10已知点A、B的一面投影，又知点A距H面15mm，点B 在V面上，试分别求作A、B另两面投影。

2-11已知点B在点A的正左方15mm;点C是点A对V面的重影点（c'不可见），且距点A为10mm。

补全点A的侧面投影，求做其他各点的三面投影，并判别可见性。

72-12 已知A、B两点的两面投影,求做第三面投影并判断A、B两点的相互位置。

2-14 在三视图中标出A、B、C三点的三面投影。

2-13 判断A、B二点的相互位置。

2-15 已知三棱锥底面的三面投影和顶点S的坐标为（20，13，20），完成三棱锥的三面投影图。

892-17 已知线段两端点A(25,10,5)、B(5,20,25)，画出其三面投影，并求4B实长及其对H的倾角α及V面夹角2-18 已知线段AB的投影ab及a '和对V面的倾角β=30°，画出其三面投影图。

2-20 在线段AB上取一点K，使AK=15mm，求K的两面投影。

2-19已知线段AB的V面投影α 'b‘及a，又知B在A的后方，AB实长为26，画出其水平投影图。

10111213142-28 在立体图中标出端点A 、B 、C 、D 的位置（立体图中用大写字母标出），并填写线段AB 、CD 的名称，及其对各投影面的相对位置。

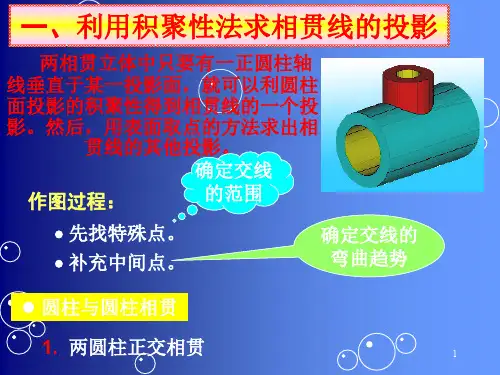
第二节相贯线的作图求解一、轴线互相垂直的两圆柱的相贯线当圆柱体轴线垂直于投影面时，其圆柱表面在该投影面上的投影有积聚性，所以两圆柱轴线互相垂直的相贯线可利用积聚性投影取点作图法求解。

1、轴线正交两圆柱的相贯线图10－2如图10-2所示两圆柱轴线垂直相交，且分别垂直于Ｈ面和Ｗ面，因此俯视图中相贯线的投影积聚在小圆柱的投影（圆）上；左视图中相贯线的投影积聚在小圆柱两条转向轮廓线之间的大圆柱面投影（圆）上。

这样由相贯线的两个已知投影，可作出它的Ｖ面投影。

利用积聚性投影取点作图求相贯线的作图步骤如图10-3所示：图10－3 柱－柱相交相贯线作图步骤（1）求特殊点图10-3.b所示相贯线上Ｉ、Ｖ两点分别位于两圆柱对Ｖ面的转向线上，是相贯线上的最高点，也分别是相贯线上的最左点和最右点。

Ⅲ、Ⅶ两点分别位于小圆柱对Ｗ面的转向线上，它们是相贯线上的最低点，也分别是相贯线上的最前点和最后点。

在投影图上可直接作投影连线求得1’、3’、5’、7’。

（2）求一般点先在俯视图中的小圆柱投影圆上，适当地确定出若干个一般点的投影，如图10-3.c所示中的2、4、6、8等点，再按点的三面投影规律，作出Ｗ面投影2"（4"）、8" （6"）和Ｖ面投影2’（8’）4’（6’）点。

（3）判断可见性及圆滑连接由于该相贯线前后前部分对称，且形状相同，所以在Ｖ面投影中可见与不可见部分重合，按1’-2’-3’-4’-5’顺序用粗实线圆滑地连接起来。

（4）按图线要求描深各图线，完成两圆柱正交立体的三视图（图10-3.d）。

2、轴线正交内、外圆柱面的相贯线由于圆柱有实体圆柱和空心圆柱之分，因此圆柱面又有外圆柱面和内圆柱面之别。

故两圆柱面相交会产生三种情况：(1）两外圆柱面相交，如图10-4.a所示；(2）外圆柱面与内圆柱面相交，即圆柱与圆孔相交，如图10-4.b所示；(3）两内圆柱面相交，即圆孔与圆孔相交，如图10-4.c所示。